Denis, ich habe diesen Kommentar zu dem Artikel.
Was die Theorie angeht, so gibt es keine Fragen, alles ist ausführlich dargestellt.
Was die Praxis betrifft, so möchte ich Ihre Aufmerksamkeit auf die Abbildungen lenken, in denen Sie empirische Histogramme zeigen, insbesondere auf Abbildung 2. Der Punkt ist, dass Sie zwei sehr bedeutende Ungenauigkeiten in Ihrer Analyse gemacht haben.
Erstens haben Sie für das Skript, das die Histogramme generiert, eine zu geringe Anzahl von Klassen festgelegt - nur 9, was an sich schon ein großer Schlag für die Aussagekraft des Pearson-Kriteriums ist und seine Anwendung unwirksam macht. Nehmen Sie für die Zukunft 200-300 Klassen, um sicher zu sein, dass Sie keinen Fehler machen, wenn der Stichprobenumfang es zulässt (und das tut er). Hätten Sie genau das getan, hätten Sie sich vergewissern können, dass der Test auf die Lognormalverteilung ein negatives Ergebnis geliefert hätte, ebenso wie der Test der Renditen für Hypersecans. Übrigens ist es sehr einfach, sich zu vergewissern, dass zwei solche Verteilungen nicht gleichzeitig einen bestimmten Wert und seinen Modulus repräsentieren können: Nehmen Sie einfach die "Hälfte" der Hypersekante und falten Sie sie mit sich selbst (analog zur Entnahme des Moduls einer Zufallsvariablen): Sie werden definitiv keine Lognormalverteilung erhalten.
Die zweite Ungenauigkeit besteht darin, dass Sie nicht das A-priori-Wissen verwendet haben, dass der Scheitelpunkt (auch Erwartungswert genannt) der Renditeverteilung genau bei 0 liegen muss (sonst wären wir alle schon längst Milliardäre). Aus diesem Grund sieht das Histogramm in Abbildung 2 nach rechts verschoben aus, obwohl es das nicht sein sollte. Auch hier würde die Berücksichtigung dieser Tatsache bei der Erstellung des Histogramms die Zuverlässigkeit der Tests erhöhen.
P.S. Ich schreibe gerade einen Artikel über die Grundlagen der Modellierung, daher dieses große Interesse. Vielen Dank für Ihren Artikel, er ist im Thema enthalten. Mit freundlichen Grüßen.
...Erstens haben Sie für das Skript, das die Histogramme erzeugt, eine zu geringe Anzahl von Klassen festgelegt - nur 9, was an sich schon ein großer Schlag für die Aussagekraft des Pearson-Kriteriums ist und seine Anwendung unwirksam macht. Für die Zukunft sollten Sie 200-300 Klassen nehmen, um sicher zu sein, dass Sie keinen Fehler machen, wenn die Stichprobengröße es zulässt (und das tut sie). Hätten Sie es so gemacht, könnten Sie sicher sein, dass der Test für die Lognormalverteilung ein negatives Ergebnis liefern würde, ebenso wie der Test der Renditen für Hypersecans. Übrigens ist es sehr einfach, sich zu vergewissern, dass zwei solche Verteilungen nicht gleichzeitig einen bestimmten Wert und seinen Modulus repräsentieren können, nehmen Sie einfach die "Hälfte" der Hypersekanz und falten Sie sie mit sich selbst (analog zur Entnahme des Moduls eines Zufallswertes): Sie werden definitiv keine Lognormalverteilung erhalten.
Lieber alsu, vielen Dank für deine Meinung!
Gehen wir der Reihe nach vor.
Die Anzahl der Klassen wird nicht willkürlich festgelegt, sondern nach einer bestimmten Formel. In meinem Fall ist es die Sturgis-Formel. Es ist eine der populärsten Regeln. Sie ist nicht perfekt, da stimme ich zu. Aber trotzdem...
Und Sie nehmen 200-300 Klassen nach welcher Regel?
Die zweite Ungenauigkeit besteht darin, dass Sie nicht das A-priori-Wissen verwendet haben, dass die Spitze (aka Erwartung) der Verteilung der Renditen genau bei 0 liegen muss (sonst wären wir alle schon längst Milliardäre). Aus diesem Grund sieht das Histogramm in Abbildung 2 nach rechts verschoben aus, obwohl es das nicht sein sollte. Auch hier würde die Berücksichtigung dieses Punktes bei der Konstruktion des Histogramms die Zuverlässigkeit der Tests erhöhen.
Ich analysiere die Stichprobe auf einer sachlichen Grundlage. Ich analysiere, was ich habe. Und auf welcher Grundlage sollte die Spitze der Ertragsverteilung genau am Punkt 0 liegen? Vielleicht verstehe ich etwas falsch...
Und außerdem, wenn man sich die Verteilung ansieht, auf die die Anpassung angewendet wurde (nämlich X~HS(-0,00, 1,00)), kann man leicht feststellen, dass der erste Parameter - der Verschiebungsparameter - genau 0 ist. In der Tat ist er gleich dem Erwartungswert.
Hier ist ein weiterer html-Bericht über die Probenahme der Standardwerte. Ich hoffe, dass die Abbildung mehr oder weniger lesbar ist. Sie ist aber nicht identisch mit der Abbildung im Artikel. Ich habe gerade die neuesten Daten genommen.
Wie Sie sehen können, ist der Mittelwert =0. Und die beste Anpassung ist die Hyperbolic Secant Verteilung: X~HS(0.00, 1.00).
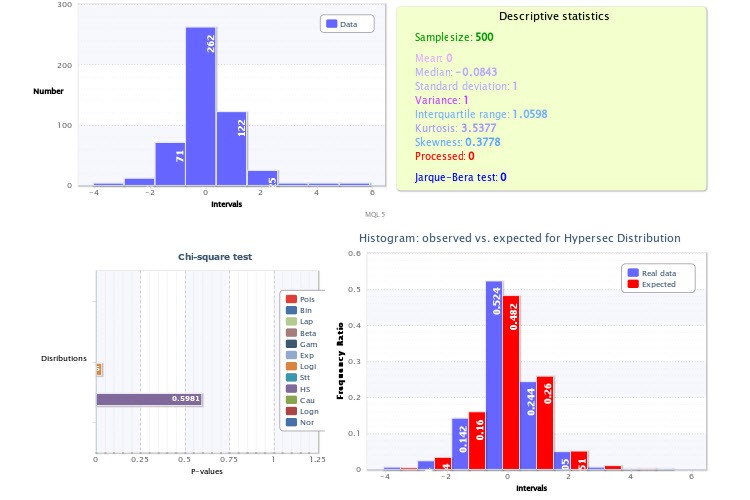
Genau, die Formel von Sturges ergab genau 9 Klassen, aber das ist eher ein Grund, über eine Erhöhung des Stichprobenumfangs nachzudenken (wenn ich die Formel umkehre, sehe ich, dass Sie etwa 256 Werte haben).
Außerdem funktioniert diese Formel nur für allgemeine Populationen mit Normalverteilung (für die sie abgeleitet wurde), und der Stichprobenumfang beträgt nicht mehr als 200 Werte. Sie können alternative Formeln verwenden - Diakonis, Scott....
Im Allgemeinen hat Sturges nie eine logische Begründung für seine Formel gegeben - ja, sie basiert auf der Annäherung der Normalverteilung durch die Binomialverteilung, na und? Wie kann dies die Frage nach der Effizienz der Wahl der Anzahl der Klassen beeinflussen? Das Optimalitätskriterium wurde vom Autor nie definiert, und die Formel selbst wurde nach dem Zufallsprinzip geschrieben. Aber der Punkt ist, dass der Ansatz von Sturges lange Zeit der einzige war, der in irgendeiner Weise formalisiert wurde, und er wurde automatisch (und meiner Meinung nach ziemlich gedankenlos!) in alle Statistikpakete aufgenommen, was übrigens ziemlich ärgerlich ist, gerade weil diese Formel fast immer eine extrem unterschätzte Anzahl von Klassen ergibt.
Auch hier gibt es alternative Formeln, aber es ist das Vorhandensein eines Personalcomputers, der uns paradoxerweise die Möglichkeit gibt, unseren eigenen Kopf als Hilfsmittel zu benutzen, d.h. eine visuelle Methode, um eine mehr oder weniger optimale Anzahl von Klassen für diese bestimmte Stichprobe zu bestimmen, wenn wir durch sanftes Verändern dieses Indikators einen Kompromiss zwischen der Glätte des Graphen und der Auflösung des Histogramms erreichen. Übrigens ist diese Methode oft besser und schneller als jede Formel.
Ich sage immer: Bevor man Zahlen in Formeln einsetzt, sollte man sich fragen, was sie bedeuten und wie (und ob) man sie anwenden soll. Kurz gesagt, ich bin gegen die Verwendung der Formel von Sturges, ich halte sie für veraltet und unzureichend).
Was den Mittelwert betrifft. Die Renditeerwartung sollte bei 0 liegen, denn sonst könnte man dummerweise immer in eine Richtung wetten, die dem Vorzeichen dieser MO entspricht, und hätte die Garantie, eine Rendite in beliebiger Höhe zu erhalten. Nun, die Spitze sollte aus reinen Symmetriegründen mit der MO übereinstimmen: Die linke Hälfte des Graphen sollte ein Spiegelbild der rechten sein (die Steigerungs- und die Abnahmerate sind statistisch gleich, und es sollte keine Unterschiede zwischen ihnen geben), so dass das Symmetriezentrum mit der Mitte übereinstimmt.
Da Sie HS(0.00, 1.00) nehmen, sollten Sie also die Klassen zentrieren - d. h. die Nullklasse sollte die Indexwerte in einem symmetrischen Intervall (-x0;x0) umfassen, andernfalls führen wir in die Berechnungen einen systematischen Fehler ein, der mit der Verschiebung der Klassen relativ zur Null zusammenhängt und sich schließlich in das Ergebnis des chi^2-Tests einschleicht. Ihr Punkt 0 liegt nicht in der Mitte der Nullklasse.
Die Frage, wie die Klassen bei diskreten Daten symmetrisch gemacht werden können, ist in der Tat nicht trivial, und auch hier ist es gut, sie für jede einzelne Stichprobe individuell und sehr sorgfältig zu lösen, da wir sonst Gefahr laufen, auch wegen der falschen Wahl der Grenzen für die Einteilung in Klassen unzureichende Ergebnisse zu erhalten.
alsu, Sie haben ein Thema angesprochen, das zwar nicht Gegenstand meines Artikels ist, aber sehr interessant ist. Ich werde dieses Thema, soweit es mir möglich ist, weiter recherchieren.
Ich danke Ihnen für Ihre konstruktive Kritik!
Mir gefällt Ihre Meinung über die Anwendbarkeit wissenschaftlicher Erkenntnisse im Handel.
Könnten Sie mir bitte sagen, welche Bücher Sie einer Person empfehlen würden, die mit der Wahrscheinlichkeitstheorie und der mathematischen Statistik vertraut ist?
Denis, guten Tag.
Mir gefällt Ihre Meinung über die Anwendbarkeit von wissenschaftlichen Erkenntnissen im Handel.
Bitte sagen Sie mir, welche Bücher Sie einer Person empfehlen würden, die mit der Wahrscheinlichkeitstheorie und der mathematischen Statistik vertraut ist.
Ich danke Ihnen für Ihre Meinung!
Ich denke, dass man dann etwas für Anfänger suchen sollte, irgendeine Lit-Rolle. Die Hauptsache ist, dass der Text des Buches einen nicht davon abhält, es weiter zu lesen :-))).
Ich mochte etwas Gaidyshev, und etwas Bulashev.....
- rsdn.org
Die zweite Ungenauigkeit besteht darin, dass Sie das a priori Wissen nicht genutzt haben, dass die Spitze (aka Erwartung) der Renditeverteilung genau bei 0 liegen muss (sonst wären wir alle schon längst Milliardäre).
Ganz und gar nicht. Eine Verschiebung der Spitze der Verteilung relativ zu 0 (Wachstum/Abnahme eines Instruments) bedeutet nicht, dass sie in der Zukunft gleich sein wird. Das ist der Grund, warum die meisten Händler keine Milliardäre sind, nicht weil.
Mit freundlichen Grüßen.
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Neuer Artikel Die Rolle von statistischen Verteilungen für die Arbeit eines Händlers :
Dieser Beitrag ist eine logische Fortsetzung meines Beitrags Statistische Verteilungen von Wahrscheinlichkeiten in MQL5, in dem die Klassen für die Arbeit mit einigen theoretischen statistischen Verteilungen dargelegt wurden. Da wir nun über die theoretische Grundlage verfügen, schlage ich vor, dass wir direkt mit realen Datensätzen fortfahren und versuchen, diese Grundlage für Informationszwecke zu nutzen.
Wir zeigen das Histogramm mithilfe der Tools an, die im vorher erwähnten Beitrag erwähnt werden. Zu diesem Zweck habe ich die Funktion histogramSave geschrieben, die das Histogramm für die beobachtete Serie in HTML darstellen wird. Die Funktion nimmt 2 Parameter auf: Array von Klassen (f) und Array von Klassenmittelpunkten (b).
Als Beispiel habe ich ein Histogramm für die absoluten Differenzen zwischen Maximal- und Minimalwerten von 500 Balken des Paares EURUSD auf dem vierstündigen Timeframe in Punkten mithilfe des Scripts volatilityTest.mq5 erstellt.
Abbildung 1. Datenhistogramm (absolute Volatilität des EURUSD H4)
Wie im Histogramm (Abb. 1) dargestellt, verfügt die erste Klasse über 146 Beobachtungen, die zweite über 176 usw. Die Funktion des Histogramms ist die Bereitstellung einer visuellen Darstellung der empirischen Verteilung der beobachteten Stichprobe.
Autor: Dennis Kirichenko