Statistische Verteilungen von Wahrscheinlichkeiten in MQL5

MetaTrader 5 — Beispiele | 7 April 2016, 14:25

872

Denis Kirichenko

Die gesamte Wahrscheinlichkeitstheorie beruht auf der Philosophie der Unerwünschtheit.
(Leonid Suchorukow)

Einleitung

Aufgrund seiner Tätigkeit stößt ein Händler sehr oft auf Kategorien wie Wahrscheinlichkeit und Zufälligkeit. Der Gegenpol zur Zufälligkeit ist die Vorstellung einer "Regelmäßigkeit". Es ist erstaunlich, dass die Zufälligkeit sich dank allgemeinphilosophischer Gesetzmäßigkeiten grundsätzlich zur Regelmäßigkeit hin entwickelt. Über das Gegenteil werden wir an dieser Stelle nicht sprechen. Grundsätzlich ist die Relation zwischen Zufälligkeit und Regelmäßigkeit eine wichtige Relation, da sie – im Kontext des Marktes – sich direkt auf die Höhe des Gewinns auswirkt, den ein Händler erhält.

In diesem Beitrag werde ich die zugrunde liegenden theoretischen Instrumente darlegen, die uns in der Zukunft helfen werden, bestimmte Regelmäßigkeiten des Marktes zu finden.

1. Verteilungen, Essenz, Typen

Um also eine bestimmte zufällige Variable zu beschreiben, brauchen wir eine eindimensionale statistische Wahrscheinlichkeitsverteilung. Sie beschreibt eine Stichprobe von zufälligen Variablen nach einem bestimmten Gesetz, d. h. die Anwendung jedes beliebigen Verteilungsgesetztes wird einen Satz von zufälligen Variablen erfordern.

Warum analysieren wir [theoretische] Verteilungen? Sie erleichtern die Erkennung von Veränderungsmustern der Häufigkeit in Abhängigkeit von den Werten der Variablenattribute. Außerdem kann man bestimmte statistische Parameter der erforderlichen Verteilung erhalten.

Was die Typen von Wahrscheinlichkeitsverteilungen betrifft, ist es in der Fachliteratur gebräuchlich, die Verteilungsfamilie in kontinuierliche und diskrete Verteilungen aufzuteilen, je nach Typ des Satzes der zufälligen Variablen. Es existieren allerdings auch andere Klassifikationen, zum Beispiel nach Kriterien wie der Symmetrie der Verteilungskurve f(x) in Bezug auf die Linie x=x0, dem Lageparameter, der Anzahl von Modi, zufälligen Variablenintervallen und sonstigen.

Es gibt mehrere Arten, das Verteilungsgesetz zu definieren. Wir sollten auf die geläufigsten darunter eingehen:

2. Theoretische Wahrscheinlichkeitsverteilungen

Versuchen wir nun, im Kontext von MQL5 Klassen zu erstellen, die statistische Verteilungen beschreiben. Ferner möchte ich hinzufügen, dass die Fachliteratur zahlreiche Codebeispiele in C++ bietet, die erfolgreich auf die MQL5-Codierung angewendet werden können. Ich habe also das Rad nicht neu erfunden und habe in manchen Fällen die Best Practices des C++-Codes angewendet.

Die größte Herausforderung war für mich die fehlende Unterstützung einer Mehrfachvererbung in MQL5. Deshalb habe ich es nicht geschafft, komplexe Klassenhierarchien zu benutzen. Das Buch mit dem Titel Numerical Recipes: The Art of Scientific Computing [2] wurde für mich zur optimalen Quelle von C++-Code, der ich den Großteil der Funktionen entnehme. In den meisten Fällen mussten sie gemäß den Anforderungen von MQL5 verfeinert werden.

2.1.1 Normalverteilung

Traditionell beginnen wir mit der Normalverteilung.

Die Normalverteilung, auch Gauß-Verteilung genannt, ist eine Wahrscheinlichkeitsverteilung aus der Funktion der Wahrscheinlichkeitsdichte:

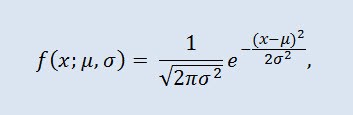
wobei der Parameter µ der Mittelwert (der erwartete Wert) einer zufälligen Variable ist und auf die höchste Koordinate der Kurve der Verteilungsdichte deutet. σ² ist die Varianz.

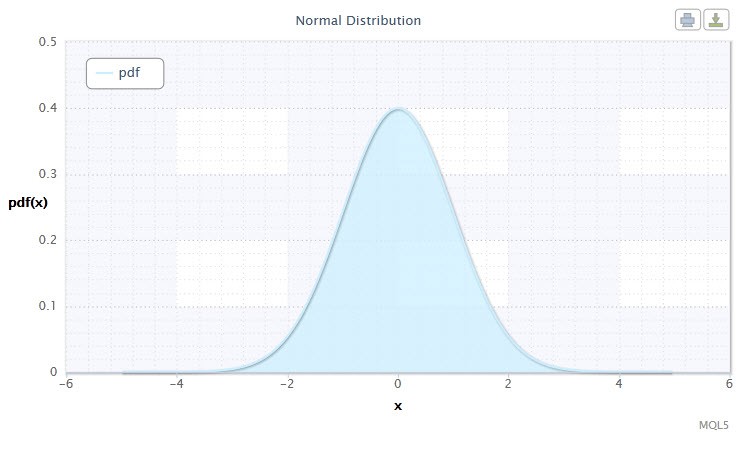
Abbildung 1. Dichte der Normalverteilung Nor(0,1)

Ihre Darstellung hat das folgende Format: X ~ Nor(μ, σ²), wobei:

X eine zufällige Variable aus der Normalverteilung Nor ist;
µ der Parameter des Mittelpunkt ist (-∞ ≤ μ ≤ +∞);
σ der Parameter der Varianz ist (0<σ).

Gültiger Bereich der zufälligen Variable X: -∞ ≤ X ≤ +∞.

Die in diesem Beitrag bereitgestellten Formeln unterscheiden sich möglicherweise von Formeln aus anderen Quellen. Solche Unterschiede sind mathematisch manchmal nicht ausschlaggebend. In manchen Fällen sind sie durch eine unterschiedliche Parametrierung bedingt.

Die Normalverteilung spielt eine wichtige Rolle in der Statistik, da sie Regelmäßigkeit widerspiegelt, die als Ergebnis der Interaktion zwischen einer großen Menge zufälliger Ursachen entsteht, von denen keine überwiegt. Und obwohl die Normalverteilung auf Finanzmärkten nur selten vorkommt, ist es dennoch wichtig, sie mit empirischen Verteilungen zu vergleichen, um das Ausmaß und die Art ihrer Unregelmäßigkeit bestimmen zu können.

Definieren wir die Klasse CNormaldist für die Normalverteilung, wie folgt:

//+------------------------------------------------------------------+
//|                Normal Distribution class definition              |
//+------------------------------------------------------------------+
class CNormaldist : CErf // Erf class inheritance
  {
public:
   double            mu, //mean parameter (μ)
   sig;                 //variance parameter (σ)
   //+------------------------------------------------------------------+
   //| CNormaldist class constructor                                    |
   //+------------------------------------------------------------------+
   void  CNormaldist()
     {
      mu=0.0;sig=1.0; //default parameters μ and σ
      if(sig<=0.) Alert("bad sig in Normal Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return(0.398942280401432678/sig)*exp(-0.5*pow((x-mu)/sig,2));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      return 0.5*erfc(-0.707106781186547524*(x-mu)/sig);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf)                |
   //| quantile function                                                |
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(!(p>0. && p<1.))
         Alert("bad p in Normal Distribution!");
      return -1.41421356237309505*sig*inverfc(2.*p)+mu;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };

//+------------------------------------------------------------------+

Wie Sie sehen können, leitet sich die Klasse CNormaldist von der Basisklasse CErf ab, die ihrerseits die Klasse der Fehlerfunktion definiert. Sie wird bei der Berechnung einiger Methoden der Klasse CNormaldist benötigt. Die Klasse CErf und die Hilfsfunktion erfcc sehen etwa so aus:

//+------------------------------------------------------------------+
//|                Error Function class definition                   |
//+------------------------------------------------------------------+
class CErf
  {
public:
   int               ncof;    // coefficient array size
   double            cof[28]; // Chebyshev coefficient array
   //+------------------------------------------------------------------+
   //| CErf class constructor                                           |
   //+------------------------------------------------------------------+
   void CErf()
     {
      int Ncof=28;
      double Cof[28]=//Chebyshev coefficients
        {
         -1.3026537197817094,6.4196979235649026e-1,
         1.9476473204185836e-2,-9.561514786808631e-3,-9.46595344482036e-4,
         3.66839497852761e-4,4.2523324806907e-5,-2.0278578112534e-5,
         -1.624290004647e-6,1.303655835580e-6,1.5626441722e-8,-8.5238095915e-8,
         6.529054439e-9,5.059343495e-9,-9.91364156e-10,-2.27365122e-10,
         9.6467911e-11, 2.394038e-12,-6.886027e-12,8.94487e-13, 3.13092e-13,
         -1.12708e-13,3.81e-16,7.106e-15,-1.523e-15,-9.4e-17,1.21e-16,-2.8e-17
        };
      setCErf(Ncof,Cof);
     };
   //+------------------------------------------------------------------+
   //| Set-method for ncof                                              |
   //+------------------------------------------------------------------+
   void setCErf(int Ncof,double &Cof[])
     {
      ncof=Ncof;
      ArrayCopy(cof,Cof);
     };
   //+------------------------------------------------------------------+
   //| CErf class destructor                                            |
   //+------------------------------------------------------------------+
   void ~CErf(){};
   //+------------------------------------------------------------------+
   //| Error function                                                   |
   //+------------------------------------------------------------------+
   double erf(double x)
     {
      if(x>=0.0) return 1.0-erfccheb(x);
      else return erfccheb(-x)-1.0;
     }
   //+------------------------------------------------------------------+
   //| Complementary error function                                     |
   //+------------------------------------------------------------------+
   double erfc(double x)
     {
      if(x>=0.0) return erfccheb(x);
      else return 2.0-erfccheb(-x);
     }
   //+------------------------------------------------------------------+
   //| Chebyshev approximations for the error function                  |
   //+------------------------------------------------------------------+
   double erfccheb(double z)
     {
      int j;
      double t,ty,tmp,d=0.0,dd=0.0;
      if(z<0.) Alert("erfccheb requires nonnegative argument!");
      t=2.0/(2.0+z);
      ty=4.0*t-2.0;
      for(j=ncof-1;j>0;j--)
        {
         tmp=d;
         d=ty*d-dd+cof[j];
         dd=tmp;
        }
      return t*exp(-z*z+0.5*(cof[0]+ty*d)-dd);
     }
   //+------------------------------------------------------------------+
   //| Inverse complementary error function                             |
   //+------------------------------------------------------------------+
   double inverfc(double p)
     {
      double x,err,t,pp;
      if(p >= 2.0) return -100.0;
      if(p <= 0.0) return 100.0;
      pp=(p<1.0)? p : 2.0-p;
      t = sqrt(-2.*log(pp/2.0));
      x = -0.70711*((2.30753+t*0.27061)/(1.0+t*(0.99229+t*0.04481)) - t);
      for(int j=0;j<2;j++)
        {
         err=erfc(x)-pp;
         x+=err/(M_2_SQRTPI*exp(-pow(x,2))-x*err);
        }
      return(p<1.0? x : -x);
     }
   //+------------------------------------------------------------------+
   //| Inverse error function                                           |
   //+------------------------------------------------------------------+
   double inverf(double p)
     {return inverfc(1.0-p);}
  };
//+------------------------------------------------------------------+
double erfcc(const double x)
/* 
 complementary error function erfc(x) with
 a relative error of 1.2 * 10^(-7)               
*/
  {
   double t,z=fabs(x),ans;
   t=2./(2.0+z);
   ans=t*exp(-z*z-1.26551223+t*(1.00002368+t*(0.37409196+t*(0.09678418+
             t*(-0.18628806+t*(0.27886807+t*(-1.13520398+t*(1.48851587+
             t*(-0.82215223+t*0.17087277)))))))));
   return(x>=0.0 ? ans : 2.0-ans);
  }
//+------------------------------------------------------------------+

2.1.2 Lognormalverteilung

Sehen wir uns nun die Lognormalverteilung an.

Die Lognormalverteilung in der Wahrscheinlichkeitstheorie ist eine zweiparametrige Familie von absolut kontinuierlichen Verteilungen. Wenn eine zufällige Variable lognormal verteilt ist, hat ihr Logarithmus eine Normalverteilung.

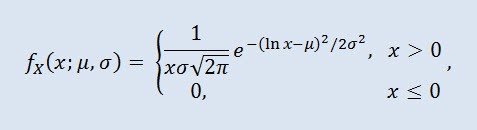
wobei µ der Lageparameter (0<µ) und σ der Skalierungsparameter (0<σ) ist.

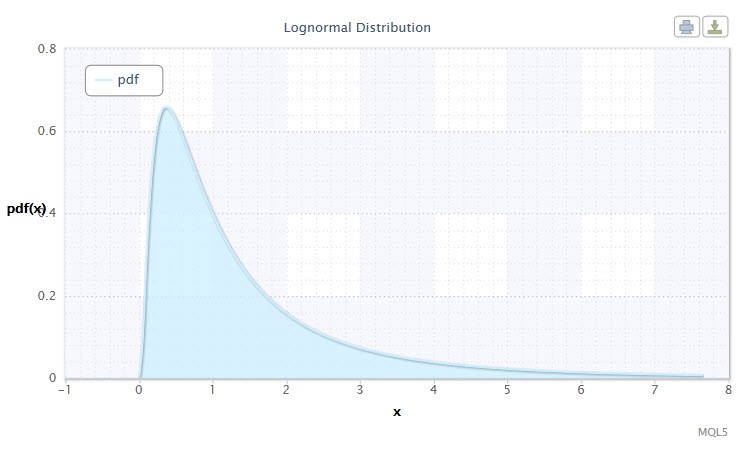
Abbildung 2. Dichte der Lognormalverteilung Logn(0,1)

Ihre Darstellung hat das folgende Format: X ~ Logn(μ, σ²), wobei:

X eine zufällige Variable aus der Lognormalverteilung Logn ist;
µ der Lageparameter ist (0<µ);
σ der Skalierungsparameter ist (0<σ).

Gültiger Bereich der zufälligen Variable X: 0 ≤ X ≤ +∞.

Erstellen wir die Klasse CLognormaldist, die die Lognormalverteilung beschreibt. Sie sieht so aus:

//+------------------------------------------------------------------+
//|                Lognormal Distribution class definition           |
//+------------------------------------------------------------------+
class CLognormaldist : CErf // Erf class inheritance
  {
public:
   double            mu, //location parameter (μ)
   sig;                 //scale parameter (σ)
   //+------------------------------------------------------------------+
   //| CLognormaldist class constructor                                 |
   //+------------------------------------------------------------------+
   void  CLognormaldist()
     {
      mu=0.0;sig=1.0; //default parameters μ and σ
      if(sig<=0.) Alert("bad sig in Lognormal Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      if(x<0.) Alert("bad x in Lognormal Distribution!");
      if(x==0.) return 0.;
      return(0.398942280401432678/(sig*x))*exp(-0.5*pow((log(x)-mu)/sig,2));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      if(x<0.) Alert("bad x in Lognormal Distribution!");
      if(x==0.) return 0.;
      return 0.5*erfc(-0.707106781186547524*(log(x)-mu)/sig);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf)(quantile)      |
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(!(p>0. && p<1.))
         Alert("bad p in Lognormal Distribution!");
      return exp(-1.41421356237309505*sig*inverfc(2.*p)+mu);
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

Wie Sie sehen können, unterscheidet sich die Lognormalverteilung nicht sehr von der Normalverteilung. Der Unterschied ist, dass der Parameter x durch den Parameter log(x) ersetzt wird.

2.1.3 Cauchy-Verteilung

Die Cauchy-Verteilung in der Wahrscheinlichkeitstheorie (in der Physik auch als Lorentz-Verteilung oder Breit-Wigner-Verteilung bezeichnet) ist eine Klasse von absolut kontinuierlichen Verteilungen. Eine zufällige Variable mit Cauchy-Verteilung ist ein bekanntes Beispiel einer Variable, die keine Erwartung und keine Varianz hat. Die Dichte sieht so aus:

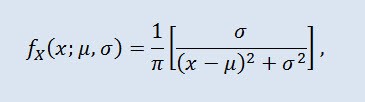
wobei µ der Lageparameter (-∞ ≤ μ ≤ +∞) und σ der Skalierungsparameter (0<σ) ist.

Die Darstellung der Cauchy-Verteilung hat das folgende Format: X ~ Cau(μ, σ), wobei:

X eine zufällige Variable aus der Cauchy-Verteilung Cau ist;
µ der Lageparameter ist (-∞ ≤ μ ≤ +∞);
σ der Skalierungsparameter ist (0<σ).

Gültiger Bereich der zufälligen Variable X: -∞ ≤ X ≤ +∞.

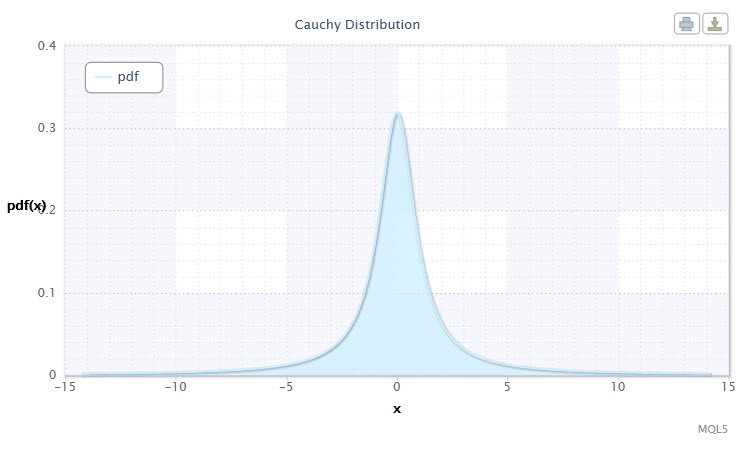
Abbildung 3. Dichte der Cauchy-Verteilung Cau(0,1)

Erstellt mithilfe der Klasse CCauchydist im MQL5-Format, sieht sie so aus:

//+------------------------------------------------------------------+
//|                Cauchy Distribution class definition              |
//+------------------------------------------------------------------+
class CCauchydist //
  {
public:
   double            mu,//location parameter (μ)
   sig;                 //scale parameter (σ)
   //+------------------------------------------------------------------+
   //| CCauchydist class constructor                                    |
   //+------------------------------------------------------------------+
   void  CCauchydist() 
     {
      mu=0.0;sig=1.0; //default parameters μ and σ
      if(sig<=0.) Alert("bad sig in Cauchy Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return 0.318309886183790671/(sig*(1.+pow((x-mu)/sig,2)));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      return 0.5+0.318309886183790671*atan2(x-mu,sig); //todo      
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(!(p>0. && p<1.))
         Alert("bad p in Cauchy Distribution!");
      return mu+sig*tan(M_PI*(p-0.5));
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

Beachten Sie, dass die Funktion atan2() verwendet wird, die den Hauptwert des Arkustangens im Bogenmaß ausgibt:

double atan2(double y,double x)
/*
 Returns the principal value of the arc tangent of y/x,
 expressed in radians. To compute the value, the function 
 uses the sign of both arguments to determine the quadrant.
 y - double value representing an y-coordinate.
 x - double value representing an x-coordinate. 
*/
  {
   double a;
   if(fabs(x)>fabs(y))
      a=atan(y/x);
   else
     {
      a=atan(x/y); // pi/4 <= a <= pi/4
      if(a<0.)
         a=-1.*M_PI_2-a; //a is negative, so we're adding
      else
         a=M_PI_2-a;
     }
   if(x<0.)
     {
      if(y<0.)
         a=a-M_PI;
      else
         a=a+M_PI;
     }
   return a;
  }

2.1.4 Secans-Hyperbolicus-Verteilung

Die Secans-Hyperbolicus-Verteilung ist für all jene interessant, die mit der Analyse finanzieller Risiken arbeiten.

In der Wahrscheinlichkeitstheorie und Statistik ist die Secans-Hyperbolicus-Verteilung eine kontinuierliche Wahrscheinlichkeitsverteilung, deren Funktion der Wahrscheinlichkeitsdichte und charakteristische Funktion proportional zur Secans-Hyperbolicus-Funktion sind. Die Dichte wird der folgenden Formel entnommen:

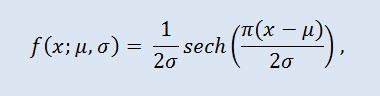
wobei µ der Lageparameter (-∞ ≤ μ ≤ +∞) und σ der Skalierungsparameter (0<σ) ist.

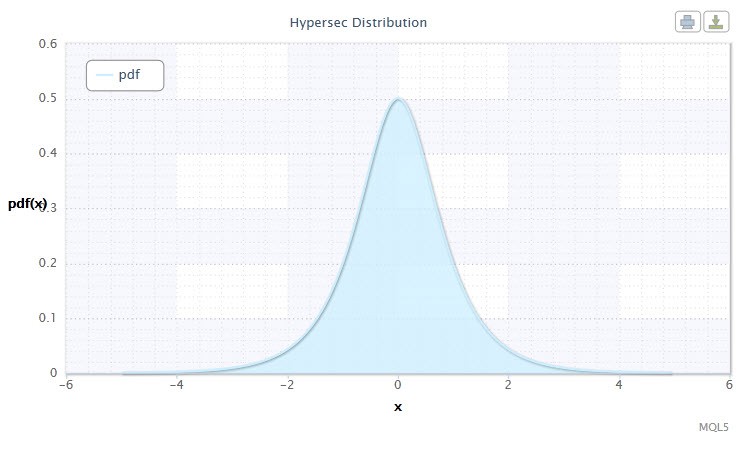
Abbildung 4. Dichte der Secans-Hyperbolicus-Verteilung HS(0,1)

Ihre Darstellung hat das folgende Format: X ~ HS(μ, σ), wobei:

X eine zufällige Variable ist;
µ der Lageparameter ist (-∞ ≤ μ ≤ +∞);
σ der Skalierungsparameter ist (0<σ).

Gültiger Bereich der zufälligen Variable X: -∞ ≤ X ≤ +∞.

Beschreiben wir sie mithilfe der Klasse CHypersecdist, wie folgt:

//+------------------------------------------------------------------+
//|        Hyperbolic Secant Distribution class definition           |
//+------------------------------------------------------------------+
class CHypersecdist //
  {
public:
   double            mu,// location parameter (μ)
   sig;                 //scale parameter (σ)
   //+------------------------------------------------------------------+
   //| CHypersecdist class constructor                                 |
   //+------------------------------------------------------------------+
   void  CHypersecdist()
     {
      mu=0.0;sig=1.0; //default parameters μ and σ
      if(sig<=0.) Alert("bad sig in Hyperbolic Secant Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return sech((M_PI*(x-mu))/(2*sig))/2*sig;
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      return 2/M_PI*atan(exp((M_PI*(x-mu)/(2*sig))));
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(!(p>0. && p<1.))
         Alert("bad p in Hyperbolic Secant Distribution!");
      return(mu+(2.0*sig/M_PI*log(tan(M_PI/2.0*p))));
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

Es ist nicht schwer zu erkennen, dass diese Verteilung ihren Namen von der Secans-Hyperbolicus-Funktion erhält, deren Funktion der Wahrscheinlichkeitsverteilung proportional zur Sekans-Hyperbolicus-Funktion ist.

Die Secans-Hyperbolicus-Funktion sech sieht so aus:

//+------------------------------------------------------------------+
//|              Hyperbolic Secant Function                          |
//+------------------------------------------------------------------+
double sech(double x)
// Hyperbolic Secant Function
  {
   return 2/(pow(M_E,x)+pow(M_E,-x));
  }

2.1.5 Studentsche t-Verteilung

Die Studentsche t-Verteilung ist eine wichtige Verteilung in der Statistik.

In der Wahrscheinlichkeitstheorie ist die Studentsche t-Verteilung meistens eine einparametrige Familie aus absolut kontinuierlichen Verteilungen. Allerdings kann sie auch als dreiparametrige Verteilung betrachtet werden, die aus der Funktion der Verteilungsdichte hervorgeht:

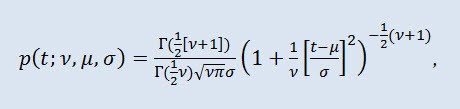
wobei Г die Eulersche Gammafunktion ist, v der Formparameter (v>0), µ der Lageparameter (-∞ ≤ μ ≤ +∞), σ der Skalierungsparameter (0<σ).

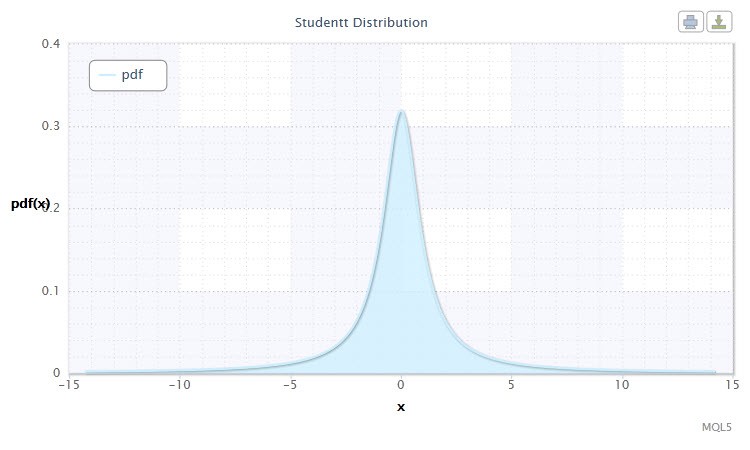
Abbildung 5. Dichte der Studentschent-Verteilung Stt(1,0,1)

Ihre Darstellung hat das folgende Format: t ~ Stt(ν,μ,σ), wobei:

t eine zufällige Variable aus der Studentschent-Verteilung Stt ist;
v der Formparameter ist (v>0);
µ der Lageparameter ist (-∞ ≤ μ ≤ +∞);
σ der Skalierungsparameter ist (0<σ).

Gültiger Bereich der zufälligen Variable X: -∞ ≤ X ≤ +∞.

Häufig, insbesondere bei Hypothesentests, wird eine standardmäßige t-Verteilung mit µ=0 und σ=1 verwendet. Somit wird daraus eine einparametrige Verteilung mit dem Parameter v.

Diese Verteilung wird häufig zum Schätzen der Erwartung, voraussichtlicher Werte und sonstiger Merkmale mithilfe von Konfidenzintervallen beim Testen von Erwartungswerthypothesen, Regressionsverhältniskoeffizienten, Homogenitätshypothesen usw. benutzt.

Beschreiben wir die Verteilung mithilfe der Klasse CStudenttdist:

//+------------------------------------------------------------------+
//|                Student's t-distribution class definition         |
//+------------------------------------------------------------------+
class CStudenttdist : CBeta // CBeta class inheritance
  {
public:
   int               nu;     // shape parameter (ν)
   double            mu,     // location parameter (μ)
   sig,                     // scale parameter (σ)
   np,                      // 1/2*(ν+1)
   fac;                     // Г(1/2*(ν+1))-Г(1/2*ν)
   //+------------------------------------------------------------------+
   //| CStudenttdist class constructor                                  |
   //+------------------------------------------------------------------+
   void  CStudenttdist()
     {
      int Nu=1;double Mu=0.0,Sig=1.0; //default parameters ν, μ and σ
      setCStudenttdist(Nu,Mu,Sig);
     }
   void setCStudenttdist(int Nu,double Mu,double Sig)
     {
      nu=Nu;
      mu=Mu;
      sig=Sig;
      if(sig<=0. || nu<=0.) Alert("bad sig,nu in Student-t Distribution!");
      np=0.5*(nu+1.);
      fac=gammln(np)-gammln(0.5*nu);
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return exp(-np*log(1.+pow((x-mu)/sig,2.)/nu)+fac)/(sqrt(M_PI*nu)*sig);
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double t)
     {
      double p=0.5*betai(0.5*nu,0.5,nu/(nu+pow((t-mu)/sig,2)));
      if(t>=mu) return 1.-p;
      else return p;
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(p<=0. || p>=1.) Alert("bad p in Student-t Distribution!");
      double x=invbetai(2.*fmin(p,1.-p),0.5*nu,0.5);
      x=sig*sqrt(nu*(1.-x)/x);
      return(p>=0.5? mu+x : mu-x);
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
   //+------------------------------------------------------------------+
   //| Two-tailed cumulative distribution function (aa) A(t|ν)          |
   //+------------------------------------------------------------------+
   double aa(double t)
     {
      if(t < 0.) Alert("bad t in Student-t Distribution!");
      return 1.-betai(0.5*nu,0.5,nu/(nu+pow(t,2.)));
     }
   //+------------------------------------------------------------------+
   //| Inverse two-tailed cumulative distribution function (invaa)      |
   //| p=A(t|ν)                                                         |
   //+------------------------------------------------------------------+
   double invaa(double p)
     {
      if(!(p>=0. && p<1.)) Alert("bad p in Student-t Distribution!");
      double x=invbetai(1.-p,0.5*nu,0.5);
      return sqrt(nu*(1.-x)/x);
     }
  };
//+------------------------------------------------------------------+

Die Liste der Klasse CStudenttdist zeigt, dass CBeta eine Basisklasse ist, die die unvollständige Betafunktion beschreibt.

CBeta sieht so aus:

//+------------------------------------------------------------------+
//|            Incomplete Beta Function class definition             |
//+------------------------------------------------------------------+
class CBeta : public CGauleg18
  {
private:
   int               Switch;                     //when to use the quadrature method
   double            Eps,Fpmin;
public:
   //+------------------------------------------------------------------+
   //| CBeta class constructor                                          |
   //+------------------------------------------------------------------+
   void CBeta()
     {
      int swi=3000;
      setCBeta(swi,EPS,FPMIN);
     };
   //+------------------------------------------------------------------+
   //| CBeta class set-method                                           |
   //+------------------------------------------------------------------+
   void setCBeta(int swi,double eps,double fpmin)
     {
      Switch=swi;
      Eps=eps;
      Fpmin=fpmin;
     };
   double            betai(const double a,const double b,const double x); //incomplete beta function Ix(a,b)
   double            betacf(const double a,const double b,const double x);//continued fraction for incomplete beta function
   double            betaiapprox(double a,double b,double x); //Incomplete beta by quadrature
   double            invbetai(double p,double a,double b);    //Inverse of incomplete beta function
  };

Diese Klasse hat auch die Basisklasse CGauleg18, die Koeffizienten für numerische Integrationsmethoden wie die Gauß-Legendre-Quadratur bereitstellt.

2.1.6 Logistische Verteilung

Ich schlage vor, dass wir als Nächstes die logistische Verteilung betrachten.

In der Wahrscheinlichkeitstheorie und Statistik ist die logistische Verteilung eine kontinuierliche Wahrscheinlichkeitsverteilung. Ihre kumulative Verteilungsfunktion ist die logistische Funktion. Ihre Form erinnert an die Normalverteilung, allerdings mit schwereren Enden. Verteilungsdichte:

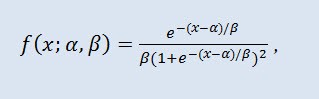
wobei α der Lageparameter ist (-∞ ≤ α ≤ +∞), β der Skalierungsparameter (0<β).

Abbildung 6. Dichte derlogistischen Verteilung Logi(0,1)

Ihre Darstellung hat das folgende Format: X ~ Logi(α,β), wobei:

X eine zufällige Variable ist;
α der Lageparameter ist (-∞ ≤ α ≤ +∞);
β der Skalierungsparameter ist (0<β).

Gültiger Bereich der zufälligen Variable X: -∞ ≤ X ≤ +∞.

CLogisticdist ist die Umsetzung der oben beschriebenen Verteilung:

//+------------------------------------------------------------------+
//|                Logistic Distribution class definition            |
//+------------------------------------------------------------------+
class CLogisticdist
  {
public:
   double            alph,//location parameter (α)
   bet;                   //scale parameter (β)
   //+------------------------------------------------------------------+
   //| CLogisticdist class constructor                                  |
   //+------------------------------------------------------------------+
   void  CLogisticdist() 
     {
      alph=0.0;bet=1.0; //default parameters μ and σ
      if(bet<=0.) Alert("bad bet in Logistic Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return exp(-(x-alph)/bet)/(bet*pow(1.+exp(-(x-alph)/bet),2));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      double et=exp(-1.*fabs(1.81379936423421785*(x-alph)/bet));
      if(x>=alph) return 1./(1.+et);
      else return et/(1.+et);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(p<=0. || p>=1.) Alert("bad p in Logistic Distribution!");
      return alph+0.551328895421792049*bet*log(p/(1.-p));
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

2.1.7 Exponentielle Verteilung

Sehen wir uns auch die exponentielle Verteilung einer zufälligen Variable an.

Eine zufällige Variable X hat die exponentielle Verteilung mit dem Parameter λ > 0, wenn ihre Dichte so aussieht:

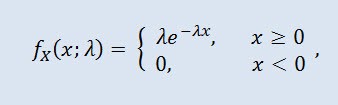
wobei λ der Skalierungsparameter ist (λ>0).

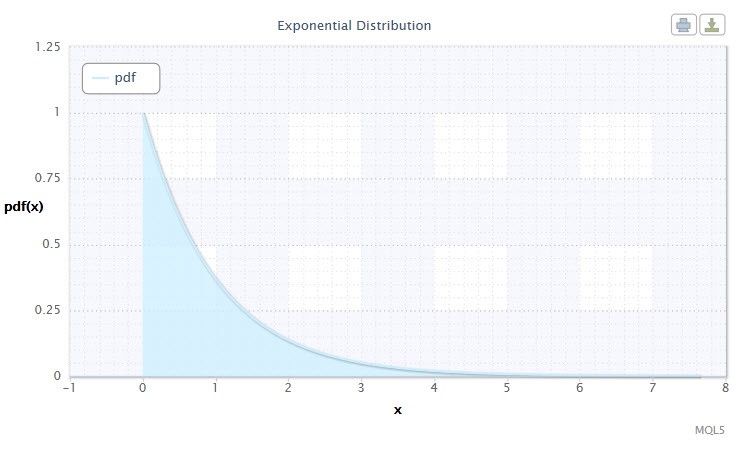
Abbildung 7. Dichte derexponentiellen Verteilung Exp(1)

Ihre Darstellung hat das folgende Format: X ~ Exp(λ), wobei:

X eine zufällige Variable ist;
λ der Skalierungsparameter ist (λ>0).

Gültiger Bereich der zufälligen Variable X: 0 ≤ X ≤ +∞.

Diese Verteilung ist deshalb interessant, weil sie eine Sequenz von Ereignissen beschreibt, die zu bestimmten Zeiten eines nach dem anderen auftreten. Somit kann ein Händler mithilfe dieser Verteilung eine Reihe von Verlustgeschäften und Sonstiges analysieren.

In MQL5-Code wird diese Verteilung über die Klasse CExpondist beschrieben:

//+------------------------------------------------------------------+
//|                Exponential Distribution class definition         |
//+------------------------------------------------------------------+
class CExpondist
  {
public:
   double            lambda;   //scale parameter (λ)
   //+------------------------------------------------------------------+
   //| CExpondist class constructor                                     |
   //+------------------------------------------------------------------+
   void  CExpondist()
     {
      lambda=1.0;              //default parameter λ
      if(lambda<=0.) Alert("bad lambda in Exponential Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      if(x<0.) Alert("bad x in Exponential Distribution!");
      return lambda*exp(-lambda*x);
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      if(x < 0.) Alert("bad x in Exponential Distribution!");
      return 1.-exp(-lambda*x);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(p<0. || p>=1.) Alert("bad p in Exponential Distribution!");
      return -log(1.-p)/lambda;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

2.1.8 Gammaverteilung

Ich habe mich für die Gammaverteilung als nächsten Typ der kontinuierlichen Verteilung einer zufälligen Variable entschieden.

In der Wahrscheinlichkeitstheorie ist die Gammaverteilung eine zweiparametrige Familie aus absolut kontinuierlichen Wahrscheinlichkeitsverteilungen. Wenn der Parameter α ganzzahlig ist, wird eine solche Gammaverteilung auch als Erlang-Verteilung bezeichnet. Die Dichte sieht so aus:

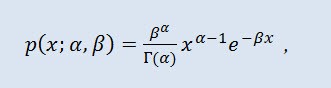
wobei Г die Eulersche Gammafunktion ist, α der Formparameter (0<α), β der Skalierungsparameter (0<β).

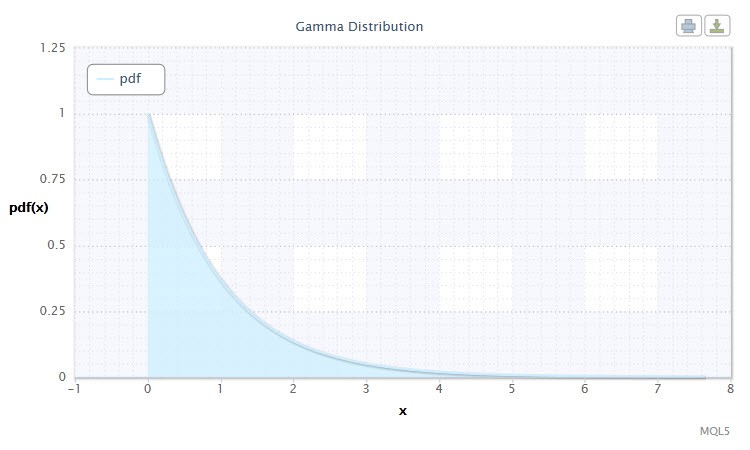
Abbildung 8. Dichte der Gammaverteilung Gam(1,1).

Ihre Darstellung hat das folgende Format: X ~ Gam(α,β), wobei:

X eine zufällige Variable ist;
α der Formparameter ist (0<α);
β der Skalierungsparameter ist (0<β).

Gültiger Bereich der zufälligen Variable X: 0 ≤ X ≤ +∞.

In der durch die Klasse CGammadist definierten Variante sieht es so aus:

//+------------------------------------------------------------------+
//|                Gamma Distribution class definition               |
//+------------------------------------------------------------------+
class CGammadist : CGamma // CGamma class inheritance
  {
public:
   double            alph,//continuous shape parameter (α>0)
   bet,                   //continuous scale parameter  (β>0)
   fac;                   //factor
   //+------------------------------------------------------------------+
   //| CGammaldist class constructor                                    |
   //+------------------------------------------------------------------+
   void  CGammadist()
     {
      setCGammadist();
     }
   void setCGammadist(double Alph=1.0,double Bet=1.0)//default parameters α and β
     {
      alph=Alph; bet=Bet;
      if(alph<=0. || bet<=0.) Alert("bad alph,bet in Gamma Distribution!");
      fac=alph*log(bet)-gammln(alph);
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      if(x<=0.) Alert("bad x in Gamma Distribution!");
      return exp(-bet*x+(alph-1.)*log(x)+fac);
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      if(x<0.) Alert("bad x in Gamma Distribution!");
      return gammp(alph,bet*x);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(p<0. || p>=1.) Alert("bad p in Gamma Distribution!");
      return invgammp(p,alph)/bet;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

Die Klasse der Gammaverteilung wird von der Klasse CGamma abgeleitet, die die unvollständige Gammafunktion beschreibt.

Die Klasse CGamma ist auf folgende Art definiert:

//+------------------------------------------------------------------+
//|            Incomplete Gamma Function class definition            |
//+------------------------------------------------------------------+
class CGamma : public CGauleg18
  {
private:
   int               ASWITCH;
   double            Eps,
   Fpmin,
   gln;
public:
   //+------------------------------------------------------------------+
   //| CGamma class constructor                                         |
   //+------------------------------------------------------------------+
   void CGamma()
     {
      int aswi=100;
      setCGamma(aswi,EPS,FPMIN);
     };
   void setCGamma(int aswi,double eps,double fpmin) //CGamma set-method
     {
      ASWITCH=aswi;
      Eps=eps;
      Fpmin=fpmin;
     };
   double            gammp(const double a,const double x); //incomplete gamma function
   double            gammq(const double a,const double x); //incomplete gamma function Q(a,x)
   void              gser(double &gamser,double a,double x,double &gln); //incomplete gamma function P(a,x)
   double            gcf(const double a,const double x); //incomplete gamma function Q(a,x)
   double            gammpapprox(double a,double x,int psig); //incomplete gamma by quadrature
   double            invgammp(double p,double a); //inverse of incomplete gamma function
  };
//+------------------------------------------------------------------+

Die Klassen CGamma und CBeta basieren auf CGauleg18 als Basisklasse.

2.1.9 Betaverteilung

Sehen wir uns nun die Betaverteilung an.

In der Wahrscheinlichkeitstheorie und Statistik ist die Betaverteilung eine zweiparametrige Familie aus absolut kontinuierlichen Verteilungen. Sie wird zum Beschreiben von zufälligen Variablen genutzt, deren Werte in einem endlichen Intervall definiert sind. Ihre Dichte ist auf folgende Art definiert:

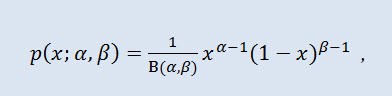
wobei B die Betafunktion ist, α der 1. Formparameter (0<α), β der 2. Formparameter (0<β).

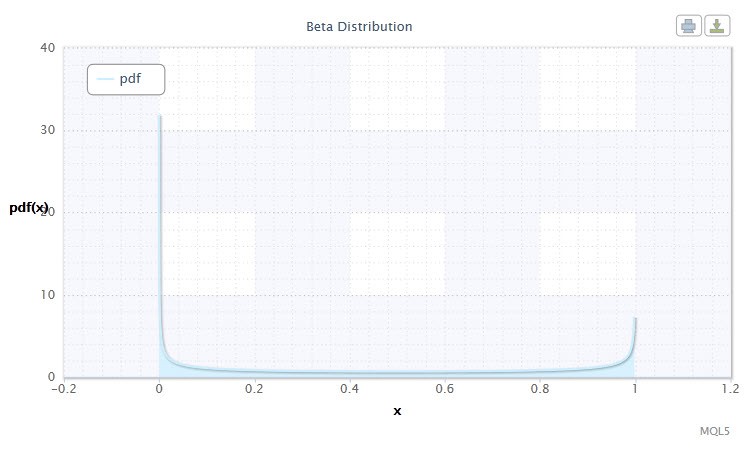
Abbildung 9. Dichte der Betaverteilung Beta(0.5,0.5)

Ihre Darstellung hat das folgende Format: X ~ Beta(α,β), wobei:

X eine zufällige Variable ist;
α der 1. Formparameter ist (0<α);
β der 2. Formparameter ist (0<β).

Gültiger Bereich der zufälligen Variable X: 0 ≤ X ≤ 1.

Die Klasse CBetadist beschreibt diese Verteilung folgendermaßen:

//+------------------------------------------------------------------+
//|                Beta Distribution class definition                |
//+------------------------------------------------------------------+
class CBetadist : CBeta // CBeta class inheritance
  {
public:
   double            alph,//continuous shape parameter (α>0)
   bet,                   //continuous shape parameter (β>0)
   fac;                   //factor
   //+------------------------------------------------------------------+
   //| CBetadist class constructor                                      |
   //+------------------------------------------------------------------+
   void  CBetadist()
     {
      setCBetadist();
     }
   void setCBetadist(double Alph=0.5,double Bet=0.5)//default parameters α and β
     {
      alph=Alph; bet=Bet;
      if(alph<=0. || bet<=0.) Alert("bad alph,bet in Beta Distribution!");
      fac=gammln(alph+bet)-gammln(alph)-gammln(bet);
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      if(x<=0. || x>=1.) Alert("bad x in Beta Distribution!");
      return exp((alph-1.)*log(x)+(bet-1.)*log(1.-x)+fac);
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      if(x<0. || x>1.) Alert("bad x in Beta Distribution");
      return betai(alph,bet,x);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(p<0. || p>1.) Alert("bad p in Beta Distribution!");
      return invbetai(p,alph,bet);
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

2.1.10 Laplace-Verteilung

Eine weitere bemerkenswerte kontinuierliche Verteilung ist die Laplace-Verteilung (doppelte Exponentialverteilung).

Die Laplace-Verteilung (doppelte Exponentialverteilung) ist in der Wahrscheinlichkeitstheorie eine kontinuierliche Verteilung einer zufälligen Variable mit der folgenden Wahrscheinlichkeitsdichte:

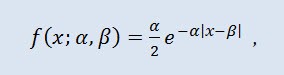
wobei α der Lageparameter ist (-∞ ≤ α ≤ +∞), β der Skalierungsparameter (0<β).

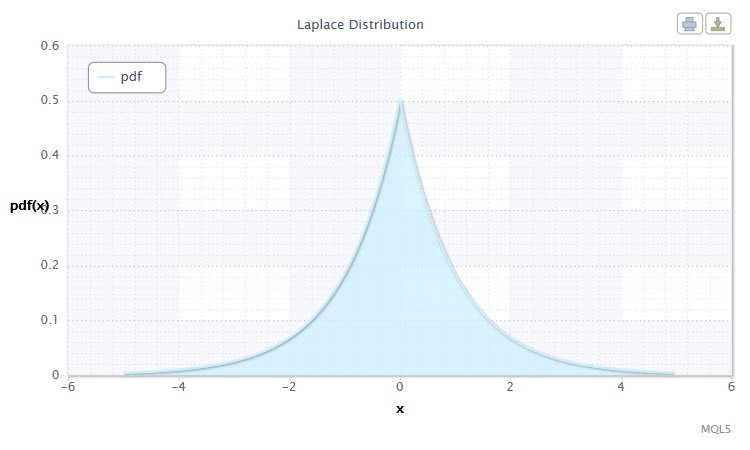
Abbildung 10. Dichte der Laplace-Verteilung Lap(0,1)

Ihre Darstellung hat das folgende Format:X ~ Lap(α,β), wobei:

X eine zufällige Variable ist;
α der Lageparameter ist (-∞ ≤ α ≤ +∞);
β der Skalierungsparameter ist (0<β).

Gültiger Bereich der zufälligen Variable X: -∞ ≤ X ≤ +∞.

Für die Zwecke dieser Verteilung ist die Klasse CLaplacedist folgendermaßen definiert:

//+------------------------------------------------------------------+
//|                 Laplace Distribution class definition            |
//+------------------------------------------------------------------+
class CLaplacedist
  {
public:
   double            alph;   //location parameter (α)
   double            bet;    //scale parameter (β)
   //+------------------------------------------------------------------+
   //| CLaplacedist class constructor                                   |
   //+------------------------------------------------------------------+
   void  CLaplacedist()
     {
      alph=.0;               //default parameter α
      bet=1.;                //default parameter β
      if(bet<=0.) Alert("bad bet in Laplace Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return exp(-fabs((x-alph)/bet))/2*bet;
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      double temp;
      if(x<0)
         temp=0.5*exp(-fabs((x-alph)/bet));
      else
         temp=1.-0.5*exp(-fabs((x-alph)/bet));
      return temp;
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      double temp;
      if(p<0. || p>=1.) Alert("bad p in Laplace Distribution!");
      if(p<0.5)
         temp=bet*log(2*p)+alph;
      else
         temp=-1.*(bet*log(2*(1.-p))+alph);
      return temp;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

Und so haben wir mithilfe von MQL5-Code 10 Klassen für die zehn kontinuierlichen Verteilungen erstellt. Davon abgesehen wurden noch einige weitere Klassen erstellt, die sozusagen ergänzender Art sind, da sie in bestimmten Funktionen und Methoden benötigt wurden (z. B. CBeta und CGamma).

Fahren wir nun mit diskreten Verteilungen fort und erstellen ein paar Klassen für diese Kategorie der Verteilungen.

2.2.1 Binomialverteilung

Fangen wir mit der Binomialverteilung an.

In der Wahrscheinlichkeitstheorie ist die Binomialverteilung eine Verteilung der Anzahl der Erfolge in einer Sequenz aus unabhängigen zufälligen Experimenten, wobei die Erfolgswahrscheinlichkeit für jedes einzelne gleich hoch ist. Die Wahrscheinlichkeitsdichte wird der folgenden Formel entnommen:

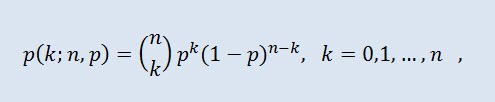
wobei (n k) der Binomialkoeffizient ist, n die Menge der Versuche (0 ≤ n), p die Erfolgswahrscheinlichkeit (0 ≤ p ≤1).

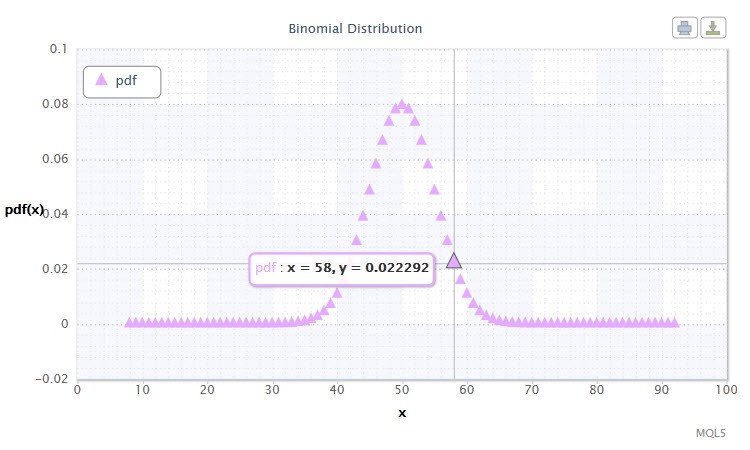
Abbildung 11. Dichte der Binomialverteilung Bin(100,0.5).

Ihre Darstellung hat das folgende Format: k ~ Bin(n,p), wobei:

k eine zufällige Variable ist;
n die Anzahl der Versuche ist (0 ≤ n);
p die Erfolgswahrscheinlichkeit ist (0 ≤ p ≤1).

Gültiger Bereich der zufälligen Variable X: 0 oder 1.

Bringt Sie der Bereich der möglichen Werte der zufälligen Variable X auf irgendeinen Gedanken? Tatsächlich, diese Verteilung kann uns helfen, die angesammelten Gewinne (1) und Verluste (0) im Handelssystem zu analysieren.

Erstellen wir die Klasse CBinomialdist auf die folgende Weise:

//+------------------------------------------------------------------+
//|               Binomial Distribution class definition             |
//+------------------------------------------------------------------+
class CBinomialdist : CBeta // CBeta class inheritance
  {
public:
   int               n;      //number of trials
   double            pe,     //success probability
   fac;                      //factor
   //+------------------------------------------------------------------+
   //| CBinomialdist class constructor                                  |
   //+------------------------------------------------------------------+
   void              CBinomialdist()
     {
      setCBinomialdist();
     }
   void setCBinomialdist(int N=100,double Pe=0.5)//default parameters n and pe
     {
      n=N; pe=Pe;
      if(n<=0 || pe<=0. || pe>=1.) Alert("bad args in Binomial Distribution!");
      fac=gammln(n+1.);
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(int k)
     {
      if(k<0) Alert("bad k in Binomial Distribution!");
      if(k>n) return 0.;
      return exp(k*log(pe)+(n-k)*log(1.-pe)+fac-gammln(k+1.)-gammln(n-k+1.));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(int k)
     {
      if(k<0) Alert("bad k in Binomial Distribution!");
      if(k==0) return 0.;
      if(k>n) return 1.;
      return 1.-betai((double)k,n-k+1.,pe);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   int invcdf(double p)
     {
      int k,kl,ku,inc=1;
      if(p<=0. || p>=1.) Alert("bad p in Binomial Distribution!");
      k=fmax(0,fmin(n,(int)(n*pe)));
      if(p<cdf(k))
        {
         do
           {
            k=fmax(k-inc,0);
            inc*=2;
           }
         while(p<cdf(k));
         kl=k; ku=k+inc/2;
           } else {
         do
           {
            k=fmin(k+inc,n+1);
            inc*=2;
           }
         while(p>cdf(k));
         ku=k; kl=k-inc/2;
        }
      while(ku-kl>1)
        {
         k=(kl+ku)/2;
         if(p<cdf(k)) ku=k;
         else kl=k;
        }
      return kl;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(int k)
     {
      return 1.-cdf(k);
     }
  };
//+------------------------------------------------------------------+

2.2.2 Poisson-Verteilung

Die nächste zu betrachtende Verteilung ist die Poisson-Verteilung.

Die Poisson-Verteilung modelliert eine zufällige Variable, die durch eine Anzahl von Ereignissen dargestellt wird, die über einen festen Zeitraum eintreten. Die Voraussetzung ist, dass diese Ereignisse mit einer festen durchschnittlichen Intensität und Unabhängigkeit voneinander eintreten. Die Dichte sieht so aus:

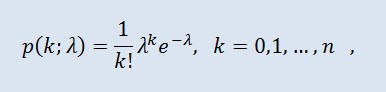
wobei k! die Fakultät ist, λ der Lageparameter (0 < λ).

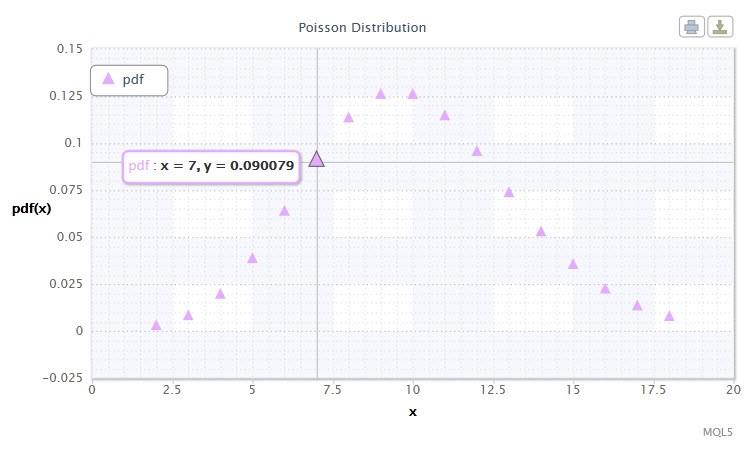
Abbildung 12. Dichteder Poisson-Verteilung Pois(10).

Ihre Darstellung hat das folgende Format: k ~ Pois(λ), wobei:

k eine zufällige Variable ist;
λ der Lageparameter ist (0 < λ).

Gültiger Bereich der zufälligen Variable X: 0 ≤ X ≤ +∞.

Die Poisson-Verteilung beschreibt das "Gesetz der seltenen Ereignisse", das für die Beurteilung des Risikogrades von Bedeutung ist.

Die Klasse CPoissondist dient den Zwecken dieser Verteilung:

//+------------------------------------------------------------------+
//|               Poisson Distribution class definition              |
//+------------------------------------------------------------------+
class CPoissondist : CGamma // CGamma class inheritance
  {
public:
   double            lambda;   //location parameter (λ)
   //+------------------------------------------------------------------+
   //| CPoissondist class constructor                                   |
   //+------------------------------------------------------------------+
   void CPoissondist()
     {
      lambda=15.;
      if(lambda<=0.) Alert("bad lambda in Poisson Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(int n)
     {
      if(n<0) Alert("bad n in Poisson Distribution!");
      return exp(-lambda+n*log(lambda)-gammln(n+1.));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(int n)
     {
      if(n<0) Alert("bad n in Poisson Distribution!");
      if(n==0) return 0.;
      return gammq((double)n,lambda);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   int invcdf(double p)
     {
      int n,nl,nu,inc=1;
      if(p<=0. || p>=1.) Alert("bad p in Poisson Distribution!");
      if(p<exp(-lambda)) return 0;
      n=(int)fmax(sqrt(lambda),5.);
      if(p<cdf(n))
        {
         do
           {
            n=fmax(n-inc,0);
            inc*=2;
           }
         while(p<cdf(n));
         nl=n; nu=n+inc/2;
           } else {
         do
           {
            n+=inc;
            inc*=2;
           }
         while(p>cdf(n));
         nu=n; nl=n-inc/2;
        }
      while(nu-nl>1)
        {
         n=(nl+nu)/2;
         if(p<cdf(n)) nu=n;
         else nl=n;
        }
      return nl;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(int n)
     {
      return 1.-cdf(n);
     }
  };
//+=====================================================================+

Natürlich ist es unmöglich, innerhalb eines Beitrags auf alle statistischen Verteilungen einzugehen, und wahrscheinlich ist es auch nicht notwendig. Wenn der Benutzer es wünscht, kann er die oben dargelegte Verteilungsgalerie erweitern. Die erstellten Verteilungen finden Sie in der Datei Distribution_class.mqh.

3. Erstellen von Verteilungsdiagrammen

Ich schlage vor, dass wir uns nun ansehen, wie die Klassen, die wir für die Verteilung erstellt haben, für unsere zukünftige Arbeit genutzt werden können.

Hier habe ich unter erneuter Zuhilfenahme der OOP die Klasse CDistributionFigure erstellt, die benutzerdefinierte Parameterverteilungen verarbeitet und sie mit den im Beitrag "Diagramme in HTML" beschriebenen Mitteln auf dem Bildschirm abbildet.

//+------------------------------------------------------------------+
//|           Distribution Figure class definition                   |
//+------------------------------------------------------------------+
class CDistributionFigure
  {
private:
   Dist_type         type;  //distribution type
   Dist_mode         mode;  //distribution mode
   double            x;     //step start
   double            x11;   //left side limit
   double            x12;   //right side limit
   int               d;     //number of points
   double            st;    //step

public:
   double            xAr[]; //array of random variables
   double            p1[];  //array of probabilities
   void              CDistributionFigure();  //constructor 
   void              setDistribution(Dist_type Type,Dist_mode Mode,double X11,double X12,double St); //set-method
   void              calculateDistribution(double nn,double mm,double ss); //distribution parameter calculation
   void              filesave(); //saving distribution parameters
  };
//+------------------------------------------------------------------+

Die Umsetzung lasse ich aus. Beachten Sie, dass diese Klasse Datenmitglieder wie type und mode hat, die sich entsprechend auf Dist_type und Dist_mode beziehen. Diese Typen sind Aufzählungen der beobachteten Verteilungen und deren Typen.

Versuchen wir nun endlich, ein Diagramm für eine Verteilung zu erstellen.

Ich habe das Script continuousDistribution.mq5 für kontinuierliche Verteilungen geschrieben, seine wichtigsten Zeilen sind die folgenden:

//+------------------------------------------------------------------+
//|                     Input variables                              |
//+------------------------------------------------------------------+

input Dist_type dist;  //Distribution Type
input Dist_mode distM; //Distribution Mode
input int nn=1;        //Nu
input double mm=0.,    //Mu
            ss=1.;    //Sigma
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//(Normal #0,Lognormal #1,Cauchy #2,Hypersec #3,Studentt #4,Logistic #5,Exponential #6,Gamma #7,Beta #8 , Laplace #9)
   double Xx1,      //left side limit
          Xx2,     //right side limit          
          st=0.05; //step
   if(dist==0) //Normal
     {
      Xx1=mm-5.0*ss/1.25;
      Xx2=mm+5.0*ss/1.25;
     }
   if(dist==2 || dist==4 || dist==5) //Cauchy,Studentt,Logistic
     {
      Xx1=mm-5.0*ss/0.35;
      Xx2=mm+5.0*ss/0.35;
     }
   else if(dist==1 || dist==6 || dist==7) //Lognormal,Exponential,Gamma
     {
      Xx1=0.001;
      Xx2=7.75;
     }
   else if(dist==8) //Beta
     {
      Xx1=0.0001;
      Xx2=0.9999;
      st=0.001;
     }
   else 
     {
      Xx1=mm-5.0*ss;
      Xx2=mm+5.0*ss;
     }
//---
   CDistributionFigure F;        //creation of the CDistributionFigure class instance 
   F.setDistribution(dist,distM,Xx1,Xx2,st);
   F.calculateDistribution(nn,mm,ss);
   F.filesave();
   string path=TerminalInfoString(TERMINAL_DATA_PATH)+"\\MQL5\\Files\\Distribution_function.htm";
   ShellExecuteW(NULL,"open",path,NULL,NULL,1);
  }
//+------------------------------------------------------------------+

Für diskrete Verteilungen wurde das Script discreteDistribution.mq5 geschrieben.

Ich habe das Script mit Standardparametern für die Cauchy-Verteilung ausgeführt und ein Diagramm wie im nachfolgend eingebetteten Video erhalten.

Fazit

Dieser Beitrag stellt einige theoretische Verteilungen einer zufälligen Variable im MQL5-Format vor. Ich bin überzeugt, dass der Handel auf dem Markt und somit auch die Arbeit eines Handelssystems auf den grundlegenden Gesetzen der Wahrscheinlichkeit basieren sollten.

Ich hoffe, dass dieser Beitrag für den interessierten Leser von praktischem Interesse sein wird. Ich werde meinerseits dieses Thema weiter verfolgen und praktische Beispiele aufführen, um zu zeigen, wie statistische Wahrscheinlichkeitsverteilungen für die Analyse von Wahrscheinlichkeitsmodellen genutzt werden können.

Ablageort der Dateien:

#	Datei	Pfad	Beschreibung
1	Distribution_class.mqh	%MetaTrader%\MQL5\Include	Galerie von Verteilungsklassen
2	DistributionFigure_class.mqh	%MetaTrader%\MQL5\Include	Klassen für die grafische Darstellung von Verteilungen
3	continuousDistribution.mq5	%MetaTrader%\MQL5\Scripts	Script für die Erstellung einer kontinuierlichen Verteilung
4	discreteDistribution.mq5	%MetaTrader%\MQL5\Scripts	Script für die Erstellung einer diskreten Verteilung
5	dataDist.txt	%MetaTrader%\MQL5\Files	Daten für die Darstellung der Verteilung
6	Distribution_function.htm	%MetaTrader%\MQL5\Files	HTML-Diagramm für kontinuierliche Verteilungen
7	Distribution_function_discr.htm	%MetaTrader%\MQL5\Files	HTML-Diagramm für diskrete Verteilungen
8	exporting.js	%MetaTrader%\MQL5\Files	Java-Script für den Export eines Diagramms
9	highcharts.js	%MetaTrader%\MQL5\Files	JavaScript-Bibliothek
10	jquery.min.js	%MetaTrader%\MQL5\Files	JavaScript-Bibliothek

Literatur:

K. Krishnamoorthy. Handbook of Statistical Distributions with Applications, Chapman and Hall/CRC 2006.
W.H. Press, et al. Numerical Recipes: The Art of Scientific Computing, Dritte Edition, Cambridge University Press: 2007. - 1256 pp.
S.V. Bulaschew Statistics for Traders. - M.: Kompania Sputnik +, 2003. - 245 pp.
I. Gaidyschew Datenanalyse und -verarbeitung: Spezielles Nachschlagewerk - SPb: Piter, 2001. - 752 pp.: Ill.
A.I. Kibzun, E.R. Gorjainowa – Wahrscheinlichkeitstheorie und mathematische Statistik. Basiskurs mit Beispielen und Aufgaben
N.Sh. KremerProbability Theory and Mathematical Statistics.M.: Unity-Dana, 2004. — 573 pp.

Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/271

Beigefügte Dateien |

ZIP herunterladen

distribution_class.mqh (108.26 KB)

continuousdistribution.mq5 (2.45 KB)

discretedistribution.mq5 (2.01 KB)

distribution_function.zip (59.99 KB)

distributionfigure_class.mqh (19.68 KB)

Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.

Andere Artikel von diesem Autor

Zur Diskussion im Händlerforum

Tracing, Debugging und strukturelle Analyse von Quellcodes

Die gesamte Problematik der Erstellung einer Struktur eines auszuführenden Codes und dessen Tracing lässt sich ohne ernsthafte Schwierigkeiten lösen. Diese Möglichkeit trat mit MetaTrader 5 dank einer neuen Funktion der MQL5-Sprache in Erscheinung: der automatischen Erstellung von Variablen eines komplexen Datentyps (Strukturen und Klassen) und deren Beseitigung beim Verlassen des lokalen Umfelds. Dieser Beitrag beschreibt die Methoden und liefert ein vorgefertigtes Tool.

3 Methoden zur Beschleunigung von Indikatoren anhand des Beispiels der linearen Regression

Dieser Beitrag behandelt die Methoden zur Optimierung der Berechnungsalgorithmen von Indikatoren. Jeder wird eine Methode finden, der seine/ihre Anforderungen am besten erfüllt. Drei Methoden werden hier beschrieben. Eine ist ziemlich simpel, die zweite erfordert solide mathematische Kenntnisse und die dritte benötigt einen gewissen Scharfsinn. Für die Realisierung der meisten beschriebenen Methoden werden Indikatoren oder Designmerkmale des MetaTrader 5 Terminals verwendet. Die Methoden sind weitestgehend universell einsatzfähig und können nicht nur für die Beschleunigung der Berechnung der linearen Regression verwendet werden, sondern auch für viele andere Indikatoren.

Statistische Schätzungen

Die Schätzung der statistischen Parameter einer Sequenz ist sehr wichtig, weil die meisten mathematischen Modelle und Methoden auf unterschiedlichen Annahmen basieren, beispielsweise dem Normalverteilungsgesetz oder dem Streuungswert oder anderen Parametern. Beim Analysieren und Prognostizieren von Zeitreihen brauchen wir deshalb ein einfaches und bequemes Werkzeug, das es uns ermöglicht, die wichtigsten statistischen Parameter schnell und deutlich zu schätzen. Dieser Beitrag beschreibt kurz die einfachsten statistischen Parameter einer zufälligen Sequenz und mehrere Methoden für die visuelle Analyse. Er liefert die Umsetzung dieser Methoden in MQL5 und die Methoden der Visualisierung des Ergebnisses der Berechnung mithilfe der Anwendung Gnuplot.

Filtern von Signalen auf Basis statistischer Daten von Preiskorrelationen

Gibt es irgendeine Korrelation zwischen dem Verhalten des Preises in der Vergangenheit und seinen zukünftigen Trends? Warum legt der Preis heute die gleichen Merkmale an den Tag wie bei seinen gestrigen Bewegungen? Können die Statistiken zum Prognostizieren der Preisdynamiken genutzt werden? Es gibt eine Antwort und sie ist positiv. Wenn Sie Zweifel haben, ist dieser Beitrag genau das Richtige für Sie. Ich werde Ihnen erzählen, wie ein funktionierender Filter für ein Handelssystem in MQL5 erstellt wird, und ein interessantes Muster in Preisveränderungen offenlegen.