Entwicklung des Price Action Analysis Toolkit (Teil 41): Aufbau eines statistischen Preis-Level EA in MQL5

Inhalt

• Einführung
• Strategische Logik
• Code-Aufschlüsselung
• Ergebnisse
• Schlussfolgerung

Einführung

Die Statistik ist seit jeher von zentraler Bedeutung für die Finanzanalyse, weil sie aus verrauschten Marktdaten messbare, vergleichbare Größen macht. In dieser Ausgabe des Price Action Analysis Toolkit wenden wir dieselben statistischen Werkzeuge direkt auf Kerzen an: Anstatt jeden Balken als einen einzelnen Klick mit Informationen zu behandeln, komprimieren wir viele Balken zu reproduzierbaren Preisniveaus und Verteilungsmerkmalen, die das jüngste Marktverhalten interpretierbar machen.

Jede Kerze lässt sich in einem typischen Preis zusammenfassen, der hier als arithmetisches Mittel ihrer drei Hauptkomponenten definiert ist: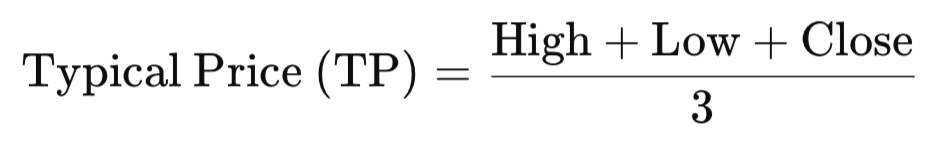

Die Verwendung von TP zur Ableitung von Mittelwert, Median, Modus und Perzentilwerten ist daher von wesentlicher Bedeutung: Der Modus hebt das Preiscluster hervor, in dem sich der Markt die meiste Zeit aufhält, und stellt oft eine praktische Unterstützung oder einen Widerstand dar; der Median identifiziert das robuste Zentrum der Verteilung und zeigt Richtungsänderungen auf, wenn der Preis dieses Zentrum durchquert; der Mittelwert (und der daraus abgeleitete z-Score) bietet einen Gleichgewichtspunkt, der auf große Bewegungen anspricht und für volatilitätsnormierte Signale nützlich ist; Perzentile (P25/P75) schließlich umrahmen die mittleren 50 % des Preisgeschehens (IQR) und helfen, eine enge Konsolidierung von einer breiten Streuung zu unterscheiden. Kurz gesagt, TP-basierte Statistiken liefern Referenzwerte, die sowohl statistisch aussagekräftig als auch für das Intraday-Kursverhalten direkt relevant sind.

In diesem Artikel zeigen wir, wie diese Metriken in praktische, chartfreundliche Signale umgesetzt werden: Sie werden zu horizontalen Referenzlinien (Mittelwert, Median, P25/P75, Modalwerte), zu Eingaben für ATR-skalierte Schwellenwerte, die Ausbrüche von Umkehrungen unterscheiden, und zur Grundlage für eine Z-Score-Signal-Engine, die ungewöhnlich extreme Preisaktionen kennzeichnet. Bei der von uns vorgestellten Implementierung (KDE Level Sentinel EA) stehen Reproduzierbarkeit und Nutzerfreundlichkeit im Vordergrund: Snapshots frieren Referenzniveaus für die Vorwärtsüberwachung ein, Etiketten werden stabil und überschneidungsfrei gehalten, und Signale werden als präzise Chartpfeile gezeichnet, die den genauen auslösenden Kurs markieren.

Lesen Sie weiter, um die Mathematik hinter jeder Metrik, die Implementierungsdetails in MQL5 und die Interpretation der EA-Ausgaben zu erfahren, damit Sie von rohen Kerzen zu klaren, überprüfbaren Handelshypothesen übergehen können.

Strategische Logik

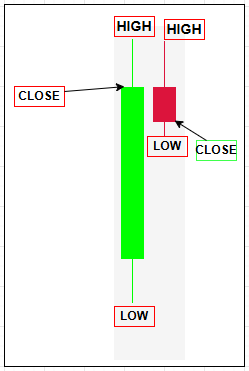
Wie ich bereits erwähnt habe, versuchen wir, statistische Methoden in die Kursentwicklung zu implementieren, weshalb wir für alle statistischen Berechnungen typische Kurse verwenden. Der typische Preis (TP) wird berechnet, indem der Höchst-, Tiefst- und Schlusskurs eines Balkens addiert und die Summe durch drei geteilt wird; er gleicht die Handelsspanne mit dem Schlussniveau aus, glättet isolierte Spitzen und erzeugt eine stabilere Serie als der Schlusskurs allein. Durch die Einbeziehung von Intra-Bar-Extremen, ohne dass die Öffnung erforderlich ist, bietet TP umfangreichere Eingaben für Verteilungsstatistiken – Mittelwert, Median und Kernel-Dichte-Schätzungen – und verbessert so die Stabilität und Signalqualität für nachgelagerte Modelle. Im Vergleich zu Alternativen wie Close, HL/2 oder OHLC4 bietet TP einen pragmatischen Mittelweg: Es erfasst sowohl die Spanne als auch die Richtung in einem kompakten, robusten Input, der sich ideal für die statistische Analyse von Preisaktionen eignet.

Nachfolgend finden Sie die statistischen Kennziffern, die wir aus dem typischen Preis (TP) ableiten. Jede Kennzahl beleuchtet einen anderen Aspekt des Preisverhaltens im Zeitverlauf – von der zentralen Tendenz und Streuung bis hin zu Häufigkeit und Struktur. 

Von TP abgeleitete Metriken:

• Mittelwert (Durchschnitt)
• Median
• Modus
• Standard Deviation
• Varianz
• Bereich (Hoch-Tief-Spanne)
• Schiefe und Kurtosis (optional für Fortgeschrittene)

Schauen wir sie uns einzeln an, um zu sehen, wie sich die Rohdaten der Kerzen in aussagekräftige Kursniveaus und Signale verwandeln, die die Preisaktionsanalyse leiten.

1. Mittelwert (Durchschnitt)

Der Mittelwert stellt den zentralen Wert aller typischen Preise innerhalb einer Stichprobe dar. Er ist zwar anfällig für extreme Ausschläge, bietet aber einen zuverlässigen Überblick darüber, wo sich die Preise im Durchschnitt bewegen. Wenn zum Beispiel eine Person in drei Monaten 1000, 1200 und 1100 Dollar verdient, ist das mittlere Gehalt (1000+1200+1100)/3=1100, was das Gesamteinkommensniveau widerspiegelt. Auch im Handel zeigt der mittlere TP den Durchschnittspreis, um den der Markt schwankt.

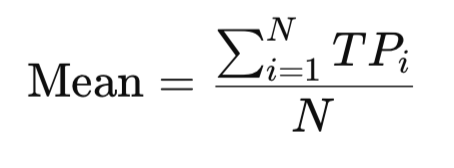
MQL5-Implementierung:

double Mean(const double &values[])
{
   double sum = 0.0;
   for(int i=0; i<ArraySize(values); i++)
      sum += values[i];
   return sum / ArraySize(values);
}

2. Median

Der Median ist der mittlere Wert in einer geordneten Menge typischer Preise. Anders als der Mittelwert wird er nicht von extremen Höchst- oder Tiefstwerten beeinflusst, was ihn zu einem robusten Maß der zentralen Tendenz macht. Bei Testergebnissen von 50, 55, 60, 95 und 100 liegt der Median bei 60, was den wahren Mittelwert der Leistung darstellt. Beim Handel zeigt der Median-TP das ausgewogene Zentrum der Preisaktion ohne Verzerrung durch ungewöhnliche Ausschläge.

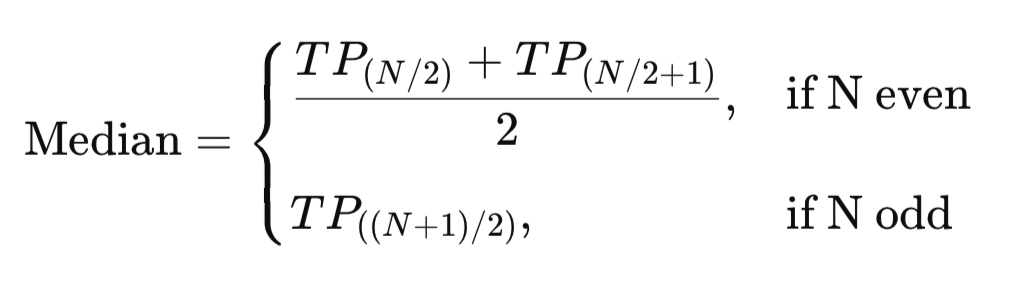
MQL5-Implementierung:

double Median(double &values[])
{
   ArraySort(values, WHOLE_ARRAY, 0, MODE_ASCEND);
   int size = ArraySize(values);
   if(size % 2 == 0)
      return (values[size/2 - 1] + values[size/2]) / 2.0;
   else
      return values[size/2];
}

3. Modus

Der Modus identifiziert den am häufigsten vorkommenden Wert in einem Datensatz und bietet einen Einblick in die natürliche Clusterbildung. In einer Gruppe mit den Schuhgrößen 7, 8, 8, 9, 8, 7, 10, 8, 9 und 7 ist die häufigste Größe die 8 – der Modus. Ähnlich verhält es sich beim Handel: Der Modus des TP weist auf Preisniveaus hin, auf denen sich der Markt die meiste Zeit aufhält und die oft mit starken Unterstützungs- oder Widerstandszonen übereinstimmen.

MQL5-Implementierung:

double Mode(const double &values[])
{
   double mode = values[0];
   int maxCount = 0;

   for(int i=0; i<ArraySize(values); i++)
   {
      int count = 0;
      for(int j=0; j<ArraySize(values); j++)
      {
         if(values[j] == values[i]) count++;
      }
      if(count > maxCount)
      {
         maxCount = count;
         mode = values[i];
      }
   }
   return mode;
}

4. Standardabweichung

Die Standardabweichung misst, wie weit die Werte vom Mittelwert abweichen, und gibt so den Grad der Variabilität an. Nehmen wir zwei Personen mit denselben durchschnittlichen täglichen Schritten: Die eine protokolliert 7900, 8000 und 8100 Schritte, die andere 2000, 15.000 und 5000. Beide liegen im Durchschnitt bei 8000, aber die zweite weist weitaus größere Schwankungen auf. Auf den Handel angewandt, unterscheidet die Standardabweichung der TP ruhige, beständige Märkte von volatilen, instabilen Märkten.

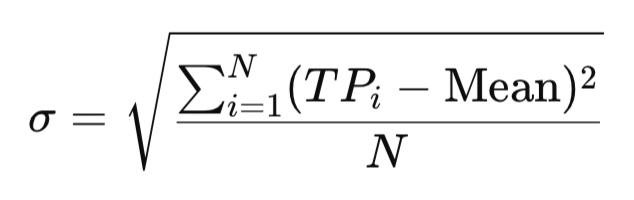
MQL5-Implementierung:

double StandardDeviation(const double &values[])
{
   double mean = Mean(values);
   double sum = 0.0;
   for(int i=0; i<ArraySize(values); i++)
      sum += MathPow(values[i] - mean, 2);
   return MathSqrt(sum / ArraySize(values));
}

5. Varianz

Die Varianz ist das Quadrat der Standardabweichung und quantifiziert die Streuung der Werte um den Mittelwert in quadratischen Einheiten. Sie ist zwar weniger intuitiv als die Standardabweichung, aber sie vergrößert große Abweichungen und bietet eine konsistente Grundlage für den Vergleich der Volatilität verschiedener Instrumente. Im Zusammenhang mit Verrechnungspreisen verdeutlicht die Varianz, wie weit die Preisniveaus auseinanderklaffen, und bietet einen weiteren Blick auf die Marktstabilität.

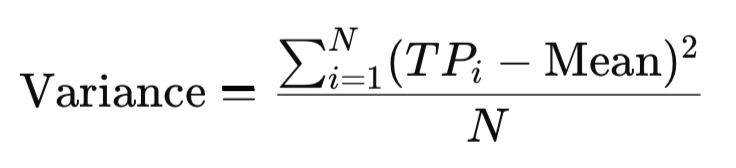
MQL5-Implementierung:

double Variance(const double &values[])
{
   double mean = Mean(values);
   double sum = 0.0;
   for(int i=0; i<ArraySize(values); i++)
      sum += MathPow(values[i] - mean, 2);
   return sum / ArraySize(values);
}

6. Bereich

Der Bereich erfasst die Differenz zwischen dem höchsten und dem niedrigsten Wert in einem Datensatz. Wenn beispielsweise die wöchentlichen Temperaturen zwischen 20°C und 35°C schwanken, beträgt die Spanne 15°C. Beim Handel zeigt der TP-Bereich die Breite der Marktbewegung an und hilft Händlern, schnell zwischen engen Konsolidierungen und großen Ausschlägen zu unterscheiden.

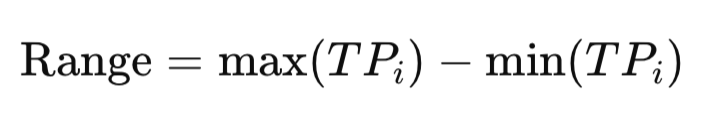
MQL5-Implementierung:

double Range(const double &values[])
{
   double minVal = values[ArrayMinimum(values)];
   double maxVal = values[ArrayMaximum(values)];
   return maxVal - minVal;
}

7. Schiefe oder Kurtosis

Die Schiefe (Skewness) misst die Asymmetrie einer Verteilung.

double Skewness(const double &values[])
{
   int n = ArraySize(values);
   double mean = Mean(values);
   double sd   = StandardDeviation(values);

   double sum = 0.0;
   for(int i=0; i<n; i++)
      sum += MathPow((values[i] - mean)/sd, 3);

   return (double)n / ((n-1)*(n-2)) * sum;
}

In einem Unternehmen, in dem die meisten Mitarbeiter 3.000 Dollar verdienen, der CEO aber 50.000 Dollar, wird das Durchschnittsgehalt nach oben gezogen, was zu einer positiven Schieflage führt. In ähnlicher Weise gibt die Schiefe der TP Aufschluss darüber, ob die Preise eher zu den Extremen nach oben oder nach unten tendieren, was auf ein Ungleichgewicht in der Marktstruktur hinweist.

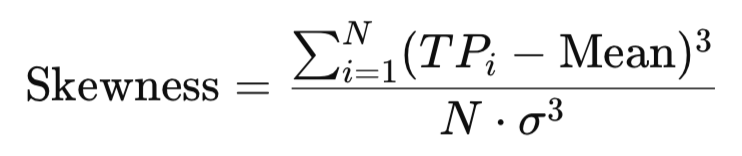
Die Kurtosis bewertet die Größe der „Ausläufer“ einer Verteilung oder die Wahrscheinlichkeit extremer Ergebnisse. Auf einer Autobahn, auf der die meisten Autos zwischen 60 und 70 km/h fahren, ist die Kurtosis gering. Wenn Autos normalerweise in diesem Bereich fahren, aber gelegentlich mit 20 kriechen oder auf 150 ansteigen, ist die Kurtosis hoch.

double Kurtosis(const double &values[])
{
   int n = ArraySize(values);
   double mean = Mean(values);
   double sd   = StandardDeviation(values);

   double sum = 0.0;
   for(int i=0; i<n; i++)
      sum += MathPow((values[i] - mean)/sd, 4);

   return ((double)n*(n+1) / ((n-1)*(n-2)*(n-3))) * sum
          - (3.0*MathPow(n-1,2) / ((n-2)*(n-3)));
}

Beim Handel deutet eine hohe Kurtosis von TP auf Märkte hin, die die meiste Zeit ruhig sind, aber zu plötzlichen, dramatischen Bewegungen neigen.

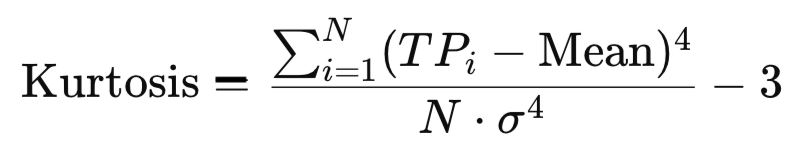
8. Perzentile (P25 und P75)

Perzentile unterteilen den Datensatz in Rangpositionen und ermöglichen es uns zu verstehen, wo die Werte innerhalb der Verteilung liegen. Das 25. Perzentil (P25) markiert den Punkt, unter dem 25 % der typischen Preise liegen, während das 75. Perzentil (P75) das Niveau markiert, unter dem 75 % der Preise liegen. Zusammen bilden diese beiden Werte den Interquartilsbereich (IQR), der die mittleren 50 % aller Beobachtungen darstellt.

double p25 = Percentile(values, 0.25);
double p75 = Percentile(values, 0.75);

Print("P25 = ", DoubleToString(p25, _Digits), 
      " | P75 = ", DoubleToString(p75, _Digits));

In Bezug auf den Handel hebt P25 die „untere Gruppe“ der Preisaktivität hervor und zeigt oft an, wo Käufer durchgängig einsteigen, während P75 die „obere Gruppe“ hervorhebt, in der tendenziell die Verkäufer dominieren. Kombiniert man diese Grenzen, erhält man ein differenzierteres Bild der Marktkonzentration als bei Mittelwert oder Median allein. Ein enger IQR deutet auf eine Konsolidierung hin, während ein breiter IQR auf eine größere Marktstreuung hindeutet.

Die Logik der Signalerzeugung basiert auf dem Z-Score des letzten typischen Preises, der als (TP – Mittelwert) / stddev unter Verwendung des aktuellen Statistikfensters berechnet wird. Wenn diese standardisierte Abweichung die konfigurierte Einstiegsschwelle (ZScoreSignalEnter) überschreitet, generiert der EA ein Kaufsignal, wenn der Preis ausreichend unter dem Mittelwert liegt (negativer Z-Score) oder ein Verkaufssignal, wenn er ausreichend darüber liegt (positiver Z-Score). Signale werden nur bestätigt, wenn die entsprechenden Einstellungen AllowLongSignals oder AllowShortSignals aktiviert sind. Im Signalzustand wartet der EA, bis der Z-Score wieder in das definierte Exit-Band (ZScoreSignalExit) fällt, bevor er das Signal löscht und möglicherweise eine Umkehr meldet. Jeder Signalübergang löst EmitAlertWithArrow aus, das einen Richtungspfeil auf dem Chart zeichnet und, je nach Nutzereinstellungen, auch einen Pop-up-Alarm, einen Ton oder eine Push-Benachrichtigung auslösen kann.

Code-Aufschlüsselung

In diesem Abschnitt werden die Implementierungsdetails von KDE Level Sentinel.mq5 beschrieben, wobei der Schwerpunkt auf der Architektur, dem Datenfluss, den Kernalgorithmen und den wichtigen Hilfsroutinen zur Unterstützung der Diagrammdarstellung und der Pegelüberwachung liegt. Die Präsentation ist so aufgebaut, dass sie dem Leser hilft, das konzeptionelle Design den entsprechenden Codeabschnitten und Konfigurationsoptionen zuzuordnen.

Konfiguration und Initialisierung

Alle vom Nutzer konfigurierbaren Optionen werden am Anfang des Quelltextes als Eingabeparameter angegeben. Dazu gehören das Analysefenster (Lookback), der Ausschluss des aktuellen Formbalkens, KDE- und Histogramm-Einstellungen (ModeBins, KDEGridPoints, KDEBandwidthFactor), Z-Score-Schwellenwerte für Signale, Snapshot- und Überwachungssteuerungen (AutoSnapshotLevels, MonitorBars, TouchTolerancePips, BreakoutPips, ReversalPips, UseATRforThresholds) und UI/Cleanup-Timing (TimerIntervalSeconds, CleanupIntervalSeconds). Dieser einzelne Abschnitt fungiert als Bedienfeld des EA; die Änderung einer Eingabe verändert die statistische Linse und das Überwachungsverhalten des EA, ohne den Code zu ändern.

// ---------- user inputs (control panel) ----------
input int    Lookback               = 1000;
input bool   ExcludeCurrent         = true;
input bool   UseWeightedByVol       = true;
input int    ModeBins               = 30;
input int    KDEGridPoints          = 100;
input double KDEBandwidthFactor     = 1.0;
input bool   DrawHistogramOnChart   = false;
input int    RefreshEveryXTicks     = 1;
input double ZScoreSignalEnter      = 2.0;
input double ZScoreSignalExit       = 0.8;
input bool   AutoSnapshotLevels     = true;
input int    MonitorBars            = 20;
input double TouchTolerancePips     = 3.0;
input bool   UseATRforThresholds    = true;
input double ATRMultiplier          = 0.5;
input int    ATRperiod              = 14;
input int    TimerIntervalSeconds   = 60;
input int    CleanupIntervalSeconds = 3600;

// ---------- OnInit (build names, cleanup, placeholders, start timer) ----------
int OnInit()
  {
   S_base = StringFormat("CSTATS_%s_%d", _Symbol, (int)TF);
   S_mean = S_base + "_MEAN";
   S_p25  = S_base + "_P25";
   // remove leftovers from previous runs
   RemoveExistingEAObjects();
   // create panel + placeholder HLINEs
   CreatePanel();
   CreateHLine(S_mean, 0.0, clrBlack, 2);
   CreateHLine(S_p25,  0.0, clrTeal,  1);
   // optionally clear previous snapshot
   if(ClearSnapshotOnStart) ClearSnapshot();
   // start periodic timer for housekeeping
   EventSetTimer(TimerIntervalSeconds);
   return(INIT_SUCCEEDED);
  }

In OnInit konstruiert der EA kanonische Objekt- und globale Variablennamen-Präfixe mit S_base = StringFormat(“CSTATS_%s_%d“, _Symbol, (int)TF). Durch diese deterministische Benennung werden mehrere Chart-Instanzen vor versehentlichen Kollisionen geschützt und die Bereinigung zentralisiert. Bei der Initialisierung werden übrig gebliebene Objekte aus früheren Instanzen entfernt, ein kompaktes Panel in einer Ecke (zusammenfassende Beschriftungen) erstellt, horizontale Platzhalterlinien für jede Kernstatistik (Mittelwert, ±SD, P25/P75, Median, beide Modi) platziert, optional frühere Schnappschüsse gelöscht und ein periodischer Timer für die Haushaltsführung gestartet.

Datenerfassung und Hauptschleife

Die Hauptberechnung findet in OnTickstatt und wird gedrosselt durch RefreshEveryXTicks, um eine übermäßige CPU-Nutzung bei hochfrequenten Ticks zu vermeiden. Die Routine kopiert Lookback-Balken aus dem konfigurierten Zeitrahmen in rates[] über CopyRates, mit start = ExcludeCurrent ? 1 : 0, um optional sich bildende Kerzen zu vermeiden. Aus rates[] werden Arrays typischer Preise vals[] = (high + low + close) / 3.0 und die der Tick-Volumina vols[] (wenn die Volumengewichtung aktiviert ist) berechnet.

void OnTick()
  {
   tick_count++;
   if(tick_count < RefreshEveryXTicks) return;
   tick_count = 0;

   int start = ExcludeCurrent ? 1 : 0;
   int needed = Lookback;
   if(Bars(_Symbol, TF) - start < needed) return;

   MqlRates rates[];
   int copied = CopyRates(_Symbol, TF, start, needed, rates);
   if(copied <= 0) { Print("CopyRates failed: ", GetLastError()); return; }

   double vals[], vols[];
   ArrayResize(vals, copied);
   ArrayResize(vols, copied);
   for(int i = 0; i < copied; i++)
     {
      vals[i] = (rates[i].high + rates[i].low + rates[i].close) / 3.0; // typical price
      vols[i] = (double)rates[i].tick_volume;
     }

   // pass vals/vols into statistics routines...
  }

Statistische Berechnungen folgen sofort: arithmetisches Mittel, optionales volumengewichtetes Mittel, Stichprobenvarianz und Standardabweichung, Median, 25. und 75. Perzentile, ein zwei Modi (ModeBins und ModeKDE). Die KDE-Bandbreite verwendet eine Silverman-ähnliche Regel h = 1,06 * sd * n^-0,2, skaliert mit KDEBandwidthFactor, bewertet dann die Dichte auf einem einheitlichen Gitter von KDEGridPoints und gibt den Gitterpunkt mit der größten geschätzten Dichte zurück. Der letzte typische Preis (latest) wird zur Berechnung eines z-score (latest – mean) / stddev verwendet, der einfache z-score Einstiegs-/Ausstiegssignale auslöst.
Die berechneten Statistiken werden als horizontale Linien und Textbeschriftungen im Chart angezeigt und als globale Variablen mit dem Präfix S_base exportiert, damit sie von anderen Skripten oder Indikatoren gelesen werden können.

Snapshotting und Überwachung auf Referenzniveau

Wenn AutoSnapshotLevels aktiviert ist, sperrt der EA einen einzelnen Snapshot, der die aktuellen Pegelschätzungen (Mittelwert, Mittelwert±sd, P25, P75, Median, Modi) enthält und ein Array refLevels[] erzeugt, das aus RefLevel-Strukturen besteht. Jedes RefLevel enthält name, price, touched, touchTime, monitorLeft, highest, lowest, result (0 unknown, 1 breakout, -1 reversal, 2 no-follow), und resolvedTime. Snapshot-HLINEs heißen S_base + „_REF_“ + name und aktualisieren entweder kanonische TXT-Objekte (wenn ein kanonisches Label existiert) oder verwenden REF-spezifische Kennzeichnungen.

// take snapshot (single-shot)
void SnapshotReferenceLevels(double mean_val, double p25, double p75, double median_val, double mode_b, double mode_k)
  {
   snapshot_mean = mean_val;
   snapshot_p25  = p25;
   snapshot_p75  = p75;
   snapshot_median= median_val;
   // build refLevels
   ArrayResize(refLevels, 6);
   refLevels[0].name = "MEAN"; refLevels[0].price = snapshot_mean; refLevels[0].touched=false; refLevels[0].result=0;
   // ... fill others ...
   refSnapshotTaken = true;
   snapshotTakenTime = TimeCurrent();
  }

// monitor reference levels (called from OnTick)
void MonitorReferenceLevels(const MqlRates &rates[], int copied)
  {
   if(!refSnapshotTaken || copied <= 0) return;
   double barHigh = rates[0].high;
   double barLow  = rates[0].low;
   double barClose= rates[0].close;
   double pipPoints = pipToPointMultiplier();
   double touchTol = TouchTolerancePips * pipPoints;
   // compute thresholds (fixed or ATR-scaled)
   double breakoutThreshold = BreakoutPips * pipPoints;
   if(UseATRforThresholds)
     {
      int hATR = iATR(_Symbol, TF, ATRperiod);
      double atrBuf[];
      CopyBuffer(hATR,0,0,1,atrBuf);
      IndicatorRelease(hATR);
      breakoutThreshold = atrBuf[0] * ATRMultiplier;
     }

   for(int i=0;i<ArraySize(refLevels);i++)
     {
      RefLevel L = refLevels[i];
      if(L.result != 0) continue;
      if(!L.touched)
        {
         if(barHigh >= L.price - touchTol && barLow <= L.price + touchTol)
           {
            L.touched = true;
            L.touchTime = rates[0].time;
            L.monitorLeft = MonitorBars;
            L.highest = barHigh; L.lowest = barLow;
            refLevels[i] = L;
           }
        }
      else
        {
         // update highest/lowest and evaluate breakout/reversal
         if(barHigh > L.highest) L.highest = barHigh;
         if(barLow  < L.lowest)  L.lowest  = barLow;
         bool breakout = (L.highest >= L.price + breakoutThreshold);
         bool reversal = (L.lowest  <= L.price - breakoutThreshold);
         if(breakout && !reversal) { L.result = 1; L.resolvedTime = rates[0].time; DrawOutcome(L, true); }
         else if(reversal && !breakout) { L.result = -1; L.resolvedTime = rates[0].time; DrawOutcome(L, false); }
         else { if(--L.monitorLeft <= 0) { L.result = 2; L.resolvedTime = rates[0].time; DrawOutcome(L, false); } }
         refLevels[i] = L;
        }
     }
  }

Die Überwachung ist in MonitorReferenceLevels implementiert. Für jede nicht aufgelöste Referenz wird der Höchst-/Tiefst-/Schlusskurs des letzten Balkens mit einer Berührungstoleranz (TouchTolerancePips, die mit pipToPointMultiplier() in Preiseinheiten umgewandelt werden) verglichen. Eine Berührung setzt monitorLeft = MonitorBars und zeichnet den anfänglichen Höchst-/Tiefstwert auf. Während des Überwachungsfensters verfolgt der EA die höchsten und niedrigsten Preise und bewertet die Ausbruchs- und Umkehrbedingungen. Schwellenwerte sind entweder feste Pip-Werte oder von ATR abgeleitet, wenn UseATRforThresholds wahr ist; ATR wird über iATR + CopyBuffer ermittelt und mit ATRMultiplier skaliert, um adaptive Schwellenwerte zu erzeugen. Eine optionale Bestätigung durch den Schlusskurs des Balken (UseCloseForConfirm) wird unterstützt. Die Ergebnisse werden entweder sofort bei der Bestätigung oder am Ende des Überwachungsfensters durch den Vergleich der beobachteten Extremwerte mit den Schwellenwerten ermittelt und anschließend aufgezeichnet und über DrawOutcome gezeichnet.

Bildmaterial und Platzierung von Kennzeichnungen

Der EA bevorzugt stabile, sich nicht überschneidende Chart-Anmerkungen. Horizontale Linien für Statistiken und Snapshot-Referenzen verwenden CreateHLine, das vorhandene Objekte aktualisiert, falls vorhanden, und einen Zeitstempel für die Metadaten setzt. Textbeschriftungen werden von CreateOrUpdateLineText behandelt, einer Platzierungsroutine, die versucht, das Ziel von Zeit & Preis über ChartTimePriceToXY auf Bildschirmkoordinaten abzubilden.

void CreateOrUpdateLineText(string name, datetime t, double price, string text)
  {
   long chart_id = ChartID();
   int x0 = 0, y0 = 0;
   bool ok = ChartTimePriceToXY(chart_id, 0, t, price, x0, y0);
   int fontSize = 10;
   int pixelThresh = MathMax(18, fontSize * 2);

   // collect used Y positions from existing OBJ_TEXT objects
   int usedYPositions[];
   ArrayResize(usedYPositions,0);
   int total = ObjectsTotal(0);
   for(int oi=0; oi<total; oi++)
     {
      string oname = ObjectName(0, oi);
      if(oname == name) continue;
      if(ObjectGetInteger(0, oname, OBJPROP_TYPE) != OBJ_TEXT) continue;
      long ot = (long)ObjectGetInteger(0, oname, OBJPROP_TIME);
      double op = ObjectGetDouble(0, oname, OBJPROP_PRICE);
      int xp=0, yp=0;
      if(ChartTimePriceToXY(chart_id,0,(datetime)ot,op,xp,yp))
        {
         ArrayResize(usedYPositions, ArraySize(usedYPositions)+1);
         usedYPositions[ArraySize(usedYPositions)-1] = yp;
        }
     }

   // attempt to find free Y slot
   int chosenY = y0;
   if(!IsYFree(chosenY, usedYPositions, pixelThresh))
     {
      int step = pixelThresh;
      bool found = false;
      for(int s=1; s<=20 && !found; s++)
        {
         int yUp = y0 - s*step;
         if(yUp >= 0 && IsYFree(yUp, usedYPositions, pixelThresh)) { chosenY = yUp; found = true; break; }
         int yDn = y0 + s*step;
         if(IsYFree(yDn, usedYPositions, pixelThresh)) { chosenY = yDn; found = true; break; }
        }
     }

   // convert chosen XY back to time/price; fallback if needed
   datetime tt = t; double pp = price;
   if(!ChartXYToTimePrice(chart_id, 0, x0, chosenY, tt, pp))
     { // fallback: nudge price slightly
      double point = SymbolInfoDouble(_Symbol, SYMBOL_POINT);
      int slotDelta = (chosenY - y0) / pixelThresh;
      pp = price + slotDelta * pixelThresh * point;
     }

   // create or update the OBJ_TEXT
   KeepSingleTextLabel(name);
   if(ObjectFind(0, name) >= 0)
     {
      ObjectSetInteger(0, name, OBJPROP_TIME, (long)tt);
      ObjectSetDouble(0, name, OBJPROP_PRICE, pp);
      ObjectSetString(0, name, OBJPROP_TEXT, text);
     }
   else
     {
      ObjectCreate(0, name, OBJ_TEXT, 0, tt, pp);
      ObjectSetString(0, name, OBJPROP_TEXT, text);
     }
   SetObjTimestamp(name);
  }

Sie sammelt die Y-Pixel-Positionen vorhandener OBJ_TEXT-Objekte (und kanonischer statistischer TXT-Peers), damit neue Beschriftungen nicht kollidieren.

Sie sucht in Pixelschritten (abgeleitet von der Schriftgröße) nach oben/unten, um einen freien Platz zu finden (IsYFree) und konvertiert den gewählten XY-Slot mit ChartXYToTimePrice zurück in Zeit & Preis. Wenn Konvertierungen fehlschlagen, ändert ein robuster Ausweichlösung die Position ungefähr, um Abstürze zu vermeiden.

Sie erzwingt ein _TXT-Objekt für jede HLINE mit KeepSingleTextLabel.

Dieser Ansatz führt zu lesbaren Beschriftungen mit minimalem Zittern beim Scrollen des Charts oder bei der Größenänderung. Signal- und Ergebnispfeile werden mit DrawArrowAt gezeichnet, das auch eine dünne, exakte HLINE am Pfeilpreis erstellt, um eine genaue Ausrichtung zu gewährleisten.

Histogramm und KDE

DrawHistogram berechnet ein Häufigkeitshistogramm typischer Preise über ModeBins, zeichnet HLINEs in den Bin-Mitten mit einer zur Anzahl proportionalen Breite und erstellt kompakte Zähletiketten. ModeBins berechnet eine schnelle modale Schätzung, indem es den Mittelpunkt des am stärksten besetzten Wertes zurückgibt. ModeKDE liefert eine glattere modale Schätzung, indem es eine naive Kernel-Dichte-Schätzung über ein nutzerspezifisches Raster durchführt; seine Berechnungskomplexität ist O(n × gridPts) und sollte daher auf die gewählte Lookback- und Intrabar-Rate abgestimmt werden.

// histogram drawing (bin counts => HLINE widths)
void DrawHistogram(const double &arr[], int n, int bins, int maxWidth)
  {
   double minv = ArrayMin(arr, n);
   double maxv = ArrayMax(arr, n);
   double binw = (maxv - minv) / bins;
   int counts[]; ArrayResize(counts, bins); ArrayInitialize(counts,0);
   for(int i=0;i<n;i++)
     {
      int b = (int)MathFloor((arr[i]-minv)/binw);
      if(b < 0) b=0; if(b >= bins) b=bins-1;
      counts[b]++;
     }
   // draw HLINE per bin with width proportional to counts[b]
  }

// KDE-based modal estimate
double ModeKDE(const double &a[], int n, int gridPts, double bwFactor)
  {
   double mn = ArrayMin(a,n), mx = ArrayMax(a,n);
   double sd = MathSqrt(Variance(a, n, false));
   double h = 1.06 * sd * MathPow((double)n, -0.2);
   if(h <= 0) h = (mx - mn) / 20.0;
   h *= bwFactor;
   double bestX = mn, bestD = -1.0;
   const double SQRT2PI = 2.5066282746310002;
   for(int g=0; g<gridPts; g++)
     {
      double x = mn + (double)g/(gridPts-1) * (mx - mn);
      double s = 0.0;
      for(int i=0;i<n;i++)
        {
         double u = (x - a[i]) / h;
         s += MathExp(-0.5 * u * u);
        }
      double dens = s / (n * h * SQRT2PI);
      if(dens > bestD) { bestD = dens; bestX = x; }
     }
   return(bestX);
  }

Metadaten und Lebenszyklusmanagement

Jedes erstellte Diagrammobjekt ist mit einem Metadaten-Zeitstempel verbunden, der in einer globalen Variablen mit dem Schlüssel S_base + „_META_“ + objectName über SetObjTimestamp gespeichert wird. Dies ermöglicht RemoveOldObjects (aufgerufen in OnTimer), eine Liste von Kandidatenobjekten zu scannen und diejenigen zu löschen, die älter als CleanupIntervalSeconds sind, um visuelle Unordnung in lang laufenden Diagrammen zu vermeiden. RemoveExistingEAObjects und CleanupAllMetaGlobals unterstützen eine kontrollierte Initialisierung und einen kontrollierten Abriss durch das Entfernen früherer Objekte und ihrer Metadaten.

// store timestamp meta
void SetObjTimestamp(string name)
  {
   string g = S_base + "_META_" + name;
   GlobalVariableSet(g, (double)TimeCurrent());
  }

// read meta timestamp
datetime GetObjTimestamp(string name)
  {
   string g = S_base + "_META_" + name;
   if(GlobalVariableCheck(g)) return (datetime)GlobalVariableGet(g);
   return 0;
  }

// remove objects older than ageSec
void RemoveOldObjects(int ageSec)
  {
   datetime now = TimeCurrent();
   string candidates[] = { S_mean, S_mean + "_TXT", S_p25, S_p25 + "_TXT", S_panel /* ... */ };
   for(int j=0;j<ArraySize(candidates);j++)
     {
      string nm = candidates[j];
      datetime ts = GetObjTimestamp(nm);
      if(ts == 0) continue;
      if((int)(now - ts) >= ageSec)
        {
         if(ObjectFind(0, nm) >= 0) ObjectDelete(0, nm);
         string g = S_base + "_META_" + nm;
         if(GlobalVariableCheck(g)) GlobalVariableDel(g);
        }
     }
  }

Warnmeldungen und Signalverarbeitung

Z-Score-Signale werden bei jedem Tick ausgewertet und unterliegen AllowLongSignals bzw. AllowShortSignals. ZScoreSignalEnter ist die Schwelle zum Eröffnen und ZScoreSignalExit die zum Schließen. Bei einer Änderung des Signalzustands zeichnet EmitAlertWithArrow den Diagrammpfeil und löst optional Plattformwarnungen (Alert()), Töne (PlaySound()) und Push-Benachrichtigungen (SendNotification()) aus, während entgegengesetzte Signalpfeile entfernt werden, um das Rauschen auf dem Chart zu begrenzen.

// z-score signal logic (called from OnTick after stats computed)
int newSig = currentSignal;
if(zscore >= ZScoreSignalEnter && AllowLongSignals) newSig = 1;
else if(zscore <= -ZScoreSignalEnter && AllowShortSignals) newSig = -1;
else if(currentSignal == 1 && zscore < ZScoreSignalExit) newSig = 0;
else if(currentSignal == -1 && zscore > -ZScoreSignalExit) newSig = 0;

if(newSig != currentSignal)
  {
   if(newSig == 1)
     EmitAlertWithArrow("CSTATS LONG " + _Symbol + " z=" + DoubleToString(zscore,3), t_now, latest, true, S_arrow_long);
   else if(newSig == -1)
     EmitAlertWithArrow("CSTATS SHORT " + _Symbol + " z=" + DoubleToString(zscore,3), t_now, latest, false, S_arrow_short);
   else // clear arrows on exit
     {
      if(ObjectFind(0, S_arrow_long) >= 0) ObjectDelete(0, S_arrow_long);
      if(ObjectFind(0, S_arrow_short) >= 0) ObjectDelete(0, S_arrow_short);
     }
   currentSignal = newSig;
  }

// emit alert helper
void EmitAlertWithArrow(string message, datetime when, double price, bool isBuy, string arrowName)
  {
   DrawArrowAt(arrowName, when, price, isBuy);
   if(SendAlertOnSignal) Alert(message);
   if(PlaySoundOnSignal) PlaySound(SoundFileOnSignal);
   if(SendPushOnSignal) SendNotification(message);
  }

Statistische Hilfsmittel und numerische Überlegungen

Der Code implementiert standardmäßige Array-basierte Statistiken: Mittelwert, gewichteter Mittelwert, Stichprobenvarianz, Median (einschließlich Even-n-Mittelung) und linear-interpolierte Perzentile – angepasst an die MQL5-Array-Semantik. Hilfsroutinen berechnen Schiefe und Kurtosis, falls dies für die Erweiterung erforderlich ist. In der Praxis sollten die KDE-Auflösung (KDEGridPoints) und die Bandbreite (KDEBandwidthFactor) so gewählt werden, dass ein Gleichgewicht zwischen Glätte, Genauigkeit und CPU-Kosten besteht. Die Erstellung und Freigabe von ATR-Handles erfolgt pro Auswertung; für eine hochfrequente Ausführung wird die Wiederverwendung von Indikator-Handles oder die Berechnung von ATR nur bei einem neuen Balken empfohlen, um den Overhead zu reduzieren.

double Mean(const double &a[], int n)
  {
   if(n<=0) return 0.0;
   double s=0.0;
   for(int i=0;i<n;i++) s += a[i];
   return s / n;
  }

double WeightedMean(const double &a[], const double &w[], int n)
  {
   if(n<=0) return 0.0;
   double sw=0.0, s=0.0;
   for(int i=0;i<n;i++) { s += a[i] * w[i]; sw += w[i]; }
   if(sw == 0.0) return Mean(a, n);
   return s / sw;
  }

double Variance(const double &a[], int n, bool sample)
  {
   if(n <= 1) return 0.0;
   double mu = Mean(a,n), s = 0.0;
   for(int i=0;i<n;i++) { double d = a[i] - mu; s += d * d; }
   return sample ? s / (n-1) : s / n;
  }

double Median(const double &a[], int n)
  {
   if(n <= 0) return 0.0;
   double tmp[]; ArrayResize(tmp, n); ArrayCopy(tmp, a); ArraySort(tmp);
   if((n % 2) == 1) return tmp[n/2];
   return (tmp[n/2 - 1] + tmp[n/2]) / 2.0;
  }

double Percentile(const double &a[], int n, double q)
  {
   if(n <= 0) return 0.0;
   double tmp[]; ArrayResize(tmp, n); ArrayCopy(tmp, a); ArraySort(tmp);
   if(q <= 0.0) return tmp[0];
   if(q >= 1.0) return tmp[n-1];
   double idx = q * (n - 1);
   int i0 = (int)MathFloor(idx); double frac = idx - i0;
   if(i0 + 1 < n) return tmp[i0] * (1.0 - frac) + tmp[i0+1] * frac;
   return tmp[i0];
  }

Ergebnisse

In diesem Abschnitt wird die Leistung des EA auf dem Chart untersucht. Es ist wichtig, das System gründlich zu testen, sowohl durch Backtests als auch auf einem Demokonto, bevor man es mit echtem Kapital einsetzt, denn Live-Signale können selbst disziplinierte Händler zu voreiligen Handelsgeschäften verleiten. Der EA zeigt ein kompaktes Metrik-Panel an und zeichnet horizontale Referenzlinien für jede berechnete Statistik; jede Linie enthält eine Textbeschriftung, die ihre Bedeutung beschreibt (Mittelwert, Median, Modi, P25/P75, usw.). Anhand dieser visuellen Hinweise lässt sich leicht beurteilen, wie der Preis mit statistisch aussagekräftigen Niveaus interagiert, und das Verhalten des EA in historischen und zukünftigen Tests validieren.

Die nachstehende Abbildung zeigt das statistische Panel des EA und die entsprechenden horizontalen Ebenen, die auf dem Stufenindex (M5) aufgetragen sind. Der Mittelwert und der gewichtete Mittelwert konvergieren bei 8114,8 und bilden einen stabilen zentralen Gleichgewichtspunkt. Die Standardabweichung (15,6) deutet auf eine mäßige Volatilität innerhalb der aktuellen Stichprobe hin, während der Median (8113,3) nahe am Mittelwert bleibt, was eine symmetrische Verteilung der Preise widerspiegelt. Sowohl der diskrete Modus (8112,4) als auch der von der KDE geschätzte Modus (8113,2) gruppieren sich knapp unter dem Mittelwert und markieren eine dichte Handelszone, die als natürliche Unterstützungs-/Widerstandsregion fungiert. Die Perzentile (P25 = 8105,7, P75 = 8121,6) bilden den Interquartilsbereich von 16 Punkten ab, der die mittleren 50 % der Aktivität einrahmt und das Konsolidierungsband hervorhebt, in dem die Preise am häufigsten schwanken. Schließlich zeigt der z-Score (2,676), dass sich der Kurs mehr als zwei Standardabweichungen über dem Mittelwert bewegt hat, was auf eine vorübergehende Übertreibung hindeutet und die Wahrscheinlichkeit einer Mittelwertumkehr erhöht.

Zusammengenommen zeigen diese Ergebnisse, wie statistische Werte, die aus dem typischen Preis abgeleitet werden, als handlungsrelevante Referenzpunkte dienen können. Die Anzeige des EA auf dem Chart ermöglicht es Händlern, visuell zu bestätigen, ob das Marktverhalten diese Zonen respektiert, ablehnt oder übersteigt, was es einfacher macht, Handelsentscheidungen an objektiv gemessenen Strukturen statt an subjektiven Einschätzungen auszurichten.

Schlussfolgerung

Der EA berechnet die Verteilungsreferenzniveaus aus dem typischen Preis (TP = (H+L+C)/3) und veröffentlicht sie direkt im Chart: beschriftete horizontale Linien (Mittelwert, gewichteter Mittelwert, Median, Bin- & KDE-Modi, P25/P75), ein kompaktes Metrik-Panel und visuelle Signale (Pfeile, Touch/Outcome-Marker). Es exportiert auch globale Variablen für die programmatische Verwendung und enthält eine Überwachungslogik, die Berührungen aufzeichnet und die Ergebnisse als Ausbruch, Umkehr oder No-Follow klassifiziert.

Diese Niveaus wandeln die Clusterbildung, die zentrale Tendenz und die Streuung in objektive Referenzpunkte auf dem Chart um, die Sie auf einen Blick erkennen können. Verwenden Sie sie als Entscheidungshilfe: Bestätigen Sie, wie der Preis mit diesen Zonen interagiert, bevor Sie handeln, und betrachten Sie die Ausgaben des EA als Kontext, nicht als automatische Handelsausführung. In zukünftigen Projekten werden wir fortgeschrittenere statistische Methoden und Ensemble-Techniken erforschen, um die Stabilität der Pegel und die Vorhersagekraft zu verbessern.

Siehe meine anderen Artikel.