Einführung in MQL5 (Teil 20): Einführung in „Harmonic Patterns“
91
0
Einführung
Willkommen zurück zu Teil 20 der Serie Einführung in MQL5! In diesem Teil werden wir ein weiteres fortgeschrittenes Chartmuster untersuchen, das harmonische Muster. Diese Muster stützen sich auf präzise Fibonacci-Verhältnisse, um potenzielle Umkehrzonen abzubilden, und sind in der technischen Analyse weithin anerkannt.
Wenn Sie versucht haben, dieses Konzept im Detail zu verstehen, ist dieser Artikel genau das Richtige für Sie. Dieser Artikel führt Sie in das Konzept ein und behandelt die Struktur harmonischer Muster sowie die wesentlichen Fibonacci-Extension- und Retracement-Tools, die zur Definition dieser Muster verwendet werden.
Wir werden die wesentlichen Elemente einiger der bekanntesten harmonischen Strukturen erforschen, darunter das Gartley-, Fledermaus-, Schmetterlings- und Krebsmuster, sowie die genauen Fibonacci-Messungen, die sie definieren. Da schon eine geringe Abweichung das Setup ungültig machen kann, ist es wichtig, diese Verhältnisse zu verstehen. Der nächste Artikel wird sich darauf konzentrieren, dieses Wissen zu nutzen, um es programmatisch auf MQL5 anzuwenden, was die automatische Identifizierung von bärischen und bullischen harmonischen Mustern ermöglicht.
In diesem Artikel erfahren Sie mehr über Folgendes:
- Die Grundlagen der harmonischen Muster und wie sie beim Handel angewendet werden.
- Mathematische Konzepte hinter den Fibonacci-Retracements und warum sie für die Mustererkennung wichtig sind.
- Wie Fibonacci-Erweiterungen funktionieren und welche Rolle sie bei der Bestimmung potenzieller Kursziele spielen.
- Implementierung der Erkennung harmonischer Muster in MQL5, einschließlich der programmatischen Verwendung von Fibonacci-Verhältnissen.
- Die Struktur der verschiedenen harmonischen Muster und wie man sie in einem Chart erkennt
Fibonacci-Erweiterung und -Retracement
Sie müssen die Fibonacci-Extension und das Fibonacci-Retracement verstehen, bevor wir das Konzept der harmonischen Muster diskutieren können. Die Objekte Fibonacci Retracement und Fibonacci Extension sind Ihnen wahrscheinlich aus Ihrer MetaTrader 5 Toolbox bekannt, aber haben Sie sich jemals gefragt, welche mathematischen Formeln zur Bestimmung dieser Levels verwendet werden?
Wenn ja, dann ist das fantastisch; in diesem Abschnitt werden Sie mehr erfahren. Wenn nicht, keine Sorge, ich kümmere mich um Sie. Am Ende dieser Diskussion werden Sie genau wissen, wie diese Fibonacci-Levels bestimmt werden und warum sie für die Erkennung harmonischer Muster entscheidend sind.
Fibonacci RetracementSowohl Fibonacci-Retracement als auch Extension arbeiten mit Prozentsätzen. Man kann sich das so vorstellen, dass man damit misst, wie viel der Markt „zurückgekommen“ oder über sich „hinausgewachsen“ ist. Nehmen wir ein einfaches Beispiel. Stellen Sie sich vor, der Markt macht ein deutliches Hin und Her, erst ein tiefer Umkehrpunkt, dann ein hoher.
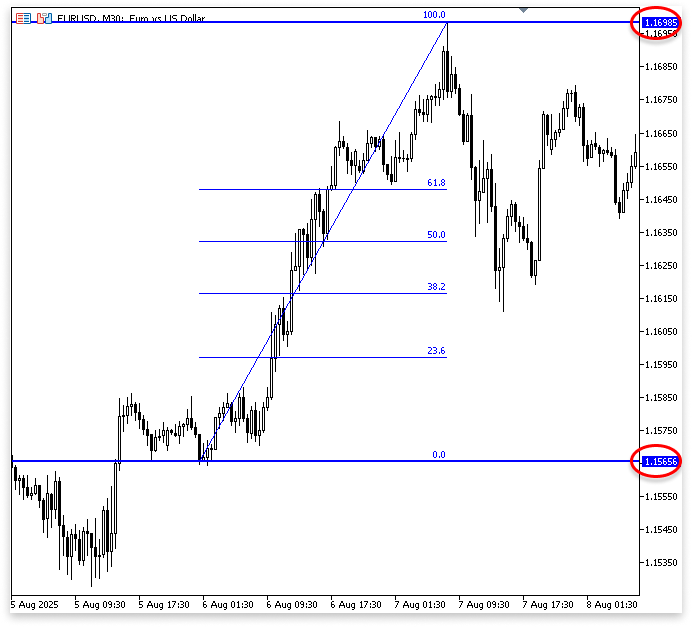
Um die Fibonacci-Retracement-Levels zu berechnen, wird die Differenz zwischen diesen beiden Punkten (die Höhe der Bewegung) herangezogen.
Beispiel:
double price_differecence; double swing_high; double swing_low; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- //--- return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- } //+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- swing_high = 1.16985; swing_low = 1.15656; price_differecence = swing_high - swing_low; }
Ziehen Sie immer swing_low von swing_high ab, um eine positive Preisdifferenz zu erhalten. Die umgekehrte Reihenfolge ergibt einen negativen Wert.
Was würde passieren, wenn der Markt auf halbem Weg von diesem Höchststand aus eine Kehrtwende machen würde? Es handelt sich um ein 50%-Retracement. Er zeigt an, dass die Hälfte der Aufwärtsbewegung des Kurses wieder zurückgenommen wurde.
Beispiel:
double price_diff_50_percent; //+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- swing_high = 1.16985; swing_low = 1.15656; price_differecence = swing_high - swing_low; price_diff_50_percent = (50.0/100.0) * price_differecence; // (Fibonacci Retracement level / 100) * Price Difference }
In dieser Zeile werden 50 % der gesamten Preisdifferenz berechnet, und die Berechnung wird als Fließkommadivision durchgeführt, da 50,0 und 100,0 verwendet werden und nicht einfache Ganzzahlen. Da eine Gleitkommadivision einen genauen Dezimalwert ergibt, ist dies von Bedeutung. Einige Computersprachen würden 50/100 als ganzzahlige Division lesen, wenn wir es in ganzen Zahlen ausgedrückt hätten.
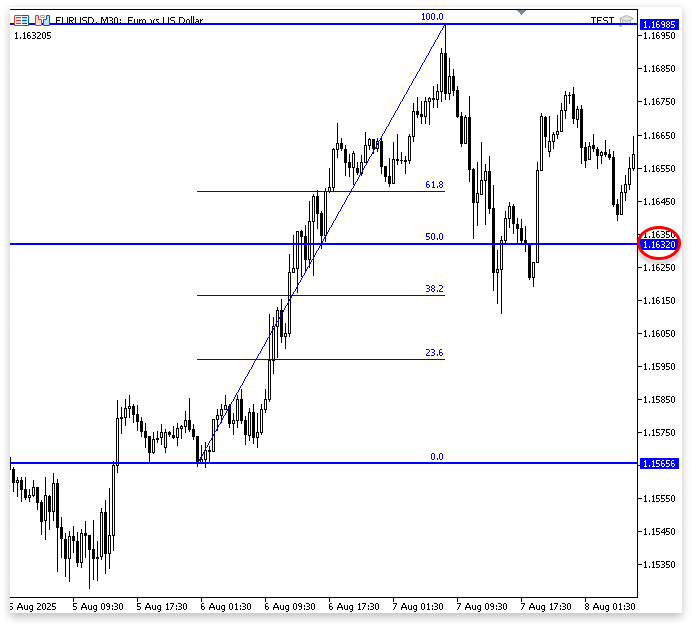
Stellen Sie sich vor, Sie gehen zehn Stufen auf einer Treppe hinauf. Sie haben die Hälfte Ihres Aufstiegs zurückgelegt, wenn Sie fünf Schritte zurückgehen. Sie können bestimmte Prozentsätze im Fibonacci-Retracement betrachten. An diesen Niveaus, die häufig als unsichtbare Unterstützungs- oder Widerstandszonen fungieren, kann der Kurs innehalten oder umkehren. Nach den Fibonacci-Proportionen hat der Kurs einfach fast zwei Drittel des Weges vom hohen zum tiefen Umkehrpunkt zurückgelegt, wenn Sie hören: „Der Markt ist bis zum 61,8 %-Niveau zurückgekehrt.“
Fibonacci-ErweiterungDie Fibonacci-Extension konzentriert sich auf die Einschätzung, wie weit die nächste Bewegung über den anfänglichen Bewegung hinausgehen könnte, während das Fibonacci-Retracement vor allem dazu dient, abzuschätzen, wie weit der Markt von einer früheren Bewegung zurückgekommen ist. Obwohl beide Werte in Prozent ausgedrückt sind, übersteigen die Erweiterungsstufen die ursprünglichen Bewegung um 100 Prozent.
Wenn Sie etwas auf dem Markt messen wollen, können Sie Fibonacci-Erweiterungen auf zwei verschiedene Arten verwenden.
Erstes Szenario (Standardeinsatz mit Retracement):
Bei der normalen Anwendung erfordert das Fibonacci-Extension-Tool, dass der Markt einen Rückschritt macht, bevor die Extension-Levels eingezeichnet werden. Hier werden Sie drei Anker verwenden:
- Der erste Anker wird am Punkt X gesetzt.
- Der zweite Anker wird am Punkt A gesetzt.
- Der dritte Anker wird am Punkt B gesetzt, wobei B ein Retracement der XA-Bewegung ist.
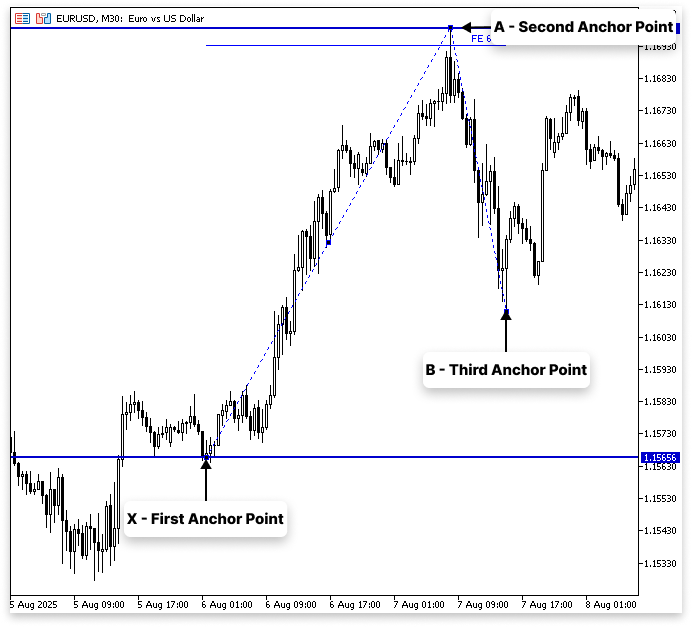
Wir beginnen im ersten Szenario der Fibonacci-Extensions mit einem Kursausschlag, den wir als XA bezeichnen. In diesem Fall stehen X und A für den Anfangs- bzw. Endpunkt des Zuges. In der Regel geht der Markt nach dieser ersten Kursbewegung bis zum Punkt B zurück, der auf halbem Weg zwischen X und A liegt. X, A und B sind die drei Anker, die wir zur Berechnung der Fibonacci-Erweiterungen verwenden. Das Erweiterungs-Tool gibt Ihnen ein Gefühl dafür, wohin sich der Markt entwickeln könnte, sobald der Rücksetzer abgeschlossen ist, indem es mögliche Kursziele über Punkt A hinaus projiziert.
Mathematisch berechnet man zunächst die Preisdifferenz zwischen X und A:
price difference=A−X
Dies ergibt die Gesamtgröße der Bewegung XA. Als Nächstes nehmen wir das gewählte Fibonacci-Erweiterungsverhältnis, z. B. 61,8 %, und drücken es als Dezimalzahl aus, indem wir es durch 100 dividieren:
fibo ratio= 61.8/100.0
Nun multiplizieren wir dieses Verhältnis mit der Preisdifferenz, um zu ermitteln, wie weit die Verlängerung über Punkt A hinausgehen wird:
extension distance = fibo ratio×price difference
Schließlich addieren wir diese Ausdehnungsdistanz zu Punkt B, um das Fibonacci-Ausdehnungsniveau zu erhalten:
fibo extension = B+extension distance
In der Praxis bedeutet dies, dass das Erweiterungs-Tool vorhersagt, wo die nachfolgende Aufwärtsbewegung über A hinaus enden könnte, wenn XA eine Aufwärtsbewegung ist und B ein Retracement dieser Bewegung ist. Auch in einem negativen Markt hilft das Erweiterungs-Tool bei der Lokalisierung möglicher Abwärtsziele außerhalb von A. Fibonacci-Erweiterungen sind dank dieses mathematischen Verfahrens garantiert systematische Prognosen, die auf proportionalen Beziehungen innerhalb des Preisschwungs basieren und nicht nur auf zufälligen Linien auf einem Chart.
Zweites Szenario (direkte Verwendung in harmonischen Mustern):
Die Fibonacci-Extension wird bei der Arbeit mit harmonischen Mustern anders als das herkömmliche Retracement angewendet. Der erste Anker wird am Punkt X und der zweite und dritte Anker am Punkt A positioniert, anstatt das Werkzeug für einen Rückzug zu verwenden. Anstatt Korrekturen zu messen, konzentriert sich dieses Setup auf die Schätzung zukünftiger Kursziele.
Obwohl die Fibonacci-Extension und das Retracement in diesem Fall vergleichbar zu sein scheinen, sind sie es nicht. Wenn es sich bei Punkt A um einem hohen Umkehrpunkt handelt, ziehen wir oft den Fibonacci-Prozentsatz der Strecke XA davon ab; wenn es sich um ein tiefen Umkehrpunkt handelt, addieren wir ihn. Bei Verlängerungen wird jedoch der Wert addiert und nicht abgezogen, wenn Punkt A ein hoher Umkehrpunkt (swing high) ist; es handelt sich also eher um eine Verlängerung als um ein Retracement.
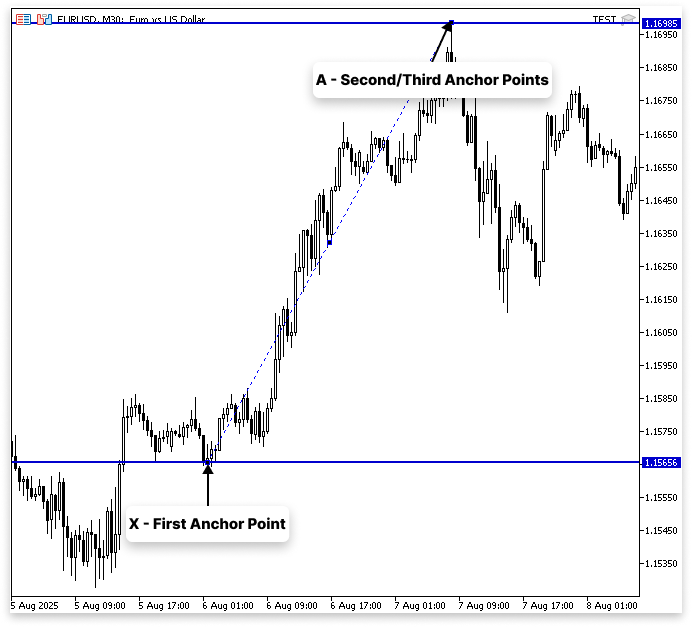
Beispiel:
double price_differecence; double swing_high; //A double swing_low; //X double price_diff_161_8_percent; double fibo_extension_161_8; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- //--- return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- } //+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- swing_high = 1.16985; swing_low = 1.15656; price_differecence = swing_high - swing_low; price_diff_161_8_percent = (61.8/100.0) * price_differecence; fibo_extension_161_8 = swing_high + price_diff_161_8_percent; }
Zum Beispiel wird X zu A als 100 % angesehen. Das Fibonacci-Niveau von XA liegt bei 61,8 Prozent, was uns eine Erweiterung über Punkt A hinaus bietet. Wenn der Wert zu Punkt A addiert wird, anstatt ihn zu subtrahieren, ergibt sich ein Niveau von 161,8. Aus diesem Grund werden Ausdehnungen wie 127,2 oder 161,8 häufig in harmonischen Mustern verwendet; sie sind keine Rückschritte innerhalb der ursprünglichen XA-Bewegung, sondern ragen über diese hinaus.
Diese Methode macht einen tatsächlichen Rückzug von XA überflüssig und erleichtert die Identifizierung des wahrscheinlichen Ortes des nachfolgenden Schwungs in harmonischen Mustern. Vielmehr wird die Kursbewegung von X nach A mathematisch gestreckt, und diese Prognosen helfen bei der Bestimmung entscheidender Punkte, an denen der Markt umkehren oder die harmonische Struktur beenden kann.
Harmonisches Muster
Es ist viel einfacher, harmonische Muster zu diskutieren, nachdem die Ideen des Fibonacci-Retracements und der Fibonacci-Extension geklärt sind. Das liegt daran, dass die Fibonacci-Verhältnisse die Grundlage aller harmonischen Muster sind. In der Tat ist es das Ausmaß, in dem die Kursschenkel bestimmten Fibonacci-Retracement- und Verlängerungsniveaus entsprechen, das neben dem Erscheinungsbild des Musters auf dem Chart jedes harmonische Muster auszeichnet.
Geometrische Preisstrukturen, die sich über verschiedene Zeiträume hinweg wiederholen, werden als harmonische Muster bezeichnet. Sie bestehen aus aufeinanderfolgenden Schwüngen oder Schenkeln, wie XA, AB, BC und CD, und um das Muster zu bestätigen, muss jeder Schenkel die exakten Fibonacci-Anforderungen erfüllen. Harmonische Muster sind anders und objektiver als einfache Chartmuster wie Dreiecke oder Flaggen, da sie sich in hohem Maße auf mathematische Verhältnisse stützen.
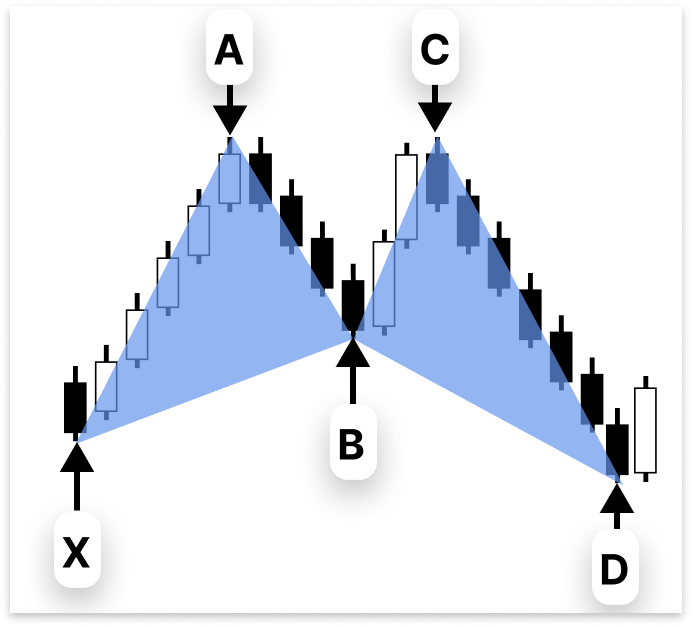
Die Muster Gartley, Fledermaus, Schmetterling und Krabbe sind einige der beliebtesten harmonischen Muster. Die Verbindung zwischen den Beinen wird durch ein einzigartiges Fibonacci-“Rezept“ für jedes dieser Muster definiert. Damit ein Muster als legitim angesehen werden kann, muss zum Beispiel das Retracement von AB im Verhältnis zu XA oder die Ausdehnung von CD im Verhältnis zu BC innerhalb bestimmter Fibonacci-Spannen liegen und darf nicht willkürlich sein.
Das Harmonische Muster des SchmetterlingsBei einem typischen Schmetterlingsmuster beginnt das erste Bein von Punkt X nach A, was die anfängliche Kursbewegung darstellt.
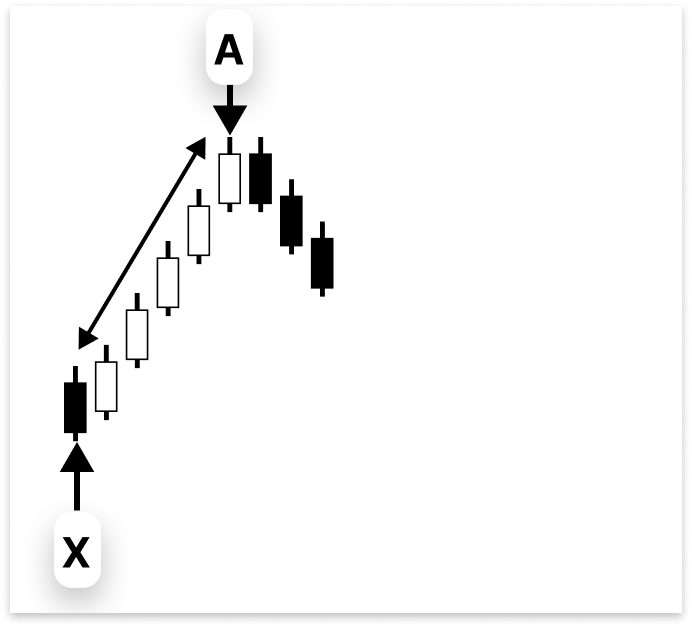
Punkt B sollte die Strecke A-B zwischen 76 % und 79 % der Strecke von X-A zurückverfolgen. Auch wenn 78,6 % häufig als „ideales“ Retracement genannt wird, erreicht der Kurs nur selten genau dieses Niveau. Aus diesem Grund ist es sicherer, einen Bereich anstelle eines Festpunkts zu verwenden.
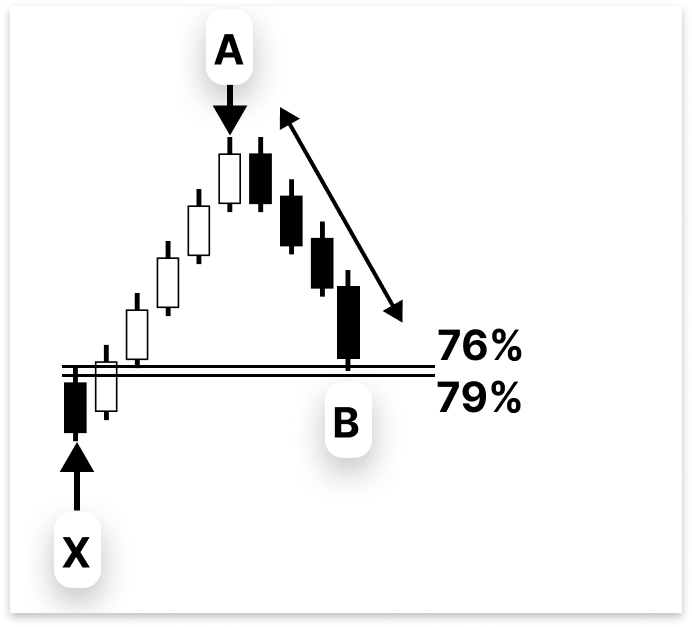
Beispiel:
double swing_low_x; //X double swing_high_x; //A double price_differecence; double fib_ret_79; double fib_ret_76; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- //--- return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- } //+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- swing_low_x = 1.15656; swing_high_x = 1.16985; price_differecence = swing_high_a - swing_low_x; fib_ret_79 = swing_high_x - ((79.0/100.0) * price_differecence); fib_ret_76 = swing_high_x - ((76.0/100.0) * price_differecence); /* if(B <= fib_ret_76 && B>= fib_ret_79) { } */ }
Erläuterung:
Dieser Algorithmus berechnet die Fibonacci-Retracement-Levels zwischen den Umkehrpunkten X und A und legt damit den Grundstein für die Lokalisierung von Punkt B in einem harmonischen Fledermaus-Muster. Die Preisdifferenz wird ermittelt, und die 79 %- und 76 %-Retracement-Niveaus werden berechnet, um den Bereich zu bestimmen, in dem sich Punkt B idealerweise bilden sollte.
Nach der Berechnung der Retracement-Levels können wir den Preis des B-Punktes mit dieser Spanne vergleichen. In dem kommentierten Block:
if(B <= fib_ret_76 && B >= fib_ret_79) { } Diese Bedingung bestimmt, ob der B-Punkt innerhalb des Retracements der angegebenen XA-Strecke liegt. Der Punkt B erfüllt die Regeln des harmonischen Fledermaus-Musters, wenn die Bedingung erfüllt ist. In diesem Fall können wir mit der zusätzlichen Validierung der Punkte C und D fortfahren.
Zwischen etwa 38,2 % und fast 88,6 % der vorherigen A-B-Bewegung werden in der Regel durch das B-C-Segment wieder aufgefangen. In diesem Segment gibt es im Vergleich zu den anderen eine gewisse Flexibilität. Solange dieser Rückzug nicht innerhalb der vorgesehenen Grenzen bleibt, wird das gesamte Muster als ordnungsgemäß angesehen.
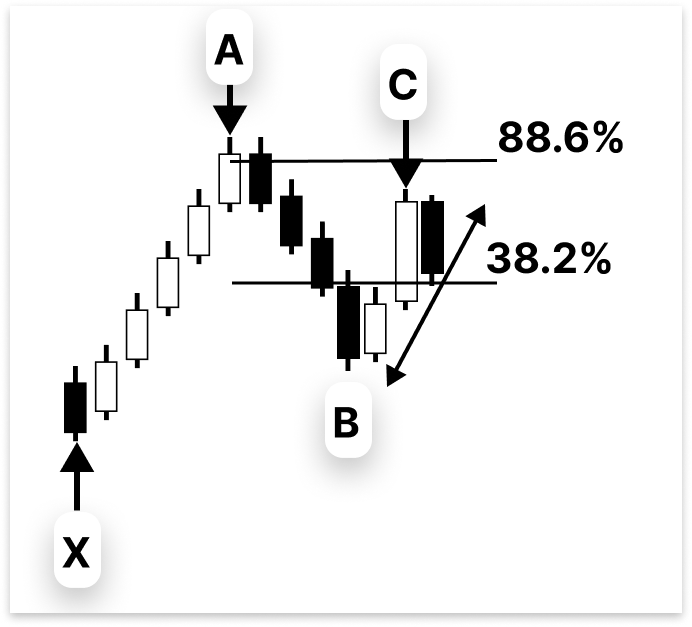
double swing_low_x; //X double swing_high_a; //A double price_differecence; double fib_ret_79; double fib_ret_76; double swing_low_b; //B double price_differecence_ab; double fib_ret_88_6_ab; double fib_ret_38_2_ab; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- //--- return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- } //+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- swing_low_x = 1.15656; swing_high_a = 1.16985; price_differecence = swing_high_a - swing_low_x; fib_ret_79 = swing_high_a - ((79.0/100.0) * price_differecence); fib_ret_76 = swing_high_a - ((76.0/100.0) * price_differecence); price_differecence_ab = swing_high_a - swing_low_b; fib_ret_88_6_ab = swing_low_b + ((88.6/100.0) * price_differecence_ab); fib_ret_38_2_ab = swing_low_b + ((38.2/100.0) * price_differecence_ab); /* if(B <= fib_ret_76 && B>= fib_ret_79 && C >= fib_ret_38_2_ab && C <= fib_ret_88_6_ab) { } */ }
Erläuterung:
In diesem Abschnitt wird die Gesamtpreisbewegung zwischen zwei wichtigen Marktpunkten berechnet. Auf der Grundlage dieser Bewegung werden bestimmte Fibonacci-Retracement-Levels ermittelt, die mögliche Umkehrpunkte oder Unterstützungs- und Widerstandsbereiche für den Kurs anzeigen. Das 38,2 %-Niveau verwendet einen kleineren Teil der Bewegung, der zum selben Punkt addiert wird, während das 88,6 %-Retracement-Niveau zwei Referenzniveaus für die Analyse findet, indem es den Großteil der gesamten Kursbewegung nimmt und zum unteren Punkt addiert.
Diese Niveaus helfen bei der Lokalisierung potenzieller Preisreaktionszonen während einer Retracement-Bewegung. Als Teil einer Logik zur Bestätigung des Musters bestimmt die kommentierte if-Anweisung schließlich, ob Punkt B zwischen zwei bestimmten Retracement-Levels liegt und ob Punkt C ebenfalls innerhalb der angegebenen Fibonacci-Spanne liegt.
Schließlich ist die C-D-Strecke, der die potenzielle Umkehrzone (PRZ) abgrenzt, die wichtigste Komponente des Schmetterling-Musters. Der D-Punkt in einem gültigen Schmetterling erstreckt sich von 127,2% bis 161,8% der ursprünglichen Strecke X-A. Die Abschlusszone, in der Händler nach möglichen Umkehrsignalen suchen, wird durch diese Verlängerung gebildet. Da X-A 100 % beträgt, wird D nach einer Verlängerung um 61,8 % etwa 161,8 % von X-A betragen.
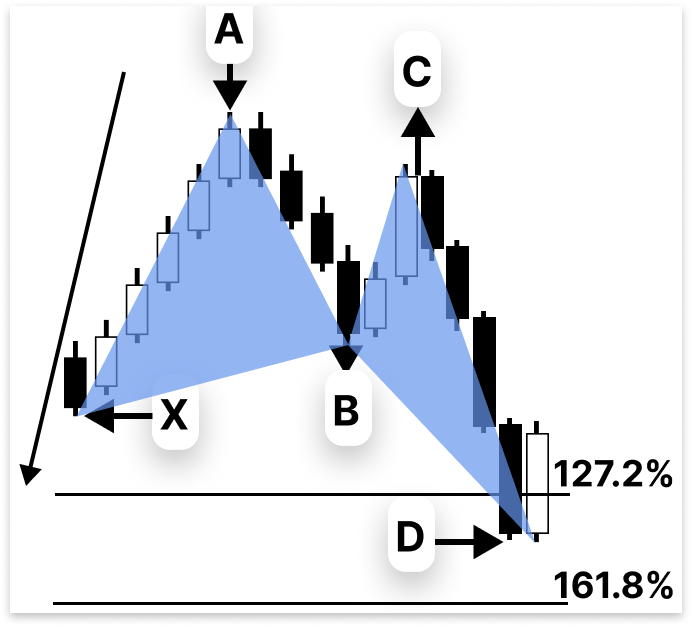
Beispiel:
double swing_low_x; //X double swing_high_a; //A double price_differecence; double fib_ret_79; double fib_ret_76; double swing_low_b; //B double price_differecence_ab; double fib_ret_88_6_ab; double fib_ret_38_2_ab; double xa_price_differecence; double fib_ext_127_2_xa; double fib_ext_161_8_xa; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- //--- return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- } //+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- swing_low_x = 1.15656; swing_high_a = 1.16985; price_differecence_ab = swing_high_a - swing_low_b; fib_ret_79 = swing_high_a - ((79.0/100.0) * price_differecence); fib_ret_76 = swing_high_a - ((76.0/100.0) * price_differecence); fib_ret_88_6_ab = swing_low_b + ((88.6/100.0) * price_differecence_ab); fib_ret_38_2_ab = swing_low_b + ((38.2/100.0) * price_differecence_ab); xa_price_differecence = swing_high_a - swing_low_x; fib_ext_127_2_xa = MathAbs(swing_low_x - ((127.2/100.0) * xa_price_differecence)); fib_ext_161_8_xa = MathAbs(swing_low_x - ((161.8/100.0) * xa_price_differecence)); /* if(B <= fib_ret_76 && B>= fib_ret_79 && C >= fib_ret_38_2_ab && C <= fib_ret_88_6_ab && D <= fib_ext_127_2_xa && D >= fib_ext_161_8_xa) { } */ }
Erläuterung:
Dieser Teil des Codes berechnet den Abstand zwischen zwei wichtigen Marktmuster-Schwungpunkten. Die Kursbewegung wird dann zur Bestimmung der Fibonacci-Erweiterungsstufen für dieses Mustersegment verwendet. Durch die Berechnung der Differenz zwischen dem Anfangs- und dem Endpunkt des Schwungs und die Verwendung der Fibonacci-Verhältnisse von 127,2 % und 161,8 % wird im Wesentlichen vorhergesagt, wohin sich der Kurs als Nächstes entwickeln könnte. Um sicherzustellen, dass die Berechnung sowohl für Aufwärts- als auch für Abwärtsbewegungen funktioniert, verwendet der Code eine Funktion, die jedes Ergebnis in eine positive ganze Zahl umwandelt. Diese Verhältnisse werden dann auf die anfängliche Kursbewegung angewandt, wobei sie je nach Richtung der Bewegung entweder hinzugefügt oder gestrichen werden, um die prognostizierten Verlängerungsniveaus zu erhalten.
Die mathematischen Grundlagen der Fibonacci-Extensions und -Retracements sowie ihre Anwendung in MQL5 sind inzwischen gut verstanden. Um harmonische Muster zu verifizieren, wissen wir jetzt, wie man Fibonacci-Verhältnisse verwendet, die Preisdifferenzen zwischen den Umkehrpunkten berechnet und wichtige Niveaus ermittelt. Dieselbe Logik, die wir hier angewandt haben, kann auch für andere harmonische Muster verwendet werden, da sie alle ähnliche Fibonacci-basierte Berechnungen verwenden, um potenzielle Umkehr- und Fortsetzungszonen zu identifizieren. Nachdem wir nun diesen Rahmen abgesteckt haben, können wir uns getrost weiteren harmonischen Mustern zuwenden. Diese Konzepte werden angewandt, um potenzielle Handelsmöglichkeiten anhand von Preisbewegungen und Fibonacci-Verbindungen zu identifizieren.
Das Muster von Gartley: Auf die Schritte XA, AB, BC und CD folgt das Gartley-Muster. Punkt D befindet sich innerhalb der 127,2-161,8 %-Ausdehnung von XA, Punkt B geht um 61,8 % von XA zurück, und Punkt C geht um 38,2-88,6 % von AB zurück. Dies deutet auf eine mögliche Umkehrzone für den Handel hin.
Das Fledermaus-Muster: Bestimmte Fibonacci-Verhältnisse definieren eine harmonische Struktur, die als Fledermaus-Muster bekannt ist. Punkt D, der in der Regel innerhalb der 88,6 %-Retracement-Zone von XA liegt, markiert den Abschluss des Musters, wobei Punkt B 38,2 % bis 50 % des XA-Segments zurückverfolgt.
Schlussfolgerung
Die Grundsätze der harmonischen Muster und ihre Verwendung im Handel wurden in diesem Artikel erörtert. Sie wissen nun, wie Sie Fibonacci-Retracements und -Extensions in MQL5 anwenden können und welche mathematischen Prinzipien ihnen zugrunde liegen. Indem wir harmonische Muster verwenden, um einen voll funktionsfähigen Expert Advisor (EA) zu konstruieren, werden wir im nächsten Artikel von der Theorie zur Praxis übergehen. Darüber hinaus erfahren Sie, wie Sie diese Muster mit Hilfe der Chart-Elemente von MQL5 auf Ihren Trading-Charts visuell erkennen und hervorheben können. Am Ende des folgenden Artikels werden Sie über die Informationen und Ressourcen verfügen, die Sie benötigen, um Handelsmethoden, die auf harmonischen Mustern basieren, erfolgreich zu automatisieren.
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/19179
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
CRUD-Operationen in Firebase mit MQL
MQL5-Handelswerkzeuge (Teil 8): Verbessertes informatives Dashboard mit verschiebbaren und minimierbaren Funktionen
Automatisieren von Handelsstrategien in MQL5 (Teil 25): Trendlinien-Händler mit der Anpassung der kleinsten Quadrate und dynamischer Signalgenerierung
MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 78): Gator- und AD-Oszillator-Strategien für Marktresilienz
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.