MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 76): Verwendung von Mustern des Awesome Oszillators und der Envelope-Kanäle mit überwachtem Lernen

Einführung

In unserem letzten Artikel haben wir das Indikatorpaar des Awesome Oszillators und der Envelope-Kanäle vorgestellt, und beim Testen dieses Paares sind 7-8 der 10 Muster in einem 2-Jahres-Testfenster nach vorne gegangen. Im Anschluss an die Einführung eines Indikatorpaares untersuchen wir in der Regel, wie sich maschinelles Lernen auf die Leistung dieser Indikatorsignale auswirken kann, wenn überhaupt. Dieser Artikel bildet da keine Ausnahme, und so werden wir untersuchen, wie die Muster 4, 8 und 9 beeinflusst werden können, wenn wir ihre Signale mit einem Netz des überwachten Lernens als Filter ergänzen. Für unser Netzwerk verwenden wir ein CNN, dessen Kernel/Kanäle durch den Punktprodukt-Kernel mit zeitübergreifender Aufmerksamkeit dimensioniert sind.

Punktprodukt-Kernel mit zeitübergreifender Berücksichtigung

Dieser Kernel ist eine Form des Aufmerksamkeitsmechanismus, bei dem man bei zwei Sequenzen, die in der Regel Merkmale aus verschiedenen Zeitschritten oder Schichten sind, einen Aufmerksamkeitswert zwischen jedem Paar berechnet, indem man ihr Punktprodukt verwendet. Dieser Ansatz würde die Beziehungen über die Zeit hinweg hervorheben und aufzeigen, wie ein vergangenes oder zukünftiges Merkmal für ein aktuelles relevant ist. Wenn Sie die folgenden zwei Sequenzen haben, funktioniert es folgendermaßen:

X=[x1,x2,...,xT]

Y=[y1,y2,...,yS]

Für jedes Paar (xi,yj) würden Sie die Punktproduktwertung wie folgt berechnen: 

Scorei,j = xi⋅yj

Alternativ kann ein Soft-Max über j oder i angewendet werden, um Aufmerksamkeitsgewichte zu erhalten, wobei die Gewichte dann verwendet werden, um die Merkmale über die Zeit zu mischen/zu gewichten. Dies ist nützlich, weil es parametereffizient ist und keine zusätzlichen gelernten Parameter über die Projektionen hinaus benötigt. Es ist flexibel, da es Sequenzen variabler Länge, unregelmäßige Abtastungen und modale/zeitliche Wechselwirkungen verarbeiten kann. Sie ist auch deshalb so wirkungsvoll, weil sie sich auf relevante Momente konzentriert und nicht nur auf die lokalen Faltungsbezirke. Anwendungen finden sich in der Zeitreihenvorhersage, insbesondere dort, wo eine Verzögerung wichtig ist, in der Videoanalyse, wo Bilder über die Zeit miteinander verknüpft sind, in der Sprachanalyse und in allen Bereichen, in denen zeitliche/zeitbasierte Abhängigkeiten nicht trivial sind.

Warum wählen wir dann diesen Kernel, um unsere CNN-Kernel-/Kanalgrößen zu bestimmen? Was die Kerne betrifft, so haben sie räumliche und zeitliche Merkmale. Erstens sagen Ihnen die Aufmerksamkeitskerne, welche Zeitschritte am wichtigsten sind. Dies ist bei kleinen Kernel-Instanzen, die sehr fokussiert sind, vielleicht nicht so bedeutsam, aber je weiter sich die Kernel ausbreiten, desto mehr Kontext wird erfasst. CNNs sind auch von Natur aus lokal, daher kann die Aufmerksamkeit das effektive rezeptive Feld adaptiv erweitern/fokussieren, indem die Kernelgröße in Abhängigkeit von der zeitlichen Dynamik der Datensequenz beeinflusst wird.

Für die Kanäle kann der Aufmerksamkeitskern erkennen, welche Merkmalskanäle oder Dimensionen „am meisten beachtet“ werden. Es ist ein Leitfaden für die Beschneidung der Kanäle. Wenn bestimmte Kanäle konsequent ignoriert werden, sind sie totes Gewicht und reduzieren die Gesamtgröße des Kanals effektiv. Sie ist auch ein Indikator für Expansion. Wenn die Aufmerksamkeit diffus ist und keinen klaren Fokus hat, dann brauchen Sie möglicherweise eine reichhaltigere Darstellung mit mehr Kanälen. Unser Ansatz ist daher, ähnlich wie in früheren Artikeln, in denen wir CNN-Verbesserungen genutzt haben, ein dynamisches Design für das CNN anstelle von statischen Kernel-/Kanalgrößen, die für alle geeignet sind. Wir nutzen Aufmerksamkeitsmuster beim Training und bei der Inferenz, um CNNs zu rekonfigurieren – mit dem Ziel, effizientere, effektivere Modelle für nicht-stationäre Finanzmarktdaten zu erhalten.

Trotz unseres dynamischen Ansatzes, der darauf abzielt, die Anpassungsfähigkeit und Leistung der Modelle zu verbessern, gibt es einige Nachteile, die erwähnenswert sind. Zunächst einmal haben wir einen Rechenaufwand von O(N^2) mit der Länge der Eingabedatenfolge, während statische CNNs typischerweise O(N) sind. Für lange Sequenzen ist dies unerschwinglich. Zweitens haben wir ein Paradoxon der Interpretierbarkeit. Aufmerksamkeitsbewertungen sind zwar „nett“, aber wenn man sie mit der dynamischen Kernel-/Kanalauswahl kombiniert, wird das Modell komplexer, wenn es darum geht, Informationen zu interpretieren und sinnvoll abzuleiten, um sie auf Situationen in Drittländern anzuwenden.

Außerdem sind sie nicht immer besser, denn einige Tests haben gezeigt, dass bei rein lokalen Aufgaben wie der Kantenerkennung in Bildern klassische CNNs aufmerksamkeitsintensive Modelle übertreffen können. Darüber hinaus sind die Datenanforderungen für Aufmerksamkeitskerne beim Training/Optimierung deutlich höher als die der klassischen CNNs, um sinnvolle zeitübergreifende Abhängigkeiten zu lernen. Schließlich besteht das Risiko einer Überanpassung. Wenn die Aufmerksamkeit die architektonischen Veränderungen steuert, kann es passieren, dass man durch übermäßige Anpassungsfähigkeit dem Rauschen oder der Zufälligkeit der getesteten Daten hinterherläuft.

Mögliche Alternativen zu unserem Ansatz sind: dilatierte Faltungen, bei denen das rezeptive Feld erweitert wird, ohne die Kernelgröße zu erhöhen, um große, aber spärliche zeitliche Unterschiede abzudecken; oder dynamische/adaptive Faltungen, bei denen die Kernelgewichte auf der Grundlage der Art der Eingabedaten oder der Aufmerksamkeitssignale festgelegt werden; oder wir könnten tiefenweise trennbare Faltungen haben, bei denen unsere Variable nur die Kanalgröße ist und unser Ziel die Recheneffizienz ist; oder wir könnten Press- und und Ausbruchsblöcke verwenden; oder temporale Faltungsnetzwerke. Jedes dieser Verfahren stellt eine neue Variante unseres Ansatzes mit einigen Vorteilen und Herausforderungen dar, wird hier aber der Vollständigkeit halber vorgestellt, um zu zeigen, was beim Tuning von CNNs möglich ist.

Das Netzwerk

Nach dieser kurzen Einführung in den Punktprodukt-Kreuz-Zeit-Aufmerksamkeits-Kernel wollen wir uns nun dem Code zuwenden. Der Hauptteil des Codes für dieses Netz als Klasse wird im Folgenden vorgestellt:

import torch
import torch.nn as nn
import torch.nn.functional as F

class DotProductAttentionConv1D(nn.Module):
    def __init__(self, input_length=100):
        super(DotProductAttentionConv1D, self).__init__()
        self.input_length = input_length

        # Deeper and wider design with attention
        self.kernel_sizes, self.channels = self._design_architecture()

        self.conv_layers = nn.ModuleList()
        self.attention_layers = nn.ModuleList()  # For cross-time attention
        in_channels = 1

        for i, (out_channels, kernel_size) in enumerate(zip(self.channels, self.kernel_sizes)):
            # Convolutional block
            conv_layer = nn.Sequential(
                nn.Conv1d(in_channels, out_channels, kernel_size=kernel_size, padding=kernel_size // 2),
                nn.BatchNorm1d(out_channels),
                nn.ReLU(),
                nn.Dropout(0.2))
            self.conv_layers.append(conv_layer)
            
            # Attention block (cross-time attention)
            if i % 2 == 0:  # Apply attention to every other layer
                attn_layer = nn.MultiheadAttention(embed_dim=out_channels, num_heads=4)
                self.attention_layers.append(attn_layer)
            else:
                self.attention_layers.append(None)
            
            in_channels = out_channels

        # Fully connected head (same as original)
        self.head = nn.Sequential(
            nn.AdaptiveAvgPool1d(1),
            nn.Flatten(),
            nn.Linear(in_channels, 128),
            nn.ReLU(),
            nn.Dropout(0.2),
            nn.Linear(128, 64),
            nn.ReLU(),
            nn.Linear(64, 1),
            nn.Sigmoid()
        )

    def _dot_product_kernel(self, x):
        """Dot product similarity kernel with positional encoding"""
        # x shape: (B, C, L)
        x = x.permute(0, 2, 1)  # (B, L, C)
        # Compute dot product attention
        attention_scores = torch.bmm(x, x.transpose(1, 2))  # (B, L, L)
        attention_weights = F.softmax(attention_scores / (x.size(-1) ** 0.5), dim=-1)
        return torch.bmm(attention_weights, x).permute(0, 2, 1)  # (B, C, L)

    def _design_architecture(self):
        # Simulate attention response pattern
        num_layers = 10
        kernel_sizes = [3 + (i % 4) * 2 for i in range(num_layers)]  # cyclic 3, 5, 7, 9
        channels = [32 * (i + 1) for i in range(num_layers)]  # 32, 64, ..., 320
        
        return kernel_sizes, channels

    def forward(self, x):
        x = x.unsqueeze(1)  # (B, 1, L)
        
        for conv_layer, attn_layer in zip(self.conv_layers, self.attention_layers):
            x = conv_layer(x)
            
            if attn_layer is not None:
                # Reshape for attention (MultiheadAttention expects seq_len first)
                attn_input = x.permute(2, 0, 1)  # (L, B, C)
                attn_output, _ = attn_layer(attn_input, attn_input, attn_input)
                x = attn_output.permute(1, 2, 0)  # (B, C, L)
                
                # Also apply dot product kernel
                x = self._dot_product_kernel(x)
        
        return self.head(x)

Erstens erbt unsere Klasse vom nn.Modul, einem Standard für Netzwerke mit PyTorch. Der Parameter input-length legt die erwartete Sequenzlänge fest, jedoch kann die Klasse bei Anpassungen auch Eingabesequenzen mit variabler Länge annehmen. Die Super-Direktive stellt sicher, dass die Basisklasse initialisiert wird, ein sehr wichtiger Schritt, damit „die ganze Magie“ in PyTorch funktioniert, und daher sicherlich nicht übersprungen werden sollte. Damit sind wir bei der Architektur bzw. dem Kernel und der Kanaldimensionierung angelangt.

Wie bereits erwähnt, verwenden wir einen dynamischen Ansatz. Anstelle einer festen Kodierung wählt unser Modell die Kernel- und Kanalgrößen algorithmisch aus bzw. legt sie fest und ermöglicht so eine Anpassung an die Aufmerksamkeitsmuster in den Eingangsdaten, die bei jedem Vorwärtsdurchlauf verarbeitet werden. Als Leitfaden könnte es sinnvoll sein, Aufmerksamkeitsstatistiken aus früheren Durchläufen oder Meta-Lernen mit den tatsächlichen Kernel-/Kanalwahlen für jede Schicht zu verknüpfen.

Sobald wir die Design-Architektur-Funktion ausgeführt haben, beginnen wir mit der Konstruktion der Schichten. Hier können Sie mit der Funktion der Modul-Liste ein variables tiefes Netz aufbauen. Dieser Schritt ist sehr wichtig, wenn Ebenen dynamisch gestapelt werden. Dann kommen wir zur for-Schleife für das Stapeln von Schichten. In diesem Stadium wird die Kernelgröße für jede Faltungsschicht separat festgelegt. Dies ermöglicht breite oder schmale Filter, je nach Fall. Der Aufmerksamkeitskern kann später Auskunft darüber geben, was optimal ist. Unser Padding, bei dem die Kernelgröße durch 2 geteilt wird, bietet das gleiche Padding, wobei die Ausgabelänge für die meisten Kernel gleich der Eingabelänge ist. Dies ist bei Zeitreihen, bei denen man die Zeitschritte angleichen muss, von entscheidender Bedeutung. Schließlich helfen Batch-Normalisierung, ReLU-Aktivierung und Drop-out, das klassische Deep-Learning-Rezept, das Training zu stabilisieren, die Konvergenz zu beschleunigen und das Modell zu regulieren.

Innerhalb der for-Schleife gibt es neben dem oben erwähnten Faltungsblock auch noch einen „Aufmerksamkeitsblock“. Hier fügen wir abwechselnd mehrköpfige Aufmerksamkeitsschichten an, den Kern des Transformators, der alle Abhängigkeiten erfasst. Wir führen diese Anfügung abwechselnd und nicht für jeden Ebenen-Slot durch, vor allem um Rechenressourcen zu sparen. Dadurch kann das Modell zwischen einem lokalen CNN und einer globalen Argumentation wechseln. Schließlich wird unserem Parameter in-channels der Wert out-channels zugewiesen. Das liegt daran, dass jeder Merkmalskartenkanal zu einer Einbettungsdimension wird, die die CNN- und Aufmerksamkeitsdarstellungen vereint.

Dann kommen wir zum letzten Teil unserer Klasseninitialisierungsfunktion, wo wir den vollständig verbundenen Kopf definieren. Hier verwenden wir das adaptive Pooling, um die Zeitdimension unabhängig von der Eingabelänge auf 1 zu reduzieren, da die Ausgabegröße fest ist, und bereiten uns dann auf vollständig verbundene Schichten vor. Es handelt sich um dichte Schichten, die einen Stapel nichtlinearer Transformationen darstellen, die in einem einzigen sigmoiden Ausgang enden. Dieser Wert kann als binäre Vorhersage oder als normalisierte Punktzahl abgeleitet werden, ist aber letztlich unsere Preistrendprognose, wobei Werte unter 0,5 fallend und solche über 0,5 steigend sind. Der Dropout verhindert eine Überanpassung auf der Stufe der dichten Schicht.

Nachdem wir uns die Klasseninitialisierung dieses Netzes angesehen haben, folgt nun die Kernel-Funktion des Punktprodukts. Bei der Berechnung des Kerns schalten wir als Erstes die Eingabe auf B-L-C um, um die Punktprodukte über die Vektorenfolge der Eingabedaten zu vereinfachen. Anschließend führen wir eine Batch-Matrixmultiplikation (bmm) durch, bei der wir alle paarweisen Punktprodukte für jeden Batch effizient berechnen. Mit GPUs kann dieser Prozess noch schneller ablaufen. Anschließend führen wir eine Soft-Max-Skalierung durch, ein Standard für den Aufmerksamkeitskern, bei dem die Temperatur die Quadratwurzel aus der Größe des Eingangsvektors oder der eingebetteten Dimension ist.

Anschließend führen wir die abschließende Batch-Matrix-Multiplikation durch, bei der wir Merkmale aus verschiedenen Zeitpunkten nach Aufmerksamkeit gewichtet mischen. Darüber hinaus wird die Multiplikationsausgabe wieder in die Form des Eingangsvektors gebracht und für die nachfolgende Verwendung vorbereitet. Diese Funktion verleiht dem Netzwerk ein zeitübergreifendes Bewusstsein, das über das hinausgeht, was eine normale Faltung allein erreichen kann, und wir nennen sie die Vorwärtspassfunktion des Netzwerks.

Unsere nächste spezielle Funktion innerhalb der Netzwerkklasse ist der Architekturentwurfsassistent. Wir haben ähnliche Funktionen bei der Anpassung des CNN in früheren Artikeln verwendet, und in diesem Fall durchlaufen wir eine Reihe von Kernelgrößen, um eine „aufmerksamkeitsgesteuerte“ Variante zu simulieren. Wir erhöhen auch stetig die Anzahl der Kanäle – ein klassischer Deep-Learning-Ansatz, bei dem wir versuchen, in späteren Schichten abstraktere und höherdimensionale Darstellungen zu lernen.

Unsere letzte Funktion in der Netzklasse ist, wie üblich, die Vorwärtspassfunktion. Als Erstes wird der Eingangsvektor vorverarbeitet, indem die zusätzliche mittlere Dimension oder der Kanal hinzugefügt wird, die für 1D-Faltungen erforderlich sind. Danach beginnen wir für jede Schicht mit einer Faltung, bei der wir lokale Merkmale aus der Eingabe extrahieren. Dann verarbeiten wir die bedingte Aufmerksamkeit, d. h. wir prüfen, ob es eine Aufmerksamkeitsebene gibt. Erinnern Sie sich daran, dass wir in der Initialisierungsfunktion dieser Klasse diese Aufmerksamkeitsebenen abwechselnd und nicht bei jedem Slot zugewiesen haben.

Wenn wir eine Aufmerksamkeitsebene haben, müssen wir sie umgestalten, da PyTorchs Multikopf ein bestimmtes Format (Kanal, Stapel, Länge) erwartet, wir aber (Stapel, Kanal, Länge) haben. Sobald wir die Aufmerksamkeitsausgabe haben, führen wir den Punktprodukt-Kernel durch, indem wir die oben definierte Funktion aufrufen. Nebenbei bemerkt, verwenden wir sowohl den Transformator als auch das Punktprodukt in einem Vorwärtsdurchlauf, obwohl nur eines davon als Alternative verwendet werden könnte. Dieser Wechsel kann mit dem Ziel erfolgen, festzustellen, welcher Algorithmus die Genauigkeit des Modells „trägt“. Die endgültige Ausgabe wird dann in den Kopf zur Klassifizierung/Regression eingespeist.

Zusammenfassung des Kodex nach Abschnitten

Abschnitt	Was es bewirkt	Warum es wichtig ist
__init__ + super	Einrichtung der Basisklasse	Wesentlich für die PyTorch-Funktionalität
self.kernel_sizes, channels	Dynamischer CNN-Entwurf	Maßgeschneiderte, adaptive Merkmalsextraktion
ModuleList layers	Modulare, erweiterbare Architektur	Skalierbarkeit, Experiment
Convolution blocks	Lokale Merkmalsextraktion	Traditionelle CNN-Stärken, Batch-Normalisierung usw.
MultiheadAttention blocks	Globale zeitübergreifende Abhängigkeiten	Erfasst weitreichende Abhängigkeiten
_dot_product_kernel	Explizite Berechnung der Aufmerksamkeit	Redundantes/verknüpftes Signal für zeitübergreifende Verbindungen
Fully connected head	Aggregation, Ausgabe	Flexibel für jede Aufgabe (Klassifizierung, Regression usw.)
forward logic	Datenfluss durch das Netz	Gewährleistet die korrekte Anwendung jedes Vorgangs
_design_architecture	Wie Kernel/Kanäle ausgewählt werden	Kann daten- oder aufmerksamkeitsorientiert gestaltet werden

Funktion des Awesome Oszillators

Die in MQL5 verwendeten Indikatorfunktionen werden nicht importiert, wenn wir das Modul von MetaTrader 5 in Python verwenden. Wir müssen daher immer vorhandene Bibliotheken verwenden oder eigene programmieren. Wir haben uns für die letztere Option entschieden und werden sie auch beibehalten und unseren Awesome Oszillator wie folgt in Python implementieren:

def Awesome_Oscillator(df: pd.DataFrame, short_period: int = 5, long_period: int = 34) -> pd.DataFrame:
    """
    Calculate the Bill Williams Awesome Oscillator (AO) and append it to the input DataFrame.
    
    AO = SMA(Median Price, short_period) - SMA(Median Price, long_period)

    Args:
        df (pd.DataFrame): DataFrame with 'high' and 'low' columns.
        short_period (int): Short period for SMA (default 5).
        long_period (int): Long period for SMA (default 34).

    Returns:
        pd.DataFrame: Input DataFrame with 'AO' column added.
    """
    required_cols = {'high', 'low'}
    if not required_cols.issubset(df.columns):
        raise ValueError("DataFrame must contain 'high' and 'low' columns")
    if not all(p > 0 for p in [short_period, long_period]):
        raise ValueError("Period values must be positive integers")

    result_df = df.copy()
    median_price = (result_df['high'] + result_df['low']) / 2
    short_sma = median_price.rolling(window=short_period).mean()
    long_sma = median_price.rolling(window=long_period).mean()
    result_df['AO'] = short_sma - long_sma

    return result_df

Zu den von uns importierten Modulen für diese Funktion gehört pandas für tabellenähnliche/Zeitreihenmanipulationen – es ist gut im Umgang mit Datenrahmen und Rolling-Window-Tricks. Wir importieren auch NumPy, das Rückgrat der schnellen Mathematik, das viel unter der Haube verwendet wird, auch wenn wir es hier nicht explizit aufrufen. Unsere Funktionssignatur, die Textzeile nach „def“, ist eine saubere Signatur, die Hinweise auf die Art der Eingabedaten gibt, die zum Aufruf der Funktion erforderlich sind. Diese Übersichtlichkeit wird mit der IDE-Autokomplettierung kombiniert, da Standardwerte für Mittelungszeiträume vordefiniert sind. Diese stehen im Einklang mit den klassischen Einstellungen von Bill Williams.

Nach der Signatur beginnen wir mit der Validierung der Dateneingabe der Funktion, wobei wir mit den erforderlichen Daten beginnen. Der Datenrahmen. Die Spalten „high“ und „low“ müssen vorhanden sein. Dies ist eine Sicherheitsüberprüfung, die spätere kryptische Fehler verhindert, wenn Spalten fehlen. Außerdem wird überprüft, ob die eingegebenen Perioden gültige Ganzzahlen ohne Vorzeichen sind. Durch nutzerfreundliche Fehlermeldungen erzwingen wir frühzeitige Ausfälle, die zu einer aussagekräftigen Diagnose beitragen können. Diese defensive Haltung bei der Überprüfung der Eingabedaten ist sehr wichtig, um NaN-Werte zu vermeiden. Vertrauen Sie niemals fremden Daten.

Als Nächstes erstellen wir eine Kopie des Eingabedatenrahmens, um sicherzustellen, dass die ursprünglichen Daten in ihrem ursprünglichen Zustand bleiben. Dies ist „nicht-destruktiv“ und für Pipelines, in denen Indikatorfunktionen geschichtet sind, unerlässlich. Anschließend berechnen wir den Medianpreis aus dem kopierten Datenrahmen. Dies ist eine der Haupteingaben für der AO und spiegelt den durchschnittlichen gehandelten Preis für den Balken wider – nicht nur den Schlusskurs – und soll das „Open-Price/Close-Price Whipsaw“ verhindern. Anschließend berechnen wir die geglätteten gleitenden Durchschnitte für die kurze und lange Laufzeit. Die Verwendung von rolling().mean() erzeugt einen gleitenden Durchschnitt, der ein glattes Trendsignal darstellt. Der Vergleich zwischen kurz und lang ist das Herzstück der Oszillatorlogik. Sie misst die Dynamik als den Abstand zwischen schnellen und langsamen Trends.

Zum Schluss fügen wir unserem kopierten Datenrahmen eine neue Spalte hinzu, „AO“. Dies ist der tatsächliche AO-Wert. Wenn das positive kurzfristige Momentum höher ist als das langfristige, ist dies eine Aufwärtsstimmung. Wenn das negative kurzfristige Momentum niedriger ist, ist dies ein Zeichen für eine Abwärtsstimmung Wie im letzten Artikel hervorgehoben wurde, ist der AO von der Nulllinie abhängig, sodass Überkreuzungen von Bedeutung sind.

Funktion der Envelope-Kanäle

Wir implementieren die Envelope-Kanäle in Python wie folgt:

def Envelope_Channels(df: pd.DataFrame, period: int = 20, deviation: float = 0.025) -> pd.DataFrame:
    """
    Calculate Envelope Channels (Upper & Lower Bands) and append to the input DataFrame.

    Envelope Channels = SMA(close, period) * (1 ± deviation)

    Args:
        df (pd.DataFrame): DataFrame with 'close' column.
        period (int): Period for SMA calculation (default 20).
        deviation (float): Deviation as a decimal (e.g., 0.025 for 2.5%, default 0.025).

    Returns:
        pd.DataFrame: Input DataFrame with 'Envelope_Upper' and 'Envelope_Lower' columns added.
    """
    required_cols = {'close'}
    if not required_cols.issubset(df.columns):
        raise ValueError("DataFrame must contain 'close' column")
    if period <= 0 or deviation < 0:
        raise ValueError("Period must be positive and deviation non-negative")

    result_df = df.copy()
    sma = result_df['close'].rolling(window=period).mean()
    result_df['Envelope_Upper'] = sma * (1 + deviation)
    result_df['Envelope_Lower'] = sma * (1 - deviation)
    result_df['Envelope_Mid'] = 0.5 * (result_df['Envelope_Upper'] + result_df['Envelope_Lower'])

    return result_df

Wie bei der AO ist die Signatur mit einem Typ-Hinweis versehen, und für die Eingaben von Periode und Abweichung werden „vernünftige“ Standardwerte verwendet. Unsere Validierung des Eingabedatenrahmens konzentriert sich darauf, nur die Spalte „close“ zu überprüfen. Dies ist unsere einzige Anforderung an den Datenrahmen, um Garbage-in und Garbage-out zu verhindern. Wir prüfen auch, ob die Eingabeperiode nicht Null ist und ob die Abweichung nicht negativ ist. Werden diese Anforderungen nicht erfüllt, erhalten wir einen Fehlerwert, der die Ausführung des Skripts abbricht. 

Wir erstellen auch eine Kopie des Eingabedatenrahmens, die wir als Ergebnisdatenrahmen bezeichnen, eine sichere Praxis, wie bereits oben und in früheren Artikeln dargelegt. Unsere erste Berechnung bezieht sich auf einen geglätteten gleitenden Durchschnitt des Schlusskurses. Die Envelope-Kanäle werden auf dieser Basis aufgebaut. Ein glatterer SMA bedeutet weniger „Whipsaw“, aber mehr Verzögerung. Er dient als Schwerpunkt der Bänder. Mit dieser Grundlage können wir nun die oberen und unteren Envelopepuffer berechnen. Dies sind die Kanäle.

Ein Preis oberhalb des oberen Bereichs könnte auf eine überkaufte Situation hindeuten, während ein Preis unterhalb dieses Bereichs eine überverkaufte Situation bedeuten könnte. Die Abweichung wird als Dezimalzahl mit einem Standardwert von 2,5 % oder 0,025 verwendet. Die Wahl des Abweichungswerts sollte für den gehandelten Vermögenswert optimal sein, da es sich in der Regel um einen sehr empfindlichen Wert handelt. Bei volatileren Vermögenswerten können die Abweichungen bis zu 5 Prozent betragen. Der zusätzliche Puffer, den wir an den Datenrahmen anhängen, ist die Mittellinie der Hüllkurve, und wir nehmen einfach den Mittelwert des oberen und unteren Bandes, um seinen Wert zu ermitteln.

Die Merkmale

Wir testen 3 der 10 Signalmuster, die wir im letzten Artikel vorgestellt haben. Wir bezeichnen diese Signalmuster in diesem Artikel als Merkmale, da sie als Input für ein Netzwerk dienen, aber für unsere Zwecke können die beiden Bezeichnungen austauschbar verwendet werden. Wie im letzten Artikel und auch in dieser Artikelserie ist jedes Merkmal ein Vektor, der die Signale von zwei Indikatoren zusammenfasst. Es handelt sich um eine Bitfolge von Nullen und Einsen. In früheren Artikeln haben wir uns damit beschäftigt, die Größe unserer Merkmale von der 2er-Größe zu erweitern und sie jedem Indikator zuzuordnen – um zu prüfen, ob es sich um ein Auf- oder Abwärtssignal handelt. Die Ergebnisse dieser Tests waren enttäuschend im Vergleich zu den Ergebnissen, die wir erhielten und erhalten, wenn wir uns auf ein steigendes oder fallendes Gesamtsignal konzentrieren.

Wir überarbeiten Feature_4, Feature_8 und Feature_9. Die allgemeine Struktur dieser Merkmalsfunktionen, wie wir sie hier übernehmen, weicht also nicht wesentlich von dem ab, was wir bisher verwendet haben. Jede Funktion gibt ein 2D-NumPy-Array aus, dessen Form der Anzahl der Zeilen im Datenrahmen entspricht und dessen Spalten zwei sind. Der [0]-Index jeder Zeile ist ein eindeutiges Aufwärts- oder Kaufmuster, während der [1]-Index jeder Zeile eine eindeutige Abwärts- oder Verkaufsmarke darstellt. In unserem Format bedeutet 1, dass es ein Kauf-/Verkaufsmuster gibt, während 0 bedeutet, dass es keines gibt. Jedes Muster ist eine Kombination aus Signalen von zwei Indikatoren, dem AO und den Envelope-Kanälen. Wir verwenden die Verschiebung[n] in jedem Datenrahmen, wenn wir mehrere Balken vergleichen. Jeder geladene Datenrahmen muss daher ausreichend Daten enthalten.

Feature_4

Zusammenfassend lässt sich sagen, dass die Kernlogik dieses Musters darin besteht, dass wir ein Aufwärtssignal setzen, wenn der AO einen Dip über Null bildet und der Kurs sich innerhalb der unteren Hälfte der Hüllkurve befindet. Umgekehrt liegt ein Abwärtssignal vor, wenn der AO eine Spitze unter Null bildet und der Kurs in der oberen Hälfte der Envelopes liegt. Wir implementieren dies in Python wie folgt:

def feature_4(df):
    """
//+------------------------------------------------------------------+
//| Check for Pattern 4.                                             |
//+------------------------------------------------------------------+

    """
    feature = np.zeros((len(df), 2))
    
    feature[:, 0] = ((df['AO'].shift(2) > df['AO'].shift(1)) &
                     (df['AO'].shift(1) < df['AO']) &
                     (df['AO'].shift(1) > 0.0) &
                     (df['close'].shift(2) >= df['Envelope_Mid'].shift(2)) &
                     (df['close'].shift(2) <= df['Envelope_Lower'].shift(2)) &
                     (df['close'].shift(1) >= df['Envelope_Mid'].shift(1)) &
                     (df['close'].shift(1) <= df['Envelope_Lower'].shift(1)) &
                     (df['close'] >= df['Envelope_Mid']) &
                     (df['close'] <= df['Envelope_Lower'])).astype(int)
    
    feature[:, 1] = ((df['AO'].shift(2) < df['AO'].shift(1)) &
                     (df['AO'].shift(1) > df['AO']) &
                     (df['AO'].shift(1) < 0.0) &
                     (df['close'].shift(2) <= df['Envelope_Mid'].shift(2)) &
                     (df['close'].shift(2) >= df['Envelope_Upper'].shift(2)) &
                     (df['close'].shift(1) <= df['Envelope_Mid'].shift(1)) &
                     (df['close'].shift(1) >= df['Envelope_Upper'].shift(1)) &
                     (df['close'] <= df['Envelope_Mid']) &
                     (df['close'] >= df['Envelope_Upper'])).astype(int)
    
    
    feature[0, :] = 0
    feature[1, :] = 0
    
    return feature

In unserem obigen Code beginnen wir, indem wir das Ausgabe-Array so vorbereiten, dass es keine Signale widerspiegelt/annimmt, indem wir es mit Nullen füllen und sicherstellen, dass es 2 Spalten hat. Dann weisen wir der ersten Spalte einen Index zu, indem wir prüfen, ob alle Voraussetzungen für einen Aufwärtsindikator erfüllt sind. Es müssen sowohl die Anforderungen des AO wie der Envelopes erfüllt sein, damit eine Spalte eine 1 erhält. Die AO-Bedingungen sind die Form eines „V“, ein Zeichen für ein sinkendes und dann steigendes Momentum oder ein Hinweis auf eine Aufwärtsumkehr. Diese V-Form muss ebenfalls vollständig über Null oder im Aufwärtsbereich liegen. Die Envelope-Bedingungen bedeuten, dass sich der Kurs nahe oder unter der Mittellinie der Hüllkurve befindet, aber nicht überverkauft ist. Dies kann mit einem Rücksetzer, aber nicht mit einem Durchbruch gleichgesetzt werden, der sich für ein Fading oder eine Wiederaufnahme des Trends eignet.

Wird einer Spalte der Wert 1 zugewiesen, so bedeutet dies mit Sicherheit, dass die andere Spalte den Wert Null hat, da sich diese Signale gegenseitig spiegeln. Unsere Abwärtslogik ist also eine Umkehrung der obigen Aussage. Voraussetzung dafür ist ein AO-“Peak“ unter Null und ein Preis, der in der oberen Envelope-Hälfte festsitzt. Das letzte, was wir in der Funktion Feature_4 tun, ist, den ersten beiden Zeilen Nullen zuzuweisen, da wir Vergleiche durchgeführt haben, die bis zu 2 Indizes umfassen. Wie bereits in der Vergangenheit argumentiert wurde, verhindert dies unbeabsichtigte Signale durch verschiebungsbedingte NaNs zu Beginn einer Reihe.

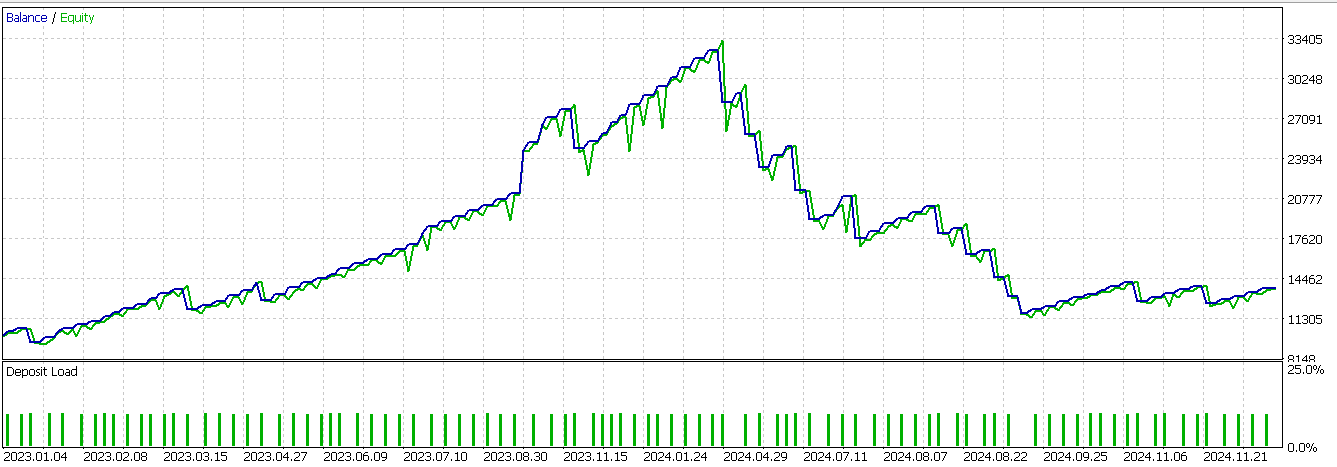
Wir führen Optimierungen und Vorlauftests für Feature_4 durch, wenn wir es mit unserem CNN als Filter ergänzen. Um den letzten Artikel zu rekapitulieren, unser Symbol ist USD JPY, der Zeitrahmen ist 30 Minuten und wie immer, zumindest für dieses Jahr, ist das Testfenster 2023 und 2024. Feature_4 ist in der Lage, besser vorwärts zu gehen, wenn auch mit einem Verlust, als das, was wir im letzten Artikel hatten. Dieser Bericht wird nachstehend wiedergegeben:

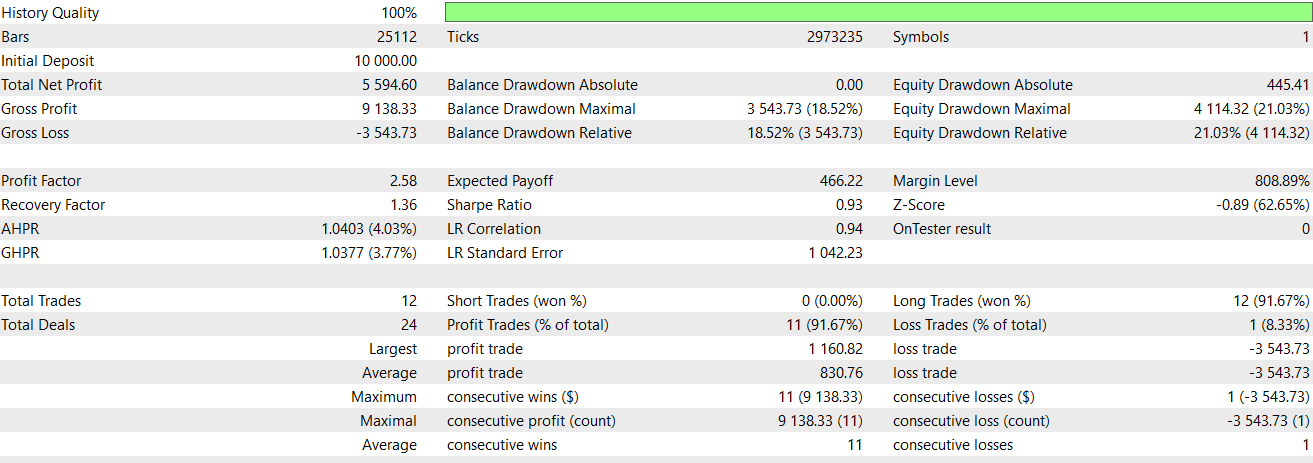
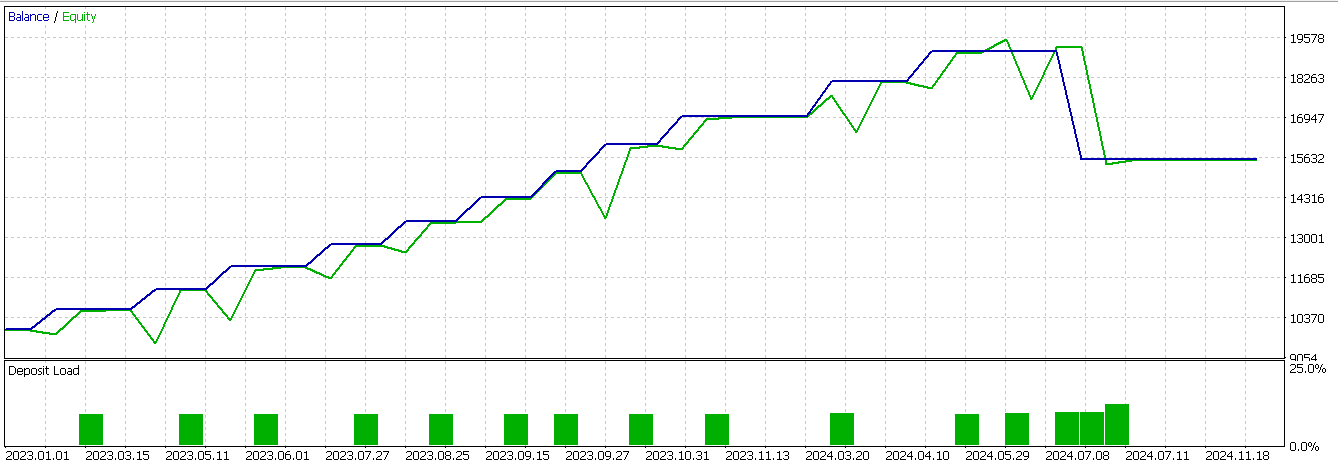
Feature_8

Wie im letzten Artikel beschrieben, weist dieses Signalmuster ein Aufwärtssignal des AO und einen beständig steigenden Kurs auf, wobei der AO über Null liegt und der Kurs sich von demunteren Envelope-Band entfernt. Nach der Abwärtslogik befinden sich AO und Preis in einem Abwärtstrend, wobei AO unter Null liegt und der Preis unter das untere Band fällt. Wir implementieren diese Funktion in Python wie folgt:

def feature_8(df):
    """
//+------------------------------------------------------------------+
//| Check for Pattern 8.                                             |
//+------------------------------------------------------------------+
    """
    feature = np.zeros((len(df), 2))
    
    feature[:, 0] = ((df['AO'].shift(2) > 0.0) &
                     (df['AO'].shift(1) > df['AO'].shift(2)) &
                     (df['AO'] > df['AO'].shift(1)) &
                     (df['close'].shift(2) > df['Envelope_Lower'].shift(2)) &
                     (df['close'].shift(1) > df['close'].shift(2)) &
                     (df['close'] > df['close'].shift(1))).astype(int)
    
    feature[:, 1] = ((df['AO'].shift(2) < 0.0) &
                     (df['AO'].shift(1) < df['AO'].shift(2)) &
                     (df['AO'] > df['AO'].shift(1)) &
                     (df['close'].shift(2) < df['Envelope_Lower'].shift(2)) &
                     (df['close'].shift(1) < df['close'].shift(2)) &
                     (df['close'] < df['close'].shift(1))).astype(int)
    
    
    feature[0, :] = 0
    feature[1, :] = 0
    
    return feature

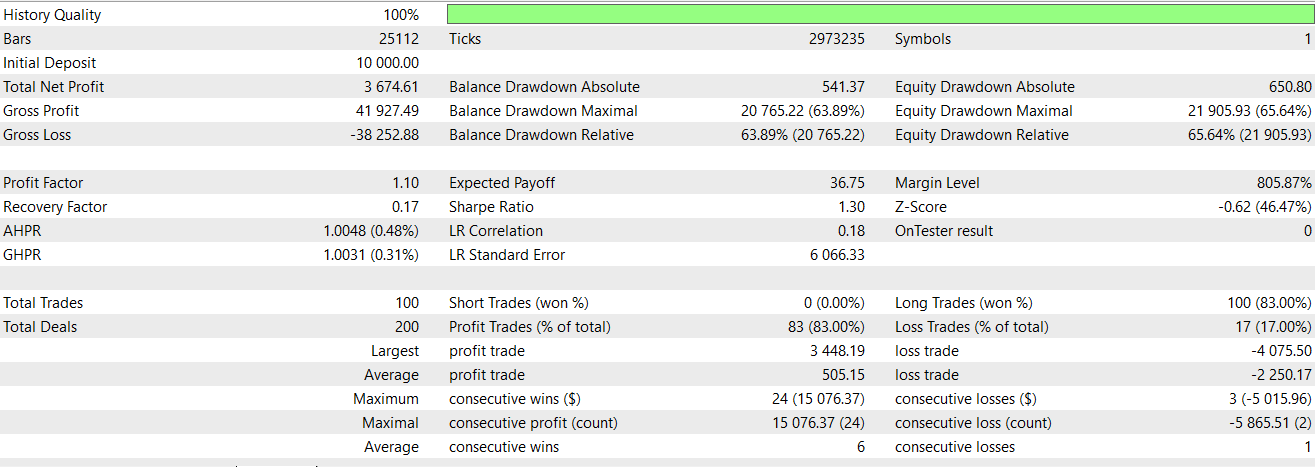
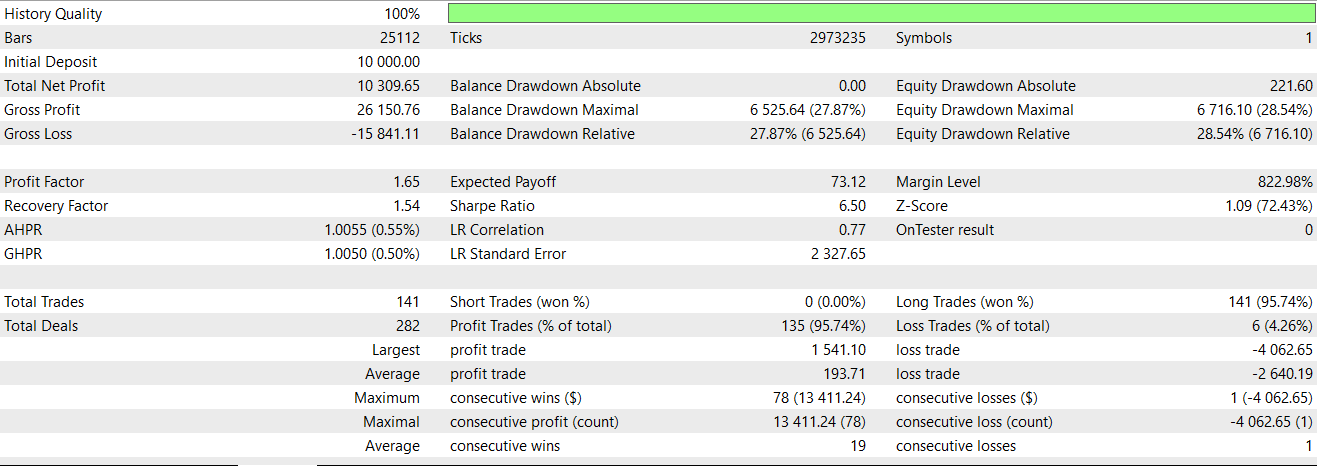
Daher geben wir in unserem obigen Code dem ersten Index eine 1, was bestätigt, dass ein Aufwärtssignal vorliegt, wenn der AO sich weiter nach oben bewegt und der Preis eine deutliche Beschleunigung aus einer positiven Zone erfährt. Wir müssen uns auch vergewissern, dass der Kurs oberhalb der unteren Hüllkurve bleibt und dass es sich nicht um einen „dead cat bounce“ handelt. Der zweite Index erhält eine 1, wenn der AO zunächst negativ ist, nachdem sie gefallen ist, dann aber möglicherweise in einem Retracement ansteigt, während der Kurs in einem starken Abwärtstrend unterhalb der unteren Hüllkurve weiter fällt. Anschließend werden die ersten 2 Indizes wie bei Merkmal 4 auf Null gesetzt. Beim Testen von Merkmal 8 gelingt es uns immer noch nicht, einen profitablen Vorwärtsgang zu erreichen. Dieser Bericht wird nachstehend wiedergegeben:

Feature_9

Wie bereits im letzten Artikel erwähnt, besteht die Hauptlogik unseres endgültigen Signalmusters darin, dass der AO umkippt, aber über Null bleibt, während der Kurs bis zur Mittellinie eintaucht und dann abprallt, um ein Aufwärtssignal zu erzeugen. Für das Abwärtssignal rollt der AO nach oben, bleibt aber unter Null, und der Kurs steigt bis zur Mittellinie an, scheitert dann aber daran, darüber hinaus zu steigen. Wir implementieren es in Python wie folgt:

def feature_9(df):
    """
//+------------------------------------------------------------------+
//| Check for Pattern 9.                                             |
//+------------------------------------------------------------------+
    """
    feature = np.zeros((len(df), 2))
    
    feature[:, 0] = ((df['AO'].shift(2) > df['AO'].shift(1)) &
                     (df['AO'].shift(1) > df['AO']) &
                     (df['AO'] > 0.0) &
                     (df['close'].shift(2) > df['Envelope_Mid'].shift(2)) &
                     (df['close'].shift(1) <= df['Envelope_Mid'].shift(1)) &
                     (df['close'] > df['Envelope_Mid'])).astype(int)
    
    feature[:, 1] = ((df['AO'].shift(2) < df['AO'].shift(1)) &
                     (df['AO'].shift(1) < df['AO']) &
                     (df['AO'] < 0.0) &
                     (df['close'].shift(2) < df['Envelope_Mid'].shift(2)) &
                     (df['close'].shift(1) >= df['Envelope_Mid'].shift(1)) &
                     (df['close'] < df['Envelope_Mid'])).astype(int)
    
    
    feature[0, :] = 0
    feature[1, :] = 0
    
    return feature

Unser Umsetzungsethos steht im Einklang mit den beiden oben genannten Funktionen, sodass ich die bereits behandelten Kernpunkte nicht noch einmal wiederholen werde. Die Prüfung unseres endgültigen Musters ergibt einen fast günstigen Vorwärtsgang. Dieser Bericht ist unten abgebildet;

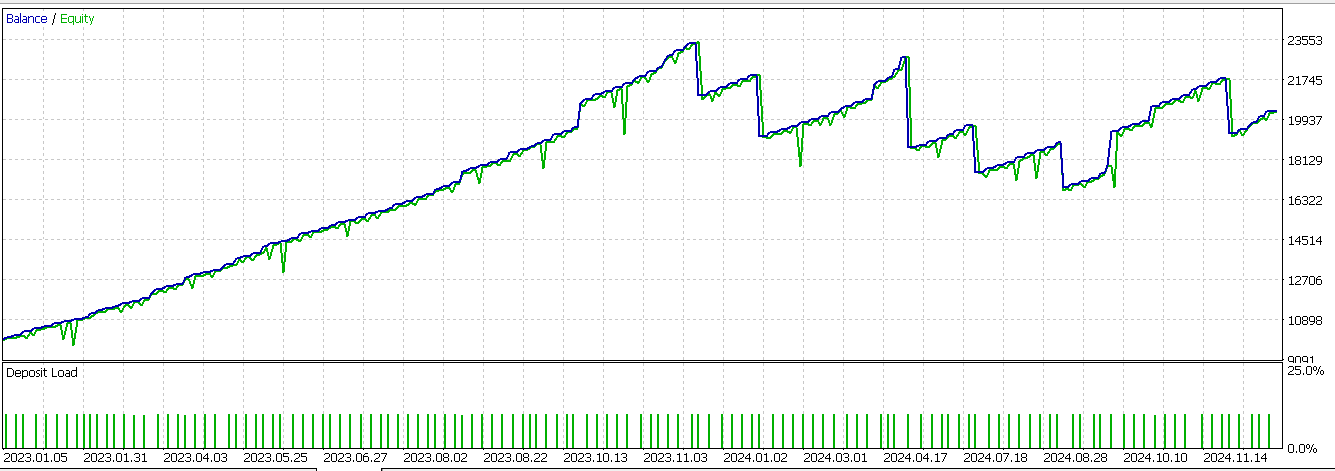
Schlussfolgerung

Zusammenfassend lässt sich sagen, dass wir die Integration des maschinellen Lernens erforscht haben, insbesondere durch den Einsatz eines CNN, das durch einen Punktproduktkern mit zeitübergreifender Aufmerksamkeit gesteuert wird, um die Signale der AO und Envelope-Kanäle zu verbessern. Unsere Testläufe konzentrierten sich auf die drei zuvor getesteten Muster (Muster-4, Muster-8 und Muster-9), um festzustellen, ob die Hinzufügung einer fortgeschrittenen neuronalen Filterung ihre Vorhersageleistung verbessern könnte.

Unsere dynamische CNN-Methode erwies sich als fruchtbar, insbesondere bei Feature_4 und Feature_9, bei denen wir die zuvor miserablen Walk-Forwards in Läufe umwandelten, bei denen sich die Verluste in Grenzen hielten. Der Aufmerksamkeitsmechanismus unseres Kerns ermöglichte es dem Netzwerk, sowohl die Kerngröße als auch die Kanaldimensionen dynamisch an die zeitliche Relevanz anzupassen, was dazu führte, dass tiefere Muster im Marktverhalten erfasst werden konnten. Diese Anpassungsfähigkeit kam uns zugute, da wir mit nicht-stationären Finanzmärkten zu tun haben. In diesem Fall ist es so, dass starre Modelle in der Regel aufgrund von Veränderungen der Volatilität, der Trenddynamik oder des Marktregimes unterdurchschnittlich abschneiden.

Allerdings waren nicht alle Ergebnisse positiv. Feature_8, das sich stark auf eine anhaltende Richtungsdynamik verlässt, hat selbst mit der verbesserten Anpassungsfähigkeit des CNN keine Rentabilität erreicht. Dies deutet darauf hin, dass bestimmte Signale unabhängig von den Modellverbesserungen begrenzt sind, was die Bedeutung der Indikator- und Signalauswahl für die Handelsstrategie unterstreicht. Neben dem überwachten Lernen, das wir in diesem Artikel erforscht haben, können wir das Verstärkungslernen als Mittel zur Verbesserung unserer Signale wieder aufgreifen. In den nächsten oder künftigen Artikeln könnte dies für die hier erörterten Merkmale untersucht werden.

Name	Beschreibung
WZ-76.mq5	Der Assistent hat einen Expert Advisor zusammengestellt, dessen Header-Highlights Dateien enthalten
SignalWZ-76.mqh	Nutzerdefinierte Signalklasse, die vom MQL5-Assistenten in der Baugruppe verwendet wird
76-4.onnx	Exportiertes Netzwerk für Signalmuster-4
76-8.onnx	Exportiertes Netz für Signalmuster-8
76-9.onnx	Exportiertes Netz für Signalmuster-9