MQL5で自己最適化エキスパートアドバイザーを構築する（第11回）：初心者向け線形代数入門

前回の記事では、行列分解について解説し、MQL5の線形代数コマンドを活用する多くの利点を紹介しました。ただし、その際には読者が時系列モデルや統計解析の基礎知識を持っていることを前提としていました。しかし振り返ると、この前提はすべての読者に当てはまるとは限りません。

初めてこれらの概念に触れる読者にとっては、前回の記事は意図したほど役立たなかった可能性があります。内容が急速に進み、多くの概念が連続して紹介されたためです。そこで本稿では、数学的背景のない読者でも理解できるように、基礎から丁寧に説明します。

本記事では、予備知識がないことを前提に解説します。そのため、すべての読者が内容を理解し、MQL5の行列・ベクトルAPIの価値を実感することができます。このAPIは強力ですが、それだけでは十分ではなく、単独では機能しません。線形代数の原理を理解することで、知的かつ効果的に活用できるようになります。

本記事は、正式な数学教育を受けていない読者への橋渡しとして位置づけます。比較のために、線形代数の知識がないMQL5開発者が書いたコードと、基礎原理を理解している開発者が書いたコードを並べて示します。この並列比較により、線形代数の利点が直感的に明確になります。

理論的な概念はすべて、MetaTrader 5ターミナル上での実際の市場データを用いた実践的な応用例に結び付けて解説します。数学理論を手を動かして適用することで、MQL5の線形代数コマンドの柔軟性と実用性を実感できます。

今日は、複数のターゲットを同時に予測できる統計モデルを構築します。通常、線形回帰モデルは単一のターゲット（例：将来の価格変動）を予測するために使用されますが、今回は次の4つの異なるターゲットを予測します。

• 将来の終値の移動平均
• 将来の高値の移動平均
  
• 将来の安値の移動平均
  
• 将来の価格

これらの予測は、取引戦略におけるエントリーおよびエグジットのルール、さらにポジション決済のフィルタとして活用します。MQL5の行列・ベクトルAPIは、現代的な機械学習アプリケーションを構築するための強力なツールです。しかし、このAPIの潜在能力を十分に引き出すには、線形代数の基本原理を理解することが不可欠です。

線形代数はしばしば抽象的で理論的な学問と考えられますが、本記事ではその概念を具体化し、価値を明確に示します。まず議論の動機を提示し、必要な数学的表記と理論を解説します。そして最後に、複数ターゲットを同時に予測できる数値駆動型の取引アルゴリズムの具体例を紹介します。 

保守可能なコードベース

市場価格、例えば始値、高値、安値、終値のコレクションを扱う際には、これらのデータを行列形式で格納することが便利です。MQL5では、行列は行優先で、次に列の順にインデックスが付けられます。そこでまず、3行5列で初期値がすべてゼロの新しい行列Aを定義します。つまり、行列Aは3行5列を持ち、すべての要素が初期状態でゼロに設定されます。続いて、現在の状態の行列Aを表示します。図1に示されている通り、確かにすべての要素がゼロで埋められています。

//--- Let's first create an empty matrix
matrix A=matrix::Zeros(3,5);

//--- Peek at the matrix
Print("Original A matrix");
Print(A);

図1：空の行列Aの可視化

次に、各行にラベルを付けます。1行目はすべて1で、2行目はすべて2で、3行目はすべて3で埋めます。

ご覧のように、MQL5で行列の要素にアクセスする際の表記は、必ず行インデックスを先に、次に列インデックスを角括弧内に書き、行列に対応する識別子の隣に置く形になります。行列Aを再度確認すると、値が正しく入力されていることがわかります。図2でもその通りであることが示されています。

//--- The notation A[R,C] describes the Row and Column we want to manipulate
//--- We will set all the values in Row 1 to be 1
A[0,0] = 1;
A[0,1] = 1;
A[0,2] = 1;
A[0,3] = 1;
A[0,4] = 1;

//--- We will set all the values in Row 2 to be 2
A[1,0] = 2;
A[1,1] = 2;
A[1,2] = 2;
A[1,3] = 2;
A[1,4] = 2;

//--- We will set all the values in Row 3 to be 3
A[2,0] = 3;
A[2,1] = 3;
A[2,2] = 3;
A[2,3] = 3;
A[2,4] = 3;

Print("Current A matrix");
Print(A);

図2：演習用に行列Aの各行にラベルを付ける

次に、行列内の値を操作してみましょう。たとえば、行列Aの2行目のすべての値を5倍にしたいとします。単純な実装方法としては、forループを作成し、2行目の各要素を順番に処理して5倍し、その結果を格納する方法が考えられます。この方法でも、目的の結果を得ることができ、機能テストも問題なく通過するでしょう。

しかし、なぜこの作業でforループの使用を避けたいのか、理由が思い浮かびますか。

//--- Let's multiply all the values of Row 2 by 5 and leave all the other rows the same.

//--- Bad performing code
//--- Copy matrix A
matrix example_1;
example_1.Assign(A);

//--- Loop over matrix A and multiply each element by 5 and then replace the original elements
for(int i =0;i<5;i++)
{
   example_1[1,i] = example_1[1,i] * 5;
}

//--- Done
Print("Example 1: ");
Print(example_1);

図3：行列Aに対してforループで操作すると、Aが大きくなると処理が遅くなる可能性がある

少し改善した方法を考えてみましょう。ループを使う代わりに、行列の2行目を行ベクトルとして選択し、それに5を掛けて、結果を元の位置に戻す方法です。この方法でも同じ効果を得られ、よりエレガントです。それでも、読者の皆さんに改めて質問します。この方法も最適ではない理由が思い浮かびますか。

//--- Slightly better code
//--- Copy the row, multiply it and then put it back
matrix example_2;
vector copy_vector;

example_2.Assign(A);

copy_vector = example_2.Row(1);

example_2.Row(copy_vector*5,1);

Print("Example 2");
Print(example_2);

図4：行列Aに対してベクトル操作を使う方法は、従来のforループよりも優れているが、最適とは言えない

最後に、この文脈で適切とされる方法を示します。まずスケーリングベクトルを作成し、そのベクトルを行列Aに適用するために行列積を使用します。示した通り、3つのコード例はいずれも同じ結果を出します。しかし、読者の皆さんは、いくつかの重要な違いに気づくはずです。

3つ目の方法は、最も少ない行数でコードを書くことができます。これは、日々の取引業務で線形代数を活用する大きな利点の1つを示しています。すなわち、より簡潔で保守可能なコードを作成できるということです。多くの開発者にとって、これだけでも線形代数の学習に時間を投資する十分な理由になると思います。しかし、これ以外にも多くの利点があり、それらは今後順に示していきます。これは単なる良い出発点にすぎません。

//--- Reliable code
matrix example_3,scaler;
vector scale = {1,5,1};

scaler.Diag(scale);
example_3 = scaler.MatMul(A);

//--- Done 
Print("Example 3");
Print(example_3);

図5：専用の行列・ベクトルメソッドが存在する場合は、それを使うのが常に最良である

では、この例をさらに発展させてみましょう。これまでは2行目のみを5倍しましたが、今回は1行目を2倍、最終行を10倍、中央の行は変更せずに処理してみます。この時点で、forループを使う際の問題点が見えてくるかもしれません。行列Aに対する操作の数が増えるにつれて、ループの長さも増え、書くコードの行数も増えます。さらに、行列Aが十分に大きい場合、ループのように各値を1つずつ順番に処理すると、特にバックテスト中に実行速度が大幅に低下する可能性があります。 

//--- Now, multiply the first and last rows by 2 and 10, but leave the middle row as it is.

//--- Loops can slow us down during backtests, especially if they must be repeated often.
for(int i =0;i<5;i++)
{
   example_1[0,i] = example_1[0,i] * 2;
   example_1[2,i] = example_1[2,i] * 10;
}

//--- Done
Print("Example 1");
Print(example_1);

図6：同じ効果を得るためだけに、forループではさらに多くの行数のコードを書く必要があります。

同様に、行を選択して再代入する方法も、操作の数が増えるにつれて複雑さが増していきます。この方法は単純なforループよりは優れていますが、それでもコードが冗長になり、エラーが発生する可能性が高くなります。

//--- The difference between example 2 and 3 starts to show
//--- Copy the row, multiply it and then put it back
vector copy_vector_2;

copy_vector = example_2.Row(0);
copy_vector_2 = example_2.Row(2);

example_2.Row(copy_vector*2,0);
example_2.Row(copy_vector_2*10,2);

//--- Done
Print("Example 2");
Print(example_2);

図7：汎用の行列・ベクトルメソッドを連鎖させる方法でも作業は達成できるが、さらに効率的な方法がある

行列積を活用することで、より良い方法が可能です。このアプローチでは、変更されるのはスケーリング値だけで、関わる行数にかかわらず、コードの他の部分はほとんど同じままです。3つの方法はいずれも同じ出力を生成します。しかし、これらを並べて見た後で、読者の皆さんに質問です。大量の過去の市場データを扱う場合、どのアプローチが最も適切に思えるでしょうか。

//--- Reliable code
vector scale_2 = {2,1,10};
scaler.Diag(scale_2);
example_3 = scaler.MatMul(example_3);

//--- Done
Print("Example 3");
Print(example_3);

図8：より少ないコード行数で同じ出力を得るには、より簡潔にプログラミングすることができる

バックテストに必要な時間

従来のforループを使う場合、特にバックテストのような時間が重要な処理では、すべてのデータポイントを効率的に処理できないことがあります。ここで第2の重要なポイントです。行列・ベクトルAPIを適切に使用することで、コードベースの保守性が向上するだけでなく、取引戦略の実行時間もより効率的になります。

結局のところ、多くの読者はおそらく、取引に役立つ強力なAIモデルを構築したいと考えているでしょう。モデルは有益な意思決定をおこなうために、多くのデータへのアクセスが必要です。そして、そのデータをモデルに投入する前に、特定の前処理や操作をおこなう必要があります。

これらの操作を非効率的におこなうと、アプリケーションを構築するために必要なコード行数が急速に増加します。特にforループに依存する場合は顕著です。コード量が増えると、バックテストに必要な時間も比例して増加します。

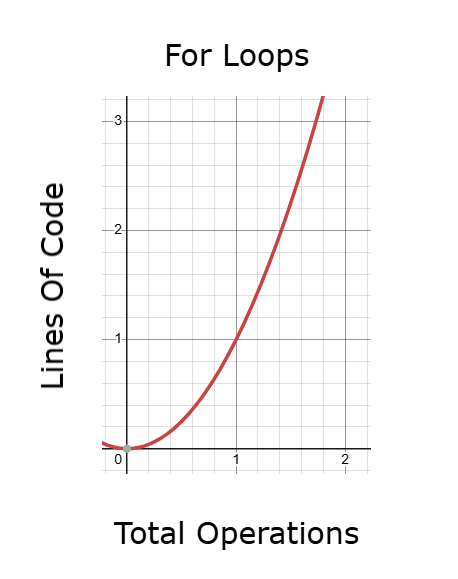
図9：forループはバックテスト中に実行時間が長くなりすぎるコードを生成する可能性がある

より良い代替策は、ベクトルや行列操作を連鎖させる方法です。この方法は従来のループよりもはるかに高速ですが、行を繰り返しコピー、修正、再代入するような操作が多くなると、やはり扱いが面倒になります。そのような操作が増えると、コードの実行に必要な時間も増加し、バックテストのパフォーマンスやモデル最適化に影響を与えます。

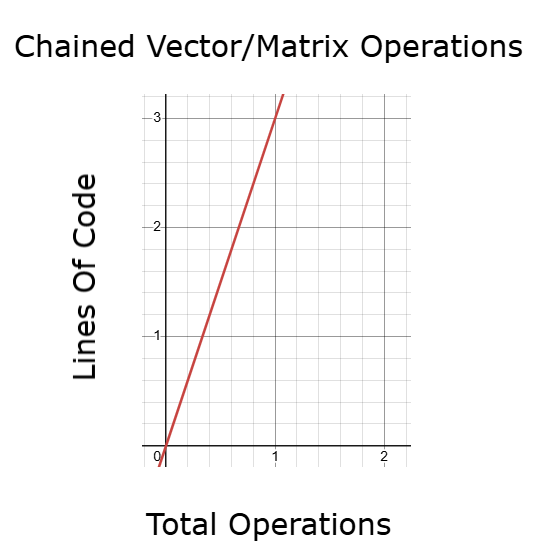
図10：行列・ベクトルAPIを連鎖させる方法はforループよりも高速だが、さらに改善の余地がある

一方で、線形代数に基づいた適切なベクトル・行列操作を使用することで、データ量が増えても、実行時間を制御し、コードの行数やバックテスト時間をほぼ一定に保つことができます。これはどんなアプリケーションにおいても非常に望ましい性質です。つまり、コード量を比例して増やさなくても、より多くの操作を実行でき、実行時間も増加させずに済むため、機械学習モデルの反復や最適化をより効率的におこなえます。多くの読者は、線形代数のいくつかの基本概念を理解するだけで、これほどの進歩が可能であることに驚くでしょう。実践で意味のある改善を得るために、高度な理論は必ずしも必要ではありません。

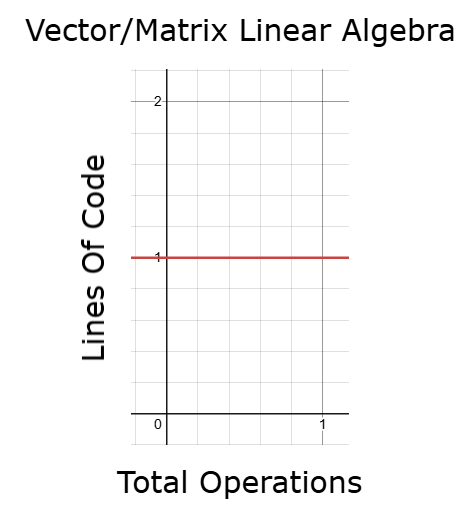
図11：線形代数を活用することで、アプリケーションの実行時間をほぼ一定に保つことができる

精度

ここで、技術的な議論ではしばしば見過ごされがちな重要な問題についても触れておきたいと思います。それは精度です。私は、このテーマは十分な注意や検討を受けていないと考えています。精度は、信頼性の高い取引戦略を構築するうえで欠かせない要素の1つです。バックテストから得られる結果は正確である必要があり、アプリケーション内部でおこなわれる計算や意思決定も、正確で信頼できるものでなければなりません。

次のシナリオを考えてみましょう。例として示したコードスニペットでは、基本的な浮動小数点の引き算「0.3 - 0.1」をおこなっています。しかし、コンピュータは結果を0.199999…と報告し、期待される0.2にはなりません。これは浮動小数点演算に関連するコンピュータサイエンス上のよく知られた問題であり、MQL5に特有のものではありません。 

ここで私が強調したいポイントは次の通りです。このような引き算をループ内で繰り返す状況を想像してください。さらに、行列Aのように100万行以上ある行列をループして、各行でこの演算を行うことを想像してください。すると、わずかな精度の誤差が累積し、最終的に結果に重大な数値的不安定性をもたらすことが簡単に理解できます。

大きな行列に対してこのような単純な引き算を直接おこなうなど、計算を不注意におこなうことは非効率的であり、精度が高く数値的に安定した結果を生み出しません。

さらに、前述の例のように、値を繰り返しコピーしたり、新しいオブジェクトを作成したり、データを再割り当てしたり、メモリを常に割り当てたり解放したりするアルゴリズムを考えると、この問題はさらに深刻になります。コンピュータには限られたメモリしかありません。行列操作を非効率的におこない、オブジェクトを生成・破棄し続けると、不要にメモリの負荷を増大させることになります。見過ごされがちですが、このような雑なメモリ管理は実際に大きな影響を及ぼします。

さらに、MQL5の行列・ベクトルAPIや、今後紹介するサポートライブラリの多くには、これらの問題を考慮して設計された既知のアルゴリズムが実装されています。これらの実装は、浮動小数点誤差を最小化し、数値的安定性を最大化するように最適化されています。対照的に、開発者が手動のforループのような非効率的な方法を選択すると、これらの問題に直面する可能性を知らず知らずのうちに高めてしまいます。

//--- Why should you care?
//--- Let's start with an often overlooked need, precision!
Print("Our computers have limited memory to store numbers with precision");
Print("What is 0.3 - 0.1");
Print(0.3-0.1);
Print("You and I know the correct answer is 0.2");

図12：線形代数に基づいた適切な行列・ベクトル操作を使うことで、こうした誤差を最小化できる

トレーダーとして線形代数をどのように活用できるか

線形代数を学ぶ利点を理解したところで、次に、線形代数を使って意思決定をおこなう際の基本的なルールについて考えてみましょう。これらの核心的なルールを理解することは、非常に有益なスキルです。

初心者向けの注意点 ：ここでの目標は、公式を暗記させることではありません。むしろ、原理を深く理解し、自然に直感的に思い出せるレベルにすることです。

線形代数の理解を始めるには、まず基本的な代数をしっかり把握する必要があります。代数とは本質的に、未知の量に関する数学です。まず簡単な例から始めましょう（図13）。この方程式は、「ある未知の値xに2を掛けると4になる」と示しています。xを求めるには、両辺を2で割ります。解を確認したければ、元の方程式にx = 2を代入し、2 × 2が確かに4になるかどうかを確認すればよいのです。 基本的な内容に感じるかもしれませんが、より高度な概念を理解するための土台となります。

図13：xの値が2であることを示す、代数の簡単な問題の可視化

次に、少し変化させて考えてみましょう。方程式が「A × 2 = 4」であった場合です。この場合、両辺をAで割り、解はx = 4 ÷ Aとなります。ここでAの値は与えられていないため、これで問題の解答は完了です。

図14：図13の問題の少し複雑なバージョンの考察

では、Aが単なる数値ではなく行列であった場合はどうなるでしょうか。ここで、高校で学んだ代数から、線形代数へと移行します。ここでAは行列です。前回のように両辺をAで割ろうと考えがちですが、線形代数では行列の割り算は定義されていません。代わりに、行列の逆行列を用います。行列が逆行列を持つ場合、両辺にその逆行列を掛けることで方程式を解くことができます。

図15：線形代数は簡単な例と同じ論理に基づいているが、いくつかのルールを変更する必要がある

これを市場データの文脈で考えるとどうなるでしょうか。行列Aが現在の市場データ（例えば価格レベル）を表すとします。ベクトルyは、予測したい将来の価格です。私たちは、「現在のデータに係数ベクトルを掛けると、将来の価格レベルが得られる」のような係数ベクトルを求めたいわけです。

しかし、ここに問題があります。すべての行列が逆行列を持つわけではありません。実際、逆行列を持たない行列を無理に逆行列化すると、取引アルゴリズムがクラッシュしたり、信頼できない結果を返したりします。このため、遭遇した行列を盲目的に逆行列化することは避けます。代わりに、多くの場合は、信頼して逆行列化できる部分行列や、数値的に安定した方法（QR分解、SVD、擬似逆行列など）で処理できるデータの一部を扱う方が安全で安定しています。

図16：任意の線形方程式系への解の一般化

線形代数を活用して取引を改善する

線形代数を用いた線形方程式系の解法の基本ルールにある程度慣れたところで、次は係数ベクトルxを求める方法を実際に応用していきます。この例では、前に説明した公式が単一のターゲットだけでなく、複数のターゲットyに対しても同様に解を求められることを示したいと思います。まず、システムの定数を定義しましょう。今回は、モデルがいくつの入力を受け取るかを指定する必要があります。このモデルでは、8つの入力を受け取ることにします。

//+------------------------------------------------------------------+
//|                                            Linear Regression.mq5 |
//|                                               Gamuchirai Ndawana |
//|                    https://www.mql5.com/ja/users/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Ndawana"
#property link      "https://www.mql5.com/ja/users/gamuchiraindawa"
#property version   "1.00"

//+------------------------------------------------------------------+
//| System constants                                                 |
//+------------------------------------------------------------------+
#define TOTAL_INPUTS 8

次に、重要なシステムパラメータを定義する必要があります。たとえば、取得する過去のバーの本数、将来予測をおこなう期間、使用する時間枠、その他関連する設定などです。これらのすべての詳細は、システムパラメータとして格納されます。

//+------------------------------------------------------------------+
//| System parameters                                                |
//+------------------------------------------------------------------+
int bars = 90;                                        //Number of historical bars to fetch
int horizon = 1;                                      //How far into the future should we forecast
int MA_PERIOD = 2;                                    //Moving average period
ENUM_TIMEFRAMES TIME_FRAME = PERIOD_D1;               //User Time Frame
ENUM_TIMEFRAMES RISK_TIME_FRAME = PERIOD_D1;          //Time Frame for our ATR stop loss
double sl_size = 2;                                   //ATR Stop loss size

どのアプリケーションにおいても、依存関係は重要です。なぜなら、依存関係を利用することで、プロジェクトごとに書き直す必要があるコードの総量を減らせるからです。そこで、いくつかの重要な依存関係を読み込みます。たとえば、Trade Impedanceという依存関係は、MetaTrader 5のすべてのバージョンにあらかじめインストールされています。残りの2つの依存関係は、私たちの取引活動のためにカスタムで作成したものです。

//+------------------------------------------------------------------+
//| Dependencies                                                     |
//+------------------------------------------------------------------+
#include <Trade\Trade.mqh>
#include <VolatilityDoctor\Time\Time.mqh>
#include <VolatilityDoctor\Trade\TradeInfo.mqh>

本システムでは、アプリケーション内のさまざまな文脈で使用される重要なグローバル変数も定義します。たとえば、現在のインジケーターの値を格納するグローバル変数があります。また、依存関係で使用される値を格納する変数や、データから学習した係数を保持する変数もあります。これには、ATRの値やシステム内のさまざまな可動要素に関する値などが含まれます。

//+------------------------------------------------------------------+
//| Global Variables                                                 |
//+------------------------------------------------------------------+
int        ma_close_handler,ma_high_handler,ma_low_handler;
double     ma_close[],ma_high[],ma_low[];
Time       *Timer;
TradeInfo  *TradeInformation;
vector     bias,temp,temp_2,temp_3,temp_4,temp_5,Z1,Z2;
matrix     X,y,prediction,b;
int        time;
CTrade Trade;
int state;
int atr_handler;
double atr[];

初期化時に、システムは読み込んだカスタム依存関係の新しいオブジェクトを作成します。タイマーは、新しいローソク足の形成を追跡する役割を担います。取引形成モジュールは、最小取引量、Ask、Bidなどの重要な情報を返します。また、移動平均を追跡するためのハンドラも作成し、行列やベクトルを開始用のプレースホルダー値1で初期化して、処理をスタートできる状態にします。

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---
   Timer                   = new Time(Symbol(),TIME_FRAME);
   TradeInformation        = new TradeInfo(Symbol(),TIME_FRAME);
   ma_close_handler        = iMA(Symbol(),TIME_FRAME,MA_PERIOD,0,MODE_SMA,PRICE_CLOSE);
   ma_high_handler        = iMA(Symbol(),TIME_FRAME,MA_PERIOD,0,MODE_SMA,PRICE_HIGH);
   ma_low_handler        = iMA(Symbol(),TIME_FRAME,MA_PERIOD,0,MODE_SMA,PRICE_LOW);

   bias = vector::Ones(TOTAL_INPUTS);
   Z1 = vector::Ones(TOTAL_INPUTS);
   Z2 = vector::Ones(TOTAL_INPUTS);
   X = matrix::Ones(TOTAL_INPUTS,bars);
   y = matrix::Ones(1,bars);
   time = 0;
   state = 0;
   atr_handler = iATR(Symbol(),RISK_TIME_FRAME,14);
//---
   return(INIT_SUCCEEDED);
  }

アプリケーションの使用が終了した際には、メモリリソースに紐づくオブジェクトを解放します。これはMQL5における良い習慣であり、私たちは常にこれを守ります。

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//---
   IndicatorRelease(atr_handler);
   IndicatorRelease(ma_close_handler);
   IndicatorRelease(ma_high_handler);
   IndicatorRelease(ma_low_handler);
  }

OnTickハンドラで価格の更新を受け取るたびに、まず新しいローソク足が完全に形成されたかどうかを確認します。もし形成されていれば、すべてのインジケーター値を対応する配列にコピーし、モデルが市場予測をおこなえるように準備します。その後、現在の終値を追跡し、買い・売りの両方のストップロスを計算します。

次に、モデルが予測する価格レベルを表示します。ここで予測しているのは、終値の移動平均、高値の移動平均、安値の移動平均、そして価格そのものです。現在ポジションが開かれていない場合は、まず関連する状態変数をリセットします。その後、将来の予想終値と予想終値移動平均の関係を確認します。

一般的には、アルゴリズムが終値の移動平均が現在の終値を上回ると予想しているかを確認したいです。これは、現在の価格がモデルが考える公正価値よりも低く取引されていることを示唆しており、価格が過小評価されている可能性があります。

さらに確認のため、ストップロスがヒットする可能性が低いことも確認します。買い条件では、安値移動平均が買いストップロスを下回ることが予想されないかを確認します。売り条件では、高値移動平均が売りストップロスを上回ることが予想されないかを確認します。いずれかの条件が破られた場合は、ポジションのエントリーを避けます。

加えて、各移動平均をその補完ペアと比較します。買いの場合は、将来の安値移動平均が現在の値より高くなることを期待します。売りの場合は、将来の安値移動平均が現在の値より低くなることを期待します。同様に、買いの場合は、将来の高値移動平均が現在の値を上回ると予想します。

ポジションをクローズするタイミングでは、まず価格が逆方向に動く可能性があるかどうかを確認します。もし任意の移動平均がストップロスを超える可能性があると予想される場合は、即座に取引を終了します。そうでなければ、ストップロスをより有利な方向にトレーリングさせ続けます。

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//---
   if(Timer.NewCandle())
     {
      CopyBuffer(atr_handler,0,0,1,atr);
      CopyBuffer(ma_close_handler,0,0,1,ma_close);
      CopyBuffer(ma_low_handler,0,0,1,ma_low);
      CopyBuffer(ma_high_handler,0,0,1,ma_high);

      setup();

      double c =  iClose(Symbol(),TIME_FRAME,0);
      double buy_sl = (TradeInformation.GetBid() - (sl_size * atr[0]));
      double sell_sl = (TradeInformation.GetAsk() + (sl_size * atr[0]));


      Comment("Forecasted MA: ",prediction[0,0],"\nForecasted MA High: ",prediction[1,0],"\nForecasted MA Low: ",prediction[2,0],"\nForecasted Price: ",prediction[3,0]);

      if(PositionsTotal() == 0)
        {
         state = 0;
         if((prediction[0,0] > c) && (prediction[2,0] > buy_sl) && (prediction[3,0] > c) && (prediction[2,0] > ma_low[0]) && (prediction[1,0] > ma_high[0]))
           {
            Trade.Buy(TradeInformation.MinVolume(),Symbol(),TradeInformation.GetAsk(),buy_sl,0);
            state = 1;
           }
         if((prediction[0,0] < c) && (prediction[1,0] < sell_sl) && (prediction[3,0] < c) && (prediction[2,0] < ma_low[0]) && (prediction[1,0] < ma_high[0]))
           {
            Trade.Sell(TradeInformation.MinVolume(),Symbol(),TradeInformation.GetBid(),sell_sl,0);
            state = -1;
           }
        }

      if(PositionsTotal() > 0)
        {
         double current_sl = PositionGetDouble(POSITION_SL);
        
         if(((state == -1) && (prediction[0,0] > c) && (prediction[1,0] > current_sl)) || ((state == 1)&&(prediction[0,0] < c)&& (prediction[2,0] < current_sl)))
            Trade.PositionClose(Symbol());
         if(PositionSelect(Symbol()))
           {
            

            if((state == 1) && ((ma_close[0] - (2 * atr[0]))>current_sl))
              {
               Trade.PositionModify(Symbol(),(ma_close[0] - (2 * atr[0])),0);
              }

            else
               if((state == -1) && ((ma_close[0] + (1 * atr[0]))<current_sl))
                 {
                  Trade.PositionModify(Symbol(),(ma_close[0] + (2 * atr[0])),0);
                 }
           }
        }
     }
  }

次に、上記のタスクに対応するために用意された個々の関数について説明します。最初の関数はprepare_data()です。この関数は1つの核心的な目的を持っています。それは、必要なすべての価格データを入力データ行列xにコピーすることです。具体的には、始値を取得し、始値の平均値と標準偏差を計算し、データを平均値で引き、標準偏差で割ることで正規化します。この処理はすべての入力に対して繰り返されます。さらに、すべての移動平均ハンドラの値もコピーされ、ターゲット配列yに格納されます。

//+------------------------------------------------------------------+
//| Prepare the training data for our model                          |
//+------------------------------------------------------------------+
void prepare_data(void)
  {
//--- Reshape the matrix
   X = matrix::Ones(TOTAL_INPUTS,bars);

//--- Store the Z-scores
   temp.CopyRates(Symbol(),TIME_FRAME,COPY_RATES_OPEN,horizon,bars);
   Z1[0] = temp.Mean();
   Z2[0] = temp.Std();
   temp = ((temp - Z1[0]) / Z2[0]);
   X.Row(temp,1);

//--- Store the Z-scores
   temp.CopyRates(Symbol(),TIME_FRAME,COPY_RATES_HIGH,horizon,bars);
   Z1[1] = temp.Mean();
   Z2[1] = temp.Std();
   temp = ((temp - Z1[1]) / Z2[1]);
   X.Row(temp,2);

//--- Store the Z-scores
   temp.CopyRates(Symbol(),TIME_FRAME,COPY_RATES_LOW,horizon,bars);
   Z1[2] = temp.Mean();
   Z2[2] = temp.Std();
   temp = ((temp - Z1[2]) / Z2[2]);
   X.Row(temp,3);

//--- Store the Z-scores
   temp.CopyRates(Symbol(),TIME_FRAME,COPY_RATES_CLOSE,horizon,bars);
   Z1[3] = temp.Mean();
   Z2[3] = temp.Std();
   temp = ((temp - Z1[3]) / Z2[3]);
   X.Row(temp,4);

//--- Store the Z-scores
   temp.CopyIndicatorBuffer(ma_close_handler,0,horizon,bars);
   Z1[4] = temp.Mean();
   Z2[4] = temp.Std();
   temp = ((temp - Z1[4]) / Z2[4]);
   X.Row(temp,5);

//--- Store the Z-scores
   temp.CopyIndicatorBuffer(ma_high_handler,0,horizon,bars);
   Z1[5] = temp.Mean();
   Z2[5] = temp.Std();
   temp = ((temp - Z1[5]) / Z2[5]);
   X.Row(temp,6);

//--- Store the Z-scores
   temp.CopyIndicatorBuffer(ma_low_handler,0,horizon,bars);
   Z1[6] = temp.Mean();
   Z2[6] = temp.Std();
   temp = ((temp - Z1[6]) / Z2[6]);
   X.Row(temp,7);

//--- Labelling our targets
   temp.CopyIndicatorBuffer(ma_close_handler,0,0,bars);
   temp_2.CopyIndicatorBuffer(ma_high_handler,0,0,bars);
   temp_3.CopyIndicatorBuffer(ma_low_handler,0,0,bars);
   temp_4.CopyRates(Symbol(),TIME_FRAME,COPY_RATES_CLOSE,0,bars);

//--- Reshape y
   y.Reshape(4,bars);

//--- Store the targets
   y.Row(temp,0);
   y.Row(temp_2,1);
   y.Row(temp_3,2);
   y.Row(temp_4,3);
  }

次に、モデルを適合させる関数を定義します。この関数は、まず適切な行列とベクトルを作成することから始まります。次に、x行列をOpenBlassライブラリを使って分解し、分解された行列を先に紹介した変数に格納します。閉形式解に従うことで、xからBを求めることができ、その後Bから学習済みの係数を出力します。

//+------------------------------------------------------------------+
//| Fit our model                                                    |
//+------------------------------------------------------------------+
void fit(void)
  {
//--- Fit the model
   matrix OB_U,OB_VT,OB_SIGMA;
   vector OB_S;

   PrintFormat("Computing Singular Value Decomposition of %s Data using OpenBLAS",Symbol());
   X.SingularValueDecompositionDC(SVDZ_S,OB_S,OB_U,OB_VT);
   OB_SIGMA.Diag(OB_S);
   b = y.MatMul(OB_VT.Transpose().MatMul(OB_SIGMA.Inv()).MatMul(OB_U.Transpose()));
   Print("OLS Solutions: ");
   Print(b);
  }

予測を生成するために、再びすべての入力データを取得します。これは、prepare_dataでおこなったのと同様です。そして、最後に行列積を1回おこない、Bから予測値を得ます。つまり、係数ベクトルを入力データに掛けるのです。

//+------------------------------------------------------------------+
//| Get a prediction from our multiple output model                  |
//+------------------------------------------------------------------+
void predict(void)
  {
//--- Prepare to get a prediction
//--- Reshape the data
   X = matrix::Ones(TOTAL_INPUTS,1);

//--- Get a prediction
   temp.CopyRates(Symbol(),TIME_FRAME,COPY_RATES_OPEN,0,1);
   temp = ((temp - Z1[0]) / Z2[0]);
   X.Row(temp,1);

   temp.CopyRates(Symbol(),TIME_FRAME,COPY_RATES_HIGH,0,1);
   temp = ((temp - Z1[1]) / Z2[1]);
   X.Row(temp,2);

   temp.CopyRates(Symbol(),TIME_FRAME,COPY_RATES_LOW,0,1);
   temp = ((temp - Z1[2]) / Z2[2]);
   X.Row(temp,3);

   temp.CopyRates(Symbol(),TIME_FRAME,COPY_RATES_CLOSE,0,1);
   temp = ((temp - Z1[3]) / Z2[3]);
   X.Row(temp,4);

   temp.CopyIndicatorBuffer(ma_close_handler,0,0,1);
   temp = ((temp - Z1[4]) / Z2[4]);
   X.Row(temp,5);
   
   temp.CopyIndicatorBuffer(ma_high_handler,0,0,1);
   temp = ((temp - Z1[5]) / Z2[5]);
   X.Row(temp,6);

   temp.CopyIndicatorBuffer(ma_low_handler,0,0,1);
   temp = ((temp - Z1[6]) / Z2[6]);
   X.Row(temp,7);

   Print("Prediction Inputs: ");
   Print(X);

//--- Get a prediction
   prediction.Reshape(1,4);
   prediction = b.MatMul(X);
   Print("Prediction");
   Print(prediction);
  }

最後に、OnTickハンドラで価格の更新を受け取るたびに、setup関数を呼び出します。この関数は、先ほど説明した3つの主要な関数を呼び出します。すなわち、データを準備し、モデルを適合させ、予測を取得するのです。

//+------------------------------------------------------------------+
//| Obtain a prediction from our model                               |
//+------------------------------------------------------------------+
void setup(void)
  {
   prepare_data();
   fit();

   Print("Training Input Data: ");
   Print(X);

   Print("Training Target");
   Print(y);

   predict();
  }
//+------------------------------------------------------------------+

#undef TOTAL_INPUTS
//+------------------------------------------------------------------+

これらすべてが整ったところで、アプリケーションを履歴データでテストする準備が整いました。下の図17に示すように、2022年から2025年までのEUR/USD市場データに対してアプリケーションを適用しました。2年間分の履歴データでバックテストをおこなっています。

図17：バックテストの対象はEUR/USD市場の過去2年分のデータにわたる

また、実際のティックに基づいたランダムな遅延設定を選択し、市場状況をできるだけ正確に再現しました。アプリケーションのパフォーマンスを現実的にシミュレーションしたい場合は、同じ設定を使用することをお勧めします。

図18：取引アプリケーションを現実的な市場条件でテストするためにランダム遅延設定を選択する

図18では、アプリケーションが4つの独立した予測を正しく生成していることがわかります。これは、関心のある各価格レベルに対して1つずつの予測をおこなっています。アプリケーションは、メイン部分で設計されたフィルターを使用し、4つの予測すべてに基づいてポジションを開きます。

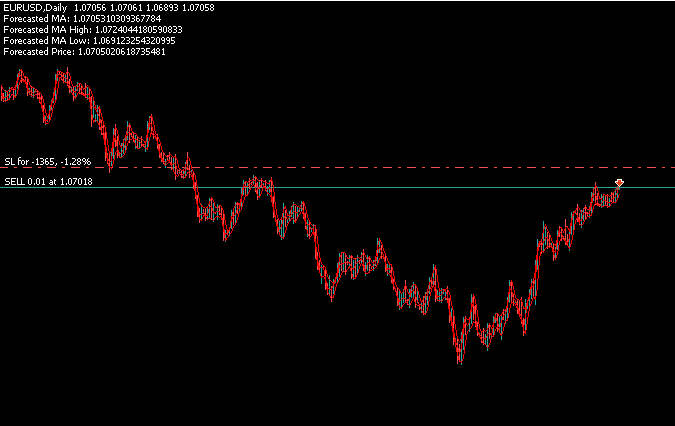
図19：取引アルゴリズムのバックテストで、4つの異なるターゲットを同時に予測する能力を検証する

また、ターミナルログのスクリーンショットを示すことで、アプリケーションが係数の行列を学習していることを確認できます。ご覧の通り、解の行列には4行あり、4つのターゲットそれぞれに対して独自の係数セットを学習しています。 アプリケーションは各ターゲットを独立して学習します。

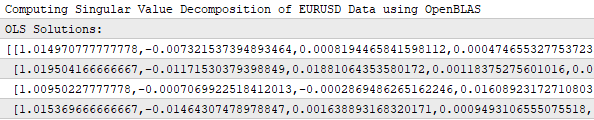
図20：取引アプリケーションは、割り当てられた4つのターゲットそれぞれに対して独自の係数セットを学習する

さらに、アプリケーションは時間の経過とともに口座残高にプラスの傾向を示しています。残高の不規則な変動は平滑化したいところですが、より一貫した成長を達成するためにシステムの改良を続けます。

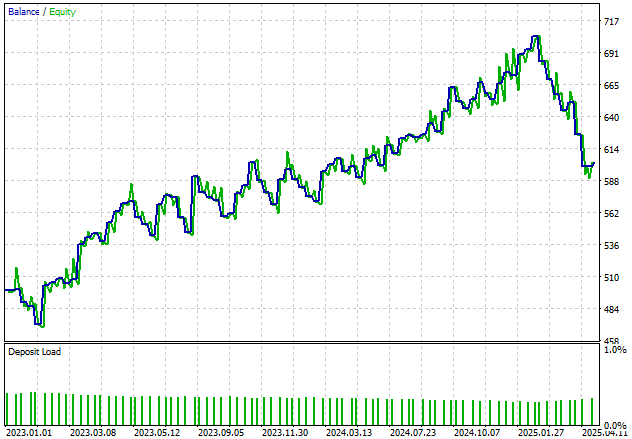
図21：2年間のバックテスト期間における口座資産曲線の成長の可視化

口座のパフォーマンスを詳細に分析すると、取引の51％が利益を上げていることがわかります。これは良い出発点ですが、将来的にはこの数値を55％、さらには60％まで引き上げることを目標としています。現時点では、平均利益が平均損失を上回り、最大利益が最大損失のほぼ2倍であるため、システムは健全であることが示唆されます。もちろん、さらなる改善も予定しています。

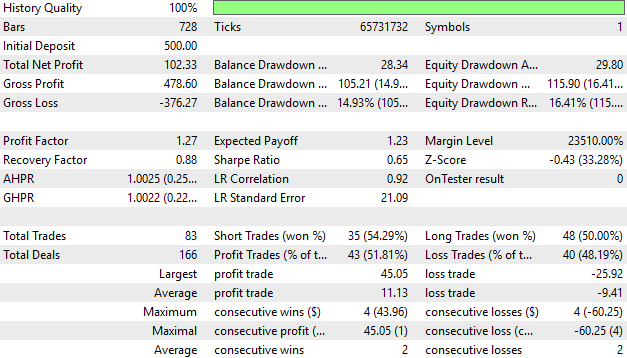
図22：バックテスト期間中の取引アプリケーションのパフォーマンス詳細分析

結論

本記事では、線形代数の概念をしっかり理解することの重要性と、それがMetaTrader 5ターミナルで市場データを扱う能力にどのように直接影響するかを示しました。この理解がなければ、大量の市場データを分析することは非常に困難になります。線形代数のいくつかの重要な原理を学び、それがMQL5でどのように実装されているかを見るだけで、市場から洞察をより速く、より信頼性高く抽出する能力を得られます。

今後の議論では、線形代数のツールをどのように使用し、MQL5で数値的に安定かつ高速な取引アルゴリズムを構築するかを紹介していきます。この記事を読んだことで、読者はほぼ一定時間で動作するアルゴリズムを設計できるようになり、複数のターゲットを同時に予測する場合でも、迅速にバックテストをおこない、アプリケーションを改善できる力を身につけました。