Technische Analyse: Was analysieren wir?

Einleitung

Heutzutage ist es sehr leicht, Handel auf Währungsfluktuationen auszuführen. Dazu muss man nur den MetaTrader (MT) auf seinem Computer installieren und in einem Dealing-Zentrum einen Account eröffnen und schon kann man mit dem Handel beginnen. Natürlich möchte jeder beim Handeln Gewinne machen. Und hier kommt uns die Welterfahrung im Handeln zu Hilfe.

Die beliebtesten Tools für technische Analyse sind im MetaTrader in Form von Indikatoren schon dabei. Und im Internet findet man dazu eine Menge Veröffentlichungen von den bekanntesten Autoren.

Doch selbst wenn Sie die Anleitungen und Empfehlungen dieser hoch gepriesenen 'Gurus' der technischen Analyse genau befolgen, erhalten Sie dennoch nicht immer das gewünschte Ergebnis. Warum? Diese Frage wird in diesem Beitrag nicht beantwortet. Stattdessen wollen wir zu verstehen versuchen, was wir analysieren.

Was analysieren wir?

Der moderne Finanzmarkt ist ein sehr sensibler Organismus, der von fast jedem Ereignis auf der Welt irgendwie beeinflusst wird. Eine ungeheure Menge unterschiedlicher Faktoren wirken sich ständig auf den Markt aus, und führen schließlich zu einer konstanten Fluktuation von Quoten. Und diese ständig sich verändernden Währungsquoten sind das einzige und ausreichende Ziel der Untersuchungen, die während einer technischen Analyse des Marktes stattfinden.

Mal angenommen, unser Computer ist via des MetaTrader Client-Terminals mit einem Dealing-Zentrum verbunden. In diesem Fall erreichen die Quoten den Terminal in einer eigenständigen Form - als separate Anzeichen (Ticks). Wir wissen, dass das ursprüngliche kontinuierliche Signal durch seine Anzeichen wieder hergestellt werden kann, wenn die Samplingfrequenz mehr als zweimal so hoch ist wie die Maximalfrequenz innerhalb des Bereichs des ursprünglichen Signals. In dieser Phase müssen wir das ursprüngliche kontinuierliche Signal nicht wieder herstellen, doch wenn es in unserem Fall theoretisch möglich ist, heißt das, dass das ursprüngliche Signal während des Samplingprozesses nicht verzerrt wurde.

Leider wird bei der Herausbildung von Ticks eine variable Samplingfrequenz verwendet. Anzeichen von Quoten (Ticks) erreichen den Terminal mit einem durchschnittlichen Zeitintervall von 0,5 Sekunden bis zu einigen Minuten. Wir kennen den Algorithmus der Änderung dieser Samplingfrequenz nicht und auch nicht die Maximalfrequenz innerhalb des Bereichs des ursprünglichen Signals. Und all das hindert uns daran, die Verzerrung einschätzen zu können, die während des Samplingprozesses entstanden ist.

Wir können also nur vermuten, dass diese Art der Quantisierung nicht zu einem Informationsverlust führt und dass das ursprüngliche kontinuierliche Signal (Marktquoten der Währungen) nicht erheblich verzerrt ist. Vor dem Hintergrund dieser Vermutung und der Tatsache, dass die Samplingfrequenz bis 2 Hz erreichen kann, erreichen wir einen Schätzwert (Näherungswert) der Obergrenze des Bereichs des ursprünglichen Signals, nämlich bei 1 Hz.

Bei einer variablen Samplingfrequenz ist die Verarbeitung des Signals ziemlich schwer, doch ist in der Praxis eine Marktanalyse nach den Ticks, die das Terminal erreichen, ziemlich selten. Die meisten Menschen arbeiten lieber mit Zeitrahmen von M30 und höher.

Wenn Sie den 'Linien-Diagramm' Modus im MetaTrader Terminal wählen, sehen Sie eine Abfolge von Anzeichen mit einem festen Sample-Intervall, das dem Wert des aktuellen Zeitrahmens entspricht. Lassen wir einige Details beiseite und gehen davon aus, dass diese Abfolge von den Ticks gebildet wird, die das Terminal erreichen.

Wenn wir dann ein Anzeichen (Tick) aus der ankommenden Abfolge alle 30 Minuten wählen, erhalten wir als Ergebnis eine Abfolge mit der festen Samplingfrequenz = 1/1800 Hz - also die Abfolge der Anzeichen für den M30 Zeitrahmen. Die Abfolgen der anderen Zeitrahmen werden auf dieselbe Art gebildet. Offensichtlich entspricht diese Art der Bildung von Anzeichen-Abfolgen fast der Quantisierung des ursprünglichen kontinuierlichen Signals, wobei das Intervall dem Wert des gewählten Zeitrahmens gleicht.

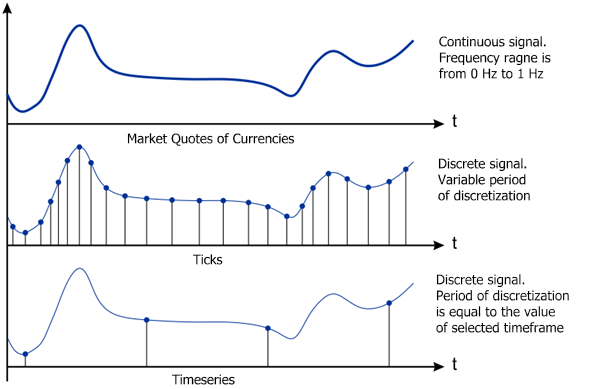
Abb. 1 Arten der Darstellung von Quoten

Aufgrund des oben gesagten kommen wir zu dem Schluss, dass der Gegenstand der technischen Analyse der ständig sich ändernde Flow von Marktquoten ist, die uns in einer eigenständigen Form als die Anzeichen mit einer variablen Frequenz der Disktreisierung (Ticks) zur Verfügung stehen sowie die Anzeichen mit einer festen Frequenz der Diskretisierung (Zeitrahmen). Und dass sich das Spektrum der ursprünglichen Quoten zwischen 0 Hz - 1 Hz befindet.

Da der Zeitraum des kleinsten Zeitrahmens M1 in MetaTrader = 1 Minute ist, erfährt also, aufgrund unseres Modells, das ursprüngliche Signal der Quoten bei der Bildung einer Abfolge von Anzeichen eine Diskretisierung von1/60 Hz Frequenz. Diese Frequenz ist 120 Mal geringer als der doppelte Wert der Obergrenze des Spektrums des ursprünglichen Signals (2 Hz). Eine solche Transformation des Signals führt auf jeden Fall zu seiner irreversiblen Verzerrung. Abbildung 2 zeigt die Art dieser Verzerrung.

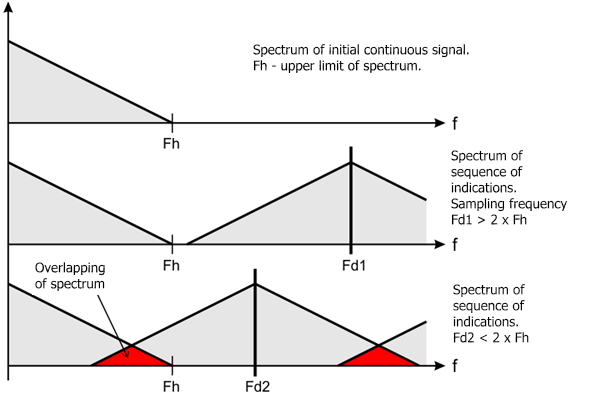
Abb. 2 Überschneidung des Spektrums

Angenommen, das Spektrum des ursprünglichen Signals sieht so aus, wie das aus Abb. 2 und seine Obergrenze entspricht Fh. Wenn die Samplingfrequenz Fd1 höher als Fh ist, weist die Abfolge der Anzeichen, die man als Ergebnis der Quantisierung erhält, kein sich überschneidendes Spektrum auf. So eine Abfolge ist eine angemessene, eigenständige Darstellung de ursprünglichen Signals.

Ein Absenken der Samplingfrequenz unterhalb des doppelten Wertes von Fh führt zur Überschneidung des Spektrums in so entstehenden Abfolge, und ist damit keine Entsprechung des ursprünglichen kontinuierliches Signals mehr. Abb. 2 zeigt ein Beispiel, in dem die Samplingfrequenz Fd2 leicht unter dem doppelten Wert von Fh liegt. Wie bereits oben erwähnt, ist die Samplingfrequenz für den Zeitrahmen M1 120 Mal geringer als die, die man akzeptieren kann.

Solch eine niedrige Frequenz der entstandenen Abfolge führt zu mehrfacher Überschneidung des Spektrums und einer weit stärkeren Verzerrung als wie im Fall , der in Abb. 2 gezeigt wurde. Wenn wir nun größere Zeitrahmen erreichen, wird die Samplingfrequenz geringer und das Niveau an Verzerrung nimmt zu. Formal gesehen spiegeln die Abfolgen der Anzeichen unterschiedlicher Zeitrahmen sich selbst nicht wider und bilden auch die ursprünglichen Quoten nicht korrekt ab.

Wenn wir also unterschiedliche Anzeichen und Systeme nehmen, die mit Zeitrahmen arbeiten, analysieren wir demzufolge eine verzerrte Darstellung von Quoten. In diesem Fall ist die technische Analyse von Quoten extrem kompliziert, und der Einsatz von streng mathematischen Methoden wird in den meisten Fällen unsinnig.

So wird z.B. ein Spektrum jedes Zeitrahmens, das durch eigenständige Fourier-Transformation erhalten wurde, niemals eine Abschätzung des Spektrums des ursprünglichen Signals der Quoten sein, sonder ein Spektrum ursprünglicher Quoten, das sich mit verzögerte Frequenz immer wieder selbst überlagert. Wiederholte Überlagerung eines Spektrums kann auch zur Bildung einer Fraktalstruktur in der daraus entstehenden Abfolge führen.

Die quantitative Abschätzung der Verzerrung, die die ursprünglichen Quoten erfahren haben, sprengt den Rahmen dieses Beitrags, daher beschränken wir uns einfach darauf, zu zeigen, dass sie existiert.

Als ursprüngliches Signal nehmen wir ein zufälliges Fragment der Abfolge der Anzeichen der GBPUSD M5 Quoten her. Abbildung 3 (grüne Linie) zeigt das Ergebnis der Filterung dieses Signals mittels des Low-Pass Filters, der analog zum SMA-Filter (einfacher gleitender Mittelwert) in Zeitraum 45 ist, der in MetaTrader verwendet wird.

Aus der ursprünglichen Abfolge wählen wir dann jedes 15. Anzeichen und bilden eine Abfolge für den M75 Zeitrahmen (gibt es in MetaTrader 4 nicht). Und mittels einfacher Ausdünnung der ursprünglichen Abfolge haben wir anschließend die Samplingfrequenz um15 Mal verringert.

Abbildung 3 (rote Linie) zeigt das Ergebnis der Filterung dieses erhaltenen Signals mittels des Low-Pass Filters, der analog zum SMA-Filter (langsames gleitendes Mittel) in Zeitraum 3 ist. Der Filter-Zeitraum wurde proportional zur Verringerung der Frequenz verringert, damit die Frequenz des Einschnitts des Lower-Pass Filters unverändert blieben kann.

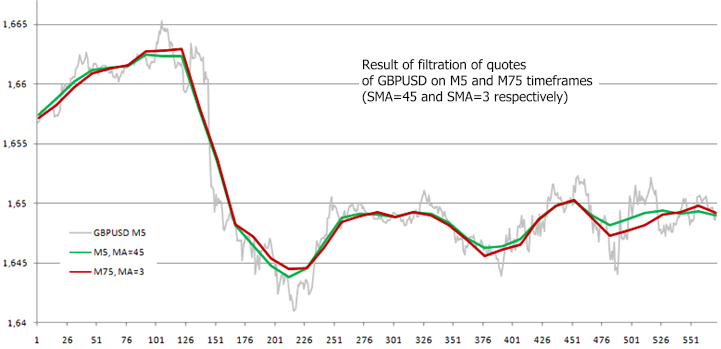
Abb. 3. Filterung der GBPUSD Quoten

Wenn wir davon ausgehen, dass das Signal während der Verringerung der Diskretisierungsfrequenz nicht verzerrt wird, sollte das Ergebnis seiner Filterung analog zur Filterung des ursprünglichen Signals sein. Abb. 3 zeigt klar den Unterschied zwischen den Kurven, die wir infolge der Verarbeitung der M5 und M75 Abfolgen erhalten haben. Höchstwahrscheinlich handelt es sich hier um eine Verzerrung, die aufgrund der Überschneidung des Spektrums entstanden ist, als die Samplingfrequenz verringert wurde.

Vielleicht ist die Verwendung eines Low-Pass Filters nicht der beste Weg, um die durch Überlagerung des Spektrums verursachte Verzerrung festzustellen, doch das Beispiel zeigt deutlich, dass sie sich auf die echten Anzeichen von Quoten auswirken kann, selbst wenn man einfache Analysemethoden verwendet.

Die Verwendung der Abfolgen unterschiedlicher Zeitrahmen ist bequem, will man Quoten visuell darstellen. Doch wenn wir zu ihrer Analyse einen mathematischen Ansatz verwenden, kann der Wechsel zu den größeren Zeitrahmen nur für die Verringerung der Menge der Berechnungen aufgrund der abnehmenden Menge an verarbeiteten Anzeichen verwendet werden.

Lässt man das Volumen der Berechnung außer acht, ist der Wechsel zu einem größeren Zeitrahmen unsinnig, außer für die zusätzliche Verzerrung des ursprünglichen Signal. Theoretisch ist die optimale Variante die Analyse von Quoten nach Ticks, die das Terminal erreichen. Wenn wir die History der Ticks hätten, könnten wir mit Hilfe der Interpolation (z.B. Verzahnungen) zur Abfolge mit der festen Samplingfrequenz wechseln und eine ziemlich hohe wählen.

Gibt es vom Standpunkt der Verzerrung von Quoten keinerlei derartige Information, ist es für eine Analyse besser, die Abfolge auf dem kleineren Zeitrahmen M1 zu verwenden. Wir können ggf. die Samplingfrequenz dieser Abfolge verringern, doch bevor wir dies tun, sollten wir ihre Frequenzen, die höher als die Hälfte der neuen Diskretisierungsfrequenzen sind, unterdrücken.

Die Höhe der Auswirkung der beschriebenen Verzerrung auf das Analyseergebnis von Quoten hängt daher stark von der Empfindlichkeit der für eine derartige Analyse verwendeten Algorithmen ab. In manchen Fällen mag diese Verzerrung durchaus keinerlei gravierende Auswirkungen auf das erhaltene Ergebnis haben, doch sollten Sie für eine korrekte Interpretation der Berechnungen immer daran denken, dass eine Verzerrung vorhanden ist.

Alles bisher Gesagte lässt eine ganze Reihe von Annahmen zu, um die Verzerrung zu unterstreichen, die mit der Überlagerung des Spektrums zusammenhängt. Und tatsächlich gibt es viele Faktoren, die uns in MetaTrader daran hindern, strikte mathematische Methoden digitaler Verarbeitung anzuwenden - das Vorhandensein von Lücken zwischen den Anzeichen von Quoten, übersprungene Bars, die in MetaTrader verwendete Methode der Bildung von Zeitreihen, die den Wert eines Ticks als den Anzeichenwert akzeptiert, bei dem die Zeit dieses Ticks nicht mit der Zeit der Bildung dieses Anzeichens übereinstimmt.

Und es stellt sich noch eine weitere Frage bzgl. der Darstellung von Quoten im Client-Terminal. Diese Frage möchte ich jetzt kurz ansprechen. Bislang haben wir noch nicht über den Darstellungsmodus in Form von Kerzen gesprochen.

Es gibt viele Arbeiten, die sich mit der Analyse von Kerzen befassen. Sie betrachten unterschiedliche Prognosemethoden für das Verhalten von Quoten auf Basis der Form der Kerzen oder ihrer Kombination. An ihrer Wirksamkeit besteht kein Zweifel, also sehen wir uns mal an, was wir erhalten, wenn wir eine mathematische Analyse der Werte «Niedrig» und «Hoch» in jedem Zeitrahmen durchführen.

Wie Sie wissen entsprechen «Niedrig» und «Hoch» dem Minimal- und Maximalwert von Quoten innerhalb des Zeitraums eines gewählten Zeitrahmens. Wann diese Werte erreicht wurden wissen wir nicht. Die Werte «Niedrig» und «Hoch» sind nicht definitiv an eine Zeitachse gebunden, sodass wir einzig und allein wissen, dass die Quoten beide Werte an irgendeinen Moment innerhalb des ausgewählten Zeitrahmens erreicht haben. Sie beide, «Niedrig» und «Hoch» sind die Abfolgen von Anzeichen mit dem variablen Diskretisierungszeitraum, der einen Zufallswert im Bereich von "0" bis zum Wert, der dem gewählten Zeitrahmen entspricht, annehmen kann.

Vom Standpunkt der mathematischen Methoden digitaler Verarbeitung von Signalen, ist eine derartige Darstellung der «Niedrig» und «Hoch» Werte - als eine zeitliche Funktion - ziemlich fremdartig. Natürlich können wird zur Verarbeitung dieser Abfolgen die Standard-Algorithmen verwenden, doch wie sollen wir die daraus entstehenden Ergebnisse interpretieren? Zum Beispiel: Was ist die Frequenz des Einschnitts eines einfachen First-Order Low-Pass Filters bei der Filterung solcher Signale?

Um mit den Funktionen zu arbeiten, die in Form einer Abfolge mit einer zufällig sich ändernden Samplingfrequenz dargestellt sind, braucht man vermutlich einen mathematischen Apparat. Und das Anwenden von Algorithmen, die für Abfolgen mit einer festen Samplingfrequenz entwickelt wurden, führt vermutlich zu einer Unsicherheit bei den erhaltenen Ergebnissen in einer Analyse von «Niedrig» und «Hoch». Daher müssen wir bei Prognosen des Verhaltens von Quoten auf Basis mathematischer Analyen der Abfolgen von «Niedrig» und «Hoch» vorsichtig sein.

Werden Quoten in Form von Kerzen dargestellt, besitzt jede Quote nicht nur die «Niedrig» und «Hoch» Werte, sondern auch ihre «Öffnen» und «Schließen» Werte - denn sie alle bilden die Kerze. Sehen wir uns mal an, wie eindeutig die Darstellung von Quoten in Form einer Kerze auf einem Intervall eines Zeitrahmens ist. 

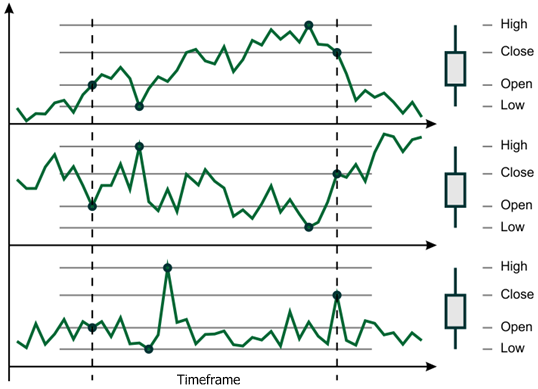
Abb. 4 Bildung einer Kerze

Abbildung 4 zeigt drei vollständig unterschiedliche Abfolgen, die zur Bildung derselben Kerze führen. Wie Sie sehen kann man das Verhalten von Quoten durch die Form einer Kerze nahezu unmöglich festlegen - und ihre «Niedrig» und «Hoch» Werte sind zeitlich auch nicht gebunden.

Uns derlei Beispiele gibt es schier endlos. Vielleicht ist die Darstellung von Quoten als Kerzen ein bequemes Werkzeug für eine schnelle visuelle Einschätzung ihres Verhaltens, doch die «Niedrig» und «Hoch» Anzeichen, die die Schatten der Kerze bilden, sind für eine mathematische Analyse nicht wirklich geeignet. «Öffnen» und «Schließen» Anzeichen sind nur etwas besser, da man hier nämlich das Problem der Unsicherheit hat, im Hinblick auf de verstrichene Zeit zu Beginn dieser Abfolgen.

Als «Öffnen» Wert nehmen wir z.B. den Wert des ersten Ticks her, der im analysierten Zeitraum auftaucht. Gibt es im Zeitraum des Zeitrahmens überhaupt keine Ticks, dann wird auch keine Kerze gebildet. Des Weiteren sollten wir bei der Verwendung von «Öffnen» und «Schließen» auch nicht die Fehler vergessen, die im Zusammenhang mit der Überschneidung des Spektrums entstehen.

Als Schlussfolgerung dieser Betrachtung ergibt sich: die beste Art für eine mathematische Analyse von Quoten ist die Verwendung der Abfolge der «Schließen» Werte aus dem kleinsten Zeitrahmen. Die zusätzlichen Anzeichen «Niedrig», «Hoch» und «Öffnen», die eine Kerze bilden, enthalten mit großer Wahrscheinlichkeit eben keine neuen Informationen.

Anstelle des «Schließen» Wertes können Sie bei der Analyse von Quoten auch versuchen, die Summe aus «Öffnen» des aktuellen Bars und «Schließen» des vorherigen Bars zu verwenden, die dann halbiert wird. Vielleicht erlaubt dieser Ansatz eine Verringerung der Auswirkungen der Unsicherheit in den Momenten des Starts der «Öffnen» und «Schließen» Anzeichen und eine exaktere Begrenzung der Startzeit des Zeitrahmens.

Fazit

Der in diesem Beitrag beschriebene Ansatz zur Darstellung von Quoten ist weit verbreitet. Er wird nicht nur in MetaTrader, sondern auch in anderen Plattformen verwendet. Die gleichen Zeitrahmen, Bars und Kerzen kann man auch im neuen MetaTrader 5 vorfinden. Daher kann man durchaus sagen, dass eine derartige Darstellung von Quoten traditionell ist und mit ziemlicher Sicherheit auch einige Vorteile bietet. Doch von einem formellen Blickwinkel aus betrachtet, sind diese Quoten, die der Anwender bekommt, für eine mathematische Analyse zu verzerrt.

Die ständig zunehmende Rechnerleistung erlaubt den Einsatz immer komplexerer mathematischer Algorithmen für eine technische Analyse - und diese Algorithmen reagieren sehr oft extrem empfindlich auf unterschiedliche Ungenauigkeiten. Ein gutes Beispiel hierfür ist der Algorithmus zur Hochrechnung von Funktionen. Trotz all dem enthält eine technische Dokumentation von Indikatoren jedoch keine Warnungen über mögliche Ungenauigkeiten, die beim Wechseln zwischen Zeitrahmen entstehen können.

Das primäre Ziel dieses Beitrags war es, die Aufmerksamkeit von Entwicklern technischer Indikatoren und Handelssysteme auf die Tatsache zu lenken, dass sie bei der Analyse der Dynamik von Marktquoten, die mit einem verzerrten Abbild ihrer selbst arbeiten, die Auswirkungen dieser Verzerrung auf die Analyseergebnisse mit berücksichtigen sollten - es sei denn eine derartige Auswirkung ist unwesentlich.