Technische Analyse: Wie analysieren wir?

Einleitung

Beim Blick in verschiedene Veröffentlichungen, die sich irgendwie mit der Anwendung von technischer Analyse beschäftigen, stoßen wir auf viele Informationen, die einen einerseits einfach kalt lassen und andererseits den Wunsch wecken, doch etwas dazu zu sagen. Und aus diesem Wunsch heraus ist dieser Beitrag entstanden, der zunächst einmal den Versuch wagen möchte, unsere Handlungen und Ergebnisse mit Hilfe einer bestimmten Analysemethode erneut zu analysieren.

Neuzeichnung

Wenn man sich die Kommentare zu Indikatoren betrachtet, die auf https://www.mql5.com/de/code zu finden sind, stellt man schnell fest, dass die überwiegende Mehrheit der Anwender diesen Indikatoren extrem negativ gegenübersteht, deren zuvor berechnete Werte sich verändern und während der Bildung des nächsten Bars neu gezeichnet werden.

Sobald klar wird, dass der Indikator neu gezeichnet wird, interessiert er niemanden mehr. Diese Haltung gegenüber der Neuzeichnung von Indikatoren ist oft ziemlich nachvollziehbar, doch in manchen Fällen ist eine derartige Neuzeichnung gar nicht so schlimm, wie es zunächst den Anschein hat. Und dies versuchen wir durch die Analyse des einfachsten SMA (einfacher gleitender Mittelwert) zu zeigen.

In Abbildung 1 zeigt die blaue Farbe die Impulseigenschaften des Niedrig-Kurs Filters, der dem SMA (15)-Indikator entspricht. In dem abgebildeten Fall ist der SMA (15) die Summe der letzten 15 Zählungen der Inputabfolge, wobei jeder der Inputzählungen mit 1/15 multipliziert wird - entsprechend der gezeigten Impulseigenschaft. Angesichts des nun auf dem Intervall von 15 Zählungen berechneten SMA (15) Werts, müssen wir entscheiden, welchen Zeitpunkt wir diesem Wert zuweisen sollten. 

Da wir den SMA (15) als einen Durchschnitt der vorigen 15 Input-Zählungen annehmen, sollte der Wert so wie im oberen Diagramm gezeigt, erscheinen, also einem 0-Bar entsprechen. Falls wir den SMA (15) als einen Niedrig-Rate Filter mit einer Impulseigenschaft endlicher Länge akzeptieren, muss also der berechnete Wert unter Berücksichtigung der Filterverzögerung der Barziffer 7 entsprechen, sowie im unteren Diagramm gezeigt.

Durch eine einfache Verschiebung wandeln wir das Diagramm des gleitenden Mittelwerts in ein Diagramm eines Niedrig-Kurs Filters mit Null-Latenzzeit um.

Hinweis: Bei der Verwendung von Null-Latenzzeit Diagrammen verändern sich einige traditionelle Analysemethode leicht in ihrer Bedeutung. So ereignen sich z.B. der Schnittpunkt der zwei MA-Plots mit unterschiedlichen Zeiträumen und der Schnittpunkt der gleichen Plots mit ausgeglichener Verzögerung zu unterschiedlichen Zeitpunkten. Im zweiten Fall erhalten wir Zeitpunkte des Schnittpunkts, die nur durch die MA-Zeiträume festgelegt sind, jedoch nicht durch ihre Latenz.

Doch zurück zu Abbildung 1: Im unteren Plot erkennt man gut, dass die SMA (15) Kurve, die jüngsten Zählungen des Inputsignals durch den Wert = der Hälfte des durchschnittlichen Zeitraums, nicht erreicht. Es entsteht ein Bereich von 7 Zählungen, wo der SMA (15) Wert nicht definiert ist. Wir können annehmen, dass wir infolge der Verzögerungsausgleich einige Informationen verloren haben, da sich ein mehrdeutiger Bereich herausgebildet hat - doch das ist komplett falsch.

Die gleiche Mehrdeutigkeit findet sich auch im oberen Diagramm (Abb. 1), doch aufgrund der Verschiebung ist sie recht verborgen, dort wo es keine Input-Zählungen gibt. Das MA Diagramm büßt seine Zeitbindung an die Input-Abfolge ein und die Verzögerungsgröße hängt aufgrund der Verschiebung vom MA-Glättungszeitraum ab.

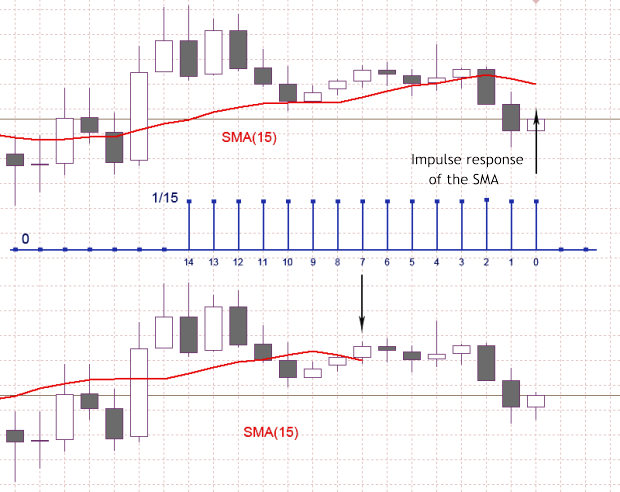
 Abb. 1 Impulsantwort des SMA (15)

Wenn man bei der Anwendung eines MA mit unterschiedlichen Zeiträumen alle auftretenden Verzögerungen immer kompensiert, führt das zu Diagrammen mit einer gewissen Zeitbindung an die Input-Abfolge und an einander. Doch jenseits der unbestreitbaren Vorteile, nimmt dieser Ansatz Bereich der Mehrdeutigkeit in Kauf. Der Grund für ihr Auftreten liegt in den allseits bekannten Features der Verarbeitung von Abfolgen mit zeitlichen endlichen Länge, und nicht in Fehler unserer Überlegungen.

Wir stoßen auf Probleme, die sich an den Kanten solcher Abfolgen mit Hilfe von Interpolation-Algorithmen abspielen, unterschiedlichen Filterungen, Glättung usw. Und niemand ist auf die Idee gekommen, den Ergebnisteil durch Verschiebung zu verbergen.

Ich gebe ja zu, dass MA-Diagrammen mit einem gewissen nicht-gezeichneten Teil Filterung korrekter darstellen, doch diese Diagrammen sehen einfach komisch aus. Vom formellen Standpunkt aus gesehen, können wir den Wert des Filters SMA (15), Shift=-7 für Output-Zählungen mit einem Index < 7 nicht berechnen. Gibt es also noch einen Weg, die Zählungen an der Kante der Input-Abfolge nach unten zu glätten?

Versuchen wir eine Filterung dieser Zählungen mit Hilfe desselben SMA-Algorithmus, doch verringern wir seinen Glättungszeitraum bei jedem Bar in Richtung "0". Und wir sollten auch den Verzögerungsausgleich des verwendeten Filters nicht vergessen.

 

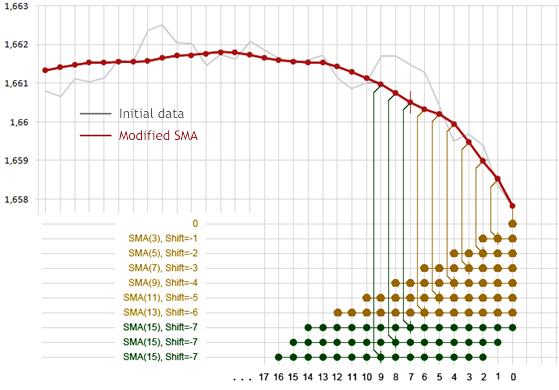
Abb. 2 Veränderter SMA

Abb. 2 zeigt, wie sich in diesem Fall Output-Zählungen mit Indices von 0 bis zu 6 herausbilden. Die Zählungen, die für die Berechnung des Durchschnittswerts hergenommen werden, sind unten in der Abbildung zur besseren Sichtbarkeit mit roten Punkte markiert. Senkrechte Linien geben an, bis zu welcher Output-Zählung dieser Durchschnitt zugewiesen wird. Auf dem "0"-Bar findet keine Verarbeitung statt, der Wert der Input-Abfolge wir der Output 1 zugewiesen. Für die Output-Abfolge mit Indices 7 oder höher, erfolgen die Berechnungen mit dem üblichen SMA (15) Verschiebung =- 7.

Wenn man so einen Ansatz verwendet, ist es ganz klar, dass das Output-Diagramm auf dem Index-Intervall von 0 bis zu 6 bei jedem Erscheinen eines neuen Bars erneut gezeichnet wird - und die Intensität dieser Neuzeichnung nimmt mit abnehmendem Index zu. Zugleich wird auch die Verzögerung für jede Zählung der Output-Abfolge ausgeglichen.

Im analysierten Beispiel haben wir einen Neuzeichnungs-Indikator erhalten, der analog zum Standard-SMA (15) ist, doch mit einer Verzögerung von "0" und extra Informationen an der Kante der Input-Abfolge, die im Standard SMA (15) nicht vorhanden ist. Vor dem Hintergrund dieser Verzögerung von "0" und der extra Informationen als Vorteile, haben wir zwar trotzdem einen Neuzeichnungs-Indikator erhalten, der jedoch mehr Informationen enthält als der Standard-SMA Indikator.

Hier sei auch darauf hingewiesen, dass die Neuzeichnung in diesem Beispiel zu keinerlei katastrophalen Folgen führt. Auf dem entstandenen Plot ist die gleiche Information verzeichnet wie im Standard-SMA, mit ihren Zählungen nach links verschoben.

Im soeben behandelten Beispiel wurde der ungerade SMA-Zeitraum gewählt, der die zeitliche Verzögerung komplett ausgeglichen hat, die für SMA:

t = (N-1)/2 ist,

wobei N ein Glättungszeitraum ist.

Aufgrund der Tatsache, dass bei geraden Werten für 'N' die Verzögerung bei diesem Ansatz nicht vollständig ausgeglichen werden kann und die angebotene Methode zur Glättung der Zählungen an der Kante der Abfolge nicht die einzig mögliche ist, wird die Variante des Indikatoraufbaus hier nur als Beispiel betrachtet und nicht als vollständiger Indikator.

Multi-Zeitrahmen

Auf den MQL4 und MQL5 Webseiten finden sie die sog. Multi-Zeitrahmen Indikatoren. Versuchen wir jetzt herauszufinden, was uns diese Multi-Zeitrahmen bringen. Dazu nehmen wir als Beispiel den "

---

" Indikator.

Angenommen, wir befinden uns im untersten M1 Zeitrahmenfenster und wir zeigen an Öffnen oder Schließen des M30 Zeitrahmen-Werts im selben Fenster an und wenden zur Glättung, SMA (3) an. Wir wissen, dass sich die M30 Zeitrahmen-Abfolge aus der M1 Zeitrahmen-Abfolge durch Samplen des 30. Werts und der Verwerfung der restlichen 29 Werte bildet. Hier kommen Zweifel auf, ob es sinnvoll ist, die M30 Zeitrahmen-Abfolge zu verwenden. 

Wenn wir beim M1 Zeitrahmen auf ein gewisses Maß Information zugreifen können, warum sollten wir uns dann mit dem M30 Zeitrahmen beschäftigen, der ja nur ein Dreißigstel dieser Information enthält? In unserem speziellen Fall beseitigen wir absichtlich den Großteil der vorhandenen Information und verarbeiten das, was vom SMA (3) übrig bleibt und zeigen das Ergebnis im M1 Zeitrahmen Quellfenster.

Klar sehen die oben beschriebenen Handlungen reichlich komisch aus. Ist es nicht einfach leichter, den SMA (90) auf eine komplette Abfolge des M1 Zeitrahmens anzuwenden? Die Frequenz des SMA (90) Filterteils auf dem M1 Zeitrahmen gleicht der Frequenz des SMA (3) Filterteils auf dem M30 Zeitrahmen.

Abb. 3 zeigt ein Beispiel der Verwendung des Multi-Zeitrahmen Indikators "iUniMA MTF" auf dem Diagramm EURUSD M1 Währungspaar. Die blaue Kurve ist das Ergebnis der Anwendung von SMA (3) auf die M30 Zeitrahmen Abfolge. In der selben Abbildung ist die rote Kurve das Ergebnis, das wir mit dem normalen "Gleitenden Mittelwert" Indikator bekommen. Also erscheint das Ergebnis der Anwendung des Standard SMA (90)-Indikators natürlicher.

Und außerdem erfordert dies dazu keine speziellen Techniken.

 

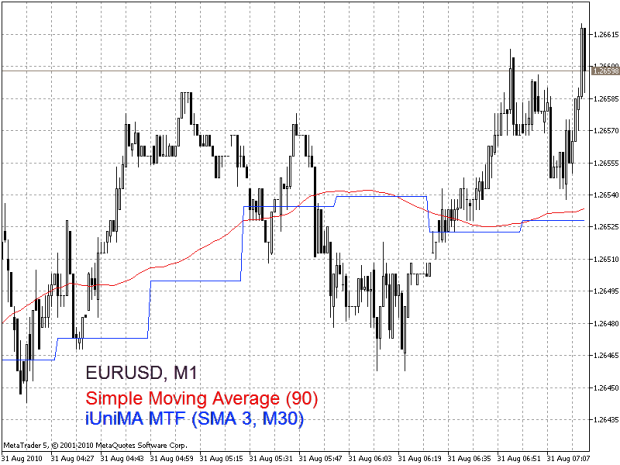
Abb. 3. Verwendung des Multi-Zeitrahmen Indikators

Doch es ist noch eine andere Variante der Anwendung von Multi-Zeitrahmen Indikatoren möglich, wenn eine Information aus dem untersten Zeitrahmen, wie dem aktuellen, auf einem Terminal angezeigt wird Diese Variante kann nützlich sein, wenn man den Umfang der Quotenanzeige weit mehr komprimieren muss als es das Terminal auf dem untersten Zeitrahmen erlaubt. Doch auch hier erhält man keine zusätzlichen Informationen über die Quoten.

Daher ist es einfacher sich dem untersten Zeitrahmen zuzuwenden und die gesamte Datenverarbeitung mit normalen Indikatoren zu machen, und eher nicht mit Multi-Zeitrahmen Indikatoren.

Bei der Entwicklung von angepassten Indikatoren oder Expert Advisors kann es zu speziellen Situationen kommen, bei denen eine Organisation des Zugriffs auf verschiedenen Zeitrahmen-Abfolgen vernünftig und zudem auch die einzig mögliche Lösung ist. Doch auch hier sollten wir daran denken, dass die höheren Zeitrahmen-Abfolgen aus den niedrigen gebildet werden und daher keine weiteren, einmaligen Informationen umfassen

Kerzendiagramme

In Publikationen zur technischen Analyse stoßen wir immer wieder auf begeisterte Verweise auf alles, was mit Kerzendiagrammen zu tun hat. So spricht z.B. der Beitrag "Die Analyse von Kerzen-Muster" davon, dass: "Der Vorteil von Kerzen darin liegt, dass sie Daten so repräsentieren können, dass man auch die Eigendynamik innerhalb der Daten erkennen kann". ... Mit japanischen Kerzendiagrammen können Sie in das "Innere" der Finanzmärkte vordringen, was mit anderen grafischen Methoden nur schwierig zu bewerkstelligen ist.

Und derlei Aussagen finden sich natürlich nicht nur hier. Versuchen wir also herauszufinden, ob wir mit Kerzendiagrammen ins "Innere" der Finanzmärkte vordringen können.

"Niedrig", "Hoch", "Öffnen" und "Schließen" Werte-Abfolgen werden zur Darstellung von Kursen in Form von Kerzendiagrammen verwendet. Erinnern wir uns kurz, um welche Art von Werten es sich hier handelt. "Niedrig" und "Hoch" Werte entsprechen den Minimal- und Maximalkurswerte im Zeitraum eines gewählten Zeitrahmen. Der "Öffnen" Wert entspricht dem ersten bekannten Wert der Kurse im analysierten Zeitraum. Der "Schließen" Wert entspricht dem letzten bekannten Wert der Kurse im analysierten Zeitraum. Was ist damit gemeint?

Zunächst einmal, dass es irgendwo Marktkurse gibt, aus denen sich "Niedrig", "Hoch", "Öffnen" und "Schließen" Abfolgen bilden. «Niedrig», «Hoch», «Öffnen» und «Schließen» Werte sind in dieser Methode ihrer Bildung nicht streng an Zeit geknüpft. Außerdem gibt es keine Möglichkeit, ursprüngliche Kurse via dieser Abfolgen wieder herzustellen. Am interessantesten ist, dass die gleiche Kombination an «Niedrig», «Hoch», «Öffnen» und «Schließen» Werten auf jedem bar in jedem Zeitrahmen aus einer unendlichen Anzahl an Varianten der ursprünglichen Kursabfolge gebildet werden kann. Diese Schlussfolgerungen sind trivial und beruhen auf allseits bekannten Tatsachen.

Daher ist die ursprüngliche Information, wenn man Marktkurse in Form von Kerzendiagrammen heranzieht, unwiederbringlich verzerrt. Bei Anwendung rein mathematischer Methoden der Analyse einer Bewertung des Kursverhaltens jeder der «Niedrig», «Hoch», «Öffnen» oder «Schließen» Abfolgen, sind die Ergebnisse nicht mit Marktkursen verknüpft, sondern schlicht an ihre verzerrte Abbildung. Trotz alledem müssen wir zugeben, dass sich Kerzendiagramme großer Beliebtheit erfreuen

Kann man das irgendwie erklären Die Antwort liegt vielleicht darin, dass anfangs das Ziel der Darstellung von Kursen in Form von Kerzendiagrammen eine schnelle visuelle und intuitive Marktanalyse bedeutete, und keine Anwendung von mathematischen Analysemethoden auf Kerzendiagramme.

Um also verstehen zu können wie die Darstellung von Kursen in Form von Kerzendiagrammen in der technischen Analyse verwendet werden kann, werfen wir kurz einen Blick auf die Theorie zur Mustererkennung, die der menschlichen Entscheidungsmethode weit näher ist, als die formellen mathematischen Analysemethoden.

Abbildung 4 zeigt, gemäß der Theorie zur Mustererkennung, ein vereinfachtes Schema der Entscheidungsfindung. In diesem Fall kann eine Entscheidung eine Definition des Start- oder Endmoments eines Trends sein und die Entdeckung der optimalen Moments zur Öffnung einer Position von Zeit-Momenten, usw.

 

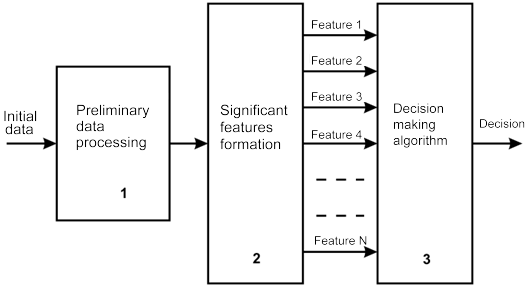
Abb. 4. Schema der Entscheidungsfindung

Wie in Abb. 4 gezeigt, werden die ursprünglichen Daten (Kurse) vorläufig behandelt und aus ihnen in Block 2 signifikante Merkmale gebildet. In unserem Fall handelt es sich bei diesen Werten um «Niedrig», «Hoch», «Öffnen» und «Schließen». Auf die Vorgänge in Block 1 und 2 haben wir keinen Einfluss. Auf der Terminal-Seite sind nur die Merkmale vorhanden, die uns sowieso schon zur Verfügung stehen. Diese Merkmale gelangen dann zu Block 3, wo aufgrund dieser Merkmal dann Entscheidungen getroffen werden.

Algorithmen zur Entscheidungsfindung können unter strenger Befolgung der Spezifikationen in die Software oder auch manuell implementiert werden. Wir können derartige Algorithmen entwickeln und auch bis zu einem gewissen Grad implementieren, aber wir können keine signifikanten Merkmale aus der analysierten Kursabfolge wählen, da uns diese Abfolge nicht zur Verfügung steht.

Vom Standpunkt der Anhebung der Wahrscheinlichkeit die richtige Entscheidung zu treffen ist der entscheidende Schritt die Wahl der signifikante Merkmale und in ihrer entscheidenden Menge - doch diese wichtige Möglichkeit haben wir nicht . Und deshalb ist es hier sehr schwierig, auf die Zuverlässigkeit dieser oder jener Erkenntnis der Marktsituation Einfluss zu nehmen, da selbst der fortschrittlichste Algorithmus zur Entscheidungsfindung auch nicht in der Lage ist, die Nachteile im Zusammenhang mit einer nicht optimalen Auswahl von Merkmalen zu kompensieren.

Was ist denn überhaupt ein Algorithmus zur Entscheidungsfindung, gemäß dieses Schemas? In unserem Fall ist er eine Reihe von Regeln, die in der Forschung der Kerzendiagrammanalyse publiziert wurde. Zum Beispiel die Definition der Arten an Kerzendiagrammen, die Darlegung der Bedeutung, was ihre verschiedenen Kombinationen bedeuten, usw..

Unter Bezugnahme auf die Theorie zur Mustererkennung können wir schlussfolgern, dass die Kerzendiagramm-Analyse zum Schema dieser Theorie passt, wir jedoch keinerlei Grund haben, mit Sicherheit sagen zu können, dass die Wahl der «Niedrig», «Hoch», «Öffnen» und «Schließen» Werte als bedeutsame Merkmale das Optimum ist. Zudem kann eine nicht optimale Wahl an Merkmalen die Wahrscheinlichkeit, in einem Analyseprozess von Kursen auch wirklich die richtige Entscheidungen zu treffen, erheblich schmälern.

Um zum Zitat von oben zurückzukommen: Wir können ziemlich sicher sagen, dass eine Kerzendiagramm-Analyse wohl kaum bis ins "Innere der Finanzmärkte vordringen" würde oder die "Eigendynamik innerhalb der Daten erkennen kann" erkennen kann. Ganz im Gegenteil: ihre Wirksamkeit, verglichen mit anderen Methoden der technischen Analyse kann ernsthafte Zweifel aufkommen lassen.

Fazit

Die technische Analyse ist ein reichlich konservatives Feld. Die Formulierung der grundlegenden Axiome der technischen Analyse hatte ihren Ursprung bereits im 18. und 19. Jahrhundert - und die Grundlagen haben sich bis heute nur unwesentlich verändert. Doch haben sich gleichzeitig im vergangenen Jahrzehnt die globalen Marktstrukturen während seiner Entwicklung drastisch verändert. Die Entwicklung des Online-Handels hat maßgeblich zur Art des Marktverhaltens beigetragen.

Vor diesem Hintergrund, werden uns der Einsatz der bekanntesten und beliebtesten Theorien und Methoden klassischer technischer Analyse eben nicht zuverlässig eine ausreichende Handels-Effizienz garantieren.

Nichtsdestotrotz kann sich die Verfügbarkeit von Computern und das Interesse am Handeln auf Märkten, das sich bei Menschen unterschiedlichster Berufe zeigt, nur anregend auf die Entwicklung der technische Analysemethoden auswirken. Es ist ganz klar, dass eine moderne Analyse des aktuellen Marktes die Entwicklung weitaus exakterer und empfindlicherer Analysetools benötigt.