La teoria del caos nel trading (Parte 1): Introduzione, applicazione ai mercati finanziari ed esponente di Lyapunov

Introduzione alla teoria del caos e al suo rapporto con i mercati finanziari

Che cos'è la teoria del caos e come può essere applicata ai mercati finanziari? Affronteremo questo tema nel corso dell'articolo.

Scriverò una serie di articoli che risponderanno alle domande su cosa sia la teoria del caos e in che modo il concetto di caos nel mercato, proposto da Bill Williams, differisca dalla teoria convenzionale, scientificamente fondata. In che modo la teoria descrive il mercato? Come e in quali aree del trading può essere applicata? 

Analizzeremo sia le basi teoriche che la creazione di una serie di strumenti che possono aiutare i trader nel trading.

Concetti di base della teoria del caos: Attrattori, frattali ed effetto farfalla

La teoria del caos è un interessante campo della matematica e della fisica che ci aiuta a comprendere meglio i sistemi complessi, come i mercati finanziari. Vediamo le tre idee principali di questa teoria:

1. Attrattori: Questi sono come calamite per gli stati del sistema - il sistema gravita verso di essi nel tempo. Nei mercati finanziari, questi possono essere prezzi specifici o schemi ripetuti che il mercato ripropone più volte. Gli attrattori strani, che si possono trovare nei sistemi caotici, sono di particolare interesse. Sembrano complessi e possono rivelare un ordine nascosto nel comportamento casuale del mercato.

2. Frattali: Si tratta di forme geometriche che hanno lo stesso aspetto a qualsiasi livello di ingrandimento. Nei mercati finanziari, i frattali possono essere osservati nei grafici dei prezzi - lo stesso schema può essere visto sia su brevi che su timeframe lunghi. Ciò consente di applicare gli stessi metodi di analisi a diversi intervalli di tempo, aiutando ad analizzare le variazioni dei prezzi e a valutare i rischi.

3. Effetto farfalla: Questo effetto dimostra che anche i cambiamenti più piccoli all'inizio possono portare a grandi e inaspettate conseguenze. Nel mondo della finanza, questo significa che piccoli cambiamenti nei dati o nel modello possono modificare drasticamente le previsioni. Ciò rende difficile la previsione a lungo termine nei mercati finanziari e sottolinea l'importanza di aggiornare e adattare continuamente i nostri modelli alle nuove condizioni.

La comprensione di queste idee aiuta gli analisti e i trader a guardare i mercati in modo nuovo, scoprendo modelli nascosti e possibili punti di ingresso o di uscita per le operazioni. La teoria del caos apre nuove strade per l'analisi e la previsione che vanno oltre i modelli convenzionali.

Sistemi caotici nel contesto dei mercati finanziari

I mercati finanziari hanno le caratteristiche di sistemi caotici, il che è importante per la loro analisi e previsione.

• Non linearità: Piccoli cambiamenti causano fluttuazioni sproporzionate.
• Sensibilità alle condizioni iniziali: Piccoli eventi possono portare a grandi movimenti.
• Auto-organizzazione: Formazione di trend e pattern senza controllo esterno.
• Struttura frattale: I grafici dei prezzi presentano proprietà frattali.
• Prevedibilità limitata: L'accuratezza delle previsioni diminuisce con l'aumentare dell'orizzonte.
• Strani attrattori: Fluttuazioni intorno a determinati livelli o stati.
• Transizioni tra stati: Improvvise transizioni dalla stabilità alla volatilità.

La comprensione di questo aspetto aiuta a sviluppare sofisticati metodi di analisi, gestione del rischio e algoritmi di trading.

Volatilità nel trading

La volatilità è un concetto chiave nel trading e nella finanza, legato alla teoria del caos. Misura la variazione del prezzo di un'asset in un determinato periodo di tempo. Nel trading, la volatilità aiuta a valutare il rischio, a prezzare le opzioni e a sviluppare strategie di trading.

I mercati finanziari si comportano spesso come sistemi caotici. Possono reagire in modo inaspettato a piccoli cambiamenti, come l'effetto farfalla. I mercati possono anche auto-organizzarsi, creando trend e pattern senza alcun intervento esterno, e i grafici dei prezzi mostrano somiglianze tra i diversi timeframe, che sono chiamate proprietà frattali.

La teoria del caos offre strumenti unici per l'analisi della volatilità, come la ricostruzione dello spazio di fase e l'esponente di Lyapunov, che aiutano a trovare modelli nascosti e a valutare la prevedibilità. Questi modelli caotici possono integrare i metodi tradizionali come i modelli GARCH, in particolare per identificare i regimi di mercato e prevedere brusche variazioni della volatilità.

La comprensione della natura caotica della volatilità apre nuove opportunità per un'analisi e previsioni più accurate delle dinamiche di mercato, che portano allo sviluppo di strategie di trading efficienti e di metodi di gestione del rischio.

La teoria del caos convenzionale e l'approccio di Bill Williams

La teoria del caos convenzionale e il concetto di "caos" di Bill Williams sono molto diversi. Il primo si basa su principi matematici rigorosi e utilizza strumenti sofisticati per analizzare i sistemi. Quest'ultimo, invece, utilizza un approccio intuitivo e indicatori tecnici, come Alligator e Fractals, che non hanno un legame diretto con la teoria matematica del caos.

La teoria del caos convenzionale si basa su principi matematici rigorosi e sulla ricerca scientifica nel campo della dinamica non lineare. Utilizza metodi matematici rigorosi e considera il caos come un comportamento deterministico ma imprevedibile. Williams usa il termine "caos" in modo più generico, riferendosi all'imprevedibilità generale dei mercati. I suoi metodi sono finalizzati all'applicazione pratica nel trading, piuttosto che all'analisi approfondita della natura caotica dei mercati.

Sebbene Williams abbia adattato alcuni termini della teoria del caos, il suo approccio si basa più sull'analisi tecnica e sull'interpretazione personale dei movimenti di mercato. Ciò ha attirato le critiche dei teorici del caos, che ritengono fuorviante l'uso del termine "caos" in questo contesto.

La teoria del caos nell'analisi di mercato

La teoria del caos offre una nuova prospettiva di analisi delle dinamiche di mercato, riconoscendo la complessità e l'imprevedibilità dei mercati finanziari. A differenza dei metodi tradizionali, la teoria del caos tiene conto della non linearità e della complessità dei processi di mercato.

Questo approccio aiuta a spiegare perché piccoli eventi possono portare a grandi movimenti di mercato e perché le previsioni a lungo termine sono spesso inaccurate. La teoria del caos ci permette di analizzare fenomeni come i crolli e le bolle di mercato, fornendo nuovi strumenti per un'analisi di mercato più accurata e adattabile.

L'esponente di Lyapunov e la sua applicazione nell'analisi delle serie temporali finanziarie

L'esponente di Lyapunov è uno strumento della teoria del caos che ci aiuta a capire quanto un sistema sia sensibile alle condizioni iniziali. Nei mercati finanziari, questo è importante perché permette di stimare quanto cambieranno i prezzi con piccole variazioni delle condizioni di mercato.

Se l'esponente di Lyapunov è positivo, significa che il sistema si comporta in modo caotico: piccoli cambiamenti possono portare a grandi fluttuazioni nel futuro. Se l'esponente è negativo, il sistema è più stabile e i prezzi cambiano meno.

Utilizzando questo esponente, è possibile determinare quando il mercato diventa più volatile e prevedibile. Valori elevati possono indicare possibili brusche variazioni di prezzo, utili per valutare il rischio e adeguare le strategie di trading.

Per calcolare l'esponente di Lyapunov nei dati finanziari, è necessario creare uno spazio di fase analizzando la divergenza dei punti più vicini in questo spazio. Questo processo richiede la scelta dei parametri giusti, come la dimensione e il ritardo.

Un aspetto importante dell'utilizzo dell'esponente di Lyapunov è quello di stimare per quanto tempo le previsioni saranno accurate. Più alto è il valore dell'esponente, più breve è il periodo durante il quale le previsioni rimangono affidabili. È particolarmente utile per il trading a breve termine e la gestione del rischio.

Ora possiamo iniziare a implementare l'esponente di Lyapunov in MQL5.

Implementazione dell'esponente di Lyapunov utilizzando MQL5

Questo indicatore implementa il calcolo dell'esponente di Lyapunov per l'analisi delle serie temporali finanziarie. Consente di valutare il grado di caos del mercato e la potenziale prevedibilità dei movimenti dei prezzi.

Inputs:

input int    InpTimeLag = 1;       // Time lag
input int    InpEmbedDim = 2;      // Embedding dimension
input int    InpDataLength = 1000; // Data length for calculation

• InpTimeLag - ritardo per la ricostruzione dello spazio di fase.
• InpEmbedDim - dimensione di incorporamento per la ricostruzione dello spazio di fase.
• InpDataLength - numero di candele utilizzate per calcolare l'indicatore.

Esiste una variabile globale:

double LyapunovBuffer[];

Inizializzazione:

int OnInit()
{
   SetIndexBuffer(0, LyapunovBuffer, INDICATOR_DATA);
   IndicatorSetInteger(INDICATOR_DIGITS, 5);
   IndicatorSetString(INDICATOR_SHORTNAME, "Lyapunov Exponent");
   return(INIT_SUCCEEDED);
}

Nella funzione OnInit() configuriamo il buffer dell'indicatore, impostiamo la precisione di visualizzazione a 5 cifre decimali e stabiliamo un nome breve per l'indicatore.

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   int start;
   if(prev_calculated == 0)
      start = InpDataLength;
   else
      start = prev_calculated - 1;
   
   for(int i = start; i < rates_total; i++)
   {
      LyapunovBuffer[i] = CalculateLyapunovExponent(close, i);
   }
   
   return(rates_total);
}

La funzione OnCalculate() viene richiamata a ogni tick ed esegue il calcolo dell'esponente di Lyapunov per ogni candela a partire da InputDataLength.

Calcolo dell'esponente di Lyapunov:

double CalculateLyapunovExponent(const double &price[], int index)
{
   if(index < InpDataLength)
      return 0;
   
   double sum = 0;
   int count = 0;
   
   for(int i = 0; i < InpDataLength - (InpEmbedDim - 1) * InpTimeLag; i++)
   {
      int nearestNeighbor = FindNearestNeighbor(price, index - InpDataLength + i, index);
      if(nearestNeighbor != -1)
      {
         double initialDistance = MathAbs(price[index - InpDataLength + i] - price[nearestNeighbor]);
         double finalDistance = MathAbs(price[index - InpDataLength + i + InpTimeLag] - price[nearestNeighbor + InpTimeLag]);
         
         if(initialDistance > 0 && finalDistance > 0)
         {
            sum += MathLog(finalDistance / initialDistance);
            count++;
         }
      }
   }
   
   if(count > 0)
      return sum / (count * InpTimeLag);
   else
      return 0;
}

La funzione CalculateLyapunovExponent() implementa l'algoritmo per il calcolo dell'esponente di Lyapunov locale. Utilizza il metodo del nearest neighbor per stimare la divergenza delle traiettorie nello spazio delle fasi ricostruito.

Ricerca del vicino più prossimo:

int FindNearestNeighbor(const double &price[], int startIndex, int endIndex)
{
   double minDistance = DBL_MAX;
   int nearestIndex = -1;
   
   for(int i = startIndex; i < endIndex - (InpEmbedDim - 1) * InpTimeLag; i++)
   {
      if(MathAbs(i - startIndex) > InpTimeLag)
      {
         double distance = 0;
         for(int j = 0; j < InpEmbedDim; j++)
         {
            distance += MathPow(price[startIndex + j * InpTimeLag] - price[i + j * InpTimeLag], 2);
         }
         distance = MathSqrt(distance);
         
         if(distance < minDistance)
         {
            minDistance = distance;
            nearestIndex = i;
         }
      }
   }
   
   return nearestIndex;
}

La funzione FindNearestNeighbor() trova il punto più vicino nello spazio di fase ricostruito utilizzando la distanza euclidea.

Interpretazione dei risultati

• Valori positivi dell'indicatore indicano la presenza di un comportamento caotico del mercato.
• I valori negativi indicano dinamiche di prezzo più stabili e potenzialmente prevedibili.
• Più alto è il valore assoluto dell'indicatore, più pronunciata è la caratteristica corrispondente (caotica o stabile).

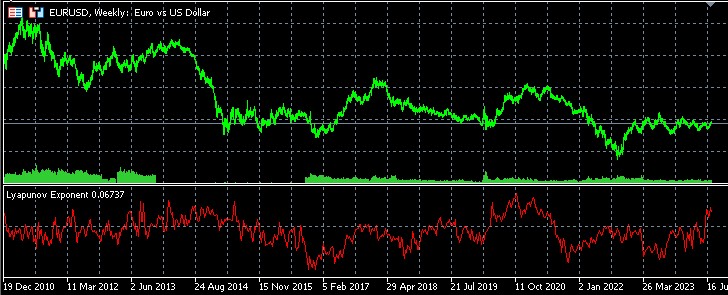
Analisi statistica delle inversioni e delle continuazioni di trend utilizzando l'esponente di Lyapunov

Ho sviluppato uno script speciale nel linguaggio MQL5 per uno studio approfondito della relazione tra l'esponente di Lyapunov e la dinamica dei mercati finanziari. Questo strumento consente un'analisi statistica dettagliata delle inversioni e delle continuazioni dei trend nel contesto dei valori degli esponenti di Lyapunov, fornendo a trader e analisti preziose indicazioni sul comportamento del mercato.

Lo script lavora con i dati storici dello strumento finanziario selezionato, analizzando un numero specifico di barre. Per ogni barra, l'esponente di Lyapunov locale viene calcolato utilizzando il metodo di ricostruzione dello spazio di fase e di ricerca dei vicini. Questo approccio ci permette di valutare il grado di caos del sistema in ogni specifico momento.

Contemporaneamente, lo script analizza la dinamica dei prezzi, identificando le inversioni e le continuazioni dei trend. Un'inversione è definita come una situazione in cui il prezzo di chiusura attuale è superiore a quello precedente e quello successivo è inferiore a quello attuale (o viceversa). Tutti gli altri casi sono considerati una continuazione del trend.

La caratteristica principale dello script è la capacità di confrontare i momenti di inversione e continuazione del trend con i valori dell'esponente di Lyapunov. Questo ci permette di identificare modelli statistici tra il comportamento caotico del mercato e le sue dinamiche di prezzo. Lo script calcola il numero di inversioni e continuazioni dei trend che si verificano con valori positivi e negativi dell'esponente di Lyapunov.

Al termine dell'analisi, lo script visualizza statistiche dettagliate, compresi i valori assoluti e le percentuali delle inversioni di trend e delle prosecuzioni per i valori positivi e negativi dell'esponente di Lyapunov. Queste informazioni consentono ai trader di valutare quanto spesso le inversioni di trend coincidano con periodi di maggiore volatilità del mercato e viceversa, quanto spesso le prosecuzioni dei trend corrispondano a periodi più stabili.

Interpretazione dei risultati dell'analisi statistica

I risultati ottenuti dall'analisi statistica delle inversioni e delle continuazioni dei trend utilizzando l'esponente di Lyapunov forniscono dati interessanti sulla dinamica del mercato EURUSD sul timeframe orario.

Innanzitutto, si nota una distribuzione quasi uguale degli eventi tra valori positivi e negativi dell'esponente di Lyapunov. Sia le inversioni che le prosecuzioni dei trend si osservano in circa la metà dei casi con esponenti di Lyapunov positivi e negativi. Ciò potrebbe indicare che il mercato EURUSD su H1 mostra un equilibrio tra periodi di relativa stabilità e caos.

Valori positivi dell'esponente di Lyapunov, tipicamente associati a un comportamento più caotico e imprevedibile, si osservano in poco più della metà dei casi (50,61% per le inversioni e 51,09% per le continuazioni). Ciò potrebbe indicare una leggera prevalenza di periodi di maggiore volatilità o incertezza sul mercato.

Valori negativi dell'esponente di Lyapunov, solitamente interpretati come segno di un comportamento più ordinato e meno caotico del sistema, si osservano nel 49,39% delle inversioni e nel 48,91% delle prosecuzioni dei trend. Questi periodi possono essere caratterizzati da movimenti di prezzo più prevedibili, che seguono determinati schemi.

È interessante notare che la percentuale di inversioni e di continuazione dei trend è quasi identica per i valori di Lyapunov sia positivi che negativi. La differenza è inferiore allo 0,5% in entrambi i casi. Ciò potrebbe indicare che l'esponente di Lyapunov in sé non è un fattore determinante per prevedere l'inversione o la continuazione di un trend.

Questa distribuzione uniforme degli eventi tra valori di Lyapunov positivi e negativi può indicare la natura complessa del mercato EURUSD, in cui i periodi di stabilità e caos si alternano con una frequenza approssimativamente uguale. 

Conclusioni

La teoria del caos offre un approccio innovativo all'analisi dei mercati finanziari, consentendo una comprensione più approfondita della loro natura complessa e non lineare. In questo articolo abbiamo analizzato i concetti chiave della teoria del caos (attrattori, frattali ed effetto farfalla) e la loro applicazione alle serie temporali finanziarie. Particolare attenzione è stata dedicata all'esponente di Lyapunov come strumento per valutare il grado di caos nelle dinamiche di mercato.