La théorie du chaos dans le trading (1ère partie) : Introduction, application aux marchés financiers et exposant de Lyapunov

Introduction à la théorie du chaos et à sa relation avec les marchés financiers

Qu'est-ce que la théorie du chaos et comment peut-elle être appliquée aux marchés financiers ? Nous aborderons cette question dans l'article.

Je vais écrire une série d'articles qui répondront aux questions suivantes : qu'est-ce que la théorie du chaos et en quoi le concept de chaos sur le marché, proposé par Bill Williams, diffère de la théorie conventionnelle, fondée sur des données scientifiques. Comment la théorie décrit-elle le marché ? Comment et dans quels domaines de trading peut-elle être appliquée ? 

Nous analyserons à la fois la base théorique et la création d'un certain nombre d'outils qui peuvent aider les traders dans leur activité.

Concepts de base de la théorie du chaos : Attracteurs, fractales et effet papillon

La théorie du chaos est un domaine intéressant des mathématiques et de la physique qui nous aide à mieux comprendre les systèmes complexes, tels que les marchés financiers. Examinons les trois idées principales de cette théorie :

1. Attracteurs: Ceux-ci sont comme des aimants pour les états du système - le système gravite autour d'eux au fil du temps. Sur les marchés financiers, il peut s'agir de prix spécifiques ou de schémas répétitifs auxquels le marché revient sans cesse. Les attracteurs étranges, que l'on peut trouver dans les systèmes chaotiques, sont particulièrement intéressants. Ils semblent complexes et peuvent révéler un ordre caché dans le comportement aléatoire du marché.

2. Fractales: Il s'agit de formes géométriques qui se ressemblent quel que soit le niveau de grossissement. Sur les marchés financiers, les fractales peuvent être observées dans les graphiques de prix - le même schéma peut être observé à la fois à court et à long terme. Cela permet d'appliquer les mêmes méthodes d'analyse à différents intervalles de temps, ce qui facilite l'analyse des variations de prix et l'évaluation des risques.

3. Effet papillon: Cet effet montre que même les plus petits changements au départ peuvent avoir des conséquences importantes et inattendues. Dans le monde de la finance, cela signifie que de petits changements dans les données ou dans le modèle peuvent modifier les prévisions de façon spectaculaire. Cela rend difficile les prévisions à long terme sur les marchés financiers et souligne l'importance d'une mise à jour et d'une adaptation permanentes de nos modèles aux nouvelles conditions.

La compréhension de ces idées permet aux analystes et aux traders d'envisager les marchés sous un angle nouveau, en découvrant des schémas cachés et des points d'entrée ou de sortie possibles pour les transactions. La théorie du chaos ouvre de nouvelles voies d'analyse et de prédiction qui vont au-delà des modèles conventionnels.

Systèmes chaotiques dans le contexte des marchés financiers

Les marchés financiers présentent les caractéristiques de systèmes chaotiques, ce qui est important pour leur analyse et leurs prévisions.

• Non-linéarité : De petites modifications entraînent des fluctuations disproportionnées.
• Sensibilité aux conditions initiales : De petits événements peuvent entraîner de grands mouvements.
• Auto-organisation : Formation de tendances et de modèles sans contrôle externe.
• Structure fractale : Les graphiques de prix présentent des propriétés fractales.
• Prévisibilité limitée : La précision des prévisions diminue avec l'augmentation de l'horizon.
• Attracteurs étranges : Fluctuations autour de certains niveaux ou états.
• Transitions entre les états : Transitions soudaines de la stabilité à la volatilité.

Comprendre cela permet de développer des méthodes d'analyse sophistiquées, des algorithmes de gestion des risques et de trading.

Volatilité des échanges

La volatilité est un concept clé du trading et de la finance, lié à la théorie du chaos. Elle mesure l'évolution du prix d'un actif sur une période donnée. En matière de trading, la volatilité permet d'évaluer les risques, de fixer le prix des options et d'élaborer des stratégies de trading.

Les marchés financiers se comportent souvent comme des systèmes chaotiques. Ils peuvent réagir de manière inattendue à de petits changements, un peu comme l'effet papillon. Les marchés peuvent également s'auto-organiser, créant des tendances et des modèles sans intervention extérieure, les graphiques de prix présentant des similitudes entre différentes périodes, ce que l'on appelle des propriétés fractales.

La théorie du chaos offre des outils uniques pour l'analyse de la volatilité, tels que la reconstruction de l'espace de phase et l'exposant de Lyapounov, qui permettent de trouver des modèles cachés et d'évaluer la prévisibilité. Ces modèles chaotiques peuvent compléter les méthodes traditionnelles telles que les modèles GARCH, notamment pour identifier les régimes de marché et prédire les changements brusques de volatilité.

La compréhension de la nature chaotique de la volatilité ouvre de nouvelles possibilités d'analyse et de prévision plus précises de la dynamique des marchés, ce qui permet de développer des stratégies de trading et des méthodes de gestion des risques efficaces.

La théorie conventionnelle du chaos et l'approche de Bill Williams

La théorie conventionnelle du chaos et le concept de "chaos" de Bill Williams sont très différents. La première s'appuie sur des principes mathématiques rigoureux et utilise des outils sophistiqués pour analyser les systèmes. Le second, en revanche, utilise une approche intuitive et des indicateurs techniques, tels que l'Alligator et les Fractales, qui n'ont pas de lien direct avec la théorie mathématique du chaos.

La théorie conventionnelle du chaos repose sur des principes mathématiques rigoureux et sur la recherche scientifique dans le domaine de la dynamique non linéaire. Elle utilise des méthodes mathématiques rigoureuses et considère que le chaos présente un comportement déterministe mais imprévisible. Williams utilise le terme "chaos" de manière plus vague, en faisant référence à l'imprévisibilité générale des marchés. Ses méthodes visent une application pratique dans le domaine du trading, plutôt qu'une analyse approfondie de la nature chaotique des marchés.

Bien que Williams ait adapté certains termes de la théorie du chaos, son approche est davantage basée sur l'analyse technique et l'interprétation personnelle des mouvements du marché. Cela a suscité des critiques de la part des théoriciens du chaos, qui considèrent que l'utilisation du terme "chaos" dans ce contexte est trompeuse.

La théorie du chaos dans l'analyse du marché

La théorie du chaos offre une nouvelle perspective sur l'analyse de la dynamique des marchés, en reconnaissant la complexité et l'imprévisibilité des marchés financiers. Contrairement aux méthodes traditionnelles, la théorie du chaos tient compte de la non-linéarité et de la complexité des processus de marché.

Cette approche permet d'expliquer pourquoi de petits événements peuvent entraîner de grands mouvements de marché et pourquoi les prévisions à long terme sont souvent inexactes. La théorie du chaos nous permet d'analyser des phénomènes tels que les krachs boursiers et les bulles, en fournissant de nouveaux outils pour une analyse plus précise et adaptative des marchés.

L'exposant de Lyapounov et son application à l'analyse des séries temporelles financières

L'exposant de Lyapounov est un outil de la théorie du chaos qui nous aide à comprendre la sensibilité d'un système aux conditions initiales. Sur les marchés financiers, cet aspect est important car il permet d'estimer l'ampleur des variations de prix en cas de changements mineurs des conditions du marché.

Si l'exposant de Lyapounov est positif, cela signifie que le système se comporte de manière chaotique : de petits changements peuvent entraîner de grandes fluctuations à l'avenir. Si l'exposant est négatif, le système est plus stable et les prix varient moins.

Cet exposant permet de déterminer à quel moment le marché devient plus volatil et plus prévisible. Des valeurs élevées peuvent indiquer la possibilité de fortes variations de prix, ce qui est utile pour évaluer les risques et ajuster les stratégies de trading.

Pour calculer l'exposant de Lyapounov dans les données financières, il est nécessaire de créer un espace de phase en analysant la divergence des points proches dans cet espace. Ce processus nécessite de choisir les bons paramètres, tels que la dimension et le délai.

Un aspect important de l'utilisation de l'exposant de Lyapounov est l'estimation de la durée de validité des prévisions. Plus la valeur de l'exposant est élevée, plus la période pendant laquelle les prévisions restent fiables est courte. Cette fonction est particulièrement utile pour les opérations à court terme et la gestion des risques.

Nous pouvons maintenant commencer à implémenter l'exposant de Lyapounov dans MQL5.

Mise en œuvre de l'exposant de Lyapounov à l'aide de MQL5

Cet indicateur implémente le calcul de l'exposant de Lyapounov pour l'analyse des séries temporelles financières. Il permet d'évaluer le degré de chaos sur le marché et la prévisibilité potentielle des mouvements de prix.

Entrées :

input int    InpTimeLag = 1;       // Time lag
input int    InpEmbedDim = 2;      // Embedding dimension
input int    InpDataLength = 1000; // Data length for calculation

• InpTimeLag - délai de reconstruction de l'espace de phase.
• InpEmbedDim - dimension d'intégration pour la reconstruction de l'espace de phase.
• InpDataLength - nombre de bougies utilisées pour calculer l'indicateur.

Il existe une variable globale :

double LyapunovBuffer[];

Initialisation :

int OnInit()
{
   SetIndexBuffer(0, LyapunovBuffer, INDICATOR_DATA);
   IndicatorSetInteger(INDICATOR_DIGITS, 5);
   IndicatorSetString(INDICATOR_SHORTNAME, "Lyapunov Exponent");
   return(INIT_SUCCEEDED);
}

Dans la fonction OnInit(), nous configurons la mémoire tampon de l'indicateur, nous fixons la précision de l'affichage à 5 décimales et nous définissons un nom court pour l'indicateur.

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   int start;
   if(prev_calculated == 0)
      start = InpDataLength;
   else
      start = prev_calculated - 1;
   
   for(int i = start; i < rates_total; i++)
   {
      LyapunovBuffer[i] = CalculateLyapunovExponent(close, i);
   }
   
   return(rates_total);
}

La fonction OnCalculate() est appelée à chaque tick et effectue le calcul de l'exposant de Lyapunov pour chaque bougie à partir de InpDataLength.

Calcul de l'exposant de Lyapounov :

double CalculateLyapunovExponent(const double &price[], int index)
{
   if(index < InpDataLength)
      return 0;
   
   double sum = 0;
   int count = 0;
   
   for(int i = 0; i < InpDataLength - (InpEmbedDim - 1) * InpTimeLag; i++)
   {
      int nearestNeighbor = FindNearestNeighbor(price, index - InpDataLength + i, index);
      if(nearestNeighbor != -1)
      {
         double initialDistance = MathAbs(price[index - InpDataLength + i] - price[nearestNeighbor]);
         double finalDistance = MathAbs(price[index - InpDataLength + i + InpTimeLag] - price[nearestNeighbor + InpTimeLag]);
         
         if(initialDistance > 0 && finalDistance > 0)
         {
            sum += MathLog(finalDistance / initialDistance);
            count++;
         }
      }
   }
   
   if(count > 0)
      return sum / (count * InpTimeLag);
   else
      return 0;
}

La fonction CalculateLyapunovExponent() implémente l'algorithme de calcul de l'exposant de Lyapounov local. Il utilise la méthode du plus proche voisin pour estimer la divergence des trajectoires dans l'espace des phases reconstruit.

Recherche du plus proche voisin :

int FindNearestNeighbor(const double &price[], int startIndex, int endIndex)
{
   double minDistance = DBL_MAX;
   int nearestIndex = -1;
   
   for(int i = startIndex; i < endIndex - (InpEmbedDim - 1) * InpTimeLag; i++)
   {
      if(MathAbs(i - startIndex) > InpTimeLag)
      {
         double distance = 0;
         for(int j = 0; j < InpEmbedDim; j++)
         {
            distance += MathPow(price[startIndex + j * InpTimeLag] - price[i + j * InpTimeLag], 2);
         }
         distance = MathSqrt(distance);
         
         if(distance < minDistance)
         {
            minDistance = distance;
            nearestIndex = i;
         }
      }
   }
   
   return nearestIndex;
}

La fonction FindNearestNeighbor() trouve le point le plus proche dans l'espace des phases reconstruit en utilisant la distance euclidienne.

Interprétation des résultats

• Des valeurs positives de l'indicateur indiquent la présence d'un comportement chaotique du marché.
• Des valeurs négatives indiquent une dynamique des prix plus stable et potentiellement prévisible.
• Plus la valeur absolue de l'indicateur est élevée, plus la caractéristique correspondante est prononcée (chaotique ou stable).

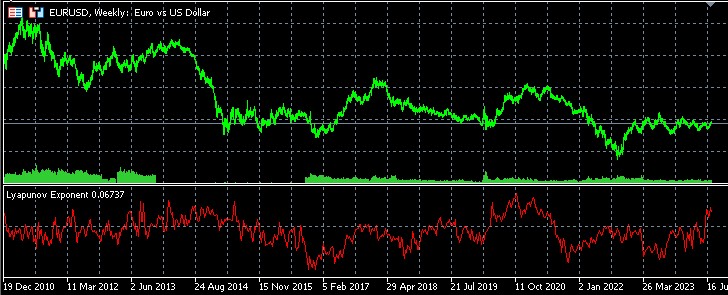
Analyse statistique des inversions et des prolongements de tendance à l'aide de l'exposant de Lyapounov

J'ai développé un script spécialisé dans le langage MQL5 pour une étude approfondie de la relation entre l'exposant de Lyapounov et la dynamique des marchés financiers. Cet outil permet une analyse statistique détaillée des renversements et des prolongements de tendance dans le contexte des valeurs de l'exposant de Lyapounov, fournissant aux traders et aux analystes des informations précieuses sur le comportement du marché.

Le script travaille avec les données historiques de l'instrument financier sélectionné, en analysant un nombre spécifié de barres. Pour chaque barre, l'exposant local de Lyapounov est calculé en utilisant la reconstruction de l'espace de phase et la méthode de recherche du plus proche voisin. Cette approche nous permet d'évaluer le degré de chaos dans le système à chaque moment précis.

Simultanément, le script analyse la dynamique des prix, identifiant les renversements et les prolongements de tendance. Un renversement est défini comme une situation dans laquelle le cours de clôture actuel est supérieur au cours précédent et le cours suivant est inférieur au cours actuel (ou vice versa). Tous les autres cas sont considérés comme une continuation de la tendance.

La principale caractéristique du script est sa capacité à comparer les moments des renversements et des prolongements de tendance avec les valeurs de l'exposant de Lyapounov. Cela nous permet d'identifier des modèles statistiques entre le comportement chaotique du marché et la dynamique de ses prix. Le script calcule le nombre de renversements et de prolongements de tendance qui se produisent avec des valeurs positives et négatives de l'exposant de Lyapounov.

Une fois l'analyse terminée, le script affiche des statistiques détaillées, y compris les valeurs absolues et les pourcentages d'inversion et de poursuite des tendances pour les valeurs positives et négatives de l'exposant de Lyapounov. Ces informations permettent aux traders d'évaluer la fréquence des renversements de tendance qui coïncident avec des périodes de volatilité accrue du marché et, inversement, la fréquence des prolongements de tendance qui correspondent à des périodes plus stables.

Interprétation des résultats de l'analyse statistique

Les résultats obtenus de l'analyse statistique des renversements et des prolongements de tendance à l'aide de l'exposant de Lyapounov fournissent des données intéressantes sur la dynamique du marché EURUSD sur l'échelle de temps de 1 heure.

Tout d'abord, l'attention est attirée sur la répartition presque égale des événements entre les valeurs positives et négatives de l'exposant de Lyapounov. Des inversions et des prolongements de tendance sont observés dans environ la moitié des cas avec des exposants de Lyapounov positifs et négatifs. Cela peut indiquer que le marché EURUSD sur H1 montre un équilibre entre des périodes de stabilité relative et de chaos.

Les valeurs positives de l'exposant de Lyapounov, qui sont généralement associées à un comportement plus chaotique et imprévisible, sont observées dans un peu plus de la moitié des cas (50,61% pour les inversions et 51,09% pour les continuations). Cela peut indiquer une légère prédominance des périodes de volatilité accrue ou d'incertitude sur le marché.

Des valeurs négatives de l'exposant de Lyapounov, généralement interprétées comme le signe d'un comportement plus ordonné et moins chaotique du système, sont observées dans 49,39% des inversions et 48,91% des prolongements de tendance. Ces périodes peuvent être caractérisées par des mouvements de prix plus prévisibles, suivant certains schémas.

Il est intéressant de noter que le pourcentage d'inversions et de prolongements de tendance est presque identique pour les valeurs de Lyapounov positives et négatives. La différence est inférieure à 0,5% dans les deux cas. Cela peut indiquer que l'exposant de Lyapounov lui-même n'est pas un facteur déterminant pour prédire le renversement ou la poursuite d'une tendance.

Cette répartition uniforme des événements entre valeurs de Lyapounov positives et négatives peut indiquer la nature complexe du marché EURUSD, où les périodes de stabilité et de chaos alternent à une fréquence à peu près égale. 

Conclusion

La théorie du chaos offre une approche novatrice de l'analyse des marchés financiers, permettant de mieux comprendre leur nature complexe et non linéaire. Dans cet article, nous avons examiné les concepts clés de la théorie du chaos (attracteurs, fractales et effet papillon) et leur application aux séries chronologiques financières. Une attention particulière a été accordée à l'exposant de Lyapounov en tant qu'outil permettant d'évaluer le degré de chaos dans la dynamique du marché.