트레이딩에서 카오스 이론(1부): 소개, 금융 시장에서의 적용 및 리아푸노프 지수

카오스 이론과 금융 시장과의 관계 소개

카오스 이론이란 무엇이며 금융 시장에 어떻게 적용할 수 있을까요? 그것이 이 글에서 다룰 예정입니다.

저는 카오스 이론이 무엇인지 그리고 빌 윌리엄스가 제안한 시장에서의 카오스 개념이 기존의 과학적 기반 이론과 어떻게 다른지에 대한 질문에 답하는 일련의 글을 작성할 것입니다. 이 이론은 시장을 어떻게 설명하나요? 이 이론을 거래의 어떤 영역에 어떻게 적용할 수 있나요? 

우리는 이론적 근거를 분석하고 트레이더의 트레이딩에 도움이 될 수 있는 여러 도구를 만들 것입니다.

카오스 이론의 기본 개념: 유인자, 프랙탈, 나비 효과

카오스 이론은 금융 시장과 같은 복잡한 시스템을 이해하는 데 도움이 되는 수학과 물리학의 흥미로운 분야입니다. 이 이론의 세 가지 주요 아이디어에 대해 살펴보겠습니다:

1. 어트랙터(Attractors): 이는 시스템 상태의 자석과 같습니다 - 시간이 지남에 따라 시스템이 그쪽으로 끌리게 됩니다. 금융 시장에서는 시장에 자주 보이는 반복적인 패턴 혹은 특정 가격일 수 있습니다. 혼란스러운 시장에서 발견할 수 있는 이상한 어트랙터는 특히 흥미롭습니다. 복잡해 보이지만 시장의 무작위적인 행동에 숨겨진 질서를 드러낼 수 있습니다.

2. 프랙탈(Fractals): 프랙탈은 어떤 배율의 수준이던지 동일하게 보이는 기하학적 도형으로 금융 시장의 가격 차트에서 볼 수 있으며 동일한 패턴을 단기 및 장기 차트 모두에서볼 수 있습니다. 이는 서로 다른 시간 간격에 걸쳐 동일한 분석 방법을 적용할 수 있다는 것을 의미하며 가격 변화를 분석하고 위험을 평가하는 데 도움이 됩니다.

3. 나비 효과(Butterfly effect): 이 효과는 처음에 아주 작은 변화라도 예상치 못한 큰 결과를 초래할 수 있음을 보여줍니다. 금융 분야에서의 측면에서 이는 데이터나 모델의 작은 변화로도 예측이 크게 달라질 수 있다는 뜻이기도 하며 금융 시장의 장기 예측을 어렵게 만들고 새로운 조건에 맞게 모델을 지속적으로 업데이트하고 조정하는 것의 중요성을 강조합니다.

이들을 이해하면 분석가와 트레이더가 새로운 방식으로 시장을 바라보고 숨겨진 패턴과 거래 진입 또는 청산 시점을 발견하는 데 도움이 됩니다. 카오스 이론은 기존의 모델을 뛰어넘는 새로운 분석 및 예측의 길을 열어줍니다.

금융 시장이란 측면에서 혼란스러운 시스템

금융 시장은 혼란스러운 시스템이란 특성을 가지고 있으며 이러한 특성은 분석과 예측시 중요합니다.

• 비선형성: 작은 변화가 불균형적인 변동을 일으킵니다.
• 초기 조건에 대한 민감도: 작은 이벤트가 큰 움직임으로 이어질 수 있습니다.
• 자기 조직화: 외부 통제 없이 트렌드와 패턴을 형성합니다.
• 프랙탈 구조: 가격 차트는 프랙탈 속성을 나타냅니다.
• 제한된 예측 가능성: 예측 정확도는 지평선이 길어질수록 감소합니다.
• 이상한 어트랙터: 특정 레벨 또는 상태 주변의 변동.
• 상태 간 전환: 안정에서 변동으로의 갑작스러운 전환.

이들을 이해하면 정교한 분석 방법 위험 관리 및 트레이딩 알고리즘을 개발하는 데 도움이 됩니다.

거래 변동성

변동성은 카오스 이론과 관련된 트레이딩 및 금융에서의 핵심 개념으로 특정 기간 동안 자산 가격이 얼마나 변했는지를 측정합니다. 트레이딩에 변동성은 위험 평가, 옵션 가격 책정, 트레이딩 전략의 개발에 도움이 됩니다.

금융 시장은 종종 혼란스러운 시스템처럼 작동하며 나비 효과와 비슷하게 작은 변화에 예기치 않게 반응할 수 있습니다. 또한 시장은 외부의 개입 없이도 스스로를 조직화 하여 추세와 패턴을 만들 수 있으며 가격 차트는 프랙탈 속성이라고 하는 여러 시간대에 걸친 유사성을 보여줍니다.

카오스 이론은 위상 공간 재구성 및 리아푸노프 지수 등 변동성을 분석하기 위한 고유한 도구를 제공하여 숨겨진 패턴을 찾고 예측 가능성을 평가하는 데 도움을 줍니다. 이러한 카오스 모델은 특히 시장 체제를 파악하고 변동성의 급격한 변화를 예측하는 데 있어 GARCH 모델과 같은 전통적인 방법을 보완할 수 있습니다.

변동성의 혼란스러운 특성을 이해하면 시장의 역학을 보다 정확하게 분석하고 예측할 수 있는 새로운 기회가 열리고 이는 효율적인 트레이딩 전략과 위험 관리 방법을 개발하는 데에 도움이 됩니다.

기존의 카오스 이론과 빌 윌리엄스의 접근 방식

기존의 카오스 이론과 빌 윌리엄스의 '카오스' 개념은 매우 다릅니다. 전자는 엄격한 수학적 원리에 의존하고 정교한 도구를 사용하여 시스템을 분석합니다. 반면 후자는 수학적 카오스 이론과 직접적인 관련이 없는 앨리게이터와 프랙탈과 같은 직관적인 접근 방식과 기술적 지표를 사용합니다.

기존의 카오스 이론은 비선형 역학의 엄격한 수학적 원리와 과학적 연구를 기반으로 하며 엄격한 수학적 방법을 사용하고 카오스는 결정론적이지만 예측할 수 없는 행동을 보이는 것으로 간주합니다. 윌리엄스는 시장의 일반적인 예측 불가능성을 언급하며 '카오스'라는 용어를 좀 더 느슨하게 사용합니다. 윌리엄스의 경우 시장의 혼란스러운 특성에 대한 심층 분석보다는 트레이딩에 실제 적용하는 데 초점을 맞추고 있습니다.

윌리엄스는 카오스 이론으로부터 일부 용어를 차용했지만 그의 접근 방식은 기술적 분석과 시장의 움직임에 대한 개인적인 해석에 더 기반을 두고 있습니다. 이러한 맥락에서 '카오스'라는 용어를 사용하는 것이 오해의 소지가 있다는 카오스 관련 이론가들의 비판이 제기되었습니다.

시장 분석에서 카오스 이론

카오스 이론은 금융 시장의 복잡성과 예측 불가능성을 인식하여 시장 역학 분석에 새로운 관점을 제시합니다. 기존의 전통적 방법과 달리 카오스 이론은 시장 프로세스의 비선형성과 복잡성을 고려합니다.

이러한 접근 방식은 작은 이벤트가 큰 시장의 움직임으로 이어질 수 있는 이유와 장기 예측이 종종 부정확한 이유를 설명하는 데 도움이 됩니다. 카오스 이론을 통해 시장 붕괴 및 거품과 같은 현상을 분석하여 보다 정확하고 적응력 있는 시장 분석을 위한 새로운 도구를 제공할 수 있습니다.

리아푸노프 지수와 금융 시계열 분석에의 적용

리아푸노프 지수는 카오스 이론의 도구로 시스템이 초기 조건에 얼마나 민감한지 이해하는 데 도움이 됩니다. 금융 시장에서는 시장 상황의 작은 변화에 따라 가격이 얼마나 변할지 예측할 수 있기 때문에 이 점이 중요합니다.

리아푸노프 지수가 양수이면 시스템이 혼란스럽게 작동한다는 의미로 작은 변화가 향후 큰 변동으로 이어질 수 있다는 것이며 음수이면 시스템이 더 안정적이고 가격 변동이 적습니다.

이 지수를 사용하면 시장의 변동성이 커지고 예측 가능한 시점을 확인할 수 있습니다. 값이 높으면 급격한 가격 변동이 일어날 것이란 가능성을 의미할 수 있으므로 위험을 평가하고 트레이딩 전략을 조정하도록 하는데에 유용합니다.

금융 데이터에서 리아푸노프 지수를 계산하려면 이 공간에서 가까운 점들이 얼마나 갈라지는지 분석하여 위상 공간을 만들어야 합니다. 이 프로세스에서는 차원 및 시간 지연과 같은 올바른 매개변수를 선택해야 합니다.

리아푸노프 지수를 사용할 때 중요한 측면 중 하나는 예측이 얼마나 오랫동안 정확할지를 측정하는 것입니다. 지수의 값이 높을수록 예측의 신뢰성이 유지되는 기간이 짧아집니다. 이는 단기 트레이딩과 리스크 관리에 특히 유용합니다.

이제 MQL5에서 리아푸노프 지수를 구현할 수 있습니다.

MQL5를 사용한 리아푸노프 지수 구현

이 지표는 재무 시계열 분석을 위한 리아푸노프 지수 계산을 구현합니다. 이를 통해 시장의 혼란 정도와 가격 변동에 대한 잠재적 예측 가능성을 평가할 수 있습니다.

입력:

input int    InpTimeLag = 1;       // Time lag
input int    InpEmbedDim = 2;      // Embedding dimension
input int    InpDataLength = 1000; // Data length for calculation

• InpTimeLag - 위상 공간 재구성을 위한 시간 지연입니다.
• InpEmbedDim - 위상 공간 재구성을 위한 임베딩 차원입니다.
• InpDataLength - 지표를 계산하는 데 사용되는 캔들 수입니다.

전역 변수가 하나 있습니다:

double LyapunovBuffer[];

초기화:

int OnInit()
{
   SetIndexBuffer(0, LyapunovBuffer, INDICATOR_DATA);
   IndicatorSetInteger(INDICATOR_DIGITS, 5);
   IndicatorSetString(INDICATOR_SHORTNAME, "Lyapunov Exponent");
   return(INIT_SUCCEEDED);
}

OnInit() 함수에서 지표 버퍼를 구성하고 표시 정밀도를 소수점 이하 5자리로 설정한 다음 지표의 이름을 설정합니다.

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   int start;
   if(prev_calculated == 0)
      start = InpDataLength;
   else
      start = prev_calculated - 1;
   
   for(int i = start; i < rates_total; i++)
   {
      LyapunovBuffer[i] = CalculateLyapunovExponent(close, i);
   }
   
   return(rates_total);
}

OnCalculate() 함수는 매 틱마다 호출되며 InpDataLength에서 시작하는 각 캔들에 대한 리아푸노프 지수 계산을 수행합니다.

리아푸노프 지수 계산:

double CalculateLyapunovExponent(const double &price[], int index)
{
   if(index < InpDataLength)
      return 0;
   
   double sum = 0;
   int count = 0;
   
   for(int i = 0; i < InpDataLength - (InpEmbedDim - 1) * InpTimeLag; i++)
   {
      int nearestNeighbor = FindNearestNeighbor(price, index - InpDataLength + i, index);
      if(nearestNeighbor != -1)
      {
         double initialDistance = MathAbs(price[index - InpDataLength + i] - price[nearestNeighbor]);
         double finalDistance = MathAbs(price[index - InpDataLength + i + InpTimeLag] - price[nearestNeighbor + InpTimeLag]);
         
         if(initialDistance > 0 && finalDistance > 0)
         {
            sum += MathLog(finalDistance / initialDistance);
            count++;
         }
      }
   }
   
   if(count > 0)
      return sum / (count * InpTimeLag);
   else
      return 0;
}

CalculateLyapunovExponent() 함수는 로컬 리아푸노프 지수를 계산하는 알고리즘을 구현합니다. 최근접 이웃 방법을 사용하여 재구성된 위상 공간에서 궤적의 발산을 추정합니다.

가장 가까운 이웃을 검색합니다:

int FindNearestNeighbor(const double &price[], int startIndex, int endIndex)
{
   double minDistance = DBL_MAX;
   int nearestIndex = -1;
   
   for(int i = startIndex; i < endIndex - (InpEmbedDim - 1) * InpTimeLag; i++)
   {
      if(MathAbs(i - startIndex) > InpTimeLag)
      {
         double distance = 0;
         for(int j = 0; j < InpEmbedDim; j++)
         {
            distance += MathPow(price[startIndex + j * InpTimeLag] - price[i + j * InpTimeLag], 2);
         }
         distance = MathSqrt(distance);
         
         if(distance < minDistance)
         {
            minDistance = distance;
            nearestIndex = i;
         }
      }
   }
   
   return nearestIndex;
}

FindNearestNeighbor() 함수는 유클리드 거리를 사용하여 재구성된 위상 공간에서 가장 가까운 점을 찾습니다.

결과 해석

• 지표의 양수 값은 혼란스러운 시장 움직임이 있음을 나타냅니다.
• 음수 값은 보다 안정적이고 잠재적으로 예측 가능한 가격 역학을 나타냅니다.
• 지표의 절대값이 높을수록 해당 특성(혼돈 또는 안정)이 더 뚜렷하게 나타납니다.

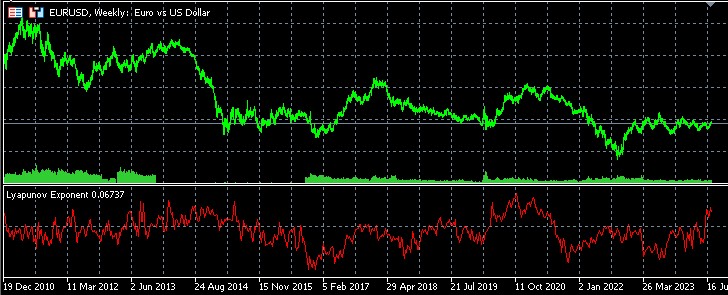
리아푸노프 지수를 사용한 추세 반전 혹은 지속에 대한 통계 분석

저는 리아푸노프 지수와 금융 시장의 역학 관계를 심층적으로 연구하기 위해 MQL5 언어로 된 특수 스크립트를 개발했습니다. 이 도구를 사용하면 리아푸노프 지수 값의 측면에서 추세 반전 및 지속에 대한 자세한 통계 분석을 통해 트레이더와 분석가에게 시장 움직임에 대한 귀중한 통찰력을 제공할 수 있습니다.

스크립트는 선택한 금융 상품의 과거 데이터를 기반으로 작동하며 지정된 수의 바를 분석합니다. 각각의 바에 대해 로컬 리아푸노프 지수는 위상 공간의 재구성 및 최근접 이웃 검색 메서드를 사용하여 계산됩니다. 이 접근 방식을 통해 각 특정 시점에서 시스템의 카오스 정도를 평가할 수 있습니다.

동시에 스크립트는 가격 역학을 분석하여 반전 및 추세의 지속을 식별합니다. 반전은 현재 종가가 이전 종가보다 높고 다음 종가가 현재 종가보다 낮은 상황(또는 그 반대)으로 정의됩니다. 다른 모든 사례는 추세의 연속으로 간주됩니다.

이 스크립트의 핵심 기능은 추세 반전 및 지속의 순간을 리아푸노프 지수 값과 비교하는 기능입니다. 이를 통해 시장의 혼란스러움과 가격 역학 사이의 통계적 패턴을 파악할 수 있습니다. 이 스크립트는 리아푸노프 지수의 양수 및 음수 값으로 발생하는 추세 반전 및 지속의 횟수를 계산합니다.

분석이 완료되면 스크립트는 리아푸노프 지수의 양수 및 음수 값에 대한 추세 반전 및 지속의 절대값과 백분율을 포함한 자세한 통계를 표시합니다. 이 정보를 통해 트레이더는 추세 반전이 시장 변동성이 커진 기간과 얼마나 자주 일치하는지 반대로 추세 지속이 더 안정된 기간과 얼마나 자주 일치하는지 평가할 수 있습니다.

통계 분석 결과 해석

리아푸노프 지수를 사용한 추세 반전 및 지속에 대한 통계 분석의 결과는 시간대별 EURUSD 시장의 역학에 대한 흥미로운 데이터를 제공합니다.

우선 리아푸노프 지수의 양수 값과 음수 값 사이의 이벤트 분포가 거의 동일하다는 점에 주목할 필요가 있습니다. 양수 및 음수 리아푸노프 지수를 가진 경우의 약 절반에서 반전과 추세 지속이 모두 관찰됩니다. 이는 EURUSD H1 시장이 상대적으로 안정된 시기와 혼란스러운 시기 사이에 균형을 이루고 있음을 나타낼 수 있습니다.

일반적으로 더 혼란스럽고 예측 불가능한 행동과 관련된 양의 리아푸노프 지수 값은 전체 사례의 절반 이상에서 관찰됩니다(반전의 경우 50.61%, 지속의 경우 51.09%). 이는 시장의 변동성이 커지거나 불확실성이 높아지는 시기가 약간 더 많다는 것을 나타낼 수 있습니다.

일반적으로 시스템이 좀 더 질서정연하고 덜 혼란스러운 행동의 신호로 해석되는 리아푸노프 지수의 음수 값은 반전의 49.39%와 추세 지속의 48.91%에서 관찰됩니다. 이 기간에는 특정 패턴에 따른 가격 변동이 더 예측 가능한 것이 특징일 수 있습니다.

흥미롭게도 추세 반전과 지속의 비율은 양수 및 음수 리아푸노프 값 모두에서 거의 동일합니다. 두 경우 모두 그 차이는 0.5% 미만입니다. 이는 리아푸노프 지수 자체가 추세의 반전이나 지속을 예측하는 결정 요인이 아니라는 것을 나타낼 수 있습니다.

양수 및 음수 리아푸노프 값 사이의 이벤트가 고르게 분포하는 것은 안정기와 혼돈기가 거의 동일한 빈도로 번갈아 나타나는 EURUSD 시장의 복잡한 특성을 나타낼 수 있습니다. 

결론

카오스 이론은 금융 시장 분석에 대한 혁신적인 접근 방식을 제공하여 복잡하고 비선형적인 금융 시장의 특성을 더 깊이 이해할 수 있게 해줍니다. 이 글에서는 카오스 이론의 핵심 개념(어트랙터, 프랙탈, 나비 효과)과 이를 금융 시계열에 적용하는 방법을 살펴봤습니다. 시장 역학에서 혼란의 정도를 평가하는 도구로 리아푸노프 지수에 특히 주목했습니다.