Datenwissenschaft und maschinelles Lernen (Teil 16): Ein frischer Blick auf die Entscheidungsbäume
284
0
Ein kurzer Rückblick
Ich habe in dieser Artikelserie einen Artikel über Entscheidungsbäume geschrieben, in dem ich erklärt habe, worum es bei Entscheidungsbäumen geht, und wir haben einen Algorithmus entwickelt, der uns bei der Klassifizierung der Wetterdaten hilft. Allerdings waren der Code und die Erklärungen in dem Artikel nicht prägnant genug. Da ich immer wieder Anfragen erhalte, einen besseren Ansatz zur Erstellung von Entscheidungsbäumen zu liefern, glaube ich, dass es besser wäre, einen zweiten Artikel zu schreiben und besseren Code für den Entscheidungsbaum bereitzustellen. Die Klärung der Entscheidungsbäume wird das Verständnis der Random-Forest-Algorithmen erleichtern, zu denen in Kürze ein Artikel erscheinen wird.
Was ist ein Entscheidungsbaum?
Ein Entscheidungsbaum ist eine Flussdiagramm-ähnliche Baumstruktur, bei der jeder interne Knoten einen Test auf ein Attribut (oder ein Merkmal) darstellt, jeder Zweig das Ergebnis des Tests und jeder Blattknoten ein Klassenlabel oder einen kontinuierlichen Wert darstellt. Der oberste Knoten in einem Entscheidungsbaum wird als „Wurzel“ bezeichnet, und die Blätter sind die Ergebnisse oder Vorhersagen.
Was ist ein Knotenpunkt?
In einem Entscheidungsbaum ist ein Knoten eine grundlegende Komponente, die einen Entscheidungspunkt auf der Grundlage eines bestimmten Merkmals oder Attributs darstellt. Es gibt zwei Haupttypen von Knoten in einem Entscheidungsbaum: interne Knoten und Blattknoten.
Interner Knotenpunkt- Ein interner Knoten ist ein Entscheidungspunkt in der Baumstruktur, an dem ein Test für ein bestimmtes Merkmal durchgeführt wird. Der Test beruht auf einer bestimmten Bedingung, z. B. ob ein Merkmalswert größer als ein Schwellenwert ist oder zu einer bestimmten Kategorie gehört.
- Interne Knoten haben Verzweigungen (Kanten), die zu Unterknoten führen. Das Ergebnis des Tests bestimmt, welcher Verzweigung man folgt.
- Die internen Knoten, d. h. zwei linke und rechte Kindknoten, sind Knoten innerhalb des zentralen Baumknotens.
- Ein Blattknoten markiert einen Endpunkt im Baum, an dem er eine endgültige Entscheidung oder Vorhersage trifft. Er bezeichnet das Klassenlabel in einer Klassifizierungsaufgabe oder den vorhergesagten Wert in einer Regressionsaufgabe.
- Blattknoten haben keine ausgehenden Verzweigungen; sie sind die Endpunkte des Entscheidungsprozesses.
- Wir kodieren dies als eine Doppelvariable.
class Node { public: // for decision node uint feature_index; double threshold; double info_gain; // for leaf node double leaf_value; Node *left_child; //left child Node Node *right_child; //right child Node Node() : left_child(NULL), right_child(NULL) {} // default constructor Node(uint feature_index_, double threshold_=NULL, Node *left_=NULL, Node *right_=NULL, double info_gain_=NULL, double value_=NULL) : left_child(left_), right_child(right_) { this.feature_index = feature_index_; this.threshold = threshold_; this.info_gain = info_gain_; this.value = value_; } void Print() { printf("feature_index: %d \nthreshold: %f \ninfo_gain: %f \nleaf_value: %f",feature_index,threshold, info_gain, value); } };
Im Gegensatz zu einigen ML-Algorithmen, die wir in dieser Serie von Grund auf kodiert haben, kann der Entscheidungsbaum schwierig zu kodieren und manchmal verwirrend sein, da es rekursive Klassen und Funktionen erfordert, was meiner Erfahrung nach in einer anderen Sprache als Python schwer zu kodieren ist.
Komponenten eines Knotens:
Ein Knoten in einem Entscheidungsbaum enthält normalerweise die folgenden Informationen:
01. Testbedingungen
Interne Knoten haben eine Prüfbedingung, die auf einem bestimmten Merkmal und einem Schwellenwert oder einer Kategorie basiert. Diese Bedingung legt fest, wie die Daten in Unterknoten aufgeteilt (split) werden.
Node *build_tree(matrix &data, uint curr_depth=0);
02. Merkmal und Schwellenwert
Gibt an, welches Merkmal an dem Knoten getestet wird und welcher Schwellenwert oder welche Kategorie für die Aufteilung verwendet wird.
uint feature_index; double threshold;
03. Klasse Bezeichnung oder Wert
Ein Blattknoten speichert die vorhergesagte Klassenbezeichnung (bei Klassifizierung) oder den Wert (bei Regression)
double leaf_value; 04. Kind-Knoten
Interne Knoten haben Unterknoten, die den verschiedenen Ergebnissen der Testbedingung entsprechen. Jeder untergeordnete Knoten stellt eine Teilmenge der Daten dar, die die Bedingung erfüllt.
Node *left_child; //left child Node Node *right_child; //right child Node
Beispiel:
Betrachten wir einen einfachen Entscheidungsbaum, um anhand der Farbe einer Frucht festzustellen, ob es sich um einen Apfel oder eine Orange handelt;
[Knoten]
Merkmal: Farbe
Testbedingung: Ist die Farbe Rot?
Bei „True“ zum linken Kind gehen, bei „False“ zum rechten Kind gehen
[Blattknoten - Apfel]
-Klassenbezeichnung: Apple
[Blattknoten - Orange]
-Klassenbezeichnung: Orange
Arten von Entscheidungsbäumen:
CART (Klassifizierungs- und Regressionsbäume): Wird sowohl für Klassifizierungs- als auch für Regressionsaufgaben verwendet. Teilt die Daten auf der Grundlage der Gini-Verunreinigung für die Klassifizierung und des mittleren quadratischen Fehlers für die Regression auf.
ID3 (Iterativer Dichotomisierer 3): Wird in erster Linie für Klassifizierungsaufgaben verwendet. Nutzt das Konzept der Entropie und des Informationsgewinns, um Entscheidungen zu treffen.
C4.5: Eine verbesserte Version von ID3, C4.5, wird für die Klassifizierung verwendet. Es verwendet ein Verstärkungsverhältnis, um die Vorliebe für Attribute mit mehr Stufen zu berücksichtigen.
Da wir den Entscheidungsbaum für Klassifizierungszwecke verwenden wollen, werden wir den ID3-Algorithmus erstellen, der sich durch Informationsgewinn, Unreinheitsberechnung und kategoriale Merkmale auszeichnet:
ID3 (Iterativer Dichotomisierer 3)
ID3 verwendet den Informationsgewinn, um zu entscheiden, welches Merkmal an jedem internen Knoten aufgespalten werden soll. Der Informationsgewinn misst die Verringerung der Entropie oder Unsicherheit nach der Aufteilung eines Datensatzes.double CDecisionTree::information_gain(vector &parent, vector &left_child, vector &right_child) { double weight_left = left_child.Size() / (double)parent.Size(), weight_right = right_child.Size() / (double)parent.Size(); double gain =0; switch(m_mode) { case MODE_GINI: gain = gini_index(parent) - ( (weight_left*gini_index(left_child)) + (weight_right*gini_index(right_child)) ); break; case MODE_ENTROPY: gain = entropy(parent) - ( (weight_left*entropy(left_child)) + (weight_right*entropy(right_child)) ); break; } return gain; }
Entropie ist ein Maß für die Unsicherheit oder Unordnung in einem Datensatz. In ID3 versucht der Algorithmus, die Entropie zu reduzieren, indem er Merkmalsaufteilungen wählt, die zu Teilmengen mit homogeneren Klassenbezeichnungen führen.
double CDecisionTree::entropy(vector &y) { vector class_labels = matrix_utils.Unique_count(y); vector p_cls = class_labels / double(y.Size()); vector entropy = (-1 * p_cls) * log2(p_cls); return entropy.Sum(); }
Um flexibler zu sein, kann man zwischen der Entropie und dem Gini-Index wählen, der ebenfalls eine Funktion ist, die häufig in Entscheidungsbäumen verwendet wird und dieselbe Arbeit wie die Entropiefunktion leistet. Beide bewerten die Unreinheit oder Unordnung im Datensatz.
double CDecisionTree::gini_index(vector &y) { vector unique = matrix_utils.Unique_count(y); vector probabilities = unique / (double)y.Size(); return 1.0 - MathPow(probabilities, 2).Sum(); }
Gegeben durch die Formeln in der folgenden Abbildung:
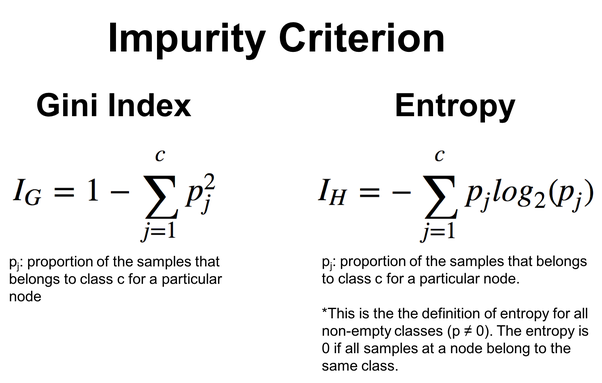
ID3 ist besonders für kategorische Merkmale geeignet, und die Auswahl der Merkmale und Schwellenwerte basiert auf der Entropiereduktion für kategorische Splits. Nachfolgend wird dies am Beispiel des Entscheidungsbaum-Algorithmus erläutert.
Entscheidungsbaum-Algorithmus
01. Splitting-Kriterien
Für die Klassifizierung sind die Gini-Verunreinigung und die Entropie die üblichen Aufteilungskriterien, während für die Regression häufig der mittlere quadratische Fehler verwendet wird. Betrachten wir nun die Aufteilungsfunktionen des Entscheidungsbaumalgorithmus, die mit der Struktur beginnen, um Informationen für die Daten zu erhalten, die aufgeteilt werden.
//A struct containing splitted data information struct split_info { uint feature_index; double threshold; matrix dataset_left, dataset_right; double info_gain; };
Anhand des Schwellenwerts werden die Merkmale, deren Werte unter dem Schwellenwert liegen, in die Matrix dataset_left aufgeteilt, während der Rest in der Matrix dataset_right verbleibt. Zum Schluss wird die Instanz der split_info-Struktur zurückgegeben.
split_info CDecisionTree::split_data(const matrix &data, uint feature_index, double threshold=0.5) { int left_size=0, right_size =0; vector row = {}; split_info split; ulong cols = data.Cols(); split.dataset_left.Resize(0, cols); split.dataset_right.Resize(0, cols); for (ulong i=0; i<data.Rows(); i++) { row = data.Row(i); if (row[feature_index] <= threshold) { left_size++; split.dataset_left.Resize(left_size, cols); split.dataset_left.Row(row, left_size-1); } else { right_size++; split.dataset_right.Resize(right_size, cols); split.dataset_right.Row(row, right_size-1); } } return split; }
Der Algorithmus muss aus einer Vielzahl von Aufteilungen die beste Aufteilung herausfinden, diejenige mit dem größten Informationsgewinn.
split_info CDecisionTree::get_best_split(matrix &data, uint num_features) { double max_info_gain = -DBL_MAX; vector feature_values = {}; vector left_v={}, right_v={}, y_v={}; //--- split_info best_split; split_info split; for (uint i=0; i<num_features; i++) { feature_values = data.Col(i); vector possible_thresholds = matrix_utils.Unique(feature_values); //Find unique values in the feature, representing possible thresholds for splitting. for (uint j=0; j<possible_thresholds.Size(); j++) { split = this.split_data(data, i, possible_thresholds[j]); if (split.dataset_left.Rows()>0 && split.dataset_right.Rows() > 0) { y_v = data.Col(data.Cols()-1); right_v = split.dataset_right.Col(split.dataset_right.Cols()-1); left_v = split.dataset_left.Col(split.dataset_left.Cols()-1); double curr_info_gain = this.information_gain(y_v, left_v, right_v); if (curr_info_gain > max_info_gain) // Check if the current information gain is greater than the maximum observed so far. { #ifdef DEBUG_MODE printf("split left: [%dx%d] split right: [%dx%d] curr_info_gain: %f max_info_gain: %f",split.dataset_left.Rows(),split.dataset_left.Cols(),split.dataset_right.Rows(),split.dataset_right.Cols(),curr_info_gain,max_info_gain); #endif best_split.feature_index = i; best_split.threshold = possible_thresholds[j]; best_split.dataset_left = split.dataset_left; best_split.dataset_right = split.dataset_right; best_split.info_gain = curr_info_gain; max_info_gain = curr_info_gain; } } } } return best_split; }
Diese Funktion durchsucht alle Merkmale und möglichen Schwellenwerte, um die beste Aufteilung zu finden, die den Informationsgewinn maximiert. Das Ergebnis ist eine split_info-Struktur, die Informationen über das Merkmal, den Schwellenwert und die Teilmengen enthält, die mit dem besten Split verbunden sind.
02. Den Baum bauen
Entscheidungsbäume werden konstruiert, indem der Datensatz auf der Grundlage von Merkmalen rekursiv aufgeteilt wird, bis eine Abbruchbedingung erfüllt ist (z. B. Erreichen einer bestimmten Tiefe oder Mindestanzahl von Stichproben).
Node *CDecisionTree::build_tree(matrix &data, uint curr_depth=0) { matrix X; vector Y; matrix_utils.XandYSplitMatrices(data,X,Y); //Split the input matrix into feature matrix X and target vector Y. ulong samples = X.Rows(), features = X.Cols(); //Get the number of samples and features in the dataset. Node *node= NULL; // Initialize node pointer if (samples >= m_min_samples_split && curr_depth<=m_max_depth) { split_info best_split = this.get_best_split(data, (uint)features); #ifdef DEBUG_MODE Print("best_split left: [",best_split.dataset_left.Rows(),"x",best_split.dataset_left.Cols(),"]\nbest_split right: [",best_split.dataset_right.Rows(),"x",best_split.dataset_right.Cols(),"]\nfeature_index: ",best_split.feature_index,"\nInfo gain: ",best_split.info_gain,"\nThreshold: ",best_split.threshold); #endif if (best_split.info_gain > 0) { Node *left_child = this.build_tree(best_split.dataset_left, curr_depth+1); Node *right_child = this.build_tree(best_split.dataset_right, curr_depth+1); node = new Node(best_split.feature_index,best_split.threshold,left_child,right_child,best_split.info_gain); return node; } } node = new Node(); node.leaf_value = this.calculate_leaf_value(Y); return node; }
if (best_split.info_gain > 0):
Die obige Codezeile prüft, ob eine Information vorliegt.
Innerhalb dieses Blocks:
Node *left_child = this.build_tree(best_split.dataset_left, curr_depth+1);
Rekursiver Aufbau des linken Kindknotens:
Node *right_child = this.build_tree(best_split.dataset_right, curr_depth+1);
Rekursives Erstellen des richtigen untergeordneten Knotens:
node = new Node(best_split.feature_index, best_split.threshold, left_child, right_child, best_split.info_gain);
Erstelle einen Entscheidungsknoten mit den Informationen aus der besten Aufteilung:
node = new Node(); Wenn keine weitere Aufteilung erforderlich ist, erstelle einen neuen Blattknoten:
node.value = this.calculate_leaf_value(Y); Setzen des Wertes des Blattknotens mit der Funktion calculate_leaf_value:
return node; Gibt den Knoten zurück, der den aktuellen Split oder das aktuelle Blatt darstellt.
Um die Funktionen bequem und nutzerfreundlich zu gestalten, kann die Funktion build_tree in der Funktion fit untergebracht werden, die üblicherweise in den Modulen des maschinellen Lernens in Python verwendet wird:
void CDecisionTree::fit(matrix &x, vector &y) { matrix data = matrix_utils.concatenate(x, y, 1); this.root = this.build_tree(data); }
Prognosen über Training und Tests des Modells treffen:
vector CDecisionTree::predict(matrix &x) { vector ret(x.Rows()); for (ulong i=0; i<x.Rows(); i++) ret[i] = this.predict(x.Row(i)); return ret; }
Vorhersagen in Echtzeit treffen:
double CDecisionTree::predict(vector &x) { return this.make_predictions(x, this.root); }
Die Funktion make_predictions ist der Ort, an dem die ganze Drecksarbeit gemacht wird:
double CDecisionTree::make_predictions(vector &x, const Node &tree) { if (tree.leaf_value != NULL) // This is a leaf leaf_value return tree.leaf_value; double feature_value = x[tree.feature_index]; double pred = 0; #ifdef DEBUG_MODE printf("Tree.threshold %f tree.feature_index %d leaf_value %f",tree.threshold,tree.feature_index,tree.leaf_value); #endif if (feature_value <= tree.threshold) { pred = this.make_predictions(x, tree.left_child); } else { pred = this.make_predictions(x, tree.right_child); } return pred; }
Weitere Einzelheiten zu dieser Funktion:
if (feature_value <= tree.threshold): Innerhalb dieses Blocks:
Rekursiver Aufruf von make_predictions für den linken Kindknoten:
pred = this.make_predictions(x, *tree.left_child); Andernfalls, wenn der Merkmalswert größer als der Schwellenwert ist:
Rekursiver Aufruf der Funktion make_predictions für den rechten nachgeordneten Knoten.
pred = this.make_predictions(x, *tree.right_child); return pred; Rückgabe der Vorhersage.
Berechnungen des Blattwerts
Mit der folgenden Funktion wird der Wert des Blattes berechnet:
double CDecisionTree::calculate_leaf_value(vector &Y) { vector uniques = matrix_utils.Unique_count(Y); vector classes = matrix_utils.Unique(Y); return classes[uniques.ArgMax()]; }
Diese Funktion gibt das Element aus Y mit der höchsten Anzahl zurück und findet so das häufigste Element in der Liste.
Das Ganze wird in der Klasse CDecisionTree verpackt.
enum mode {MODE_ENTROPY, MODE_GINI}; class CDecisionTree { CMatrixutils matrix_utils; protected: Node *build_tree(matrix &data, uint curr_depth=0); double calculate_leaf_value(vector &Y); //--- uint m_max_depth; uint m_min_samples_split; mode m_mode; double gini_index(vector &y); double entropy(vector &y); double information_gain(vector &parent, vector &left_child, vector &right_child); split_info get_best_split(matrix &data, uint num_features); split_info split_data(const matrix &data, uint feature_index, double threshold=0.5); double make_predictions(vector &x, const Node &tree); void delete_tree(Node* node); public: Node *root; CDecisionTree(uint min_samples_split=2, uint max_depth=2, mode mode_=MODE_GINI); ~CDecisionTree(void); void fit(matrix &x, vector &y); void print_tree(Node *tree, string indent=" ",string padl=""); double predict(vector &x); vector predict(matrix &x); };
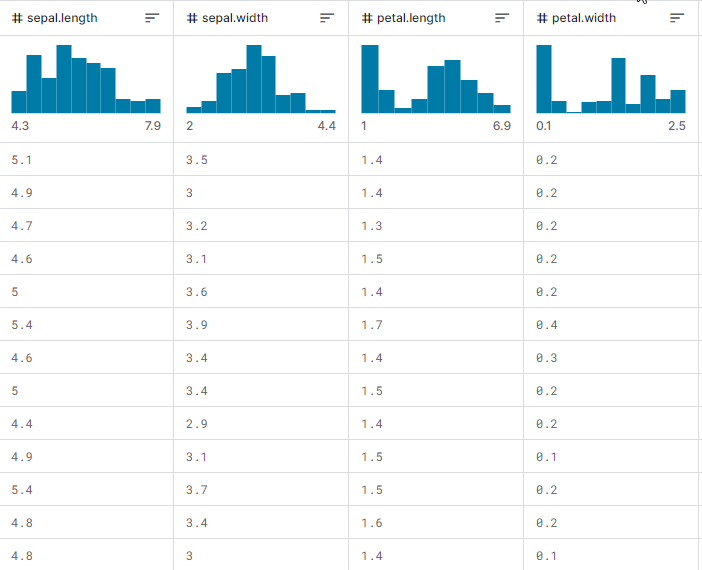
Nachdem wir das gezeigt haben, wollen wir uns ansehen, wie das Ganze in der Praxis funktioniert, wie man den Baum aufbaut und wie man ihn verwendet, um Vorhersagen beim Training und beim Testen zu treffen, ganz zu schweigen vom Echtzeithandel. Wir werden den am meisten verbreiteten Iris-CSV-Datensatz verwenden, um zu testen, ob er funktioniert.
Angenommen, wir trainieren das Entscheidungsbaummodell bei jeder EA-Initialisierung, indem wir zunächst die Trainingsdaten aus einer CSV-Datei laden:
int OnInit() { matrix dataset = matrix_utils.ReadCsv("iris.csv"); //loading iris-data decision_tree = new CDecisionTree(3,3, MODE_GINI); //Initializing the decision tree matrix x; vector y; matrix_utils.XandYSplitMatrices(dataset,x,y); //split the data into x and y matrix and vector respectively decision_tree.fit(x, y); //Building the tree decision_tree.print_tree(decision_tree.root); //Printing the tree vector preds = decision_tree.predict(x); //making the predictions on a training data Print("Train Acc = ",metrics.confusion_matrix(y, preds)); //Measuring the accuracy return(INIT_SUCCEEDED); }
So sieht die Matrix des Datensatzes aus, wenn sie ausgedruckt wird. Die letzte Spalte wurde kodiert. Eins (1) steht für Setosa, zwei (2) steht für Versicolor und drei (3) steht für Virginica
Print("iris-csv\n",dataset);
MS 0 08:54:40.958 DecisionTree Test (EURUSD,H1) iris-csv PH 0 08:54:40.958 DecisionTree Test (EURUSD,H1) [[5.1,3.5,1.4,0.2,1] CO 0 08:54:40.958 DecisionTree Test (EURUSD,H1) [4.9,3,1.4,0.2,1] ... ... NS 0 08:54:40.959 DecisionTree Test (EURUSD,H1) [5.6,2.7,4.2,1.3,2] JK 0 08:54:40.959 DecisionTree Test (EURUSD,H1) [5.7,3,4.2,1.2,2] ... ... NQ 0 08:54:40.959 DecisionTree Test (EURUSD,H1) [6.2,3.4,5.4,2.3,3] PD 0 08:54:40.959 DecisionTree Test (EURUSD,H1) [5.9,3,5.1,1.8,3]]
Den Baum drucken
Wenn Sie sich den Code ansehen, ist Ihnen vielleicht die Funktion print_tree aufgefallen, die die Baumwurzel als eines ihrer Argumente annimmt. Mit dieser Funktion wird versucht, das Gesamtbild des Baumes zu drucken; eine genauere Betrachtung finden Sie weiter unten.
void CDecisionTree::print_tree(Node *tree, string indent=" ",string padl="") { if (tree.leaf_value != NULL) Print((padl+indent+": "),tree.leaf_value); else //if we havent' reached the leaf node keep printing child trees { padl += " "; Print((padl+indent)+": X_",tree.feature_index, "<=", tree.threshold, "?", tree.info_gain); print_tree(tree.left_child, "left","--->"+padl); print_tree(tree.right_child, "right","--->"+padl); } }
Weitere Einzelheiten zu dieser Funktion:
Struktur des Knotens:
Die Funktion geht davon aus, dass eine Knotenklasse den Entscheidungsbaum darstellt. Jeder Knoten kann entweder ein Entscheidungsknoten oder ein Blattknoten sein. Entscheidungsknoten haben einen feature_index, einen threshold und einen info_gain, die das Merkmal (feature_index), den Schwellenwert (threshold), den Informationsgewinn (info_gain) und den Blattwert (leaf_value) angeben.
Entscheidungs-Knoten drucken:
Wenn der aktuelle Knoten kein Blattknoten ist (d.h. tree.leaf_value ist NULL), werden Informationen über den Entscheidungsknoten ausgegeben. Er gibt die Bedingung für die Aufteilung aus, z. B. „X_2 <= 1,9 ? 0,33“ und die Größe der Einrückung.
Blattknoten drucken:
Wenn der aktuelle Knoten ein Blattknoten ist (d.h. tree.leaf_value ist nicht NULL), wird der Blattwert zusammen mit der Einrückungsebene ausgegeben. Zum Beispiel: „left: 0.33“.
Rekursion:
Die Funktion ruft sich dann selbst rekursiv für die linken und rechten Kinder des aktuellen Knotens auf. Das Argument padl fügt der Druckausgabe eine Einrückung hinzu, wodurch die Baumstruktur besser lesbar wird.
Die Ausgabe von print_tree für den in der Funktion OnInit erstellten ist:
CR 0 09:26:39.990 DecisionTree Test (EURUSD,H1) : X_2<=1.9?0.3333333333333334 HO 0 09:26:39.990 DecisionTree Test (EURUSD,H1) ---> left: 1.0 RH 0 09:26:39.990 DecisionTree Test (EURUSD,H1) ---> right: X_3<=1.7?0.38969404186795487 HP 0 09:26:39.990 DecisionTree Test (EURUSD,H1) --->---> left: X_2<=4.9?0.08239026063100136 KO 0 09:26:39.990 DecisionTree Test (EURUSD,H1) --->--->---> left: X_3<=1.6?0.04079861111111116 DH 0 09:26:39.990 DecisionTree Test (EURUSD,H1) --->--->--->---> left: 2.0 HM 0 09:26:39.990 DecisionTree Test (EURUSD,H1) --->--->--->---> right: 3.0 HS 0 09:26:39.990 DecisionTree Test (EURUSD,H1) --->--->---> right: X_3<=1.5?0.2222222222222222 IH 0 09:26:39.990 DecisionTree Test (EURUSD,H1) --->--->--->---> left: 3.0 QM 0 09:26:39.990 DecisionTree Test (EURUSD,H1) --->--->--->---> right: 2.0 KP 0 09:26:39.990 DecisionTree Test (EURUSD,H1) --->---> right: X_2<=4.8?0.013547574039067499 PH 0 09:26:39.990 DecisionTree Test (EURUSD,H1) --->--->---> left: X_0<=5.9?0.4444444444444444 PE 0 09:26:39.990 DecisionTree Test (EURUSD,H1) --->--->--->---> left: 2.0 DP 0 09:26:39.990 DecisionTree Test (EURUSD,H1) --->--->--->---> right: 3.0 EE 0 09:26:39.990 DecisionTree Test (EURUSD,H1) --->--->---> right: 3.0
Beeindruckend.
Im Folgenden wird die Genauigkeit unseres trainierten Modells dargestellt:
vector preds = decision_tree.predict(x); //making the predictions on a training data Print("Train Acc = ",metrics.confusion_matrix(y, preds)); //Measuring the accuracy
Ausgaben:
PM 0 09:26:39.990 DecisionTree Test (EURUSD,H1) Confusion Matrix CE 0 09:26:39.990 DecisionTree Test (EURUSD,H1) [[50,0,0] HR 0 09:26:39.990 DecisionTree Test (EURUSD,H1) [0,50,0] ND 0 09:26:39.990 DecisionTree Test (EURUSD,H1) [0,1,49]] GS 0 09:26:39.990 DecisionTree Test (EURUSD,H1) KF 0 09:26:39.990 DecisionTree Test (EURUSD,H1) Classification Report IR 0 09:26:39.990 DecisionTree Test (EURUSD,H1) MD 0 09:26:39.990 DecisionTree Test (EURUSD,H1) _ Precision Recall Specificity F1 score Support EQ 0 09:26:39.990 DecisionTree Test (EURUSD,H1) 1.0 50.00 50.00 100.00 50.00 50.0 HR 0 09:26:39.990 DecisionTree Test (EURUSD,H1) 2.0 51.00 50.00 100.00 50.50 50.0 PO 0 09:26:39.990 DecisionTree Test (EURUSD,H1) 3.0 49.00 50.00 100.00 49.49 50.0 EH 0 09:26:39.990 DecisionTree Test (EURUSD,H1) PR 0 09:26:39.990 DecisionTree Test (EURUSD,H1) Accuracy 0.99 HQ 0 09:26:39.990 DecisionTree Test (EURUSD,H1) Average 50.00 50.00 100.00 50.00 150.0 DJ 0 09:26:39.990 DecisionTree Test (EURUSD,H1) W Avg 50.00 50.00 100.00 50.00 150.0 LG 0 09:26:39.990 DecisionTree Test (EURUSD,H1) Train Acc = 0.993
Wir erreichten eine Genauigkeit von 99,3 %, was auf die erfolgreiche Implementierung unseres Entscheidungsbaums hinweist. Diese Genauigkeit entspricht dem, was man von den Modellen Scikit-Learn erwarten würde, wenn es um ein einfaches Datenproblem geht.
Fahren wir mit dem Training fort und testen wir das Modell mit Daten, die nicht in der Stichprobe enthalten sind.
matrix train_x, test_x; vector train_y, test_y; matrix_utils.TrainTestSplitMatrices(dataset, train_x, train_y, test_x, test_y, 0.8, 42); //split the data into training and testing samples decision_tree.fit(train_x, train_y); //Building the tree decision_tree.print_tree(decision_tree.root); //Printing the tree vector preds = decision_tree.predict(train_x); //making the predictions on a training data Print("Train Acc = ",metrics.confusion_matrix(train_y, preds)); //Measuring the accuracy //--- preds = decision_tree.predict(test_x); //making the predictions on a test data Print("Test Acc = ",metrics.confusion_matrix(test_y, preds)); //Measuring the accuracy
Ausgaben:
QD 0 14:56:03.860 DecisionTree Test (EURUSD,H1) : X_2<=1.7?0.34125 LL 0 14:56:03.860 DecisionTree Test (EURUSD,H1) ---> left: 1.0 QK 0 14:56:03.860 DecisionTree Test (EURUSD,H1) ---> right: X_3<=1.6?0.42857142857142855 GS 0 14:56:03.860 DecisionTree Test (EURUSD,H1) --->---> left: X_2<=4.9?0.09693877551020412 IL 0 14:56:03.860 DecisionTree Test (EURUSD,H1) --->--->---> left: 2.0 MD 0 14:56:03.860 DecisionTree Test (EURUSD,H1) --->--->---> right: X_3<=1.5?0.375 IS 0 14:56:03.860 DecisionTree Test (EURUSD,H1) --->--->--->---> left: 3.0 QR 0 14:56:03.860 DecisionTree Test (EURUSD,H1) --->--->--->---> right: 2.0 RH 0 14:56:03.860 DecisionTree Test (EURUSD,H1) --->---> right: 3.0 HP 0 14:56:03.860 DecisionTree Test (EURUSD,H1) Confusion Matrix FG 0 14:56:03.860 DecisionTree Test (EURUSD,H1) [[42,0,0] EO 0 14:56:03.860 DecisionTree Test (EURUSD,H1) [0,39,0] HK 0 14:56:03.860 DecisionTree Test (EURUSD,H1) [0,0,39]] OL 0 14:56:03.860 DecisionTree Test (EURUSD,H1) KE 0 14:56:03.860 DecisionTree Test (EURUSD,H1) Classification Report QO 0 14:56:03.860 DecisionTree Test (EURUSD,H1) MQ 0 14:56:03.860 DecisionTree Test (EURUSD,H1) _ Precision Recall Specificity F1 score Support OQ 0 14:56:03.860 DecisionTree Test (EURUSD,H1) 1.0 42.00 42.00 78.00 42.00 42.0 ML 0 14:56:03.860 DecisionTree Test (EURUSD,H1) 3.0 39.00 39.00 81.00 39.00 39.0 HK 0 14:56:03.860 DecisionTree Test (EURUSD,H1) 2.0 39.00 39.00 81.00 39.00 39.0 OE 0 14:56:03.860 DecisionTree Test (EURUSD,H1) EO 0 14:56:03.860 DecisionTree Test (EURUSD,H1) Accuracy 1.00 CG 0 14:56:03.860 DecisionTree Test (EURUSD,H1) Average 40.00 40.00 80.00 40.00 120.0 LF 0 14:56:03.860 DecisionTree Test (EURUSD,H1) W Avg 40.05 40.05 79.95 40.05 120.0 PR 0 14:56:03.860 DecisionTree Test (EURUSD,H1) Train Acc = 1.0 CD 0 14:56:03.861 DecisionTree Test (EURUSD,H1) Confusion Matrix FO 0 14:56:03.861 DecisionTree Test (EURUSD,H1) [[9,2,0] RK 0 14:56:03.861 DecisionTree Test (EURUSD,H1) [1,10,0] CL 0 14:56:03.861 DecisionTree Test (EURUSD,H1) [2,0,6]] HK 0 14:56:03.861 DecisionTree Test (EURUSD,H1) DQ 0 14:56:03.861 DecisionTree Test (EURUSD,H1) Classification Report JJ 0 14:56:03.861 DecisionTree Test (EURUSD,H1) FM 0 14:56:03.861 DecisionTree Test (EURUSD,H1) _ Precision Recall Specificity F1 score Support QM 0 14:56:03.861 DecisionTree Test (EURUSD,H1) 2.0 12.00 11.00 19.00 11.48 11.0 PH 0 14:56:03.861 DecisionTree Test (EURUSD,H1) 3.0 12.00 11.00 19.00 11.48 11.0 KD 0 14:56:03.861 DecisionTree Test (EURUSD,H1) 1.0 6.00 8.00 22.00 6.86 8.0 PP 0 14:56:03.861 DecisionTree Test (EURUSD,H1) LJ 0 14:56:03.861 DecisionTree Test (EURUSD,H1) Accuracy 0.83 NJ 0 14:56:03.861 DecisionTree Test (EURUSD,H1) Average 10.00 10.00 20.00 9.94 30.0 JR 0 14:56:03.861 DecisionTree Test (EURUSD,H1) W Avg 10.40 10.20 19.80 10.25 30.0 HP 0 14:56:03.861 DecisionTree Test (EURUSD,H1) Test Acc = 0.833
Das Modell ist bei den Trainingsdaten zu 100 % und bei den Out-of-Sample-Daten zu 83 % genau.
Entscheidungsbaum-KI im Handel
All dies nützt nichts, wenn wir den Handelsaspekt nicht mit Hilfe der Entscheidungsbaummodelle untersuchen. Um dieses Modell im Handel anzuwenden, formulieren wir ein Problem, das wir lösen wollen.
Das zu lösende Problem:
Wir möchten das KI-Entscheidungsbaummodell verwenden, um Vorhersagen über den aktuellen Balken zu treffen, die uns möglicherweise sagen, wohin sich der Markt bewegt, entweder nach oben oder nach unten.
Wie bei jedem Modell wollen wir dem Modell einen Datensatz zum Lernen geben; nehmen wir an, wir entscheiden uns für die beiden Oszillator-Indikatoren, den RSI-Indikator und den Stochastik-Oszillator; im Grunde wollen wir, dass das Modell die Muster dieser beiden Indikatoren versteht und wie sie die Preisbewegung für den aktuellen Balken beeinflussen.
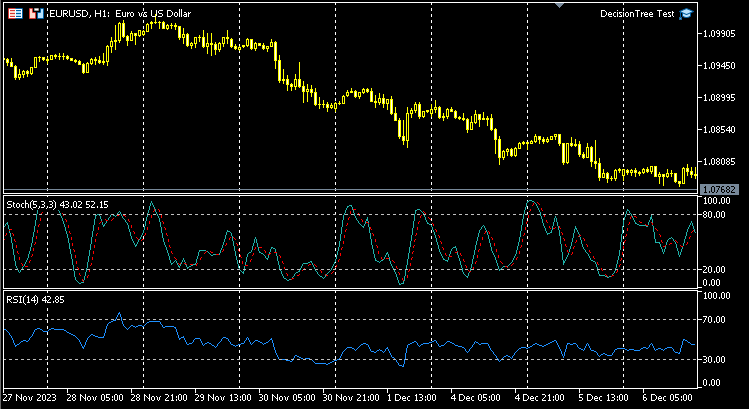
Datenstruktur:
Sobald die Daten für Trainings- und Testzwecke gesammelt wurden, werden sie in der unten stehenden Struktur gespeichert. Das Gleiche gilt für Daten, die zur Erstellung von Echtzeitprognosen verwendet werden.
struct data{ vector stoch_buff, signal_buff, rsi_buff, target; } data_struct;
Datenerfassung, Training und Testen des Entscheidungsbaums
void TrainTree() { matrix dataset(train_bars, 4); vector v; //--- Collecting indicator buffers data_struct.rsi_buff.CopyIndicatorBuffer(rsi_handle, 0, 1, train_bars); data_struct.stoch_buff.CopyIndicatorBuffer(stoch_handle, 0, 1, train_bars); data_struct.signal_buff.CopyIndicatorBuffer(stoch_handle, 1, 1, train_bars); //--- Preparing the target variable MqlRates rates[]; ArraySetAsSeries(rates, true); int size = CopyRates(Symbol(), PERIOD_CURRENT, 1,train_bars, rates); data_struct.target.Resize(size); //Resize the target vector for (int i=0; i<size; i++) { if (rates[i].close > rates[i].open) data_struct.target[i] = 1; else data_struct.target[i] = -1; } dataset.Col(data_struct.rsi_buff, 0); dataset.Col(data_struct.stoch_buff, 1); dataset.Col(data_struct.signal_buff, 2); dataset.Col(data_struct.target, 3); decision_tree = new CDecisionTree(min_sample,max_depth_, tree_mode); //Initializing the decision tree matrix train_x, test_x; vector train_y, test_y; matrix_utils.TrainTestSplitMatrices(dataset, train_x, train_y, test_x, test_y, 0.8, 42); //split the data into training and testing samples decision_tree.fit(train_x, train_y); //Building the tree decision_tree.print_tree(decision_tree.root); //Printing the tree vector preds = decision_tree.predict(train_x); //making the predictions on a training data Print("Train Acc = ",metrics.confusion_matrix(train_y, preds)); //Measuring the accuracy //--- preds = decision_tree.predict(test_x); //making the predictions on a test data Print("Test Acc = ",metrics.confusion_matrix(test_y, preds)); //Measuring the accuracy }
Die Mindeststichprobe wurde auf 3 und die maximale Tiefe auf 5 festgelegt.
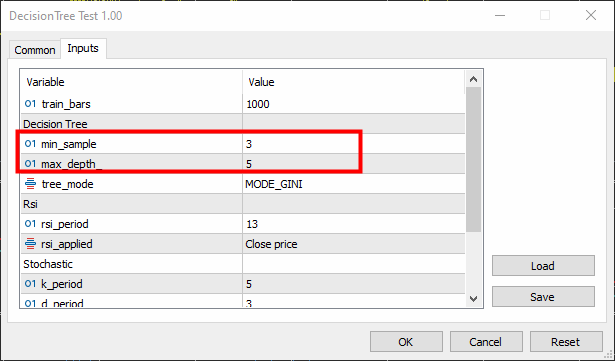
Ausgaben:
KR 0 16:26:53.028 DecisionTree Test (EURUSD,H1) : X_0<=65.88930872549261?0.0058610536710859695 CN 0 16:26:53.028 DecisionTree Test (EURUSD,H1) ---> left: X_0<=29.19882857713344?0.003187469522387243 FK 0 16:26:53.028 DecisionTree Test (EURUSD,H1) --->---> left: X_1<=26.851851851853503?0.030198175526895188 RI 0 16:26:53.028 DecisionTree Test (EURUSD,H1) --->--->---> left: X_2<=7.319205739522295?0.040050858232676456 KG 0 16:26:53.028 DecisionTree Test (EURUSD,H1) --->--->--->---> left: X_0<=23.08345903222593?0.04347468770545693 JF 0 16:26:53.028 DecisionTree Test (EURUSD,H1) --->--->--->--->---> left: X_0<=21.6795921184317?0.09375 PF 0 16:26:53.028 DecisionTree Test (EURUSD,H1) --->--->--->--->--->---> left: -1.0 ER 0 16:26:53.028 DecisionTree Test (EURUSD,H1) --->--->--->--->--->---> right: -1.0 QF 0 16:26:53.028 DecisionTree Test (EURUSD,H1) --->--->--->--->---> right: X_2<=3.223853479489069?0.09876543209876543 LH 0 16:26:53.028 DecisionTree Test (EURUSD,H1) --->--->--->--->--->---> left: -1.0 FJ 0 16:26:53.028 DecisionTree Test (EURUSD,H1) --->--->--->--->--->---> right: 1.0 MM 0 16:26:53.028 DecisionTree Test (EURUSD,H1) --->--->--->---> right: -1.0 MG 0 16:26:53.028 DecisionTree Test (EURUSD,H1) --->--->---> right: 1.0 HH 0 16:26:53.028 DecisionTree Test (EURUSD,H1) --->---> right: X_0<=65.4606831930956?0.0030639039663222234 JR 0 16:26:53.028 DecisionTree Test (EURUSD,H1) --->--->---> left: X_0<=31.628407983040333?0.00271101025966336 PS 0 16:26:53.028 DecisionTree Test (EURUSD,H1) --->--->--->---> left: X_0<=31.20436037455599?0.0944903581267218 DO 0 16:26:53.028 DecisionTree Test (EURUSD,H1) --->--->--->--->---> left: X_2<=14.629981942657205?0.11111111111111116 EO 0 16:26:53.028 DecisionTree Test (EURUSD,H1) --->--->--->--->--->---> left: 1.0 IG 0 16:26:53.028 DecisionTree Test (EURUSD,H1) --->--->--->--->--->---> right: -1.0 EI 0 16:26:53.028 DecisionTree Test (EURUSD,H1) --->--->--->--->---> right: 1.0 LO 0 16:26:53.028 DecisionTree Test (EURUSD,H1) --->--->--->---> right: X_0<=32.4469112469684?0.003164795835173595 RO 0 16:26:53.028 DecisionTree Test (EURUSD,H1) --->--->--->--->---> left: X_1<=76.9736842105244?0.21875 RO 0 16:26:53.028 DecisionTree Test (EURUSD,H1) --->--->--->--->--->---> left: -1.0 PG 0 16:26:53.028 DecisionTree Test (EURUSD,H1) --->--->--->--->--->---> right: 1.0 MO 0 16:26:53.028 DecisionTree Test (EURUSD,H1) --->--->--->--->---> right: X_0<=61.82001028403415?0.0024932856070305487 LQ 0 16:26:53.028 DecisionTree Test (EURUSD,H1) --->--->--->--->--->---> left: -1.0 EQ 0 16:26:53.029 DecisionTree Test (EURUSD,H1) --->--->--->--->--->---> right: 1.0 LE 0 16:26:53.029 DecisionTree Test (EURUSD,H1) --->--->---> right: X_2<=84.68660541575225?0.09375 ED 0 16:26:53.029 DecisionTree Test (EURUSD,H1) --->--->--->---> left: -1.0 LM 0 16:26:53.029 DecisionTree Test (EURUSD,H1) --->--->--->---> right: -1.0 NE 0 16:26:53.029 DecisionTree Test (EURUSD,H1) ---> right: X_0<=85.28191275702572?0.024468404842877933 DK 0 16:26:53.029 DecisionTree Test (EURUSD,H1) --->---> left: X_1<=25.913621262458935?0.01603292204455742 LE 0 16:26:53.029 DecisionTree Test (EURUSD,H1) --->--->---> left: X_0<=72.18709160232456?0.2222222222222222 ED 0 16:26:53.029 DecisionTree Test (EURUSD,H1) --->--->--->---> left: X_1<=15.458937198072245?0.4444444444444444 QQ 0 16:26:53.029 DecisionTree Test (EURUSD,H1) --->--->--->--->---> left: 1.0 CS 0 16:26:53.029 DecisionTree Test (EURUSD,H1) --->--->--->--->---> right: -1.0 JE 0 16:26:53.029 DecisionTree Test (EURUSD,H1) --->--->--->---> right: -1.0 QM 0 16:26:53.029 DecisionTree Test (EURUSD,H1) --->--->---> right: X_0<=69.83504428897093?0.012164425148527835 HP 0 16:26:53.029 DecisionTree Test (EURUSD,H1) --->--->--->---> left: X_0<=68.39798826749553?0.07844460227272732 DL 0 16:26:53.029 DecisionTree Test (EURUSD,H1) --->--->--->--->---> left: X_1<=90.68322981366397?0.06611570247933873 DO 0 16:26:53.029 DecisionTree Test (EURUSD,H1) --->--->--->--->--->---> left: 1.0 OE 0 16:26:53.029 DecisionTree Test (EURUSD,H1) --->--->--->--->--->---> right: 1.0 LI 0 16:26:53.029 DecisionTree Test (EURUSD,H1) --->--->--->--->---> right: X_1<=88.05704099821516?0.11523809523809525 DE 0 16:26:53.029 DecisionTree Test (EURUSD,H1) --->--->--->--->--->---> left: 1.0 DM 0 16:26:53.029 DecisionTree Test (EURUSD,H1) --->--->--->--->--->---> right: -1.0 LG 0 16:26:53.029 DecisionTree Test (EURUSD,H1) --->--->--->---> right: X_0<=70.41747488780877?0.015360959832756427 OI 0 16:26:53.029 DecisionTree Test (EURUSD,H1) --->--->--->--->---> left: 1.0 PI 0 16:26:53.029 DecisionTree Test (EURUSD,H1) --->--->--->--->---> right: X_0<=70.56490391752676?0.02275277028755862 CF 0 16:26:53.029 DecisionTree Test (EURUSD,H1) --->--->--->--->--->---> left: -1.0 MO 0 16:26:53.029 DecisionTree Test (EURUSD,H1) --->--->--->--->--->---> right: 1.0 EG 0 16:26:53.029 DecisionTree Test (EURUSD,H1) --->---> right: X_1<=97.0643939393936?0.10888888888888892 CJ 0 16:26:53.029 DecisionTree Test (EURUSD,H1) --->--->---> left: 1.0 GN 0 16:26:53.029 DecisionTree Test (EURUSD,H1) --->--->---> right: X_0<=90.20261550045987?0.07901234567901233 CP 0 16:26:53.029 DecisionTree Test (EURUSD,H1) --->--->--->---> left: X_0<=85.94461490761033?0.21333333333333332 HN 0 16:26:53.029 DecisionTree Test (EURUSD,H1) --->--->--->--->---> left: -1.0 GE 0 16:26:53.029 DecisionTree Test (EURUSD,H1) --->--->--->--->---> right: X_1<=99.66856060606052?0.4444444444444444 GK 0 16:26:53.029 DecisionTree Test (EURUSD,H1) --->--->--->--->--->---> left: -1.0 IK 0 16:26:53.029 DecisionTree Test (EURUSD,H1) --->--->--->--->--->---> right: 1.0 JM 0 16:26:53.029 DecisionTree Test (EURUSD,H1) --->--->--->---> right: -1.0 KE 0 16:26:53.029 DecisionTree Test (EURUSD,H1) Confusion Matrix DO 0 16:26:53.029 DecisionTree Test (EURUSD,H1) [[122,271] QF 0 16:26:53.029 DecisionTree Test (EURUSD,H1) [51,356]] HS 0 16:26:53.029 DecisionTree Test (EURUSD,H1) LF 0 16:26:53.029 DecisionTree Test (EURUSD,H1) Classification Report JR 0 16:26:53.029 DecisionTree Test (EURUSD,H1) ND 0 16:26:53.029 DecisionTree Test (EURUSD,H1) _ Precision Recall Specificity F1 score Support GQ 0 16:26:53.029 DecisionTree Test (EURUSD,H1) 1.0 173.00 393.00 407.00 240.24 393.0 HQ 0 16:26:53.029 DecisionTree Test (EURUSD,H1) -1.0 627.00 407.00 393.00 493.60 407.0 PM 0 16:26:53.029 DecisionTree Test (EURUSD,H1) OG 0 16:26:53.029 DecisionTree Test (EURUSD,H1) Accuracy 0.60 EO 0 16:26:53.029 DecisionTree Test (EURUSD,H1) Average 400.00 400.00 400.00 366.92 800.0 GN 0 16:26:53.029 DecisionTree Test (EURUSD,H1) W Avg 403.97 400.12 399.88 369.14 800.0 LM 0 16:26:53.029 DecisionTree Test (EURUSD,H1) Train Acc = 0.598 GK 0 16:26:53.029 DecisionTree Test (EURUSD,H1) Confusion Matrix CQ 0 16:26:53.029 DecisionTree Test (EURUSD,H1) [[75,13] CK 0 16:26:53.029 DecisionTree Test (EURUSD,H1) [86,26]] NI 0 16:26:53.029 DecisionTree Test (EURUSD,H1) RP 0 16:26:53.029 DecisionTree Test (EURUSD,H1) Classification Report HH 0 16:26:53.029 DecisionTree Test (EURUSD,H1) LR 0 16:26:53.029 DecisionTree Test (EURUSD,H1) _ Precision Recall Specificity F1 score Support EM 0 16:26:53.029 DecisionTree Test (EURUSD,H1) -1.0 161.00 88.00 112.00 113.80 88.0 NJ 0 16:26:53.029 DecisionTree Test (EURUSD,H1) 1.0 39.00 112.00 88.00 57.85 112.0 LJ 0 16:26:53.029 DecisionTree Test (EURUSD,H1) EL 0 16:26:53.029 DecisionTree Test (EURUSD,H1) Accuracy 0.51 RG 0 16:26:53.029 DecisionTree Test (EURUSD,H1) Average 100.00 100.00 100.00 85.83 200.0 ID 0 16:26:53.029 DecisionTree Test (EURUSD,H1) W Avg 92.68 101.44 98.56 82.47 200.0 JJ 0 16:26:53.029 DecisionTree Test (EURUSD,H1) Test Acc = 0.505
Das Modell lag beim Training in 60 % der Fälle richtig, während es beim Test nur 50,5 % richtig lag; nicht gut. Dafür kann es viele Gründe geben, z. B. die Qualität der Daten, die wir zur Erstellung des Modells verwendet haben, oder vielleicht gibt es schlechte Prädiktoren. Der häufigste Grund ist, dass wir die Parameter für das Modell nicht richtig eingestellt haben.
Um dies zu beheben, müssen Sie möglicherweise die Parameter anpassen, um festzustellen, was für Ihre Bedürfnisse am besten geeignet ist.
Lassen Sie uns nun eine Funktion für Echtzeit-Vorhersagen programmieren.
int desisionTreeSignal() { //--- Copy the current bar information only data_struct.rsi_buff.CopyIndicatorBuffer(rsi_handle, 0, 0, 1); data_struct.stoch_buff.CopyIndicatorBuffer(stoch_handle, 0, 0, 1); data_struct.signal_buff.CopyIndicatorBuffer(stoch_handle, 1, 0, 1); x_vars[0] = data_struct.rsi_buff[0]; x_vars[1] = data_struct.stoch_buff[0]; x_vars[2] = data_struct.signal_buff[0]; return int(decision_tree.predict(x_vars)); }
Lassen Sie uns nun eine einfache Handelslogik entwickeln:
Wenn der Entscheidungsbaum -1 vorhersagt, bedeutet das, dass die Kerze nach tiefer schließen wird, wir eröffnen eine Verkaufsposition; wenn er die Klasse 1 vorhersagt, bedeutet das, dass die Kerze höher schließen wird als sie eröffnet wurde, wir eröffnen eine Kaufposition.
void OnTick() { //--- if (!train_once) // You want to train once during EA lifetime TrainTree(); train_once = true; if (isnewBar(PERIOD_CURRENT)) // We want to trade on the bar opening { int signal = desisionTreeSignal(); double min_lot = SymbolInfoDouble(Symbol(), SYMBOL_VOLUME_MIN); SymbolInfoTick(Symbol(), ticks); if (signal == -1) { if (!PosExists(MAGICNUMBER, POSITION_TYPE_SELL)) // If a sell trade doesnt exist m_trade.Sell(min_lot, Symbol(), ticks.bid, ticks.bid+stoploss*Point(), ticks.bid - takeprofit*Point()); } else { if (!PosExists(MAGICNUMBER, POSITION_TYPE_BUY)) // If a buy trade doesnt exist m_trade.Buy(min_lot, Symbol(), ticks.ask, ticks.ask-stoploss*Point(), ticks.ask + takeprofit*Point()); } } }
Ich habe einen Test für einen einzelnen Monat 2023.01.01 - 2023.02.01 mit Eröffnungspreisen durchgeführt, um zu sehen, ob alles funktioniert.
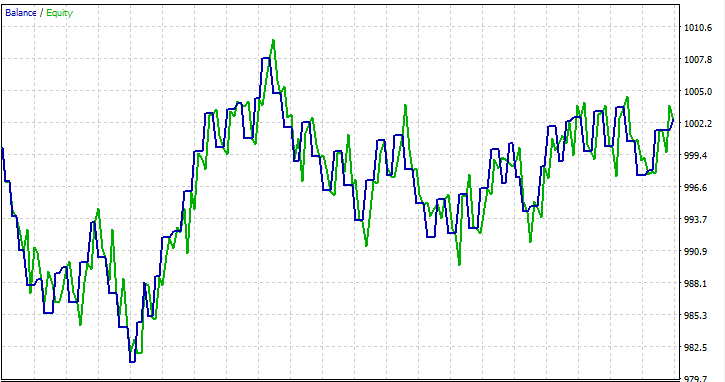
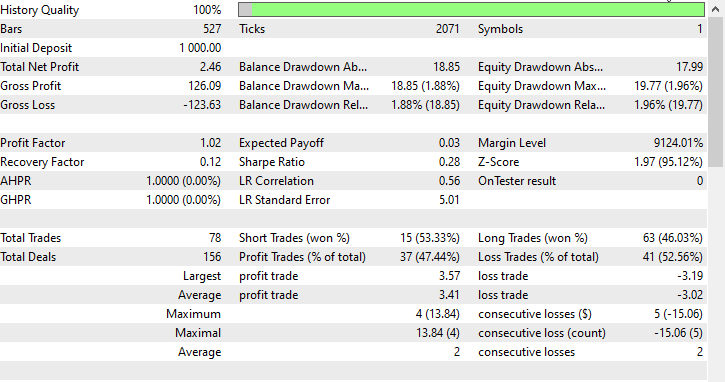
FAQs zu Entscheidungsbäumen im Handel:
| Frage | Antwort |
|---|---|
| Ist die Normalisierung der Eingabedaten für Entscheidungsbäume wichtig? | Nein, die Normalisierung ist im Allgemeinen für Entscheidungsbäume überhaupt nicht entscheidend. Entscheidungsbäume teilen auf der Grundlage von Merkmalsschwellenwerten auf, und die Skala der Merkmale hat keinen Einfluss auf die Baumstruktur. Es ist jedoch empfehlenswert, die Auswirkungen der Normalisierung auf die Modellleistung zu überprüfen. |
| Wie gehen Entscheidungsbäume mit kategorialen Variablen in Handelsdaten um? | Entscheidungsbäume können natürlich mit kategorialen Variablen umgehen. Sie führen binäre Aufteilungen (Splits) durch, je nachdem, ob eine Bedingung erfüllt ist, einschließlich Bedingungen für kategoriale Variablen. Der Baum bestimmt die optimalen Splitpunkte für kategoriale Merkmale. |
| Können Entscheidungsbäume für Zeitreihenprognosen im Handel verwendet werden? | Entscheidungsbäume können zwar für Zeitreihenprognosen im Handel eingesetzt werden, sie erfassen jedoch komplexe zeitliche Muster nicht so effektiv wie Modelle wie rekurrente neuronale Netze (RNNs). Ensemble-Methoden wie Random Forests könnten eine größere Robustheit bieten |
| Leiden Entscheidungsbäume unter Overfitting? | Entscheidungsbäume, insbesondere tiefe Entscheidungsbäume, können durch die Erfassung von Rauschen in den Trainingsdaten zu einer Überanpassung neigen. Techniken wie das Beschneiden und die Begrenzung der Baumtiefe können eingesetzt werden, um die Überanpassung bei Handelsanwendungen zu vermindern. |
| Sind Entscheidungsbäume für die Analyse der Bedeutung von Merkmalen in Handelsmodellen geeignet? | Ja, Entscheidungsbäume bieten eine natürliche Methode zur Bewertung der Bedeutung von Merkmalen. Merkmale, die mehr zu den Aufteilungsentscheidungen an der Spitze des Baums beitragen, sind im Allgemeinen kritischer. Diese Analyse kann Aufschluss über die Faktoren geben, die die Handelsentscheidungen beeinflussen. |
| Wie empfindlich sind Entscheidungsbäume gegenüber Ausreißern in Handelsdaten? | Entscheidungsbäume können empfindlich auf Ausreißer reagieren, insbesondere wenn der Baum tief ist. Ausreißer können zu spezifischen Aufteilungen führen, die Rauschen erfassen. Vorverarbeitungsschritte, wie die Erkennung und Entfernung von Ausreißern, können diese Empfindlichkeit verringern. |
| Gibt es bestimmte Hyperparameter, die für Entscheidungsbäume in Handelsmodellen eingestellt werden müssen? | Ja, zu den wichtigsten abzustimmenden Hyperparametern gehören:
Man kann die Kreuzvalidierung verwenden, um optimale Hyperparameterwerte für bestimmte Datensätze zu finden. |
| Können Entscheidungsbäume Teil eines Ensemble-Ansatzes sein? | Ja, Entscheidungsbäume können Teil von Ensemble-Methoden wie Random Forests sein, die mehrere Bäume kombinieren, um die Gesamtvorhersageleistung zu verbessern. Ensemble-Methoden sind oft robust und effektiv in Handelsanwendungen. |
Vorteile von Entscheidungsbäumen:
Interpretierbarkeit:
- Entscheidungsbäume sind leicht zu verstehen und zu interpretieren. Die grafische Darstellung der Baumstruktur ermöglicht eine klare Visualisierung der Entscheidungsprozesse.
Umgang mit Nicht-Linearität:
- Entscheidungsbäume können nicht-lineare Beziehungen in Daten erfassen und eignen sich daher für Probleme, bei denen die Entscheidungsgrenzen nicht linear sind.
Umgang mit gemischten Datentypen:
- Entscheidungsbäume können sowohl numerische als auch kategoriale Daten verarbeiten, ohne dass eine umfangreiche Vorverarbeitung erforderlich ist.
Merkmal Wichtigkeit:
- Entscheidungsbäume bieten eine natürliche Möglichkeit, die Bedeutung von Merkmalen zu bewerten und helfen dabei, kritische Faktoren zu identifizieren, die die Zielvariable beeinflussen.
Keine Annahmen über die Datenverteilung:
- Entscheidungsbäume machen keine Annahmen über die Datenverteilung, was sie vielseitig und für verschiedene Datensätze anwendbar macht.
Robustheit gegenüber Ausreißern:
- Entscheidungsbäume sind relativ robust gegenüber Ausreißern, da die Aufteilung auf relativen Vergleichen basiert und nicht durch absolute Werte beeinflusst wird.
Automatische Variablenauswahl:
- Der Prozess der Baumerstellung umfasst eine automatische Variablenauswahl, wodurch sich die Notwendigkeit einer manuellen Merkmalskonstruktion verringert.
Kann mit fehlenden Werten umgehen:
- Entscheidungsbäume können mit fehlenden Werten in Merkmalen umgehen, ohne dass eine Imputation erforderlich ist, da Aufteilungen auf der Grundlage der verfügbaren Daten vorgenommen werden.
Nachteile von Entscheidungsbäumen:
Überanpassung:
- Entscheidungsbäume neigen zur Überanpassung, insbesondere wenn sie tief sind und Rauschen in den Trainingsdaten erfassen. Techniken wie das Beschneiden werden eingesetzt, um dieses Problem zu lösen.
Instabilität:
- Kleine Änderungen in den Daten können zu erheblichen Änderungen in der Baumstruktur führen, was die Entscheidungsbäume etwas instabil macht.
Voreingenommenheit gegenüber den dominanten Klassen:
- In Datensätzen mit unausgewogenen Klassen können Entscheidungsbäume in Richtung der dominanten Klasse voreingenommen sein, was zu einer suboptimalen Leistung für Minderheitsklassen führt.
Globales Optimum vs. Lokale Optima:
- Entscheidungsbäume konzentrieren sich auf die Suche nach lokalen optimalen Aufteilungen an jedem Knoten, was nicht unbedingt zu einer global optimalen Lösung führen muss.
Begrenzte Ausdruckskraft:
- Entscheidungsbäume können im Vergleich zu komplexeren Modellen wie neuronalen Netzen Schwierigkeiten haben, komplexe Beziehungen in Daten auszudrücken.
Nicht geeignet für kontinuierliche Ausgabe:
- Während sich Entscheidungsbäume für Klassifizierungsaufgaben eignen, sind sie für Aufgaben, die eine kontinuierliche Ausgabe erfordern, möglicherweise weniger gut geeignet.
Empfindlich gegenüber verrauschten Daten:
- Entscheidungsbäume können empfindlich auf verrauschte Daten reagieren, und Ausreißer können zu spezifischen Aufteilungen führen, die eher Rauschen als sinnvolle Muster erfassen.
Voreingenommenheit für dominante Merkmale:
- Merkmale mit mehreren Ebenen oder Kategorien können aufgrund der Art und Weise, wie die Aufteilung vorgenommen wird, kritischer erscheinen, was zu Verzerrungen führen kann. Dies kann durch Techniken wie die Skalierung von Merkmalen erreicht werden.
Das war's, Leute, danke fürs Lesen.
Verfolgen Sie die Entwicklung des Entscheidungsbaum-Algorithmus und vieler weiterer KI-Modelle auf meinem GitHub-Repositorium: https://github.com/MegaJoctan/MALE5/tree/master
Anhänge:
| tree.mqh | Das Haupt-Include, Datei. Enthält den Entscheidungsbaum-Code, den wir oben hauptsächlich besprochen haben. |
| metrics.mqh | Enthält Funktionen und Code zur Messung der Leistung von ML-Modellen. |
| matrix_utils.mqh | Enthält zusätzliche Funktionen für Matrixmanipulationen. |
| preprocessing.mqh | Die Bibliothek für die Vorverarbeitung von rohen Eingabedaten, um sie für die Verwendung von Modellen des maschinellen Lernens geeignet zu machen. |
| DecisionTree Test.mq5(EA) | Die Hauptdatei. Ein Expert Advisor für die Ausführung des Entscheidungsbaums. |
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/13862
Filterung und Merkmalsextraktion von Frequenzen
MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 08): Perceptrons
MQL5-Assistent-Techniken, die Sie kennen sollten (Teil 09): K-Means-Clustering mit fraktalen Wellen
Wie man einen einfachen Multi-Currency Expert Advisor mit MQL5 erstellt (Teil 4): Triangulärer gleitender Durchschnitt — Indikatorensignale
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.