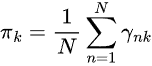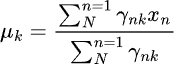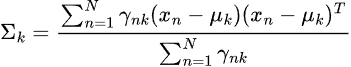
Datenwissenschaft und ML (Teil 43): Erkennen verborgener Muster in Indikatordaten unter Verwendung Latenter Gaußscher Mischmodelle (LGMM)
119
0
Inhalt
- Einführung
- Was ist ein Latentes Gaußsches Mischmodell?
- Die Mathematik hinter LGMM
- Schulung des LGMM anhand von Indikatorendaten
- Ein MQL5-Indikator auf der Grundlage des LGMM
- Suche nach der besten Anzahl von Komponenten für LGMM
- Das Latentes Gaußsches Mischmodell neben einem Klassifikatormodell
- LGMM-basierter Handelsroboter
- Schlussfolgerung
Einführung
Fast alle verfügbaren Handelsstrategien, die wir als Händler verwenden, basieren auf der Identifizierung und Erkennung von bestimmten Mustern. Wir untersuchen Indikatoren auf Muster und Bestätigungen, und manchmal zeichnen wir sogar Objekte und Linien, wie Unterstützungs- und Widerstandslinien, um den Zustand des Marktes zu erkennen.
Während die Erkennung von Mustern auf den Finanzmärkten für uns Menschen eine leichte Aufgabe ist, stellt die Programmierung und Automatisierung dieses Prozesses aufgrund der Beschaffenheit der Märkte (verrauscht und chaotisch) eine Herausforderung dar.
Einige Händler haben sich für diese Aufgabe auf den Einsatz von Künstlicher Intelligenz (KI) und maschinellem Lernen verlegt und verwenden verschiedene auf Computer Vision basierende Techniken, die Bilddaten ähnlich wie Menschen verarbeiten, wie wir in einem der vorherigen Artikel beschrieben haben.
In diesem Artikel wird ein probabilistisches Modell namens Latentes Gaußsches Mischmodell (LGMM) vorgestellt, das in der Lage ist, Muster zu erkennen. Anhand der Indikatordaten werden wir die Wirksamkeit dieses Modells bei der Erkennung verborgener Muster und der Erstellung präziser Vorhersagen auf den Finanzmärkten untersuchen.
Was ist ein Latentes Gaußsches Mischmodell (LGMM)?
Das Latente Gaußsche Mischmodell, GaussianMixture, ist ein probabilistisches Modell, das davon ausgeht, dass die Daten aus einer Mischung mehrerer Gaußscher Verteilungen generiert werden, die jeweils mit einer latenten (versteckten) Variable verbunden sind.
Es ist eine Erweiterung des Gaußschen Mischmodells (GMM), das latente Variablen einbezieht, die die Clusterzuordnung für jede Beobachtung erklären.
Latente Gauß-Modelle werden zur Analyse von Daten verwendet, bei denen die zugrunde liegenden Prozesse, die die Daten erzeugen, nicht direkt beobachtbar sind und bei denen eine Gaußsche (normale) Verteilung angenommen wird.
Der „latente“ Teil bezieht sich auf diese unbeobachteten Variablen, ähnlich wie die unsichtbaren elektrischen Signale in einem Schaltkreis, die das Verhalten des Systems beeinflussen, aber nicht direkt gemessen werden.
Auf den Finanzmärkten können diese latenten Variablen zugrunde liegende Handelsmuster in den Daten darstellen, die wir oft falsch interpretieren oder übersehen.
Kurz gesagt, das Rückgrat des LGMM besteht aus:
- Latente Variablen
Dabei handelt es sich um unbeobachtete Variablen, die als gaußförmig angenommen werden und zugrunde liegende Faktoren darstellen, die die beobachteten Daten beeinflussen. - Beobachtungen
Die tatsächlich erhobenen Daten, die in der Regel nicht gaußförmig sind und einer beliebigen Verteilung folgen können, die mit den latenten Variablen durch eine bekannte Funktion verknüpft ist. - Parameter
Diese regeln die Beziehung zwischen latenten Variablen und Beobachtungen, einschließlich der Mittelwerte und Varianzen der Verteilungen.
Die Mathematik hinter LGMM
LGMM ist ein generatives Modell (Wahrscheinlichkeit) mit einer Cluster-Technik als Kernstück. Es hat:
Latente Variablen
- Diese werden nicht direkt beobachtet
- Sie stellen die Komponente (Cluster) dar, aus der ein Datenpunkt stammt.
- Sie werden häufig als kategoriale (diskrete) Verteilung modelliert, z. B.
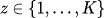
Das Mischmodell
Die Wahrscheinlichkeitsverteilung der Daten ist eine gewichtete Summe aus mehreren Gauß-Verteilungen.
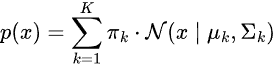
wobei:
-
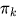ist der Mischungskoeffizient (Vorwahrscheinlichkeit einer Komponente 
, 
-
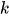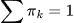
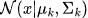= Gaußsche Verteilung mit Mittelwert 
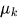und Kovarianz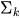 
Repräsentation latenter Variablen
Anstatt p(x) direkt zu modellieren, betrachten wir:
wobei:
Ziel dieses Modells ist es, latente Variablen und die Parameter 
zu schätzen.
Die gebräuchlichste Methode zur Bestimmung dieser Variablen ist der Algorithmus Erwartungs-Maximierung (EM).
Erwartungs-Maximierung (EM) für LGMM
Dies umfasst zwei Schritte: Erwartung und Minimierung.
Schritt 01, Erwartungen.
Dies beinhaltet die Schätzung der Posteriorwahrscheinlichkeit, dass jeder Datenpunkt zu jedem Gauß gehört.
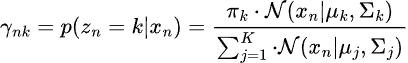
Schritt 02, Minimierung
In diesem Schritt werden die Parameter mit Hilfe von 
aktualisiert.
Beim Training werden sowohl Schritt 01 als auch Schritt 02 wiederholt, bis das Modell konvergiert.
LGMM wurde in verschiedenen Anwendungen in der realen Welt eingesetzt, z. B. beim Clustering von Daten mit Unsicherheit (Soft Clustering), bei der Erkennung von Anomalien, bei der Dichteschätzung und bei Aufgaben im Zusammenhang mit der Spracherkennung.
LGMM-Training mit den Indikatorendaten
Wir wissen, dass es in den Indikatordaten Muster gibt, die wir als Händler nutzen, um fundierte Handelsentscheidungen zu treffen. Unser Ziel ist es, mit LGMM diese Muster zuerst zu erkennen.
Wir beginnen mit dem Sammeln von Indikatordaten aus dem MetaTrader 5, indem wir zunächst die Sprache MQL5 verwenden.
- Symbol = XAUUSD.
- Zeitrahmen = DAILY.
Dateiname: XAUUSD-Daten abrufen.mq5
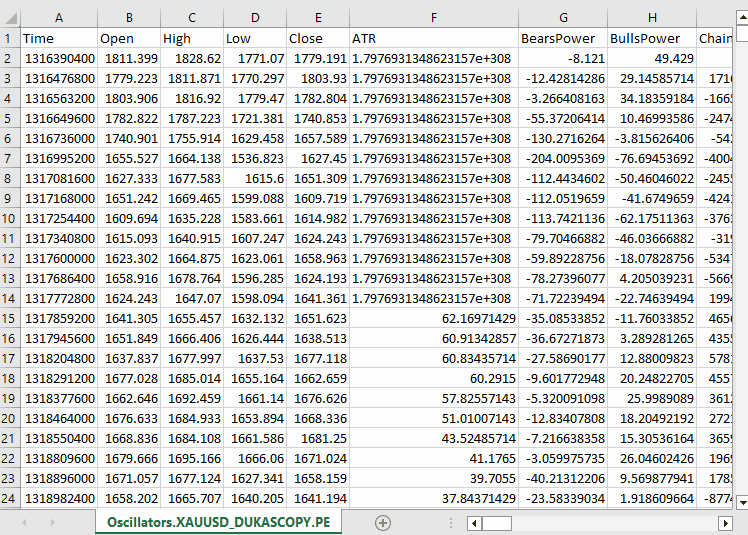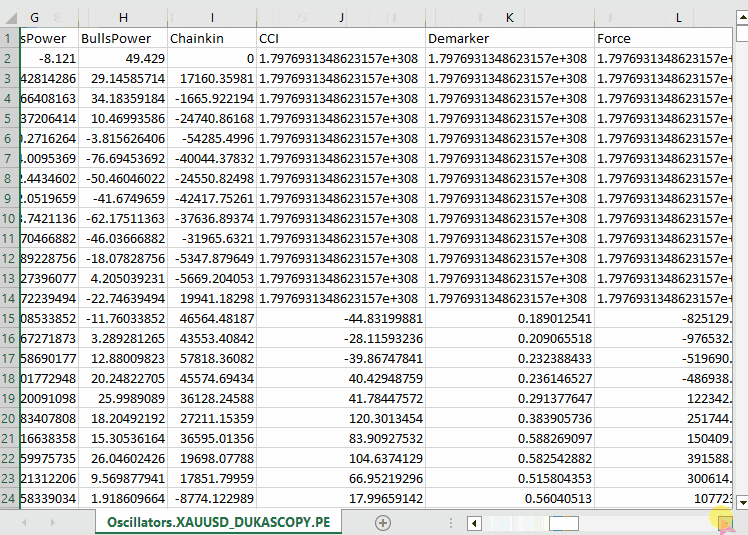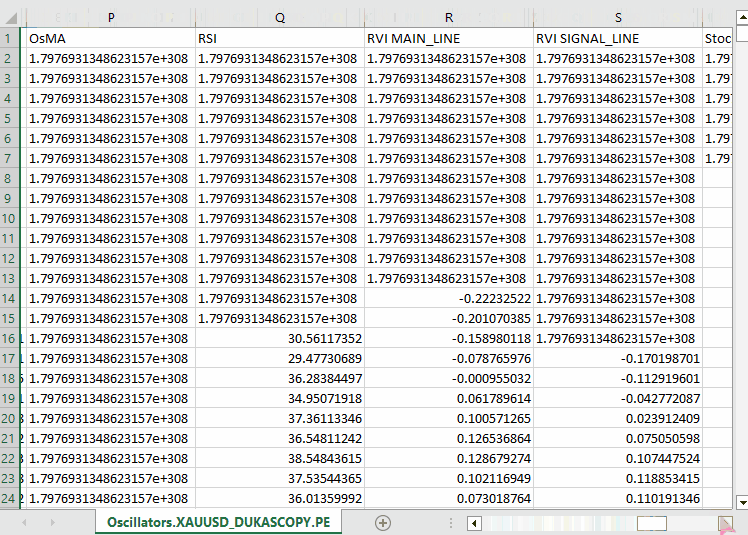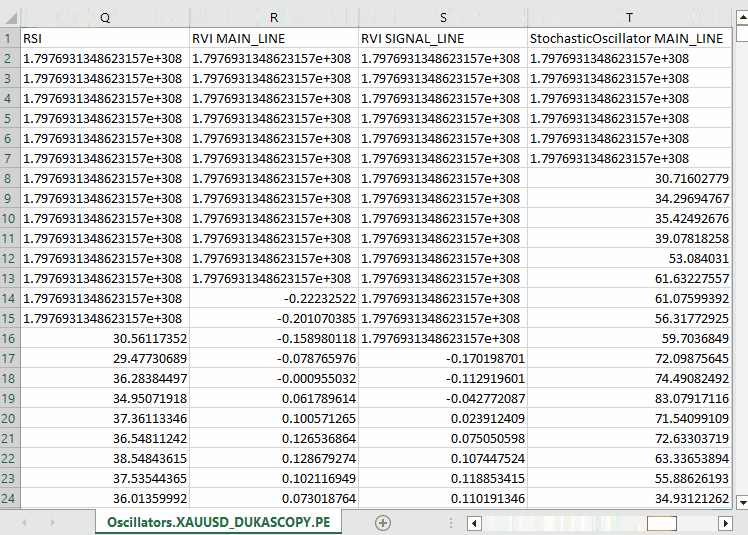
#include <Arrays\ArrayString.mqh> #include <Arrays\ArrayObj.mqh> #include <pandas.mqh> //https://www.mql5.com/en/articles/17030 input datetime start_date = D'2005.01.01'; input datetime end_date = D'2023.01.01'; input string symbol = "XAUUSD"; input ENUM_TIMEFRAMES timeframe = PERIOD_D1; struct indicator_struct { long handle; CArrayString buffer_names; //buffer_names array }; indicator_struct indicators[15]; //Structure for keeping indicator handle alongside its buffer names //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- vector time, open, high, low, close; if (!SymbolSelect(symbol, true)) { printf("%s failed to select symbol %s, Error = %d",__FUNCTION__,symbol,GetLastError()); return; } //--- time.CopyRates(symbol, timeframe, COPY_RATES_TIME, start_date, end_date); open.CopyRates(symbol, timeframe, COPY_RATES_OPEN, start_date, end_date); high.CopyRates(symbol, timeframe, COPY_RATES_HIGH, start_date, end_date); low.CopyRates(symbol, timeframe, COPY_RATES_LOW, start_date, end_date); close.CopyRates(symbol, timeframe, COPY_RATES_CLOSE, start_date, end_date); CDataFrame df; df.insert("Time", time); df.insert("Open", open); df.insert("High", high); df.insert("Low", low); df.insert("Close", close); //--- Oscillators indicators[0].handle = iATR(symbol, timeframe, 14); indicators[0].buffer_names.Add("ATR"); indicators[1].handle = iBearsPower(symbol, timeframe, 13); indicators[1].buffer_names.Add("BearsPower"); indicators[2].handle = iBullsPower(symbol, timeframe, 13); indicators[2].buffer_names.Add("BullsPower"); indicators[3].handle = iChaikin(symbol, timeframe, 3, 10, MODE_EMA, VOLUME_TICK); indicators[3].buffer_names.Add("Chainkin"); indicators[4].handle = iCCI(symbol, timeframe, 14, PRICE_OPEN); indicators[4].buffer_names.Add("CCI"); indicators[5].handle = iDeMarker(symbol, timeframe, 14); indicators[5].buffer_names.Add("Demarker"); indicators[6].handle = iForce(symbol, timeframe, 13, MODE_SMA, VOLUME_TICK); indicators[6].buffer_names.Add("Force"); indicators[7].handle = iMACD(symbol, timeframe, 12, 26, 9, PRICE_OPEN); indicators[7].buffer_names.Add("MACD MAIN_LINE"); indicators[7].buffer_names.Add("MACD SIGNAL_LINE"); indicators[8].handle = iMomentum(symbol, timeframe, 14, PRICE_OPEN); indicators[8].buffer_names.Add("Momentum"); indicators[9].handle = iOsMA(symbol, timeframe, 12, 26, 9, PRICE_OPEN); indicators[9].buffer_names.Add("OsMA"); indicators[10].handle = iRSI(symbol, timeframe, 14, PRICE_OPEN); indicators[10].buffer_names.Add("RSI"); indicators[11].handle = iRVI(symbol, timeframe, 10); indicators[11].buffer_names.Add("RVI MAIN_LINE"); indicators[11].buffer_names.Add("RVI SIGNAL_LINE"); indicators[12].handle = iStochastic(symbol, timeframe, 5, 3,3,MODE_SMA,STO_LOWHIGH); indicators[12].buffer_names.Add("StochasticOscillator MAIN_LINE"); indicators[12].buffer_names.Add("StochasticOscillator SIGNAL_LINE"); indicators[13].handle = iTriX(symbol, timeframe, 14, PRICE_OPEN); indicators[13].buffer_names.Add("TEMA"); indicators[14].handle = iWPR(symbol, timeframe, 14); indicators[14].buffer_names.Add("WPR"); //--- Get buffers for (uint ind=0; ind<indicators.Size(); ind++) //Loop through all the indicators { for (uint buffer_no=0; buffer_no<(uint)indicators[ind].buffer_names.Total(); buffer_no++) //Their buffer names resemble their buffer numbers { string name = indicators[ind].buffer_names.At(buffer_no); //Get the name of the buffer, it is helpful for the DataFrame and CSV file vector buffer = {}; if (!buffer.CopyIndicatorBuffer(indicators[ind].handle, buffer_no, start_date, end_date)) //Copy indicator buffer { printf("func=%s line=%d | Failed to copy %s indicator buffer, Error = %d",__FUNCTION__,__LINE__,name,GetLastError()); continue; } df.insert(name, buffer); //Insert a buffer vector and its name to a dataframe object } } df.to_csv(StringFormat("Oscillators.%s.%s.csv",symbol,EnumToString(timeframe)), true); //Save all the data to a CSV file }
Ausgabe:
Beachten Sie, dass wir ungefähr alle Oszillator-Indikatoren gesammelt haben, die MQL5 anbietet. Die meisten von ihnen produzieren stationäre Daten, da sie normalerweise Mindest- und Höchstwerte haben. Zum Beispiel: Der RSI-Indikator liefert Werte zwischen 0 und 100.
Obwohl das LGMM in der Lage ist, mit Daten unterschiedlicher statistischer Eigenschaften, wie z. B. nicht-stationären Daten, zu arbeiten. Stationäre Daten erleichtern es dem LGMM, aussagekräftige Strukturen und Muster zu finden, da die statistischen Eigenschaften stationärer Daten über die Zeit hinweg konstant bleiben.
Sie können jede Art von Daten verwenden, die Sie bevorzugen.
Wir sammelten Open-, High-, Low-, Close- und Time-Variablen (OHLCT) zusammen mit Indikatordaten für die Nutzung des maschinellen Lernens. Diese Informationen können bei der Visualisierung und bei der Festlegung der Zielvariablen für prädiktive maschinelle Lernmodelle (abgesehen von LGMM) verwendet werden.
In einem Python-Skript (Jupyter Notebook) laden wir diese Daten als erstes, kurz nachdem wir die Abhängigkeiten importiert und die MetaTrader 5-Desktop-App initialisiert haben.
Dateiname: main.ipynb
import pandas as pd import numpy as np import MetaTrader5 as mt5 import os from Trade.TerminalInfo import CTerminalInfo import matplotlib.pyplot as plt import seaborn import warnings warnings.filterwarnings("ignore") seaborn.set_style("darkgrid") if not mt5.initialize(): print("Failed to Initialize MetaTrade5, Error = ",mt5.last_error()) mt5.shutdown() terminal = CTerminalInfo() # similarly to CTerminalInfo from MQL5. For getting information about the MetaTrader5 app
Wir importieren die Daten aus dem gemeinsamen Pfad (Ordner), in dem wir sie mit MQL5 gespeichert haben.
common_path = os.path.join(terminal.common_data_path(), "Files") symbol = "XAUUSD" timeframe = "PERIOD_D1" df = pd.read_csv(os.path.join(common_path, f"Oscillators.{symbol}.{timeframe}.csv")) # the same naming pattern as the one used in the MQL5 script # Identify max float value max_float = np.finfo(float).max # Replace all max float (double) values with NaN produced by preliminary indicator calculations df = df.replace(max_float, np.nan) df.dropna(inplace=True) df["Time"] = pd.to_datetime(df["Time"], unit="s") df.head()
Ausgabe:
Time Open High Low Close ATR BearsPower BullsPower Chainkin CCI ... MACD SIGNAL_LINE Momentum OsMA RSI RVI MAIN_LINE RVI SIGNAL_LINE StochasticOscillator MAIN_LINE StochasticOscillator SIGNAL_LINE TEMA WPR 0 2005-01-03 438.45 438.71 426.72 429.55 5.481429 -12.314215 -0.324215 -1079.046551 -51.013015 ... 0.175727 99.870165 -0.582169 46.666555 -0.082596 0.018515 26.976532 32.920132 -0.000089 -85.144357 1 2005-01-04 429.52 430.18 423.71 427.51 5.450000 -13.677899 -7.207899 -1129.324384 -235.622347 ... -0.000779 98.615544 -1.252741 37.393138 -0.158362 -0.048541 22.158658 27.150101 -0.000190 -82.774252 2 2005-01-05 427.50 428.77 425.10 426.58 5.162143 -10.743913 -7.073913 -1496.644248 -196.837418 ... -0.247283 97.044402 -1.816758 35.666584 -0.227422 -0.119850 17.070979 22.068723 -0.000325 -86.990027 3 2005-01-06 426.31 427.85 420.17 421.37 5.234286 -13.606211 -5.926211 -3349.884147 -164.038728 ... -0.576309 97.480164 -2.194161 34.651526 -0.269634 -0.187300 14.096364 17.775334 -0.000482 -95.312500 4 2005-01-07 421.39 425.48 416.57 419.02 5.605000 -15.098181 -6.188181 -4970.426959 -168.301515 ... -1.015433 95.440750 -2.669414 30.754440 -0.305796 -0.243045 11.442611 14.203318 -0.000670 -91.609589
Bereiten wir die Zielvariable für ein Klassifizierungsproblem zur späteren Verwendung in Klassifizierungsmodellen für maschinelles Lernen vor. Nicht-indikatorische Merkmale lassen wir auf dem Weg fallen.
lookahead = 1 df["future_close"] = df["Close"].shift(-lookahead) new_df = df.dropna() new_df["Direction"] = np.where(new_df["future_close"]>new_df["Close"], 1, -1) # if a the close value in the next bar(s)=lookahead is above the current close price, thats a long signal otherwise that's a short signal
from sklearn.model_selection import train_test_split X = new_df.drop(columns=[ "Time", "Open", "High", "Low", "Close", "future_close", "Direction" ]) y = new_df["Direction"] X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, shuffle=True, random_state=42)
Wir müssen uns vergewissern, dass wir die erforderlichen „Indikatordaten“ haben.
X_train.head()
Ausgabe:
ATR BearsPower BullsPower Chainkin CCI Demarker MACD MAIN_LINE MACD SIGNAL_LINE Momentum OsMA RSI RVI MAIN_LINE RVI SIGNAL_LINE StochasticOscillator MAIN_LINE StochasticOscillator SIGNAL_LINE TEMA WPR 1057 30.139286 34.958195 62.858195 16280.794393 268.371098 251356.076923 -1.759289 -15.645899 107.768519 13.886610 62.077386 0.229591 0.108028 92.301971 83.886543 -0.002663 -8.048595 3806 3.096429 0.724299 3.314299 -1279.189840 69.806094 696.923077 -0.121217 -0.952863 100.299538 0.831645 52.157089 0.096237 0.080054 67.031250 71.466497 -0.000077 -21.325052 38884 5.927143 -8.488258 -3.858258 -2005.866698 -213.672289 -3333.080000 -0.049837 0.496440 99.774916 -0.546277 39.550361 -0.022395 0.035070 28.046540 49.606252 0.000012 -73.130342 10351 2.060714 -0.491108 1.158892 723.246254 40.384615 2508.735385 1.293179 0.953618 100.533084 0.339561 58.791715 0.217352 0.294053 57.239819 69.770534 0.000123 -19.070322 38170 5.632143 -5.682364 -3.262364 -1321.008995 -109.039933 -1673.607692 -0.609996 0.785433 99.712893 -1.395429 41.917705 -0.062258 -0.053202 13.322009 9.490964 0.000035 -77.826942
Lassen Sie uns endlich das LGMM trainieren.
from sklearn.mixture import GaussianMixture from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType components = 3 gmm = GaussianMixture(n_components=components, covariance_type="full", random_state=42) gmm.fit(X_train) latent_features_train = gmm.predict_proba(X_train) latent_features_test = gmm.predict_proba(X_test)
Ich verwende 3 Komponenten für das Gaußsche Mischmodell, in der Hoffnung, dass es die in den Indikatoren beobachteten Muster in 3 Clustern zusammenfassen kann. Angeblich steht ein Cluster für einen Aufwärtstrend (Signal), der andere Cluster für ein Abwärtssignal und der andere für eine Konsolidierung oder ein Range-Signal. Nochmals, dies ist nur eine Vermutung.
Ähnlich wie bei anderen Techniken des maschinellen Lernens und des Clusterings ist es schwierig, die vom Modell erzeugten Komponenten (Ergebnisse) zu interpretieren. Im Moment können wir nur davon ausgehen, dass jede der Komponenten zu den drei gerade beschriebenen Klassen gehört.
Sie fragen sich vielleicht, warum ich das Modell als Latentes Gaußsches Mischmodell (LGMM) bezeichne, aber am Ende ein Modell mit dem Namen GaussianMixture von Scikit-Learn einsetze?
Das importierte GaussianMixture hat eine Funktionalität, die dem LGMM entspricht, wie im Abschnitt über Mathematik in diesem Beitrag beschrieben. Diese beiden sind theoretisch gleich.
Lassen Sie uns das Array latent_features_train ausdrucken.
latent_features_train
Ausgabe:
array([[9.48947877e-13, 1.08107288e-62, 1.00000000e+00], [9.71935407e-01, 2.80542130e-02, 1.03801388e-05], [5.35722226e-03, 9.94642667e-01, 1.10916653e-07], ..., [7.72441751e-08, 8.80712550e-41, 9.99999923e-01], [9.99975623e-01, 1.07924534e-33, 2.43771745e-05], [1.91968188e-01, 8.08030586e-01, 1.22621110e-06]], shape=(3760, 3))
Das LGMM hat in jeder Zeile der Vorhersagen ein Feld mit 3 Elementen erzeugt, wobei jede Spalte die Wahrscheinlichkeit darstellt, dass der empfangene Dateninput zu einem der 3 Cluster gehört. Die Summe der Wahrscheinlichkeiten für alle 3 Spalten ist in jeder Zeile gleich 1.
Da dies in seiner jetzigen Form schwer zu interpretieren ist, wollen wir dieses Modell in das ONNX-Format konvertieren, die Cluster in MQL5 visualisieren und sehen, welche Schlussfolgerungen wir aus den Ergebnissen dieses probabilistischen Modells ziehen können.
Ein MQL5-Indikator auf der Grundlage von dem Latenten Gaußschen Mischmodell (LGMM)
Wir beginnen damit, LGMM im ONNX-Format zu speichern.
# Define input type (shape should match your training data) initial_type = [("float_input", FloatTensorType([None, X_train.shape[1]]))] # Convert the pipeline to ONNX format onnx_model = convert_sklearn(gmm, initial_types=initial_type) # Save the model to a file with open(os.path.join(common_path, f"LGMM.{symbol}.{timeframe}.onnx"), "wb") as f: f.write(onnx_model.SerializeToString())
Nachfolgend sehen Sie die Architektur des Modells, wenn es in Netron geöffnet wurde.
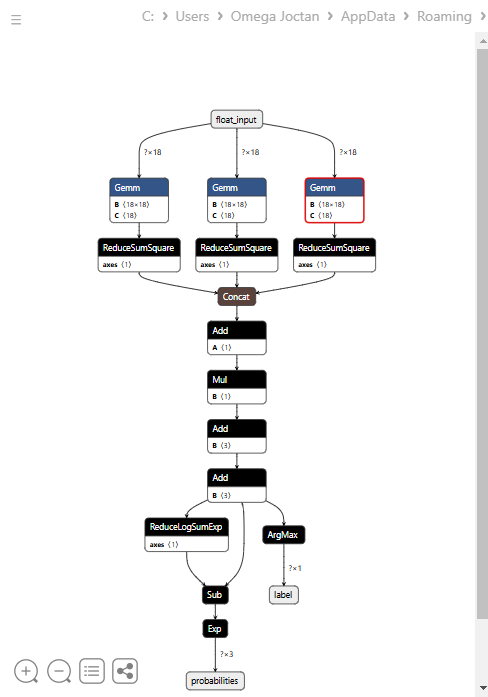
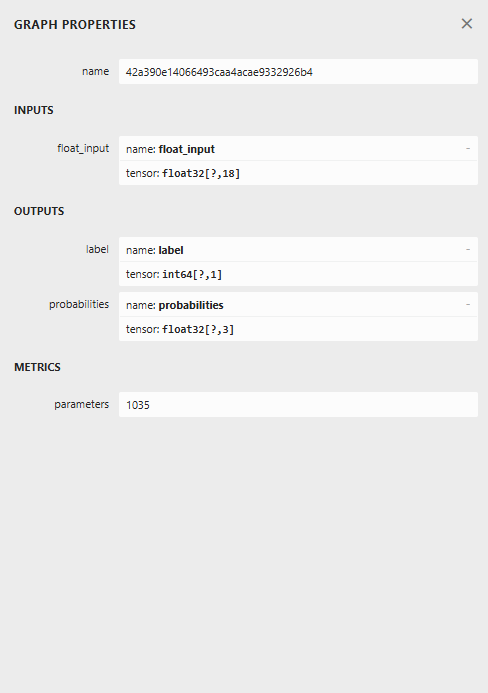
Dieses Modell hat eine merkwürdige Architektur mit zwei Ausgängen im Endknoten, einem für das vorhergesagte Label und einem für die Wahrscheinlichkeiten. Dies müssen wir bei der Implementierung des Ladecodes für dieses Modell in MQL5 berücksichtigen.
LGMM in MQL5 laden
Dateiname: Gaussian Mixture.mqh
Wir benötigen die Ausgabestruktur, die mehrere Arrays von Werten aufnimmt, um zwei Ausgabeknoten mit jeweils einem Array von Ausgaben unterzubringen.
class CGaussianMixture { protected: bool initialized; long onnx_handle; void PrintTypeInfo(const long num,const string layer,const OnnxTypeInfo& type_info); ulong inputs[]; //Inputs of a model in dimensions [nxn] struct outputs_struct { ulong outputs[]; } model_output_structure[]; //Outputs of the model structure array
Dann
bool CGaussianMixture::OnnxLoad(long &handle) { //--- since not all sizes defined in the input tensor we must set them explicitly //--- first index - batch size, second index - series size, third index - number of series (only Close) OnnxTypeInfo type_info; //Getting onnx information for Reference In case you forgot what the loaded ONNX is all about long input_count=OnnxGetInputCount(handle); if (MQLInfoInteger(MQL_DEBUG)) Print("model has ",input_count," input(s)"); for(long i=0; i<input_count; i++) { string input_name=OnnxGetInputName(handle,i); if (MQLInfoInteger(MQL_DEBUG)) Print(i," input name is ",input_name); if(OnnxGetInputTypeInfo(handle,i,type_info)) { if (MQLInfoInteger(MQL_DEBUG)) PrintTypeInfo(i,"input",type_info); ArrayCopy(inputs, type_info.tensor.dimensions); } } long output_count=OnnxGetOutputCount(handle); if (MQLInfoInteger(MQL_DEBUG)) Print("model has ",output_count," output(s)"); ArrayResize(model_output_structure, (int)output_count); for(long i=0; i<output_count; i++) { string output_name=OnnxGetOutputName(handle,i); if (MQLInfoInteger(MQL_DEBUG)) Print(i," output name is ",output_name); if(OnnxGetOutputTypeInfo(handle,i,type_info)) { if (MQLInfoInteger(MQL_DEBUG)) PrintTypeInfo(i,"output",type_info); ArrayCopy(model_output_structure[i].outputs, type_info.tensor.dimensions); } //--- Set the output shape replace(model_output_structure); if(!OnnxSetOutputShape(handle, i, model_output_structure[i].outputs)) { if (MQLInfoInteger(MQL_DEBUG)) { printf("Failed to set the Output[%d] shape Err=%d",i,GetLastError()); DebugBreak(); } return false; } } //--- replace(inputs); //--- Setting the input size for (long i=0; i<input_count; i++) if (!OnnxSetInputShape(handle, i, inputs)) //Giving the Onnx handle the input shape { if (MQLInfoInteger(MQL_DEBUG)) printf("Failed to set the input shape Err=%d",GetLastError()); DebugBreak(); return false; } initialized = true; if (MQLInfoInteger(MQL_DEBUG)) Print("ONNX model Initialized"); return true; } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ bool CGaussianMixture::Init(string onnx_filename, uint flags=ONNX_DEFAULT) { onnx_handle = OnnxCreate(onnx_filename, flags); if (onnx_handle == INVALID_HANDLE) return false; return OnnxLoad(onnx_handle); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ bool CGaussianMixture::Init(const uchar &onnx_buff[], ulong flags=ONNX_DEFAULT) { onnx_handle = OnnxCreateFromBuffer(onnx_buff, flags); //creating onnx handle buffer if (onnx_handle == INVALID_HANDLE) return false; return OnnxLoad(onnx_handle); }
Wir haben die Methode Predict dieser Klasse so gestaltet, dass sie zwei Variablen zurückgibt, das vorhergesagte Kennzeichen und einen Wahrscheinlichkeitsvektor in einer Struktur.
struct pred_struct { vector proba; long label; };
pred_struct CGaussianMixture::predict(const vector &x) { pred_struct res; if (!this.initialized) { if (MQLInfoInteger(MQL_DEBUG)) printf("%s The model is not initialized yet to make predictions | call Init function first",__FUNCTION__); return res; } //--- vectorf x_float; //Convert inputs from a vector of double values to those float values x_float.Assign(x); vector label = vector::Zeros(model_output_structure[0].outputs[1]); //outputs[1] we get the second shape (columns) from an array vector proba = vector::Zeros(model_output_structure[1].outputs[1]); //outputs[1] we get the second shape (columns) from an array if (!OnnxRun(onnx_handle, ONNX_DATA_TYPE_FLOAT, x_float, label, proba)) //Run the model and get the predicted label and probability { if (MQLInfoInteger(MQL_DEBUG)) printf("Failed to get predictions from Onnx err %d",GetLastError()); DebugBreak(); return res; } //--- res.label = (long)label[label.Size()-1]; //Get the last item available at the label's array res.proba = proba; return res; }
Rufen wir die Vorhersagefunktion innerhalb der Hauptfunktion eines Indikators auf, um uns mit latenten Merkmalen zu versorgen.
Dateiname: LGMM Indicator.mq5
int OnCalculate(const int32_t rates_total, const int32_t prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int32_t &spread[]) { //--- Main calculation loop int lookback = 20; for (int i = prev_calculated; i < rates_total && !IsStopped(); i++) { if (i+1<lookback) //prevent data not found errors during copy buffer continue; int reverse_index = rates_total - 1 - i; //--- Get the indicators data vector x = getX(reverse_index, lookback); if (x.Size()==0) continue; pred_struct res = lgmm.predict(x); vector proba = res.proba; long label = res.label; ProbabilityBuffer[i] = proba.Max(); // Determine color based on histogram value if (label == 0) ColorBuffer[i] = 0; else if (label == 1) ColorBuffer[i] = 1; else ColorBuffer[i] = 2; Comment("bars [",i+1,"/",rates_total,"]"," Proba: ",proba," label: ",label); } //--- return(rates_total); }
In der Funktion getX() müssen wir alle Indikatorpuffer auf die gleiche Weise sammeln, wie wir es im Skript beim Sammeln der Daten für das Training getan haben.
vector getX(uint start=0, uint count=10) { //--- Get buffers CDataFrame df; for (uint ind=0; ind<indicators.Size(); ind++) //Loop through all the indicators { uint buffers_total = indicators[ind].buffer_names.Total(); for (uint buffer_no=0; buffer_no<buffers_total; buffer_no++) //Their buffer names resemble their buffer numbers { string name = indicators[ind].buffer_names.At(buffer_no); //Get the name of the buffer, it is helpful for the DataFrame and CSV file vector buffer = {}; if (!buffer.CopyIndicatorBuffer(indicators[ind].handle, buffer_no, start, count)) //Copy indicator buffer { printf("func=%s line=%d | Failed to copy %s indicator buffer, Error = %d",__FUNCTION__,__LINE__,name,GetLastError()); continue; } df.insert(name, buffer); //Insert a buffer vector and its name to a dataframe object } } return df.iloc(-1); //Return the latest information from the dataframe which is the most recent buffer }
Anmerkung: Alle Indikatoren wurden in der Funktion Init initialisiert, nachdem das Modell aus dem gemeinsamen Ordner, in dem wir es mit Python gespeichert haben, initialisiert wurde.
#include <Gaussian Mixture.mqh> #include <Arrays\ArrayString.mqh> #include <MALE5\Pandas\pandas.mqh> CGaussianMixture lgmm; input string symbol = "XAUUSD"; input ENUM_TIMEFRAMES timeframe = PERIOD_D1; struct indicator_struct { long handle; CArrayString buffer_names; }; indicator_struct indicators[15]; //--- Indicator buffers double ProbabilityBuffer[]; double ColorBuffer[]; double MaBuffer[]; //+------------------------------------------------------------------+ //| Custom indicator initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- indicator buffers mapping Comment(""); // Setting indicator properties SetIndexBuffer(0, ProbabilityBuffer, INDICATOR_DATA); SetIndexBuffer(1, ColorBuffer, INDICATOR_COLOR_INDEX); // Setting histogram drawing style PlotIndexSetInteger(0, PLOT_DRAW_TYPE, DRAW_COLOR_HISTOGRAM); // Set indicator labels IndicatorSetString(INDICATOR_SHORTNAME, "3-Color Histogram"); IndicatorSetInteger(INDICATOR_DIGITS, _Digits); //--- string filename = StringFormat("LGMM.%s.%s.onnx",symbol, EnumToString(timeframe)); if (!lgmm.Init(filename, ONNX_COMMON_FOLDER)) { printf("%s Failed to initialize the GaussianMixture model (LGMM) in ONNX format file={%s}, Error = %d",__FUNCTION__,filename,GetLastError()); } //--- Oscillators indicators[0].handle = iATR(symbol, timeframe, 14); indicators[0].buffer_names.Add("ATR"); //... //... //... indicators[14].handle = iWPR(symbol, timeframe, 14); indicators[14].buffer_names.Add("WPR"); for (uint i=0; i<indicators.Size(); i++) if (indicators[i].handle==INVALID_HANDLE) { printf("%s Invalid %s handle, Error = %d",__FUNCTION__,indicators[i].buffer_names[0],GetLastError()); return INIT_FAILED; } //--- return(INIT_SUCCEEDED); }
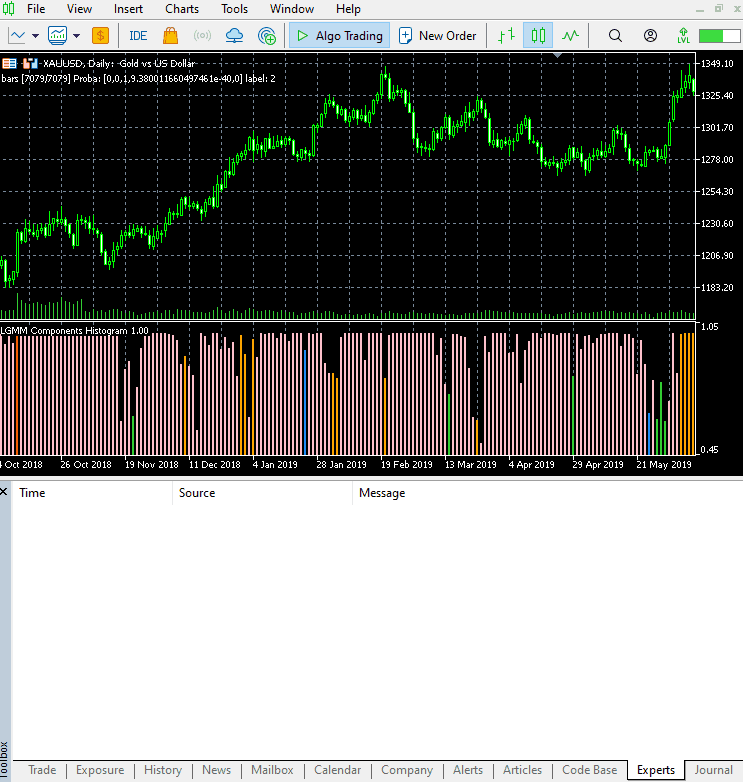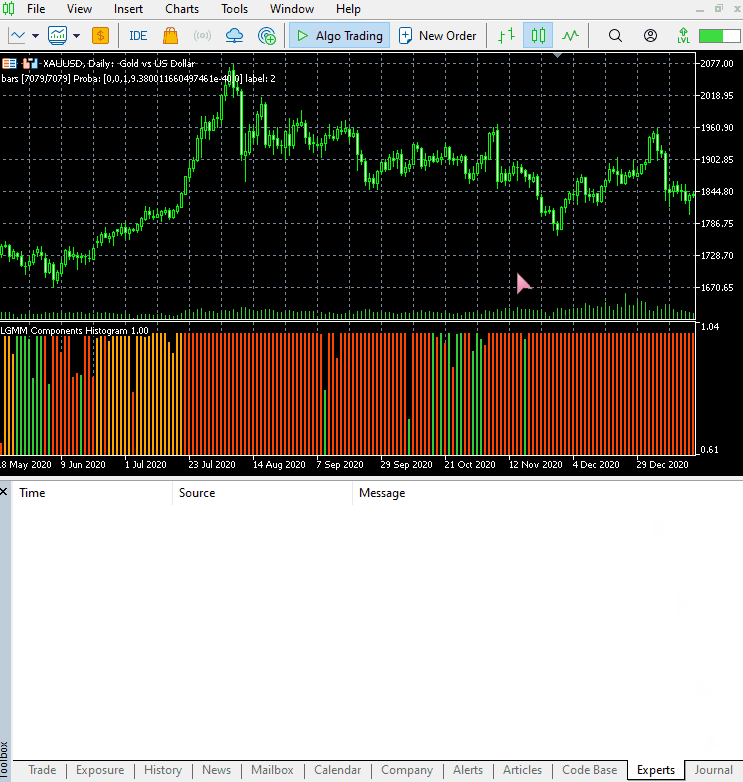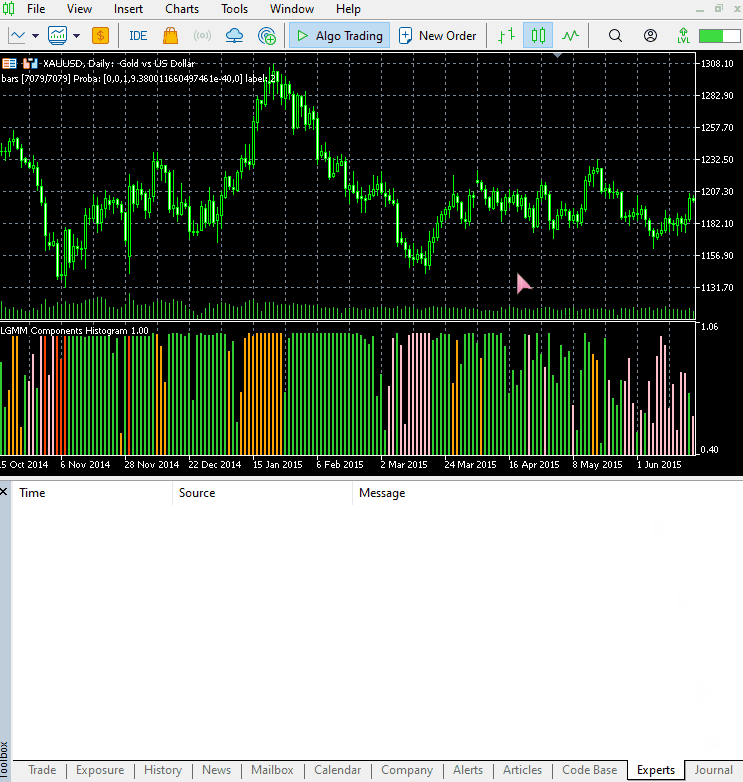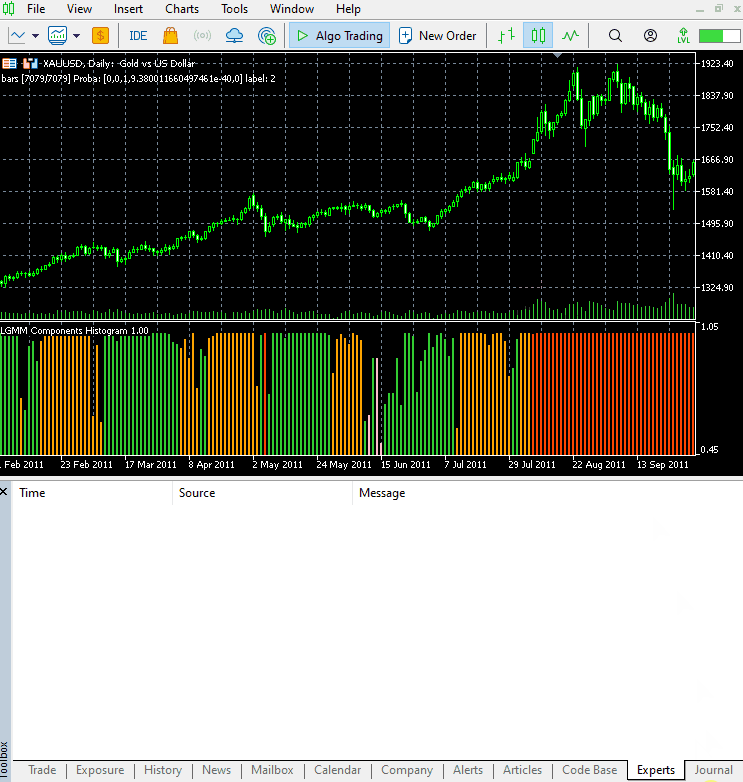
Zum Schluss lassen wir diesen Indikator auf dem XAUUSD-Chart und demselben Zeitrahmen laufen, auf dem das Modell trainiert wurde.
Dieser Indikator ist immer noch schwer zu interpretieren, aber ein Muster scheint vorherrschend zu sein, und das ist die Komponente, die in roter Farbe dargestellt ist. Es scheint, dass dieses Muster auftritt, wenn der Markt in einem Aufwärts- oder Abwärtstrend volatil ist (die Volatilität ist hoch). Das könnte daran liegen, dass wir uns nicht sicher sind, wie viele Komponenten wir für dieses Modell verwendet haben. Lassen Sie uns also die beste Anzahl von Komponenten für dieses Modell finden.
Suche nach der besten Anzahl von Komponenten für LGMM
Da das von Scikit-Learn angebotene Mixture-Modell Informationskriteriumswerte erzeugt, Akaike Information Criterion (AIC) und Bayesian Information Criterion (BIC). Stellen wir diese Werte gegen ihren Komponentenbereich in einem Diagramm dar und erkennen wir den oder die Knickpunkte.
Der Ellbogenpunkt in einem Diagramm ist der Punkt, an dem das Hinzufügen weiterer Komponenten zum Modell nur zu einer marginalen Verbesserung der Leistung führt, d. h. die Kurve flacht ab.
Dateiname: main.ipynb
lowest_bic = np.inf bic = [] aic = [] n_components_range = range(1, 10) for n_components in n_components_range: gmm = GaussianMixture(n_components=n_components, random_state=42) gmm.fit(X) bic.append(gmm.bic(X_train)) aic.append(gmm.aic(X_train)) if bic[-1] < lowest_bic: best_gmm = gmm lowest_bic = bic[-1] # Plot the BIC and AIC scores plt.figure(figsize=(8, 5)) plt.plot(n_components_range, bic, label='BIC', marker='o') plt.plot(n_components_range, aic, label='AIC', marker='o') plt.xlabel('Number of components') plt.ylabel('Score') plt.title('LGMM selection: AIC vs BIC') plt.legend() plt.grid(True) plt.show()
Ausgabe:
Sowohl die AIC- als auch die BIC-Kurve fallen bei den Komponenten 1 bis 2 stark ab und nehmen dann weiter ab, aber die Verbesserungsrate verlangsamt sich bei beiden nach 5 Komponenten merklich. Das bedeutet, dass die beste Anzahl von Komponenten, die wir für dieses Modell verwenden sollten, 5 ist.
Gehen wir zurück, trainieren wir das Modell neu und aktualisieren wir den Indikator.
Dateiname: main.ipynb
components = 5 # according to the elbow point gmm = GaussianMixture(n_components=components, covariance_type="full", random_state=42) gmm.fit(X_train) latent_features_train = gmm.predict_proba(X_train) latent_features_test = gmm.predict_proba(X_test)
Da wir nun 5 Komponenten innerhalb von 3 haben, was bedeutet, dass das Modell 5 Wahrscheinlichkeiten erzeugt, die wir darstellen können, müssen wir die Anzahl der Farben im Indikator auf 5 für das farbige Histogramm erhöhen und 5 verschiedene Fälle für die vorhergesagten Labels behandeln.
Dateiname: LGMM Indicator.mq5
#property indicator_color1 clrDodgerBlue, clrLimeGreen, clrCrimson, clrOrange, clrYellow
Innerhalb der Funktion OnCalculate.
int OnCalculate(const int32_t rates_total, const int32_t prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int32_t &spread[]) { //--- Main calculation loop int lookback = 20; for (int i = prev_calculated; i < rates_total && !IsStopped(); i++) { if (i+1<lookback) //prevent data not found errors during copy buffer continue; //... //... //... // Determine color based on predicted label if (label == 0) ColorBuffer[i] = 0; else if (label == 1) ColorBuffer[i] = 1; else if (label == 2) ColorBuffer[i] = 2; else if (label == 3) ColorBuffer[i] = 3; else ColorBuffer[i] = 4; Comment("bars [",i+1,"/",rates_total,"]"," Proba: ",proba," label: ",label); }
Das neue Erscheinungsbild des Indikators.
Er sieht gut aus, ist aber dennoch schwer zu lesen, da wir oft an einfache Oszillatoren gewöhnt sind, die oft überverkaufte und überkaufte Bereiche anzeigen. Zögern Sie nicht, diesen Indikator zu erkunden, und teilen Sie uns Ihre Meinung im Diskussionsbereich mit.
Lassen Sie uns nun das LGMM zusammen mit einem maschinellen Lernmodell verwenden.
Latentes Gaußsches Mischmodell neben einem Klassifikatormodell
Wir haben nun gesehen, wie wir LGMM verwenden können, um latente Merkmale zu erzeugen, die die Wahrscheinlichkeit darstellen, dass ein Etikett zu einem bestimmten Cluster gehört, da es schwierig ist, diese Merkmale zu verstehen. Lassen Sie uns diese in einer Random-Forest-Klassifizierung zusammen mit den Indikatormerkmalen verwenden, in der Hoffnung, dass dieses maschinelle Lernmodell herausfinden kann, wie latente Merkmale die Handelssignale beeinflussen.
Dateiname: main.ipynb
Wir haben die Zielvariable bereits bei der Aufteilung der Trainings- und Testdaten erstellt, hier noch einmal als Referenz.
from sklearn.model_selection import train_test_split X = new_df.drop(columns=[ "Time", "Open", "High", "Low", "Close", "future_close", "Direction" ]) y = new_df["Direction"] X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, shuffle=True, random_state=42)
Nachdem wir das LGMM trainiert hatten, verwendeten wir es, um Vorhersagen für die Trainings- und Testdaten zu treffen.
latent_features_train = gmm.predict_proba(X_train) latent_features_test = gmm.predict_proba(X_test)
Da diese Daten schwer zu lesen sind, fügen wir ihnen einige Merkmalsnamen hinzu, damit die Merkmale identifizierbar sind.
latent_features_train_df = pd.DataFrame(latent_features_train, columns=[f"LATENT_FEATURE_{i}" for i in range(latent_features_train.shape[1])]) latent_features_test_df = pd.DataFrame(latent_features_test, columns=[f"LATENT_FEATURE_{i}" for i in range(latent_features_test.shape[1])])
latent_features_train_df
Ausgabe:
| LATENT_FEATURE_0 | LATENT_FEATURE_1 | LATENT_FEATURE_2 | LATENT_FEATURE_3 | LATENT_FEATURE_4 | |
|---|---|---|---|---|---|
| 0 | 0.000000e+00 | 5.368039e-08 | 9.999999e-01 | 1.566000e-57 | 8.541983e-37 |
| 1 | 3.316692e-124 | 8.262106e-01 | 2.931424e-06 | 1.725415e-01 | 1.244990e-03 |
| 2 | 6.572730e-49 | 7.441120e-08 | 3.481699e-08 | 9.461818e-01 | 5.381811e-02 |
| 3 | 0.000000e+00 | 1.165057e-126 | 1.413762e-05 | 4.101964e-16 | 9.999859e-01 |
| 4 | 0.000000e+00 | 4.446778e-289 | 1.000000e+00 | 1.717945e-36 | 4.234123e-21 |
Lassen Sie uns diese Merkmale mit den Daten der Primärindikatoren kombinieren.
all_columns = X_train.columns.tolist() + latent_features_train_df.columns.tolist() X_latent_train_arr = np.hstack([X_train, latent_features_train_df]) X_latent_test_arr = np.hstack([X_test, latent_features_test_df]) X_Train_latent = pd.DataFrame(X_latent_train_arr, columns=all_columns) X_Test_latent = pd.DataFrame(X_latent_test_arr, columns=all_columns) X_Train_latent.columns
Ausgabe:
Index(['ATR', 'BearsPower', 'BullsPower', 'Chainkin', 'CCI', 'Demarker', 'Force', 'MACD MAIN_LINE', 'MACD SIGNAL_LINE', 'Momentum', 'OsMA', 'RSI', 'RVI MAIN_LINE', 'RVI SIGNAL_LINE', 'StochasticOscillator MAIN_LINE', 'StochasticOscillator SIGNAL_LINE', 'TEMA', 'WPR', 'LATENT_FEATURE_0', 'LATENT_FEATURE_1', 'LATENT_FEATURE_2', 'LATENT_FEATURE_3', 'LATENT_FEATURE_4'], dtype='object')
Übergeben wir diese kombinierten Daten an einen Random-Forest-Klassifikator.
from sklearn.ensemble import RandomForestClassifier from sklearn.utils.class_weight import compute_class_weight classes = np.unique(y_train) weights = compute_class_weight(class_weight='balanced', classes=classes, y=y_train) class_weights_dict = dict(zip(classes, weights)) params = { "n_estimators": 100, "min_samples_split": 2, "max_depth": 10, "max_leaf_nodes": 10, "criterion": "gini", "random_state": 42 } model = RandomForestClassifier(**params, class_weight=class_weights_dict) model.fit(X_Train_latent, y_train)
Die Bewertung des Modells.
y_train_pred = model.predict(X_Train_latent) print("Train classification report\n", classification_report(y_train, y_train_pred)) y_test_pred = model.predict(X_Test_latent) print("Test classification report\n", classification_report(y_test, y_test_pred))
Ausgabe:
Train classification report precision recall f1-score support -1 0.60 0.67 0.63 1766 1 0.68 0.61 0.64 1994 accuracy 0.64 3760 macro avg 0.64 0.64 0.64 3760 weighted avg 0.64 0.64 0.64 3760 Test classification report precision recall f1-score support -1 0.45 0.47 0.45 445 1 0.50 0.48 0.49 495 accuracy 0.47 940 macro avg 0.47 0.47 0.47 940 weighted avg 0.47 0.47 0.47 940
Das resultierende Modell hat eine schlechte Leistung auf der Validierungsstichprobe, es gibt eine Menge, was wir tun können, um es zu verbessern, aber im Augenblick wenden wir uns der Darstellung der vom Modell erzeugten Bedeutung des Merkmals zu.
importances = model.feature_importances_ feature_names = X_Train_latent.columns if hasattr(X_Train_latent, 'columns') else [f'feature_{i}' for i in range(X_Train_latent.shape[1])] # Create DataFrame and sort importance_df = pd.DataFrame({'feature': all_columns, 'importance': importances}) importance_df = importance_df.sort_values('importance', ascending=False) # Plot plt.figure(figsize=(8, 6)) plt.barh(importance_df['feature'], importance_df['importance'], color='red') plt.title('RFC Feature Importance (Gini Importance)') plt.xlabel('Importance Score') plt.gca().invert_yaxis() # Most important on top plt.show()
Ausgabe:
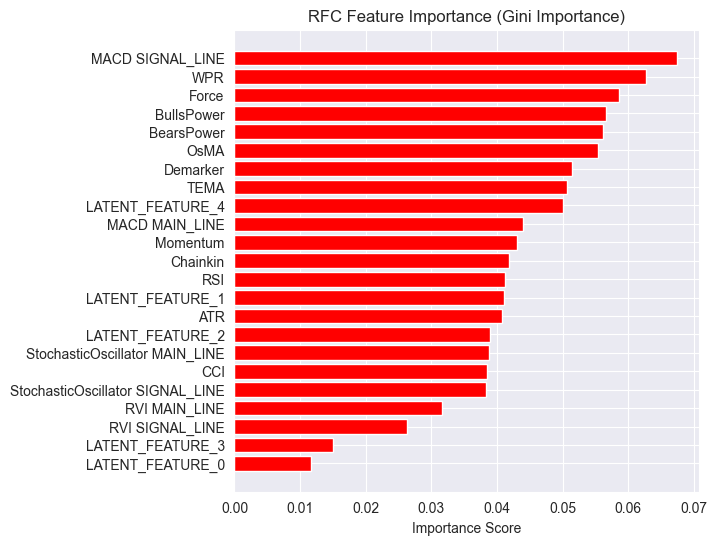
Latente Merkmale erweisen sich als wichtig für das Modell, d. h. sie enthalten bestimmte Muster und Informationen, die zu den Vorhersagen des Modells beitragen.
Der Grund für diese schwache Leistung des Modells könnte in der Art der verwendeten Zielvariablen liegen. Der Wert von 1 für die Vorausschau könnte falsch sein.
Wenn wir diese Indikatoren verwenden, um fundierte Handelsentscheidungen zu treffen, verwenden wir sie normalerweise nicht, um den nächsten Balken vorherzusagen. Wenn der RSI-Wert beispielsweise unter dem Schwellenwert von 30 (überverkauft) liegt, können wir sagen, dass der Markt in den nächsten paar Balken einen Aufwärtstrend erleben könnte. Nicht erst beim nächsten Balken, so wie wir unser Modell derzeit trainieren.
Legen wir also die Zielvariable mit dem Vorausschauwert 5 neu an.
lookahead = 5 df["future_close"] = df["Close"].shift(-lookahead) new_df = df.dropna() new_df["Direction"] = np.where(new_df["future_close"]>new_df["Close"], 1, -1) # if a the close value in the next bar(s)=lookahead is above the current close price, thats a long signal otherwise that's a short signal
Die Auswertung des Modells anhand von Trainings- und Validierungsdaten führt nun zu einem anderen Ergebnis.
Train classification report precision recall f1-score support -1 0.56 0.70 0.62 1706 1 0.69 0.54 0.61 2050 accuracy 0.61 3756 macro avg 0.62 0.62 0.61 3756 weighted avg 0.63 0.61 0.61 3756 Test classification report precision recall f1-score support -1 0.46 0.61 0.52 392 1 0.63 0.48 0.55 548 accuracy 0.54 940 macro avg 0.55 0.55 0.53 940 weighted avg 0.56 0.54 0.54 940
Und eine andere Darstellung der Bedeutung des Merkmals.
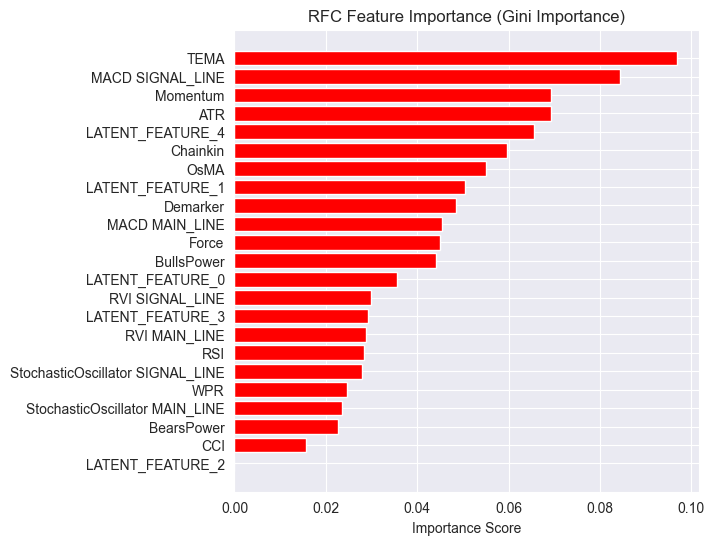
Das Modell hatte eine Gesamtgenauigkeit von 54 %, nicht gut, aber gut genug, um uns glauben zu machen, was wir auf dem Diagramm der Merkmalsbedeutung sehen.
Einige der vom LGMM erzeugten latenten Merkmale schafften es an die Spitze der prädiktivsten Merkmale des Modells.
LATENT_FEATURE_4 ist das fünftwichtigste Merkmal für den Random-Forest-Klassifikator, die übrigen latenten Merkmale wie LATENT_FEATURE_0 und LATENT_FEATURE_1 schnitten recht gut ab und übertrafen einige Rohindikatoren.
Insgesamt weisen die meisten von LGMM erzeugten Merkmale Muster auf, die für das Klassifizierungsmodell von Vorteil sind.
Mit diesen Informationen haben Sie nun einen Ausgangspunkt für das Verständnis des Indikators.
Die Anordnung der Farben ähnelt den verborgenen Merkmalen.
LGMM-basierter Handelsroboter
Innerhalb des Expert Advisors (EA) beginnen wir mit dem Import der erforderlichen Bibliotheken.
Dateiname: LGMM BASED EA.mq5
#include <Random Forest.mqh> #include <Arrays\ArrayString.mqh> #include <pandas.mqh> //https://www.mql5.com/en/articles/17030 #include <Trade\Trade.mqh> #include <Trade\PositionInfo.mqh> #include <Trade\SymbolInfo.mqh> #include <errordescription.mqh> CSymbolInfo m_symbol; CTrade m_trade; CPositionInfo m_position; CRandomForestClassifier rfc;
Auch hier müssen wir sicherstellen, dass wir dasselbe Symbol und denselben Zeitrahmen wie bei den Trainingsdaten verwenden.
#define MAGICNUMBER 11062025 input string SYMBOL = "XAUUSD"; input ENUM_TIMEFRAMES TIMEFRAME = PERIOD_D1; input uint LOOKAHEAD = 5; input uint SLIPPAGE = 100;
Wir initialisieren beide Modelle, LGMM und den Random-Forest-Klassifikator, innerhalb der Funktion OnInit.
int OnInit() { if (!MQLInfoInteger(MQL_DEBUG) && !MQLInfoInteger(MQL_TESTER)) { ChartSetSymbolPeriod(0, SYMBOL, TIMEFRAME); if (!SymbolSelect(SYMBOL, true)) { printf("%s failed to select SYMBOL %s, Error = %s",__FUNCTION__,SYMBOL,ErrorDescription(GetLastError())); return INIT_FAILED; } } //--- Loading the Gaussian Mixture model string filename = StringFormat("LGMM.%s.%s.onnx",SYMBOL, EnumToString(TIMEFRAME)); if (!lgmm.Init(filename, ONNX_COMMON_FOLDER)) { printf("%s Failed to initialize the GaussianMixture model (LGMM) in ONNX format file={%s}, Error = %s",__FUNCTION__,filename,ErrorDescription(GetLastError())); } //--- Loading the RFC model filename = StringFormat("rfc.%s.%s.onnx",SYMBOL,EnumToString(TIMEFRAME)); Print(filename); if (!rfc.Init(filename, ONNX_COMMON_FOLDER)) { printf("func=%s line=%d, Failed to Load the RFC in ONNX file={%s}, Error = %s",__FUNCTION__,__LINE__,filename,ErrorDescription(GetLastError())); return INIT_FAILED; } //... //... other lines of code //... }
In der Funktion getX rufen wir LGMM auf, um die latenten Merkmale vorzubereiten, die zusammen mit den Indikatordaten als endgültige Eingaben für das Random-Forest-Klassifizierungsmodell verwendet werden können.
vector getX(uint start=0, uint count=10) { //--- Get buffers CDataFrame df; for (uint ind=0; ind<indicators.Size(); ind++) //Loop through all the indicators { uint buffers_total = indicators[ind].buffer_names.Total(); for (uint buffer_no=0; buffer_no<buffers_total; buffer_no++) //Their buffer names resemble their buffer numbers { string name = indicators[ind].buffer_names.At(buffer_no); //Get the name of the buffer, it is helpful for the DataFrame and CSV file vector buffer = {}; if (!buffer.CopyIndicatorBuffer(indicators[ind].handle, buffer_no, start, count)) //Copy indicator buffer { printf("func=%s line=%d | Failed to copy %s indicator buffer, Error = %d",__FUNCTION__,__LINE__,name,GetLastError()); continue; } df.insert(name, buffer); //Insert a buffer vector and its name to a dataframe object } } if ((uint)df.shape()[0]==0) return vector::Zeros(0); //--- predict the latent features vector indicators_data = df.iloc(-1); //index=-1 returns the last row from the dataframe which is the most recent buffer from all indicators //--- Given the indicators let's predict the latent features vector latent_features = lgmm.predict(indicators_data).proba; if (latent_features.Size()==0) return vector::Zeros(0); return hstack(indicators_data, latent_features); //Return indicators data stacked alongside latent features }
Schließlich entwickeln wir eine einfache Handelsstrategie, die sich auf Handelssignale stützt, die vom Random-Forest-Klassifikator erzeugt werden.
void OnTick() { //--- Close trades after AI predictive horizon is over CloseTradeAfterTime(MAGICNUMBER, PeriodSeconds(TIMEFRAME)*LOOKAHEAD); //--- Refresh tick information if (!m_symbol.RefreshRates()) { printf("func=%s line=%s. Failed to copy rates, Error = %s",__FUNCTION__,ErrorDescription(GetLastError())); return; } //--- vector x = getX(); //Get all the input for the model if (x.Size()==0) return; long signal = rfc.predict(x).cls; //the class predicted by the random forest classifier double proba = rfc.predict(x).proba; //probability of the predictions double volume = m_symbol.LotsMin(); if (!PosExists(POSITION_TYPE_SELL, MAGICNUMBER) && !PosExists(POSITION_TYPE_BUY, MAGICNUMBER)) //no position is open { if (signal == 1) //If a model predicts a bullish signal m_trade.Buy(volume, SYMBOL, m_symbol.Ask()); //Open a buy trade else if (signal == -1) // if a model predicts a bearish signal m_trade.Sell(volume, SYMBOL, m_symbol.Bid()); //open a sell trade } }
Wir schließen Handelsgeschäfte, nachdem die LOOKAHEAD-Anzahl der Balken auf dem Zeitrahmen, auf dem das Modell trainiert wurde, vergangen ist. Der LOOKAHEAD-Wert muss mit dem Wert übereinstimmen, der bei der Erstellung der Zielvariablen im Trainingsskript verwendet wurde.
Konfigurationen des Testers
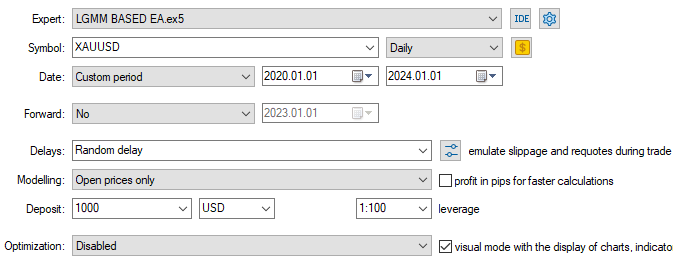
Eingänge
Ergebnisse des Testers
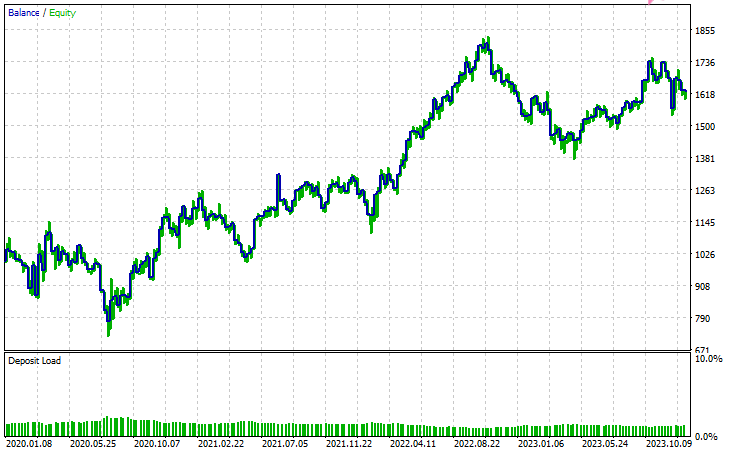
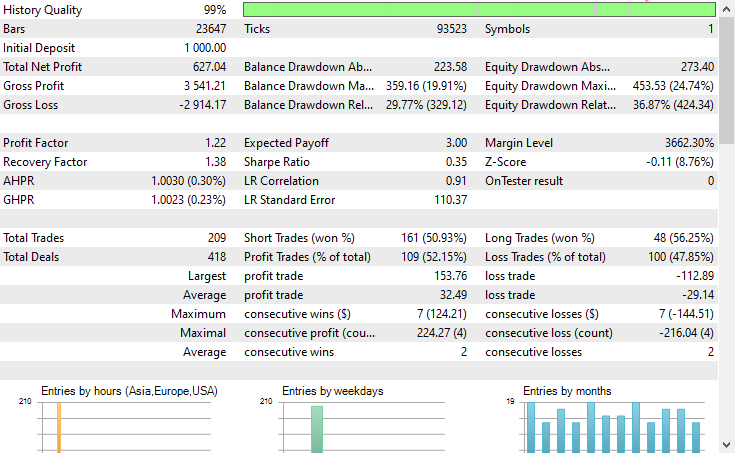
Schlussfolgerung
Das Latente Gaußsche Mischmodell (LGMM) ist ein geeignetes Verfahren, das uns aussagekräftige Merkmale liefert, die nicht beobachtbare Muster umfassen, die für Modelle des maschinellen Lernens oft nützlich sind. Wie alle anderen Modelle des maschinellen Lernens und Vorhersagetechniken hat sie jedoch auch einige Nachteile.
Latentes Gaußsches Mischmodell (LGMM): Übersicht
| Aspekt | Beschreibung |
|---|---|
| Was ist LGMM | Eine Methode zur Extraktion latenter (versteckter) Merkmale, die nicht beobachtbare Muster in Daten darstellen. Diese Merkmale können für Modelle des maschinellen Lernens nützlich sein. |
| Hauptvorteil | Erfasst sinnvolle verborgene Strukturen in Daten, die die Modellleistung verbessern können. |
Beschränkungen des LGMM
| Begrenzung | Erklärung |
|---|---|
| Geht von einer Gaußschen Verteilung aus | Das LGMM geht davon aus, dass jeder Datenpunkt einer multivariaten Normalverteilung folgt, was bei Finanzdaten, die in der Regel chaotisch und nichtlinear sind, selten der Fall ist. |
| Empfindlich auf Initialisierung | Das Modell erfordert eine sorgfältige Auswahl der Anzahl der Komponenten. Eine schlechte Initialisierung oder die Wahl falscher Parameter kann die Effektivität des Systems erheblich beeinträchtigen. |
| Schwer zu interpretierende Ergebnisse | Die dabei entstehenden latenten Merkmale sind schwer zu verstehen oder zu erklären. Da es sich um eine unbeaufsichtigte Methode handelt, werden die erkannten Muster nicht gekennzeichnet, sondern nur geclustert. |
| Empfindlich gegenüber Ausreißern | Gaußsche Verteilungen sind nicht robust gegenüber Ausreißern. Einige wenige Extremwerte können den Mittelwert verzerren und die Varianz aufblähen, wodurch die Ergebnisse des Modells verzerrt werden. |
Dieses Modell ist am nützlichsten, wenn es darum geht, die Dimensionen zu reduzieren (die Anzahl der Merkmale auf einige wenige aussagekräftige zu reduzieren) und neue Merkmale einzuführen, um das Modell mit mehr nützlichen Informationen anzureichern. Ich glaube, dass es am besten ist, sie auf diese Weise zu verwenden.
Mit freundlichen Grüßen.
Bleiben Sie dran und tragen Sie zur Entwicklung von Algorithmen für maschinelles Lernen für die Sprache MQL5 in diesem GitHub Repository bei.
Tabelle der Anhänge
| Dateiname | Beschreibung und Verwendung |
|---|---|
| Include\errordescription.mqh | Enthält die Beschreibung aller von MetaTrader 5 erzeugten Fehlercodes in der Sprache MQL5. |
| Include\Gaussian Mixture.mqh | Eine Bibliothek, die die Klasse für die Initialisierung und den Einsatz des im ONNX-Format gespeicherten Gaußschen Mischmodells enthält. |
| Include\pandas.mqh | Enthält eine Klasse zur Datenspeicherung und -manipulation, ähnlich wie Pandas in der Programmiersprache Python. |
| Include\Random Forest.mqh | Eine Bibliothek, die die Klasse für die Initialisierung und den Einsatz des Random-Forest-Klassifikators enthält, der im ONNX-Format gespeichert ist. |
| Indicators\LGMM Indicator.mq5 | Ein Indikator für die Anzeige latenter Merkmale, die durch das Latente Gaußsche Mischmodell (LGMM) erzeugt werden. |
| Scripts\Get XAUUSD Data.mq5 | Ein Skript zum Sammeln von Oszillator-Indikatoren und OHLCT-Werten aus MetaTrader 5 und zum Speichern in einer CSV-Datei. |
| Experts\LGMM BASED EA.mq5 | Ein Expert Advisor (EA), der auf der Grundlage der Vorhersagen des Random-Forest-Klassifikators unter Verwendung der Daten, d. h. der Kombination aus latenten Merkmalen, die von LGMM- und Oszillator-Indikatoren erzeugt werden, Trades eröffnet und schließt. |
| Python Code\main.ipynb | Ein Jupyter-Notebook (Python-Skript) für die Datenanalyse, das Training von Modellen des maschinellen Lernens usw. |
| Python Code\Trade\TerminalInfo.py | Es hat eine Klasse, die CTerminalInfo in MQL5 ähnelt, um Informationen über die ausgewählte MetaTrader 5 Desktop-Anwendung zu erhalten. |
| Python\requirements.txt | Enthält alle Python-Abhängigkeiten und ihre Versionsnummern, die in diesem Projekt verwendet werden. |
| Common\Files\* | Verfügt über ein CSV-Beispiel, das Trainingsdaten und einige ONNX-Modelldateien enthält, die in diesem Artikel verwendet werden, nur als Referenz. |
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/18497
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
Vom Neuling zum Experten: Animierte Nachrichtenüberschrift mit MQL5 (II)
Vom Neuling zum Experten: Animierte Nachrichtenüberschrift mit MQL5 (I)
Datenwissenschaft und ML (Teil 45): Forex Zeitreihenprognosen mit dem Modell PROPHET von Facebook
Umstellung auf MQL5 Algo Forge (Teil 3): Verwendung externer Repositories für die eigenen Projekte
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.