神经网络实践：绘制神经元

概述

大家好，欢迎阅读另一篇关于神经网络的文章。

在上一篇文章神经网络实践：伪逆（二）中，我讨论了专用计算系统的重要性及其发展背后的原因。在这篇关于神经网络的新文章中，我们将更深入地探讨这个主题。为这个阶段创建材料并不是一项简单的任务。尽管看起来很简单，但解释一些经常引起严重混淆的事情可能相当具有挑战性。

现阶段我们将涵盖哪些内容？在本系列中，我的目标是演示神经网络是如何学习的。到目前为止，我们已经探索了神经网络如何在不同数据点之间建立相关性。然而，到目前为止讨论的方法仅适用于处理预处理和过滤的数据集。这使得神经网络能够基于现有信息识别最优解。但是，当数据未经过滤时会发生什么？在这种情况下，神经网络如何建立相关性？这就是许多人错误地认为神经网络具有某种形式的智能的地方。他们认为它“学习”了如何以一种自主的、类似人类的方式对事物进行分类。

这种常见的误解使得解释神经网络特别具有挑战性。通常，那些试图理解它们的人缺乏如何对不同类型的信息进行排序的基本知识，即使数据之间存在某种关系。对于那些不使用它的人来说，这是最令人困惑的一点。因此，他们可能会误解解释，导致对神经网络如何运作的进一步困惑。

澄清一下，我并不是说神经网络以人类的方式学习。它们内心没有隐藏的智慧。任何持有相反观点的人都是错误的。神经网络只不过是一个复杂的数学方程。然而，该方程在分析和分类数据方面具有显著的能力。一旦对数据集进行了分类，任何与现有分类类似的新数据点将被赋予属于已知类别的概率。

这个概念在前面的文章中已经介绍过，但在这里，我们将采取一种略有不同的方法。这种方法既基础又有趣。我们将从绝对基础开始，逐步构建使用人工神经元的神经网络。

基础知识

为了真正理解神经网络在显示信息时是如何学习的，我要求你忘记你认为你知道的关于人工智能和神经网络的一切。您所（认为）知道的大部分内容可能纯属无稽之谈或错误信息，尤其是如果您在新闻网站或其他类似来源上看到它的话。神经网络的话题之所以进入公众视野，主要是因为一些企业家将其视为赚钱的机会，但神经网络已经发展了几十年。它们既不是新的，也不像人们经常描绘的那样运作。虽然非常有用，但它们主要与那些对编程有浓厚兴趣的人有关。

所有神经网络（有些人称之为人工智能）的核心都是基于前几篇文章中讨论的简单数学原理。在这里，我们将更详细地研究这个概念，这就是割线。不管别人怎么说，神经网络中的一切都归结为这个基本概念 — 找到一条近似切线的割线。事实上它非常简单。

在之前的讨论中，我们绕过了这一步，直接跳到识别切线。这解释了前面介绍的公式。这些公式是专门为缩短过程并直接到达切线而设计的。所有这些材料都与一个非常具体的事实有关：当我们在数据库中过滤、选择信息时，当这种情况发生时，我们不需要割线，我们直接去求切线，创建一个最能反映此数据集内容的公式。因此，当搜索程序查询此数据集时，它可以返回关于给定信息的近乎完美的结果。许多人将这种类型的程序称为人工智能。然而，在数据集不完整或非结构化的情况下，需要采用不同的方法。神经网络必须能够在看似无关的数据点之间建立相关性。这个过程称为训练。简单地说，我们有原始数据，最初似乎没有相关性。这些数据被系统地输入神经网络，神经网络逐渐学会近似切线。这个过程最终会产生一个数学方程，使人工智能系统能够生成有用的预测。当使用网络未知但由人类排序的数据来测试方程时，这一点得到了证实。

我不知道你是否理解了这一切是如何运作的，但我会尽力为那些还不是程序员但已经有金融市场工作经验的人更清楚地解释一下。当你开始在市场上工作时，你需要做的第一件事就是所谓的回溯测试。我们选择一个交易模型，转到图表并查找该模型出现的所有信号。这相当于神经网络的训练阶段。一旦模型经过一定时间的全面测试，我们将进入测试阶段。在这里，我们选择随机时间框架来验证模型是否仍然有效。如果我们能够始终如一地识别模型，即使它的模式不太明显，我们也能有效地将其内化，并用数学方法表达出来。最后一步是盲测。在这里，我们使用模拟账户进入市场，以评估我们的数学模型是否可靠。如果你以前这样做过，那么你就知道它永远不会 100% 准确，系统总是有误差的空间。无论如何，误差较小的模型被认为是有效的。

这正是神经网络试图实现的：制定一个方程，使其能够识别模式，无论是手写、面部识别、分子结构、植物物种、动物、声音、图像还是任何其他形式的分类。

现在，让我们继续下一个主题，探索如何实现这一目标。

神经元

现在我们已经介绍了上一个主题，让我们从可以创建的最简单的东西开始：单个神经元。但是，不要低估它的重要性。虽然我们将从一个神经元开始，但复杂性将迅速升级。因此，我鼓励你们有条不紊地进行，在我们进行的过程中了解每个组成部分。当我们开始构建整个神经网络架构时，这种渐进的方法将是至关重要的。

那么，让我们从以下代码开始。

//+------------------------------------------------------------------+
#property copyright "Daniel Jose"
//+------------------------------------------------------------------+
void OnStart()
{
    Print("The first neuron...");
}
//+------------------------------------------------------------------+

这个看似无趣的代码只是向终端打印一条消息。就是这样！但请记住，这是一个脚本，尽管它可以成为一个服务。现在，我们将把它作为一个简单的脚本。那么，神经元应该做什么呢？你可以想到一千件不同的事情，但试着把它们归结为一个共同的目标。这是第一部分，一切都归结为神经元必须执行的一项任务。

神经元需要知道如何执行计算。这很重要，因为它必须返回一些信息。然而，我们还不知道这些计算是什么，我们只有训练神经元所需的数据。因此，上面的代码被修改并变成了下面显示的代码。

//+------------------------------------------------------------------+
#property copyright "Daniel Jose"
//+------------------------------------------------------------------+
void OnStart()
{
    double Train[][2] {
                        {0, 0},
                        {1, 2},
                        {2, 4},
                        {3, 6},
                        {4, 8},
                      };

    Print("The first neuron...");
}
//+------------------------------------------------------------------+

显然，只需查看训练数据，就会立即清楚其中存在某种模式。也就是说，我们将第一个数字乘以 2。但我们的神经元还不知道这一点。我们想要的是让它学习如何推导一个方程，这样当给定一个数字时，它就可以提供正确的答案。然后，神经元将使用它创建的方程，根据它所学到的知识生成输出。

听起来不错，但我们如何让神经元发现这个公式呢？这里有一个问题：我们不能只使用以前文章中的知识。那么，亲爱的读者，我们如何让神经元找到最能代表训练数据的方程呢？

这就是许多人容易感到困惑的地方。我们要做的就是简单地告诉神经元从一个随机值开始，并以此为基础找到正确的数学方程。这是一个关键的误解点。我们并没有告诉神经元搜索乘法中应该使用的确切数字。毕竟，我们可以使用加法、除法，甚至随机数据。我们真正想要的是神经元找到一个方程，而不仅仅是一个值。我们让它使用的初始值只不过是一个起点，仅此而已。现在，让我们进一步优化我们的代码，如下所示。

//+------------------------------------------------------------------+
#property copyright "Daniel Jose"
//+------------------------------------------------------------------+
#define macroRandom (rand() / (double)SHORT_MAX)
//+------------------------------------------------------------------+
void OnStart()
{
    double Train[][2] {
                        {0, 0},
                        {1, 2},
                        {2, 4},
                        {3, 6},
                        {4, 8},
                      };
    double weight;

    Print("The first neuron...");
    MathSrand(512);
    weight = (double)macroRandom;
}
//+------------------------------------------------------------------+

好的，我们正在取得进展！但在继续之前，让我们先讨论一些重要的事情。通常，在使用 MathSrand 函数时，我们使用系统时钟中的值对其进行初始化。这确保了每次启动随机数生成器时，它都从不同的点开始。只是一个简短的提醒：生成的数字不是真正的随机数字，它们是伪随机的。这意味着，尽管它们不是完全随机的，但很难预测序列中的下一个数字。由于我们想控制起点，我们明确地向 MathSrand 提供了一个初始值，从而允许更一致的测试。现在，这里真正重要的是存储在变量 “weight” 中的值。这个值告诉我们的神经元是否在正确的轨道上。由于它以随机值开始，因此还没有定义方向。

这是另一个关键点：weight（权重）值在 0 和 1 之间。这是因为，在我们的宏中，'rand' 函数的结果除以了其最大可能返回值。您可以查看文档以了解更多详细信息。我将权重限制在这个范围内以简化接下来的步骤。但是，如果你愿意，你可以自由使用原始随机值；请注意，稍后我们探索进一步的计算时，需要进行一些调整。

现在，让我们开始实现目标吧！我们的神经元开始成形。但在我们继续前进之前，我们首先需要为它定义一个初始的数学公式。没有什么是从无到有的 — 我们必须告诉神经网络它应该如何运作。它不能从零开始创造自己。如果你对数学计算有基本的了解，你就会知道，从最简单的方程到最复杂的多项式，一切都可以简化为一个基本概念。我讲的是导数。但我们所需要的并不是任何导数 — 我们需要的是尽可能简单的导数。在之前的文章中，我证明了直线方程是最简单的方程。任何多项式或方程，当微分到其最基本的形式时，都可以简化为这个线性方程。如果我们继续微分，我们最终可能会得到一个常数。但这对我们没有用，我们需要的是一个作为最小计算工具的导数。这让我们回到下面所示的方程式。

在这个阶段，导数的顺序并不重要。重要的是，如果我们简化得太多，我们最终会得到一个常数，在这种情况下这是无用的。然而，常数 < b >（截距）现在应该被视为零。同时，常数< a >（斜率）将被设置为权重中存储的值。通过这种方法，我们现在可以进一步优化我们的代码，如下所示：

//+------------------------------------------------------------------+
#property copyright "Daniel Jose"
//+------------------------------------------------------------------+
#define macroRandom (rand() / (double)SHORT_MAX)
//+------------------------------------------------------------------+
void OnStart()
{
    double Train[][2] {
                        {0, 0},
                        {1, 2},
                        {2, 4},
                        {3, 6},
                        {4, 8},
                      };
    double weight, fx, x;

    Print("The first neuron...");
    MathSrand(512);
    weight = (double)macroRandom;

    for (uint c = 0; c < Train.Size() / 2; c++)
    {
        x = Train[c][0];
        fx = x * weight;
        Print("Actual: ", fx , " expected: ", x);
    }
}
//+------------------------------------------------------------------+

运行此代码后，您将在 MetaTrader 终端中看到一个类似于下图所示的图像。

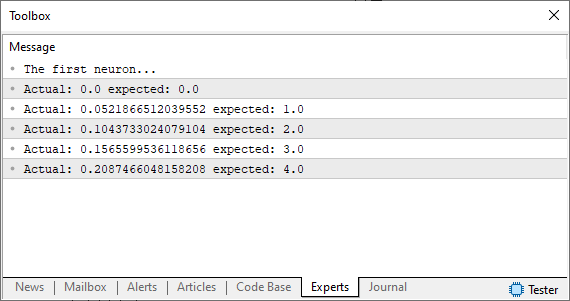
请注意，我们使用的是一个假设，这是一个与我们想要或期望得到的随机数不同的随机数。我们如何才能改善这种情况？好了，我们的基本神经元正在路上。现在我们需要使用与前几篇文章中相同的原则。换句话说，我们将定义一个误差系统，以便神经元知道在哪里移动以找到最合适的方程。这很容易做到，如下面的代码所示。

//+------------------------------------------------------------------+
#property copyright "Daniel Jose"
//+------------------------------------------------------------------+
#define macroRandom (rand() / (double)SHORT_MAX)
//+------------------------------------------------------------------+
void OnStart()
{
    double Train[][2] {
                        {0, 0},
                        {1, 2},
                        {2, 4},
                        {3, 6},
                        {4, 8},
                      };
    double weight, fx, dx, x, err;
    const uint nTrain = Train.Size() / 2;

    Print("The first neuron...");
    MathSrand(512);
    weight = (double)macroRandom;
    err = 0;
        
    for (uint c = 0; c < nTrain; c++)
    {
        x = Train[c][0];
        fx = x * weight;
        Print("Actual: ", fx , " expected: ", x);
        dx = fx - Train[c][1];
        err += MathPow(dx, 2);
    }
    Print("Err: ", err / nTrain);
}
//+------------------------------------------------------------------+

好吧，当你运行这段代码时，你应该看到类似于下图的东西。

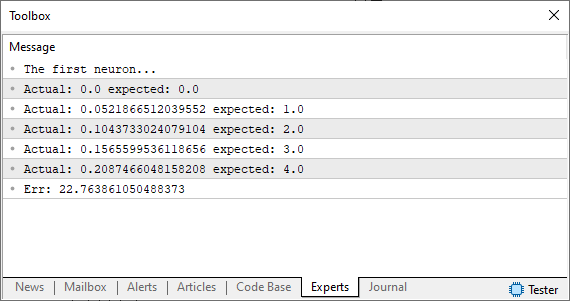
此刻，我们正处在一个十字路口。这正是以前我们必须手动调整值以尽量减少误差的时刻。如果你不确定我的意思，请查看前面的文章以了解背景。然而，这次我们不会像以前那样手动调整，而是让电脑来做这项工作。我们将使用割线来接近切线，而不是像以前那样找到切线。这就是事情开始变得有趣的地方 — 机器现在将开始“疯狂”，因为它在寻找最合适的东西。有时，它会收敛到正确的解，而在其他时候，它会完全发散。

我们的目标是减少变量 “err” 的值。这就是导致机器不可预测行为的原因。为了更好地理解这一点，让我们转向一个新的话题。

使用割线

在文章“神经网络实践：割线“中，我简要提到过割线在神经网络中起着根本性的作用。在那里，我展示了一张图表，您可以在下面查看。

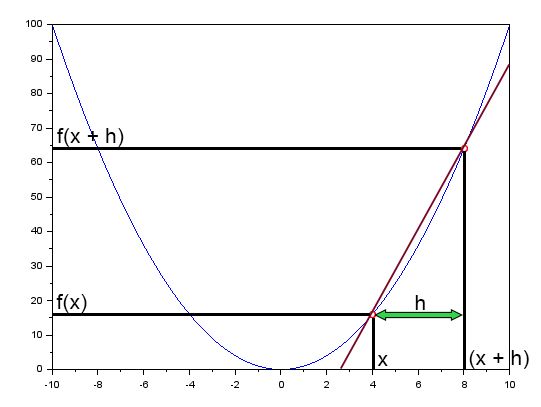
此图沿直线显示了误差曲线。这就是割线。通过简化图表并仅保留割线，我们得到了下面显示的图像。

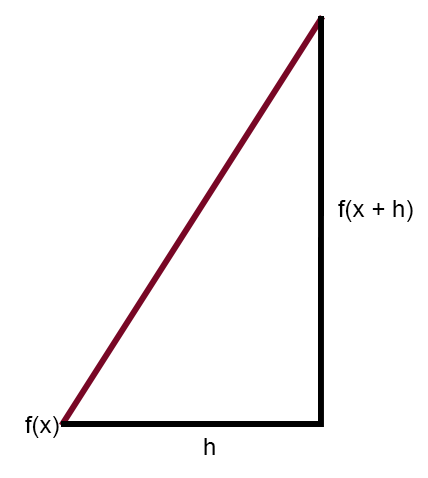
现在，如果修改此图使得常数 < h > 等于零，则会得到以下表达式：

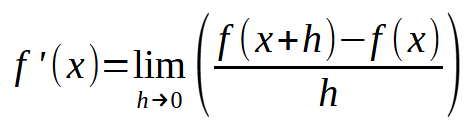
这就是它变得令人兴奋的地方。上述公式本质上是一个“神奇公式”，它允许神经网络从误差中学习。通过应用这个方程，我们可以迫使计算机找到表示输入数据的最佳拟合线。这使机器能够学习如何解决给定的问题，无论它是什么。无论你向神经网络输入什么数据，底层计算都是一样的。但请密切注意：关键是为 < h > 选择合适的值。如果该值超过某个限制，机器将“疯狂”地试图找到最佳的直线方程。如果该值太小，机器将花费大量时间搜索最佳拟合方程，因此在这件事上有一点常识并没有坏处。因此，这里需要一点良好的判断力。不要要求过高，但也不要太粗心。找到一个平衡的方法。

现在，我们如何将其整合到我们的神经元中？在做出任何更改之前，让我们先做一个小测试。下面是我们更新后的代码应该是什么样子的。

//+------------------------------------------------------------------+
#property copyright "Daniel Jose"
//+------------------------------------------------------------------+
#define macroRandom (rand() / (double)SHORT_MAX)
//+------------------------------------------------------------------+
double Train[][2] {
                    {0, 0},
                    {1, 2},
                    {2, 4},
                    {3, 6},
                    {4, 8},
                  };
//+------------------------------------------------------------------+
const uint nTrain = Train.Size() / 2;
const double eps = 1e-3;
//+------------------------------------------------------------------+
double Cost(const double w)
{
    double err;

    err = 0;
    for (uint c = 0; c < nTrain; c++)
        err += MathPow((Train[c][0] * w) - Train[c][1], 2);

    return err / nTrain;
}
//+------------------------------------------------------------------+
void OnStart()
{
    double weight;

    Print("The first neuron...");
    MathSrand(512);
    weight = (double)macroRandom;

    Print("Err: ", Cost(weight));
    Print("Err: ", Cost(weight + eps));
}
//+------------------------------------------------------------------+

哇！现在，这开始感觉像是一个真正的程序。当你运行它时，你应该看到类似于下图的东西。

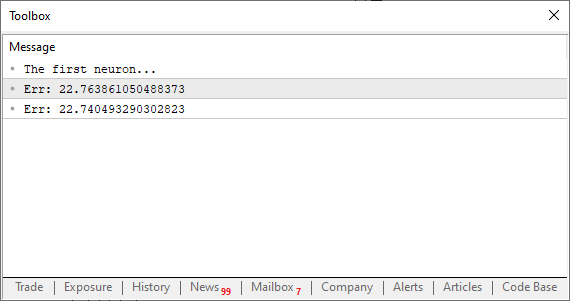
在这个阶段，真正重要的是误差值是减小还是增大。实际数值本身并不重要。现在，请密切注意：变量“eps”对应于我们之前在公式中看到的 <h>。这个值越接近零，每次迭代就越接近切线。这是因为割线将开始向极限点收敛。那么，我们的下一步是什么？一些非常简单的事情：我们需要创建一个循环，不断减少每次迭代的错误（或成本）。最终，我们将达到一个错误停止减少并开始增加的点。在那个确切的时刻，程序应该检测到这种变化并退出循环。否则，我们就有可能陷入无限循环。或者，我们可以引入另一种类型的保护措施来防止无限循环。一种常见的方法是限制迭代次数，确保程序在无法收敛或开始“疯狂”时停止。如果步长选择不当，可能会出现这种不稳定性。我们稍后将更详细地探讨这个问题。所以现在，不要太担心。也就是说，你可以自由地微调程序，以追求尽可能低的成本价值。何时结束循环完全取决于你。但为了简单起见，让我们看看这在实践中是什么样子的。查看下面的代码，了解它是如何工作的。

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. #define macroRandom (rand() / (double)SHORT_MAX)
05. //+------------------------------------------------------------------+
06. double Train[][2] {
07.                     {0, 0},
08.                     {1, 2},
09.                     {2, 4},
10.                     {3, 6},
11.                     {4, 8},
12.                   };
13. //+------------------------------------------------------------------+
14. const uint nTrain = Train.Size() / 2;
15. const double eps = 1e-3;
16. //+------------------------------------------------------------------+
17. double Cost(const double w)
18. {
19.     double err;
20. 
21.     err = 0;
22.     for (uint c = 0; c < nTrain; c++)
23.         err += MathPow((Train[c][0] * w) - Train[c][1], 2);
24. 
25.     return err / nTrain;
26. }
27. //+------------------------------------------------------------------+
28. void OnStart()
29. {
30.     double weight, err;
31. 
32.     Print("The first neuron...");
33.     MathSrand(512);
34.     weight = (double)macroRandom;
35. 
36.     for(ulong c = 0; c < 10; c++)
37.     {
38.         err = ((Cost(weight + eps) - Cost(weight)) / eps);
39.         weight -= (err * eps);
40.         Print(c, "  -->  ", weight, " :: ", err);
41.     }
42.     Print("Weight: ", weight);
43. }
44. //+------------------------------------------------------------------+

运行此代码时，您将在终端中看到与下图类似的内容。

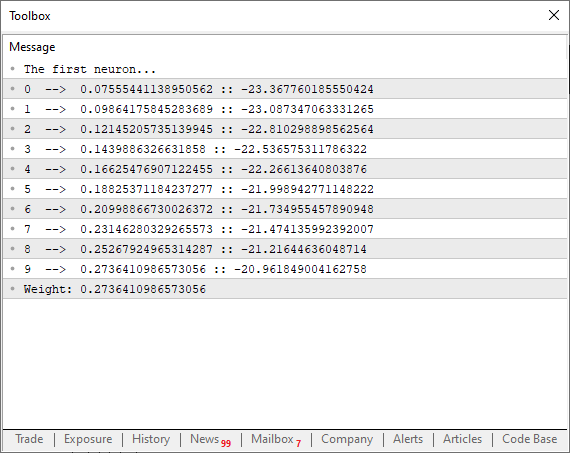
现在，仔细看看一个有趣的细节。在第 38 行，我们正在执行前面讨论的精确计算，在那里我们强制割线搜索最低可能极限，帮助函数收敛。然而，在第 39 行中，请注意，我们不仅仅是使用原始误差或总成本值来调整曲线点。但是为什么呢？如果我们这样做，程序将开始沿着函数的曲线混乱地来回跳跃。而这并不是我们想要的。我们需要平稳和可控的调整。但是为什么不使用“eps”来微调抛物线上的下一个点呢？好吧，如果我们这样做了，我们必须不断检查误差是在增加还是在减少。如果我们应用第 39 行中的因式分解，这将变得完全不必要。这种方法还有另一个优点，因为它迫使神经元在过程开始时更快地收敛。然后，当它接近理想值时，衰减曲线会平滑，表现得像一个倒对数衰减函数。这真的很棒！这意味着我们将更快地达到最佳误差值。

但我们可以让这段代码变得更好！我们可以添加额外的分析工具来更好地了解正在发生的事情。同时，我们可以引入一个额外的测试，允许循环在达到最小收敛点后立即终止，甚至在达到最大迭代次数之前。考虑到这一点，以下是代码的改进版本：

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. #define macroRandom (rand() / (double)SHORT_MAX)
05. //+------------------------------------------------------------------+
06. double Train[][2] {
07.                     {0, 0},
08.                     {1, 2},
09.                     {2, 4},
10.                     {3, 6},
11.                     {4, 8},
12.                   };
13. //+------------------------------------------------------------------+
14. const uint nTrain = Train.Size() / 2;
15. const double eps = 1e-3;
16. //+------------------------------------------------------------------+
17. double Cost(const double w)
18. {
19.     double err;
20. 
21.     err = 0;
22.     for (uint c = 0; c < nTrain; c++)
23.         err += MathPow((Train[c][0] * w) - Train[c][1], 2);
24. 
25.     return err / nTrain;
26. }
27. //+------------------------------------------------------------------+
28. void OnStart()
29. {
30.     double weight, err, e1;
31.     int f = FileOpen("Cost.csv", FILE_COMMON | FILE_WRITE | FILE_CSV);
32. 
33.     Print("The first neuron...");
34.     MathSrand(512);
35.     weight = (double)macroRandom;
36. 
37.     for(ulong c = 0; (c < ULONG_MAX) && ((e1 = Cost(weight)) > eps); c++)
38.     {
39.         err = (Cost(weight + eps) - e1) / eps;
40.         weight -= (err * eps);
41.         if (f != INVALID_HANDLE)
42.             FileWriteString(f, StringFormat("%I64u;%f;%f\n", c, err, e1));
43.     }
44.     if (f != INVALID_HANDLE)
45.         FileClose(f);
46.     Print("Weight: ", weight);
47. }
48. //+------------------------------------------------------------------+

这段代码的美妙之处在于，它的实验非常有趣。它的设计使您可以研究、调整和使用它。我决定不将值输出到 MetaTrader 5 终端，而是输出到一个文件中。这样，我们可以生成一个图表，更仔细地分析正在发生的事情。在当前配置下，结果图如下：

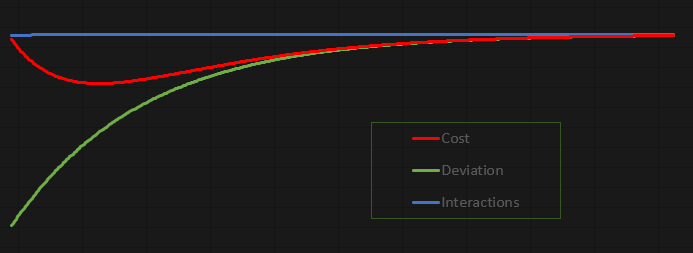
该图表是在 Excel 中创建的，基于神经元生成的文件中存储的值。现在，我承认创建文件的方式有点笨拙。但由于这是一项教育性和有趣的练习，我认为我们如何将数据传输到文件中没有问题。

最后的探讨

在这篇文章中，我们构建了一个基本的神经元。当然，这很简单，有些人可能会认为代码太基本或毫无意义。但我希望您，我的读者，能玩得开心。不要害怕修改代码，完全理解它才是目标。代码已附上，这样你就可以探索一个简单的神经元是如何工作的。慢慢阅读这篇文章。尝试从头开始键入代码，而不是复制粘贴。测试每个步骤，直到达到最终版本。不要只是复制我的方法，而是以一种对你有意义的方式构建它。关键是要实现相同的最终结果：找到数组中训练数据之间的相关性。事实上它非常简单。

由于代码包含在附件中，因此您可以尝试进行一些有趣的修改。记住要冷静地检查每一个修改。第一个元素是训练数组，位于应用程序代码的第六行。你可以把不同的值放在那里，让神经元尝试找到它们之间的相关性。

另一个非常有趣的点是第 15 行常量值的变化。将其更改为更高或更低的值，并观察神经元在工作结束时报告的结果。您会注意到，较低的值需要更长的时间来处理，但结果将更接近理想值。

另一个同样有趣的点是第 35 行，在那里我们分配了一个在 0 和 1 之间波动的权重。您可以通过将宏返回的值相乘来更改它。例如，试着把这样的东西放在第 35 行。

weight = (double)macroRandom * 50;

你会注意到，一切都会完全不同，仅仅是因为你改变了神经元开始的初始权重。当你完全确定发生了什么时，你可以将第 34 行中的代码更改为下面显示的代码。

MathSrand(GetTickCount()); 

你会注意到，一切都比许多人想象的有趣得多。但最重要的是，你将开始了解神经网络中的单个神经元是如何学习的。在下一篇文章中，我们将把这个神经元变成更有趣的东西。因此，在继续阅读下一篇文章之前，请研究这段代码并进行实验。因为这仅仅是一个开始。