
Neuronale Netze leicht gemacht (Teil 53): Aufteilung der Belohnung
Einführung
Wir studieren weiterhin die Methoden des Reinforcement Learning bzw. des Verstärkungslernens. Wie Sie wissen, basieren alle Algorithmen zum Trainieren von Modellen in diesem Bereich des maschinellen Lernens auf dem Paradigma der Maximierung von Belohnungen aus der Umwelt. Die Belohnungsfunktion spielt eine Schlüsselrolle bei der Modellbildung. Seine Signale sind in der Regel ziemlich zweideutig.
Um einen Anreiz für den Agenten zu schaffen, das gewünschte Verhalten zu zeigen, führen wir zusätzliche Boni und Strafen in die Belohnungsfunktion ein. Zum Beispiel haben wir die Belohnungsfunktion oft komplexer gestaltet, um den Agenten zu ermutigen, die Umgebung zu erkunden, und Strafen für Untätigkeit eingeführt. Gleichzeitig bleiben die Architektur des Modells und die Belohnungsfunktion das Ergebnis der subjektiven Überlegungen des Modellarchitekten.
Während der Ausbildung kann das Modell auch bei sorgfältiger Planung auf verschiedene Schwierigkeiten stoßen. Es kann sein, dass der Agent aus vielen verschiedenen Gründen nicht die gewünschten Ergebnisse erzielt. Aber wie können wir verstehen, dass der Agent unsere Signale in der Belohnungsfunktion richtig interpretiert? Um dieses Problem zu verstehen, wird versucht, die Belohnung in verschiedene Komponenten aufzuteilen. Die Verwendung von aufgeteilten (decomposed) Belohnungen und die Analyse des Einflusses einzelner Komponenten kann sehr nützlich sein, um Wege zur Optimierung des Modelltrainings zu finden. So können wir besser verstehen, wie verschiedene Aspekte das Verhalten des Agenten beeinflussen, die Ursachen von Problemen ermitteln und die Modellarchitektur, den Trainingsprozess oder die Belohnungsfunktion effektiv anpassen.
1. Die Notwendigkeit der Aufteilung von Belohnungen
Die Funktion der Aufteilung von Belohnungswerten ist eine einfache und weithin anwendbare Methode, die eine Vielzahl von Herausforderungen bewältigen kann. Beim Verstärkungslernen erhält der Agent eine Belohnung, die sich oft aus mehreren Komponenten zusammensetzt. Jedes dieser Elemente soll einen Aspekt des gewünschten Verhaltens des Agenten kodieren. Aus dieser zusammengesetzten Belohnung lernt der Agent eine einzige komplexe Wichtigkeitsfunktion. Mit Hilfe der Werteaufteilung lernt der Agent eine Wichtigkeitsfunktion für jede Belohnungskomponente. Jede einzelne Funktion, die von ihnen übernommen wird, hat höchstwahrscheinlich eine einfachere Form.
Zur Optimierung der Strategie wird die zusammengesetzte Wichtigkeitsfunktion durch eine gewichtete Summe der einzelnen Wichtigkeitsfunktionen rekonstruiert.
Die Aufteilung von Belohnungen kann in einer Vielzahl verschiedener Methoden enthalten sein, einschließlich der hier betrachteten Actor-Critic-Familie.
Die zusätzlichen Diagnose- und Trainingsmöglichkeiten durch die Aufteilung der Belohnung werden jedoch durch eine komplexere Vorhersageaufgabe erkauft: Anstatt eine einzige Wichtigkeitsfunktion zu trainieren, sollten mehrere Funktionen trainiert werden. Die Analyse des Einflusses dieses Faktors auf die Leistung des Agenten wird in dem Artikel „Value Function Decomposition for Iterative Design of Reinforcement Learning Agents“ durchgeführt. Die Autoren des Artikels fanden heraus, dass die Trainingsergebnisse des Modells schlechter sind als die des ursprünglichen Algorithmus, wenn man dem Soft Actor-Critic-Algorithmus die Aufteilung der Belohnungsfunktion hinzufügt. Die Autoren schlagen jedoch Möglichkeiten zur Verbesserung des Algorithmus vor. Dadurch konnten wir die Leistung des ursprünglichen Soft Actor-Critic-Algorithmus nicht nur erreichen, sondern manchmal sogar übertreffen. Diese Verbesserungen können auf die Aufteilung von Belohnungsfunktionen und auf andere Algorithmen der Actor-Critic-Familie angewendet werden.
Die zahlreichen Algorithmen des Reinforcement Learning können so angepasst werden, dass sie eine Aufteilung der Belohnungsfunktion nach dem folgenden Muster verwenden:
- Ändern wir das Q-Funktionsmodell so, dass wir am Ausgang des Modells ein Element für jede Komponente der Belohnungsfunktion erhalten.
- Wir verwenden den grundlegenden Q-Funktions-Lernalgorithmus, um jede Komponente zu aktualisieren.
Dieses Muster gilt sowohl für diskrete als auch für kontinuierliche Algorithmen zum Lernen von Aktionsraummodellen.
Die Idee ist ganz einfach. Aber wie bereits erwähnt, entdeckten die Autoren des Artikels die Ineffizienz der „Kopf-an-Kopf-Lösung“ bei der Verwendung der Reward-Decomposition im Rahmen des Soft Actor-Critic-Algorithmus. Ich möchte Sie an die Optimierungsgleichungen für die Q-Funktion in diesem Algorithmus erinnern.
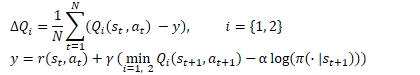
Hier sehen wir die Verwendung der minimalen Schätzung des zukünftigen Zustands aus den beiden Zielmodellen der Kritiker. Wie in Punkt 2 des Musters angegeben, verwenden wir den grundlegenden Algorithmus, um die Parameter der einzelnen Komponenten der Q-Funktion zu aktualisieren. Die Praxis hat jedoch gezeigt, dass die Verwendung eines komponentenweisen Mindestwerts zu einer Unausgewogenheit des Modells führt. Die Auswahl eines Modells mit der geringsten Gesamtpunktzahl ist effizienter, ebenso wie die Verwendung der Komponentenschätzungen zum Trainieren von Modellen.
Im Allgemeinen wird davon ausgegangen, dass die Belohnungsfunktion des Modells eine lineare Funktion seiner Komponenten ist.
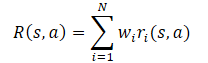
Die Anwendung der Linearität des Erwartungswertes zeigt, dass die Q-Funktion die lineare Struktur der Belohnungsfunktion erbt.
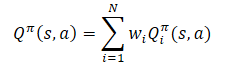
Wenn nicht anders angegeben, nehmen wir an, dass Wi=1 für alle i. Da die Gewichte der Komponenten aus der Q-Funktion herausgenommen werden, können sie geändert werden, ohne die Zielprognose der Komponente zu verändern. So kann die Politik für jede beliebige Kombination von Gewichten bewertet werden.
Der zweite Punkt, den es zu beachten gilt, ist, dass die Optimierung der Funktion der aufgeteilten Belohnungen eine Optimierung des Modells nach vielen Kriterien ist. Sie weist Probleme auf, die für die multikriterielle Optimierung charakteristisch sind: widersprüchliche Gradienten, starke Krümmung und große Unterschiede in den Gradientenwerten. Um die negativen Auswirkungen dieses Faktors zu minimieren, schlagen die Autoren der Methode vor, den Conflict-Averse Gradient Descent (CAGrad) Gradienten zu verwenden, der für eine Multi-Task-Verstärkungslernumgebung entwickelt wurde. Diese Methode zielt darauf ab, die oben genannten Probleme der Mehrzieloptimierung zu entschärfen. Die Grundidee besteht darin, den Gradienten einer Multi-Task-Zielfunktion durch eine gewichtete Summe der Gradienten für jede einzelne Aufgabe zu ersetzen. Zu diesem Zweck wird das folgende Optimierungsproblem gelöst:
![]()
wobei d ein Aktualisierungsvektor ist,
g₀ — durchschnittliche Steigung,
с — Konvergenzkoeffizient im Bereich [0, 1).
Die Lösung dieses Optimierungsproblems ermöglicht es uns, den Einfluss der einzelnen Komponenten auf die Optimierung zu berücksichtigen und uns darauf zu konzentrieren, die schlechteste Schätzung in jedem Schritt zu verbessern.
2. Implementierung mit MQL5
2.1 Erstellen einer neuen Modellklasse
Wir implementieren unsere Version der Aufteilung der Belohnungsfunktion auf der Grundlage des Algorithmus SAC+DICE. Aufgrund der Besonderheiten der Algorithmus-Implementierung werden wir nicht von der im vorherigen Artikel erstellten Klasse CNet_SAC_DICE erben. Aber wir werden die bisherigen Entwicklungen weiter nutzen. Wir werden die Klasse CNet_SAC_D_DICE ähnlich wie CNet_SAC_DICE erstellen. Die Struktur der neuen Klasse ist im Folgenden dargestellt.
class CNet_SAC_D_DICE : protected CNet { protected: CNet cActorExploer; CNet cCritic1; CNet cCritic2; CNet cTargetCritic1; CNet cTargetCritic2; CNet cZeta; CNet cNu; CNet cTargetNu; vector<float> fLambda; vector<float> fLambda_m; vector<float> fLambda_v; int iLatentLayer; float fCAGrad_C; int iCAGrad_Iters; int iUpdateDelay; int iUpdateDelayCount; //--- float fLoss1; float fLoss2; vector<float> fZeta; vector<float> fQWeights; //--- vector<float> GetLogProbability(CBufferFloat *Actions); vector<float> CAGrad(vector<float> &grad); public: //--- CNet_SAC_D_DICE(void); ~CNet_SAC_D_DICE(void) {} //--- bool Create(CArrayObj *actor, CArrayObj *critic, CArrayObj *zeta, CArrayObj *nu, int latent_layer = -1); //--- virtual bool Study(CArrayFloat *State, CArrayFloat *SecondInput, CBufferFloat *Actions, vector<float> &Rewards, CBufferFloat *NextState, CBufferFloat *NextSecondInput, float discount, float tau); virtual void GetLoss(float &loss1, float &loss2) { loss1 = fLoss1; loss2 = fLoss2; } virtual bool TargetsUpdate(float tau); //--- virtual void SetQWeights(vector<float> &weights) { fQWeights=weights; } virtual void SetCAGradC(float c) { fCAGrad_C=c; } virtual void SetLambda(vector<float> &lambda) { fLambda=lambda; fLambda_m=vector<float>::Zeros(lambda.Size()); fLambda_v=fLambda_m; } virtual void TargetsUpdateDelay(int delay) { iUpdateDelay=delay; iUpdateDelayCount=delay; } //--- virtual bool Save(string file_name, bool common = true); bool Load(string file_name, bool common = true); };
Die geliehenen Modellobjekte können wir in der bereitgestellten Klassenstruktur sehen. Anstelle von Variablen zur Speicherung des Lagrange-Koeffizienten und seiner Mittelwerte werden wir jedoch Vektoren verwenden, deren Größe der Anzahl der Komponenten der Belohnungsfunktion entspricht. Hier fügen wir den Vektor fQWeights hinzu, um die Gewichtungskoeffizienten der einzelnen Komponenten zu speichern. Wir wählen die Variable fCAGrad_C, um den Konvergenzkoeffizienten der CAGrad-Methode zu erfassen.
Natürlich werden diese Änderungen im Klassenkonstruktor berücksichtigt. In der Anfangsphase initialisieren wir alle Vektoren mit einer Einheitslänge.
CNet_SAC_D_DICE::CNet_SAC_D_DICE(void) : fLoss1(0), fLoss2(0), fCAGrad_C(0.5f), iCAGrad_Iters(15), iUpdateDelay(100), iUpdateDelayCount(100) { fLambda = vector<float>::Full(1, 1.0e-5f); fLambda_m = vector<float>::Zeros(1); fLambda_v = vector<float>::Zeros(1); fZeta = vector<float>::Zeros(1); fQWeights = vector<float>::Ones(1); }
Die Methode zur Initialisierung einer Klasse und zur Erstellung verschachtelter Modelle wurde ohne wesentliche Änderungen aus dem früheren Artikel übernommen. Die Änderungen betreffen nur die Vektorgrößen.
bool CNet_SAC_D_DICE::Create(CArrayObj *actor, CArrayObj *critic, CArrayObj *zeta, CArrayObj *nu, int latent_layer = -1) { ResetLastError(); //--- if(!cActorExploer.Create(actor) || !CNet::Create(actor)) { PrintFormat("Error of create Actor: %d", GetLastError()); return false; } //--- if(!opencl) { Print("Don't opened OpenCL context"); return false; } //--- if(!cCritic1.Create(critic) || !cCritic2.Create(critic)) { PrintFormat("Error of create Critic: %d", GetLastError()); return false; } //--- if(!cZeta.Create(zeta) || !cNu.Create(nu)) { PrintFormat("Error of create function nets: %d", GetLastError()); return false; } //--- if(!cTargetCritic1.Create(critic) || !cTargetCritic2.Create(critic) || !cTargetNu.Create(nu)) { PrintFormat("Error of create target models: %d", GetLastError()); return false; } //--- cActorExploer.SetOpenCL(opencl); cCritic1.SetOpenCL(opencl); cCritic2.SetOpenCL(opencl); cZeta.SetOpenCL(opencl); cNu.SetOpenCL(opencl); cTargetCritic1.SetOpenCL(opencl); cTargetCritic2.SetOpenCL(opencl); cTargetNu.SetOpenCL(opencl); //--- if(!cTargetCritic1.WeightsUpdate(GetPointer(cCritic1), 1.0) || !cTargetCritic2.WeightsUpdate(GetPointer(cCritic2), 1.0) || !cTargetNu.WeightsUpdate(GetPointer(cNu), 1.0)) { PrintFormat("Error of update target models: %d", GetLastError()); return false; } //--- cZeta.getResults(fZeta); ulong size = fZeta.Size(); fLambda = vector<float>::Full(size,1.0e-5f); fLambda_m = vector<float>::Zeros(size); fLambda_v = vector<float>::Zeros(size); fQWeights = vector<float>::Ones(size); iLatentLayer = latent_layer; //--- return true; }
Beachten Sie, dass wir hier den Vektor fQWeights der Gewichte mit Einzelwerten initialisieren. Wenn Ihre Belohnungsfunktion andere Koeffizienten vorsieht, müssen wir die Methode SetQWeights verwenden. Sie sollte jedoch aufgerufen werden, nachdem die Klasse mit der Methode Create initialisiert wurde, da sonst die Koeffizienten mit Einzelwerten überschrieben werden.
Wir haben den Conflict-Averse Gradient Descent-Algorithmus in eine separate CAGrad-Methode ausgelagert. In den Parametern erhält diese Methode einen Vektor von Gradienten und gibt den angepassten Vektor zurück.
Zunächst müssen wir einige vorbereitende Arbeiten im Methodenkörper durchführen:
- den Durchschnittswert der Steigung bestimmen;
- den Skalengradienten, um die Stabilität der Berechnungen zu verbessern;
- die lokale Variablen und Vektoren vorbereiten.
vector<float> CNet_SAC_D_DICE::CAGrad(vector<float> &grad) { matrix<float> GG = grad.Outer(grad); GG.ReplaceNan(0); if(MathAbs(GG).Sum() == 0) return grad; float scale = MathSqrt(GG.Diag() + 1.0e-4f).Mean(); GG = GG / MathPow(scale,2); vector<float> Gg = GG.Mean(1); float gg = Gg.Mean(); vector<float> w = vector<float>::Zeros(grad.Size()); float c = MathSqrt(gg + 1.0e-4f) * fCAGrad_C; vector<float> w_best = w; float obj_best = FLT_MAX; vector<float> moment = vector<float>::Zeros(w.Size());
Nach Abschluss der vorbereitenden Arbeiten wird ein Zyklus zur Lösung des Optimierungsproblems eingerichtet. Im Schleifenkörper lösen wir das Problem der Suche nach dem optimalen Aktualisierungsvektor iterativ mit der Methode des Gradientenabstiegs.
for(int i = 0; i < iCAGrad_Iters; i++) { vector<float> ww; w.Activation(ww,AF_SOFTMAX); float obj = ww.Dot(Gg) + c * MathSqrt(ww.MatMul(GG).Dot(ww) + 1.0e-4f); if(MathAbs(obj) < obj_best) { obj_best = MathAbs(obj); w_best = w; } if(i < (iCAGrad_Iters - 1)) { float loss = -obj; vector<float> derev = Gg + GG.MatMul(ww) * c / (MathSqrt(ww.MatMul(GG).Dot(ww) + 1.0e-4f) * 2) + ww.MatMul(GG) * c / (MathSqrt(ww.MatMul(GG).Dot(ww) + 1.0e-4f) * 2); vector<float> delta = derev * loss; ulong size = delta.Size(); matrix<float> ident = matrix<float>::Identity(size, size); vector<float> ones = vector<float>::Ones(size); matrix<float> sm_der = ones.Outer(ww); sm_der = sm_der.Transpose() * (ident - sm_der); delta = sm_der.MatMul(delta); if(delta.Ptp() != 0) delta = delta / delta.Ptp(); moment = delta * 0.8f + moment * 0.5f; w += moment; if(w.Ptp() != 0) w = w / w.Ptp(); } }
Nach Abschluss der Schleifeniterationen werden die Fehlergradienten anhand der optimalen Gewichte angepasst. Das Ergebnis wird an das aufrufende Programm zurückgegeben.
w_best.Activation(w,AF_SOFTMAX); float gw_norm = MathSqrt(w.MatMul(GG).Dot(w) + 1.0e-4f); float lmbda = c / (gw_norm + 1.0e-4f); vector<float> result = ((w * lmbda + 1.0f / (float)grad.Size()) * grad) / (1 + MathPow(fCAGrad_C,2)); //--- return result; }
Genau wie in der Klasse CNet_SAC_DICE wird das gesamte Training in der Methode CNet_SAC_D_DICE::Study durchgeführt. Doch trotz der Einheitlichkeit der Ansätze und der äußeren Ähnlichkeit gibt es viele Unterschiede im Algorithmus und in der Struktur der Methode. Wir haben die ersten Änderungen an den Methodenparametern vorgenommen. Hier haben wir die Variable „reward“ (Belohnung) durch den Vektor Rewards der aufgeteilten Belohnungen ersetzt.
Außerdem haben wir den Logarithmusvektor für die Aktionswahrscheinlichkeit ActionsLogProbab ausgeschlossen. Wie Sie wissen, wird der Algorithmus Soft Actor-Critic verwendet, um die Entropiekomponente in die Belohnungsfunktion einfließen zu lassen und den Agenten zu ermutigen, Aktionen mit geringer Wahrscheinlichkeit zu wiederholen. Bei der Aufteilung der Belohnungsfunktion wird jeder Komponente ein eigenes Element zugewiesen. Die Wahrscheinlichkeitslogarithmen sind also bereits im aufgeteilten Belohnungsvektor Rewards enthalten, und wir brauchen sie nicht in einem separaten Vektor zu duplizieren.
bool CNet_SAC_D_DICE::Study(CArrayFloat *State, CArrayFloat *SecondInput, CBufferFloat *Actions, vector<float> &Rewards, CBufferFloat *NextState, CBufferFloat *NextSecondInput, float discount, float tau) { //--- if(!Actions) return false;
Im Hauptteil der Methode wird die Relevanz des Zeigers auf den resultierenden Puffer der abgeschlossenen Aktionen geprüft. Damit ist der Kontrollblock unserer Methode abgeschlossen.
In der nächsten Phase muss festgestellt werden, dass beim Training des Modells ein ziemlich großer, unangemessener Anstieg der Schätzungen der nachfolgenden Zustände durch die Zielmodelle zu verzeichnen war. Diese Schätzungen lagen weit über den tatsächlichen Belohnungen, was zu einer gegenseitigen Anpassung des trainierten Modells und seiner Zielkopie führte, ohne die tatsächlichen Belohnungen der Umgebung zu berücksichtigen.
Um diesen Effekt zu minimieren, wurde beschlossen, das Modell in der Anfangsphase anhand der tatsächlichen kumulativen Belohnung zu trainieren. Eine völlige Verweigerung der Verwendung von Zielmodellen hat ebenfalls negative Auswirkungen. Im Erfahrungswiederholungspuffer ist die kumulative Bewertung auf einen Trainingszeitraum beschränkt. Sie kann für ähnliche Zustände und Handlungen sehr unterschiedlich sein, je nach Abstand zum Ende der Trainingsmenge. Dieser Unterschied wird durch das Zielmodell geglättet. Darüber hinaus hilft das Zielmodell bei der Einschätzung von Zuständen, die auf aktuellen politischen Maßnahmen beruhen. Mit zunehmender Anzahl von Iterationen der Aktualisierung von Agentenparametern weicht die aktuelle Strategie zunehmend von der Strategie im Erfahrungswiedergabepuffer ab, was nicht ignoriert werden kann. Aber wir brauchen ein Zielmodell mit angemessenen Schätzungen. Daher benötigen wir zwei Modi für den Betrieb der Methode: mit und ohne Verwendung von Zielmodellen.
Bei der Ausgestaltung des Methodenalgorithmus lassen wir uns von folgenden Überlegungen leiten:
- Wenn es notwendig ist, Zielmodelle zu verwenden, übergibt der Nutzer in den Parametern Zeiger auf zukünftige Zustände. Der Belohnungsvektor enthält eine aufgeteilte Belohnung nur für die im aktuellen Zustand ausgeführte Aktion.
- Nach der Ablehnung der Verwendung von Zielmodellen, kann ein Nutzer keine Zeiger auf zukünftige Zustände übergeben (die Parametervariablen sind auf NULL gesetzt). Der Belohnungsvektor Rewards enthält eine kumulative, aufgeteilte Belohnung.
Daher überprüfen wir als Nächstes den Zeiger auf den zukünftigen Zustand und bestimmen gegebenenfalls eine Aktion im zukünftigen Zustand auf der Grundlage der aktuellen Politik. Außerdem bewerten wir das Zustand-Aktion-Paar.
if(!!NextState) if(!CNet::feedForward(NextState, 1, false, NextSecondInput)) return false; if(!cTargetCritic1.feedForward(GetPointer(this), iLatentLayer, GetPointer(this), layers.Total() - 1) || !cTargetCritic2.feedForward(GetPointer(this), iLatentLayer, GetPointer(this), layers.Total() - 1)) return false; //--- if(!cTargetNu.feedForward(GetPointer(this), iLatentLayer, GetPointer(this), layers.Total() - 1)) return false;
Als Nächstes nehmen wir einen direkten Durchgang der konservativen Politik im aktuellen Zustand. Wir ersetzen die Aktionen und führen einen direkten Durchlauf durch die DICE-Blockmodelle durch.
if(!CNet::feedForward(State, 1, false, SecondInput)) return false; CBufferFloat *output = ((CNeuronBaseOCL*)((CLayer*)layers.At(layers.Total() - 1)).At(0)).getOutput(); output.AssignArray(Actions); output.BufferWrite(); if(!cNu.feedForward(GetPointer(this), iLatentLayer, GetPointer(this))) return false; if(!cZeta.feedForward(GetPointer(this), iLatentLayer, GetPointer(this))) return false;
Dann bestimmen wir die Werte der Verlustfunktionen der Blockmodelle der Verteilungskorrekturschätzung. Dieser Schritt wurde in dem vorangegangenen Artikel ausführlich beschrieben. Ich weise nur darauf hin, dass im Falle der Weigerung, das Zielmodell zu verwenden, der Vektor für die Bewertung des zukünftigen Zustands next_nu mit Nullwerten gefüllt wird.
vector<float> nu, next_nu, zeta, ones; cNu.getResults(nu); cZeta.getResults(zeta); if(!!NextState) cTargetNu.getResults(next_nu); else next_nu = vector<float>::Zeros(nu.Size()); ones = vector<float>::Ones(zeta.Size()); vector<float> log_prob = GetLogProbability(output); int shift = (int)(Rewards.Size() - log_prob.Size()); if(shift < 0) return false; float policy_ratio = 0; for(ulong i = 0; i < log_prob.Size(); i++) policy_ratio += log_prob[i] - Rewards[shift + i] / LogProbMultiplier; policy_ratio = MathExp(policy_ratio / log_prob.Size()); vector<float> bellman_residuals = (next_nu * discount + Rewards) * policy_ratio - nu; vector<float> zeta_loss = MathPow(zeta, 2.0f) / 2.0f - zeta * (MathAbs(bellman_residuals) - fLambda) ; vector<float> nu_loss = zeta * MathAbs(bellman_residuals) + MathPow(nu, 2.0f) / 2.0f; vector<float> lambda_los = fLambda * (ones - zeta);
Als Nächstes aktualisieren wir den Vektor der Lagrange-Koeffizienten mit Hilfe der Adam-Optimierungsmethode.
Bitte beachten Sie, dass wir den Vektor der Fehlergradienten mit der oben beschriebenen CAGrad-Methode korrigieren. Die Verwendung von Vektoroperationen ermöglicht es uns, mit Vektoren genauso einfach zu arbeiten wie mit einfachen Variablen.
Wir speichern die angepassten Werte in dem entsprechenden Vektor.
vector<float> grad_lambda = CAGrad((ones - zeta) * (lambda_los * (-1.0f))); fLambda_m = fLambda_m * b1 + grad_lambda * (1 - b1); fLambda_v = fLambda_v * b2 + MathPow(grad_lambda, 2) * (1.0f - b2); fLambda += fLambda_m * lr / MathSqrt(fLambda_v + lr / 100.0f);
Der nächste Schritt ist die Aktualisierung der Modellparameter v, ζ. Der Algorithmus für diese Operationen bleibt derselbe. Wir ersetzen einfach die Variablen durch Vektoren und verwenden Vektoroperationen.
CBufferFloat temp; temp.BufferInit(MathMax(Actions.Total(), SecondInput.Total()), 0); temp.BufferCreate(opencl); //--- update nu int last_layer = cNu.layers.Total() - 1; CLayer *layer = cNu.layers.At(last_layer); if(!layer) return false; CNeuronBaseOCL *neuron = layer.At(0); if(!neuron) return false; CBufferFloat *buffer = neuron.getGradient(); if(!buffer) return false; vector<float> nu_grad = CAGrad(nu_loss * (zeta * bellman_residuals / MathAbs(bellman_residuals) - nu)); if(!buffer.AssignArray(nu_grad) || !buffer.BufferWrite()) return false; if(!cNu.backPropGradient(output, GetPointer(temp))) return false;
Wir korrigieren die Vektoren der Fehlergradienten notwendigerweise mit Hilfe des Algorithmus Conflict-Averse Gradient Descent in der Methode CNet_SAC_D_DICE::CAGrad.
//--- update zeta last_layer = cZeta.layers.Total() - 1; layer = cZeta.layers.At(last_layer); if(!layer) return false; neuron = layer.At(0); if(!neuron) return false; buffer = neuron.getGradient(); if(!buffer) return false; vector<float> zeta_grad = CAGrad(zeta_loss * (zeta - MathAbs(bellman_residuals) + fLambda) * (-1.0f)); if(!buffer.AssignArray(zeta_grad) || !buffer.BufferWrite()) return false; if(!cZeta.backPropGradient(output, GetPointer(temp))) return false;
In diesem Stadium beenden wir die Arbeit mit den Objekten des Blocks „Schätzung der Verteilungskorrektur“ und gehen zum Training unserer Kritiker-Modelle über. Zunächst führen wir ihren Vorwärtsdurchgang aus. Wir haben die Vorwärtsdurchgänge des Akteurs bereits früher durchgeführt.
//--- feed forward critics if(!cCritic1.feedForward(GetPointer(this), iLatentLayer, output) || !cCritic2.feedForward(GetPointer(this), iLatentLayer, output)) return false;
Der nächste Schritt besteht darin, den Vektor der Referenzwerte für die Aktualisierung der Parameter des Kritikers zu bestimmen. Hier gibt es zwei Nuancen. Beide betreffen Zielmodelle. Zunächst prüfen wir die Notwendigkeit ihrer Verwendung zur Bewertung des späteren Zustands und der Maßnahmen. Zu diesem Zweck wird ein Zeiger auf den späteren Zustand des Systems geprüft.
Wenn wir Zielmodelle verwenden, um das nachfolgende Zustands-Aktions-Paar zu bewerten, dann müssen wir den Zielkritiker mit der geringsten kumulativen Punktzahl auswählen. Die kumulative Schätzung lässt sich leicht durch Multiplikation des Vektors der Gewichtungskoeffizienten der Komponenten der Belohnungsfunktion mit dem Vektor der aufgeteilten prädiktiven Belohnung aus einem Vorwärtsdurchlauf der Zielmodelle erhalten. Als Nächstes müssen wir nur noch die minimale Schätzung auswählen und den Vektor der vorhergesagten Werte des ausgewählten Modells speichern.
Wenn wir uns weigern, die nachfolgenden Zustände zu schätzen, wird der Vektor der Prognosewerte mit Nullwerten gefüllt.
vector<float> result; if(fZeta.CompareByDigits(vector<float>::Zeros(fZeta.Size()),8) == 0) fZeta = MathAbs(zeta); else fZeta = fZeta * 0.9f + MathAbs(zeta) * 0.1f; zeta = MathPow(MathAbs(zeta), 1.0f / 3.0f) / (MathPow(fZeta, 1.0f / 3.0f) * 10.0f); vector<float> target = vector<float>::Zeros(Rewards.Size()); if(!!NextState) { cTargetCritic1.getResults(target); cTargetCritic2.getResults(result); if(fQWeights.Dot(result) < fQWeights.Dot(target)) target = result; }
Wir passen die Prognoseschätzungen um den Abzinsungsfaktor an und addieren sie mit der Belohnung des aktuellen Zustands.
target = (target * discount + Rewards); ulong total = log_prob.Size(); for(ulong i = 0; i < total; i++) target[shift + i] = log_prob[i] * LogProbMultiplier;
Im resultierenden Vektor wird der Logarithmus der Aktionswahrscheinlichkeit in der aktuellen Politik angepasst. Die Logarithmen der Handlungswahrscheinlichkeiten, die im Erfahrungswiedergabepuffer gespeichert sind, sind bereits im Belohnungsvektor enthalten. Wir ersetzen ihre Werte durch Logarithmen der aktuellen Politik, um den Kritiker darauf zu trainieren, Bewertungen unter Berücksichtigung der aktuellen Politik vorzunehmen.
Nach der Bestimmung der Zielwerte berechnen wir den Vorhersagefehler des ersten Kritikers und den Fehlergradienten für jede Komponente der Q-Funktion. Die sich daraus ergebenden Gradienten werden mit dem Algorithmus Conflict-Averse Gradient Descent angepasst.
//--- update critic1 cCritic1.getResults(result); vector<float> loss = zeta * MathPow(result - target, 2.0f); if(fLoss1 == 0) fLoss1 = MathSqrt(fQWeights.Dot(loss) / fQWeights.Sum()); else fLoss1 = MathSqrt(0.999f * MathPow(fLoss1, 2.0f) + 0.001f * fQWeights.Dot(loss) / fQWeights.Sum()); vector<float> grad = CAGrad(loss * zeta * (target - result) * 2.0f);
Wir übertragen die korrigierten Fehlergradienten in den entsprechenden Critic1-Puffer und führen einen umgekehrten Modelldurchlauf durch.
last_layer = cCritic1.layers.Total() - 1; layer = cCritic1.layers.At(last_layer); if(!layer) return false; neuron = layer.At(0); if(!neuron) return false; buffer = neuron.getGradient(); if(!buffer) return false; if(!buffer.AssignArray(grad) || !buffer.BufferWrite()) return false; if(!cCritic1.backPropGradient(output, GetPointer(temp)) || !backPropGradient(SecondInput, GetPointer(temp), iLatentLayer)) return false;
Hier führen wir auch einen teilweisen Rückwärtsdurchlauf des Actors durch, um den Block der Vorverarbeitung der Quelldaten anzupassen.
Wir wiederholen die Vorgänge für den zweiten Kritiker.
//--- update critic2 cCritic2.getResults(result); loss = zeta * MathPow(result - target, 2.0f); if(fLoss2 == 0) fLoss2 = MathSqrt(fQWeights.Dot(loss) / fQWeights.Sum()); else fLoss2 = MathSqrt(0.999f * MathPow(fLoss2, 2.0f) + 0.001f * fQWeights.Dot(loss) / fQWeights.Sum()); grad = CAGrad(loss * zeta * (target - result) * 2.0f); last_layer = cCritic2.layers.Total() - 1; layer = cCritic2.layers.At(last_layer); if(!layer) return false; neuron = layer.At(0); if(!neuron) return false; buffer = neuron.getGradient(); if(!buffer) return false; if(!buffer.AssignArray(grad) || !buffer.BufferWrite()) return false; if(!cCritic2.backPropGradient(output, GetPointer(temp)) || !backPropGradient(SecondInput, GetPointer(temp), iLatentLayer)) return false;
Im nächsten Block unserer Methode werden wir die Richtlinien aktualisieren. Ich möchte Sie daran erinnern, dass der Algorithmus SAC+DICE das Training von zwei Akteurs-Strategien vorsieht: konservativ und optimistisch. Zunächst werden wir die konservative Politik aktualisieren. Wir haben den Vorwärtsdurchgang für dieses Modell bereits durchgeführt.
Für das Training der Akteure wird der Kritiker mit dem geringsten mittleren Fehler verwendet. Definieren wir ein solches Modell und speichern wir einen Zeiger darauf in einer lokalen Variablen.
vector<float> mean; CNet *critic = NULL; if(fLoss1 <= fLoss2) { cCritic1.getResults(result); cCritic2.getResults(mean); critic = GetPointer(cCritic1); } else { cCritic1.getResults(mean); cCritic2.getResults(result); critic = GetPointer(cCritic2); }
Hier werden wir die voraussichtlichen Bewertungen der einzelnen Kritiker hochladen. Dann werden wir die Referenzwerte für den Rückwärtsdurchlauf der Modelle anhand der Gleichung bestimmen.
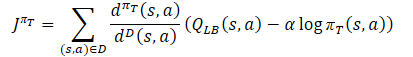
Gleichzeitig stellen wir sicher, dass wir den Vektor der Fehlergradienten mit der Methode des konfliktfreien Gradientenabstiegs korrigieren.
vector<float> var = MathAbs(mean - result) / 2.0f; mean += result; mean /= 2.0f; target = mean; for(ulong i = 0; i < log_prob.Size(); i++) target[shift + i] = discount * log_prob[i] * LogProbMultiplier; target = CAGrad(zeta * (target - var * 2.5f) - result) + result;
Als Nächstes müssen wir nur noch die empfangenen Daten in den Puffer übertragen und einen Rückwärtsdurchlauf von Critic und Actor durchführen. Um eine gegenseitige Anpassung der Modelle zu verhindern, schalten wir den Critic-Trainingsmodus aus, bevor wir mit den Arbeiten beginnen. In diesem Fall verwenden wir ihn nur, um den Fehlergradienten an den Akteur weiterzugeben.
CBufferFloat bTarget; bTarget.AssignArray(target); critic.TrainMode(false); if(!critic.backProp(GetPointer(bTarget), GetPointer(this)) || !backPropGradient(SecondInput, GetPointer(temp))) { critic.TrainMode(true); return false; }
Wir haben das Modell eines optimistischen Akteurs im Gegensatz zu einem konservativen Akteur noch nicht verwendet. Daher müssen wir, bevor wir mit der Aktualisierung seiner Parameter beginnen, einen direkten Durchlauf mit dem aktuellen Zustand der Umgebung durchführen.
//--- update exploration policy if(!cActorExploer.feedForward(State, 1, false, SecondInput)) { critic.TrainMode(true); return false; } output = ((CNeuronBaseOCL*)((CLayer*)cActorExploer.layers.At(layers.Total() - 1)).At(0)).getOutput(); output.AssignArray(Actions); output.BufferWrite();
Wie im Falle eines konservativen Akteurs ersetzen wir den Vektor der Aktionen und erhalten Logarithmen der Wahrscheinlichkeiten, wobei wir die optimistische Politik berücksichtigen.
cActorExploer.GetLogProbs(log_prob);
Wir bestimmen den Vektor der Referenzwerte für den umgekehrten Durchlauf der Modelle gemäß der Gleichung der optimistischen Politik.
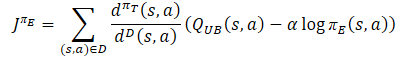
Der Vektor der Fehlergradienten wird mit der Methode des konfliktfreien Gradientenabstiegs korrigiert.
target = mean; for(ulong i = 0; i < log_prob.Size(); i++) target[shift + i] = discount * log_prob[i] * LogProbMultiplier; target = CAGrad(zeta * (target + var * 2.0f) - result) + result;
Dann führen wir einen Rückwärtsdurchlauf durch die Modelle durch und versetzen den Kritiker wieder in den Modell-Trainingsmodus.
bTarget.AssignArray(target); if(!critic.backProp(GetPointer(bTarget), GetPointer(cActorExploer)) || !cActorExploer.backPropGradient(SecondInput, GetPointer(temp))) { critic.TrainMode(true); return false; } critic.TrainMode(true);
Als Nächstes müssen wir die Zielmodelle aktualisieren. Hier habe ich weitere Ergänzungen vorgenommen, um eine Verzerrung der Schätzungen künftiger Zustände und eine Anpassung der Modelle der Kritiker an die Werte ihrer Zielkopien zu verhindern.
Die Parameter der Zielmodelle werden bei jeder Iteration nur dann aktualisiert, wenn sie nicht mehr zur Schätzung des nachfolgenden Zustands verwendet werden. Wenn die Zielmodelle beim Training verwendet werden, wird ihre Aktualisierung mit einer Verzögerung durchgeführt.
Daher prüfen wir zunächst, ob die Modelle aktualisiert werden müssen, und führen erst dann die Operationen durch.
if(!!NextState) { if(iUpdateDelayCount > 0) { iUpdateDelayCount--; return true; } iUpdateDelayCount = iUpdateDelay; } if(!cTargetCritic1.WeightsUpdate(GetPointer(cCritic1), tau) || !cTargetCritic2.WeightsUpdate(GetPointer(cCritic2), tau) || !cTargetNu.WeightsUpdate(GetPointer(cNu), tau)) { PrintFormat("Error of update target models: %d", GetLastError()); return false; } //--- return true; }
Nach erfolgreichem Abschluss aller Iterationen der Methode beenden wir ihre Arbeit mit dem „wahren“ Ergebnis.
Die Aufteilung von Belohnungen und die Verwendung von Vektoren führten zu Veränderungen bei anderen Methoden, einschließlich der Arbeit mit Dateien. Aber wir wollen uns jetzt nicht damit aufhalten. Sie finden sie, ebenso wie den vollständigen Code aller Methoden der neuen Klasse, in der beigefügten Datei „MQL5\Experts\SAC-D&DICE\Net_SAC_D_DICE.mqh“.
2.2 Anpassen der Datenspeicherstrukturen
Richten wir nun unsere Aufmerksamkeit auf die Datei „MQL5\Experts\SAC-D&DICE\Trajectory.mqh“. Wir haben hier die Architektur der Modelle verändert. Jetzt haben wir sie praktisch unverändert gelassen. Wir müssen nur die Anzahl der Neuronen am Ausgang des Critic ändern. Sie sollten ausreichen, um die Belohnungsfunktion zu zerlegen. Doch bevor wir ihre Anzahl festlegen, sollten wir die Struktur der aufgeteilten Belohnung definieren.
Wir geben die relative Veränderung des Saldos im ersten Element mit dem Index „0“ an. Wie Sie wissen, ist es unser Hauptziel, die Gewinne auf dem Markt zu maximieren.
Der Parameter mit dem Index „1“ enthält den relativen Wert der Kapitalveränderung. Ein negativer Wert weist auf eine unerwünschte Absenkung hin. Ein positiver Wert zeigt einen schwankenden Gewinn an.
Ein weiteres Element ist für Sanktionen wegen des Mangels an offenen Stellen vorgesehen.
Als Nächstes werden die Logarithmen der Handlungswahrscheinlichkeiten addiert. Wie Sie wissen, ist die Länge des Wahrscheinlichkeitslogarithmusvektors gleich dem Aktionsvektor.
//+------------------------------------------------------------------+ //| Rewards structure | //| 0 - Delta Balance | //| 1 - Delta Equity ( "-" Drawdown / "+" Profit) | //| 2 - Penalty for no open positions | //| 3... - LogProbs vector | //+------------------------------------------------------------------+
Somit ist die Größe der neuronalen Schicht der Critic-Ergebnisse um 3 Elemente größer als die Anzahl der Aktionen.
#define NActions 6 //Number of possible Actions #define NRewards 3+NActions //Number of rewards
bool CreateDescriptions(CArrayObj *actor, CArrayObj *critic) { //--- CLayerDescription *descr; //--- if(!actor) { actor = new CArrayObj(); if(!actor) return false; } if(!critic) { critic = new CArrayObj(); if(!critic) return false; } //--- Actor ........ ........ //--- Critic critic.Clear(); //--- Input layer ........ ........ //--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = NRewards; descr.optimization = ADAM; descr.activation = None; if(!critic.Add(descr)) { delete descr; return false; } //--- return true; }
Durch die Aufteilung der Belohnung wurde auch die Struktur der Datenspeicherung im Erfahrungswiedergabepuffer geändert. Nun reicht eine Variable nicht aus, um die Belohnung festzulegen. Wir brauchen ein Datenfeld. Gleichzeitig haben wir die Entropiekomponente in das Array der Belohnungen aufgenommen und benötigen kein separates Array, um diese Werte zurückzusetzen. Daher ersetzen wir in der Struktur der Zustandsbeschreibung das Array „log_prob“ durch "rewards" und passen die Methoden zum Kopieren der Struktur und zur Behandlung der Dateien an.
struct SState { float state[HistoryBars * BarDescr]; float account[AccountDescr - 4]; float action[NActions]; float rewards[NRewards]; //--- SState(void); //--- bool Save(int file_handle); bool Load(int file_handle); //--- overloading void operator=(const SState &obj) { ArrayCopy(state, obj.state); ArrayCopy(account, obj.account); ArrayCopy(action, obj.action); ArrayCopy(rewards, obj.rewards); } };
Wir löschen in der Struktur STrajectory das Array Rewards, da wir die Belohnung jetzt in der Struktur SState beschreiben werden. Außerdem sollten wir die Strukturmethoden gezielt ändern.
struct STrajectory { SState States[Buffer_Size]; int Total; float DiscountFactor; bool CumCounted; //--- STrajectory(void); //--- bool Add(SState &state); void CumRevards(void); //--- bool Save(int file_handle); bool Load(int file_handle); };
Der vollständige Code der genannten Strukturen und ihrer Methoden ist im Anhang verfügbar.
2.3 Erstellen von EAs für das Modelltraining
Es ist an der Zeit, an der Modellbildung von EAs zu arbeiten. Während des Trainings verwenden wir wie zuvor drei EAs:
- Research — Sammlung von Beispieldatenbanken
- Study — Modelltraining
- Test — Überprüfung der erzielten Ergebnisse.
In den Forschungs- und Test-EAs betrafen die Änderungen nur die Vorbereitung der Struktur zur Beschreibung des Umgebungszustands und die am Ende der OnTick-Methode erhaltene Belohnung. Während wir zuvor Belohnungen und Geldstrafen addiert haben, fügen wir jetzt jede Komponente zu einem eigenen Array-Element hinzu. In diesem Fall ist es wichtig, dass die oben genannte Datenstruktur eingehalten wird. Jedes Element des Arrays muss ausgefüllt werden. Fehlt der Wert der Komponente, so wird dem entsprechende Array-Element „0“ zugewiesen. Dieser Ansatz gibt uns Vertrauen in die Gültigkeit der verwendeten Daten.
void OnTick() { //--- ........ ........ //--- sState.rewards[0] = bAccount[0]; sState.rewards[1] = 1.0f-bAccount[1]; vector<float> log_prob; Actor.GetLogProbs(log_prob); if((buy_value + sell_value) == 0) sState.rewards[2] -= (float)(atr / PrevBalance); else sState.rewards[2] = 0; for(ulong i = 0; i < NActions; i++) { sState.action[i] = ActorResult[i]; sState.rewards[i + 3] = log_prob[i] * LogProbMultiplier; } if(!Base.Add(sState)) ExpertRemove(); }
Die vollständigen Codes der EAs finden Sie in der Anlage.
Wie üblich wird das Modelltraining im EA Study durchgeführt. Wie bereits erwähnt, unterteilen wir den Prozess der Modellbildung in zwei Phasen:
- Training mit tatsächlicher kumulativer Belohnung (keine Zielmodelle),
- Training mit Zielmodellen.
Die Dauer der ersten Stufe wird durch eine Konstante bestimmt.
#define StartTargetIteration 20000
Es ist erwähnenswert, dass das Training ohne die Verwendung von Zielmodellen nur dann durchgeführt wird, wenn Sie die Study EA zum ersten Mal starten, wenn keine vortrainierten Modelle vorhanden sind.
Wenn es dem Trainings-EA beim Start gelingt, bereits trainierte Modelle zu laden, werden die Zielmodelle ab der ersten Trainingsiteration verwendet.
Diese Kontrolle wird in der Methode OnInit des EA implementiert.
int OnInit() { //--- ResetLastError(); if(!LoadTotalBase()) { PrintFormat("Error of load study data: %d", GetLastError()); return INIT_FAILED; } //--- load models if(!Net.Load(FileName, true)) { CArrayObj *actor = new CArrayObj(); CArrayObj *critic = new CArrayObj(); if(!CreateDescriptions(actor, critic)) { delete actor; delete critic; return INIT_FAILED; } if(!Net.Create(actor, critic, critic, critic, LatentLayer)) { delete actor; delete critic; return INIT_FAILED; } delete actor; delete critic; StartTargetIter = StartTargetIteration; } else StartTargetIter = 0; //--- if(!EventChartCustom(ChartID(), 1, 0, 0, "Init")) { PrintFormat("Error of create study event: %d", GetLastError()); return INIT_FAILED; } //--- return(INIT_SUCCEEDED); }
Wie Sie sehen, erhält die Variable StartTargetIter beim Erstellen neuer Modelle den konstanten Wert StartTargetIteration. Wenn bereits trainierte Modelle geladen sind, wird in der Verzögerungsvariablen „0“ gespeichert.
Die Trainingsiterationen sind in der Methode Train angeordnet. Zu Beginn der Methode bestimmen wir wie üblich die Anzahl der gespeicherten Trajektorien im Erfahrungswiedergabepuffer und richten eine Trainingsschleife mit der im externen Parameter EA angegebenen Anzahl von Iterationen ein.
void Train(void) { int total_tr = ArraySize(Buffer); uint ticks = GetTickCount(); //--- for(int iter = 0; (iter < Iterations && !IsStopped()); iter ++) { int tr = (int)((MathRand() / 32767.0) * (total_tr - 1)); int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2)); if(i < 0) { iter--; continue; }
Im Hauptteil der Schleife wird der Zustand in einer der gespeicherten Trajektorien zufällig ausgewählt. Danach geben wir Informationen über den ausgewählten Zustand an die Datenpuffer und den Vektor weiter.
//--- bState.AssignArray(Buffer[tr].States[i].state); float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0]; float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1]; bAccount.Clear(); bAccount.Add((Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance); bAccount.Add(Buffer[tr].States[i].account[1] / PrevBalance); bAccount.Add((Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity); bAccount.Add(Buffer[tr].States[i].account[2]); bAccount.Add(Buffer[tr].States[i].account[3]); bAccount.Add(Buffer[tr].States[i].account[4] / PrevBalance); bAccount.Add(Buffer[tr].States[i].account[5] / PrevBalance); bAccount.Add(Buffer[tr].States[i].account[6] / PrevBalance); double x = (double)Buffer[tr].States[i].account[7] / (double)(D'2024.01.01' - D'2023.01.01'); bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_MN1); bAccount.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_W1); bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_D1); bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); //--- bActions.AssignArray(Buffer[tr].States[i].action); vector<float> rewards; rewards.Assign(Buffer[tr].States[i].rewards);
Bitte beachten Sie, dass wir zum jetzigen Zeitpunkt nur Informationen über den ausgewählten Zustand aufbereiten. Um keine unnötige Arbeit zu leisten, werden wir nur bei Bedarf Informationen über den nachfolgenden Zustand generieren.
Wir testen die Notwendigkeit der Verwendung von Zielmodellen zur Schätzung des nachfolgenden Zustands, indem wir die aktuelle Trainingsiteration und den Wert der Variablen StartTargetIter vergleichen. Wenn die Anzahl der Iterationen den Schwellenwert nicht erreicht hat, führen wir ein Training mit kumulierten Werten durch. Aber es gibt hier eine Nuance. Beim Speichern der Daten im Erfahrungswiedergabepuffer haben wir die kumulative Summe der Werte aller Belohnungskomponenten berechnet. Wir benötigen jedoch die Entropiekomponente ohne eine kumulative Summe. Deshalb bauen wir eine Schleife auf und entfernen die kumulierten Werte nur aus der Entropiekomponente der Belohnungsfunktion.
//--- if(iter < StartTargetIter) { ulong start = rewards.Size() - bActions.Total(); for(ulong r = start; r < rewards.Size(); r++) rewards[r] -= Buffer[tr].States[i + 1].rewards[r] * DiscFactor; if(!Net.Study(GetPointer(bState), GetPointer(bAccount), GetPointer(bActions), rewards, NULL, NULL, DiscFactor, Tau)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; } }
Dann rufen wir die Trainingsmethode unserer neuen Klasse auf. Hier geben wir in den nachfolgenden Zustandsparametern „NULL“ an.
Nach Erreichen der Schwelle für die Verwendung der Zielfunktionen werden wir zunächst Informationen über den späteren Zustand des Systems vorbereiten.
else { //--- Target bNextState.AssignArray(Buffer[tr].States[i + 1].state); PrevBalance = Buffer[tr].States[i].account[0]; PrevEquity = Buffer[tr].States[i].account[1]; if(PrevBalance == 0) { iter--; continue; } bNextAccount.Clear(); bNextAccount.Add((Buffer[tr].States[i + 1].account[0] - PrevBalance) / PrevBalance); bNextAccount.Add(Buffer[tr].States[i + 1].account[1] / PrevBalance); bNextAccount.Add((Buffer[tr].States[i + 1].account[1] - PrevEquity) / PrevEquity); bNextAccount.Add(Buffer[tr].States[i + 1].account[2]); bNextAccount.Add(Buffer[tr].States[i + 1].account[3]); bNextAccount.Add(Buffer[tr].States[i + 1].account[4] / PrevBalance); bNextAccount.Add(Buffer[tr].States[i + 1].account[5] / PrevBalance); bNextAccount.Add(Buffer[tr].States[i + 1].account[6] / PrevBalance); x = (double)Buffer[tr].States[i + 1].account[7] / (double)(D'2024.01.01' - D'2023.01.01'); bNextAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_MN1); bNextAccount.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_W1); bNextAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_D1); bNextAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
Dann entfernen wir die kumulativen Werte für alle Komponenten der Belohnungsfunktion, sodass nur die Belohnungen des aktuellen Zustands übrig bleiben.
for(ulong r = 0; r < rewards.Size(); r++) rewards[r] -= Buffer[tr].States[i + 1].rewards[r] * DiscFactor; if(!Net.Study(GetPointer(bState), GetPointer(bAccount), GetPointer(bActions), rewards, GetPointer(bNextState), GetPointer(bNextAccount), DiscFactor, Tau)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; } }
Rufen Sie die Trainingsmethode für das Klassenmodell auf. Dieses Mal geben wir Objekte mit nachfolgenden Zustandsdaten an.
Am Ende einer Schleifeniteration drucken wir eine Meldung aus, um den Nutzer zu informieren, und fahren mit der nächsten Iteration fort.
//--- if(GetTickCount() - ticks > 500) { float loss1, loss2; Net.GetLoss(loss1, loss2); string str = StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Critic1", iter * 100.0 / (double)(Iterations), loss1); str += StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Critic2", iter * 100.0 / (double)(Iterations), loss2); Comment(str); ticks = GetTickCount(); } }
Nachdem wir alle Schleifeniterationen erfolgreich abgeschlossen haben, löschen wir das Kommentarfeld im Chart. Wir erzwingen die Aktualisierung der Zielmodelle. Wir zeigen das Trainingsergebnis im MetaTrader 5 Journal an und starten das Herunterfahren des EA.
Comment(""); //--- float loss1, loss2; Net.GetLoss(loss1, loss2); Net.TargetsUpdate(Tau); PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic1", loss1); PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic2", loss2); ExpertRemove(); //--- }
Dies ist das Ende unserer Arbeit mit den EAs für das Modelltraining. Der vollständige Code aller in diesem Artikel verwendeten Programme ist im Anhang verfügbar.
3. Test
Wir haben eine Option für die Umsetzung des Ansatzes zur Aufteilung der Belohnungsfunktion auf der Grundlage des Algorithmus SAC+DICE vorgeschlagen, und jetzt können wir die Ergebnisse der Arbeit in der Praxis bewerten. Wie zuvor wurden die Modelle auf EURUSD H1 für die ersten 5 Monate des Jahres 2023 trainiert. Alle Indikatorparameter werden standardmäßig verwendet. Das Anfangsguthaben beträgt 10.000 USD.
Das Modelltraining ist ein iterativer Prozess, der sich mit den Phasen der Sammlung von Beispielen in einem Erfahrungsspeicher und der Aktualisierung der Modellparameter abwechselt.
In der ersten Phase erstellen wir eine primäre Datenbank mit Beispielen unter Verwendung von Actor-Modellen, die mit Zufallsparametern gefüllt sind. Als Ergebnis erhalten wir eine Reihe von Zufallsdurchläufen, die außerhalb der Politik liegende Datensätze „Zustand → Aktion → Neuer Zustand → Belohnung“ erzeugen.
Im Gegensatz zu allen bisher betrachteten Algorithmen sammeln wir in diesem Fall aufgeteilte Daten über die Umweltbelohnungen für die Aktionen des Agenten.
Nachdem wir Beispiele gesammelt haben, führen wir ein erstes Training unseres Modells durch. Um dies zu erreichen, starten wir den EA „..\SAC-D&DICE\Study.mq5“.
Während des primären Trainings ohne die Verwendung von Zielmodellen beobachten wir einen stetigen Trend zu einer Abnahme der Fehler beider Kritiker. Bei der Verwendung von Zielmodellen zur Schätzung des nachfolgenden Zustands werden jedoch chaotische (seltene) Spitzen im Vorhersagefehler beobachtet, gefolgt von einer sanften Rückkehr zum vorherigen Fehlerniveau.
In der zweiten Phase starten wir die Trainingsdatenerfassung EA erneut im Optimierungsmodus des Strategietesters mit einer vollständigen Parametersuche. Dieses Mal verwenden wir den optimistischen Akteur, der in der ersten Phase trainiert wurde, für alle Durchgänge. Die Streuung der Ergebnisse der einzelnen Durchgänge ist geringer als bei der ersten Datenerhebung und ist auf die Stochastizität der Politik des Akteurs zurückzuführen.
Das Sammeln von Beispielen und das Trainieren des Modells werden mehrmals wiederholt, bis das gewünschte Ergebnis erreicht ist oder ein lokales Minimum erreicht ist, wenn die nächste Iteration des Sammelns von Beispielen und des Trainierens des Modells keinen Fortschritt bringt.
Während des Trainings des Modells haben wir eine Akteurspolitik erhalten, die in der Lage ist, während des Trainingszeitraums einen kleinen Gewinn zu erzielen.
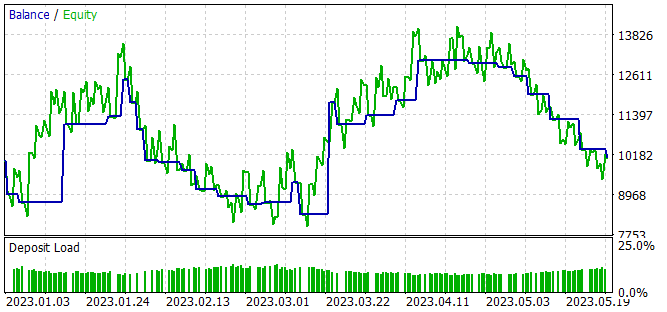
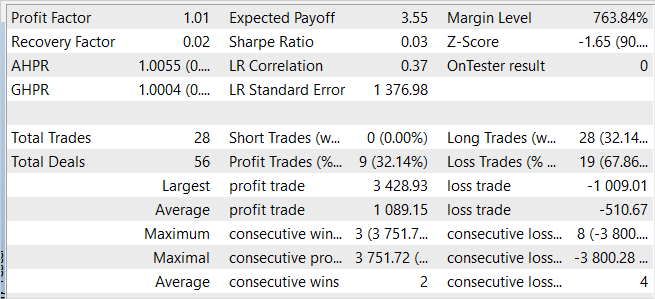
Trotz des erzielten Gewinns ist die erlernte Politik weit von dem entfernt, was wir wollen. Die Saldenkurve zeigt eine wellenförmige Bewegung mit einer ziemlich großen Amplitude. Nur 32 % von 28 Handelsgeschäften wurden mit einem Gewinn abgeschlossen. Der Gesamtgewinn wurde durch die Überschreitung des Umfangs eines gewinnbringenden Geschäfts gegenüber einem Verlustgeschäft erzielt. Der durchschnittliche Gewinn bei einem Handel übersteigt den durchschnittlichen Verlust um das Zweifache. Der maximale Gewinn pro Handel beträgt fast das 3,5-fache des maximalen Verlustes. Infolgedessen ist der Gewinnfaktor etwas höher als 1.
Der EA hat auch bei den neuen Daten Gewinne erzielt. Einen Monat nach der Trainingsperiode konnte das Modell fast 20 % des Gewinns erzielen, was über dem Ergebnis der Trainingsmenge liegt. Die statistischen Ergebnisse sind jedoch mit den Daten des Trainingssatzes vergleichbar. Während des Tests wurden nur 4 Geschäfte getätigt und nur eines davon wurde mit einem Gewinn abgeschlossen. Aber der Gewinn bei diesem Handel ist 12,8 Mal höher als der schlechteste Verlust.
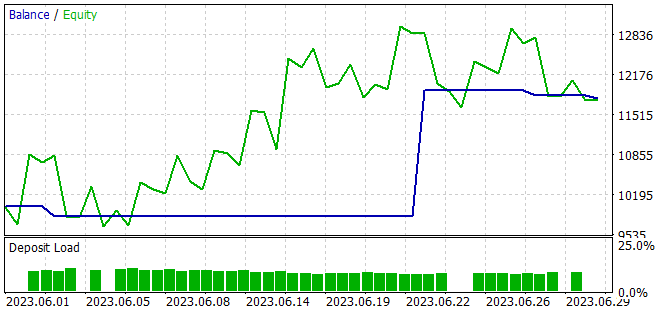
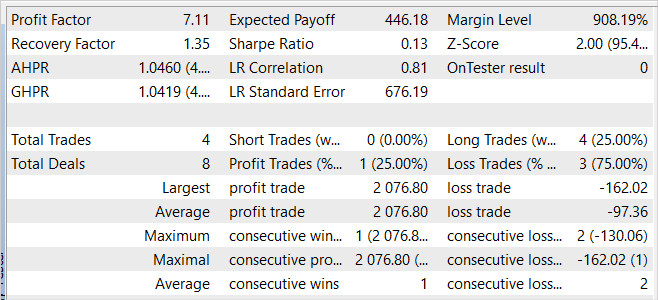
Vergleicht man die Ergebnisse für die Trainingsstichprobe und den darauffolgenden Zeitraum, so kann man davon ausgehen, dass wir bei den neuen Daten den Beginn einer Rentabilitätswelle beobachten, auf die in absehbarer Zeit ein Rückgang folgen könnte.
Insgesamt ist das Modell in der Lage, Gewinne zu erwirtschaften, aber es besteht weiterer Optimierungsbedarf.
Schlussfolgerung
In diesem Artikel haben wir den Ansatz der Aufteilung von Belohnungsfunktionen vorgestellt, mit dem wir Agenten effizienter trainieren können. Die Aufteilung der Belohnung ermöglicht es dem Nutzer, den Einfluss der verschiedenen Komponenten auf die Entscheidungen des Agenten zu analysieren.
Wir haben den Algorithmus mit MQL5 implementiert und die Aufteilung der Belohnungsfunktion in die SAC+DICE-Methode integriert.
Beim Testen des implementierten Algorithmus ist es uns gelungen, ein Modell zu erhalten, das in der Lage ist, sowohl auf der Trainingsmenge als auch außerhalb davon Gewinne zu erzielen. Dies zeigt die Verallgemeinerungsfähigkeit des Algorithmus.
Die erzielten Ergebnisse sind jedoch weit von dem entfernt, was wir wollen. Gleichzeitig ermöglicht die Aufteilung der Belohnungsfunktion eine Analyse des Einflusses der einzelnen Komponenten der Belohnungsfunktion auf das Trainingsergebnis. Ich möchte Sie ermutigen, mit der Einbeziehung und dem Ausschluss einzelner Komponenten zu experimentieren, um ihre Auswirkungen auf das Trainingsergebnis zu bewerten.
Links
- Conflict-Averse Gradient Descent for Multi-task Learning
- Value Function Decomposition for Iterative Design of Reinforcement Learning Agents
- Neuronale Netze leicht gemacht (Teil 52): Forschung mit Optimismus und Verteilungskorrektur
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | Beispielsammlung EA |
| 2 | Study.mq5 | Expert Advisor | Trainings-EA des Agenten |
| 3 | Test.mq5 | Expert Advisor | Test-EA des Modells |
| 4 | Trajectory.mqh | Klassenbibliothek | Struktur der Systemzustandsbeschreibung |
| 5 | Netz_SAC_D_DICE.mqh | Klassenbibliothek | Modellklasse |
| 6 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes |
| 7 | NeuroNet.cl | Code Base | Die Bibliothek des Programmcodes von OpenCL |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/13098
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Danke Dmitry, ich klickte auf Ihr Verkäuferprofil in der Hoffnung, einige nn EAs zu finden, die ich testen könnte.
Ich habe eine udemy MQL5 Kurs auf nn genommen, jetzt versuchen, tiefer zu gehen. Ich bin mit Ihrer Serie von Artikeln beginnen.