Ordinale Kodierung für Nominalvariablen

Einführung

Wenn man beim maschinellen Lernen mit kategorischen Daten arbeitet, stößt man häufig auf nominale Variablen. Obwohl diese Variablen wertvolle Informationsquellen für die Modellierung sein können, können viele Algorithmen des maschinellen Lernens - insbesondere solche, die ausschließlich mit numerischen Daten arbeiten - sie nicht direkt verarbeiten. Um dieses Problem zu lösen, wandeln wir häufig nominale Variablen in ordinale Variablen um. In diesem Artikel befassen wir uns mit der Komplexität der Umwandlung von nominalen Variablen in ordinale Variablen. Wir werden die Gründe für solche Umrechnungen untersuchen, verschiedene Techniken für die Zuweisung von Ordinalwerten erörtern und die möglichen Vor- und Nachteile jedes Ansatzes aufzeigen. Darüber hinaus werden wir diese Methoden in erster Linie mit Python-Code demonstrieren, aber auch zwei vielseitige Transformationsmethoden in reinem MQL5 implementieren.

Nominal- und Ordinalvariablen verstehen

Nominale Variablen stellen kategoriale Daten dar, bei denen keine inhärente Ordnung oder Rangfolge zwischen den Kategorien besteht. Beispiele für Zeitreihendaten aus dem Finanzbereich könnten sein:

• Muster von Kursbalken (z. B. Pin Bar, Spinning Top, Hammer)
• Wochentage (z. B. Montag, Dienstag, Mittwoch)
  

Diese Variablen sind rein qualitativ, d. h. es gibt keine implizite Hierarchie oder Reihenfolge zwischen den Kategorien. So ist beispielsweise eine Pin-Bar-Formation nicht per se besser als ein Spinning Top, und ein Aufwärtsbalken (bullish) auch nicht besser als ein Abwärtsbalken (bearish).

Bei numerischen Berechnungen ist es üblich, beliebige ganze Zahlen bestimmten Kategorien zuzuordnen. Wenn diese ganzen Zahlen jedoch als Eingaben für einen Algorithmus für maschinelles Lernen verwendet werden, besteht die Gefahr, dass die zugewiesenen Werte die von den ursprünglichen Daten übermittelten Informationen verfälschen können. Der Algorithmus könnte fälschlicherweise zu dem Schluss kommen, dass größere Werte eine bestimmte Beziehung oder Rangfolge implizieren, auch wenn dies nicht beabsichtigt war.

Bei Ordinalvariablen handelt es sich dagegen um kategoriale Daten mit einer inhärenten Ordnung oder Rangfolge zwischen den Kategorien. Beispiele hierfür sind:

• Trendintensität (z. B. starker Trend, leichter Trend, schwacher Trend)
• Volatilität (z. B. hohe Volatilität, geringe Volatilität)

Wenn man diese Unterscheidung versteht, wird klar, warum die einfache Zuordnung von ganzen Zahlen zu nominalen Kategorien nicht immer angemessen ist. Zum besseren Verständnis werden wir einen Datensatz mit kategorialen Variablen erstellen, die in den folgenden Abschnitten mit verschiedenen Methoden in ein ordinales Format umgewandelt werden. Wir werden Daten der Tagesbalken (Open, High, Low, Close) für Bitcoin sammeln und nominale Variablen generieren, die zur Vorhersage der Renditen am nächsten Tag verwendet werden. Die erste nominale Variable klassifiziert die Balken entweder als auf- oder abwärts. Die zweite nominale Variable enthält vier verschiedene Kategorien und gruppiert die Balken auf der Grundlage des Verhältnisses zwischen der Körpergröße eines Leuchters und seiner vollen Größe. Für die letzte nominale Variable werden drei Kategorien gebildet:

• Wenn sowohl der aktuelle als auch der vorhergehende Balken nach oben tendieren (bullish) und der Tiefst- und Höchststand des aktuellen Balkens über dem Tiefst- und Höchststand des vorhergehenden Balkens liegt, bezeichnen wir den aktuellen Balken als „höheres Hoch“.

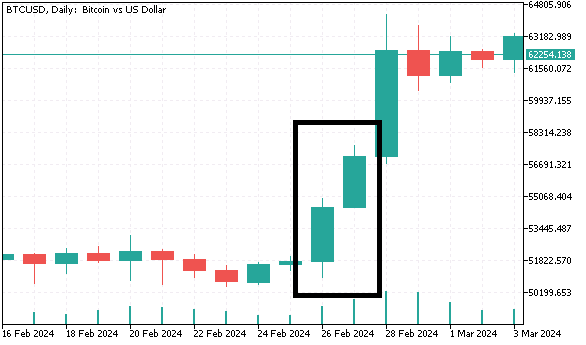
• Das gegenteilige Szenario wird als „tieferes Tief“ bezeichnet.

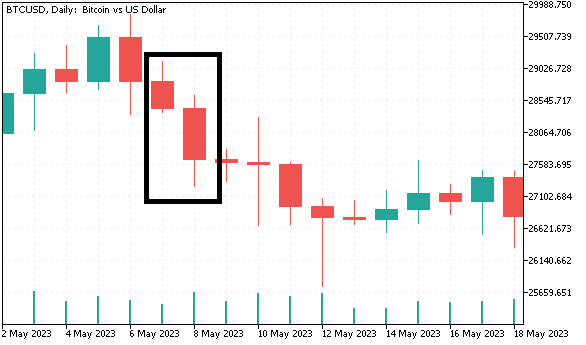
• Jedes andere Muster mit 2 Balken fällt in die dritte Kategorie.

Der Python-Code, mit dem dieser Datensatz erzeugt wird, ist unten aufgeführt.

# Copyright 2024, MetaQuotes Ltd.
# https://www.mql5.com
# imports 
from datetime import datetime
import MetaTrader5 as mt5
import pandas as pd
import numpy  as np
import pytz
import os
from category_encoders import OrdinalEncoder, OneHotEncoder, BinaryEncoder,TargetEncoder, CountEncoder, HashingEncoder, LeaveOneOutEncoder,JamesSteinEncoder

if not mt5.initialize():
    print("initialize() failed ")
    mt5.shutdown()
    exit()
 
#set up timezone infomation   
tz=pytz.timezone("Etc/UTC")

#use time zone to set correct date for history data extraction
startdate = datetime(2023,12,31,hour=23,minute=59,second=59,tzinfo=tz)
stopdate = datetime(2017,12,31,hour=23,minute=59,second=59,tzinfo=tz)

#list the symbol 
symbol = "BTCUSD"

#get price history
prices = pd.DataFrame(mt5.copy_rates_range(symbol,mt5.TIMEFRAME_D1,stopdate,startdate))

if len(prices) < 1:
    print(" Error downloading rates history ")
    mt5.shutdown()
    exit()

#shutdown mt5 tether
mt5.shutdown()

#drop unnecessary columns
prices.drop(labels=["time","tick_volume","spread","real_volume"],axis=1,inplace=True)

#initialize categorical features
prices["bar_type"] = np.where(prices["close"]>=prices["open"],"bullish","bearish")
prices["body_type"] = np.empty((len(prices),),dtype='str')
prices["bar_pattern"] = np.empty((len(prices),),dtype='str')

#set feature values
for i in np.arange(len(prices)):
    bodyratio = np.abs(prices.iloc[i,3]-prices.iloc[i,0])/np.abs(prices.iloc[i,1]-prices.iloc[i,2])
    if bodyratio >= 0.75:
        prices.iloc[i,5] = ">=0.75"
    elif bodyratio < 0.75 and bodyratio >= 0.5:
        prices.iloc[i,5]=">=0.5<0.75"
    elif bodyratio < 0.5 and bodyratio >= 0.25:
        prices.iloc[i,5]=">=0.25<0.5"
    else:
        prices.iloc[i,5]="<0.25"
    if i < 1:
      prices.iloc[i,6] = None
      continue
    if(prices.iloc[i,4]=="bullish" and prices.iloc[i-1,4]=="bullish") and (prices.iloc[i,1]>prices.iloc[i-1,1]) and (prices.iloc[i,2]>prices.iloc[i-1,2]):
        prices.iloc[i,6] = "higherHigh"
    elif(prices.iloc[i,4]=="bearish" and prices.iloc[i-1,4]=="bearish") and (prices.iloc[i,2]<prices.iloc[i-1,2]) and (prices.iloc[i,1]<prices.iloc[i-1,1]):
        prices.iloc[i,6] = "lowerLow"
    else :
        prices.iloc[i,6] = "flat"
 
#calculate target
look_ahead = 1
prices["target"] = np.log(prices["close"])
prices["target"] = prices["target"].diff(look_ahead)
prices["target"] = prices["target"].shift(-look_ahead)              

#drop rows with NA values
prices.dropna(axis=0,inplace=True,ignore_index=True)

print("Full feature matrix \n",prices.head())

Beachten Sie, dass in Python den Kategorien literale Namen zugewiesen werden, während in den folgenden MQL5-Codeauflistungen Ganzzahlen zur Unterscheidung zwischen den Kategorien verwendet werden.

//get relative shift of is and oos sets
   int trainstart,trainstop;
   trainstart=iBarShift(SetSymbol!=""?SetSymbol:NULL,tf,TrainingSampleStartDate);
   trainstop=iBarShift(SetSymbol!=""?SetSymbol:NULL,tf,TrainingSampleStopDate);
//check for errors from ibarshift calls
   if(trainstart<0 || trainstop<0)
     {
      Print(ErrorDescription(GetLastError()));
      return;
     }
//---set the size of the sample sets
   size_insample=(trainstop - trainstart) + 1;
//---check for input errors
   if(size_insample<=0)
     {
      Print("Invalid inputs ");
      return;
     }
//---
   if(!predictors.Resize(size_insample,3))
     {
      Print("ArrayResize error ",ErrorDescription(GetLastError()));
      return;
     }
//---
   if(!prices.CopyRates(SetSymbol,tf,COPY_RATES_VERTICAL|COPY_RATES_OHLC,TrainingSampleStartDate,TrainingSampleStopDate))
     {
      Print("Copyrates error ",ErrorDescription(GetLastError()));
      return;
     }
//---
   targets = log(prices.Col(3));
   targets = np::diff(targets);
//---
   double bodyratio = 0.0;
   for(ulong i = 0; i<prices.Rows(); i++)
     {
      if(prices[i][3]<prices[i][0])
         predictors[i][0] = 0.0;
      else
         predictors[i][0] = 1.0;

      bodyratio = MathAbs(prices[i][3]-prices[i][0])/MathAbs(prices[i][1]-prices[i][2]);

      if(bodyratio >=0.75)
         predictors[i][1] = 0.0;
      else
         if(bodyratio<0.75 && bodyratio>=0.5)
            predictors[i][1] = 1.0;
         else
            if(bodyratio<0.5 && bodyratio>=0.25)
               predictors[i][1] = 2.0;
            else
               predictors[i][1] = 3.0;

      if(i<1)
        {
         predictors[i][2] = 0.0;
         continue;
        }

      if(predictors[i][0]==1.0 && predictors[i-1][0]==1.0 && prices[i][1]>prices[i-1][1] && prices[i][2]>prices[i-1][2])
         predictors[i][2] = 2.0;
      else
         if(predictors[i][0]==0.0 && predictors[i-1][0]==0.0 && prices[i][2]<prices[i-1][2] && prices[i][1]>prices[i-1][1])
            predictors[i][2] = 1.0;
         else
            predictors[i][2] = 0.0;
     }

   targets = np::sliceVector(targets,1);

   prices = np::sliceMatrixRows(prices,1,predictors.Rows()-1);

   predictors = np::sliceMatrixRows(predictors,1,predictors.Rows()-1);

   matrix fullFeatureMatrix(predictors.Rows(),predictors.Cols()+prices.Cols());

   if(!np::matrixCopyCols(fullFeatureMatrix,prices,0,prices.Cols()) ||
      !np::matrixCopyCols(fullFeatureMatrix,predictors,prices.Cols()))
     {
      Print("Failed to merge matrices");
      return;
     }

Nachstehend finden Sie einen Auszug aus dem Datensatz.

Warum nominale Variablen in ordinale umwandeln?

Einige Algorithmen des maschinellen Lernens, wie z. B. Entscheidungsbäume, können direkt mit nominalen Daten umgehen. Andere jedoch - insbesondere lineare Modelle wie logistische Regression oder neuronale Netze - erfordern numerische Eingaben. Durch die Umwandlung von nominalen Variablen in ordinale Variablen können sie von diesen Modellen interpretiert werden, sodass die Algorithmen effektiver aus den Daten lernen können. Ordinalvariablen stellen zwar Kategorien dar, bieten aber auch eine klare Progression oder Rangfolge und geben Algorithmen mehr Kontext, um Beziehungen zu verstehen. Wenn eine nominale Variable wesentliche Informationen mit der Zielvariablen teilt, kann es oft von Vorteil sein, ihre Messgenauigkeit zu erhöhen. Wenn die nominale Variable aussagekräftige numerische Werte hat, können diese direkt als Eingaben für das Modell verwendet werden. Aber selbst wenn die Werte keine eigentliche numerische Bedeutung haben, können wir oft Ordinalwerte auf der Grundlage ihrer Beziehung zur Zielvariablen zuweisen.

Indem wir eine nominale Variable in eine Ordinalskala umwandeln, geben wir den Kategorien ein Gefühl von Ordnung oder Rangfolge. Dies kann die Fähigkeit des Modells verbessern, zugrunde liegende Muster und Beziehungen zwischen der Variable und dem Ziel zu erfassen. Theoretisch ist es zwar möglich, die nominale Variable auf das gleiche Messniveau wie die Zielvariable zu heben, doch in der Praxis reicht es oft aus, sie in eine Ordinalskala umzuwandeln. Dieser Ansatz stellt ein Gleichgewicht zwischen der Erhaltung des Informationsgehalts der Variablen und der Minimierung des Rauschens her. In den folgenden Abschnitten werden gängige Techniken zur Umwandlung von nominalen Variablen in ordinale Formen sowie wichtige Überlegungen zur Wahrung der Datenintegrität erläutert.

Nominale variable Umrechnungstechniken

Wir beginnen mit der einfachsten Methode: der ordinalen Kodierung. Bei dieser Methode wird jeder Kategorie einfach ein ganzzahliger Wert zugewiesen. Wie bereits erwähnt, werden die Kategorien dadurch in eine Rangfolge gebracht. Wenn der Praktiker mit den Daten vertraut ist und im Voraus weiß, wie sich die Kategorien auf die Zielvariable beziehen, sollte diese Methode ausreichen. Die ordinale Kodierung sollte jedoch beim unüberwachten Lernen nicht verwendet werden, da sie leicht zu Verzerrungen führen kann, indem sie eine Reihenfolge impliziert, die nicht existiert.

Um unseren Datensatz mit nominalen Variablen in Python zu konvertieren, verwenden wir das Paket category_encoders. Dieses Paket bietet eine breite Palette von Implementierungen kategorischer Transformationen und ist damit für die meisten Aufgaben geeignet. Weitere Informationen finden Sie im Repositorium auf GitHub des Projekts.

Für die Konvertierung von Variablen in das numerische Ordinalformat ist das Objekt OrdinalEncoder erforderlich.

#Ordinal encoding
ord_encoder = OrdinalEncoder(cols = ["bar_type","body_type","bar_pattern"])
ordinal_data = ord_encoder.fit_transform(prices)

print(" ordinal encoding\n ", ordinal_data.head())

Die transformierten Daten:

Geeignete Konvertierungstechniken für Algorithmen des unüberwachten Lernens sind die Binärkodierung, die One-Hot-Kodierung und die Frequenzkodierung. Bei der One-Hot-Kodierung wird jede Kategorie in eine binäre Spalte umgewandelt, in der das Vorhandensein einer Kategorie mit einer 1 und ihr Fehlen mit einer 0 gekennzeichnet wird. Der größte Nachteil dieser Methode besteht darin, dass sich die Zahl der Eingabevariablen erheblich erhöht. Für jede Kategorie einer kategorialen Variablen wird eine neue Variable erstellt. Wenn wir zum Beispiel die Monate des Jahres kodieren würden, hätten wir 11 zusätzliche Eingabevariablen.

Der „OneHotEncoder“ behandelt die One-Hot-Kodierung im Paket category_encoders.

#One-Hot encoding
onehot_encoder = OneHotEncoder(cols = ["bar_type","body_type","bar_pattern"])
onehot_data = onehot_encoder.fit_transform(prices)

print(" ordinal encoding\n ", onehot_data.head())

Die transformierten Daten:

Die binäre Kodierung ist eine effizientere Alternative, insbesondere wenn es um zahlreiche Kategorien geht. Bei dieser Methode wird jede Kategorie zunächst in eine eindeutige, ganze Zahl umgewandelt und diese dann als Binärzahl dargestellt. Diese binäre Darstellung wird auf mehrere Spalten verteilt, was im Vergleich zur One-Hot-Kodierung in der Regel zu weniger Spalten führt. Um beispielsweise 12 Monate zu kodieren, werden nur 4 Binärspalten benötigt. Die binäre Kodierung eignet sich gut für Szenarien, in denen die kategoriale Variable viele eindeutige Kategorien hat und Sie die Anzahl der Eingabevariablen begrenzen möchten.

Binäre Kodierung unseren BTCUSD-Datensatz.

#Binary encoding
binary_encoder = BinaryEncoder(cols = ["bar_type","body_type","bar_pattern"])
binary_data = binary_encoder.fit_transform(prices)

print(" binary encoding\n ", binary_data.head())

Die transformierten Daten:

Bei der Frequenzkodierung wird eine kategoriale Variable umgewandelt, indem jede Kategorie durch die Häufigkeit ihres Auftretens im Datensatz ersetzt wird. Anstatt mehrere Spalten zu erstellen, wird jede Kategorie durch den Anteil oder die Anzahl der Häufigkeit ihres Auftretens ersetzt. Dieser Ansatz ist nützlich, wenn eine sinnvolle Beziehung zwischen der Häufigkeit einer Kategorie und der Zielvariablen besteht, da er wertvolle Informationen in einer kompakteren Form bewahrt. Es kann jedoch zu Verzerrungen kommen, wenn bestimmte Kategorien im Datensatz dominieren. Sie wird oft als erster Schritt in einer komplexeren Entwicklungspipeline für Merkmale in Szenarien des unüberwachten Lernens verwendet.

Hier verwenden wir das Objekt „CountEncoder“.

#Frequency encoding
freq_encoder = CountEncoder(cols = ["bar_type","body_type","bar_pattern"])
freq_data = freq_encoder.fit_transform(prices)

print(" frequency encoding\n ", freq_data.head())

Die transformierten Daten:

Binäre Kodierung, One-Hot-Kodierung und Frequenzkodierung sind vielseitige Techniken, die auf die meisten kategorialen Daten angewandt werden können, ohne dass das Risiko besteht, unerwünschte Nebeneffekte einzuführen, die das Lernergebnis beeinträchtigen könnten. Diese Transformationen haben die wichtige Eigenschaft, unabhängig von der Zielvariablen zu sein.

In einigen Fällen kann ein Algorithmus für maschinelles Lernen jedoch von Transformationen profitieren, die die Assoziation einer Variablen mit dem Ziel widerspiegeln. Diese Methoden nutzen die Zielvariable, um kategoriale Daten in numerische Werte umzuwandeln, die ein gewisses Maß an Assoziativität vermitteln und so die Vorhersagekraft des Modells verbessern können.

Eine dieser Methoden ist die Zielkodierung, auch bekannt als Mittelwertkodierung. Bei diesem Ansatz wird jede Kategorie durch den Mittelwert der Zielvariablen für diese Kategorie ersetzt. Wenn wir beispielsweise die Wahrscheinlichkeit vorhersagen wollen, dass eine Aktie höher schließt (binäres Ziel), könnten wir jede Kategorie in einer nominalen Variablen - z. B. Handelsvolumenbereich - durch die durchschnittliche Wahrscheinlichkeit zu schließen für jeden Bereich ersetzen. Die Kodierung des Ziels kann bei kategorialen Variablen mit hoher Kardinalität besonders leistungsfähig sein, da sie nützliche Informationen konsolidiert, ohne die Dimensionalität des Datensatzes zu erhöhen. Diese Technik hilft bei der Erfassung von Beziehungen zwischen der kategorialen Variable und dem Ziel, was sie für überwachte Lernaufgaben effektiv macht. Sie ist vor allem dann wirksam, wenn die Kategorien eine starke Korrelation mit dem Ziel haben. Sie müssen aber auch mit überangepassten Abschwächungsverfahren gepaart werden, um eine bessere Verallgemeinerung zu gewährleisten.

#Target encoding
target_encoder = TargetEncoder(cols = ["bar_type","body_type","bar_pattern"])
target_data = target_encoder.fit_transform(prices[["open","high","low","close","bar_type","body_type","bar_pattern"]], prices["target"])

print(" target encoding\n ", target_data.head())

Die transformierten Daten:

Eine weitere zielabhängige Methode ist die Leave-One-Out-Kodierung. Sie funktioniert ähnlich wie die Zielkodierung, passt aber die Kodierung an, indem sie den Zielwert der aktuellen Zeile bei der Berechnung des Mittelwerts für diese Kategorie ausschließt. Dies trägt dazu bei, eine Überanpassung zu vermeiden, insbesondere wenn der Datensatz klein ist oder wenn bestimmte Kategorien überrepräsentiert sind. Die Leave-One-Out-Kodierung stellt sicher, dass die Transformation unabhängig von der verarbeiteten Zeile bleibt und somit die Integrität des Lernprozesses gewahrt wird.

#LeaveOneOut encoding
oneout_encoder = LeaveOneOutEncoder(cols = ["bar_type","body_type","bar_pattern"])
oneout_data = oneout_encoder.fit_transform(prices[["open","high","low","close","bar_type","body_type","bar_pattern"]], prices["target"])

print(" LeaveOneOut encoding\n ", oneout_data.head())

Die transformierten Daten:

Die James-Stein Kodierung ist ein Bayes'scher Kodierungsansatz, der die Schätzung des Zielmittelwerts einer Kategorie auf den Gesamtmittelwert reduziert, abhängig von der Menge der für jede Kategorie verfügbaren Daten. Diese Technik ist besonders nützlich für Datensätze mit geringer Kardinalität, bei denen herkömmliche Methoden wie Target Encoding oder Leave-One-Out Encoding zu einer Überanpassung führen können, insbesondere bei kleinen Datensätzen oder bei Kategorien, die eine sehr ungleichmäßige Verteilung aufweisen. Durch die Anpassung der Mittelwerte der Kategorien auf der Grundlage des Gesamtmittelwerts mindert die James-Stein-Kodierung das Risiko, dass Extremwerte das Modell unangemessen beeinflussen. Dies führt zu stabileren und robusteren Schätzungen und macht sie zu einer effektiven Alternative, wenn es um wenig (sparse) Daten oder Kategorien mit wenigen Beobachtungen geht.

#James Stein encoding
james_encoder = JamesSteinEncoder(cols = ["bar_type","body_type","bar_pattern"])
james_data = james_encoder.fit_transform(prices[["open","high","low","close","bar_type","body_type","bar_pattern"]], prices["target"])

print(" James Stein encoding\n ", james_data.head())

Transformierte Daten:

Die category_encoders-Bibliothek bietet eine Vielzahl von Kodierungsverfahren, die auf verschiedene Arten von kategorialen Daten und Aufgaben des maschinellen Lernens zugeschnitten sind. Die geeignete Kodierungsmethode hängt von der Art der Daten, dem verwendeten maschinellen Lernalgorithmus und den spezifischen Anforderungen der jeweiligen Aufgabe ab. Zusammenfassend lässt sich sagen, dass die One-Hot-Kodierung eine vielseitige Methode ist, die sich für viele Anwendungsfälle eignet, insbesondere wenn es um nominale Variablen geht. Zielkodierung, Leave-One-Out-Kodierung und James-Stein-Kodierung sollten verwendet werden, wenn die Beziehung zwischen einer Variablen und dem Ziel hervorgehoben werden muss. Schließlich sind die binäre Kodierung und die Hash-Kodierung nützliche Techniken, wenn das Ziel darin besteht, die Dimensionalität zu verringern und dennoch aussagekräftige Informationen zu erhalten.

Umwandlung von Nominal- in Ordinalzahlen in MQL5

In diesem Abschnitt implementieren wir zwei Methoden zur Kodierung von Nominalvariablen in MQL5, die beide in Klassen gekapselt sind, die in der Header-Datei nom2ord.mqh deklariert sind. Die Klasse COneHotEncoder implementiert die One-Hot-Kodierung für Datensätze und verfügt über zwei Hauptmethoden, mit denen die Nutzer vertraut sein sollten.

//+------------------------------------------------------------------+
//| one hot encoder class                                            |
//+------------------------------------------------------------------+
class COneHotEncoder
  {
private:
   vector            m_mapping[];
   ulong             m_cat_cols[];
   ulong             m_vars,m_cols;
public:
   //+------------------------------------------------------------------+
   //|  Constructor                                                     |
   //+------------------------------------------------------------------+
                     COneHotEncoder(void)
     {
     }
   //+------------------------------------------------------------------+
   //|  Destructor                                                      |
   //+------------------------------------------------------------------+
                    ~COneHotEncoder(void)
     {
      ArrayFree(m_mapping);
     }
   //+------------------------------------------------------------------+
   //| map categorical features of a training dataset                   |
   //+------------------------------------------------------------------+
   bool              fit(matrix &in_data,ulong &cols[])
     {
      m_cols = in_data.Cols();
      matrix data = np::selectMatrixCols(in_data,cols);

      if(data.Cols()!=ulong(cols.Size()))
        {
         Print(__FUNCTION__, " invalid input data ");
         return false;
        }

      m_vars = ulong(cols.Size());

      if(ArrayCopy(m_cat_cols,cols)<=0 || !ArraySort(m_cat_cols))
        {
         Print(__FUNCTION__, " ArrayCopy or ArraySort failure ", GetLastError());
         return false;
        }

      if(ArrayResize(m_mapping,int(m_vars))<0)
        {
         Print(__FUNCTION__, " Vector array resize failure ", GetLastError());
         return false;
        }

      for(ulong i = 0; i<m_vars; i++)
        {
         vector unique = data.Col(i);
         m_mapping[i] = np::unique(unique);
        }

      return true;
     }
   //+------------------------------------------------------------------+
   //| Transform abitrary feature matrix to learned category m_mapping  |
   //+------------------------------------------------------------------+

   matrix            transform(matrix &in_data)
     {
      if(in_data.Cols()!=m_cols)
        {
         Print(__FUNCTION__," Column dimension of input not equal to ", m_cols);
         return matrix::Zeros(1,1);
        }

      matrix out,input_copy;
      matrix data = np::selectMatrixCols(in_data,m_cat_cols);

      if(data.Cols()!=ulong(m_cat_cols.Size()))
        {
         Print(__FUNCTION__, " invalid input data ");
         return matrix::Zeros(1,1);
        }

      ulong unchanged_feature_cols[];

      for(ulong i = 0; i<in_data.Cols(); i++)
        {
         int found = ArrayBsearch(m_cat_cols,i);
         if(m_cat_cols[found]!=i)
           {
            if(!unchanged_feature_cols.Push(i))
              {
               Print(__FUNCTION__, " Failed array insertion ", GetLastError());
               return matrix::Zeros(1,1);
              }
           }
        }

      input_copy = unchanged_feature_cols.Size()?np::selectMatrixCols(in_data,unchanged_feature_cols):input_copy;
      ulong numcols = 0;
      vector cumsum = vector::Zeros(ulong(MathMin(m_vars,data.Cols())));

      for(ulong i = 0; i<cumsum.Size(); i++)
        {
         cumsum[i] = double(numcols);
         numcols+=m_mapping[i].Size();
        }

      out = matrix::Zeros(data.Rows(),numcols);

      for(ulong i = 0;i<data.Rows(); i++)
        {
         vector row = data.Row(i);
         for(ulong col = 0; col<row.Size(); col++)
           {
            for(ulong k = 0; k<m_mapping[col].Size(); k++)
              {
               if(MathAbs(row[col]-m_mapping[col][k])<=1.e-15)
                 {
                  out[i][ulong(cumsum[col])+k]=1.0;
                  break;
                 }
              }
           }
        }

      matrix newfeaturematrix(out.Rows(),input_copy.Cols()+out.Cols());

      if((input_copy.Cols()>0 && !np::matrixCopyCols(newfeaturematrix,input_copy,0,input_copy.Cols())) || !np::matrixCopyCols(newfeaturematrix,out,input_copy.Cols()))
        {
         Print(__FUNCTION__, " Failed matrix copy ");
         return matrix::Zeros(1,1);
        }

      return newfeaturematrix;

     }

  };
//+------------------------------------------------------------------+

Die erste Methode ist fit(), die nach der Erstellung einer Instanz der Klasse aufgerufen werden sollte. Diese Methode erfordert zwei Eingaben: eine Merkmalsmatrix (Trainingsdaten) und ein Array. Bei der Merkmalsmatrix kann es sich um den gesamten Datensatz handeln, der sowohl kategoriale als auch nicht-kategoriale Variablen enthält. Wenn dies der Fall ist, sollte das Array die Spaltenindizes der nominalen Variablen innerhalb der Matrix enthalten. Wird ein leeres Array angegeben, wird davon ausgegangen, dass alle Variablen nominal sind. Nachdem die Methode fit() erfolgreich ausgeführt wurde und „true“ zurückgibt, kann die Methode transform() aufgerufen werden, um den transformierten Datensatz zu erhalten. Diese Methode erfordert eine Matrix, die die gleiche Anzahl von Spalten hat wie die Matrix, die der fit()-Methode übergeben wurde. Wenn die Abmessungen nicht übereinstimmen, wird ein Fehler angezeigt.

Untersuchen wir die Funktionsweise der Klasse COneHotEncoder anhand einer Demonstration mit dem BTCUSD-Datensatz, der weiter oben in diesem Text vorbereitet wurde. Der folgende Ausschnitt veranschaulicht den Umwandlungsprozess. Dieser Code stammt aus dem MetaTrader 5-Skript OneHotEncoding_demo.mq5.

//+------------------------------------------------------------------+
//|                                          OneHotEncoding_demo.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<np.mqh>
#include<nom2ord.mqh>
#include<ErrorDescription.mqh>
//--- input parameters
input datetime TrainingSampleStartDate=D'2023.12.31';
input datetime TrainingSampleStopDate=D'2017.12.31';
input ENUM_TIMEFRAMES tf = PERIOD_D1;
input string   SetSymbol="BTCUSD";
//+------------------------------------------------------------------+
//|global integer variables                                          |
//+------------------------------------------------------------------+
int size_insample,                 //training set size
    size_observations,             //size of of both training and testing sets combined
    price_handle=INVALID_HANDLE;   //log prices indicator handle
//+------------------------------------------------------------------+
//|double global variables                                           |
//+------------------------------------------------------------------+

matrix       prices;                   //array for log transformed prices
vector       targets;                  //differenced prices kept here
matrix       predictors;               //flat array arranged as matrix of all predictors ie size_observations by size_predictors
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//get relative shift of is and oos sets
   int trainstart,trainstop;
   trainstart=iBarShift(SetSymbol!=""?SetSymbol:NULL,tf,TrainingSampleStartDate);
   trainstop=iBarShift(SetSymbol!=""?SetSymbol:NULL,tf,TrainingSampleStopDate);
//check for errors from ibarshift calls
   if(trainstart<0 || trainstop<0)
     {
      Print(ErrorDescription(GetLastError()));
      return;
     }
//---set the size of the sample sets
   size_insample=(trainstop - trainstart) + 1;
//---check for input errors
   if(size_insample<=0)
     {
      Print("Invalid inputs ");
      return;
     }
//---
   if(!predictors.Resize(size_insample,3))
     {
      Print("ArrayResize error ",ErrorDescription(GetLastError()));
      return;
     }
//---
   if(!prices.CopyRates(SetSymbol,tf,COPY_RATES_VERTICAL|COPY_RATES_OHLC,TrainingSampleStartDate,TrainingSampleStopDate))
     {
      Print("Copyrates error ",ErrorDescription(GetLastError()));
      return;
     }
//---
   targets = log(prices.Col(3));
   targets = np::diff(targets);
//---
   double bodyratio = 0.0;
   for(ulong i = 0; i<prices.Rows(); i++)
     {
      if(prices[i][3]<prices[i][0])
         predictors[i][0] = 0.0;
      else
         predictors[i][0] = 1.0;

      bodyratio = MathAbs(prices[i][3]-prices[i][0])/MathAbs(prices[i][1]-prices[i][2]);

      if(bodyratio >=0.75)
         predictors[i][1] = 0.0;
      else
         if(bodyratio<0.75 && bodyratio>=0.5)
            predictors[i][1] = 1.0;
         else
            if(bodyratio<0.5 && bodyratio>=0.25)
               predictors[i][1] = 2.0;
            else
               predictors[i][1] = 3.0;

      if(i<1)
        {
         predictors[i][2] = 0.0;
         continue;
        }

      if(predictors[i][0]==1.0 && predictors[i-1][0]==1.0 && prices[i][1]>prices[i-1][1] && prices[i][2]>prices[i-1][2])
         predictors[i][2] = 2.0;
      else
         if(predictors[i][0]==0.0 && predictors[i-1][0]==0.0 && prices[i][2]<prices[i-1][2] && prices[i][1]>prices[i-1][1])
            predictors[i][2] = 1.0;
         else
            predictors[i][2] = 0.0;
     }

   targets = np::sliceVector(targets,1);

   prices = np::sliceMatrixRows(prices,1,predictors.Rows()-1);

   predictors = np::sliceMatrixRows(predictors,1,predictors.Rows()-1);

   matrix fullFeatureMatrix(predictors.Rows(),predictors.Cols()+prices.Cols());

   if(!np::matrixCopyCols(fullFeatureMatrix,prices,0,prices.Cols()) ||
      !np::matrixCopyCols(fullFeatureMatrix,predictors,prices.Cols()))
     {
      Print("Failed to merge matrices");
      return;
     }

   if(predictors.Rows()!=targets.Size())
     {
      Print(" Error in aligning data structures ");
      return;
     }

   COneHotEncoder enc;

   ulong selectedcols[] = {4,5,6};

   if(!enc.fit(fullFeatureMatrix,selectedcols))
      return;

   matrix transformed = enc.transform(fullFeatureMatrix);

   Print(" Original predictors \n", fullFeatureMatrix);
   Print(" transformed predictors \n", transformed);
  }
//+------------------------------------------------------------------+

Die Merkmalsmatrix vorher:

RQ      0       16:40:41.760    OneHotEncoding_demo (BTCUSD,D1)  Original predictors 
ED      0       16:40:41.761    OneHotEncoding_demo (BTCUSD,D1) [[13743,13855,12362.69,13347,0,2,0]
RN      0       16:40:41.761    OneHotEncoding_demo (BTCUSD,D1)  [13348,15381,12535.67,14689,1,2,0]
DG      0       16:40:41.761    OneHotEncoding_demo (BTCUSD,D1)  [14232.48,15408,14110.57,15130,1,1,2]
HH      0       16:40:41.761    OneHotEncoding_demo (BTCUSD,D1)  [15114,15370,13786.18,15139,1,3,0]
QN      0       16:40:41.761    OneHotEncoding_demo (BTCUSD,D1)  [15055.8,16894,14349.84,16725,1,1,2]
RP      0       16:40:41.761    OneHotEncoding_demo (BTCUSD,D1)  [15699.53,16474,15672.99,16186,1,1,0]
OI      0       16:40:41.761    OneHotEncoding_demo (BTCUSD,D1)  [16187,16258,13639.83,14900,0,2,0]
ML      0       16:40:41.761    OneHotEncoding_demo (BTCUSD,D1)  [14884,15334,13777.33,14405,0,2,0]
GS      0       16:40:41.761    OneHotEncoding_demo (BTCUSD,D1)  [14405,14876,12969.58,14876,1,3,0]
KF      0       16:40:41.761    OneHotEncoding_demo (BTCUSD,D1)  [14876,14927,12417.22,13245,0,1,0]
ON      0       16:40:41.761    OneHotEncoding_demo (BTCUSD,D1)  [12776.79,14078.5,12355.38,13681,1,1,0…]]

Die Merkmalsmatrix nachher:

PH      0       16:40:41.762    OneHotEncoding_demo (BTCUSD,D1)  transformed predictors 
KP      0       16:40:41.762    OneHotEncoding_demo (BTCUSD,D1) [[13743,13855,12362.69,13347,1,0,1,0,0,0,1,0,0]
KP      0       16:40:41.762    OneHotEncoding_demo (BTCUSD,D1)  [13348,15381,12535.67,14689,0,1,1,0,0,0,1,0,0]
NF      0       16:40:41.762    OneHotEncoding_demo (BTCUSD,D1)  [14232.48,15408,14110.57,15130,0,1,0,1,0,0,0,1,0]
JI      0       16:40:41.762    OneHotEncoding_demo (BTCUSD,D1)  [15114,15370,13786.18,15139,0,1,0,0,1,0,1,0,0]
CL      0       16:40:41.762    OneHotEncoding_demo (BTCUSD,D1)  [15055.8,16894,14349.84,16725,0,1,0,1,0,0,0,1,0]
RL      0       16:40:41.762    OneHotEncoding_demo (BTCUSD,D1)  [15699.53,16474,15672.99,16186,0,1,0,1,0,0,1,0,0]
IS      0       16:40:41.762    OneHotEncoding_demo (BTCUSD,D1)  [16187,16258,13639.83,14900,1,0,1,0,0,0,1,0,0]
GG      0       16:40:41.762    OneHotEncoding_demo (BTCUSD,D1)  [14884,15334,13777.33,14405,1,0,1,0,0,0,1,0,0]
QK      0       16:40:41.762    OneHotEncoding_demo (BTCUSD,D1)  [14405,14876,12969.58,14876,0,1,0,0,1,0,1,0,0]
PL      0       16:40:41.762    OneHotEncoding_demo (BTCUSD,D1)  [14876,14927,12417.22,13245,1,0,0,1,0,0,1,0,0]
GS      0       16:40:41.762    OneHotEncoding_demo (BTCUSD,D1)  [12776.79,14078.5,12355.38,13681,0,1,0,1,0,0,1,0,0.]]

Die zweite in MQL5 implementierte Konvertierungsmethode arbeitet in zwei Modi, die beide Variationen der Zielkodierung sind, die modifiziert wurden, um die Auswirkungen von Overfitting zu reduzieren. Diese Technik ist in der Klasse CNomOrd gekapselt, die in nom2ord.mqh definiert ist. Die Klasse nutzt die bekannten Methoden fit() und transform(), um Variablen zu konvertieren, ohne die Dimensionalität kategorialer Eingaben zu reduzieren.

public:
   //+------------------------------------------------------------------+
   //|  constructor                                                     |
   //+------------------------------------------------------------------+

                     CNomOrd(void)
     {
     }
   //+------------------------------------------------------------------+
   //|  destructor                                                      |
   //+------------------------------------------------------------------+

                    ~CNomOrd(void)
     {
     }
   //+------------------------------------------------------------------+
   //| fit mapping to training data                                     |
   //+------------------------------------------------------------------+

   bool              fit(matrix &preds_in, ulong &cols[], vector &target)
     {
      m_dim_reduce = 0;
      mapped = false;
      //---
      if(cols.Size()==0 && preds_in.Cols())
        {
         m_pred = int(preds_in.Cols());
         if(!np::arange(m_colindices,m_pred,ulong(0),ulong(1)))
           {
            Print(__FUNCTION__, " arange error ");
            return mapped;
           }
        }
      else
        {
         m_pred = int(cols.Size());
        }
      //---
      m_rows = int(preds_in.Rows()) ;
      m_cols = int(preds_in.Cols());
      //---
      if(ArrayResize(m_mean_rankings,m_pred)<0 ||
         ArrayResize(m_rankings,m_rows)<0 ||
         ArrayResize(m_indices,m_rows)<0 ||
         ArrayResize(m_mapping,m_pred)<0  ||
         ArrayResize(m_class_counts,m_pred)<0  ||
         !m_median.Resize(m_pred) ||
         !m_class_ids.Resize(m_rows,m_pred) ||
         !shuffle_target.Resize(m_rows,2) ||
         (cols.Size()>0 && ArrayCopy(m_colindices,cols)<0) ||
         !ArraySort(m_colindices))
        {
         Print(__FUNCTION__, " Memory allocation failure ", GetLastError());
         return mapped;
        }
      //---
      for(uint col = 0; col<m_colindices.Size(); col++)
        {
         vector var = preds_in.Col(m_colindices[col]);
         m_mapping[col] = np::unique(var);
         m_class_counts[col] = vector::Zeros(m_mapping[col].Size());
         for(ulong i = 0; i<var.Size(); i++)
           {
            for(ulong j = 0; j<m_mapping[col].Size(); j++)
              {
               if(MathAbs(var[i]-m_mapping[col][j])<=1.e-15)
                 {
                  m_class_ids[i][col]=double(j);
                  ++m_class_counts[col][j];
                  break;
                 }
              }
           }
        }

      m_target = target;

      for(uint i = 0; i<m_colindices.Size(); i++)
        {
         vector cid = m_class_ids.Col(i);
         vector ccounts = m_class_counts[i];
         m_mean_rankings[i] = train(cid,ccounts,m_target,m_median[i]);
        }

      mapped = true;
      return mapped;
     }
   //+------------------------------------------------------------------+
   //|  transform nominal to ordinal based on learned mapping           |
   //+------------------------------------------------------------------+

   matrix            transform(matrix &data_in)
     {
      if(m_dim_reduce)
        {
         Print(__FUNCTION__, " Invalid method call, Use fitTransform() or call fit() ");
         return matrix::Zeros(1,1);
        }

      if(!mapped)
        {
         Print(__FUNCTION__, " Invalid method call, training either failed or was not done. Call fit() first. ");
         return matrix::Zeros(1,1);
        }

      if(data_in.Cols()!=ulong(m_cols))
        {
         Print(__FUNCTION__, " Unexpected input data shape, doesnot match training data ");
         return matrix::Zeros(1,1);
        }
      //---
      matrix out = data_in;
      //---
      for(uint col = 0; col<m_colindices.Size(); col++)
        {
         vector var = data_in.Col(m_colindices[col]);
         for(ulong i = 0; i<var.Size(); i++)
           {
            for(ulong j = 0; j<m_mapping[col].Size(); j++)
              {
               if(MathAbs(var[i]-m_mapping[col][j])<=1.e-15)
                 {
                  out[i][m_colindices[col]]=m_mean_rankings[col][j];
                  break;
                 }
              }
           }
        }
      //---
      return out;
     }

Die Methode fit() erfordert eine zusätzliche Eingabe: einen Vektor, der als entsprechende Zielvariable verwendet wird. Das Kodierungsschema unterscheidet sich von der Standard-Zielkodierung, um die Überanpassung zu minimieren, die häufig durch Ausreißer in der Verteilung der Zielvariablen entsteht. Um dieses Problem zu lösen, wird in der Klasse eine Perzentil-Transformation verwendet. Die Zielwerte werden in eine prozentuale Skala umgewandelt, wobei dem Mindestwert ein Perzentilrang von 0 zugewiesen wird, der Höchstwert einen Rang von 100 erhält und Zwischenwerte proportional skaliert werden. Bei diesem Ansatz bleibt die ordinale Beziehung zwischen den Werten erhalten, während der Einfluss von Ausreißern abgeschwächt wird.

   //+------------------------------------------------------------------+
   //|   test for a genuine relationship between predictor and target   |
   //+------------------------------------------------------------------+

   double            score(int reps, vector &test_target,ulong selectedVar=0)
     {
      if(!mapped)
        {
         Print(__FUNCTION__, " Invalid method call, training either failed or was not done. Call fit() first. ");
         return -1.0;
        }

      if(m_dim_reduce==0 && selectedVar>=ulong(m_colindices.Size()))
        {
         Print(__FUNCTION__, " invalid predictor selection ");
         return -1.0;
        }

      if(test_target.Size()!=m_rows)
        {
         Print(__FUNCTION__, " invalid targets parameter, Does not match shape of training data. ");
         return -1.0;
        }

      int i, j, irep, unif_error ;
      double dtemp, min_neg, max_neg, min_pos, max_pos, medn ;
      dtemp = 0.0;
      min_neg = 0.0;
      max_neg = -DBL_MIN;
      min_pos = DBL_MAX;
      max_pos = DBL_MIN ;

      vector id = (m_dim_reduce)?m_class_ids.Col(0):m_class_ids.Col(selectedVar);
      vector cc = (m_dim_reduce)?m_class_counts[0]:m_class_counts[selectedVar];
      int nclasses = int(cc.Size());

      if(reps < 1)
         reps = 1 ;

      for(irep=0 ; irep<reps ; irep++)
        {

         if(!shuffle_target.Col(test_target,0))
           {
            Print(__FUNCTION__, " error filling shuffle_target column ", GetLastError());
            return -1.0;
           }

         if(irep)
           {
            i = m_rows ;
            while(i > 1)
              {
               j = (int)(MathRandomUniform(0.0,1.0,unif_error) * i) ;
               if(unif_error)
                 {
                  Print(__FUNCTION__, " mathrandomuniform() error ", unif_error);
                  return -1.0;
                 }
               if(j >= i)
                  j = i - 1 ;
               dtemp = shuffle_target[--i][0] ;
               shuffle_target[i][0] = shuffle_target[j][0] ;
               shuffle_target[j][0] = dtemp ;
              }
           }

         vector totrain = shuffle_target.Col(0);
         vector m_ranks = train(id,cc,totrain,medn) ;

         if(irep == 0)
           {
            for(i=0 ; i<nclasses ; i++)
              {
               if(i == 0)
                  min_pos = max_pos = m_ranks[i] ;
               else
                 {
                  if(m_ranks[i] > max_pos)
                     max_pos = m_ranks[i] ;
                  if(m_ranks[i] < min_pos)
                     min_pos = m_ranks[i] ;
                 }
              } // For i<nclasses
            orig_max_class = max_pos - min_pos ;
            count_max_class = 1 ;

           }
         else
           {
            for(i=0 ; i<nclasses ; i++)
              {
               if(i == 0)
                  min_pos = max_pos = m_ranks[i];
               else
                 {
                  if(m_ranks[i] > max_pos)
                     max_pos = m_ranks[i] ;
                  if(m_ranks[i] < min_pos)
                     min_pos = m_ranks[i] ;
                 }
              } // For i<nclasses
            if(max_pos - min_pos >= orig_max_class)
               ++count_max_class ;

           }
        }



      if(reps <= 1)
         return -1.0;

      return double(count_max_class)/ double(reps);

     }

Die Methode score() wird verwendet, um die statistische Signifikanz der impliziten Beziehung zwischen einer ordinalen Variablen und einem Ziel zu bewerten. Ein Monte-Carlo-Permutationstest wird eingesetzt, um die Daten der Zielvariablen wiederholt zu mischen und die beobachtete Beziehung neu zu berechnen. Durch den Vergleich der beobachteten Beziehung mit der Verteilung der Beziehungen, die durch zufällige Permutationen erhalten werden, können wir die Wahrscheinlichkeit schätzen, dass die beobachtete Beziehung nur auf Zufall beruht. Um die beobachtete Beziehung zu quantifizieren, berechnen wir die Differenz zwischen dem maximalen und dem minimalen mittleren Zielperzentil über alle Kategorien der nominalen Variablen. Daher gibt die Methode score() einen Wahrscheinlichkeitswert zurück, der als Ergebnis des Hypothesentests dient, wobei die Nullhypothese besagt, dass der beobachtete Unterschied zufällig aus einer nicht verwandten nominalen Variable und einem Ziel entstanden sein könnte.

Wir wollen sehen, wie das funktioniert, indem wir die Klasse auf unseren BTCUSD-Datensatz anwenden. Diese Demonstration ist in dem MQL5-Skript TargetBasedNominalVariableConversion_demo.mq5 enthalten.

CNomOrd enc;
   
   ulong selectedcols[] = {4,5,6};
    
   if(!enc.fit(fullFeatureMatrix,selectedcols,targets))
     return;
     
   matrix transformed = enc.transform(fullFeatureMatrix);
   
   Print(" Original predictors \n", fullFeatureMatrix);
   Print(" transformed predictors \n", transformed);
   
   for(uint i = 0; i<selectedcols.Size(); i++)
      Print(" Probability that predicator at ", selectedcols[i] , " is associated with target ", enc.score(10000,targets,ulong(i)));

Die transformierten Daten:

IQ      0       16:44:25.680    TargetBasedNominalVariableConversion_demo (BTCUSD,D1)    transformed predictors 
LM      0       16:44:25.680    TargetBasedNominalVariableConversion_demo (BTCUSD,D1)   [[13743,13855,12362.69,13347,52.28360492434251,50.66453470243147,50.45172139701621]
CN      0       16:44:25.680    TargetBasedNominalVariableConversion_demo (BTCUSD,D1)    [13348,15381,12535.67,14689,47.85025875164135,50.66453470243147,50.45172139701621]
IH      0       16:44:25.680    TargetBasedNominalVariableConversion_demo (BTCUSD,D1)    [14232.48,15408,14110.57,15130,47.85025875164135,49.77386885151457,48.16372967916465]
FF      0       16:44:25.680    TargetBasedNominalVariableConversion_demo (BTCUSD,D1)    [15114,15370,13786.18,15139,47.85025875164135,49.23046392011166,50.45172139701621]
HR      0       16:44:25.680    TargetBasedNominalVariableConversion_demo (BTCUSD,D1)    [15055.8,16894,14349.84,16725,47.85025875164135,49.77386885151457,48.16372967916465]
EM      0       16:44:25.680    TargetBasedNominalVariableConversion_demo (BTCUSD,D1)    [15699.53,16474,15672.99,16186,47.85025875164135,49.77386885151457,50.45172139701621]
RK      0       16:44:25.680    TargetBasedNominalVariableConversion_demo (BTCUSD,D1)    [16187,16258,13639.83,14900,52.28360492434251,50.66453470243147,50.45172139701621]
LG      0       16:44:25.680    TargetBasedNominalVariableConversion_demo (BTCUSD,D1)    [14884,15334,13777.33,14405,52.28360492434251,50.66453470243147,50.45172139701621]
QD      0       16:44:25.680    TargetBasedNominalVariableConversion_demo (BTCUSD,D1)    [14405,14876,12969.58,14876,47.85025875164135,49.23046392011166,50.45172139701621]
HP      0       16:44:25.680    TargetBasedNominalVariableConversion_demo (BTCUSD,D1)    [14876,14927,12417.22,13245,52.28360492434251,49.77386885151457,50.45172139701621]
PO      0       16:44:25.680    TargetBasedNominalVariableConversion_demo (BTCUSD,D1)    [12776.79,14078.5,12355.38,13681,47.85025875164135,49.77386885151457,50.45172139701621…]]

Die p-Werte, die den Zusammenhang zwischen den transformierten Variablen und dem Ziel schätzen.

NS	0	16:44:29.287	TargetBasedNominalVariableConversion_demo (BTCUSD,D1)    Probability that predicator at 4 is associated with target 0.0005
IR      0       16:44:32.829    TargetBasedNominalVariableConversion_demo (BTCUSD,D1)    Probability that predicator at 5 is associated with target 0.7714
JS      0       16:44:36.406    TargetBasedNominalVariableConversion_demo (BTCUSD,D1)    Probability that predicator at 6 is associated with target 0.749

Die Ergebnisse zeigen, dass von allen kategorialen Variablen nur die Klassifizierung auf- oder abwärts (bullish/bearish) für das Ziel signifikant relevant ist. Im Gegensatz dazu weisen das Zwei-Balken-Muster und die Größe des Kerzenkörpers keine offensichtliche Übereinstimmung mit dem Ziel auf. Dies deutet darauf hin, dass umgewandelte Variablen für eine Zufallsvariable kaum von Bedeutung sind.

Die letzte Demonstration zeigt die Verwendung der Klasse zur Konvertierung eines Satzes von nominalen Variablen in Kombination mit Dimensionalitätsreduktion. Diese Funktionalität wird durch den Aufruf von fitTransform() erreicht, der die gleichen Eingabeparameter wie die fit()-Methode akzeptiert und eine Matrix zurückgibt, die eine einzelne repräsentative Variable enthält, die aus den konvertierten nominalen Variablen abgeleitet wurde. Diese Operation reduziert eine beliebige Anzahl von nominalen Variablen konsequent auf eine ordinale Variable.

   //+------------------------------------------------------------------+
   //| categorical conversion with dimensionality reduction             |
   //+------------------------------------------------------------------+
   matrix            fitTransform(matrix &preds_in, ulong &cols[], vector &target)
     {
      //---
      if(preds_in.Cols()<2)
        {
         if(!fit(preds_in,cols,target))
           {
            Print(__FUNCTION__, " error at ", __LINE__);
            return matrix::Zeros(1,1);
           }
         //---
         return transform(preds_in);
        }
      //---
      m_dim_reduce = 1;
      mapped = false;
      //---
      if(cols.Size()==0 && preds_in.Cols())
        {
         m_pred = int(preds_in.Cols());
         if(!np::arange(m_colindices,m_pred,ulong(0),ulong(1)))
           {
            Print(__FUNCTION__, " arange error ");
            return matrix::Zeros(1,1);
           }
        }
      else
        {
         m_pred = int(cols.Size());
        }
      //---
      m_rows = int(preds_in.Rows()) ;
      m_cols = int(preds_in.Cols());
      //---
      if(ArrayResize(m_mean_rankings,1)<0 ||
         ArrayResize(m_rankings,m_rows)<0 ||
         ArrayResize(m_indices,m_rows)<0 ||
         ArrayResize(m_mapping,m_pred)<0  ||
         ArrayResize(m_class_counts,1)<0  ||
         !m_median.Resize(m_pred) ||
         !m_class_ids.Resize(m_rows,m_pred) ||
         !shuffle_target.Resize(m_rows,2) ||
         (cols.Size()>0 && ArrayCopy(m_colindices,cols)<0) ||
         !ArraySort(m_colindices))
        {
         Print(__FUNCTION__, " Memory allocation failure ", GetLastError());
         return matrix::Zeros(1,1);
        }
      //---
      for(uint col = 0; col<m_colindices.Size(); col++)
        {
         vector var = preds_in.Col(m_colindices[col]);
         m_mapping[col] = np::unique(var);
         for(ulong i = 0; i<var.Size(); i++)
           {
            for(ulong j = 0; j<m_mapping[col].Size(); j++)
              {
               if(MathAbs(var[i]-m_mapping[col][j])<=1.e-15)
                 {
                  m_class_ids[i][col]=double(j);
                  break;
                 }
              }
           }
        }

      m_class_counts[0] = vector::Zeros(ulong(m_colindices.Size()));

      if(!m_class_ids.Col(m_class_ids.ArgMax(1),0))
        {
         Print(__FUNCTION__, " failed to insert new class id values ", GetLastError());
         return matrix::Zeros(1,1);
        }

      for(ulong i = 0; i<m_class_ids.Rows(); i++)
         ++m_class_counts[0][ulong(m_class_ids[i][0])];

      m_target = target;

      vector cid = m_class_ids.Col(0);
      m_mean_rankings[0] = train(cid,m_class_counts[0],m_target,m_median[0]);

      mapped = true;

      ulong unchanged_feature_cols[];

      for(ulong i = 0; i<preds_in.Cols(); i++)
        {
         int found = ArrayBsearch(m_colindices,i);
         if(m_colindices[found]!=i)
           {
            if(!unchanged_feature_cols.Push(i))
              {
               Print(__FUNCTION__, " Failed array insertion ", GetLastError());
               return matrix::Zeros(1,1);
              }
           }
        }

      matrix out(preds_in.Rows(),unchanged_feature_cols.Size()+1);
      ulong nfeatureIndex = unchanged_feature_cols.Size();

      if(nfeatureIndex)
        {
         matrix input_copy = np::selectMatrixCols(preds_in,unchanged_feature_cols);
         if(!np::matrixCopyCols(out,input_copy,0,nfeatureIndex))
           {
            Print(__FUNCTION__, " failed to copy matrix columns ");
            return matrix::Zeros(1,1);
           }
        }

      for(ulong i = 0; i<out.Rows(); i++)
        {
         ulong r = ulong(m_class_ids[i][0]);
         if(r>=m_mean_rankings[0].Size())
           {
            Print(__FUNCTION__, " critical error , index out of bounds ");
            return matrix::Zeros(1,1);
           }
         out[i][nfeatureIndex] = m_mean_rankings[0][r];
        }

      return out;
     }

Das Skript TargetBasedNominalVariableConversionWithDimReduc_demo veranschaulicht, wie dieser Prozess implementiert wird.

CNomOrd enc;
   
   ulong selectedcols[] = {4,5,6};
     
   matrix transformed = enc.fitTransform(fullFeatureMatrix,selectedcols,targets);
   
   Print(" Original predictors \n", fullFeatureMatrix);
   Print(" transformed predictors \n", transformed);
   
   Print(" Probability that predicator  is associated with target ", enc.score(10000,targets));

Die transformierte Variable.

JR      0       16:51:06.137    TargetBasedNominalVariableConversionWithDimReduc_demo (BTCUSD,D1)        transformed predictors 
JO      0       16:51:06.137    TargetBasedNominalVariableConversionWithDimReduc_demo (BTCUSD,D1)       [[13743,13855,12362.69,13347,49.36939702213909]
NS      0       16:51:06.137    TargetBasedNominalVariableConversionWithDimReduc_demo (BTCUSD,D1)        [13348,15381,12535.67,14689,49.36939702213909]
OP      0       16:51:06.137    TargetBasedNominalVariableConversionWithDimReduc_demo (BTCUSD,D1)        [14232.48,15408,14110.57,15130,49.36939702213909]
RM      0       16:51:06.137    TargetBasedNominalVariableConversionWithDimReduc_demo (BTCUSD,D1)        [15114,15370,13786.18,15139,50.64271980734179]
RL      0       16:51:06.137    TargetBasedNominalVariableConversionWithDimReduc_demo (BTCUSD,D1)        [15055.8,16894,14349.84,16725,49.36939702213909]
ON      0       16:51:06.137    TargetBasedNominalVariableConversionWithDimReduc_demo (BTCUSD,D1)        [15699.53,16474,15672.99,16186,49.36939702213909]
DO      0       16:51:06.137    TargetBasedNominalVariableConversionWithDimReduc_demo (BTCUSD,D1)        [16187,16258,13639.83,14900,49.36939702213909]
JN      0       16:51:06.137    TargetBasedNominalVariableConversionWithDimReduc_demo (BTCUSD,D1)        [14884,15334,13777.33,14405,49.36939702213909]
EN      0       16:51:06.137    TargetBasedNominalVariableConversionWithDimReduc_demo (BTCUSD,D1)        [14405,14876,12969.58,14876,50.64271980734179]
PI      0       16:51:06.137    TargetBasedNominalVariableConversionWithDimReduc_demo (BTCUSD,D1)        [14876,14927,12417.22,13245,50.64271980734179]
FK      0       16:51:06.137    TargetBasedNominalVariableConversionWithDimReduc_demo (BTCUSD,D1)        [12776.79,14078.5,12355.38,13681,49.36939702213909…]]
NQ      0       16:51:09.741    TargetBasedNominalVariableConversionWithDimReduc_demo (BTCUSD,D1)        Probability that predicator  is associated with target 0.4981

Die Überprüfung der Beziehung zwischen der neuen Variable und der Zielvariable ergibt einen relativ hohen p-Wert, was eine der Einschränkungen der Dimensionsreduktion verdeutlicht: den Verlust von Informationen. Daher ist diese Methode mit Vorsicht zu genießen. 

Schlussfolgerung

Die Umwandlung von nominalen Variablen in ordinale Variablen für das maschinelle Lernen ist ein leistungsfähiger, aber nuancierter Prozess. Sie ermöglicht es den Modellen, sinnvoll mit kategorialen Daten zu arbeiten, aber sie erfordert eine sorgfältige Überlegung, um Verzerrungen oder falsche Darstellungen zu vermeiden. Durch den Einsatz geeigneter Transformationstechniken - ob manuelle Ordnung, frequenzbasierte Kodierung, Clustering oder Zielkodierung - können Sie sicherstellen, dass Ihre Modelle für maschinelles Lernen nominale Variablen effektiv verarbeiten und gleichzeitig die Datenintegrität bewahren. Dieser Artikel gibt einen unvollständigen Überblick über gängige Methoden zur Konvertierung von Nominalvariablen. Es ist wichtig zu wissen, dass es viele fortgeschrittenere Techniken gibt. Das Hauptziel dieses Textes ist es, Praktiker in das Konzept der ordinalen Kodierung einzuführen und die Faktoren zu berücksichtigen, die bei der Auswahl der am besten geeigneten Methode für ihren spezifischen Anwendungsfall zu berücksichtigen sind. Durch das Verständnis der Auswirkungen verschiedener Kodierungstechniken können Praktiker fundiertere Entscheidungen treffen und die Leistung und Interpretierbarkeit ihrer maschinellen Lernmodelle verbessern. Alle im Artikel erwähnten Codedateien sind unten angefügt.

Datei	Beschreibung
MQL5/scripts/CategoricalVariableConversion.py	Python-Skript mit Beispielen für kategoriale Konvertierung
MQL5/scripts/CategoricalVariableConversion.ipynb	Jupyter-Notizbuch für das oben genannte Python-Skript
MQL5/scripts/ OneHotEncoding_demo.mq5	Demo-Skript für die Konvertierung von nominalen Variablen mit One-Hot-Kodierung in MQL5
MQL5/scripts/TargetBasedNominalVariableConversion_demo.mq5	Demo-Skript zur Konvertierung von nominalen Variablen mit einer nutzerdefinierten zielbasierten Kodierungsmethode
MQL5/scripts/TargetBasedNominalVariableConversionWithDimReduc_demo.mq5	Demo-Skript für die Konvertierung von nominalen Variablen unter Verwendung einer nutzerdefinierten zielbasierten Kodierungsmethode, die eine Dimensionalitätsreduktion implementiert
MQL5/include/nom2ord.mqh	Header-Datei mit der Definition der Klassen CNomOrd und COneHotEncoder
MQL5/include/np.mqh	Header-Datei mit Vektor- und Matrix-Utility-Funktionen