
预测市场价格的通用回归模型(二):自然、技术和社会暂态函数
概述
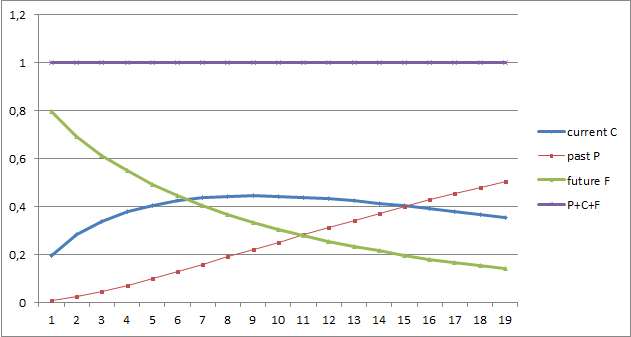
如其所证,分析交易过程中物料平衡的暂态函数 /1/ 能够充分描述人类生活当中所有领域的其它动态和静态过程。该理论基于三个参数的三个函数。 其一(当前函数 C)是微分形式,而另外两个是伽马(Gamma)函数分布密度的积分形式。 过去函数 P 是通过将 C 的 n+1 参数从 0 到无穷远积分得到的,而未来函数 F 也用到 n 参数。
所有三个函数都满足标准化和物料平衡 P+C+F=1 条件,且具有计算精度。 它们分别描述了自大爆炸以来自然或人为起源的所有可想象和不可想象的规律。 在第一篇文章中提供的方程式已被发现能适用所有参数。 而参数 n 指向自动控制领域,而参数 tau 意指时间、温度、浓度、及其测量单位中的类似概念,而参数 D 无疑代表系统或过程的潜力。 例如,相对于价格,它表示最大变化幅度。
有三个暂态函数描述了动态暂态的三个阶段,定义则是遵照伽马分布函数的各种修订形式,从而判断所研究参数的行为。 特别是,市场价格对过去(P)、当前(C)和未来(F)时间的依赖性。 甚至,研究还表明,它们的合计在任何时刻都保持不变,等于一。 本文致力于更详尽地研究这三个函数链,通常称为“PCF 函数”,以及它们在建立自然界中发生的、具有自然和技术相关特征的流程形态中所扮演的角色。 尽管如此,主要强调的还是放在对交易过程的研究上,以及在此基础上创建和应用指标。
自然、技术相关和社会暂态函数(PCF)
下图显示了过去(P)、当前(C)和未来(F)函数,以及展示其合计始终等于一的函数图,即。
P+C+F=1:
在这个函数链中,当前(C)函数是主要函数,因为所有其它函数都是从它派生出来的。 P 是通过当前 C 函数的积分得到的。当推导 F 时,P 是通过一部分积分而来的,如 /1/ 所示。 于此同时,应用不完全的欧拉伽马(Euler's Gamma)分布可得出以下结果:
![]() =过去 P
=过去 P
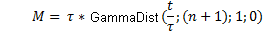 =当前 C
=当前 C
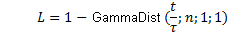 =未来 F
=未来 F
![]()
![]()
最终,我们得到:
F=1-(P+C)
在石油、采矿、冶金和电力行业应用 PCF 函数
PCF 函数已成功应用于预测塔吉克斯坦北部马赫拉姆油田 #5 生产井的油气开采动态,从而可以在生产井区检测数十万吨石油。此外, PCF 函数用于描述 JV Zeravshan LLC Hirshona 生产井废矿中黄金的堆浸。 也就是说,经证明,在不进行初步矿石研磨的情况下可额外提取 13 千克黄金,令其提取度达到 91%。 这些函数还成功地用于预测塔吉克斯坦共和国的经济指标。
PCF 曾被用作开发钢铁冶金生产动力学的数学模型的基础,根据各种因素从精矿中高压釜浸出金和银,以及 根据湿法冶金中各种试剂的时间和性质从精矿中浮选金矿。还充分描述了以石灰为特征的隔热复合材料的属性变化。 PCF 函数结果证明,在描述 合金比热容的动态形态时非常准确,尤其是铬、锰和钼合金化的 Zn5Al 对温度的依赖性。 这就有可能获得用于定义配电变压器和电力变压器在不同冷却剂温度下连续运行的可承受负荷系数的方程式。
PCF 函数在描述微观世界形态时也展示了它们的能力。 特别是,它们准确地描述了金属和矿物晶体中原子间平面相互排列的规律性,这令依据每种金属和矿物固有的特征方程来识别它们成为可能。 PCF 方程也预测了中国和美国 nCov-19 冠状病毒的传播、治愈和死亡动态。 这是一个部分任务的列表,PCF 显示了它的优势。
MetaTrader 4 和 MetaTrader 5 指标
PCF 函数也曾为 MetaTrader 4 和 MetaTrader 5 开发指标 /2,3/。 您可以在 MQL5 代码库中找到它们。
该指标由三条线组成 — 卖出线(红色)、买入线(蓝色)和交易者线(黄色)。
它以给定的回顾形式分析历史来预测期望的价格走势。
在执行交易时,我们应该遵守黄线,这是价格走势的主导线。 它还表明在趋势形成阶段,当从一条线跳到另一条线时,可能会发生趋势变化。
趋势形成后,所有的线都会组合起来,并展示出趋势目标。 图形的分支表明了市场的不稳定性。
第二个指标版本根据当前柱线和历史(历史深度可调)上匹配所有指标线的规则显示入场信号。 您可以选择生成预测的价格。 默认情况下,该版本设置为使用开盘价。 因此,信号会伴随着柱线的开立而出现,且之后不会改变。
第三个指标版本实现“跟踪”模式。

如果有许多红色箭头,它们表示下行趋势的方向。 如果有许多蓝色箭头,它们指示上行趋势的方向(当存在多于一个的状态订单时,应始终使用“许多”一词)。 否则,它们应识别为一个订单群体,指示柱线图以外的趋势方向(但不能改变柱线图的未来趋势方向)。
红色箭头当中夹杂一个蓝色箭头表示,根据之前的柱线图结果,上行趋势已被下行趋势所取代。 根据之前的条形图结果,蓝色箭头当中夹杂一个红色箭头表示下行趋势已被上行趋势所取代。 然而,它无法改变柱线的未来趋势。
当交易一篮子多个货币对时,市场上会出现一种共振现象,资本要么暴富、要么爆仓。
实验性 EA 依据 PCF 为基础的指标交易一篮子货币对
现在,我们来看看一项实验的结果,该实验旨在安排一个真正的自动交易,针对所有 33 种可用货币对,不带止损和止盈的单一订单,包括 D1 上的黄金和白银;然后在美分账户里,初始本金为 98 美元,每笔交易 0.06 手,分析在 D1 历史的最后 300 根柱线上进行交易。
实验从余额、净值和系统潜在增长开始,如下图所示:
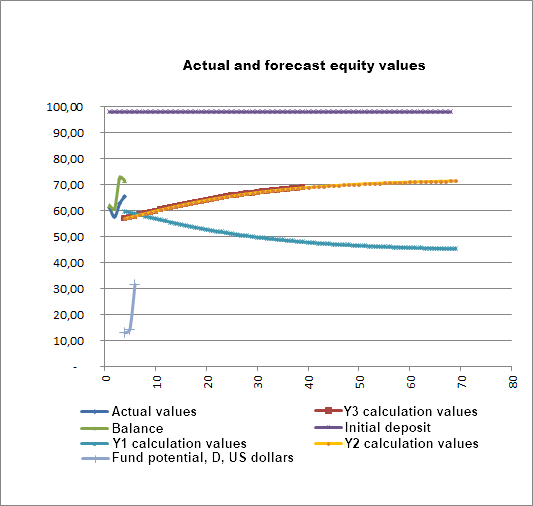
交易沿着不断增长的 PCF Y1 指示线前行。 然而,PCF 也超过了下降的 Y2 线,这表明未来净值有可能下降,事实上,交易过程很快就切换到下降的 PCF Y2 线:
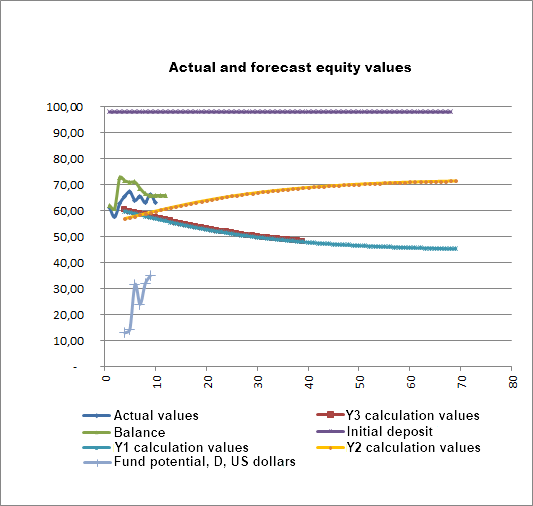
接下来,交易过程开始于图中所示的 Y2 下降线:

根据图形,第 16 点看到了一个事件,其极大地扭转了交易过程,令交易过程变得更糟,导致保证金几乎缩水了两番,从 76 美元跌至 42 美元。 该事件导致净值进一步下降至 30 美元,尽管保证金曾增加至 93.5 美元。 该增长最终导致了资金的恢复:
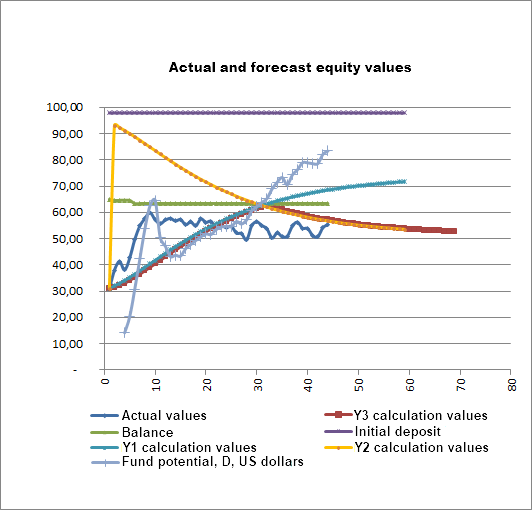
根据图形,资金从 30 美元开始恢复,并沿着上行的 PCF Y1 线上升。 与此同时,另一种可能的场景(伴随 PCF Y2 的下行线资金缩水)仍然存在。 然而,随着账户资金的恢复,交易过程切换到 PCF Y2 下行线,而余额保持相对不变。 沿 SML Y1 线净值增加的可能性仍然存在,净值预测排除了近期资金缩水的威胁。 这个过渡结论对交易者的交易是一个非常重要的激励。
如 /1/ 所示,描述过程动力学的 PCF 函数取决于三个因素 — 一个参数和两个比率。 我们试着来厘清它们在交易过程中的角色。
交易过程
“n” 交易过程仍然是最神秘的因素。 它的影响尚未完全显现。
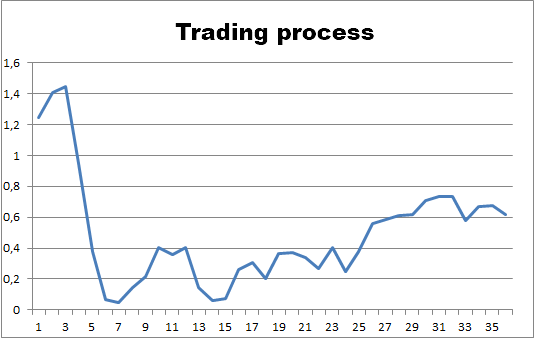
交易过程时间常数
事实证明,自然界中的每一个动态过程都是在已分配时间内发展的。 每个过程的时间都不同。 它并不取决于“我们的”时间。 过程时间的速度由“时间常数”设定。 如果在这段时间内过程条件保持不变,则 T 保持不变,就像静态和稳态过程一样(例如,上述矿物和金属的电子轨道)。
在真实的市场条件下,过程的节奏会发生变化,T 也会相应地发生变化。 T 的倒数称为系统阻抗,或系统对过程的阻力。 在 PCF 开发过程中,我找到了明确定义的 T 方程式。 T 常数的影响如下所示。 我们研究价格动态,或者,在这种情况下,依赖其值的净值变化。
我们可以通过分析 T 和净值图形来评估其影响。 正如上面所示,净值图形展示出很多关于其未来价值的信息。 根据图形,真实净值和预测净值相匹配。 这可确立交易员的信心。 甚而,T 的增加导致净值的增加:

系统潜力
根据以上图形,目前的净值直接取决于系统的潜力。
结束语
暂态函数的详细研究产生了三个阶段的动态暂态,定义则遵照各种伽马分布修订的形式。 这些修订定义了研究参数的行为,这取决于从失稳开始的过去(P)、当前(C)和未来(F)时期。
甚至,研究还表明,它们的合计在任何时刻都保持不变,等于一。 本文致力于针对这三个函数链,通常称为 “PCF 函数”,进行更详尽的研究。 具体的示例展示出它们在建立自然界中发生的、具有自然和技术相关特征的过程流形态方面所扮演的角色。 基于 PCF 的指标已成功应用于外汇交易。
参考
- Sultonov Y., 市场价格预测的通用回归模型, https://www.mql5.com/zh/articles/250;
- Sultonov 的指标,用于 MetaTrader 4, https://www.mql5.com/zh/code/10339 (俄语);
- Sultonov 的指标,用于 MetaTrader 5, https://www.mql5.com/zh/code/32939 (俄语);
- 实验,https://www.mql5.com/ru/forum/367874(俄语)。
本文由MetaQuotes Ltd译自俄文
原文地址: https://www.mql5.com/ru/articles/9868
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。
 针对交易的组合数学和概率论(第四部分):伯努利(Bernoulli)逻辑
针对交易的组合数学和概率论(第四部分):伯努利(Bernoulli)逻辑


他受到了如此多的嘲弄,我想他很快就不会再出现了。没有人受到惩罚。
所以他被耍了,我想他很快就不会出现了。没有人受到惩罚
他用 PNB 取走了自己的账户,仅此而已。
他用 PNB 取走了他的账户里的钱,仅此而已。
EOR 可以有不同的使用方式,因此放水/不放水并不能作为失踪的论据。
在研究过程中,我确信为分析金融市场(考虑到市场的非平稳性)而开发的数学模型也适用于其他非平稳过程。
特别是信息和行为系统以及技术过程。当然,要考虑到每个过程的特殊性。
事实上,本文作者已经举例说明了其方法的这种普遍性。