从头开始采用 MQL 语言进行深度神经网络编程

概述

鉴于机器学习最近变得炙手可热，许多人听说了深度学习，并希望知道如何应用 MQL 语言来实现它。 我曾见过带有激活函数的人工神经元的简单实现，但对于深度神经网络还没有真正的实现。 在本文中，我将向您介绍一个采用 MQL 语言实现的深度神经网络，它带有不同的激活函数；例如用于隐藏层的双曲正切函数，和用于输出层的 Softmax 函数。 我们将从第一步贯穿到最后，完成深度神经网络。

1. 制造人工神经元

从神经网络的基本单元开始：单个神经元。 在本文中，我将专注于深度神经网络中所用神经元类型的不同部分，尽管神经元类型之间最大的区别通常是激活函数。

1.1. 单个神经元部分

人工神经元，松散地模仿人脑中的神经元，简单地担负数学计算。 如同我们的神经元，当它受到足够的刺激时就会触发。 神经元把输入数据进行组合，这些数据含有一组或放大或抑制输入的系数或权重，从而为尝试学习任务的算法分配意义重大的输入。 在下一张图片中，可以看到神经元活动的各个部分：

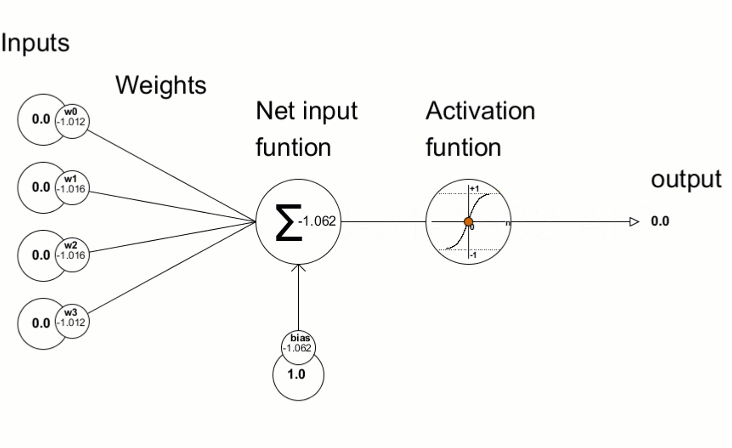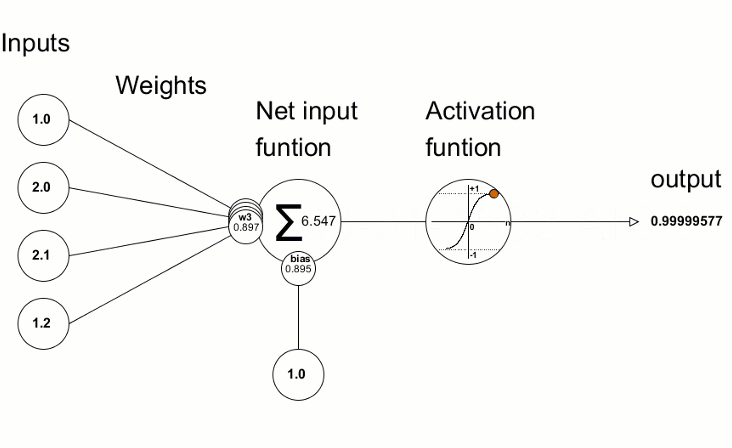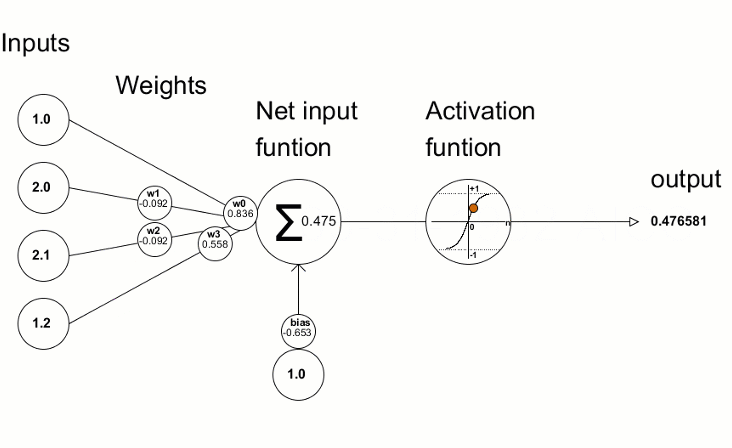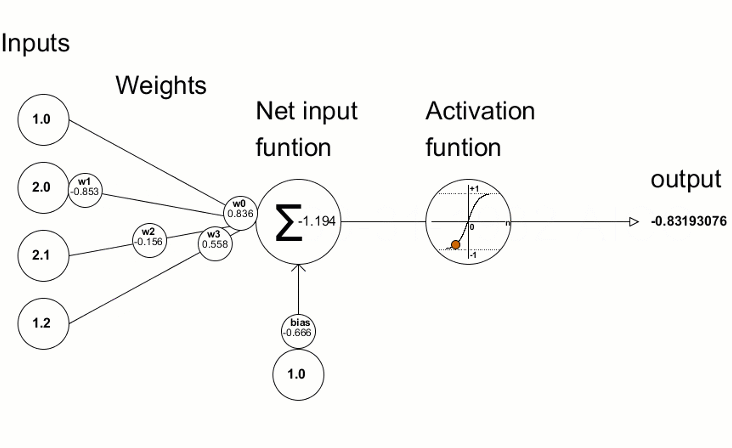
1.1.1. 输入

输入要么是来自环境的外部触发器，要么来自其它人工神经元的输出；这将由网络进行评估。 它充当神经元的“食物”，并经由神经元传递，从而变成一个输出，我们可以基于神经元所受训练，对其进行解释。 它们可以是离散值或实数值。

1.1.2. 权重

权重是与相应项目相乘的因子，增加或减少它们的值，赋予神经元内部的输入放大或缩小的意义，随之影响到输出。 神经网络训练算法的目标是判断欲解决问题的“最佳”可能权值集合。

1.1.3. 网络输入函数

在这个神经元部分，输入和权重收敛为单一结果乘积，即每项乘以其权重之和。 这个结果或数值经由激活函数传递，然后为我们衡量输入神经元对神经网络输出的影响。

1.1.4. 激活函数

激活函数引导输出。 有几种类型的激活函数（Sigmoid、Tan-h、Softmax、ReLU、等等）。 它决定神经元是否应该被激活。 本文重点介绍 Tan-h 和 Softmax 类型的函数。

1.1.5. 输出

最后，我们有了输出。 它可以被传递至另一个神经元，也可以被外部环境采样。 该值可以是离散值或实数值，具体取决于所采用的激活函数。

2. 构建神经网络

神经网络的灵感受到生物神经系统处理信息方法的启发，比如大脑。 它由多层人工神经元组成，每一层与下一层互连。 因此，前一层充当下一层的输入，然后依次充当输出层的输入。 神经网络的目的应当是通过无监督学习进行聚类，通过有监督学习或回归进行分类。 在本文中，我们将重点讨论三种状态的分类能力：买入、卖出或持有。 下面是一个带有一个隐藏层的神经网络：

3. 从神经网络按比例扩张到深度神经网络

深度神经网络与更常见的单隐层神经网络的区别在于其深度的构成层数。 超过三个层（包括输入和输出）即符合“深度”学习的资格。 因此，深度是一个严格定义的技术术语，意思是不止一个隐藏层。 若您越深入神经网络，您的神经元就能识别出更复杂的特征，因为它们汇聚并重组了来自前一层的特征。 它令深度学习网络能够处理非常庞大的高维数据集合，这些数据集合包含数十亿个经由非线性函数的参数。 在下图中，参见含有 3 个隐藏层的深度神经网络：

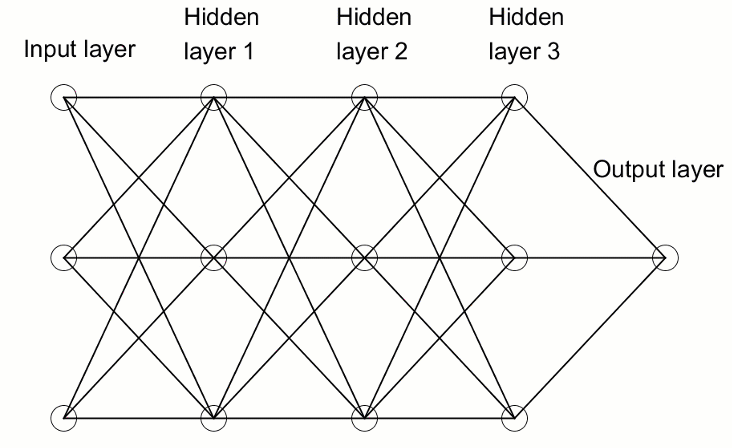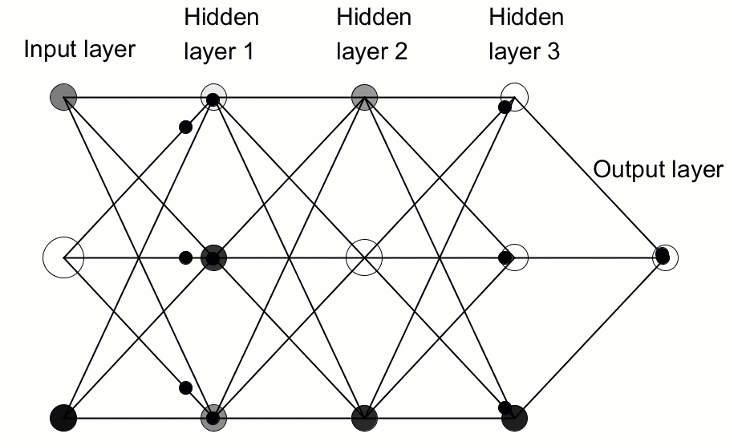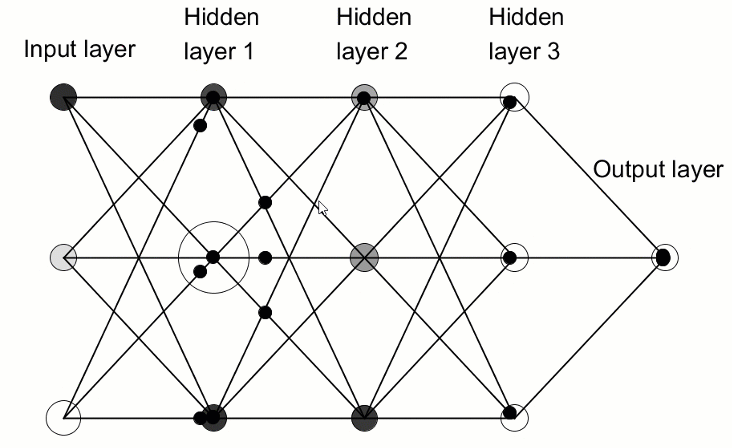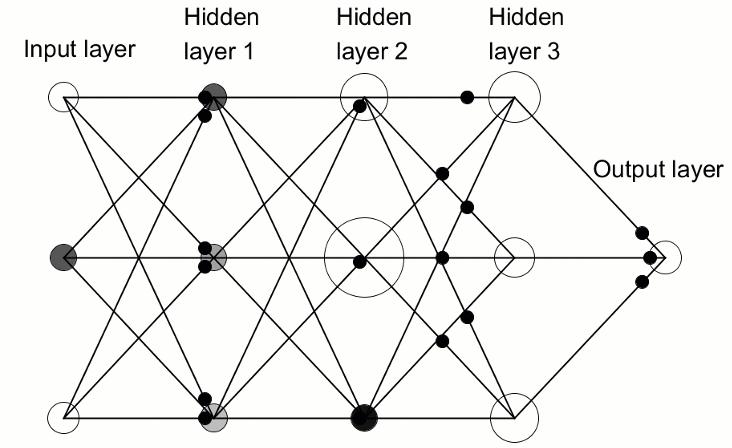
3.1. 深度神经网络类

现在我们看看将用来创建神经网络的类。 深度神经网络封装在一个名为 DeepNeuralNetwork 的程序定义类中。 主方法实例化了一个 3-4-5-3 完全连接的前馈神经网络。 稍后，在本文中的深度神经网络训练过程中，我将展示一些馈入我们网络的纪录样例，但现在我们的重点是创建网络。 该网络硬编码了两个隐藏层。 含有三层或更多层的神经网络非常少见，但是如果您想创建一个含有更多层的网络，您可以利用本文介绍的结构轻松地完成。 input-to-layer-A 的权重存储在矩阵 iaWeights 当中，layer-A-to-layer-B 的权重存储在矩阵 abWeights 当中，layer-B-to-output 的权重存储在矩阵 boWeights 当中。 由于多维数组只有第一维度能定义为静态的或动态的 — 所有其它维度都是静态的 — 因此矩阵的尺寸使用 “#define” 语句声明为常量。 除了引用顶层系统名称空间，我删除了所有其它语句，从而节省空间。 您可以在本文的附件中找到完整的源代码。

程序结构：

#define SIZEI 4
#define SIZEA 5
#define SIZEB 3
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class DeepNeuralNetwork
  {
private:

   int               numInput;
   int               numHiddenA;
   int               numHiddenB;
   int               numOutput;

   double            inputs[];

   double            iaWeights[][SIZEI];
   double            abWeights[][SIZEA];
   double            boWeights[][SIZEB];

   double            aBiases[];
   double            bBiases[];
   double            oBiases[];

   double            aOutputs[];
   double            bOutputs[];
   double            outputs[];

public:

                     DeepNeuralNetwork(int _numInput,int _numHiddenA,int _numHiddenB,int _numOutput)
     {...}
     

   void SetWeights(double &weights[])
     {...}      
    

   void ComputeOutputs(double &xValues[],double &yValues[])
     {...}     
          

   double HyperTanFunction(double x)
     {...}      
     

   void Softmax(double &oSums[],double &_softOut[])
     {...}
      

  };
//+------------------------------------------------------------------+

两个隐藏层和单个输出层均有一组对应的偏离值，分别命名为 aBiases、bBiases 和 oBiases。 针对隐藏层的局部输出存储在类作用域下的 aOutputs 和 bOutputs 的数组之中。

3.2. 计算深度神经网络输出

方法 ComputeOutputs 首先设置临时数组来暂存初步（激活前）的合计。 接着，它按照 layer-A 节点的输入数量计算权重的初步合计 ，添加偏离值，然后应用激活函数。 然后，使用刚刚计算出的 layer-A 输出作为局部输入，计算 layer-B 局部输出，最后计算最终输出。

void ComputeOutputs(double &xValues[],double &yValues[])
     {
      double aSums[]; // hidden A nodes sums scratch array
      double bSums[]; // hidden B nodes sums scratch array
      double oSums[]; // output nodes sums

      ArrayResize(aSums,numHiddenA);
      ArrayFill(aSums,0,numHiddenA,0);
      ArrayResize(bSums,numHiddenB);
      ArrayFill(bSums,0,numHiddenB,0);
      ArrayResize(oSums,numOutput);
      ArrayFill(oSums,0,numOutput,0);

      int size=ArraySize(xValues);

      for(int i=0; i<size;++i) // copy x-values to inputs
         this.inputs[i]=xValues[i];

      for(int j=0; j<numHiddenA;++j) // compute sum of (ia) weights * inputs
         for(int i=0; i<numInput;++i)
            aSums[j]+=this.inputs[i]*this.iaWeights[i][j]; // note +=

      for(int i=0; i<numHiddenA;++i) // add biases to a sums
         aSums[i]+=this.aBiases[i];

      for(int i=0; i<numHiddenA;++i) // apply activation
         this.aOutputs[i]=HyperTanFunction(aSums[i]); // hard-coded

      for(int j=0; j<numHiddenB;++j) // compute sum of (ab) weights * a outputs = local inputs
         for(int i=0; i<numHiddenA;++i)
            bSums[j]+=aOutputs[i]*this.abWeights[i][j]; // note +=

      for(int i=0; i<numHiddenB;++i) // add biases to b sums
         bSums[i]+=this.bBiases[i];

      for(int i=0; i<numHiddenB;++i) // apply activation
         this.bOutputs[i]=HyperTanFunction(bSums[i]); // hard-coded

      for(int j=0; j<numOutput;++j) // compute sum of (bo) weights * b outputs = local inputs
         for(int i=0; i<numHiddenB;++i)
            oSums[j]+=bOutputs[i]*boWeights[i][j];

      for(int i=0; i<numOutput;++i) // add biases to input-to-hidden sums
         oSums[i]+=oBiases[i];

      double softOut[];
      Softmax(oSums,softOut); // softmax activation does all outputs at once for efficiency
      ArrayCopy(outputs,softOut);

      ArrayCopy(yValues,this.outputs);

     }

在幕后，神经网络在计算两个隐藏层的输出时采用了双曲正切激活函数（Tan-h），在计算最终输出值时采用了 Softmax 激活函数。

• 双曲正切(Tan-h): 逻辑上如同 Sigmoid，Tan-h 函数也是 sigmoidal，但取而代之的输出值范围为（-1,1）。 因此，Tan-h 的强负输入将映射为负输出。 此外，只有零值输入映射到接近零的输出。 在本例中，我将展示数学公式，以及实现它的 MQL 源代码。

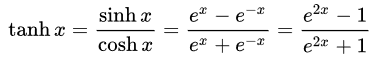
   double HyperTanFunction(double x)
     {
      if(x<-20.0) return -1.0; // approximation is correct to 30 decimals
      else if(x > 20.0) return 1.0;
      else return MathTanh(x); //Use explicit formula for MQL4 (1-exp(-2*x))/(1+exp(-2*x))
     }

• Softmax:在多个类的情况下，为每个类分配小数概率。 这些小数概率必须加上 1.0。 这种额外的限制可令训练更迅速地收敛。

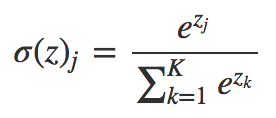
   void Softmax(double &oSums[],double &_softOut[])
     {
      // determine max output sum
      // does all output nodes at once so scale doesn't have to be re-computed each time
      int size=ArraySize(oSums);
      double max= oSums[0];
      for(int i = 0; i<size;++i)
         if(oSums[i]>max) max=oSums[i];

      // determine scaling factor -- sum of exp(each val - max)
      double scale=0.0;
      for(int i= 0; i<size;++i)
         scale+= MathExp(oSums[i]-max);

      ArrayResize(_softOut,size);
      for(int i=0; i<size;++i)
         _softOut[i]=MathExp(oSums[i]-max)/scale;

     }

4. 使用 DeepNeuralNetwork 类的演示智能交易系统

在启动开发智能交易系统之前，我们必须为深度神经网络定义将要输入的数据。 由于神经网络擅长分类形态，我们将打算采用日本蜡烛的相对值作为输入。 这些值应是上阴影的大小、主体、下阴影和蜡烛的方向（看涨或看跌）。 记录项的数量没必要太小，但作为一个测试程序的情况下，足够就行了。

演示智能交易系统：

结构为 4-4-5-3 神经网络需要总共 (4 * 4) + 4 + (4 * 5) + 5 + (5 * 3) + 3 = 63 个权重和偏离值。

#include <DeepNeuralNetwork.mqh> 

int numInput=4;
int numHiddenA = 4;
int numHiddenB = 5;
int numOutput=3;

DeepNeuralNetwork dnn(numInput,numHiddenA,numHiddenB,numOutput);


//--- weight & bias values
input double w0=1.0;
input double w1=1.0;
input double w2=1.0;
input double w3=1.0;
input double w4=1.0;
input double w5=1.0;
input double w6=1.0;
input double w7=1.0;
input double w8=1.0;
input double w9=1.0;
input double w10=1.0;
input double w11=1.0;
input double w12=1.0;
input double w13=1.0;
input double w14=1.0;
input double w15=1.0;
input double b0=1.0;
input double b1=1.0;
input double b2=1.0;
input double b3=1.0;
input double w40=1.0;
input double w41=1.0;
input double w42=1.0;
input double w43=1.0;
input double w44=1.0;
input double w45=1.0;
input double w46=1.0;
input double w47=1.0;
input double w48=1.0;
input double w49=1.0;
input double w50=1.0;
input double w51=1.0;
input double w52=1.0;
input double w53=1.0;
input double w54=1.0;
input double w55=1.0;
input double w56=1.0;
input double w57=1.0;
input double w58=1.0;
input double w59=1.0;
input double b4=1.0;
input double b5=1.0;
input double b6=1.0;
input double b7=1.0;
input double b8=1.0;
input double w60=1.0;
input double w61=1.0;
input double w62=1.0;
input double w63=1.0;
input double w64=1.0;
input double w65=1.0;
input double w66=1.0;
input double w67=1.0;
input double w68=1.0;
input double w69=1.0;
input double w70=1.0;
input double w71=1.0;
input double w72=1.0;
input double w73=1.0;
input double w74=1.0;
input double b9=1.0;
input double b10=1.0;
input double b11=1.0;

对于神经网络的输入，我们将采用以下公式来判断代表蜡烛各部分比照蜡烛总尺寸的百分比。

//+------------------------------------------------------------------+
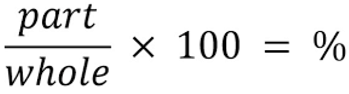
//|percentage of each part of the candle respecting total size       |
//+------------------------------------------------------------------+
int CandlePatterns(double high,double low,double open,double close,double uod,double &xInputs[])
  {
   double p100=high-low;//Total candle size   
   double highPer=0;
   double lowPer=0;
   double bodyPer=0;
   double trend=0;

   if(uod>0)
     {
      highPer=high-close;
      lowPer=open-low;
      bodyPer=close-open;
      trend=1;

     }
   else
     {
      highPer=high-open;
      lowPer=close-low;
      bodyPer=open-close;
      trend=0;
     }
   if(p100==0)return(-1);
   xInputs[0]=highPer/p100;
   xInputs[1]=lowPer/p100;
   xInputs[2]=bodyPer/p100;
   xInputs[3]=trend;

   return(1);

  }

现在我们可以处理贯穿神经网络的输入：

   MqlRates rates[];
   ArraySetAsSeries(rates,true);
   int copied=CopyRates(_Symbol,0,1,5,rates);

   //Compute the percent of the upper shadow, lower shadow and body in base of sum 100%
   int error=CandlePatterns(rates[0].high,rates[0].low,rates[0].open,rates[0].close,rates[0].close-rates[0].open,_xValues);

   if(error<0)return;
   
   dnn.SetWeights(weight);

   double yValues[];
   dnn.ComputeOutputs(_xValues,yValues);

现在，基于神经网络的计算结果，对交易时机进行决策。 记住，Softmax 函数产生的 3 个输出将基于 100% 的合计。 这些值存储在 “yValues” 数组当中，数字大于 60% 的值才会被执行。

//--- if the output value of the neuron is mare than 60%
   if(yValues[0]>0.6)
     {
      if(m_Position.Select(my_symbol))//check if there is an open position
        {
         if(m_Position.PositionType()==POSITION_TYPE_SELL) m_Trade.PositionClose(my_symbol);//Close the opposite position if exists
         if(m_Position.PositionType()==POSITION_TYPE_BUY) return;
        }
      m_Trade.Buy(lot_size,my_symbol);//open a Long position
     }
//--- if the output value of the neuron is mare than 60%
   if(yValues[1]>0.6)
     {
      if(m_Position.Select(my_symbol))//check if there is an open position
        {
         if(m_Position.PositionType()==POSITION_TYPE_BUY) m_Trade.PositionClose(my_symbol);//Close the opposite position if exists
         if(m_Position.PositionType()==POSITION_TYPE_SELL) return;
        }
      m_Trade.Sell(lot_size,my_symbol);//open a Short position
     }

   if(yValues[2]>0.6)
     {
      m_Trade.PositionClose(my_symbol);//close any position

     }

5. 利用策略优化训练深度神经网络

正如您也许已经注意到的，只有深度神经网络前馈机制已经实现，但它不执行任何训练。 此任务预留给策略测试器。 下面，我将为您展示如何训练神经网络。 请记住，由于输入和训练参数的范围数量很大，它只能在 MetaTrader 5 中训练，不过一旦获得优化值，就可以很容易地复制到 MetaTrader 4。

策略测试器配置：

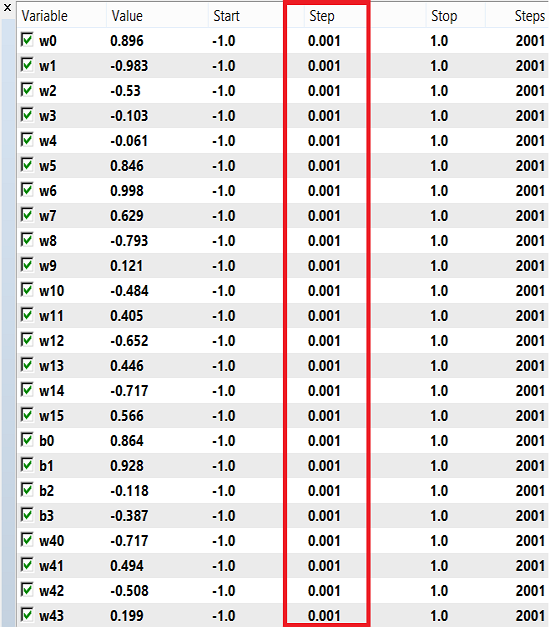
权重和偏离值可以选用一系列数字进行训练，从 -1 到 1，步长为 0.1、0.01 或 0.001。 您可以尝试这些数值，看看哪一个能得到最好的结果。 在我的例子中，我采用了 0.001 作为步长，如下图所示：

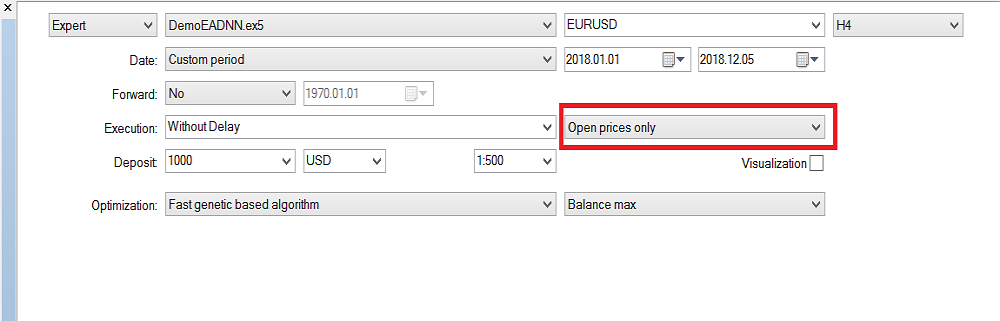
请注意，我采用的是“仅开盘价”，因为我用的是最后一根收盘的蜡烛，所以不值得在每次即时报价上运行。 现在我已经在 H4 时间帧上运行了优化，去年我在回测中得到了这个结果：

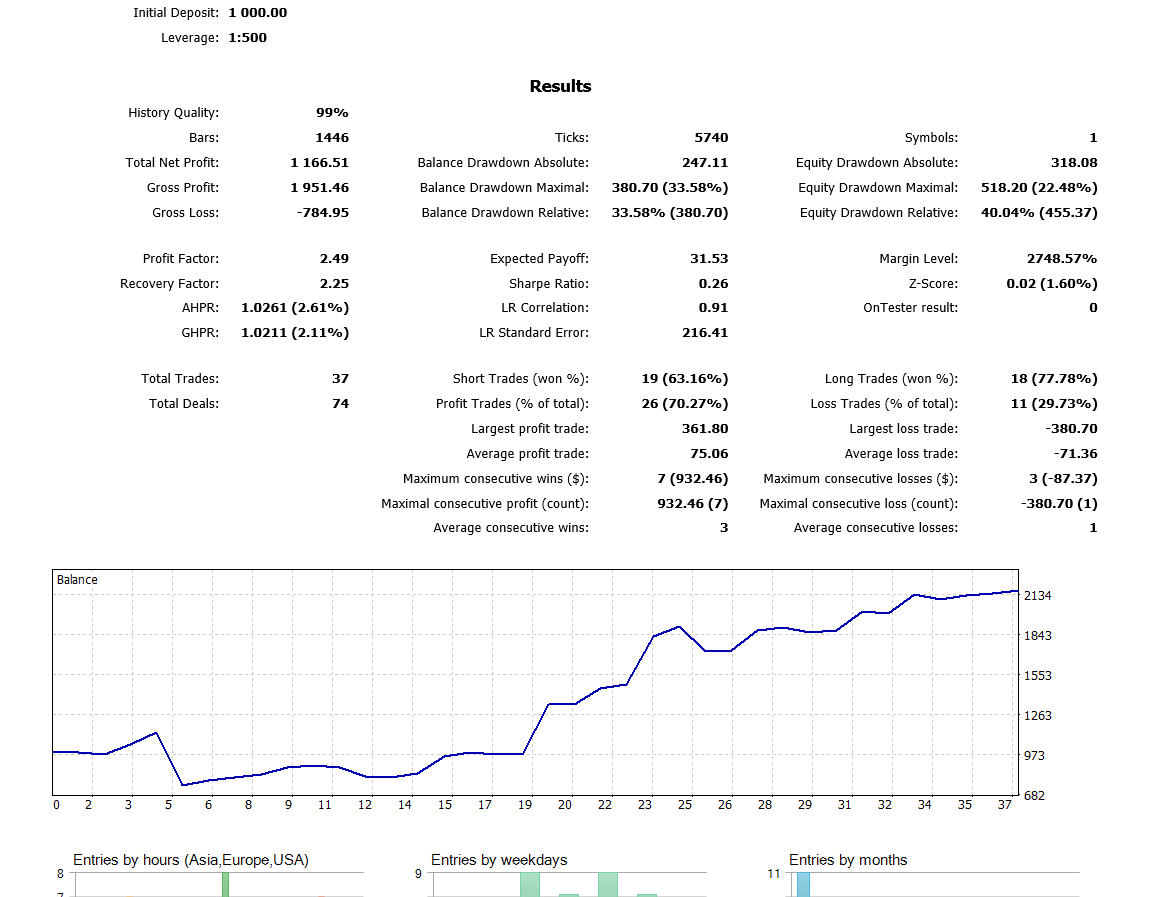
结束语

本文中的代码和解释表述，可为您理解含有两个隐藏层的神经网络提供良好的基础。 那三个或更多隐藏层会如何呢？ 研究文献中的共识是，两个隐藏层足以解决几乎所有的实际问题。 本文概括了一种采用深度神经网络来开发改进汇率预测模型的方法，其动机是深度网络从原始数据中学习抽象特征的能力。 初步结果证实，我们的深度网络产生的预测精度，明显高于已开发出的货币市场基准模型。