丹尼斯, 我对这篇文章有以下评论。
在理论方面,没有任何问题,所有内容都有详细介绍。
至于实践,我想提请你注意你展示的经验直方图,尤其是图 2。 问题是,你在分析中犯了两个非常严重的错误。
首先,你为生成直方图的脚本设置的类数太少--只有 9 个,这本身就是对皮尔逊标准威力的巨大打击,使其无法有效应用。当然,如果样本量允许(确实允许),您不会犯错。如果你能做到这一点,你就能确保对数正态分布的检验结果为负,以及超正态分布的收益检验结果为负。顺便说一句,要确保两个这样的分布不能同时代表某个值及其模数是非常容易的,只需取超正态分布的 "一半 "并与它本身相卷积(类似于从随机变量中取模数):你肯定不会得到对数正态分布。
第二个不准确之处在于,你没有利用收益分布的顶部(又称期望值)必须恰好为 0 的先验知识(否则我们早就成为亿万富翁了)。这就是为什么图 2 中的柱状图看起来向右偏移了,尽管它不应该偏移。同样,在绘制直方图 时考虑到这一点,会使测试更加可靠。
附注:我正在写一篇关于建模基础知识的文章,因此对您的文章很感兴趣。感谢您的文章,它就在主题中。谢谢。
......首先,您为生成直方图的脚本设置的类数太少了--只有 9 个,这本身就对皮尔逊标准的威力是一个很大的打击,使其无法有效应用。当然,如果样本量允许(确实允许),您不会犯错。如果你这样做了,你就能确保对数正态分布的检验结果为负,以及超正态分布的收益检验结果为负。顺便说一下,要确保两个这样的分布不能同时代表某个值及其模数,其实很简单,只需取超正态分布的 "一半 "并与它本身相卷积(类似于从随机值中取模数):你肯定不会得到对数正态分布。
亲爱的alsu,感谢您的意见!
让我们按顺序来。
类数不是自愿设定的,而是根据 某个公式设定的。在我看来,这就是 斯特吉斯公式。这是最流行的规则之一。它并不完美,我同意这一点。但是...
你是根据什么规则来参加 200-300 级比赛的?
第二个不准确之处在于,你没有使用先验知识,即收益分布的顶部(又称期望值)必须正好为 0(否则我们早就都成亿万富翁了)。这就是为什么图 2 中的直方图看起来向右偏移了,尽管它不应该偏移。同样,在绘制直方图时考虑到这一点,会使测试更加可靠。
我根据事实分析样本。我分析我所拥有的。那么,收益率分布的顶点应该恰好位于 0 点吗?也许我误解了什么...
此外,如果你看一下拟合的分布(即X~HS(-0.00,1.00)),很容易发现第一个参数--移动参数--正好是 0。事实上,它等于期望值。
下面是另一份关于标准值采样的 html 报告。我希望该图或多或少具有可读性。但它与文章中的数据并不完全相同。我刚刚采集了最新的数据。
如您所见,平均值 =0。最佳拟合是双曲正割分布:X~HS(0.00, 1.00)。
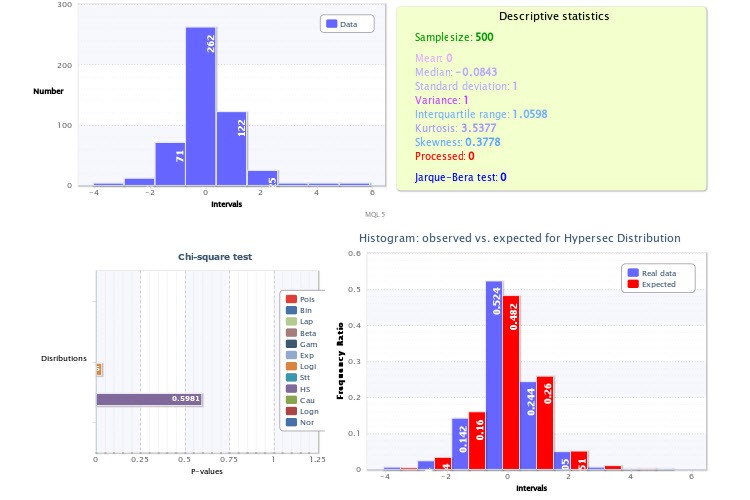
没错,斯特吉斯的公式正好给出了 9 个等级,但这也是考虑增加样本量的一个原因(反转公式,我发现你的样本量大约是 256?)
此外,这个公式只适用于正态分布的一般人群(它是针对正态分布而推导出来的),而且样本量不超过 200 个值。您可以使用其他公式 - Diakonis, Scott....
总之,你知道,斯特吉斯从未给出过他的公式的逻辑依据--是的,它是基于二项分布 对正态分布的近似,那又怎样?这对选择类数的效率问题有何影响?作者从未定义过最优性标准,公式本身也是随意写的。但问题是,在很长一段时间里,斯特吉斯的方法是唯一被正式化的方法,而且它自动(在我看来,是非常粗心大意的!)包含在所有统计软件包中,顺便说一句,这非常令人讨厌,因为这个公式几乎总是 给出一个被极度 低估的类数。
同样,也有其他公式可以替代,但矛盾的是,个人电脑的存在让我们有机会把自己的脑袋当作一个工具,也就是用一种可视化的方式来确定这个特定样本的最佳类数,当我们平滑地改变这个指标时,我们就能在图形的平滑度和直方图的分辨率之间取得折中。顺便说一句,这种方法往往比任何公式都更好更快。
我总是对每个人说--在把数字写进公式之前,先问问它的含义,以及如何(和是否)应用它。总之,我反对使用斯特吉斯的公式,我认为它已经过时,而且不够充分)。
关于平均值。收益的期望值应该为 0,因为如果不是这样,我们就可以愚蠢地总是朝着一个方向下注,与这个 MO 的符号相对应,并保证获得任何预定规模的收益。那么,顶部应该与MO重合,这纯粹是出于对称的考虑:图形的左半部分应该是右半部分的镜像(从统计学角度看,增加率和减少率是相等的,它们之间不应该有任何差异),因此对称中心与中心重合。
由于您取的是 HS(0.00,1.00),因此您应将类居中,即零类应包括某个对称 区间(-x0;x0)内的指数值,否则我们就会在计算中引入与类相对于零的移动有关的系统误差,并最终将其渗入 chi^2 检验的结果中。您的 0 点并不在零类的中间。
事实上,如何使离散数据的类对称是一个相当棘手的问题,同样,我们最好对每个特定样本进行非常仔细的逐一求解,否则我们就有可能因为错误选择了划分类的边界而得到不充分的结果。
alsu,你提到的话题虽然不是 我文章的主题,但却非常有趣。我会尽我所能进一步研究这个问题。
感谢您的建设性批评!
我喜欢您关于科学知识在交易中的适用性的观点。
能否请您告诉我,您会向熟悉概率论和数理统计的人推荐哪本书?
丹尼斯,下午好。我喜欢您关于科学知识在交易中的适用性的观点。请告诉我,您会向熟悉概率论和数理统计的人推荐哪本书。
谢谢您的意见!
我认为,应该为初学者寻找一些读物。最重要的是,书中的文字不应妨碍您继续阅读:-)))。
我喜欢 Gaidyshev 和 Bulashev.....。
这里有 一个有趣的主题。
- rsdn.org
第二个不准确之处在于,你没有利用收益分布的顶部(又称期望值)必须正好为 0 的先验知识(否则我们早就都是亿万富翁了)。
完全没有。收益率分布顶点相对于 0 的移动(投资工具的增长/下降)并不意味着未来也会如此。这就是为什么大多数交易者都不是亿万富翁,而不是因为。
谢谢。
......分布顶端相对于 0(上升/下降仪器)的移动并不一定意味着未来也会如此...
同意。
向alsu 提问。您说的零点是指市场效率吗?
新文章 统计分布在交易者工作中的作用已发布:
本文是我的《用 MQL5 表示统计概率分布》一文的续篇,该文介绍了处理某些理论统计分布的类。现在,我们已经有了理论基础,我建议我们应直接进入实际数据集,并尝试据此基础获得某些信息。
作者:Dennis Kirichenko