
突破机器学习的局限(第一部分):缺乏可互操作的度量指标
遗憾的是,盲目遵循“最优实践”的危害,也在悄然侵蚀着我们交易策略所依赖的其他工具,从业者不应认为这个问题仅存在于技术指标之中。
在本系列文章中,我们将深入探讨算法交易者每天都会面临的重大问题,这些问题正是由那些本应保障他们使用机器学习模型安全的指导方针和实践所引发的。简言之,如果每天在MQL5云上部署的机器学习模型比操控它们的从业者更早地意识到本文所讨论的事实,那么麻烦即将来临。投资者可能会迅速发现自己面临的风险远超预期。
事实上,即便是在世界领先的统计学习书籍中,这些问题也未得到足够的重视。我们讨论的核心是一个每个从业者都应知晓的简单真理
“经分析后证明,欧几里得离散度量指标(如均方根误差RMSE、平均绝对误差MAE或均方误差MSE)的一阶导数,可以通过目标均值来求解。”
已经了解这一事实及其含义的从业者,无需继续阅读。
然而,对于那些尚未理解这一点的从业者,我迫切地需要通过本文与他们沟通。简言之,我们用于构建模型的回归度量指标,并不适合用于模拟资产收益率。
本文将带您了解这一现象是如何发生的,它给您带来的风险,以及您可以实施哪些改变,以开始利用这一原则作为指南针,在数百个潜在交易市场中筛选出适合的市场。
希望深入探究证明过程的从业者,可以查阅哈佛大学关于RMSE等度量指标局限性的文献。特别是,哈佛的论文提供了样本均值最小化RMSE的分析证明。读者可点击此处的链接查看该论文。
其他机构,如社会科学研究网络(SSRN),会维护一本期刊,刊载来自各个领域已发表且经过同行评审的论文,其中有一篇论文对我们的讨论很有帮助,其探究了用于资产定价任务中替代均方根误差(RMSE)的其他损失函数。我为读者挑选的这篇论文,回顾了该领域的其他论文,并在提出一种新方法之前对当前文献进行总结。读者可点击此处轻松地获取这篇论文。
一个类比实验(有助于理解)
想象您正在参加一场彩票式的竞赛。您和另外99人被随机选中,共同角逐1,000,000美元的大奖。规则很简单:您必须猜测其他99名参与者的身高。猜测总误差最小的人即为获胜者。
现在,情况有了变化:在本例中,假设全球人类的平均身高为1.1米。如果您对每个人都猜测为1.1米,那么您实际上可能会赢得大奖,尽管从技术层面上讲,您的每一个预测都是错误的。为什么呢?因为在充满噪声和不确定性的环境中,猜测平均值往往能产生最小的总体误差。
交易领域的类比
这个类比实验旨在向读者生动展示,大多数机器学习模型是如何被选中用于金融市场的。
例如,假设您正在构建一个模型来预测标准普尔500指数的收益率。如果一个模型总是预测该指数的历史平均值,即每年大约7%,那么当使用RMSE、MAE或MSE等指标来评判时,它实际上可能会比更复杂的模型表现更好。但这里有个陷阱:那个模型并没有学习到任何有用的内容。它只是围绕着统计平均值进行预测。更糟糕的是,您所信任的指标和验证程序,反而在奖励它这种做法。
初学者须知:RMSE是一种用于评判机器学习模型预测实值目标质量的“单位”。
它会对大的偏差进行惩罚,但是并不关心模型为何出错。不过要记住,模型因某些偏差而受到惩罚,而这些偏差实际上可能是盈利的。
因此,一个总是预测平均值的模型(即使它对市场毫无理解),在用RMSE评判时,也可能在纸面上看起来非常出色。但遗憾的是,让我们创建出数学上合理但实际上毫无用处的模型。
真正发生的情况
金融数据充满噪声。我们无法观察到关键变量,如全球真正的供需情况、投资者情绪或机构订单簿的深度。因此,为了最小化误差,您的模型会采取最符合统计学逻辑的做法:预测平均值。
读者必须明白,从数学上讲,这是一种合理的做法。预测平均值能最小化大多数常见的回归误差。但交易并非要最小化统计误差,而是要在不确定性下做出盈利决策。这一点至关重要。在我们这个社区,这样的做法类似于过拟合,但构建这些模型的统计学家并不像我们这样看待问题。
不要天真地认为这个问题只存在于回归模型中。在分类任务中,模型可以通过总是预测训练样本中最常见的类别来最小化误差。此外,如果训练集中最大的类别恰好与整个总体中最大的类别相对应,那么我相信从业者很快就能看出,模型是如何轻易地伪装其技能的。
奖励黑客行为:模型通过作弊获胜
这种现象被称为奖励黑客行为:即模型通过学习不良行为来达到令人满意的性能水平。在交易中,奖励黑客行为会导致从业者选择一个看似技能高超,但实际上只是玩平均数游戏的模型,这好比统计上的一个空中楼阁。您以为模型学习到了什么;但实际上,它所做的在统计学上就相当于说“每个人的身高都是1.1米”。而RMSE每次都毫无质疑地接受这一点。
真实证据
既然我们的契机已经明确,那么让我们抛开“空中楼阁”,转而考虑真实的市场数据。我通过MetaTrader 5的Python应用程序接口(API),从我的经纪商处获取了333个市场的数据。我们筛选出了至少拥有四年真实历史数据的市场。这一筛选条件将我们的市场范围缩小到了119个。
接下来,我们为每个市场构建两个模型:
- 控制模型:总在预测未来10天的平均收益率。
- 预测模型:尝试学习并预测未来的收益率。
模型结果
经测试,有91.6%的市场情况下,控制模型胜出。也就是说,总是预测历史平均10天收益率的模型,在四年时间里,有91%的情况下产生的误差更低!从业者很快就会发现,即便我们尝试使用更深的神经网络,改进效果也微乎其微。
那么,从业者是否应该遵循机器学习的“最优实践”,总是选择产生最低误差的模型呢?记住,这个模型就是总是预测平均收益率的模型?
初学者须知:这并不意味着机器学习对您毫无用处。这意味着您在交易环境中定义“良好表现”时必须极其谨慎。如果您不够谨慎,那么我们就有理由相信,您可能会在不知不觉中选择一个因预测市场平均收益率而受到奖励的模型。
那么,现在该怎么办?
结论很明确:我们目前使用的评估指标——RMSE、MSE、MAE——并非为交易而设计。它们诞生于统计学、医学和其他自然科学领域,在这些领域里,预测平均值是有意义的。但在我们的算法交易社区中,预测平均收益率有时甚至比没有预测、没有使用AI还要糟糕,有时候不使用AI反而更安全。但缺乏理解的AI永远是不安全的!
我们需要能够奖励有用技能的评估框架,而不是奖励统计配合度的指标。我们需要能够理解盈亏的指标。此外,我们还需要训练协议来惩罚“拥抱平均值”的行为,即采用鼓励模型在学习交易现实的同时,能够体现我们社区价值观的训练流程。而这正是本系列文章的重点。这是一系列独特的问题,它们并非直接由市场引起。相反,它们源于我们希望使用的工具本身,而且在其他文章、学术统计学习书籍甚至我们自己的社区讨论中都很少被提及。
从业者必须充分了解这些事实,以确保自身交易安全。遗憾的是,我们每个社区成员对这些局限性的基本认识并非都作为信手拈来的常识。日常从业者毫不犹豫地重复着非常危险的统计实践。
开始
让我们看看迄今为止的讨论是否有价值。加载我们的标准库。
import pandas as pd import numpy as np import matplotlib.pyplot as plt import MetaTrader5 as mt5 import multiprocessing as mp
定义我们希望预测未来的时间范围。
HORIZON = 10加载MetaTrader 5终端,以便我们获取真实的市场数据。
if(not mt5.initialize()): print("Failed to load MT5")
获取所有可用交易品种的完整列表。
symbols = mt5.symbols_get()
只需提取交易品种名称。
symbols[0].name
symbol_names = []
for i in range(len(symbols)):
symbol_names.append(symbols[i].name)现在,准备好看一下我们是否能超越一个总是预测均值的模型。
from sklearn.linear_model import Ridge from sklearn.model_selection import TimeSeriesSplit,cross_val_score
创建时间序列验证拆分器。
tscv = TimeSeriesSplit(n_splits=5,gap=HORIZON)我们需要一种方法,该方法能够在总是预测市场平均收益率时返回误差水平,以及在尝试预测未来市场收益率时返回误差水平。
def null_test(name): data_amount = 365 * 4 f_data = pd.DataFrame(mt5.copy_rates_from_pos(name,mt5.TIMEFRAME_D1,0,data_amount)) if(f_data.shape[0] < data_amount): print(f"{symbol_names[i]} did not have enough data!") return(None) f_data['time'] =pd.to_datetime(f_data['time'],unit='s') f_data['target'] = f_data['close'].shift(-HORIZON) - f_data['close'] f_data.dropna(inplace=True) model = Ridge() res = [] res.append(np.mean(np.abs(cross_val_score(model,f_data.loc[:,['open']] * 0,f_data['target'],cv=tscv)))) res.append(np.mean(np.abs(cross_val_score(model,f_data.loc[:,['open','high','low','close']],f_data['target'],cv=tscv)))) return(res)
现在,我们将对所有可获取的市场进行这项测试。
res = pd.DataFrame(columns=['Mean Forecast','Direct Forecast'],index=symbol_names) for i in range(len(symbol_names)): test_score = null_test(symbol_names[i]) if(test_score is None): print(f"{symbol_names[i]} does not have enough data!") res.iloc[i,:] = [np.nan,np.nan] continue res.iloc[i,0] = test_score[0] res.iloc[i,1] = test_score[1] print(f"{i/len(symbol_names)}% complete.") res['Score'] = ((res.iloc[:,1] / res.iloc[:,0])) res.to_csv("Deriv Null Model Test.csv")
0.06606606606606606%完成。
0.06906906906906907%完成。
0.07207207207207207%完成。
...
英镑兑美元(GBPUSD)相对强弱指数(RSI)下行趋势指标数据不足!
英镑兑美元(GBPUSD)相对强弱指数(RSI)下行趋势指标数据不足!
在我们可获取的所有市场中,我们能够分析的市场有多少个?
#How many markets did we manage to investigate? test = pd.read_csv("Null Model Test.csv") print(f"{(test.dropna().shape[0] / test.shape[0]) * 100}% of Markets Were Evaluated")
35.73573573573574%的市场已获评估
现在,我们将根据与每个市场相关联的分数,对119个市场进行分组。该分数是我们预测市场时的误差与总是预测平均收益率时的误差之比。分数小于1的情况令人印象深刻,因为这意味着我们的表现优于总是预测平均收益率的模型。否则,分数大于1则验证了我们开展此项研究的契机,正如我们在本文引言部分所分享的那样。
初学者须知:我们简要概述的评分方法在机器学习领域并非新事物。它是一种通常被称为R平方(决定系数)的指标。该指标能告诉我们,通过我们提出的模型,能够解释目标变量中多少比例的方差。我们并未使用您在独立学习过程中可能熟悉的精确R平方计算公式。
首先,让我们对所有得分小于1的市场进行分组。
res.loc[res['Score'] < 1]
| 市场名称 | 平均预测值 | 直接预测值 | 得分 |
|---|---|---|---|
| 澳元兑加元 | 0.022793 | 0.018566 | 0.814532 |
| 欧元兑加元 | 0.037192 | 0.027209 | 0.731587 |
| 新西兰元兑加元 | 0.019124 | 0.015117 | 0.790466 |
| 美元兑人民币 | 0.125586 | 0.112814 | 0.898297 |
在我们过去四年测试的所有市场中,表现优于总是预测市场平均收益率模型的比例究竟有多少?大约8%。
res.loc[res['Score'] < 1].shape[0] / res.shape[0]
0.08403361344537816
因此,这也意味着在过去的四年里,在我们测试的所有市场中,大约有91.6%的表现占比未能超越总是预测平均收益率的模型。
res.loc[res['Score'] > 1].shape[0] / res.shape[0]
0.9159663865546218
至此,部分读者或许会心生质疑:“作者仅使用了简单的线性模型,倘若我们投入时间构建更灵活的模型,定能一直超越预测平均收益率的模型。这纯属无稽之谈。”此言虽有一定道理,却也并非全然正确。接下来,让我们以欧元兑美元(EURUSD)市场为例,构建一个深度神经网络模型,力求超越预测市场平均收益率的基准模型。
首先,我们需要编写一个MQL5脚本,以捕获欧元兑美元汇率的详细市场信息。我们将记录四个价格水平各自的涨幅,以及它们之间的相对涨幅情况。
//+------------------------------------------------------------------+ //| ProjectName | //| Copyright 2020, CompanyName | //| http://www.companyname.net | //+------------------------------------------------------------------+ #property copyright "Copyright 2024, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #property script_show_inputs //+------------------------------------------------------------------+ //| System constants | //+------------------------------------------------------------------+ //+------------------------------------------------------------------+ //| File name | //+------------------------------------------------------------------+ string file_name = Symbol() + " IID Candlestick Recognition.csv"; //+------------------------------------------------------------------+ //| User inputs | //+------------------------------------------------------------------+ input int size = 3000; input int HORIZON = 10; //+------------------------------------------------------------------+ //| Our script execution | //+------------------------------------------------------------------+ void OnStart() { //---Write to file int file_handle=FileOpen(file_name,FILE_WRITE|FILE_ANSI|FILE_CSV,","); for(int i=size;i>=1;i--) { if(i == size) { FileWrite(file_handle,"Time","Open","High","Low","Close","Delta Open","Delta High","Delta Low","Delta Close","O - H","O - L","O - C","H - L","H - C","L - C"); } else { FileWrite(file_handle, iTime(_Symbol,PERIOD_CURRENT,i), iOpen(_Symbol,PERIOD_CURRENT,i), iHigh(_Symbol,PERIOD_CURRENT,i), iLow(_Symbol,PERIOD_CURRENT,i), iClose(_Symbol,PERIOD_CURRENT,i), iOpen(_Symbol,PERIOD_CURRENT,i) - iOpen(_Symbol,PERIOD_CURRENT,i + HORIZON), iHigh(_Symbol,PERIOD_CURRENT,i) - iHigh(_Symbol,PERIOD_CURRENT,i + HORIZON), iLow(_Symbol,PERIOD_CURRENT,i) - iLow(_Symbol,PERIOD_CURRENT,i + HORIZON), iClose(_Symbol,PERIOD_CURRENT,i) - iClose(_Symbol,PERIOD_CURRENT,i + HORIZON), iOpen(_Symbol,PERIOD_CURRENT,i) - iHigh(_Symbol,PERIOD_CURRENT,i), iOpen(_Symbol,PERIOD_CURRENT,i) - iLow(_Symbol,PERIOD_CURRENT,i), iOpen(_Symbol,PERIOD_CURRENT,i) - iClose(_Symbol,PERIOD_CURRENT,i), iHigh(_Symbol,PERIOD_CURRENT,i) - iLow(_Symbol,PERIOD_CURRENT,i), iHigh(_Symbol,PERIOD_CURRENT,i) - iClose(_Symbol,PERIOD_CURRENT,i), iLow(_Symbol,PERIOD_CURRENT,i) - iClose(_Symbol,PERIOD_CURRENT,i) ); } } //--- Close the file FileClose(file_handle); } //+------------------------------------------------------------------+ //+------------------------------------------------------------------+ //| Undefine system constants | //+------------------------------------------------------------------+ #undef HORIZON
现在,将您的脚本拖放到图表上以获取该市场的历史数据,之后我们就可以开始操作。
#Read in market data HORIZON = 10 data = pd.read_csv('EURUSD IID Candlestick Recognition.csv') #Label the data data['Null'] = 0 data['Target'] = data['Close'].shift(-HORIZON) - data['Close'] #Drop the last HORIZON rows of data data = data.iloc[:-HORIZON,:] data
那些认为深度神经网络和复杂模型能够解决超越预测市场平均收益率模型这一难题的读者,在阅读本文接下来的内容时,一定会感到震惊。
我建议您在投入资金部署模型之前,先使用自己的经纪商平台重复这一实验。现在,让我们加载scikit-learn工具包,来对比一下我们的深度神经网络与简单线性模型的表现孰优孰劣。
#Load our models from sklearn.neural_network import MLPRegressor from sklearn.linear_model import Ridge from sklearn.model_selection import TimeSeriesSplit,train_test_split,cross_val_score
分割数据。
#Split the data into half train,test = train_test_split(data,test_size=0.5,shuffle=False)
创建时间序列验证对象。
#Create a time series validation object tscv = TimeSeriesSplit(n_splits=5,gap=HORIZON)
构建一个总是预测市场平均收益率的模型。因总是预测均值而产生的误差被称为“总平方和(TSS)”。在机器学习中,TSS是一个关键的误差基准,它为我们指明了评估模型性能的基准方向。
#Fit the model predicting the mean on the train set null_model = Ridge() null_model.fit(train[['Null']],train['Target']) tss = np.mean(np.abs(cross_val_score(null_model,test[['Null']],test['Target'],cv=tscv,scoring='neg_mean_absolute_error'))) tss
np.float64(0.011172426520738554)
定义我们的输入和目标。
X = data.iloc[:,4:-2].columns y = 'Target'
训练您的深度神经网络。我鼓励读者根据自身需求自由调整这个神经网络的结构与参数,衡量自己是否有能力超越均值预测的表现。
#Let us now try to outperform the null model model = MLPRegressor(activation='logistic',solver='lbfgs',random_state=0,shuffle=False,hidden_layer_sizes=(len(X),200,50),max_iter=1000,early_stopping=False) model.fit(train.loc[:,X],train['Target']) rss = np.mean(np.abs(cross_val_score(model,test.loc[:,X],test['Target'],cv=tscv,scoring='neg_mean_absolute_error'))) print(f"Test Passed: {rss < tss} || New R-Squared Metric {rss/tss}") res = [] res.append(rss) res.append(tss) sns.barplot(res,color='black') plt.axhline(tss,color='red',linestyle=':') plt.grid() plt.ylabel("RMSE") plt.xticks([0,1],['Deep Neural Network','Null Model']) plt.title("Our Deep Neural Network vs The Null Model") plt.show()
经过大量的配置、调整与优化,我最终成功利用深度神经网络击败了那个预测平均收益率的模型。然而,让我们深入探究这背后的具体情况。

图1:超越预测市场平均收益率的模型充满挑战性
接下来,让我们直观地展示深度神经网络所带来的改进。首先,我会搭建一个网格,以便我们评估测试集中市场收益率的分布情况,以及我们模型所预测收益率的分布情况。存储模型对测试集的预测收益率。
predictions = model.predict(test.loc[:,X])
我们先将训练集中观察到的平均市场收益率,在图表中间用红色虚线标出。
plt.title("Visualizing Our Improvements")
plt.plot()
plt.grid()
plt.xlabel("Return")
plt.axvline(train['Target'].mean(),color='red',linestyle=':')
legend = ['Train Mean']
plt.legend(legend)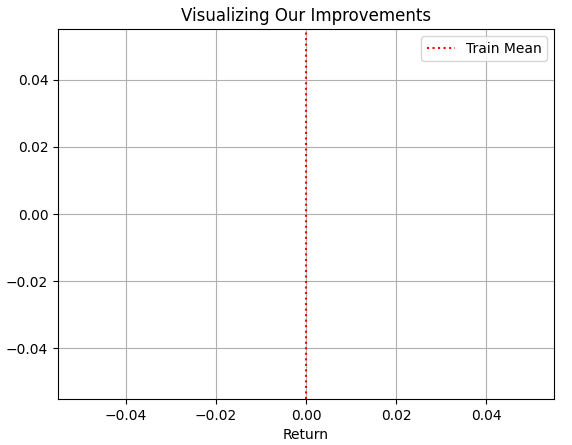
图2:可视化训练集的平均市场收益率
现在,让我们将模型对测试集的预测结果叠加在训练集的平均收益率之上。正如读者所见,模型的预测值围绕训练集均值呈分散分布。然而,当我们最终将市场实际遵循的真实分布以黑色曲线形式叠加在底层时,问题便一目了然了。
plt.title("Visualizing Our Improvements") plt.plot() plt.grid() plt.xlabel("Return") plt.axvline(train['Target'].mean(),color='red',linestyle=':') sns.histplot(predictions,color='blue') legend = ['Train Mean','Model Predictions'] plt.legend(legend)
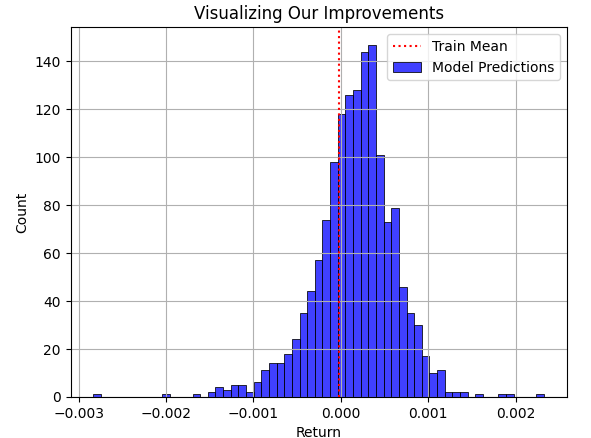
图3:可视化模型针对训练集中观察到的平均收益率所做出的预测
在图3中,模型预测的蓝色区域看似合理,但当我们最终在图4中考虑市场实际遵循的真实分布时,便会发现,该模型并不适用于当前任务。该模型未能捕捉到市场真实分布的宽度,其中一些最大的盈利和亏损情况,都超出了模型的感知范围。遗憾的是,如果负责的从业者没有仔细理解、重视并正确解读RMSE这一指标,那么RMSE往往会引导从业者选择此类模型。在真实交易中使用这样的模型,将会给您的实盘交易带来灾难性后果。
plt.title("Visualizing Our Improvements") plt.plot() plt.grid() plt.xlabel("Return") plt.axvline(train['Target'].mean(),color='red',linestyle=':') sns.histplot(test['Target'],color='black') sns.histplot(predictions,color='blue') legend = ['Train Mean','Test Distribution','Model Prediction'] plt.legend(legend)
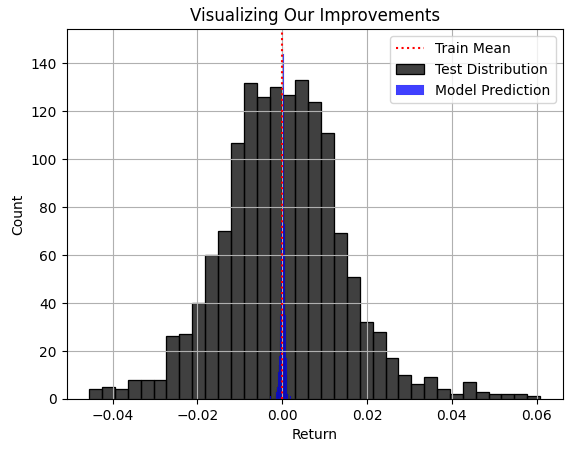
图4:模型预测与市场真实分布的可视化对比
我们提出的解决方案
至此,我们已向读者证明,诸如RMSE等指标,很容易通过总是预测市场平均收益率来优化,同时也阐述了为何这种做法缺乏吸引力——因为RMSE往往会告诉我们,这样一个毫无用处的模型,竟是我们所能获得的最好结果。我们明确指出,需要一些流程和新技术,能够切实做到以下几点:
- 检验对真实市场的理解程度。
- 理解盈利与亏损之间的差异。
- 抑制“均值依赖”行为。
我想要提出一种独特的模型架构,它可能是读者可以考虑的一个候选解决方案。我将这一策略称为“动态状态切换模型”,简称DRS。在另一篇关于高概率交易设置的讨论中,我们观察到,对交易策略产生的盈亏进行建模,可能比直接预测市场走势更为容易。尚未阅读过那篇文章的读者,可点击此处链接阅读。
现在,我们将以一种有趣的方式利用这一观察结果。我们将构建两个完全相同的模型,以模拟同一交易策略的对立版本。一个模型总是假设市场处于趋势跟踪状态,而另一个模型则总是假设市场处于均值回归状态。每个模型将单独训练,且彼此之间没有互通,也无法协调其预测结果。
读者应回忆起有效市场假说教导投资者,买入和卖出相同数量的同一资产,将使投资者实现完美对冲,且如果两个头寸同时开仓和平仓,在不考虑任何交易费用的情况下,总盈利为0。因此,我们预期模型也应一直遵循这一事实。确切地说,我们可以检验模型是否遵循此真理,否则,模型对真实市场毫无理解。
因此,我们可以通过检验DVM是否展现出对构建市场结构的这一原则的理解,来替代依赖诸如RMSE等指标。这正是我们检验对真实市场理解程度的测试所在。如果我们的两个模型都真正理解了交易的实际情况,那么无论何时,它们的预测总和应一直为0。我们将在训练集上训练模型,然后在样本外进行测试,看一下即使在模型承受压力的情况下,其预测总和是否一直为0。
请记住,模型的预测结果之间并未基于任何方式、形式或结构上的协调。模型是单独训练的,且彼此之间没有互通。因此,如果模型没有“操纵”理想的误差指标,而是真正学习了市场的底层结构,那么当两个模型的预测总和为0时,它们将证明自己是通过正当途径得出的预测结果。
在任何时刻,这两个模型中只有一个可以预期获得正回报。如果我们的模型预测总和不为0,那么模型可能无意中学习到了违反有效市场假说的方向性偏差。否则,在最优情况下,我们可以以前所未有的信心水平在这两种市场状态之间动态切换。在任何单一时刻,应预期只有一个模型获得正回报,而我们的交易理念是,相信该模型对应于市场当前所处的隐藏状态。这样可能对我们来说,比低RMSE值更有价值。
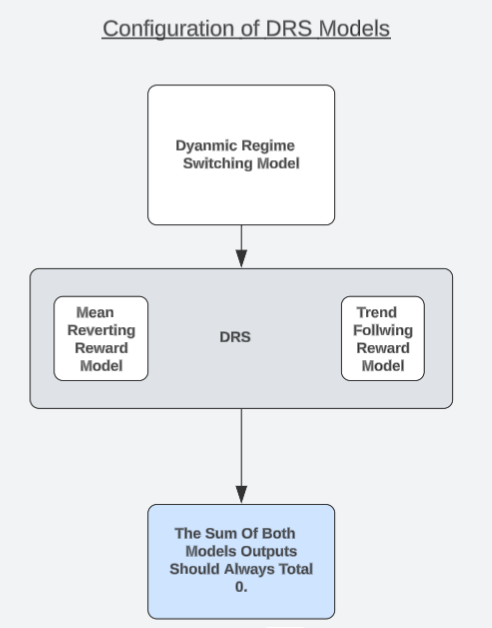
图5:理解我们的DRS模型整体架构
从交易终端获取数据
为了获得最优效果,我们的数据应尽可能详尽。因此,我们既要跟踪技术指标和价格水平的当前值,也要同时记录这些市场动态中正在发生的增长情况。
//+------------------------------------------------------------------+ //| ProjectName | //| Copyright 2020, CompanyName | //| http://www.companyname.net | //+------------------------------------------------------------------+ #property copyright "Copyright 2024, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #property script_show_inputs //--- Define our moving average indicator #define MA_PERIOD 5 //--- Moving Average Period #define MA_TYPE MODE_SMA //--- Type of moving average we have #define HORIZON 10 //--- Our handlers for our indicators int ma_handle; //--- Data structures to store the readings from our indicators double ma_reading[]; //--- File name string file_name = Symbol() + " DRS Modelling.csv"; //--- Amount of data requested input int size = 3000; //+------------------------------------------------------------------+ //| Our script execution | //+------------------------------------------------------------------+ void OnStart() { int fetch = size + (HORIZON * 2); //---Setup our technical indicators ma_handle = iMA(_Symbol,PERIOD_CURRENT,MA_PERIOD,0,MA_TYPE,PRICE_CLOSE); //---Set the values as series CopyBuffer(ma_handle,0,0,fetch,ma_reading); ArraySetAsSeries(ma_reading,true); //---Write to file int file_handle=FileOpen(file_name,FILE_WRITE|FILE_ANSI|FILE_CSV,","); for(int i=size;i>=1;i--) { if(i == size) { FileWrite(file_handle,"Time","Open","High","Low","Close","Delta O","Delta H","Delta Low","Delta Close","SMA 5","Delta SMA 5"); } else { FileWrite(file_handle, iTime(_Symbol,PERIOD_CURRENT,i), iOpen(_Symbol,PERIOD_CURRENT,i), iHigh(_Symbol,PERIOD_CURRENT,i), iLow(_Symbol,PERIOD_CURRENT,i), iClose(_Symbol,PERIOD_CURRENT,i), iOpen(_Symbol,PERIOD_CURRENT,i) - iOpen(_Symbol,PERIOD_CURRENT,(i + HORIZON)), iHigh(_Symbol,PERIOD_CURRENT,i) - iHigh(_Symbol,PERIOD_CURRENT,(i + HORIZON)), iLow(_Symbol,PERIOD_CURRENT,i) - iLow(_Symbol,PERIOD_CURRENT,(i + HORIZON)), iClose(_Symbol,PERIOD_CURRENT,i) - iClose(_Symbol,PERIOD_CURRENT,(i + HORIZON)), ma_reading[i], ma_reading[i] - ma_reading[(i + HORIZON)] ); } } //--- Close the file FileClose(file_handle); } //+------------------------------------------------------------------+
开始
为了顺利推进后续工作,我们首先导入标准库。
#Load our libraries import pandas as pd import numpy as np import matplotlib.pyplot as plt import seaborn as sns
现在我们可以读取之前导出到CSV文件中的数据。
#Read in the data data = pd.read_csv("/content/drive/MyDrive/Colab Data/Financial Data/FX/EUR USD/DRS Modelling/EURUSD DRS Modelling.csv") data
在编写MQL5脚本时,我们曾对未来10个步长进行预测。现在必须保持一致。
#Recall that in our MQL5 Script our forecast horizon was 10 HORIZON = 10 #Calculate the returns generated by the market data['Return'] = data['Close'].shift(-HORIZON) - data['Close'] #Drop the last horizon rows data = data.iloc[:-HORIZON,:]
现在对数据进行标注。需要注意的是,我们将设置两类标签:一类总是假设市场将持续趋势行情,另一类则总是假设市场处于均值回归状态。
#Now let us define the signals being generated by the moving average, in the DRS framework there are always at least n signals depending on the n states the market could be in #Our simple DRS model assumes only 2 states #First we will define the actions you should take assuming the market is in a trending state #Therefore if price crosses above the moving average, buy. Otherwise, sell. data['Trend Action'] = 0 data.loc[data['Close'] > data['SMA 5'], 'Trend Action'] = 1 data.loc[data['Close'] < data['SMA 5'], 'Trend Action'] = -1 #Now calculate the returns generated by the strategy data['Trend Profit'] = data['Trend Action'] * data['Return']
在完成趋势跟踪行为的标注后,再插入均值回归行为的标注。
#Now we will repeat the procedure assuming the market was mean reverting data['Mean Reverting Action'] = 0 data.loc[data['Close'] > data['SMA 5'], 'Mean Reverting Action'] = -1 data.loc[data['Close'] < data['SMA 5'], 'Mean Reverting Action'] = 1 #Now calculate the returns generated by the strategy data['Mean Reverting Profit'] = data['Mean Reverting Action'] * data['Return']
通过这种数据标注方式,我们期望计算机能够识别出每种策略在何种市场条件下会亏损,以及预测何时应采纳不同的策略。如果绘制累计目标值曲线,可以清晰地观察到:在我们所选的数据时间段内,欧元兑美元市场呈现均值回归特征的时间,多于趋势跟踪特征的时间。然而,需要注意的是,两条曲线均存在突发性波动。我认为这些异常波动可能对应着市场的突然状态切换。
#If we plot our cumulative profit sums, we can see the profit and losses aren't evenly distributed between the two states plt.plot(data['Trend Profit'].cumsum(),color='black') plt.plot(data['Mean Reverting Profit'].cumsum(),color='red') #The mean reverting strategy appears to have been making outsized profits with respect to the trending stratetefgy #However, closer inspection reveals, that both strategies are profitable, but never at the same time! #The profit profiles of both strategies show abrupt shocks, when the opposite strategy become more profitable. plt.legend(['Trend Profit','Mean Reverting Profit']) plt.xlabel('Time') plt.ylabel('Profit/Loss') plt.title('A DRS Model Visualizes The Market As Being in 2 Possible States') plt.grid() plt.axhline(0,color='black',linestyle=':')
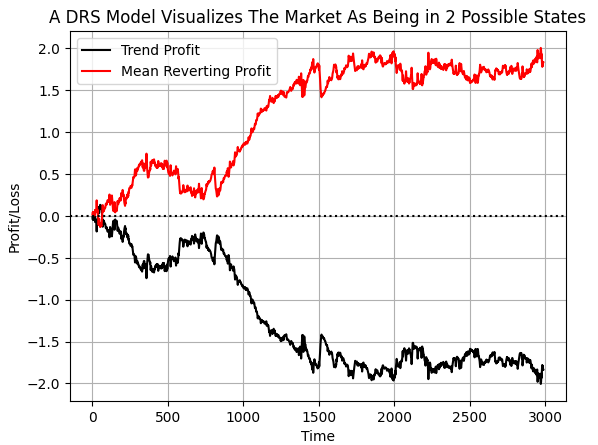
图6:可视化两种对立策略的盈利分布
定义输入与目标。
#Let's define the inputs and target X = data.iloc[:,1:-5].columns y = ['Trend Profit','Mean Reverting Profit']
选择我们的市场建模工具。
#Import the modelling tools from sklearn.model_selection import train_test_split,TimeSeriesSplit from sklearn.ensemble import RandomForestRegressor
分两次拆分数据。从而得到训练集、验证集和最终测试集。
#Split the data train , test = train_test_split(data,test_size=0.5,shuffle=False) f_train , f_validation = train_test_split(train,test_size=0.5,shuffle=False)
现在开始构建两个模型。再次提醒,这两个模型虽然会为我们提供对市场的双重视角(Dual-View),但它们之间不应存在任何形式的协同或关联。
#The trend model trend_model = RandomForestRegressor() #The mean reverting model mean_model = RandomForestRegressor()
拟合我们的模型。
trend_model.fit(f_train.loc[:,X],f_train.loc[:,y[0]]) mean_model.fit(f_train.loc[:,X],f_train.loc[:,y[1]])
验证模型的有效性。我们将记录两个模型在测试集上对各自目标变量的预测值。需注意,这两个模型并非针对同一目标进行学习。每个模型均独立学习各自的目标变量,并单独优化以降低自身误差,彼此间不存在任何关联。
pred_1 = trend_model.predict(f_validation.loc[:,X]) pred_2 = mean_model.predict(f_validation.loc[:,X])
验证集数据对模型而言属于完全未见样本。我们实质上是在用模型从未接触过的数据进行压力测试,观察其在极端市场环境下是否仍能保持"理性"行为。
我们的测试基于两个模型预测值的相加总和。如果两模型预测值之和的最大值为0.0,则判定模型通过测试。这是因为根据有效市场假说,当投资者同时遵循两个对立策略时,其收益应当相互抵消(即总和为0)。在我们实际执行时每次仅采用单个模型的预测结果。因此需要动态切换不同策略的运行状态,也就是说,实现无需人工干预的自动化策略切换机制。
test_result = pred_1 + pred_2 print(f" Test Passed: {np.linalg.norm(test_result,ord=2) == 0.0}")
NumPy库包含众多实用工具包,例如我们前文使用的线性代数模块。其中调用的norm函数可根据参数设置,返回向量所有元素的绝对值之和,或向量的最大绝对值。从逻辑上讲,这与手动验证数组内容完全等效——即确认数组中所有数值均为0。请注意,此处我已省略数组输出,但可以保证所有元素确实均为0。
array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
当我们将趋势跟踪策略的实际盈利曲线,与该策略模型的预测值进行对比时会发现:除去少数几次极端盈利波动(例如在第600-700天区间,欧元兑美元市场出现剧烈波动期间),我们的模型能够准确追踪到其他常规幅度的盈利变化。
plt.plot(f_validation.loc[:,y[0]],color='black') plt.plot(pred_1,color='red',linestyle=':') plt.legend(['Actual Profit','Predicted Profit']) plt.grid() plt.ylabel('Loss / Profit') plt.xlabel('Out Of Sample Days') plt.title('Visualizing Our Model Performance Out Of Sample on the EURUSD 10 Day Return')
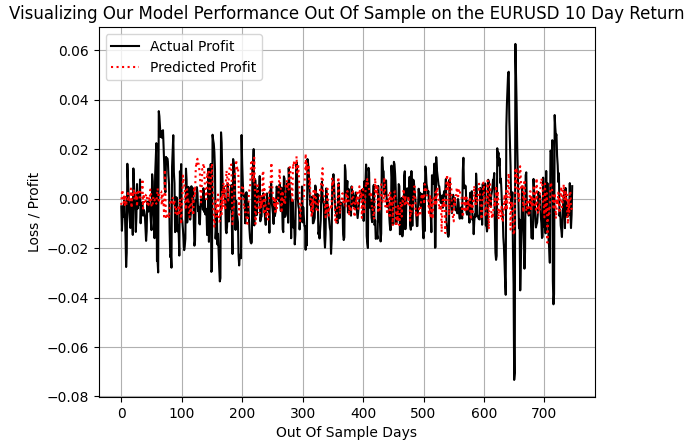
图7:我们的DRS模型未能捕捉市场真实波动性
现在,我们可将机器学习模型导出为ONNX格式,为交易系统开辟新的技术路径。ONNX是开放神经网络交换标准,通过一组通用API实现模型的构建与部署。其核心优势在于跨语言兼容性——不同编程环境均可调用同一ONNX模型文件。需注意,每个ONNX文件本质上是原机器学习模型的序列化表示。如果尚未安装skl2onnx和ONNX库,请先执行以下安装命令:
!pip install skl2onnx onnx
接下来加载模型导出所需的工具库。
import onnx from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType
定义ONNX模型的输入/输出形状。
eurusd_drs_shape = [("float_input",FloatTensorType([1,len(X)]))] eurusd_drs_output_shape = [("float_output",FloatTensorType([1,1]))]
准备DRS模型的ONNX原型。
trend_drs_model_proto = convert_sklearn(trend_model,initial_types=eurusd_drs_shape,final_types=eurusd_drs_output_shape,target_opset=12) mean_drs_model_proto = convert_sklearn(mean_model,initial_types=eurusd_drs_shape,final_types=eurusd_drs_output_shape,target_opset=12)
保存模型。
onnx.save(trend_drs_model_proto,"EURUSD RF D1 T LBFGSB DRS.onnx") onnx.save(mean_drs_model_proto,"EURUSD RF D1 M LBFGSB DRS.onnx")
恭喜!您已成功构建首个DRS模型架构。接下来,让我们进入回测环节——验证模型是否产生实际价值,以及能否有效替代设计流程中的RMSE评估指标。
MQL5入门指南
在开始之前,我们需要先定义交易系统中至关重要的常量。
//+------------------------------------------------------------------+ //| EURUSD DRS.mq5 | //| Copyright 2024, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2024, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" //+------------------------------------------------------------------+ //| System constants | //+------------------------------------------------------------------+ #define HORIZON 10 #define MA_PERIOD 5 #define MA_SHIFT 0 #define MA_MODE MODE_SMA #define TRADING_VOLUME SymbolInfoDouble(Symbol(),SYMBOL_VOLUME_MIN)
现在,我们可以加载系统资源。
//+------------------------------------------------------------------+ //| System dependencies | //+------------------------------------------------------------------+ #resource "\\Files\\DRS\\EURUSD RF D1 T DRS.onnx" as uchar onnx_proto[] //Our Trend Model #resource "\\Files\\DRS\\EURUSD RF D1 M DRS.onnx" as uchar onnx_proto_2[] //Our Mean Reverting Mode
加载交易库。
//+------------------------------------------------------------------+ //| System libraries | //+------------------------------------------------------------------+ #include <Trade/Trade.mqh> CTrade Trade;
我们还需要为技术指标定义相应的变量。
//+------------------------------------------------------------------+ //| Technical Indicators | //+------------------------------------------------------------------+ int ma_o_handle,ma_c_handle,atr_handle; double ma_o[],ma_c[],atr[]; double bid,ask; int holding_period;
指定全局变量。
//+------------------------------------------------------------------+ //| Global variables | //+------------------------------------------------------------------+ long onnx_model,onnx_model_2;
当应用程序首次加载时,我们将调用一个专门负责加载技术指标和ONNX模型的方法。
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- if(!setup()) return(INIT_FAILED); //--- return(INIT_SUCCEEDED); }
如果应用程序未处于使用状态,我们应及时释放不再需要的系统资源。
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- release(); }
最终,当接收到最新价格数据时,系统将执行两项核心操作:要么寻找交易机会,要么管理现有持仓。
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- static datetime time_stamp; datetime current_time = iTime(Symbol(),PERIOD_D1,0); if(time_stamp != current_time) { time_stamp = current_time; update_variables(); if(PositionsTotal() == 0) { find_setup(); } else if(PositionsTotal() > 0) { manage_setup(); } } } //+------------------------------------------------------------------+
这是我们为搭建整个交易系统所编写的核心功能实现代码。
//+------------------------------------------------------------------+ //| Attempt To Setup Our System Variables | //+------------------------------------------------------------------+ bool setup(void) { atr_handle = iATR(Symbol(),PERIOD_CURRENT,14); ma_c_handle = iMA(Symbol(),PERIOD_CURRENT,MA_PERIOD,MA_SHIFT,MA_MODE,PRICE_CLOSE); ma_o_handle = iMA(Symbol(),PERIOD_CURRENT,MA_PERIOD,MA_SHIFT,MA_MODE,PRICE_OPEN); holding_period = 0; onnx_model = OnnxCreateFromBuffer(onnx_proto,ONNX_DEFAULT); onnx_model_2 = OnnxCreateFromBuffer(onnx_proto_2,ONNX_DEFAULT); if(onnx_model == INVALID_HANDLE) { Comment("Failed to load Trend DRS model"); return(false); } if(onnx_model_2 == INVALID_HANDLE) { Comment("Failed to load Mean Reverting DRS model"); return(false); } ulong input_shape[] = {1,10}; ulong output_shape[] = {1,1}; if(!OnnxSetInputShape(onnx_model,0,input_shape)) { Comment("Failed to set Trend DRS Model input shape"); return(false); } if(!OnnxSetInputShape(onnx_model_2,0,input_shape)) { Comment("Failed to set Mean Reverting DRS Model input shape"); return(false); } if(!OnnxSetOutputShape(onnx_model,0,output_shape)) { Comment("Failed to set Trend DRS Model output shape"); return(false); } if(!OnnxSetOutputShape(onnx_model_2,0,output_shape)) { Comment("Failed to set Mean Reverting DRS Model output shape"); return(false); } return(true); }
当系统执行反初始化操作时,我们将手动释放不再使用的技术指标和ONNX模型资源。
//+------------------------------------------------------------------+ //| Free up system resources | //+------------------------------------------------------------------+ void release(void) { IndicatorRelease(ma_c_handle); IndicatorRelease(ma_o_handle); OnnxRelease(onnx_model); OnnxRelease(onnx_model_2); }
每当获取新的价格信息时,立即更新系统变量。
//+------------------------------------------------------------------+ //| Update our system variables | //+------------------------------------------------------------------+ void update_variables(void) { bid = SymbolInfoDouble(Symbol(),SYMBOL_BID); ask = SymbolInfoDouble(Symbol(),SYMBOL_ASK); CopyBuffer(ma_c_handle,0,1,(HORIZON*2),ma_c); CopyBuffer(ma_o_handle,0,1,(HORIZON*2),ma_o); CopyBuffer(atr_handle,0,0,1,atr); ArraySetAsSeries(ma_c,true); ArraySetAsSeries(ma_o,true); }
通过追踪10日收益率的倒计时机制,对现有持仓进行动态管理。
//+------------------------------------------------------------------+ //| Manage The Trade We Have Open | //+------------------------------------------------------------------+ void manage_setup(void) { if((PositionsTotal() > 0) && (holding_period < (HORIZON-1))) holding_period +=1; else if((PositionsTotal() > 0) && (holding_period == (HORIZON - 1))) Trade.PositionClose(Symbol()); }
通过获取当前市场状态的详细信息并输入模型,识别潜在交易机会。我们的策略核心是利用移动平均线作为投资者情绪的方向灯。当移动平均线发出做空信号时,虽然市场普遍预期投资者将做空,但我们相信在外汇市场中多数人的判断往往相反。
//+------------------------------------------------------------------+ //| Find A Trading Oppurtunity For Our Strategy | //+------------------------------------------------------------------+ void find_setup(void) { vectorf model_inputs = vectorf::Zeros(10); vectorf model_outputs = vectorf::Zeros(1); vectorf model_2_outputs = vectorf::Zeros(1); holding_period = 0; int i = 0; model_inputs[0] = (float) iOpen(Symbol(),PERIOD_CURRENT,0); model_inputs[1] = (float) iHigh(Symbol(),PERIOD_CURRENT,0); model_inputs[2] = (float) iLow(Symbol(),PERIOD_CURRENT,0); model_inputs[3] = (float) iClose(Symbol(),PERIOD_CURRENT,0); model_inputs[4] = (float)(iOpen(Symbol(),PERIOD_CURRENT,0) - iOpen(Symbol(),PERIOD_CURRENT,HORIZON)); model_inputs[5] = (float)(iHigh(Symbol(),PERIOD_CURRENT,0) - iHigh(Symbol(),PERIOD_CURRENT,HORIZON)); model_inputs[6] = (float)(iLow(Symbol(),PERIOD_CURRENT,0) - iLow(Symbol(),PERIOD_CURRENT,HORIZON)); model_inputs[7] = (float)(iClose(Symbol(),PERIOD_CURRENT,0) - iClose(Symbol(),PERIOD_CURRENT,HORIZON)); model_inputs[8] = (float) ma_c[0]; model_inputs[9] = (float)(ma_c[0] - ma_c[HORIZON]); if(!OnnxRun(onnx_model,ONNX_DEFAULT,model_inputs,model_outputs)) { Comment("Failed to run the ONNX model correctly."); } if(!OnnxRun(onnx_model_2,ONNX_DEFAULT,model_inputs,model_2_outputs)) { Comment("Failed to run the ONNX model correctly."); } if(model_outputs[0] > 0) { if(ma_c[0] < ma_o[0]) { if(iClose(Symbol(),PERIOD_CURRENT,0) > ma_c[0]) Trade.Buy(TRADING_VOLUME,Symbol(),ask,0,0,""); } else if(ma_c[0] > ma_o[0]) { if(iClose(Symbol(),PERIOD_CURRENT,0) < ma_c[0]) Trade.Sell(TRADING_VOLUME,Symbol(),bid,0,0,""); } } else if(model_2_outputs[0] > 0) { if(ma_c[0] < ma_o[0]) { if(iClose(Symbol(),PERIOD_CURRENT,0) < ma_c[0]) Trade.Buy(TRADING_VOLUME,Symbol(),ask,0,0,""); } if(ma_c[0] > ma_o[0]) { if(iClose(Symbol(),PERIOD_CURRENT,0) > ma_c[0]) Trade.Sell(TRADING_VOLUME,Symbol(),bid,0,0,""); } } Comment("0: ",model_outputs[0],"1: ",model_2_outputs[0]); }
未定义系统常量。
//+------------------------------------------------------------------+ //| Undefine system constants | //+------------------------------------------------------------------+ #undef HORIZON #undef MA_MODE #undef MA_PERIOD #undef MA_SHIFT #undef TRADING_VOLUME //+------------------------------------------------------------------+
首先,我们需要选定回测日期范围。再次提醒,我们一直选择模型训练集之外的日期进行回测,以此可靠评估模型在未来的实际表现。
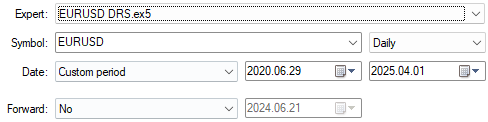
图8:请确保所选回测日期均位于模型训练集之外
为全面检验模型性能,建议选择"随机延迟"和"基于真实tick的逐tick回测"模式,以便在真实且复杂的市场环境下测试策略有效性。
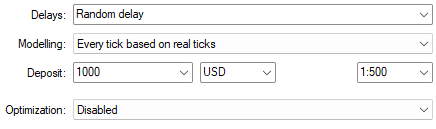
图9:选择"基于真实tick的逐tick回测"是对DRS架构进行压力测试最贴近真实市场的建模方式
以下是我们新的DRS策略的详细性能总结。有意思的是,我们首次尝试在模型构建过程中正式用DRS替代RMSE,便成功开发出盈利策略。
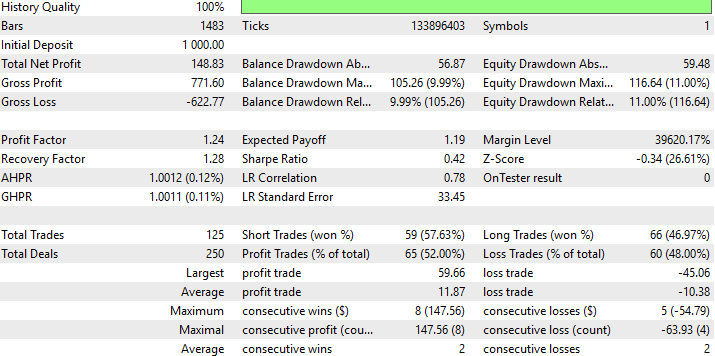
图10:策略在未参与训练数据上的详细性能表现
观察策略生成的资金曲线,可发现此前讨论的DRS模型缺陷——未能预判市场波动性,已导致策略收益出现周期性震荡。具体表现为盈利期与亏损期交替出现。然而,该策略仍展现出良好的自我修正能力,能够持续回归预期收益轨道,这符合我们的期望。
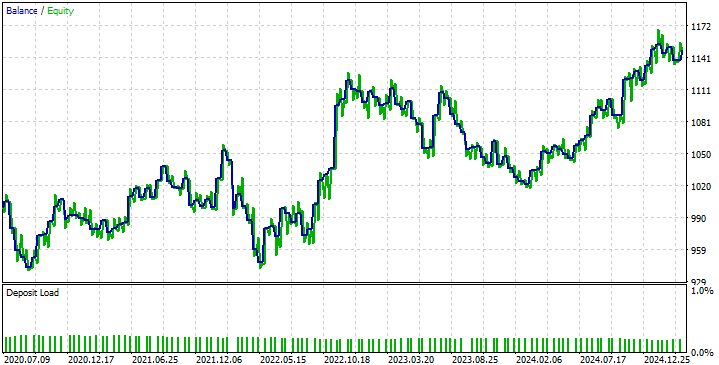
图11:新交易策略生成的资金曲线
结论
阅读本文后,原本不了解这些指标局限性的读者,其认知水平已显著提升。理解工具的局限性与掌握其优势同样重要。在构建AI模型时,优化方法在解决高难度问题时可能陷入"局部最优"困境。当从业者用这些工具模拟资产收益时,必须清醒地认识到:模型可能倾向于收敛至市场平均收益水平。
读者还获得了切合实际的见解:通过筛选能持续超越平均收益预测模型的市场,可发现其中存在的套利机会——这正暗示着市场存在低效性,值得从业者深度挖掘。
通过基于超额收益能力的市场筛选,读者将学会不再盲目依赖RMSE作为单一评估指标,而是一直将其与TSS进行相对比较。这种实践认知突破了多数同类文献的研究范畴,包括本文引用的学术文献,使读者受益匪浅。
最后,如果读者计划将机器学习模型投入实盘交易却未意识到这些局限,笔者强烈建议:请先复现本文演示的验证流程,避免在未知风险中"自毁长城"。RMSE可能让模型在测试中"作弊",但相信坚持读完本文的读者,已具备识破AI局限性的慧眼。
| 文件名 | 文件描述 |
|---|---|
| DRS Models.mq5 | 我们为获取构建DRS模型所需的详细市场数据而开发的MQL5脚本。 |
| Dynamic_Regime_Switching_Models_(DRS_Modelling).ipynb | 我们用于设计DRS模型的Jupyter笔记本。 |
| EURUSD DRS.mq5 | 我们采用DRS模型的欧元兑美元EA。 |
| EURUSD RF D1 T DRS.onnx | 趋势跟踪DRS模型总是假设市场处于趋势跟踪状态。 |
| EURUSD RF D1 M DRS.onnx | 均值回归DRS模型总是假设市场处于均值回归状态。 |
本文由MetaQuotes Ltd译自英文
原文地址: https://www.mql5.com/en/articles/17906
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。
 MQL5 中的高级订单执行算法:TWAP、VWAP 和冰山订单
MQL5 中的高级订单执行算法:TWAP、VWAP 和冰山订单
 MQL5交易工具(第一部分):构建交互式可视化挂单交易助手工具
MQL5交易工具(第一部分):构建交互式可视化挂单交易助手工具
 您应当知道的 MQL5 向导技术(第 56 部分):比尔·威廉姆斯(Bill Williams)分形
您应当知道的 MQL5 向导技术(第 56 部分):比尔·威廉姆斯(Bill Williams)分形

"然而,我们的战略展示了恢复和保持正轨的能力,这正是我们所追求的"。
我一直认为,一个人应该努力追求的是能够产生利润的战略:)
"然而,我们的战略显示出我们有能力恢复并保持正轨,这正是我们的目标"。
我一直认为,应该努力制定一项能带来利润的战略:)
谢谢你的文章,@Gamuchirai Zororo Ndawana
我同意@Maxim Dmitrievsky 的观点,最终目标是盈利。作为稳健性和缩水控制,"恢复并保持在正轨上 "的想法是有道理的,但它不能取代盈利。
实用建议:前向检验、成本和滑点、非对称或量化损失或基于效用的目标,以及惩罚换手率以避免均值拥抱。(务实的看法:使亏损与盈利方式保持一致)。
引用:的确如此,但遗憾的是,我们仍然没有标准化的机器学习指标来区分盈利和亏损。
答: 是的:只有当您的反向测试产品 或平盘与您针对后续投资组合或一篮子指数所使用的远期市场一样好时,才会存在盈亏栏。
有一些指数和新创立的 ETF `s 即将推出,或正在不断增加,用于这种预期用途,并将产生这些结果,利润率,如道琼斯 30 指数以及许多其他指数,已创建用于这种预期用途。 彼得-马蒂
谢谢你的文章, @Gamuchirai Zororo Ndawana
我同意 @Maxim Dmitrievsky 的观点,最终目标是盈利。从稳健性和控制缩水的角度来看,恢复并保持在正轨上的想法是有道理的,但它不能替代盈利。
有时我在想,我们所依赖的翻译工具是否无法捕捉到原始信息。您的回复比我从 @Maxim Dmitrievsky 的原文中理解到的更多。
感谢您指出了前瞻性偏差(带 i + HORIZON 的功能)中的疏忽,这是我最讨厌的 bug,它们需要整个重新测试。
您还提供了宝贵的反馈意见,说明了在实践中用于验证模型的验证措施,夏普比率(Sharpe Ratio)一定类似于通用的黄金标准。我需要更多地了解 Calmar 和 Sortino,才能形成自己的观点,谢谢您的建议。
我同意你的观点,这两个术语在设计上是反对称的,而检验的标准是模型应保持反对称,任何偏离这一预期的行为都是不合格的。如果一个或两个模型存在不可接受的偏差,那么它们的预测就不会像我们期望的那样保持反对称。
然而,利润的概念只是我为了突出问题而给出的一个简单说明。我们今天所拥有的衡量标准都不能告诉我们什么时候会出现均值拥抱现象。关于统计学习的文献都没有告诉我们为什么会发生均值拥抱。不幸的是,由于我们遵循的最佳实践,这种情况正在发生,而这只是我希望就最佳实践的危险性展开更多讨论的众多方法之一。
这篇文章更像是一种求助,希望我们能够团结起来,从头开始设计新的协议。新标准。我们的优化人员可以直接针对我们的利益制定新的目标。