数据科学和机器学习（第 17 部分）：摇钱树？外汇交易中随机森林的艺术与科学

MetaTrader 5 — 交易 | 9 八月 2024, 17:03

552

Omega J Msigwa

两个头总比一个好，并非因为任何一头都是万无一失的，而是因为它们不太可能在同一方向上出错。

随机森林算法

随机森林是一种融合学习方法，它通过在训练过程中构建多棵决策树来操作，并输出类别，即类的模式（分类）、或单棵树的均值预测（回归）。随机森林中的每棵树都依据不同数据子集进行训练，训练过程中引入的随机性有助于提高模型的整体性能和普适能力。

为了更好地理解这一点，我们必须在机器学习术语中研究融合学习。

融合学习

融合学习是一种方式，其中将两个或多个机器学习模型依据相同的数据拟合，并将每个模型的预测组合在一起。融合学习旨在令融合模型的性能优于任何单个模型。

随机森林是一种融合方法，它结合了多棵决策树的预测，从而提高单个/单一模型的整体预测能力。

随机森林 mql5

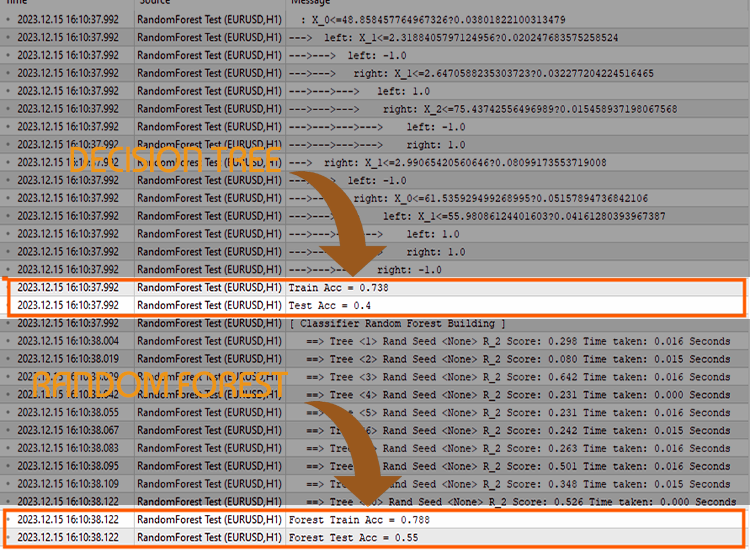
我创建了一棵决策树，以及一个十（10）棵树的随机森林集合来演示这一点。使用相同的数据集，我在使用随机森林 AI 的训练和测试阶段获得了更高的准确性。

随机森林 AI 的主要特点

01：融合学习

随机森林是一种融合方法，它结合了多个机器学习模型的预测，从而提高整体性能。

for (uint i=0; i<m_ntrees; i++) //Build a given x number of trees
  { 
    temp_data = data;
    matrix_utils.Randomize(temp_data, m_random_state, replace); //Get randomized subsets
    
    forest[i] = new CDecisionTreeClassifier(this.m_minsplit, this.m_maxdepth); //Add the tree to the forest
                  
    forest[i].fit(x_subset, y_subset); //Add the trained tree to the forest
    preds = forest[i].predict(x_subset);    
  }

02：自举聚合（Bagging）

在机器学习中，自举是一种重复采样技术，它涉及从源数据中重复抽取样本，并进行替换，通常用于估算总体参数。

随机森林中的每棵树都依据不同的数据子集进行训练，这些数据子集是通过自举（采样和替换）创建的。

matrix_utils.Randomize(temp_data, m_random_state, replace); //Get randomized subsets

源：

template<typename T>
void CMatrixutils::Randomize(matrix<T> &matrix_,int random_state=-1, bool replace=false)

replace = true 参数允许多次选择同一索引，从而模拟自举过程。

03：特征随机性：

在构造每棵树的过程中拆分节点时，会考虑特征的随机子集。

这在树之间引入了进一步的多样性，令融合更加坚固。

04：投票（或平均）机制

对于分类问题，采取预测的模式（最频繁的类别）。

对于回归问题，考虑预测的平均值。

投票过程对于随机森林分类至关重要，人们可以选择多种技术作为投票机制；有些是软性投票和投票门槛：

软性投票

每棵树的预测都与软性投票中的置信度分数（概率）相关联。然后，最终预测是这些概率的加权平均值。

由于我们的决策树类还不能预测概率，因此我们不能使用这种投票机制。我们将使用自定义投票。

投票门槛

投票机制是这样的：如果一定比例的树预测了特定的类别，则被认为是最终预测。这可以帮助应对纽带，或确保最低限度的信心。

使用树的百分比来判定要预测的类，若进行预测的类太多也许很复杂；我们将自定义 Predict 函数，以便选择大多数树预测的类，而不管预测了多少个类。

double CRandomForestClassifier::predict(vector &x)
 {
   vector predictions(m_ntrees); //predictions from all the trees
    
    for (uint i=0; i<this.m_ntrees; i++) //all trees make the predictions
      predictions[i] = forest[i].predict(x);
      
   vector uniques = matrix_utils.Unique(predictions);   
   
   return uniques[matrix_utils.Unique_count(predictions).ArgMax()]; //select the majority decision
 }

扩展决策树类

在上一篇文章中，我们讨论了分类决策树，而它适用于对二元目标变量进行分类；我不得不扩展回归决策树的类和代码。

class CDecisionTreeRegressor: public CDecisionTreeClassifier
  {
private:
   double            calculate_leaf_value(vector &Y);
   split_info        get_best_split(matrix &data, uint num_features);
   double            variance_reduction(vector &parent, vector &l_child, vector &r_child);

   Node              *build_tree(matrix &data, uint curr_depth = 0);
public:
                     CDecisionTreeRegressor(uint min_samples_split = 2, uint max_depth = 2);
                    ~CDecisionTreeRegressor(void);

   void              fit(matrix &x, vector &y);
  };

这两个类在大多数情况下是相似的，它们共享相同的节点类和许多函数，除了叶值计算、信息增益、构建树、和调用构建树函数的拟合函数。

回归器决策树中的叶值

在回归问题中，给定节点的叶值是其所有值的平均值。

double CDecisionTreeRegressor::calculate_leaf_value(vector &Y)
 {
   return Y.Mean();

计算信息增益

正如上一篇文章所说，信息增益衡量的是数据集拆分后熵或不确定性的减少。

我们替换基于概率的基尼和熵，而是用方差减少公式来测量给定节点中的杂质。

double CDecisionTreeRegressor::variance_reduction(vector &parent, vector &l_child, vector &r_child)
 {
    double weight_l = l_child.Size() / (double)parent.Size(),
           weight_r = r_child.Size() / (double)parent.Size();
     
    return parent.Var() - ((weight_l * l_child.Var()) + (weight_r * r_child.Var()));
 }

上述函数计算通过将数据集拆分为决策树中特定节点的左右子节点来实现方差减少。

构建树 & Fit 函数

构建树

Node *CDecisionTreeRegressor::build_tree(matrix &data, uint curr_depth=0)
 {
    matrix X;
    vector Y;
      
    if (!matrix_utils.XandYSplitMatrices(data,X,Y)) //Split the input matrix into feature matrix X and target vector Y.    
      {
         #ifdef DEBUG_MODE 
           printf("%s Line %d Failed to build a tree Data Empty",__FUNCTION__,__LINE__);
         #endif 
         
         return NULL; //Return a NULL pointer
      }
      
    ulong samples = X.Rows(), features = X.Cols(); //Get the number of samples and features in the dataset.
        
    ArrayResize(nodes, nodes.Size()+1); //Append the nodes to memory
    Node *left_child, *right_child;
            
    if (samples >= m_min_samples_split && curr_depth<=m_max_depth)
      {
         split_info best_split = this.get_best_split(data, (uint)features);
         
         #ifdef DEBUG_MODE
           Print(__FUNCTION__," | ",__LINE__,"\nbest_split left: [",best_split.dataset_left.Rows(),"x",best_split.dataset_left.Cols(),"]\nbest_split right: [",best_split.dataset_right.Rows(),"x",best_split.dataset_right.Cols(),"]\nfeature_index: ",best_split.feature_index,"\nInfo gain: ",best_split.info_gain,"\nThreshold: ",best_split.threshold);
         #endif 
                  
         if (best_split.info_gain > 0)
           {
             left_child = this.build_tree(best_split.dataset_left, curr_depth+1);
             right_child = this.build_tree(best_split.dataset_right, curr_depth+1);
                      
             nodes[nodes.Size()-1] = new Node(best_split.feature_index,best_split.threshold,left_child,right_child,best_split.info_gain);  
             return nodes[nodes.Size()-1];
           }
      }      
     
     nodes[nodes.Size()-1] = new Node();
     nodes[nodes.Size()-1].leaf_value = this.calculate_leaf_value(Y);
     
     return nodes[nodes.Size()-1];
 }

Fit 函数

void CDecisionTreeRegressor::fit(matrix &x, vector &y)
 {
   matrix data = matrix_utils.concatenate(x, y, 1);
      
   this.root = this.build_tree(data);
   
   is_fitted = true;
 }

Regressor 类和 Classifier 类之间 build_tree 函数的唯一区别是 variance_reduction 函数。

我使用流行的 Airfoil 噪声数据来测试构建的回归树。

   matrix data = matrix_utils.ReadCsv("airfoil_noise_data.csv");
   
   matrix x; vector y;
   
   if (!matrix_utils.XandYSplitMatrices(data, x, y))
     return INIT_FAILED;
   
   regressor_tree = new CDecisionTreeRegressor(3,3);
   regressor_tree.fit(x, y);
   regressor_tree.print_tree(regressor_tree.root);
   
   vector preds = regressor_tree.predict(x);
      
   Print("r-squared: ",metrics.r_squared(y, preds));

输出：

KS      0       00:04:11.402    RandomForest Test (EURUSD,H1)     : X_0<=3150.0?7.6482714516406745
FI      0       00:04:11.402    RandomForest Test (EURUSD,H1)   --->  left: X_4<=0.0150478?4.070223732531591
ME      0       00:04:11.402    RandomForest Test (EURUSD,H1)   --->--->   left: X_2<=0.1016?2.453283788183441
RR      0       00:04:11.402    RandomForest Test (EURUSD,H1)   --->--->--->    left: X_0<=630.0?2.3366165961173238
JR      0       00:04:11.402    RandomForest Test (EURUSD,H1)   --->--->--->--->    left: 126.94465000000002
MF      0       00:04:11.402    RandomForest Test (EURUSD,H1)   --->--->--->--->    right: 130.51523904382472
II      0       00:04:11.402    RandomForest Test (EURUSD,H1)   --->--->--->    right: X_0<=1600.0?4.999630155449349
HF      0       00:04:11.402    RandomForest Test (EURUSD,H1)   --->--->--->--->    left: 127.90983653846149
JM      0       00:04:11.402    RandomForest Test (EURUSD,H1)   --->--->--->--->    right: 122.97036507936505
JR      0       00:04:11.402    RandomForest Test (EURUSD,H1)   --->--->   right: X_4<=0.0483159?6.040280153408631
FI      0       00:04:11.402    RandomForest Test (EURUSD,H1)   --->--->--->    left: X_0<=1250.0?5.315257051142112
IG      0       00:04:11.402    RandomForest Test (EURUSD,H1)   --->--->--->--->    left: 125.68045918367342
GM      0       00:04:11.402    RandomForest Test (EURUSD,H1)   --->--->--->--->    right: 120.69493181818189
NQ      0       00:04:11.402    RandomForest Test (EURUSD,H1)   --->--->--->    right: X_0<=1250.0?13.291165881821172
GK      0       00:04:11.402    RandomForest Test (EURUSD,H1)   --->--->--->--->    left: 117.69977777777775
GH      0       00:04:11.402    RandomForest Test (EURUSD,H1)   --->--->--->--->    right: 109.80075000000001
EL      0       00:04:11.402    RandomForest Test (EURUSD,H1)   --->  right: X_4<=0.00152689?28.997059993530435
OL      0       00:04:11.402    RandomForest Test (EURUSD,H1)   --->--->   left: X_0<=6300.0?11.053304033466667
HK      0       00:04:11.402    RandomForest Test (EURUSD,H1)   --->--->--->    left: X_4<=0.000930789?9.067095683299033
FG      0       00:04:11.402    RandomForest Test (EURUSD,H1)   --->--->--->--->    left: 134.9866388888889
NO      0       00:04:11.402    RandomForest Test (EURUSD,H1)   --->--->--->--->    right: 128.59900000000002
QS      0       00:04:11.402    RandomForest Test (EURUSD,H1)   --->--->--->    right: X_4<=0.000930789?9.783359845444707
NI      0       00:04:11.402    RandomForest Test (EURUSD,H1)   --->--->--->--->    left: 128.05125581395347
GJ      0       00:04:11.402    RandomForest Test (EURUSD,H1)   --->--->--->--->    right: 120.90806666666667
RM      0       00:04:11.402    RandomForest Test (EURUSD,H1)   --->--->   right: X_4<=0.0341183?5.715854852017056
LN      0       00:04:11.402    RandomForest Test (EURUSD,H1)   --->--->--->    left: X_0<=5000.0?5.190320913085316
GN      0       00:04:11.402    RandomForest Test (EURUSD,H1)   --->--->--->--->    left: 120.08625170068028
NE      0       00:04:11.402    RandomForest Test (EURUSD,H1)   --->--->--->--->    right: 115.52968965517242
MI      0       00:04:11.402    RandomForest Test (EURUSD,H1)   --->--->--->    right: X_4<=0.0483159?4.450134400476193
IS      0       00:04:11.402    RandomForest Test (EURUSD,H1)   --->--->--->--->    left: 109.44371428571428
GQ      0       00:04:11.402    RandomForest Test (EURUSD,H1)   --->--->--->--->    right: 104.84033333333332
PH      0       00:04:11.403    RandomForest Test (EURUSD,H1)   r-squared: 0.5937442611327515

对于相同的参数，回归树似乎具有更多的分支，这会导致分类决策树中的分支更少。

在训练期间，我们的回归模型的准确率为 59%;；这是一个很好的迹象，我们做对了吗？当把预测绘制成图形时，它们如下所示：

回归预测树

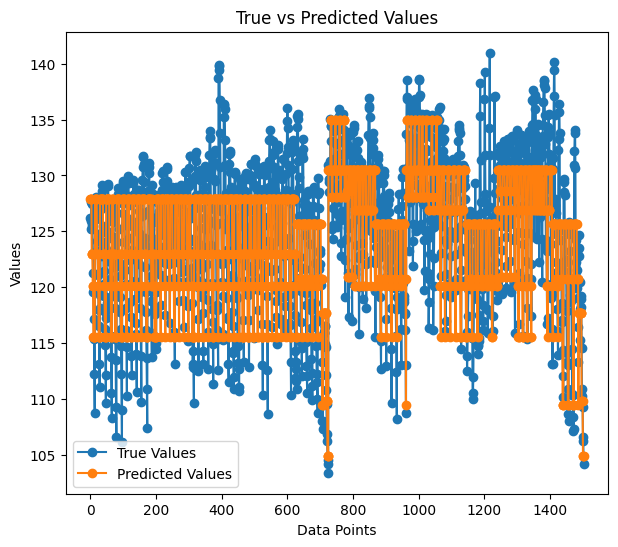
预测方式与实际值拟合，它们几乎看起来像一棵树。

为什么选择随机森林？

高精度： 随机森林通常在分类和回归任务中都能提供更高的准确性。

鲁棒性： 随机森林的融合性质令其对过拟合和噪声数据具有稳健性。

特征重要性： 随机森林可以提供有关特征重要性的信息，从而有助于特征选择。

减少方差： 树之间的多样性令模型的方差最小化，从而导致更好普适。

无需特征缩放： 与决策树一样，随机森林对特征缩放不太敏感，因此适用于具有不同尺度的数据集。

多样性： 适用于各种类型的数据，包括分类和数值特征。

构建随机森林分类器

现在我们已经看到为什么人们应该更喜欢随机森林算法而非决策树，我们来看看如何构建随机森林模型，从分类器开始。

包含 CDecisionTreeClassifier 类。

class CRandomForestClassifier
  {
CMetrics metrics;

protected:
   uint  m_ntrees;
   uint  m_maxdepth;
   uint  m_minsplit;
   int   m_random_state;
   
   CMatrixutils matrix_utils;
   CDecisionTreeClassifier *forest[];
   string ConvertTime(double seconds);
   
public:
                     CRandomForestClassifier(uint n_trees=100, uint minsplit=NULL, uint max_depth=NULL, int random_state=-1);
                    ~CRandomForestClassifier(void);
                    
                    void fit(matrix &x, vector &y, bool replace=true);
                    double predict(vector &x);
                    vector predict(matrix &x);
  };

由于随机森林分类器简单地把一个森林中 x 数量的分类器树组合到一起，因此该类指向名为 forest[] 的 CDecisionTreeClassifier 对象数组。

n_trees = 100（默认），这意味着随机森林分类器森林中有 100 棵树。

min_split 和 max_depth 是我们在上一篇文章中讨论的每棵树的参数。min_split 是树应该具有的最小树枝数量，而 max_depth 则是树的树枝应有的长度。

将树拟合到随机森林之中

这是 CRandomForestClassifier 类中最重要的函数，其中在类构造函数中选择 n_trees 数量的树组成森林。

void CRandomForestClassifier::fit(matrix &x, vector &y, bool replace=true)
 {
  matrix x_subset;
  vector y_subset;
  matrix data = this.matrix_utils.concatenate(x, y, 1);
  matrix temp_data = data;
  vector preds;
  
  datetime time_start = GetTickCount(), current_time;
  
  Print("[ Classifier Random Forest Building ]");
    
   for (uint i=0; i<m_ntrees; i++) //Build a given x number of trees
     {
       time_start = GetTickCount();
       
       temp_data = data;
       matrix_utils.Randomize(temp_data, m_random_state, replace); //Get randomized subsets
       
       if (!this.matrix_utils.XandYSplitMatrices(temp_data, x_subset, y_subset)) //split the random subset into x and y subsets
         {
            ArrayRemove(forest,i,1); //Delete the invalid tree in a forest
            printf("%s %d Failed to split data for a tree ",__FUNCTION__,__LINE__);
            continue;
         } 
       
       forest[i] = new CDecisionTreeClassifier(this.m_minsplit, this.m_maxdepth); //Add the tree to the forest
                     
       forest[i].fit(x_subset, y_subset); //Add the trained tree to the forest
       preds = forest[i].predict(x_subset);
       
       current_time = GetTickCount();
       
       printf("   ==> Tree <%d> Rand Seed <%s> Accuracy Score: %.3f Time taken: %s",i+1,m_random_state==-1?"None":string(m_random_state),metrics.accuracy_score(y_subset, preds), ConvertTime((current_time - time_start) / 1000.0));
     }
     
   m_ntrees = ArraySize(forest); //The successfully build trees
   
 }

决策树分类器对比随机森林分类器

为了证明随机分类器在分类任务中是否比决策树做得更好，我进行了 5 次测试。

测试 01：

	训练	测试
决策树	73.8%	40%
随机森林	78%	45%

测试 02：

决策树	73.8%	40%
随机森林	83%	45%

测试 03：

决策树	73.8%	40%
随机森林	80%	45%

测试 04：

决策树	73.8%	40%
随机森林	78.8%	45%

测试 05：

决策树	73.8%	40%
随机森林	78.8%	45%

根据我的经验，依据交易数据运用随机森林分类器可能会导致混淆，因为您也许会遇到随机森林的整体准确性并不比单棵决策树更好的状况；这是由于以下一个或多个因素造成的：

导致随机森林无法提供比单棵决策树准确性更好的因素：

树缺乏多样性

随机森林受益于单棵树的多样性。如果所有树都相似，则集合不会提供太多的改进。

确保在每棵树的训练过程中正确地引入随机性。随机化可能涉及选择特征的随机子集，和/或使用训练数据的不同子集。

超参数优调

试验不同的超参数，例如每次拆分时要考虑的特征数量（m_max_features）、拆分内部节点所需的最小样本数量（m_minsplit），以及树的最大深度（m_maxdepth）。

对一系列超参数值进行网格搜索，或随机搜索有助于辨别更好的配置。

交叉验证

使用交叉验证来评估模型的性能。这有助于更可靠地估算模型对于新数据的普适程度。

交叉验证还有助于检测过拟合或欠拟合问题。

在整个数据集上进行训练

确保树不会依赖训练数据过拟合。如果森林中的每棵树都依据整个数据集进行训练，则它可能会捕获噪声而不是信号。

考虑在数据的自举样本（装袋）上训练每棵树。

特征缩放

如果您的特征具有不同的伸缩，则对其进行缩放可能会有所帮助。决策树通常对特征尺度不敏感，但对特征进行常规或标准化可能会有所帮助，尤其是在将单棵树的性能与融合进行比较时。

评估度量

在您尝试用模型解决问题时，确保您正在使用适当的评估度量；对于回归的常用评估度量是 R 平方，而对于分类的常用评估度量是准确率分数。

fit() 函数的最后一个参数有一个 error 参数，它允许您选择适当的度量来衡量森林中每棵树的准确性。

enum errors_classifier
  {
   ERR_ACCURACY
  };

enum errors_regressor
  {
   ERR_R2_SCORE,
   ERR_ADJUSTED_R
  };

融合大小

对森林中的树木数量进行实验。有时，增加树木的数量可以提高融合的性能。

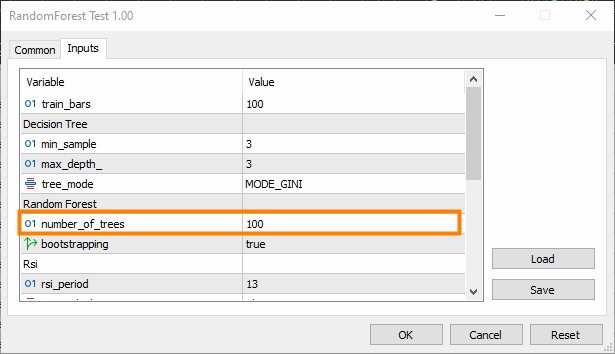
注意，这会增加复杂性；更改后，训练和测试时间可能会急剧增加。

数据品质

确保数据的品质。如果存在异常值或缺失值，则可能会影响随机森林的性能。

随机种子

确保在每次运行期间设置一致地随机种子，从而确保可重复性。

具有相同的随机种子将导致所有树产生相同的精度，这并不比单棵决策树好。

在策略测试器中继续竞争

随机森林在训练和测试阶段取得了胜利，但它也能在交易中取得胜利吗，其中它会表现出远超预测的能力从而盈利吗？

我采用从 2022.01.01 到 2023.02.01 的默认设置对这两种算法进行了测试。

其它测试器设置：

延迟：随机延迟
建模：仅限开盘价
本金： 1000$
杠杆：1/100

随机森林结果图：

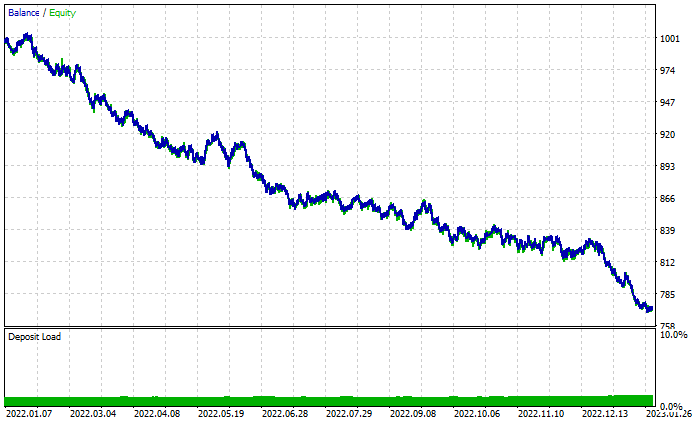
尽管总共有 46% 的盈利交易，但图形看起来很糟糕。我们看看决策树做了什么：

决策树测试结果

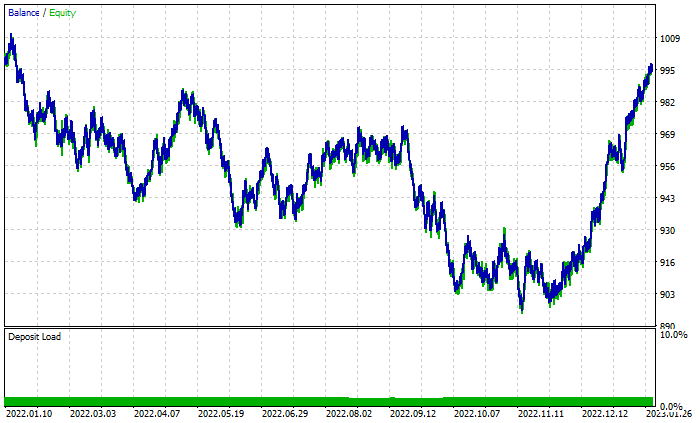
好于由 100 棵树组成的随机森林，尽管有 44% 的盈利交易。

进行了快速优化，找到了两种模型的最优止损 = 960，和止盈 = 1295，同时将最小拆分设置为 2。以下是两种模型的结果。

决策树分类器：

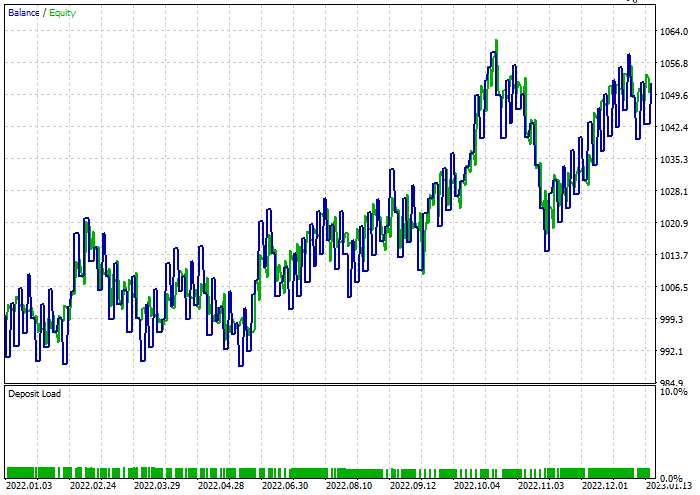
在测试期间 47.68% 的交易盈利。该模型在测试期间赚取了 52$ 的盈利。

随机森林分类器：

随机森林分类器

在测试期间 33.99%的交易盈利。该模型在测试过程中损失了 -72$。

虽然与决策树分类器相比，随机森林在纸面上看起来更准确，但对于实际交易环境来说，它并非一个更好的模型；一般来说，随机森林是决策树的后继者，但这些事情在机器学习中经常发生，有时一个简单的模型可以比一个高级模型产生更好的结果，故才有此说。您可以进行随机森林优化，并尝试不同的参数，从而找到最优参数。它仍然有改进的余地，从而令其比决策树更好。

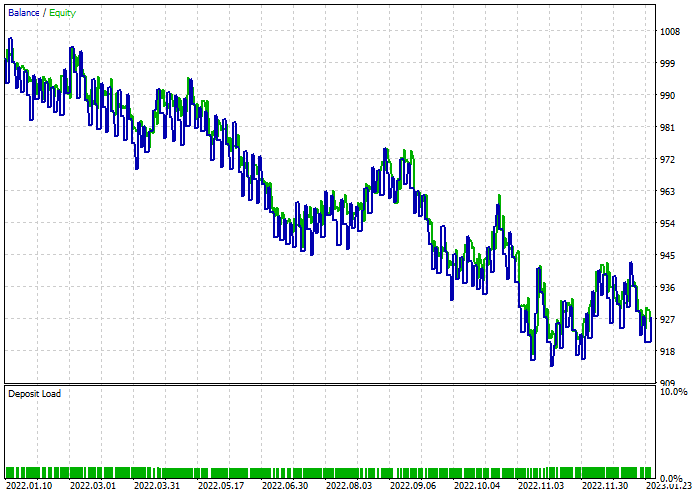
后记

随机森林已被用于许多行业的各种活动，例如金融、娱乐和医疗部门。然而，就像任何模型一样，在决定为他们的交易项目选择这个模型之前，他们必须明白会有一些挫折。

计算复杂度：

随机森林模型，尤其是含有许多树木的随机森林模型，计算成本可能很高，并且需要大量资源。

内存使用：

随着树木数量的增加，随机森林模型的内存占用量也会增加，这可能导致内存占用过高。

可解释性：

随机森林的融合性质令它们不如单棵决策树更容易解释，特别是当森林由许多树组成时。

过拟合：

尽管随机森林比单棵决策树更不容易过拟合，但它们仍然容易针对噪声数据或带有异常值的数据过拟合。

偏向主导类别：

在类分布不平衡的分类问题中，随机森林可能偏向于主导类别，从而影响模型对劣势类别的预测性能。

参数灵敏度：

虽然随机森林对于超参数的选择具有稳健性，但模型的性能仍可能对特定参数值敏感。

黑匣子性质：

随机森林的融合性质结合了多棵决策树，这令解释模型的决策过程具有挑战性。

训练时间：

训练随机森林模型可能比训练单棵决策树花费更长的时间，尤其是对于大型数据集。

交易活动延迟了 10 分钟，因为它们不得不等待训练 100 棵树。

感谢您的阅读;

我们讨论了该机器学习模型的跟踪开发，在 GitHub 存储库上有更多本系列文章中讨论的内容。

附件：

文件	用法与说明
forest.mqh（可在 include 文件夹下找到）	包含随机森林类，包括 CRandomForestClassifier 和 CRandomForestRegressor
matrix_utils.mqh（包含）	包含用于矩阵操作的附加函数。
metrics.mqh（包含）	包含用于衡量 ML 模型性能的函数和代码。
preprocessing.mqh（包含）	预处理原始输入数据的函数库，令其适合机器学习模型的用法。
tree.mqh（包含）	包含决策树类。
RandomForest Test.mq5（智能系统）	运行和测试随机森林模型的最终智能系统。

本文由MetaQuotes Ltd译自英文
原文地址： https://www.mql5.com/en/articles/13765

附加的文件 |

下载ZIP

Code.zip (22.86 KB)

注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.

该作者的其他文章

最近评论 | 前往讨论 (1)

Altan Karakaya | 24 12月 2023 在 08:48

信息量大，非常有趣

种群优化算法：进化策略，(μ,λ)-ES 和 (μ+λ)-ES

本文研究一套称为进化策略（ES）的优化算法。它们是最早使用进化原理来寻找最优解的种群算法之一。我们将针对传统的 ES 变体实现变更，并修改算法的测试函数和测试台方法。

用于时间序列挖掘的数据标签（第 5 部分）：使用 Socket 在 EA 中进行应用和测试

本系列文章介绍了几种时间序列标注方法，可以创建符合大多数人工智能模型的数据，根据需求有针对性地进行数据标注，可以使训练出来的人工智能模型更符合预期设计，提高我们模型的准确性，甚至帮助模型实现质的飞跃！

为 Metatrader 5 开发 MQTT 客户端：TDD 方法 - 第 5 部分

本文是系列文章的第五部分，介绍了我们为 MQTT 5.0 协议开发本地 MQL5 客户端的步骤。在这一部分中，我们将介绍 PUBLISH 数据包的结构、如何设置其发布标志（Publish Flag）、如何对主题名称（Topic Name）字符串进行编码，以及在需要时如何设置数据包标识符（Packet Identifier）。

在 MQL5 中实现增广迪基–富勒检验

在本文中，我们演示了增广迪基–富勒（Augmented Dickey-Fuller，ADF）检验的实现，并将其应用于使用 Engle-Granger 方法进行协整检验。