MetaTrader 5 / 示例
English Русский Español Deutsch 日本語 Português
preview
数据处理的分组方法：在MQL5中实现组合算法

数据处理的分组方法：在MQL5中实现组合算法

MetaTrader 5 — 示例 |
329 0
Francis Dube
Francis Dube

概述

GMDH（Group Method of Data Handling）的组合算法，通常被称为COMBI，是GMDH的基本形式，为该系列中更为复杂的算法奠定了基础。与多层迭代算法（MIA）一样，基于一组变量观测值的矩阵形式输入数据样本操作。数据样本被分为两部分：训练样本和测试样本。训练子样本用于评估多项式的系数，而测试子样本则用于根据所选准则的最小值选择最佳模型结构。本文描述了COMBI算法的计算过程。同时，通过扩展前一篇文章中描述的“GmdhModel”类，来展示其在MQL5中的实现。稍后，我们还将讨论与之密切相关的组合选择算法及在MQL5中的实现。最后，我们将通过构建比特币每日价格的预测模型，来总结GMDH算法的实际应用。


COMBI算法

MIA和COMBI算法之间的根本区别在于它们的网络结构不同。与MIA的多层性质相反，COMBI的特点是单层。

组合方法的网络结构

这一层的节点数量由输入数量决定。其中，每个节点代表全部输入中的一个或多个已定义的候选模型。为了说明这一点，让我们举一个想要建模的系统实例，该系统由2个输入变量定义。应用COMBI算法，会使用这些变量的所有可能组合来构建候选模型。可能的组合数量由以下公式给出：

最大组合数公式



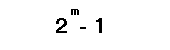
其中 ：

  • m 代表输入变量的数量。


对于这些组合中的每一种组合，都会生成一个候选模型。在第一层和唯一一层的节点处，评估得到的候选模型由下式给出：



候选多项式



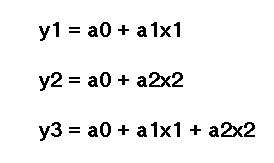
其中：

  •  “a”是系数，“a1”是第一个系数，“a2”是第二个系数。
  •  “x”是输入变量，“x1”代表第一个输入变量或预测变量，“x2”是第二个。


这个过程涉及解一个线性方程组，以推导出候选模型系数的估值。依据每个模型的性能指标选择最能描述数据的最终模型。


COMBI MQL5实现

基于之前文章中描述的GmdhModel基类实现COMBI算法的代码。它还依赖于在linearmodel.mqh中声明的中间类LinearModel。该类封装了COMBI方法最基本且独特的特征。即COMBI模型完全是线性的。

//+------------------------------------------------------------------+
//|                                                  linearmodel.mqh |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include "gmdh.mqh"
//+------------------------------------------------------------------+
//| Class implementing the general logic of GMDH linear algorithms   |
//+------------------------------------------------------------------+
class LinearModel:public GmdhModel
  {

protected:
   vector            calculatePrediction(vector& x)
     {
      if(x.Size()<ulong(inputColsNumber))
         return vector::Zeros(ulong(inputColsNumber));

      matrix modifiedX(1,x.Size()+ 1);

      modifiedX.Row(x,0);

      modifiedX[0][x.Size()] = 1.0;

      vector comb = bestCombinations[0][0].combination();
      matrix xx(1,comb.Size());
      for(ulong i = 0; i<xx.Cols(); ++i)
         xx[0][i] = modifiedX[0][ulong(comb[i])];
      vector c,b;
      c = bestCombinations[0][0].bestCoeffs();
      b = xx.MatMul(c);

      return b;
     }



   virtual matrix    xDataForCombination(matrix& x,  vector& comb) override
     {
      matrix out(x.Rows(), comb.Size());

      for(ulong i = 0; i<out.Cols(); i++)
         out.Col(x.Col(int(comb[i])),i);

      return out;
     }

   virtual string    getPolynomialPrefix(int levelIndex, int combIndex) override
     {
      return "y=";
     }

   virtual string    getPolynomialVariable(int levelIndex, int coeffIndex, int coeffsNumber, vector& bestColsIndexes) override
     {
      return ((coeffIndex != coeffsNumber - 1) ? "x" + string(int(bestColsIndexes[coeffIndex]) + 1) : "");
     }



public:
                     LinearModel(void)
     {
     }

   vector            predict(vector& x, int lags) override
     {
      if(lags <= 0)
        {
         Print(__FUNCTION__," lags value must be a positive integer");
         return vector::Zeros(1);
        }

      if(!training_complete)
        {
         Print(__FUNCTION__," model was not successfully trained");
         return vector::Zeros(1);
        }

      vector expandedX = vector::Zeros(x.Size() + ulong(lags));
      for(ulong i = 0; i<x.Size(); i++)
         expandedX[i]=x[i];

      for(int i = 0; i < lags; ++i)
        {
         vector vect(x.Size(),slice,expandedX,ulong(i),x.Size()+ulong(i)-1);
         vector res = calculatePrediction(vect);
         expandedX[x.Size() + i] = res[0];
        }

      vector vect(ulong(lags),slice,expandedX,x.Size());
      return vect;

     }

  };

//+------------------------------------------------------------------+

combi.mqh文件包含COMBI类的定义。该类继承自LinearModel，并定义了用于拟合模型的fit()方法。

//+------------------------------------------------------------------+
//|                                                        combi.mqh |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include "linearmodel.mqh"
//+------------------------------------------------------------------+
//| Class implementing combinatorial COMBI algorithm                 |
//+------------------------------------------------------------------+
class COMBI:public LinearModel
  {
private:
   Combination       getBest(CVector &combinations)
     {
      double proxys[];
      int best[];

      ArrayResize(best,combinations.size());
      ArrayResize(proxys,combinations.size());

      for(int k = 0; k<combinations.size(); k++)
        {
         best[k]=k;
         proxys[k]=combinations[k].evaluation();
        }

      MathQuickSortAscending(proxys,best,0,int(proxys.Size()-1));

      return combinations[best[0]];

     }
protected:

   virtual void      removeExtraCombinations(void) override
     {
      CVector2d realBestCombinations;
      CVector n;
      Combination top;
      for(int i = 0 ; i<bestCombinations.size(); i++)
        {
         top = getBest(bestCombinations[i]);
         n.push_back(top);
        }

      top = getBest(n);

      CVector sorted;

      sorted.push_back(top);

      realBestCombinations.push_back(sorted);

      bestCombinations = realBestCombinations;
     }

   virtual bool      preparations(SplittedData &data, CVector &_bestCombinations) override
     {
      lastLevelEvaluation = DBL_MAX;
      return (bestCombinations.push_back(_bestCombinations) && ulong(level+1) < data.xTrain.Cols());
     }

   void              generateCombinations(int n_cols,vector &out[])  override
     {
      GmdhModel::nChooseK(n_cols,level,out);
      return;
     }

public:
                     COMBI(void):LinearModel()
     {
      modelName = "COMBI";
     }

   bool              fit(vector &time_series,int lags,double testsize=0.5,CriterionType criterion=stab)
     {

      if(lags < 1)
        {
         Print(__FUNCTION__," lags must be >= 1");
         return false;
        }

      PairMVXd transformed = timeSeriesTransformation(time_series,lags);

      SplittedData splited = splitData(transformed.first,transformed.second,testsize);

      Criterion criter(criterion);

      int pAverage = 1;
      double limit  = 0;
      int kBest = pAverage;

      if(validateInputData(testsize, pAverage, limit, kBest))
         return false;

      return GmdhModel::gmdhFit(splited.xTrain, splited.yTrain, criter, kBest, testsize, pAverage, limit);
     }

   bool              fit(matrix &vars,vector &targets,double testsize=0.5,CriterionType criterion=stab)
     {

      if(vars.Cols() < 1)
        {
         Print(__FUNCTION__," columns in vars must be >= 1");
         return false;
        }

      if(vars.Rows() != targets.Size())
        {
         Print(__FUNCTION__, " vars dimensions donot correspond with targets");
         return false;
        }

      SplittedData splited = splitData(vars,targets,testsize);

      Criterion criter(criterion);

      int pAverage = 1;
      double limit  = 0;
      int kBest = pAverage;

      if(validateInputData(testsize, pAverage, limit, kBest))
         return false;

      return GmdhModel::gmdhFit(splited.xTrain, splited.yTrain, criter, kBest, testsize, pAverage, limit);
     }


  };
//+------------------------------------------------------------------+



使用COMBI类

使用COMBI类将模型拟合到数据集，与使用MIA类的方式是完全相同的。我们需要创建一个实例，并调用其中一个fit()方法。该实例通过脚本COMBI_test.mq5和COMBI_Multivariable_test.mq5来演示。 

//+------------------------------------------------------------------+
//|                                                   COMBI_test.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <GMDH\combi.mqh>

input int NumLags = 2;
input int NumPredictions = 6;
input CriterionType critType = stab;
input double DataSplitSize = 0.33;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   vector tms = {1,2,3,4,5,6,7,8,9,10,11,12};

   if(NumPredictions<1)
     {
      Alert("Invalid setting for NumPredictions, has to be larger than 0");
      return;
     }

   COMBI combi;

   if(!combi.fit(tms,NumLags,DataSplitSize,critType))
      return;

   string modelname = combi.getModelName()+"_"+EnumToString(critType)+"_"+string(DataSplitSize);

   combi.save(modelname+".json");

   vector in(ulong(NumLags),slice,tms,tms.Size()-ulong(NumLags));

   vector out = combi.predict(in,NumPredictions);

   Print(modelname, " predictions ", out);

   Print(combi.getBestPolynomial());

  }
//+------------------------------------------------------------------+

两者都使用的相同数据集将COMBI算法应用于示例脚本中，演示如何应用前一篇文章中的MIA算法。 

//+------------------------------------------------------------------+
//|                                     COMBI_Multivariable_test.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <GMDH\combi.mqh>

input CriterionType critType = stab;
input double DataSplitSize = 0.33;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   matrix independent = {{1,2,3},{3,2,1},{1,4,2},{1,1,3},{5,3,1},{3,1,9}};
   vector dependent = {6,6,7,5,9,13};

   COMBI combi;

   if(!combi.fit(independent,dependent,DataSplitSize,critType))
      return;

   string modelname = combi.getModelName()+"_"+EnumToString(critType)+"_"+string(DataSplitSize)+"_multivars";

   combi.save(modelname+".json");

   matrix unseen = {{8,6,4},{1,5,3},{9,-5,3}};

   for(ulong row = 0; row<unseen.Rows(); row++)
     {
      vector in = unseen.Row(row);
      Print("inputs ", in, " prediction ", combi.predict(in,1));
     }

   Print(combi.getBestPolynomial());

  }
//+------------------------------------------------------------------+

通过查看COMBI_test.mq5的输出，我们可以比较拟合多项式的复杂度与MIA算法生成多项式的复杂度。以下是时间序列数据集和多变量数据集分别对应的多项式。

LR      0       14:54:15.354    COMBI_test (BTCUSD,D1)  COMBI_stab_0.33 predictions [13,14,15,16,17,18.00000000000001]
PN      0       14:54:15.355    COMBI_test (BTCUSD,D1)  y= 1.000000e+00*x1 + 2.000000e+00
CI      0       14:54:29.864    COMBI_Multivariable_test (BTCUSD,D1)    inputs [8,6,4] prediction [18.00000000000001]
QD      0       14:54:29.864    COMBI_Multivariable_test (BTCUSD,D1)    inputs [1,5,3] prediction [9]
QQ      0       14:54:29.864    COMBI_Multivariable_test (BTCUSD,D1)    inputs [9,-5,3] prediction [7.00000000000001]
MM      0       14:54:29.864    COMBI_Multivariable_test (BTCUSD,D1)    y= 1.000000e+00*x1 + 1.000000e+00*x2 + 1.000000e+00*x3 - 7.330836e-15

接下来是使用MIA方法生成的多项式。

JQ      0       14:43:07.969    MIA_Test (Step Index 500,M1)    MIA_stab_0.33_1_0.0 predictions [13.00000000000001,14.00000000000002,15.00000000000004,16.00000000000005,17.0000000000001,18.0000000000001]
IP      0       14:43:07.969    MIA_Test (Step Index 500,M1)    y = - 9.340179e-01*x1 + 1.934018e+00*x2 + 3.865363e-16*x1*x2 + 1.065982e+00
II      0       14:52:59.698    MIA_Multivariable_test (BTCUSD,D1)      inputs [1,2,4] prediction [6.999999999999998]
CF      0       14:52:59.698    MIA_Multivariable_test (BTCUSD,D1)      inputs [1,5,3] prediction [8.999999999999998]
JR      0       14:52:59.698    MIA_Multivariable_test (BTCUSD,D1)      inputs [9,1,3] prediction [13.00000000000001]
NP      0       14:52:59.698    MIA_Multivariable_test (BTCUSD,D1)      f1_1 = 1.071429e-01*x1 + 6.428571e-01*x2 + 4.392857e+00
LR      0       14:52:59.698    MIA_Multivariable_test (BTCUSD,D1)      f1_2 = 6.086957e-01*x2 - 8.695652e-02*x3 + 4.826087e+00
ME      0       14:52:59.698    MIA_Multivariable_test (BTCUSD,D1)      f1_3 = - 1.250000e+00*x1 - 1.500000e+00*x3 + 1.125000e+01
DJ      0       14:52:59.698    MIA_Multivariable_test (BTCUSD,D1)      
IP      0       14:52:59.698    MIA_Multivariable_test (BTCUSD,D1)      f2_1 = 1.555556e+00*f1_1 - 6.666667e-01*f1_3 + 6.666667e-01
ER      0       14:52:59.698    MIA_Multivariable_test (BTCUSD,D1)      f2_2 = 1.620805e+00*f1_2 - 7.382550e-01*f1_3 + 7.046980e-01
ES      0       14:52:59.698    MIA_Multivariable_test (BTCUSD,D1)      f2_3 = 3.019608e+00*f1_1 - 2.029412e+00*f1_2 + 5.882353e-02
NH      0       14:52:59.698    MIA_Multivariable_test (BTCUSD,D1)      
CN      0       14:52:59.698    MIA_Multivariable_test (BTCUSD,D1)      f3_1 = 1.000000e+00*f2_1 - 3.731079e-15*f2_3 + 1.155175e-14
GP      0       14:52:59.698    MIA_Multivariable_test (BTCUSD,D1)      f3_2 = 8.342665e-01*f2_2 + 1.713326e-01*f2_3 - 3.359462e-02
DO      0       14:52:59.698    MIA_Multivariable_test (BTCUSD,D1)      
OG      0       14:52:59.698    MIA_Multivariable_test (BTCUSD,D1)      y = 1.000000e+00*f3_1 + 3.122149e-16*f3_2 - 1.899249e-15


MIA模型相对复杂，而COMBI模型则较为简单，很像序列本身。反映了该方法的线性特性。这一点也从脚本COMBI_Multivariable_test.mq5的输出中得到了证实，该脚本试图通过提供输入变量和相应的输出示例，来构建一个为三个数字求和的模型。在这里，COMBI算法成功地推断出系统的潜在特性。

COMBI算法的穷举搜索既是一个优势，也是一个劣势。从其积极的一面来看，评估所有输入组合可以确保找到描述数据的最佳多项式。然而，如果输入变量众多，这种广泛的搜索可能令计算成本变得高昂。可能导致训练时间过长。请注意，候选模型的数量由2的m次方减1给出，m越大，需要评估的候选模型数量就越多。为了解决这个问题，又开发了组合选择算法（Combinatorial Selective Algorithm）。


组合选择算法

我们称之为MULTI的组合选择算法，是对COMBI方法在效率方面所做的一种改进。它通过采用类似于GMDH多层算法中使用的程序，避免了穷举搜索。因此，它可以被视为是对原本单层性质的COMBI算法采取的一种多层解决方法。

组合选择法的网络结构


 
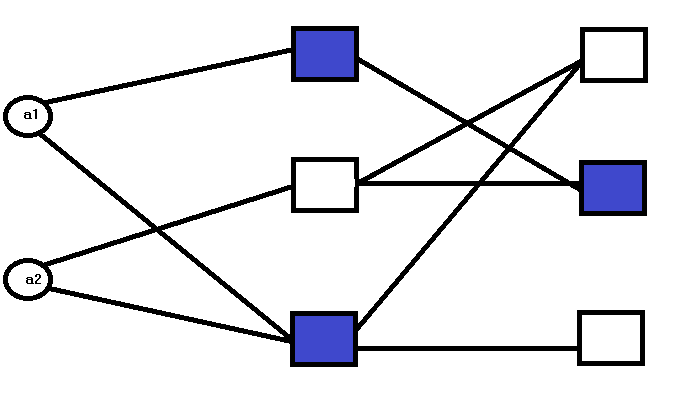
在第一层中，会估算所有包含一个输入变量的模型，并根据外部标准选择最佳模型，将其传递到下一层。在后续层中，会选择不同的输入变量并添加到这些候选模型中，期待对它们进行改进。是否添加新层取决于输出的准确性是否有所提高，以及是否有可用输入变量，尽管这些变量尚未成为候选模型的一部分。这意味着可能层的最大数量与输入变量的总数相符。

以这种方式评估候选模型通常可以避免穷举搜索，但也导致了一个问题。算法可能无法找到最能描述数据集的最优多项式。这表明在训练阶段应该考虑更多的候选模型。推导出最优多项式成为了一个需要精细化调整众多参数的过程。特别是每层评估的候选模型数量。


组合选择算法的实现

multi.mqh中提供了组合选择算法的实现方式。它包含继承自LinearModel的MULTI类的定义。 

//+------------------------------------------------------------------+
//|                                                        multi.mqh |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include "linearmodel.mqh"

//+------------------------------------------------------------------+
//|  Class implementing combinatorial selection MULTI algorithm      |
//+------------------------------------------------------------------+
class MULTI : public LinearModel
  {

protected:

   virtual void      removeExtraCombinations(void) override
     {
      CVector2d realBestCombinations;
      CVector n;
      n.push_back(bestCombinations[0][0]);
      realBestCombinations.push_back(n);
      bestCombinations = realBestCombinations;
     }

   virtual bool      preparations(SplittedData &data, CVector &_bestCombinations) override
     {
      return (bestCombinations.setAt(0,_bestCombinations) && ulong(level+1) < data.xTrain.Cols());
     }

   void              generateCombinations(int n_cols,vector &out[])  override
     {
      if(level == 1)
        {
         nChooseK(n_cols,level,out);
         return;
        }

      for(int i = 0; i<bestCombinations[0].size(); i++)
        {

         for(int z = 0; z<n_cols; z++)
           {
            vector comb = bestCombinations[0][i].combination();
            double array[];
            vecToArray(comb,array);
            int found = ArrayBsearch(array,double(z));
            if(int(array[found])!=z)
              {
               array.Push(double(z));
               ArraySort(array);
               comb.Assign(array);
               ulong dif = 1;
               for(uint row = 0; row<out.Size(); row++)
                 {
                  dif = comb.Compare(out[row],1e0);
                  if(!dif)
                     break;
                 }

               if(dif)
                 {
                  ArrayResize(out,out.Size()+1,100);
                  out[out.Size()-1] = comb;
                 }
              }

           }
        }
     }



public:
                     MULTI(void):LinearModel()
     {
      CVector members;
      bestCombinations.push_back(members);
      modelName = "MULTI";
     }

   bool              fit(vector &time_series,int lags,double testsize=0.5,CriterionType criterion=stab,int kBest = 3,int pAverage = 1,double limit = 0.0)
     {

      if(lags < 1)
        {
         Print(__FUNCTION__," lags must be >= 1");
         return false;
        }

      PairMVXd transformed = timeSeriesTransformation(time_series,lags);

      SplittedData splited = splitData(transformed.first,transformed.second,testsize);

      Criterion criter(criterion);

      if(validateInputData(testsize, pAverage, limit, kBest))
         return false;

      return GmdhModel::gmdhFit(splited.xTrain, splited.yTrain, criter, kBest, testsize, pAverage, limit);
     }

   bool              fit(matrix &vars,vector &targets,double testsize=0.5,CriterionType criterion=stab,int kBest = 3,int pAverage = 1,double limit = 0.0)
     {

      if(vars.Cols() < 1)
        {
         Print(__FUNCTION__," columns in vars must be >= 1");
         return false;
        }

      if(vars.Rows() != targets.Size())
        {
         Print(__FUNCTION__, " vars dimensions donot correspond with targets");
         return false;
        }

      SplittedData splited = splitData(vars,targets,testsize);

      Criterion criter(criterion);

      if(validateInputData(testsize, pAverage, limit, kBest))
         return false;

      return GmdhModel::gmdhFit(splited.xTrain, splited.yTrain, criter, kBest, testsize, pAverage, limit);
     }

  };
//+------------------------------------------------------------------+

MULTI类的工作方式与熟悉的COMBI类及其“fit()”方法类似。与COMBI类相比，读者应注意“fit()”方法中包含了更多的超参数。在应用MULTI类时，“kBest”和“pAverage”是两个可能需要仔细调整的参数。在MULTI_test.mq5和MULTI_Multivariable_test.mq5脚本中展示了将模型拟合到数据集的过程。以下是相关代码。 

//+----------------------------------------------------------------------+
//|                                                   MULTI_test.mq5           |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com     |
//+----------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <GMDH\multi.mqh>

input int NumLags = 2;
input int NumPredictions = 6;
input CriterionType critType = stab;
input int Average  = 1;
input int NumBest  = 3;
input double DataSplitSize = 0.33;
input double critLimit = 0;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   vector tms = {1,2,3,4,5,6,7,8,9,10,11,12};

   if(NumPredictions<1)
     {
      Alert("Invalid setting for NumPredictions, has to be larger than 0");
      return;
     }

   MULTI multi;

   if(!multi.fit(tms,NumLags,DataSplitSize,critType,NumBest,Average,critLimit))
      return;

   vector in(ulong(NumLags),slice,tms,tms.Size()-ulong(NumLags));

   vector out = multi.predict(in,NumPredictions);

   Print(" predictions ", out);

   Print(multi.getBestPolynomial());

  }
//+------------------------------------------------------------------+


//+------------------------------------------------------------------+
//|                                    MULTI_Mulitivariable_test.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <GMDH\multi.mqh>

input CriterionType critType = stab;
input double DataSplitSize = 0.33;
input int Average  = 1;
input int NumBest  = 3;
input double critLimit = 0;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   matrix independent = {{1,2,3},{3,2,1},{1,4,2},{1,1,3},{5,3,1},{3,1,9}};
   vector dependent = {6,6,7,5,9,13};

   MULTI multi;

   if(!multi.fit(independent,dependent,DataSplitSize,critType,NumBest,Average,critLimit))
      return;

   matrix unseen = {{1,2,4},{1,5,3},{9,1,3}};

   for(ulong row = 0; row<unseen.Rows(); row++)
     {
      vector in = unseen.Row(row);
      Print("inputs ", in, " prediction ", multi.predict(in,1));
     }

   Print(multi.getBestPolynomial());

  }
//+------------------------------------------------------------------+

由此可见，通过运行脚本，从我们的简单数据集中得到的多项式与应用COMBI算法得到的多项式完全相同。

IG      0       18:24:28.811    MULTI_Mulitivariable_test (BTCUSD,D1)   inputs [1,2,4] prediction [7.000000000000002]
HI      0       18:24:28.812    MULTI_Mulitivariable_test (BTCUSD,D1)   inputs [1,5,3] prediction [9]
NO      0       18:24:28.812    MULTI_Mulitivariable_test (BTCUSD,D1)   inputs [9,1,3] prediction [13.00000000000001]
PP      0       18:24:28.812    MULTI_Mulitivariable_test (BTCUSD,D1)   y= 1.000000e+00*x1 + 1.000000e+00*x2 + 1.000000e+00*x3 - 7.330836e-15
DP      0       18:25:04.454    MULTI_test (BTCUSD,D1)   predictions [13,14,15,16,17,18.00000000000001]
MH      0       18:25:04.454    MULTI_test (BTCUSD,D1)  y= 1.000000e+00*x1 + 2.000000e+00


基于比特币价格的GMDH模型

在本节中，我们将应用GMDH方法来构建比特币每日收盘价预测模型。这将通过文章末尾附带的GMDH_Price_Model.mq5脚本来实现。尽管我们的演示专门针对比特币这一交易品种，但该脚本也可以应用于任何交易品种和时间周期。该脚本具有多个用户可变参数，用于控制程序的各个方面。 

//--- input parameters
input string   SetSymbol="";
input ENUM_GMDH_MODEL modelType = Combi;
input datetime TrainingSampleStartDate=D'2019.12.31';
input datetime TrainingSampleStopDate=D'2022.12.31';
input datetime TestSampleStartDate = D'2023.01.01';
input datetime TestSampleStopDate = D'2023.12.31';
input ENUM_TIMEFRAMES tf=PERIOD_D1;    //time frame
input int Numlags = 3;
input CriterionType critType = stab;
input PolynomialType polyType = linear_cov;
input int Average  = 10;
input int NumBest  = 10;
input double DataSplitSize = 0.2;
input double critLimit = 0;
input ulong NumTestSamplesPlot = 20;

通过下表列出并加以描述。

输入参数名称
 说明
SetSymbol
设置将用作训练数据收盘价的符号名称，如果留空，则假定应用脚本的图表符号。
modeltype 它代表由GMDH算法选择的枚举
TrainingSampleStartDate
 样品期内收盘价的起始日期
TrainingSampleStopDate
 样本期内收盘价的结束日期
TestSampleStartDate
 样品期外的开始日期
TestSampleStopDate
 样品期外的结束日期
tf
应用的时间周期
Numlags
 定义用于预测下一个收盘价的历史滞后值的数量
critType
 指定模型构建过程的外部标准
polyType
 当选择MIA算法时，通过所使用的多项式类型在现有变量的基础上构造新的变量，这在训练过程中非常关键
Average
在计算停止标准时所要考虑的最优模型数量
Numbest
 对于MIA模型，它定义了最优模型的数量，基于这些模型构建后续层的新输入
而对于COMBI模型，它是在每一层选择候选模型的数量，以供后续迭代时参考
DataSplitSize
 用于评估模型的一部分输入数据
critLimit
 为了继续训练模型，外部标准必须改善一个特定的最小值
NumTestSamplePlot
 该值定义了样本外数据集中可视化的样本数量，以及与这些样本相对应的预测结果

该脚本首先从选择一个合适的观测样本作为训练数据开始。 

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//get relative shift of IS and OOS sets
   int trainstart,trainstop, teststart, teststop;
   trainstart=iBarShift(SetSymbol!=""?SetSymbol:NULL,tf,TrainingSampleStartDate);
   trainstop=iBarShift(SetSymbol!=""?SetSymbol:NULL,tf,TrainingSampleStopDate);
   teststart=iBarShift(SetSymbol!=""?SetSymbol:NULL,tf,TestSampleStartDate);
   teststop=iBarShift(SetSymbol!=""?SetSymbol:NULL,tf,TestSampleStopDate);
//check for errors from ibarshift calls
   if(trainstart<0 || trainstop<0 || teststart<0 || teststop<0)
     {
      Print(ErrorDescription(GetLastError()));
      return;
     }
//---set the size of the sample sets
   size_observations=(trainstart - trainstop) + 1 ;
   size_outsample = (teststart - teststop) + 1;
//---check for input errors
   if(size_observations <= 0  || size_outsample<=0)
     {
      Print("Invalid inputs ");
      return;
     }
//---download insample prices for training
   int try
         = 10;
   while(!prices.CopyRates(SetSymbol,tf,COPY_RATES_CLOSE,TrainingSampleStartDate,TrainingSampleStopDate) && try)
     {
      try
         --;
      if(!try)
        {
         Print("error copying to prices  ",GetLastError());
         return;
        }
      Sleep(5000);

另一组收盘价样本已被下载，用其绘制预测收盘价和实际收盘价的图表来可视化模型的性能。 

//---download out of sample prices testing
   try
         = 10;
   while(!testprices.CopyRates(SetSymbol,tf,COPY_RATES_CLOSE|COPY_RATES_TIME|COPY_RATES_VERTICAL,TestSampleStartDate,TestSampleStopDate) && try)
     {
      try
         --;
      if(!try)
        {
         Print("error copying to testprices  ",GetLastError());
         return;
        }
      Sleep(5000);
     }

该脚本的用户定义参数能够应用我们之前讨论和实现过的三种GMDH模型之一。 

//--- train and make predictions
   switch(modelType)
     {
      case Combi:
        {
         COMBI combi;
         if(!combi.fit(prices,Numlags,DataSplitSize,critType))
            return;
         Print("Model ", combi.getBestPolynomial());
         MakePredictions(combi,testprices.Col(0),predictions);
        }
      break;

      case Mia:
        {
         MIA mia;
         if(!mia.fit(prices,Numlags,DataSplitSize,polyType,critType,NumBest,Average,critLimit))
            return;
         Print("Model ", mia.getBestPolynomial());
         MakePredictions(mia,testprices.Col(0),predictions);
        }
      break;

      case Multi:
        {
         MULTI multi;
         if(!multi.fit(prices,Numlags,DataSplitSize,critType,NumBest,Average,critLimit))
            return;
         Print("Model ", multi.getBestPolynomial());
         MakePredictions(multi,testprices.Col(0),predictions);
        }
      break;

      default:
         Print("Invalid GMDH model type ");
         return;
     }
//---

以显示预测收盘价与实际样本期外数据集值的图表作为程序结收尾。 

//---
   ulong TestSamplesPlot = (NumTestSamplesPlot>0)?NumTestSamplesPlot:20;
//---
   if(NumTestSamplesPlot>=testprices.Rows())
      TestSamplesPlot = testprices.Rows()-Numlags;
//---
   vector testsample(100,slice,testprices.Col(0),Numlags,Numlags+TestSamplesPlot-1);
   vector testpredictions(100,slice,predictions,0,TestSamplesPlot-1);
   vector dates(100,slice,testprices.Col(1),Numlags,Numlags+TestSamplesPlot-1);
//---
//Print(testpredictions.Size(), ":", testsample.Size());
//---
   double y[], y_hat[];
//---
   if(vecToArray(testpredictions,y_hat) && vecToArray(testsample,y) && vecToArray(dates,xaxis))
     {
      PlotPrices(y_hat,y);
     }
//---
   ChartRedraw();
  }

以下是分别使用组合算法和多层迭代算法进行预测所得的图表。

组合模型比特币预测

MIA模型比特币预测


结论

综上所述，GMDH的组合算法为复杂系统的建模提供了一个框架，特别是在数据驱动、归纳方法领域表现出明显优势。然而，由于该算法在处理大型数据集时效率低下，其实际应用往往受到限制。组合选择算法仅在一定程度上缓解了这一缺陷。在算法中引入更多需要调整的参数，虽然可以带来速度上的提升，但也会增加调优的负担，从而影响到算法性能的发挥。GMDH方法在金融时间序列分析中的应用，显示了其可提供的有价值的潜力。

File
说明
Mql5\include\VectorMatrixTools.mqh
 定义函数的头文件，用于操作向量和矩阵
Mql5\include\JAson.mqh
 包含用于解析和生成JSON对象的自定义类型
Mql5\include\GMDH\gmdh_internal.mqh
 包含gmdh库中使用的自定义类型的头文件
Mql5\include\GMDH\gmdh.mqh
 包含定义基类GmdhModel的文件
Mql5\include\GMDH\linearmodel.mqh
 包含定义中间类LinearModel的文件，该类是COMBI和MULTI类的基础
Mql5\include\GMDH\combi.mqh
 包含定义COMBI类的文件
Mql5\include\GMDH\multi.mqh
 包含定义MULTI类的文件
Mql5\include\GMDH\mia.mqh
 包含实现多层迭代算法的MIA类
Mql5\script\COMBI_test.mq5
 演示应用COMBI类构建一个简单的时间序列模型的脚本
Mql5\script\COMBI_Multivariable_test.mq5
 演示应用COMBI类构建多变量数据集模型的脚本
Mql5\script\MULTI_test.mq5
 演示应用MULTI 类构建一个简单的时间序列模型的脚本
Mql5\script\MULTI_Multivariable_test.mq5
 演示应用MULTI类构建多变量数据集模型的脚本
Mql5\script\GMDH_Price_Model.mqh
 演示价格序列GMDH模型的脚本

本文由MetaQuotes Ltd译自英文
原文地址： https://www.mql5.com/en/articles/14804

附加的文件 |
下载ZIP
VectorMatrixTools.mqh (6.41 KB)
JAson.mqh (33.43 KB)
combi.mqh (4.02 KB)
gmdh.mqh (23.86 KB)
gmdh_internal.mqh (82.09 KB)
linearmodel.mqh (2.84 KB)
mia.mqh (12.1 KB)
multi.mqh (4.05 KB)
COMBI_Multivariable_test.mq5 (1.54 KB)
COMBI_test.mq5 (1.59 KB)
GMDH_Price_Model.mq5 (8.41 KB)
MULTI_Mulitivariable_test.mq5 (1.5 KB)
MULTI_test.mq5 (1.55 KB)
Mql5.zip (31.81 KB)

注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.

该作者的其他文章

前往讨论
神经网络变得简单（第 75 部分）：提升轨迹预测模型的性能 神经网络变得简单（第 75 部分）：提升轨迹预测模型的性能
我们创建的模型变得越来越大，越来越复杂。这不光提高了它们的训练成本，还有操作成本。不过，做出决定所需的时间往往很关键。有关于此，我们来研究在不损失品质的情况下优化模型性能的方法。
如何使用抛物线转向（Parabolic SAR）指标设置跟踪止损（Trailing Stop） 如何使用抛物线转向（Parabolic SAR）指标设置跟踪止损（Trailing Stop）
在创建交易策略时，我们需要测试多种多样的保护性止损。这时，一个随着价格变动而动态调整止损位的想法浮现在我的脑海中。抛物线转向（Parabolic SAR）指标无疑是最佳选择。很难想到有比这更简单且视觉上更清晰的指标了。
自定义指标（第一部份）：在MQL5中逐步开发简单自定义指标的入门指南 自定义指标（第一部份）：在MQL5中逐步开发简单自定义指标的入门指南
学习如何使用MQL5创建自定义指标。这篇入门文章将指引您了解创建简单自定义指标的基础知识，并向初次接触这一有趣话题的MQL5程序员展示编写各种自定义指标的方法。
如何构建和优化基于波动率的交易系统（Chaikin volatility-CHV） 如何构建和优化基于波动率的交易系统（Chaikin volatility-CHV）
在本文中，我们将介绍另一个基于波动率的指标——蔡金波动率（Chaikin Volatility）。在了解到蔡金波动率的使用方法和构建方式之后，我们将学习如何构建自定义指标。我们将分享一些可用的简单策略，并对其进行测试，以了解哪个策略更优。