Estimations Statistiques
99
0
Introduction
De nos jours,vous pouvez souvent rencontrer des articles et publication écrits sur des sujets liés à l’économétrie, la prévision des séries de prix, la sélection et l’estimation de l’adéquation d’un modèle etc. Mais dans la plupart des cas, le raisonnement est basé sur l'hypothèse qu'un lecteur connaissant les méthodes de statistiques mathématiques et peut facilement estimer les paramètres statistiques d'une séquence analysée.
L'estimation des paramètres statistiques d'une séquence est très importante, car la plupart des modèles et méthodes mathématiques sont axés sur des hypothèses différentes. Par exemple, la normalité de la loi de distribution ou la valeur de dispersion, ou d'autres paramètres. Ainsi, lors de l'analyse et de la prévision de séries chronologiques, nous avons besoin d'un outil simple et pratique qui permette d'estimer rapidement et clairement les principaux paramètres statistiques. Dans cet article, nous allons essayer de créer un tel outil.
L'article décrit brièvement les paramètres statistiques les plus simples d'une séquence aléatoire et plusieurs méthodes de son analyse visuelle. Il propose l’implémentation de ces méthodes en MQL5 et les méthodes de visualisation du résultat des calculs à l'aide de Gnuplot application. Cet article n'a en aucun cas prétendu être un manuel ou une référence ; c'est pourquoi il peut comprendre certaines familiarités admises quant à la terminologie et aux définitions.
Analyse des Paramètres sur un Échantillon
Admettons qu un processus stationnaire existant indéfiniment dans le temps, qui peut être représenté comme une séquence d'échantillons discrets. Appelons cette séquence d'échantillons la population générale. Une partie des échantillons sélectionnés dans la population générale sera appelée échantillonnage de la population générale ou échantillonnage d’échantillons N. En plus de cela, admettons qu'aucun vrai paramètre ne nous soit connu, nous allons donc les estimer sur la base d'un échantillonnage fini.
Éviter les Valeurs Aberrantes
Avant de commencer l'estimation statistique des paramètres, il convient de noter que la précision de l'estimation peut être insuffisante si l'échantillonnage comporte de grossières erreurs (cas aberrants). Les valeurs aberrantes affectent considérablement la précision des estimations si l'échantillonnage a un petit volume. Les valeurs aberrantes sont les valeurs qui divergent anormalement du milieu de la distribution. De tels écarts peuvent être causés par différents événements peu probables et des erreurs sont apparues lors de la collecte des données statistiques et de la formation de la séquence.
Il est difficile de se décider quant au filtrage des valeurs aberrantes, car dans la plupart des cas, il est impossible de détecter clairement si une valeur est une valeur aberrante ou appartient au processus analysé. Donc, si des valeurs aberrantes sont détectées et qu'il est décidé de les filtrer, une question se pose : que devons-nous faire avec ces valeurs d'erreur ? La variante la plus logique est d'exclure de l'échantillonnage, ce qui peut augmenter la précision de l'estimation des caractéristiques statistiques ; mais vous devez faire attention à l’exclusion des valeurs aberrantes de l'échantillonnage lorsque vous travaillez avec des séquences chronologiques.
Pour avoir la possibilité d'exclure les valeurs aberrantes d'un échantillonnage ou au moins de les détecter, implémentons l'algorithme décrit dans le livre"Statistics for Traders" écrit par SV Bulashev.
Selon cet algorithme, nous devons calculer cinq valeurs d'estimation du centre de distribution :
- Médiane,
- Centre de l'intervalle interquartile à 50 % (intervalle moyen-quartile, MQR) ;
- Moyenne arithmétique de l'ensemble de l'échantillonnage ;
- Moyenne arithmétique sur l'intervalle interquartile de 50 % (moyenne interquartile, IQM) ;
- Centre de gamme (milieu de gamme) - déterminé comme la valeur moyenne de la valeur maximale et minimale dans un échantillonnage.
Ensuite, les résultats de l'estimation du centre de distribution sont triés par ordre croissant ; puis la valeur moyenne ou la troisième dans l'ordre est choisie comme centre de distributionXcen. Ainsi, l'estimation choisie semble être peu affectée par les valeurs aberrantes.
De plus, en utilisant l'estimation obtenue du centre de distributionXcen, calculons l'écart types , l'excès K et le taux de censure selon la formule empirique :
où N est le nombre d'échantillons dans l'échantillonnage (volume d'échantillonnage).
Ensuite, les valeurs qui se situent en dehors de la plage :
seront comptées comme des valeurs aberrantes, ils devraient donc être exclues de l'échantillonnage.
Cette méthode est décrite en détail dans le livre"Statistics for Traders" donc, passons directement à l’implémentation de l’algorithme. L'algorithme qui permet de détecter et d'exclure les valeurs aberrantes est implémenté dans la fonction erremove().
Vous trouverez ci-dessous le script écrit pour tester cette fonction.
//---------------------------------------------------------------------------- // erremove.mq5 // Copyright 2011, MetaQuotes Software Corp. // https://www.mql5.com //---------------------------------------------------------------------------- #property copyright "Copyright 2011, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" #import "shell32.dll" bool ShellExecuteW(int hwnd,string lpOperation,string lpFile, string lpParameters,string lpDirectory,int nShowCmd); #import //---------------------------------------------------------------------------- // Script program start function //---------------------------------------------------------------------------- void OnStart() { int i; double dat[100]; double y[]; srand(1); for(i=0;i<ArraySize(dat);i++)dat[i]=rand()/16000.0; dat[25]=3; // Make Error !!! erremove(dat,y,1); } //---------------------------------------------------------------------------- int erremove(const double &x[],double &y[],int visual=1) { int i,m,n; double a[],b[5]; double dcen,kurt,sum2,sum4,gs,v,max,min; if(!ArrayIsDynamic(y)) // Error { Print("Function erremove() error!"); return(-1); } n=ArraySize(x); if(n<4) // Error { Print("Function erremove() error!"); return(-1); } ArrayResize(a,n); ArrayCopy(a,x); ArraySort(a); b[0]=(a[0]+a[n-1])/2.0; // Midrange m=(n-1)/2; b[1]=a[m]; // Median if((n&0x01)==0)b[1]=(b[1]+a[m+1])/2.0; m=n/4; b[2]=(a[m]+a[n-m-1])/2.0; // Midquartile range b[3]=0; for(i=m;i<n-m;i++)b[3]+=a[i]; // Interquartile mean(IQM) b[3]=b[3]/(n-2*m); b[4]=0; for(i=0;i<n;i++)b[4]+=a[i]; // Mean b[4]=b[4]/n; ArraySort(b); dcen=b[2]; // Distribution center sum2=0; sum4=0; for(i=0;i<n;i++) { a[i]=a[i]-dcen; v=a[i]*a[i]; sum2+=v; sum4+=v*v; } if(sum2<1.e-150)kurt=1.0; kurt=((n*n-2*n+3)*sum4/sum2/sum2-(6.0*n-9.0)/n)*(n-1.0)/(n-2.0)/(n-3.0); // Kurtosis if(kurt<1.0)kurt=1.0; gs=(1.55+0.8*MathLog10((double)n/10.0)*MathSqrt(kurt-1))*MathSqrt(sum2/(n-1)); max=dcen+gs; min=dcen-gs; m=0; for(i=0;i<n;i++)if(x[i]<=max&&x[i]>=min)a[m++]=x[i]; ArrayResize(y,m); ArrayCopy(y,a,0,0,m); if(visual==1)vis(x,dcen,min,max,n-m); return(n-m); } //---------------------------------------------------------------------------- void vis(const double &x[],double dcen,double min,double max,int numerr) { int i; double d,yma,ymi; string str; yma=x[0];ymi=x[0]; for(i=0;i<ArraySize(x);i++) { if(yma<x[i])yma=x[i]; if(ymi>x[i])ymi=x[i]; } if(yma<max)yma=max; if(ymi>min)ymi=min; d=(yma-ymi)/20.0; yma+=d;ymi-=d; str="unset key\n"; str+="set title 'Sequence and error levels (number of errors = "+ (string)numerr+")' font ',10'\n"; str+="set yrange ["+(string)ymi+":"+(string)yma+"]\n"; str+="set xrange [0:"+(string)ArraySize(x)+"]\n"; str+="plot "+(string)dcen+" lt rgb 'green',"; str+=(string)min+ " lt rgb 'red',"; str+=(string)max+ " lt rgb 'red',"; str+="'-' with line lt rgb 'dark-blue'\n"; for(i=0;i<ArraySize(x);i++)str+=(string)x[i]+"\n"; str+="e\n"; if(!saveScript(str)){Print("Create script file error");return;} if(!grPlot())Print("ShellExecuteW() error"); } //---------------------------------------------------------------------------- bool grPlot() { string pnam,param; pnam="GNUPlot\\binary\\wgnuplot.exe"; param="-p MQL5\\Files\\gplot.txt"; return(ShellExecuteW(NULL,"open",pnam,param,NULL,1)); } //---------------------------------------------------------------------------- bool saveScript(string scr1="",string scr2="") { int fhandle; fhandle=FileOpen("gplot.txt",FILE_WRITE|FILE_TXT|FILE_ANSI); if(fhandle==INVALID_HANDLE)return(false); FileWriteString(fhandle,"set terminal windows enhanced size 560,420 font 8\n"); FileWriteString(fhandle,scr1); if(scr2!="")FileWriteString(fhandle,scr2); FileClose(fhandle); return(true); } //----------------------------------------------------------------------------
Examinons en détail la fonction erremove(). Comme premier paramètre de la fonction, nous passons l'adresse du tableau x[], où sont stockées les valeurs de l'échantillonnage analysé ; le volume d'échantillonnage ne doit pas être inférieur à quatre éléments. Il est admis que la taille du tableau x[] est égale à la taille de l'échantillonnage, c'est la raison pour laquelle la valeur N du volume de l'échantillonnage n'est pas passée. Les données situées dans le tableau x[] ne sont pas modifiées suite à l'exécution de la fonction.
Le paramètre suivant est l'adresse du tableau y[]. En cas d'exécution réussie de la fonction, ce tableau comprendra la séquence d'entrée avec les valeurs aberrantes exclues. La taille du tableau y[] est inférieure à la taille du tableau x[] par le nombre de valeurs exclues de l'échantillonnage. Le tableau y[] doit être déclaré dynamique, sinon il sera impossible de modifier sa taille dans le corps de la fonction.
Le dernier paramètre (facultatif) est la balise en charge de la visualisation des résultats du calcul. Si sa valeur est égale à un (valeur par défaut), alors avant la fin de l'exécution de la fonction le graphique ,affichant les informations suivantes ,sera tracé dans une fenêtre séparée : la séquence d'entrée, la ligne de centre de distribution et les limites de portée , dont les valeurs en dehors seront considérées comme des valeurs aberrantes.
La méthode de dessin des graphiques sera décrite plus loin. En cas d'exécution réussie, la fonction renvoie le nombre de valeurs exclues de l'échantillonnage ; en cas d'erreur, il renvoie -1. Si aucune valeur d'erreur (valeurs aberrantes) n'est détectée, la fonction renverra 0 et la séquence dans le tableau y[] sera la même que dans x[].
Au début de la fonction, les informations sont copiées du tableau x[] vers le tableau a[], puis elles sont triées par ordre croissant, puis cinq estimations du centre de distribution sont effectuées.
Le milieu de la gamme (milieu de gamme) est déterminé comme la somme des valeurs extrêmes du tableau trié a[] divisée par deux.
La médiane est calculée pour les volumes impairs de l'échantillonnageNcomme suit :
et pour des volumes pairs de l'échantillonnage :
En considérant que les index du tableau trié a[] partent de zéro,nous obtenons:
m=(n-1)/2; median=a[m]; if((n&0x01)==0)b[1]=(median+a[m+1])/2.0;
Le milieu de l'intervalle interquartile de 50 % (intervalle mi-quartile, MQR) :
oùM=N/4 (division entière).
Pour le tableau trié a[]nous obtenons:
m=n/4; MQR=(a[m]+a[n-m-1])/2.0; // Midquartile range
Moyennes arithmétiques de l'intervalle interquartile de 50 % (moyenne interquartile, IQM). 25% des échantillons sont coupés des deux côtés de l'échantillonnage, et les 50% restants sont utilisés pour le calcul de la moyenne arithmétique :
oùM=N/4 (division entière).
m=n/4; IQM=0; for(i=m;i<n-m;i++)IQM+=a[i]; IQM=IQM/(n-2*m); // Interquartile mean(IQM)
La moyenne arithmétique (moyenne) est déterminée pour l'ensemble de l'échantillonnage.
Chacune des valeurs déterminées est portée dans le tableau b[], puis le tableau est trié par ordre croissant. Une valeur d'élément du tableau b[2] est choisie comme centre de la distribution. De plus, en utilisant cette valeur, nous calculerons les estimations non-biaisées de la moyenne arithmétique et du coefficient d'aplatissement ; l'algorithme de calcul sera décrit plus loin.
Les estimations obtenues sont utilisées pour le calcul du coefficient de censure et des limites de la plage de détection des valeurs aberrantes (les expressions sont présentées ci-dessus). En fin de compte, la séquence avec les valeurs aberrantes exclues est formée dans le tableau y[] et les fonctions vis() sont appelées pour tracer le graphique. Examinons brièvement la méthode de visualisation utilisée dans cet article.
Visualisation
Pour afficher les résultats de calcul, j'utilise l'application gratuite gnuplot destinée à la réalisation de divers graphes 2D et 3D. Gnuplot offre la possibilité d'afficher des graphiques à l'écran (dans une fenêtre séparée) ou de les écrire dans un fichier sous différents formats graphiques. Les commandes de tracé des cartes peuvent être exécutées à partir d'un fichier texte préalablement préparé. La page Web officielle du projet gnuplot est -gnuplot.sourceforge.net L'application est multiplateforme et distribuée à la fois sous forme de fichiers de code source et de fichiers binaires compilés pour une certaine plate-forme.
Les exemples écrits pour cet article ont été testés sous Windows XP SP3 et la version 4.2.2 de gnuplot. Le fichier gp442win32.zip peut être téléchargé àhttp://sourceforge.net/projects/gnuplot/files/gnuplot/4.4.2/ Je n'ai pas testé les exemples avec d'autres versions et builds de gnuplot.
Une fois que vous avez téléchargé l'archive gp442win32.zip, décompressez-la. En conséquence, le dossier \gnuplot est créé, il comporte l'application, le fichier d'aide, la documentation et les exemples. Pour interagir avec les applications, placez l'intégralité du dossier \gnuplot dans le dossier racine de votre terminal client MetaTrader 5.
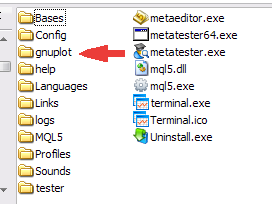
Figure 1. Placement du dossier \gnuplot
Une fois le dossier déplacé, vous pouvez modifier l'opérabilité de l'application gnuplot. Pour ce faire, exécutez le fichier \gnuplot\binary\wgnuplot.exe, puis, lorsque la commande "gnuplot>" apparaît, tapez la commande "plot sin(x)". En conséquence, une fenêtre contenant la fonction sin(x) devrait apparaître. Vous pouvez également essayer les exemples inclus dans la livraison de l'application ; pour ce faire, choisissez l'élément File\Demos et sélectionnez le fichier \gnuplot\demo\all.dem.
Maintenant que vous démarrez le script erremove.mq5, le graphique illustré dans la figure 2 sera dessiné dans une fenêtre séparée :
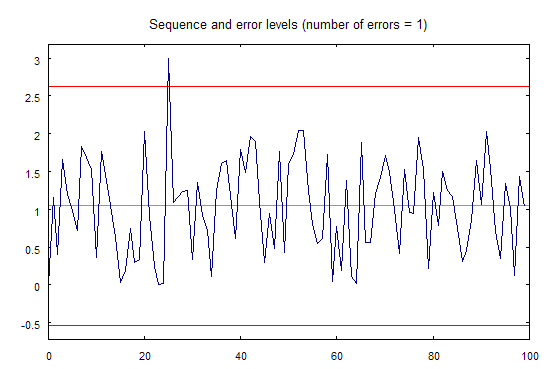
Figure 2. Le graphique qui est dessiné à l'aide du script erremove.mq5.
Plus loin dans l'article,nous allons parler un peu de certaines caractéristiques de l'utilisation de gnuplot, car les informations sur le programme et ses contrôles peuvent être facilement trouvées dans la documentation, qui y est livrée, et sur divers sites Web,tels quehttp://gnuplot.ikir.ru/.
Les exemples de programmes écrits pour cet article utilisent la méthode d'interaction la plus simple avec gnuplot pour dessiner les graphiques. Au début, le fichier texte gplot.txt est créé ; il comporte les commandes gnuplot et les informations à afficher. Ensuite, l'application wgnuplot.exe est lancée avec le nom de ce fichier passé en argument dans la ligne de commande. L'application wgnuplot.exe est appelée à l'aide de la fonction ShellExecuteW() importée de la bibliothèque système shell32.dll ; c'est la raison pour laquelle l'importation de dll externes doit être autorisée dans le terminal client.
La version donnée de gnuplot permet de dessiner des graphiques dans une fenêtre séparée pour deux types de terminaux : wxt et windows. Le terminal wxt utilise les algorithmes d'antialiasing pour le tracé de graphiques, ce qui permet d'obtenir une image de meilleure qualité par rapport au terminal Windows. Cependant, le terminal Windows a été utilisé pour écrire les exemples de cet article. La raison en est que lorsque vous travaillez avec le terminal Windows, le processus système créé à la suite de l'appel "wgnuplot.exe -p MQL5\\Files\\gplot.txt" et l'ouverture d'une fenêtre graphique est automatiquement tué lorsque la fenêtre est fermée .
Si vous choisissez le terminal wxt, lorsque vous fermez la fenêtre graphique, le processus système wgnuplot.exe ne s'arrêtera pas automatiquement. Ainsi, si vous utilisez le terminal wxt et appelez wgnuplot.exe plusieurs fois comme décrit ci-dessus, plusieurs processus sans aucun signe d'activité peuvent s'accumuler dans le système. En utilisant l'appel "wgnuplot.exe -p MQL5\\Files\\gplot.txt" et le terminal Windows, vous pouvez éviter l'ouverture d'une fenêtre supplémentaire indésirable et l'apparition de processus système non fermés.
La fenêtre, où le graphique est affiché, est interactive et traite les événements de clic de souris et de clavier. Pour obtenir les informations sur les raccourcis clavier par défaut, exécutez wgnuplot.exe, choisissez un type de terminal à l'aide de la commande "set terminal windows" et tracez n'importe quel graphique, par exemple à l'aide de la commande "plot sin(x)". Si la fenêtre graphique est active (au focus), alors vous verrez une astuce s'afficher dans la fenêtre de texte de wgnuplot.exe dès que vous appuyez sur le bouton "h".
Estimation des Paramètres
Après la brève familiarisation avec la méthode de tracé des graphiques, revenons à l'estimation des paramètres de la population générale à partir de son échantillonnage fini. En admettant qu'aucun paramètre statistique de la population générale ne soit connu, nous n'utiliserons que des estimations non-biaisées de ces paramètres.
L'estimation de l'espérance mathématique ou de la moyenne d'échantillonnage peut être considérée comme le paramètre principal qui détermine la distribution d'une séquence. La moyenne d'échantillonnage est calculée à l'aide de la formule suivante :
où N est le nombre d'échantillons dans l'échantillonnage.
La valeur moyenne est une estimation du centre de distribution et elle est utilisée pour le calcul d'autres paramètres liés aux moments centraux, ce qui rend ce paramètre particulièrement important. En plus de la valeur moyenne, nous utiliserons l'estimation de la dispersion (dispersion, variance), l'écart type, le coefficient d'asymétrie (asymétrie) et le coefficient d'aplatissement (kurtose) comme paramètres statistiques.
où m sont des moments centraux.
Les moments centraux sont des caractéristiques numériques de la distribution d'une population générale.
Les deuxième, troisième et quatrième moments centraux sélectifs sont déterminés par les expressions suivantes :
Mais ces valeurs sont non-biaisées. Ici, nous devrions mentionner k-Statistic and h-Statistic. Sous certaines conditions, ils permettent d'obtenir des estimations non biaisées des moments centraux, de sorte qu'ils peuvent être utilisés pour le calcul d'estimations non biaisées de la dispersion, de l'écart type, de l'asymétrie et de l'aplatissement.
Notez que le calcul du quatrième moment dans les estimations k et h est effectué de différentes manières. Il en découle l'obtention de différentes expressions pour l'estimation de l'aplatissement lors de l'utilisation de k ou h. Par exemple, dans Microsoft Excel, l'excédent est calculé à l'aide de la formule qui correspond à l'utilisation des k-estimations, et dans le livre "Statistics for Traders", l'estimation non biaisée de l'aplatissement est effectuée à l'aide des h-estimations.
Choisissons les h-estimations et puis en les substituant à la place de 'm' dans l'expression donnée précédemment, nous calculerons les paramètres nécessaires.
Dispersion et Écart Type :
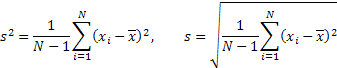
Dissymétrie
kurtose
Le coefficient d'aplatissement (kurtose) calculé selon l'expression donnée pour la séquence avec loi de distribution normale est égal à 3.
Vous devez faire attention au fait que la valeur obtenue en soustrayant 3 de la valeur calculée est souvent utilisée comme valeur d'aplatissement ; ainsi la valeur obtenue est normalisée par rapport à la loi de distribution normale. Dans le premier cas, ce coefficient est appelé kurtose ; dans le second cas, on parle d'« excès de kurtose ».
Le calcul des paramètres selon l'expression donnée est effectué dans la fonction dStat() :
struct statParam { double mean; double median; double var; double stdev; double skew; double kurt; }; //---------------------------------------------------------------------------- int dStat(const double &x[],statParam &sP) { int i,m,n; double a,b,sum2,sum3,sum4,y[]; ZeroMemory(sP); // Reset sP n=ArraySize(x); if(n<4) // Error { Print("Function dStat() error!"); return(-1); } sP.kurt=1.0; ArrayResize(y,n); ArrayCopy(y,x); ArraySort(y); m=(n-1)/2; sP.median=y[m]; // Median if((n&0x01)==0)sP.median=(sP.median+y[m+1])/2.0; sP.mean=0; for(i=0;i<n;i++)sP.mean+=x[i]; sP.mean/=n; // Mean sum2=0;sum3=0;sum4=0; for(i=0;i<n;i++) { a=x[i]-sP.mean; b=a*a;sum2+=b; b=b*a;sum3+=b; b=b*a;sum4+=b; } if(sum2<1.e-150)return(1); sP.var=sum2/(n-1); // Variance sP.stdev=MathSqrt(sP.var); // Standard deviation sP.skew=n*sum3/(n-2)/sum2/sP.stdev; // Skewness sP.kurt=((n*n-2*n+3)*sum4/sum2/sum2-(6.0*n-9.0)/n)* (n-1.0)/(n-2.0)/(n-3.0); // Kurtosis return(1);Lorsque dStat() est appelé, l'adresse du tableau x[] est transmise à la fonction. Il comporte les données initiales et le lien vers la structure statParam, qui comportera les valeurs calculées des paramètres. En cas d'erreur lorsqu'il y a moins de quatre éléments dans le tableau, la fonction renvoie -1.
Histogramme
En plus des paramètres calculés dans la fonction dStat(), la loi de distribution de la population générale est d’un intérêt majeur pour nous. Pour estimer visuellement la loi de distribution sur l'échantillonnage fini,nous pouvons tracer un histogramme. Lors du tracé de l'histogramme, la plage de valeurs de l'échantillonnage est divisée en plusieurs sections similaires. Et puis le nombre d'éléments dans chaque section est calculé (fréquences de groupe).
En outre, un diagramme à barres est tracé sur la base des fréquences de groupe. C'est ce qu'on appelle un histogramme. Après normalisation à la largeur de la plage, l'histogramme représentera une densité de distribution empirique d'une valeur aléatoire. Utilisons l'expression empirique décrite dans les "Statistics for Traders" pour déterminer un nombre optimal de sections pour dessiner l'histogramme :
où L est le nombre requis de section, N est le volume d'échantillonnage et e est l'aplatissement.
Ci-dessous, vous pouvez trouver le dHist(), qui détermine le nombre de sections, calcule le nombre d'éléments dans chacune d'elles et normalise les fréquences de groupe obtenues.
struct statParam { double mean; double median; double var; double stdev; double skew; double kurt; }; //---------------------------------------------------------------------------- int dHist(const double &x[],double &histo[],const statParam &sp) { int i,k,n,nbar; double a[],max,s,xmin; if(!ArrayIsDynamic(histo)) // Error { Print("Function dHist() error!"); return(-1); } n=ArraySize(x); if(n<4) // Error { Print("Function dHist() error!"); return(-1); } nbar=(sp.kurt+1.5)*MathPow(n,0.4)/6.0; if((nbar&0x01)==0)nbar--; if(nbar<5)nbar=5; // Number of bars ArrayResize(a,n); ArrayCopy(a,x); max=0.0; for(i=0;i<n;i++) { a[i]=(a[i]-sp.mean)/sp.stdev; // Normalization if(MathAbs(a[i])>max)max=MathAbs(a[i]); } xmin=-max; s=2.0*max*n/nbar; ArrayResize(histo,nbar+2); ArrayInitialize(histo,0.0); histo[0]=0.0;histo[nbar+1]=0.0; for(i=0;i<n;i++) { k=(a[i]-xmin)/max/2.0*nbar; if(k>(nbar-1))k=nbar-1; histo[k+1]++; } for(i=0;i<nbar;i++)histo[i+1]/=s; return(1); }
L'adresse du tableau x[] est transmise à la fonction. Elle comporte la séquence initiale. Le contenu du tableau n'est pas modifié suite à l'exécution de la fonction. Le paramètre suivant est le lien vers le tableau dynamique histo[], où les valeurs calculées seront stockées. Le nombre d'éléments de ce tableau correspondra au nombre de sections utilisées pour le calcul plus deux éléments.
Un élément comportant une valeur nulle est ajouté au début et à la fin du tableau histo[]. Le dernier paramètre est l'adresse de la structure statParam qui doit comporter les valeurs précédemment calculées des paramètres qui y sont stockés. Dans le cas où le tableau histo[] transmis à la fonction n'est pas un tableau dynamique ou le tableau d'entrée x[] comporte moins de quatre éléments, la fonction arrête son exécution et renvoie -1.
Une fois que vous avez tracé un histogramme des valeurs obtenues, vous pouvez estimer visuellement si l'échantillonnage correspond à la loi de distribution normale. Pour une représentation graphique plus visuelle de la correspondance avec la loi normale de distribution, nous pouvons tracer un graphique avec l'échelle de probabilité normale (Normal Probability Plot) en plus de l'histogramme.
Diagramme de Probabilité Normale
L'idée principale de dessiner un tel graphique est que l'axe X doit être tendu de sorte que les valeurs affichées d'une séquence avec une distribution normale se trouvent sur la même ligne. De cette façon, l'hypothèse de normalité peut être graphiquement vérifiée. Vous pouvez trouver des informations plus détaillées sur ce type de graphiques ici : «Normal probability plot«ou»e-Handbook of Statistical Methods»
Pour calculer les valeurs requises pour tracer le graphique de probabilité normale, la fonction dRankit() illustrée ci-dessous est utilisée.
struct statParam { double mean; double median; double var; double stdev; double skew; double kurt; }; //---------------------------------------------------------------------------- int dRankit(const double &x[],double &resp[],double &xscale[],const statParam &sp) { int i,n; double np; if(!ArrayIsDynamic(resp)||!ArrayIsDynamic(xscale)) // Error { Print("Function dHist() error!"); return(-1); } n=ArraySize(x); if(n<4) // Error { Print("Function dHist() error!"); return(-1); } ArrayResize(resp,n); ArrayCopy(resp,x); ArraySort(resp); for(i=0;i<n;i++)resp[i]=(resp[i]-sp.mean)/sp.stdev; ArrayResize(xscale,n); xscale[n-1]=MathPow(0.5,1.0/n); xscale[0]=1-xscale[n-1]; np=n+0.365; for(i=1;i<(n-1);i++)xscale[i]=(i+1-0.3175)/np; for(i=0;i<n;i++)xscale[i]=ltqnorm(xscale[i]); return(1); } //---------------------------------------------------------------------------- double A1 = -3.969683028665376e+01, A2 = 2.209460984245205e+02, A3 = -2.759285104469687e+02, A4 = 1.383577518672690e+02, A5 = -3.066479806614716e+01, A6 = 2.506628277459239e+00; double B1 = -5.447609879822406e+01, B2 = 1.615858368580409e+02, B3 = -1.556989798598866e+02, B4 = 6.680131188771972e+01, B5 = -1.328068155288572e+01; double C1 = -7.784894002430293e-03, C2 = -3.223964580411365e-01, C3 = -2.400758277161838e+00, C4 = -2.549732539343734e+00, C5 = 4.374664141464968e+00, C6 = 2.938163982698783e+00; double D1 = 7.784695709041462e-03, D2 = 3.224671290700398e-01, D3 = 2.445134137142996e+00, D4 = 3.754408661907416e+00; //---------------------------------------------------------------------------- double ltqnorm(double p) { int s=1; double r,x,q=0; if(p<=0||p>=1){Print("Function ltqnorm() error!");return(0);} if((p>=0.02425)&&(p<=0.97575)) // Rational approximation for central region { q=p-0.5; r=q*q; x=(((((A1*r+A2)*r+A3)*r+A4)*r+A5)*r+A6)*q/(((((B1*r+B2)*r+B3)*r+B4)*r+B5)*r+1); return(x); } if(p<0.02425) // Rational approximation for lower region { q=sqrt(-2*log(p)); s=1; } else //if(p>0.97575) // Rational approximation for upper region { q = sqrt(-2*log(1-p)); s=-1; } x=s*(((((C1*q+C2)*q+C3)*q+C4)*q+C5)*q+C6)/((((D1*q+D2)*q+D3)*q+D4)*q+1); return(x); }
L'adresse du tableau x[] est introduite dans la fonction. Le tableau comprend la séquence initiale. Les paramètres suivants sont des références aux tableaux de sortie resp[] et xscale[]. Après l'exécution de la fonction, les valeurs utilisées dans le dessin du graphique sur les axes X et Y sont respectivement écrites dans les tableaux. Ensuite, l'adresse de la structure statParam est transmise à la fonction. Elle doit comprendre les valeurs précédemment calculées des paramètres statistiques de la séquence d'entrée. En cas d'erreur, la fonction renvoie -1.
Lors de la formation des valeurs pour l'axe X, la fonction ltqnorm() est appelée. Elle calcule la fonction intégrale inverse de la distribution normale. L'algorithme utilisé pour le calcul est tiré de " "An algorithme pour calculer la fonction de distribution cumulative normale inverse".
Quatre Graphiques
Auparavant, j'ai mentionné la fonction dStat() où les valeurs des paramètres statistiques sont calculées. Répétons brièvement leur signification.
Dispersion (variance) – la valeur moyenne des carrés de l'écart d'une valeur aléatoire par rapport à son espérance mathématique (valeur moyenne). Paramètre qui indique l'ampleur de l'écart d'une valeur aléatoire par rapport à son centre de distribution. Plus la valeur de ce paramètre est élevée, plus l'écart est important.
Ecart type - puisque la dispersion est mesurée comme le carré d'une valeur aléatoire, l'écart type est souvent utilisé comme une caractéristique plus évidente de la dispersion. Elle est égale à la racine carrée de la dispersion.
Asymétrie - si nous dessinons une courbe de distribution d'une valeur aléatoire, l'asymétrie montrera à quel point la courbe de densité de probabilité est asymétrique par rapport au centre de distribution. Si la valeur d'asymétrie est supérieure à zéro, la courbe de densité de probabilité affiche une pente gauche raide et une pente droite plate. Si la valeur d'asymétrie est négative, alors la pente de gauche est plate et celle de droite est raide. Lorsque la courbe de densité de probabilité est symétrique par rapport au centre de distribution, l'asymétrie est égale à zéro.
Le coefficient d'aplatissement (kurtose) - il décrit la netteté d'un pic de la courbe de densité de probabilité et la raideur des pentes des queues de distribution. Plus le pic de la courbe près du centre de distribution est net, plus la valeur de l'aplatissement est élevée.
Malgré le fait que les paramètres statistiques mentionnés décrivent une séquence en détail, vous pouvez souvent caractériser une séquence de manière plus simple - sur la base du résultat d'estimations représentées sous forme graphique. Par exemple, un graphique ordinaire d'une séquence peut considérablement compléter une vue obtenue lors de l'analyse des paramètres statistiques.
Précédemment dans l'article, j'ai mentionné les fonctions dHist() et dRankit() qui permettent de préparer des données pour dessiner un histogramme ou un graphique avec l'échelle de probabilité normale. L'affichage de l'histogramme et du graphique de distribution normale avec le graphique ordinaire sur la même feuille, vous permet de déterminer visuellement les principales caractéristiques de la séquence analysée.
Ces trois graphiques répertoriés doivent être complétés par un autre - le graphique avec les valeurs actuelles de la séquence sur l'axe Y et ses précédentes valeurs sur l'axe X. Un tel graphique est appeléLag Plot». S'il existe une forte corrélation entre des indications adjacentes, les valeurs d'un échantillonnage s'étireront en ligne droite. Et s'il n'y a pas de corrélation entre des indications adjacentes, par exemple, lors de l'analyse d'une séquence aléatoire, alors les valeurs seront dispersées sur tout le graphique.
Pour une rapide estimation d'un échantillonnage initial, je suggère de tracer quatre graphiques sur une seule feuille et d'y afficher les valeurs calculées du paramètre statistique. Ce n'est pas une nouvelle idée; vous pouvez en savoir plus sur l'utilisation de l'analyse des quatre graphiques mentionnés ici : "4-Plot".
A la fin de l'article, il y a la section "Files" comportant le script s4plot.mq5,qui dessine ces quatre graphiques sur une seule feuille. Le tableau dat[] est créé dans la fonction OnStart() du script. Il comporte la séquence initiale. Ensuite, les fonctions dStat(), dHist() et dRankit() sont appelées en conséquence pour le calcul des données nécessaires au traçage des graphiques. La fonction vis4plot() est appelée ensuite. EIle crée un fichier texte avec les commandes gnuplot sur la base des données calculées, puis elle appelle l'application pour dessiner les graphiques dans une fenêtre séparée.
Il ne sert à rien de montrer l'intégralité du code du script dans l'article, puisque les dStat(), dHist() et dRankit() ont précédemment été décrits, la fonction vis4plot(), qui crée une séquence de commandes gnuplot, ne présente pas toutes les particularités significatives, et la description des commandes gnuplot sort des limites du sujet de l'article. En plus de cela, vous pouvez utiliser une autre méthode pour dessiner les graphiques au lieu de l'application gnuplot.
Ne montrons donc qu'une partie du s4plot.mq5 - sa fonction OnStart().
//---------------------------------------------------------------------------- // Script program start function //---------------------------------------------------------------------------- void OnStart() { int i; double dat[128],histo[],rankit[],xrankit[]; statParam sp; MathSrand(1); for(i=0;i<ArraySize(dat);i++) dat[i]=MathRand(); if(dStat(dat,sp)==-1)return; if(dHist(dat,histo,sp)==-1)return; if(dRankit(dat,rankit,xrankit,sp)==-1)return; vis4plot(dat,histo,rankit,xrankit,sp,6); }
Dans cet exemple, une séquence aléatoire est utilisée pour remplir le tableau dat[] avec les données initiales à l'aide de la fonction MathRand(). L'exécution du script doit produire les résultats suivants :
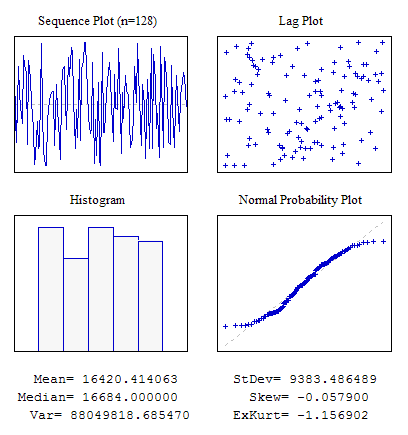
Figure 3. Quatre graphiques Script s4plot.mq5
Vous devez faire attention au dernier paramètre de la fonction vis4plot(). Elle est chargée du format des valeurs numériques sorties. Dans cet exemple, les valeurs sont sorties avec six décimales. Ce paramètre est le même que celui qui détermine le format dans la fonction DoubleToString().
Si les valeurs de la séquence d'entrée sont trop petites ou trop grandes, vous pouvez utiliser le format scientifique pour un affichage plus évident. Pour ce faire, définissez ce paramètre sur -5, par exemple. La valeur -5 est définie par défaut pour la fonction vis4plot().
Pour démontrer l'évidence de la méthode des quatre graphiques affichant les particularités d'une séquence, nous avons besoin d'un générateur de telles séquences.
Générateur d'une séquence pseudo-aléatoire
La classe RNDXor128 est destinée à générer des séquences pseudo-aléatoires.
Ci-dessous, il y a le code source du fichier d'inclusion décrivant cette classe.
//----------------------------------------------------------------------------------- // RNDXor128.mqh // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #include <Object.mqh> //----------------------------------------------------------------------------------- // Generation of pseudo-random sequences. The Xorshift RNG algorithm // (George Marsaglia) with the 2**128 period of initial sequence is used. // uint rand_xor128() // { // static uint x=123456789,y=362436069,z=521288629,w=88675123; // uint t=(x^(x<<11));x=y;y=z;z=w; // return(w=(w^(w>>19))^(t^(t>>8))); // } // Methods: // Rand() - even distribution withing the range [0,UINT_MAX=4294967295]. // Rand_01() - even distribution within the range [0,1]. // Rand_Norm() - normal distribution with zero mean and dispersion one. // Rand_Exp() - exponential distribution with the parameter 1.0. // Rand_Laplace() - Laplace distribution with the parameter 1.0 // Reset() - resetting of all basic values to initial state. // SRand() - setting new basic values of the generator. //----------------------------------------------------------------------------------- #define xor32 xx=xx^(xx<<13);xx=xx^(xx>>17);xx=xx^(xx<<5) #define xor128 t=(x^(x<<11));x=y;y=z;z=w;w=(w^(w>>19))^(t^(t>>8)) #define inidat x=123456789;y=362436069;z=521288629;w=88675123;xx=2463534242 class RNDXor128:public CObject { protected: uint x,y,z,w,xx,t; uint UINT_half; public: RNDXor128() {UINT_half=UINT_MAX>>1;inidat;}; double Rand() {xor128;return((double)w);}; int Rand(double& a[],int n) {int i;if(n<1)return(-1); if(ArraySize(a)<n)return(-2); for(i=0;i<n;i++){xor128;a[i]=(double)w;} return(0);}; double Rand_01() {xor128;return((double)w/UINT_MAX);}; int Rand_01(double& a[],int n) {int i;if(n<1)return(-1); if(ArraySize(a)<n)return(-2); for(i=0;i<n;i++){xor128;a[i]=(double)w/UINT_MAX;} return(0);}; double Rand_Norm() {double v1,v2,s,sln;static double ra;static uint b=0; if(b==w){b=0;return(ra);} do{ xor128;v1=(double)w/UINT_half-1.0; xor128;v2=(double)w/UINT_half-1.0; s=v1*v1+v2*v2; } while(s>=1.0||s==0.0); sln=MathLog(s);sln=MathSqrt((-sln-sln)/s); ra=v2*sln;b=w; return(v1*sln);}; int Rand_Norm(double& a[],int n) {int i;if(n<1)return(-1); if(ArraySize(a)<n)return(-2); for(i=0;i<n;i++)a[i]=Rand_Norm(); return(0);}; double Rand_Exp() {xor128;if(w==0)return(DBL_MAX); return(-MathLog((double)w/UINT_MAX));}; int Rand_Exp(double& a[],int n) {int i;if(n<1)return(-1); if(ArraySize(a)<n)return(-2); for(i=0;i<n;i++)a[i]=Rand_Exp(); return(0);}; double Rand_Laplace() {double a;xor128; a=(double)w/UINT_half; if(w>UINT_half) {a=2.0-a; if(a==0.0)return(-DBL_MAX); return(MathLog(a));} else {if(a==0.0)return(DBL_MAX); return(-MathLog(a));}}; int Rand_Laplace(double& a[],int n) {int i;if(n<1)return(-1); if(ArraySize(a)<n)return(-2); for(i=0;i<n;i++)a[i]=Rand_Laplace(); return(0);}; void Reset() {inidat;}; void SRand(uint seed) {int i;if(seed!=0)xx=seed; for(i=0;i<16;i++){xor32;} xor32;x=xx;xor32;y=xx; xor32;z=xx;xor32;w=xx; for(i=0;i<16;i++){xor128;}}; int SRand(uint xs,uint ys,uint zs,uint ws) {int i;if(xs==0&&ys==0&&zs==0&&ws==0)return(-1); x=xs;y=ys;z=zs;w=ws; for(i=0;i<16;i++){xor128;} return(0);}; }; //-----------------------------------------------------------------------------------
L'algorithme utilisé pour générer une séquence aléatoire est décrit en détail dans l'article "Xorshift RNGs" de George Marsaglia (voir le xorshift.zip en fin d'article). Les méthodes de la classe RNDXor128 sont décrites dans le fichier RNDXor128.mqh. En s’appuyant sur cette classe, vous pouvez obtenir des séquences avec une distribution paire, normale ou exponentielle ou avec une distribution de Laplace (double exponentielle).
Vous devez faire attention au fait que lorsqu'une instance de la classe RNDXor128 est créée, les valeurs de base de la séquence sont définies sur l'état initial. Ainsi, contrairement à l'appel de la fonction MathRand() à chaque nouveau démarrage d'un script ou d'un indicateur utilisant RNDX ou 128, une seule et même séquence sera générée. Identique à l'appel de MathSrand() et puis MathRand().
Exemples de Séquences
Ci-dessous, à titre d'exemple, vous trouverez les résultats obtenus lors de l'analyse de séquences extrêmement différentes les unes des autres avec leurs propriétés.
Exemple 1. Une Séquence Aléatoire avec la Loi de Distribution Paire.
#include "RNDXor128.mqh" RNDXor128 Rnd; //---------------------------------------------------------------------------- void OnStart() { int i; double dat[512]; for(i=0;i<ArraySize(dat);i++) dat[i]=Rnd.Rand_01(); ... }
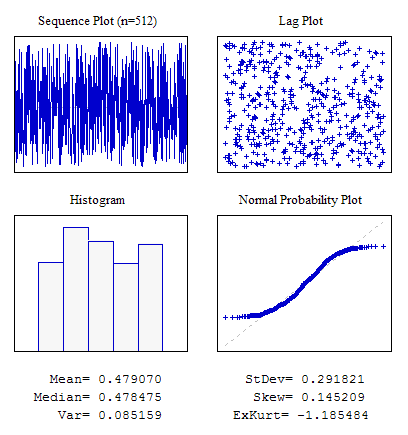
Figure 4. Distribution paire
Exemple 2. Une Séquence Aléatoire avec la Loi Normale de Distribution.
#include "RNDXor128.mqh" RNDXor128 Rnd; //---------------------------------------------------------------------------- void OnStart() { int i; double dat[512]; for(i=0;i<ArraySize(dat);i++) dat[i]=Rnd.Rand_Norm(); ... }
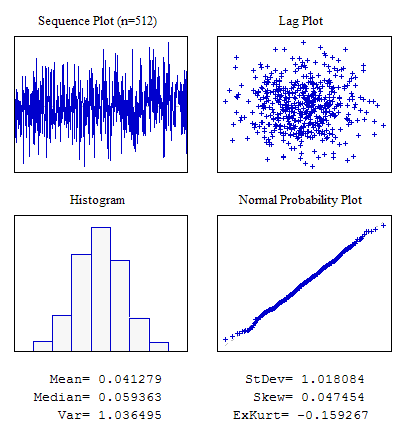
Figure 5. Distribution Normale
Exemple 3 Une séquence Aléatoire avec la Loi de Distribution Exponentielle.
#include "RNDXor128.mqh" RNDXor128 Rnd; //---------------------------------------------------------------------------- void OnStart() { int i; double dat[512]; for(i=0;i<ArraySize(dat);i++) dat[i]=Rnd.Rand_Exp(); ... }
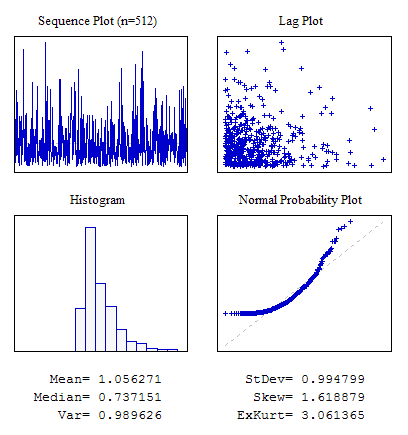
Figure 6. Distribution exponentielle
Example 4 Une Séquence Aléatoire avec Distribution de Laplace.
#include "RNDXor128.mqh" RNDXor128 Rnd; //---------------------------------------------------------------------------- void OnStart() { int i; double dat[512]; for(i=0;i<ArraySize(dat);i++) dat[i]=Rnd.Rand_Laplace(); ... }
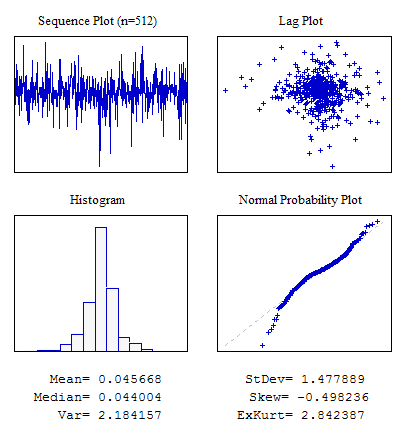
Figure 7. Laplace Distribution
Example 5 Séquence Sinusoïdale
//---------------------------------------------------------------------------- void OnStart() { int i; double dat[512]; for(i=0;i<ArraySize(dat);i++) dat[i]=MathSin(2*M_PI/4.37*i); ... }
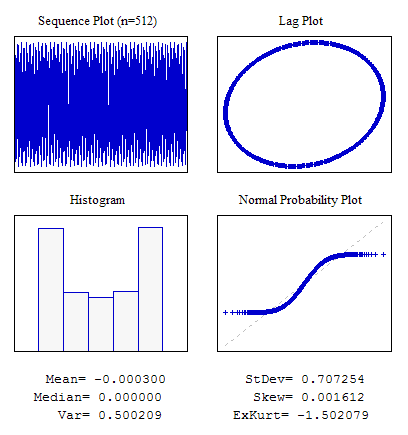
Figure 8. Séquence sinusoïdale
Exemple 6. Une Séquence avec une Corrélation Visible entre des Indications Adjacentes.
#include "RNDXor128.mqh" RNDXor128 Rnd; //---------------------------------------------------------------------------- void OnStart() { int i; double dat[512],a; for(i=0;i<ArraySize(dat);i++) {a+=Rnd.Rand_Laplace();dat[i]=a;} ... }
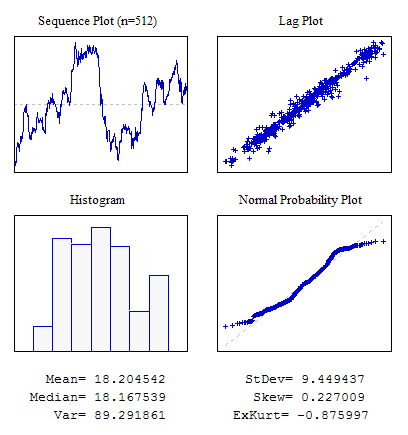
Figure 9. Corrélation entre indications adjacentes
Conclusion
L’élaboration d'algorithmes de programme qui implémentent tout type de calcul est toujours une tâche ardue à accomplir. La raison en est la nécessité de prendre en compte un grand nombre d'exigences pour minimiser les erreurs qui peuvent survenir lors de l'arrondi, de la troncature et du débordement de variables.
Lors de la rédaction des exemples de l'article, je n'ai effectué aucune analyse des algorithmes du programme. Lors de l'écriture de la fonction, les algorithmes mathématiques ont été "directement implémentés. Ainsi, si vous comptez les utiliser dans des applications "sérieuses", vous devez analyser leur stabilité et précision.
L'article ne décrit pas du tout les caractéristiques de l'application gnuplot. Ces questions dépassent le cadre de cet article. Quoi qu'il en soit, je voudrais mentionner que gnuplot peut être adapté pour une utilisation conjointe avec MetaTrader 5. Pour cela, vous devez apporter quelques corrections à son code source et le recompiler. De plus, la manière de passer des commandes à gnuplot à l'aide d'un fichier n'est probablement pas une manière optimale, puisque l'interaction avec gnuplot peut être organisée via une interface de programmation.
Fichiers
- erremove.mq5 – exemple de script qui exclut les erreurs d'un échantillonnage.
- function_dstat.mq5 – fonction de calcul des paramètres statistiques.
- function_dhist.mq5 - fonction de calcul des valeurs de l'histogramme.
- function_drankit.mq5 - fonction de calcul des valeurs utilisées lors de l'élaboration d'un graphique avec l'échelle de distribution normale.
- s4plot.mq5 - exemple d'un script qui dessine quatre graphiques sur une seule feuille.
- RNDXor128.mqh – classe du générateur d'une séquence aléatoire.
- xorshift.zip - George Marsaglia. "Xorshift RNGs".
Traduit du russe par MetaQuotes Ltd.
Article original : https://www.mql5.com/ru/articles/273
Utiliser des Cartes de Caractéristiques Auto-Organisatrices (Kohonen Maps) dans MetaTrader 5
Traçage, Débogage et Analyse Structurelle du Code Source
Création de Critères Personnalisés d’Optimisation des Expert Advisors
Distributions de Probabilités Statistiques dans MQL5
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Vous acceptez la politique du site Web et les conditions d'utilisation