MetaTrader 5 / 예
English Русский 中文 Español Deutsch 日本語 Português Français Italiano Türkçe
통계적 추정

통계적 추정

MetaTrader 5 — 예 | 4 8월 2021, 17:24
92 0
Victor
Victor

들어가며

오늘날, 여러분은 종종 경제 지표, 가격 시리즈의 예측, 모델의 선택 및 적절성 추정 등과 관련된 주제에 대해 쓰여진 기사와 출판물을 볼 수 있습니다. 그러나 대부분의 경우, 추론은 독자가 수학 통계의 방법을 알고 있고 분석된 시퀀스의 통계적 모수를 쉽게 추정할 수 있다는 전제를 깔고 시작하기 마련입니다.

대부분의 수학적 모델과 방법은 서로 다른 가정을 기반으로 하기 때문에 시퀀스의 통계적 모수 추정은 매우 중요합니다. 예를 들어 분포 법칙의 정규성이나 분산 값 또는 기타 모수가 있습니다. 따라서 시계열 분석 및 예측 시 주요 통계 모수를 빠르고 명확하게 추정할 수 있는 간단하고 편리한 도구가 필요합니다. 이 문서에서 우리는 그런 툴을 만들어 볼 것입니다.

이 문서는 랜덤 시퀀스의 가장 간단한 통계적 모수와 시각적 분석의 여러 메소드에 대해 설명할 것입니다. MQL5에서는 이러한 방법의 구현과 Gnuplot 어플리케이션을 사용한 계산 결과의 시각화 방법을 제공합니다. 본 문서는 매뉴얼이나 참고 자료가 아닙니다; 그렇기 때문에 친숙한 표현이나 정의를 이용될 수 있습니다.


샘플 패러미터 분석하기

시간 내에 끝없이 존재하는 정지된 프로세스가 있다고 가정하며, 이것을 이항 표본 시퀀스로 나타낼 수 있습니다. 이 표본 시퀀스르 일반 모집단이라고 부르겠습니다. 일반 모집단에서 선택한 표본의 일부를 일반 모집단의 표본 추출 또는 N개 표본 추출이라고 한다. 또한 실제 모수가 알려져 있지 않으므로 유한 샘플링을 기반으로 추정합니다.


아웃라이어 배제하기

모수의 통계적 추정을 시작하기 전에 샘플에 큰 오차(아웃라이어)가 포함되어 있으면 추정 정확도가 내려갈 수 있다는 점을 염두에 두어야합니다. 샘플링 크기가 작으면 작을 경우 추정 정확도에 큰 영향을 미칩니다. 아웃라이어는 분포 중간과 비교했을 때 비정상적으로 차이가 나는 값입니다. 그러한 편차는 통계 데이터를 수집하고 시퀀스를 구성하는 동안 나타나는 거의 가능성이 없는 다른 사건 및 오류에 의해 발생할 수 있습니다.

대부분의 경우 값이 아웃라이어인지 아니면 분석된 프로세스에 속하는지 여부를 명확히 탐지하는 것이 불가능하기 때문에 아웃라이어를 필터링할 것인가 말 것인가 판단하기 힘듭니다. 그러면 아웃라이어가 감지되고 이를 필터링하기로 결정하면 이러한 오류 값을 어떻게 해야 할까요?라는 의문이 생깁니다. 가장 논리적인 버전은 통계적 특성의 추정 정확도를 높일 수 있는 표본 추출에서 제외되지만, 타임 시퀀스를 다룰 때는 샘플 추출에서 아웃라이어를 제외하는 데 주의해야 합니다.

샘플 추출에서 아웃라이어를 배제하고 최소한 검출까지는 하려면 다음의 책에서 소개된 알고리즘을 이용해봅시다 - "트레이더를 위한 통계학" S.V. 불라셰프(Bulashev).

이 알고리즘에 따라 분포 중심 추정치 5개를 계산해야 합니다.

  1. 중간값;
  2. 50% 사분위간 범위의 중심 (midquartile range, MQR);
  3. 전체 샘플링의 산술 평균;
  4. 50% 사분위간 범위에서 산술 평균 (interquartile mean, IQM);
  5. 그 후 범위의 중심(중범위, 미드레인지) - 샘플링에서 최대값과 최소값의 평균값으로 결정됩니다.

그런 다음 분포 중심 추정의 결과를 오름차순으로 정렬하고 평균값 또는 세 번째 값을 분포 중심 Xcen으로 선택합니다. . 따라서 선택한 추정치는 아웃라이어의 영향을 최소로 받는 것으로 보입니다.

추가적으로, 분포 중심 추정을 통해 얻어진 Xcen을 이용하여 표준편차 s와, 경험적 공식에 따른 초과 K 및 중도 절단 비율을 계산해봅시다:

 

N는 표본 추출 과정에서 얻은 표본 수 (표본 부피).

그러면 범위를 벗어나는 값은 다음과 같습니다:

 

아웃라이어로 계산되므로 표본 추출에서 제외해야 합니다.

이 방법은 "트레이더를 위한 통계학" 책에 자세하게 설명되어있으므로 빠르게 알고리즘을 구현해봅시다. 아웃라이어를 탐지하고 제외할 수 있는 알고리즘은 erremove() 함수에 구현됩니다.

아래에서 이 기능을 테스트하기 위해 작성된 스크립트를 확인할 수 있습니다.

//----------------------------------------------------------------------------
//                                                                erremove.mq5
//                                   Copyright 2011, MetaQuotes Software Corp.
//                                                         https://www.mql5.com
//----------------------------------------------------------------------------
#property copyright "Copyright 2011, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"

#import "shell32.dll"
bool ShellExecuteW(int hwnd,string lpOperation,string lpFile,
                  string lpParameters,string lpDirectory,int nShowCmd);
#import
//----------------------------------------------------------------------------
// Script program start function
//----------------------------------------------------------------------------
void OnStart()
  {
  int i;
  double dat[100];
  double y[];
  
  srand(1);
  for(i=0;i<ArraySize(dat);i++)dat[i]=rand()/16000.0;
  
  dat[25]=3;           // Make Error !!!
  
  erremove(dat,y,1);
  
  }
//----------------------------------------------------------------------------
int erremove(const double &x[],double &y[],int visual=1)
  {
  int i,m,n;
  double a[],b[5];
  double dcen,kurt,sum2,sum4,gs,v,max,min;
  
  if(!ArrayIsDynamic(y))                           // Error
    {
    Print("Function erremove() error!");
    return(-1);
    }
  n=ArraySize(x);
  if(n<4)                                          // Error
    {
    Print("Function erremove() error!");
    return(-1);
    }
  ArrayResize(a,n);
  ArrayCopy(a,x);
  ArraySort(a);
  b[0]=(a[0]+a[n-1])/2.0;                          // Midrange
  m=(n-1)/2;
  b[1]=a[m];                                       // Median
  if((n&0x01)==0)b[1]=(b[1]+a[m+1])/2.0;
  m=n/4;
  b[2]=(a[m]+a[n-m-1])/2.0;                        // Midquartile range
  b[3]=0;
  for(i=m;i<n-m;i++)b[3]+=a[i];                    // Interquartile mean(IQM)
  b[3]=b[3]/(n-2*m);
  b[4]=0;
  for(i=0;i<n;i++)b[4]+=a[i];                      // Mean
  b[4]=b[4]/n;
  ArraySort(b);
  dcen=b[2];                                       // Distribution center
  sum2=0; sum4=0;  
  for(i=0;i<n;i++)
    {
    a[i]=a[i]-dcen;
    v=a[i]*a[i];
    sum2+=v;
    sum4+=v*v;
    }
  if(sum2<1.e-150)kurt=1.0;
  kurt=((n*n-2*n+3)*sum4/sum2/sum2-(6.0*n-9.0)/n)*(n-1.0)/(n-2.0)/(n-3.0); // Kurtosis
  if(kurt<1.0)kurt=1.0;
  gs=(1.55+0.8*MathLog10((double)n/10.0)*MathSqrt(kurt-1))*MathSqrt(sum2/(n-1));
  max=dcen+gs;
  min=dcen-gs;
  m=0;
  for(i=0;i<n;i++)if(x[i]<=max&&x[i]>=min)a[m++]=x[i];
  ArrayResize(y,m);
  ArrayCopy(y,a,0,0,m);

  if(visual==1)vis(x,dcen,min,max,n-m);
  
  return(n-m);  
  }
//----------------------------------------------------------------------------
void vis(const double &x[],double dcen,double min,double max,int numerr)
  {
  int i;
  double d,yma,ymi;
  string str;
  
  yma=x[0];ymi=x[0];
  for(i=0;i<ArraySize(x);i++)
    {
    if(yma<x[i])yma=x[i];
    if(ymi>x[i])ymi=x[i];
    }
  if(yma<max)yma=max;
  if(ymi>min)ymi=min;
  d=(yma-ymi)/20.0;
  yma+=d;ymi-=d;
  str="unset key\n";
  str+="set title 'Sequence and error levels (number of errors = "+
        (string)numerr+")' font ',10'\n";
  str+="set yrange ["+(string)ymi+":"+(string)yma+"]\n";
  str+="set xrange [0:"+(string)ArraySize(x)+"]\n";
  str+="plot "+(string)dcen+" lt rgb 'green',";
  str+=(string)min+ " lt rgb 'red',";
  str+=(string)max+ " lt rgb 'red',";
  str+="'-' with line lt rgb 'dark-blue'\n";
  for(i=0;i<ArraySize(x);i++)str+=(string)x[i]+"\n";
  str+="e\n";
  if(!saveScript(str)){Print("Create script file error");return;}
  if(!grPlot())Print("ShellExecuteW() error");
  }
//----------------------------------------------------------------------------
bool grPlot()
  {
  string pnam,param;
  
  pnam="GNUPlot\\binary\\wgnuplot.exe";
  param="-p MQL5\\Files\\gplot.txt";
  return(ShellExecuteW(NULL,"open",pnam,param,NULL,1));
  }
//----------------------------------------------------------------------------
bool saveScript(string scr1="",string scr2="")
  {
  int fhandle;
  
  fhandle=FileOpen("gplot.txt",FILE_WRITE|FILE_TXT|FILE_ANSI);
  if(fhandle==INVALID_HANDLE)return(false);
  FileWriteString(fhandle,"set terminal windows enhanced size 560,420 font 8\n");
  FileWriteString(fhandle,scr1);
  if(scr2!="")FileWriteString(fhandle,scr2);
  FileClose(fhandle);
  return(true);
  }
//----------------------------------------------------------------------------

erremove() 함수를 들여다봅시다 함수의 첫 번째 패러미터로 분석된 샘플링의 값이 저장되는 어레이 x[]의 어드레스를 전달합니다. 샘플링 량은 최소 4개 이상이어야합니다 x[] 어레이의 크기가 샘플 크기와 동일하다고 가정하기 때문에 샘플 부피의 N 값이 전달되지 않습니다. x[] 어레이에 있는 데이터는 함수 실행의 결과로 변경되지 않습니다. 

다음 패러미터는 y[] 어레이의 어드레스입니다. 함수를 성공적으로 실행할 경우 이 어레이에는 특이치가 제외된 입력 시퀀스가 포함됩니다. y[] 어레이의 크기가 샘플링에서 제외된 값의 수만큼 x[] 어레이의 크기보다 작습니다. y[] 어레이는 동적 어레이로 선언되어야 합니다. 그렇지 않으면 함수 본문에서 어레이의 크기를 변경할 수 없습니다.

마지막(옵션) 패라미터는 계산 결과의 시각화를 담당하는 플래그입니다. 값이 1(기본값)이면 함수 실행이 종료되기 전에 별도의 창에 입력 시퀀스, 분포 중심선 및 범위 한계(이 값을 벗어난 값은 이상치로 간주) 정보를 표시하는 차트가 그려집니다.

차트 그리기 방법은 나중에 설명합니다. 실행에 성공하면 함수는 샘플링에서 제외된 값의 수를 반환하고, 오류가 발생하면 -1을 반환합니다. 오류 값(아웃라이어)이 발견되지 않으면 함수는 0을 반환하고 y[] 어레이의 시퀀스는 x[]와 같습니다.

함수 시작 부분에서 정보가 x[]에서 a[] 어레이로 복사된 다음 오름차순으로 정렬되고 분포 중심 추정치 5개가 만들어집니다.

중간 범위 (midrange)는 정렬된 어레이 a[]의 양 끝 값의 합을 2로 나눈 값으로 결정됩니다.

중간값은 샘플링N의 홀수 볼륨들을 아래와 같이 다룸으로서 얻어집니다:

 

짝수 볼륨에 대해서는:

 

정렬된 어레이 a[]의 인덱스가 0부터 시작하는 것을 고려하면 다음을 얻을 수 있습니다:

m=(n-1)/2;
median=a[m];                                       
if((n&0x01)==0)b[1]=(median+a[m+1])/2.0;

50% 사분범위의 중앙 (midquartile range, MQR):

 

M=N/4 (정수 나눗셈).

정렬된 어레이 a[]일 경우 이를 얻습니다:

m=n/4;
MQR=(a[m]+a[n-m-1])/2.0;               // Midquartile range

50% 사분범위의 산술적 평균 (interquartile mean, IQM). 표본의 25%는 표본의 양쪽에서 절단되며, 나머지 50%는 산술평균의 계산에 사용된다.

 

M=N/4 (정수 나눗셈).

m=n/4; IQM=0;
for(i=m;i<n-m;i++)IQM+=a[i];
IQM=IQM/(n-2*m);                       // Interquartile mean(IQM)

산술 평균 (mean)은 전체 샘플으로 판단됩니다.

결정된 각 값은 b[] 어레이에 기록된 다음 배열이 오름차순으로 정렬됩니다. b[2] 어레이의 요소 값이 분포의 중심으로 선택됩니다. 또한 이 값을 사용하여 산술 평균과 초과 계수의 치우침 없는 추정치를 계산할 것이며, 계산 알고리즘은 나중에 설명될 것입니다.

얻어진 추정치는 아웃라이어 검출을 위한 범위의 한계와 차단 계수를 계산하는 데 사용됩니다(위 식 참조). 결국, 제외된 특이치가 있는 시퀀스는 y[] 어레이에서 형성되며, 그래프. 평균 및 초과 계수를 그리기 위해 vis() 함수가 호출됩니다. 이 기사에 사용된 시각화 방법을 간단히 살펴보겠습니다.


시각화

계산 결과를 표시하기 위해 다양한 2D 및 3D 그래프를 만들기 위한 무료 어플리케이션 gnuplot 을 사용합니다. Gnuplot은 별도의 창에 차트를 표시하거나 다른 그래픽 형식의 파일에 쓸 수 있습니다. 플로팅 차트의 커맨드는 사전 준비된 텍스트 파일에서 실행할 수 있습니다. gnuplot의 공식 홈페이지는 다음과 같습니다 - gnuplot.sourceforge.net. 이 프로그램은 여러 플랫폼을 지원하며 이며 특정 플랫폼에 대해 컴파일된 소스 코드 파일과 이진 파일로 배포됩니다.

이 문서에서 다룬 예시는 Windows XP SP3 및 4.2.2 버전의 gnuplot에서 테스트한 것입니다. gp442win32.zip 파일은 http://sourceforge.net/projects/gnuplot/files/gnuplot/4.4.2/에서 다운로드 받을 수 있습니다. 다른 버전이나 빌드는 테스트해보지 않았습니다.

gp442win32.zip 아카이브를 다운로드 받았다면 압축해제하십시오. \gnuplot 폴더가 생성되고 응용 프로그램, 도움말 파일, 문서 및 예가 포함됩니다. 응용 프로그램과 상호 작용하려면 전체 \gnuplot 폴더를 MetaTrader 5 클라이언트 터미널의 루트 폴더에 저장하십시오.

\gnuplot 

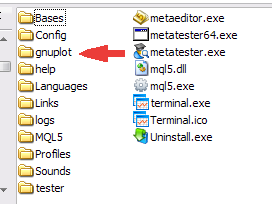
 1번 그림. \gnuplot 폴더 배치

폴더가 이동되면 gnuplot 응용 프로그램의 작동 가능 여부를 변경할 수 있습니다. 이렇게 하려면 \gnuplot\binary\wgnuplot.exe 파일을 실행한 다음 "gnuplot>" 명령 프롬프트가 나타나면 "plot sin(x)" 커맨드를 입력하십시오. 그 결과 sin(x) 함수가 그려진 창이 나타나야합니다. 또한 응용 프로그램 전송에 포함된 예를 사용해 볼 수도 있습니다. 이 작업을 수행하려면 File\Demos 항목을 선택하고 \gnuplot\demo\all.dem 파일을 선택하십시오.

이제 erremove.mq5 스크립트를 시작하면 그림 2에 표시된 그래프가 별도의 창에 그려집니다.

erremove.mq5 

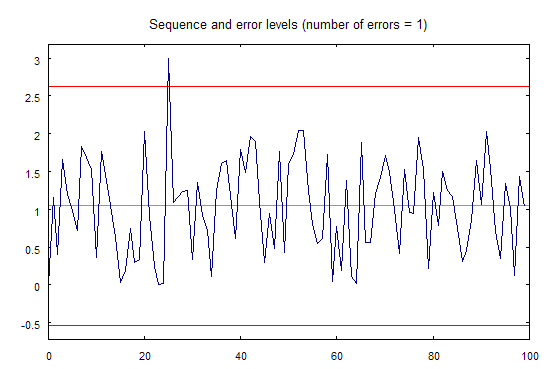
2번 그림. erremove.mq5 스크립트를 이용하여 그려진 그래프.

또한 프로그램과 프로그램 컨트롤에 대한 정보는 설명서 및 http://gnuplot.ikir.ru/와 같은 다양한 웹 사이트에서 쉽게 찾을 수 있으므로 gnuplot 사용에 대한 몇 가지 기능에 대해 잠시 설명하겠습니다.

이 기사에 대해 작성된 프로그램의 예제는 차트를 그리기 위해 gnuplot와 상호 작용하는 가장 간단한 방법을 사용합니다. 먼저 텍스트 파일 gplot.txt가 생성됩니다. txt에는 표시할 gnuplot 명령과 정보가 포함됩니다. 그리고 wgnuplot.exe 에 인수로 전달된 파일의 이름으로 exe 애플리케이션이 시작됩니다. wgnuplot.exe 애플리케이션은 시스템 라이브러리 shell32.dll에서 가져온 ShellExecuteW() 함수를 사용하여 호출됩니다. 이러한 이유로 클라이언트 터미널에서 외부 dlls 임포트가 허용되어야 합니다.

이 버전의 gnuplot에서는 wxt와 window의 두 가지 터미널 유형에 대해 별도의 창에 차트를 그릴 수 있습니다. wxt 단자는 차트 도면에 안티앨라이싱 알고리즘을 사용하므로 Windows 단자에 비해 고품질 그림을 얻을 수 있습니다. 그러나 윈도우 터미널을 이 문서의 예시 작성용으로 사용했습니다. 그 이유는 윈도우즈 터미널에서 작업중일 때, "wgnuplot.exe -p MQL5\\Files\\gplot.txt" 콜과 그래프 윈도우를 열때 만들어지는 시스템 프로세스가 창이 끄는 즉시 종료되기 때문입니다.

wxt 터미널을 선택할 경우 차트 창을 닫아도 wgnuplot.exe 시스템 프로세스가 자동으로 종료되지 않습니다. 따라서 위에서 설명한 것처럼 wxt 터미널과 wgnuplot.exe를 여러 번 사용하면 시스템에서 활동 징후가 없는 여러 프로세스가 누적될 수 있습니다. "wgnuplot.exe -p MQL5\\Files\\gplot.txt" 호출 및 윈도우 터미널을 사용하면 원치않는 추가 창이 열리는 것과 종료되지 않는 시스템 프로세스를 방지할 수 있습니다.

차트가 표시되는 창은 대화식이며 마우스 클릭 및 키보드 이벤트를 처리합니다. 기본 단축키에 대한 정보를 가져오려면 wgnuplot.exe를 실행하고 "set terminal window" 명령을 사용하여 터미널 유형을 선택하고 "plot sin(x)" 커맨드를 이용해 어떠한 차트건 그릴 수 있습니다. 차트 창이 활성(초점) 상태이면 h를 누르는 즉시 wgnuplot.exe의 텍스트 창에 팁이 표시됩니다.


패러미터 측정

도표 작성 방법에 대해 짧게 알아본 후, 유한 표본 추출을 기반으로 한 일반 모집단의 패러미터 추정으로 돌아가 보겠습니다. 일반 모집단의 통계 모수가 알려져 있지 않다고 가정할 때, 우리는 이러한 모수에 대해 편향되지않은 추정치만 사용할 것입니다.

수학 기대값 또는 표본 평균의 추정은 시퀀스의 분포를 결정하는 주요 모수로 간주할 수 있습니다. 표본 평균이란 다음의 공식을 통해 계산됩니다:

 

N 은 표본의 수.

평균 값은 분포 중심 추정치이며, 중심 모멘트와 연결된 다른 모멘트의 계산에 사용되므로 이 모수가 특히 중요합니다. 평균값 외에 분산(분산, 분산), 표준 편차, 왜도 계수(왜도) 및 초과 계수(컷토시)를 통계적 모수로 사용할 것입니다.

 

m은 중심 모먼트입니다. 

중심 모멘트는 일반 모집단의 분포에 대한 숫자 특성입니다.

두 번째, 세 번째 및 네 번째 선택적 중심 모멘트는 다음 식으로 결정됩니다.

 

그러나 이들의 값은 편향되어선 안됩니다 덤으로 k-Statistic와 h-Statistic을 언급해야겠는데요. 특정 조건에서는 중심 모멘트의 편향되지않은 추정을 얻을 수 있으므로 분산, 표준 편차, 왜도 및 첨도의 편향되지 않은 추정을 계산하는 데 사용할 수 있습니다.

k와 h 추정에서 네 번째 모멘트의 계산은 다른 방식으로 수행된다는 점에 유의해야합니다. 따라서 k 또는 h를 사용할 때 첨도 추정에 대한 다른 식을 얻을 수 있습니다. 예를 들어 Microsoft Excel에서는 k-추정의 사용에 해당하는 공식을 사용하여 초과값을 계산하고, "트레이더를 위한 통계" 책에서는 h-추정을 사용하여 첨도의 편중 추정을 수행합니다.

h-추정을 선택한 다음, 기존에 주어진 식에서 m이 아닌 m으로 치환하여 필요한 모수를 계산하겠습니다.

분산 및 표준 편차:

 

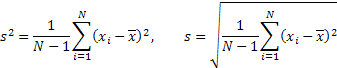
왜도:

 

첨도:

 

정규 분포 법칙을 사용하는 시퀀스에 대해 주어진 식에 따라 계산된 초과(첨도) 계수는 3과 같습니다.

계산된 값에서 3을 빼서 얻은 값은 종종 첨도 값으로 사용되므로 정규 분포 법칙에 따라 상대적으로 정규화됩니다. 첫 번째 경우에는 이 계수를 첨도라고 하고, 두 번째 경우에는 "초과 첨도"라고 합니다.

지정된 식에 따른 모수 계산은 dStat() 함수에서 수행됩니다.

struct statParam
  {
  double mean;
  double median;
  double var;
  double stdev;
  double skew;
  double kurt;
  };
//----------------------------------------------------------------------------
int dStat(const double &x[],statParam &sP)
  {
  int i,m,n;
  double a,b,sum2,sum3,sum4,y[];
  
  ZeroMemory(sP);                                      // Reset sP
  n=ArraySize(x);
  if(n<4)                                             // Error
    {
    Print("Function dStat() error!");
    return(-1);
    }
  sP.kurt=1.0;
  ArrayResize(y,n);
  ArrayCopy(y,x);
  ArraySort(y);
  m=(n-1)/2;
  sP.median=y[m];                                     // Median
  if((n&0x01)==0)sP.median=(sP.median+y[m+1])/2.0;
  sP.mean=0;
  for(i=0;i<n;i++)sP.mean+=x[i];
  sP.mean/=n;                                         // Mean
  sum2=0;sum3=0;sum4=0;  
  for(i=0;i<n;i++)
    {
    a=x[i]-sP.mean;
    b=a*a;sum2+=b;
    b=b*a;sum3+=b;
    b=b*a;sum4+=b;
    }
  if(sum2<1.e-150)return(1);
  sP.var=sum2/(n-1);                                  // Variance
  sP.stdev=MathSqrt(sP.var);                           // Standard deviation
  sP.skew=n*sum3/(n-2)/sum2/sP.stdev;                 // Skewness
  sP.kurt=((n*n-2*n+3)*sum4/sum2/sum2-(6.0*n-9.0)/n)*
                              (n-1.0)/(n-2.0)/(n-3.0); // Kurtosis
  
  return(1);  
dStat()가 호출된 경우 x[] 어레이의 주소가 함수로 전달됩니다. 여기에는 초기 데이터와 모수의 계산된 값이 포함될 statParam 스트럭쳐에 대한 링크가 포함됩니다. 어레이에 요소가 4개 미만인 경우 오류가 발생하면 함수는 -1을 반환합니다.


히스토그램

dStat() 함수에서 계산된 모수 외에도 일반 모집단의 분포 법칙은 꽤나 흥미로운 소재입니다. 유한 표본 추출에 대한 분포 법칙을 시각적으로 추정하기 위해 히스토그램을 그릴 수 있습니다. 히스토그램을 그릴 때 샘플링의 값 범위는 여러 유사한 섹션으로 나뉩니다. 그런 다음 각 섹션의 요소 수를 계산합니다(그룹 빈도).

또한 그룹 빈도를 기반으로 막대 다이어그램이 그려집니다. 이를 히스토그램이라고 부릅니다. 범위 폭으로 정규화하면 히스토그램은 임의 값의 경험적 분포 밀도를 나타냅니다. 히스토그램을 그리기 위한 최적의 섹션 수를 결정하기 위해 "거래자 통계"에 설명된 경험적 표현을 사용하겠습니다.

 

L은 필요한 섹션 수이며, N은 표본 추출 볼륨 e 는 첨도입니다.

아래에는 섹션 수를 결정하고 각 섹션의 요소 수를 계산하며 얻은 그룹 빈도를 정규화하는 dHist()가 있습니다.

struct statParam
  {
  double mean;
  double median;
  double var;
  double stdev;
  double skew;
  double kurt;
  };
//----------------------------------------------------------------------------
int dHist(const double &x[],double &histo[],const statParam &sp)
  {
  int i,k,n,nbar;
  double a[],max,s,xmin;
  
  if(!ArrayIsDynamic(histo))                           // Error
    {
    Print("Function dHist() error!");
    return(-1);
    }
  n=ArraySize(x);
  if(n<4)                                             // Error
    {
    Print("Function dHist() error!");
    return(-1);
    }
  nbar=(sp.kurt+1.5)*MathPow(n,0.4)/6.0;
  if((nbar&0x01)==0)nbar--; if(nbar<5)nbar=5;          // Number of bars
  ArrayResize(a,n);
  ArrayCopy(a,x);
  max=0.0;
  for(i=0;i<n;i++)
    {
    a[i]=(a[i]-sp.mean)/sp.stdev;                     // Normalization
    if(MathAbs(a[i])>max)max=MathAbs(a[i]);
    }
  xmin=-max;
  s=2.0*max*n/nbar;
  ArrayResize(histo,nbar+2);
  ArrayInitialize(histo,0.0);
  histo[0]=0.0;histo[nbar+1]=0.0;
  for(i=0;i<n;i++)
    {
    k=(a[i]-xmin)/max/2.0*nbar;
    if(k>(nbar-1))k=nbar-1;
    histo[k+1]++;
    }
  for(i=0;i<nbar;i++)histo[i+1]/=s;
  
  return(1);
  }

x[] 어레이의 주소가 함수로 전달됩니다. 이 안에는 초기 시퀀스가 있습니다. 함수를 실행해도 어레이의 내용은 변경되지 않습니다. 다음 패러미터는 계산된 값이 저장될 histo[] 동적 어레이에 대한 링크입니다. 해당 어레이의 요소 수는 계산에 사용된 섹션 수에 두 요소를 더한 값입니다.

값이 0인 요소 하나가 histo[] 어레이의 시작과 끝에 추가됩니다. 마지막 패러미터는 statParam 스트럭쳐에 저장된 패러미터의 이전에 계산된 값을 포함해야 하는 statParam 스트럭쳐의 주소입니다. 함수에 전달된 histo[] 어레가 동적 어레기아 아니거나 입력 배열 x[]의 요소가 4개 미만인 경우, 함수는 실행을 중지하고 -1을 반환합니다.

얻어진 값의 히스토그램을 그린 후에는 표본 추출이 정규 분포 법칙에 해당하는지 여부를 시각적으로 추정할 수 있습니다. 정규 분포 법칙에 대한 대응성을 보다 시각적으로 그래픽으로 표현하기 위해 히스토그램 외에 정규 확률도(정규 확률도)의 척도를 사용하여 그래프를 그릴 수 있습니다.


정규 확률 그림

이러한 그래프를 그릴 때의 핵심 아이디어는 정규 분포를 가진 시퀀스의 표시된 값이 동일한 선에 오도록 X축을 변형해야 한다는 것입니다. 이러한 방법으로 정규성 가설을 그래픽으로 확인할 수 있습니다. 이들 그래프에 대한 더 자세한 설명을: "정규 확률 작도" 혹은 "통계적 메소드 e-수첩"에서 찾아볼 수 있습니다.

정규 확률의 그래프를 그리는 데 필요한 값을 계산하려면 아래에 표시된 dRankit() 함수를 사용합니다.

struct statParam
  {
  double mean;
  double median;
  double var;
  double stdev;
  double skew;
  double kurt;
  };
//----------------------------------------------------------------------------
int dRankit(const double &x[],double &resp[],double &xscale[],const statParam &sp)
  {
  int i,n;
  double np;
  
  if(!ArrayIsDynamic(resp)||!ArrayIsDynamic(xscale))    // Error
    {
    Print("Function dHist() error!");
    return(-1);
    }
  n=ArraySize(x);
  if(n<4)                                            // Error
    {
    Print("Function dHist() error!");
    return(-1);
    }
  ArrayResize(resp,n);
  ArrayCopy(resp,x);
  ArraySort(resp);
  for(i=0;i<n;i++)resp[i]=(resp[i]-sp.mean)/sp.stdev;
  ArrayResize(xscale,n);
  xscale[n-1]=MathPow(0.5,1.0/n);
  xscale[0]=1-xscale[n-1];
  np=n+0.365;
  for(i=1;i<(n-1);i++)xscale[i]=(i+1-0.3175)/np;
  for(i=0;i<n;i++)xscale[i]=ltqnorm(xscale[i]);
  
  return(1);
  }
//----------------------------------------------------------------------------

double A1 = -3.969683028665376e+01, A2 =  2.209460984245205e+02,
       A3 = -2.759285104469687e+02, A4 =  1.383577518672690e+02,
       A5 = -3.066479806614716e+01, A6 =  2.506628277459239e+00;
double B1 = -5.447609879822406e+01, B2 =  1.615858368580409e+02,
       B3 = -1.556989798598866e+02, B4 =  6.680131188771972e+01,
       B5 = -1.328068155288572e+01;
double C1 = -7.784894002430293e-03, C2 = -3.223964580411365e-01,
       C3 = -2.400758277161838e+00, C4 = -2.549732539343734e+00,
       C5 =  4.374664141464968e+00, C6 =  2.938163982698783e+00;
double D1 =  7.784695709041462e-03, D2 =  3.224671290700398e-01,
       D3 =  2.445134137142996e+00, D4 =  3.754408661907416e+00;
//----------------------------------------------------------------------------
double ltqnorm(double p)
  {
  int s=1;
  double r,x,q=0;

  if(p<=0||p>=1){Print("Function ltqnorm() error!");return(0);}
  if((p>=0.02425)&&(p<=0.97575))    // Rational approximation for central region
    {
    q=p-0.5; r=q*q;
    x=(((((A1*r+A2)*r+A3)*r+A4)*r+A5)*r+A6)*q/(((((B1*r+B2)*r+B3)*r+B4)*r+B5)*r+1);
    return(x);
    }
  if(p<0.02425)                    // Rational approximation for lower region
    {
    q=sqrt(-2*log(p)); 
    s=1;
    }
  else      //if(p>0.97575)          // Rational approximation for upper region
    {
    q = sqrt(-2*log(1-p));
    s=-1;
    }
  x=s*(((((C1*q+C2)*q+C3)*q+C4)*q+C5)*q+C6)/((((D1*q+D2)*q+D3)*q+D4)*q+1);
  return(x);
  }

x[] 어레이의 주소가 함수에 들어갑니다. 어레이에 초기 시퀀스가 포함되어 있습니다. 다음 패러미터는 출력 어레이 resp[] 및 xscale[]에 대한 참조입니다. 기능 실행 후 X축과 Y축에 각각 차트를 그리는 데 사용된 값이 어레이에 기록됩니다. 그런 다음 statParam 구조의 주소가 함수로 전달됩니다. 여기에는 입력 시퀀스의 통계 패러미터에 대해 이전에 계산된 값이 포함되어야 합니다. 오류가 발생하면 함수는 -1을 반환합니다.

X축에 대한 값을 형성할 때 함수 ltqnorm()이 호출됩니다. 정규 분포의 역적분 함수를 계산합니다. 계산에 사용된 알고리즘은 "역정규분포함수를 계산하는 알고리즘"에서 가져왔습니다.


네개의 차트

앞에서 통계 파라미터의 값이 계산되는 dStat() 함수를 언급했습니다. 그 의미에 대해서 빠르게 한 번 더 짚고 가봅시다

분산 – 수학 기대값에서 랜덤 값의 편차 제곱의 평균 값(평균 값). . 분포 중심에서 랜덤 값의 편차가 얼마나 큰지를 보여 주는 모수입니다. 이 패러미터의 값이 클수록 편차가 커집니다.

표준 편차 – 분산는 무작위 값의 제곱으로 측정되기 때문에, 표준 편차는 분산보다 명확한 특성으로 종종 사용됩니다. 이는 분산의 루트값입니다.

왜도 – 무작위 값의 분포 곡선을 그린다면, 왜도는 분포 중심과 비교한 확률 밀도의 곡선이 얼마나 비대칭적인지를 보여줄 것입니다. 왜도 값이 0보다 크면 확률 밀도의 곡선은 가파른 왼쪽 기울기와 평평한 오른쪽 기울기를 가집니다. 왜도 값이 음수이면 왼쪽 기울기가 평평하고 오른쪽 기울기가 가파릅니다. 확률 밀도의 곡선이 분포의 중심과 대칭이면 왜도는 0과 같습니다.

초과 계수 (첨도) – 확률밀도 곡선의 꼭대기가 얼마나 날카로운가와, 분포 양 끝의 경사도를 나타냅니다. 분포 중심 근처의 곡선 피크가 날카로울수록 첨도 값이 커집니다.

위에서 언급된 통계 패러미터가 시퀀스에 대해 자세히 설명하긴 하지만, 그래픽 형태로 표현된 추정 결과에 기초하여 시퀀스를 그것 보다 쉽게 특성화할 수 있습니다. 예를 들어, 시퀀스의 일반 그래프는 통계 패러미터를 분석할 때 얻은 보기를 크게 완성할 수 있습니다.

앞에서 정규 확률 척도로 히스토그램 또는 차트를 그리기 위한 데이터를 준비할 수 있는 dHist() 및 dRankit() 함수를 언급했습니다. 히스토그램 및 정규 분포 그래프를 동일한 시트에 일반 그래프와 함께 표시하면 분석된 시퀀스의 주요 특징을 시각적으로 확인할 수 있습니다.

나열된 세 개의 차트는 Y축에 시퀀스의 현재 값이 있는 차트와 X축에 이전 값이 있는 차트로 보완해야 합니다. 이런 차트를 "지연 플롯"이라고 부릅니다. 인접한 인디케이션 사이에 강한 상관관계가 있는 경우, 표본 추출 값은 직선으로 늘어납니다. 예를 들어 랜덤 시퀀스를 분석할 때 인접 표시 간에 상관 관계가 없으면 차트 전체에 값이 분산됩니다.

초기 샘플링을 빠르게 추정하려면 단일 시트에 4개의 차트를 그리고 그 위에 통계 패러미터의 계산된 값을 표시하는 것이 좋습니다. 딱히 새로운 발상이 아닙니다; 언급한 4개의 차트의 분석을 이용하는 방법에 대해"4 Plot"에서 읽어볼 수 있습니다.

이 글의 마지막 부분의 "파일" 섹션에는 s4plot.mq5 스크립트가 있으며, 저 파일을 이용해서 4개의 차트를 단일 시트에 그립니다. dat[] 어레이는 스크립트의 OnStart() 함수 내에 생성됩니다. 이는 초기 시퀀스를 포함합니다. 그런 다음 차트 도면에 필요한 데이터를 계산하기 위해 dStat(), dHist() 및 dRankit() 함수가 호출됩니다. 이 다음에 vis4plot() 함수가 호출됩니다. 계산된 데이터를 기반으로 gnuplot 커맨드를 사용하여 텍스트 파일을 생성한 후, 별도의 창에 차트를 그리기 위한 응용 프로그램을 호출합니다.

dStat(), dHist() 및 dRankit()이 이전에 설명되었기 때문에 굳이 코드 전문을 보일 필요는 없을 것 같습니다. 그 외에 gnuplot 커맨드의 시퀀스를 생성하는 vis4plot() 함수는 특이한 사항이 없고, nuplot 커맨드에 대한 해설은 이 문서의 논점을 이탈하게됩니다. 이 외에도 gnuplot 애플리케이션 대신 다른 방법을 사용하여 차트를 그릴 수 있습니다.

s4plot.mq5 - 해당 OnStart() 함수의 일부만 표시하겠습니다.

//----------------------------------------------------------------------------
// Script program start function
//----------------------------------------------------------------------------
void OnStart()
  {
  int i;
  double dat[128],histo[],rankit[],xrankit[];
  statParam sp;
 
  MathSrand(1);
  for(i=0;i<ArraySize(dat);i++) dat[i]=MathRand();
  
  if(dStat(dat,sp)==-1)return;
  if(dHist(dat,histo,sp)==-1)return;
  if(dRankit(dat,rankit,xrankit,sp)==-1)return;
  
  vis4plot(dat,histo,rankit,xrankit,sp,6);
  }

이 예에서는 임의 시퀀스를 사용하여 MathRand() 기능을 사용하여 dat[] 어레이를 초기 데이터로 채웁니다. 스크립트 실행 결과는 다음과 같습니다:

4-Plot 

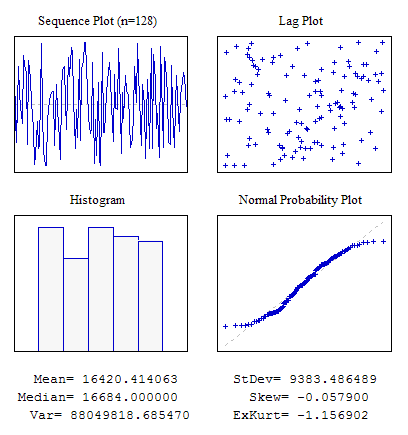
3번 그림. 4개의 차트. s4plot.mq5 스크립트

vis4plot() 기능의 마지막 패러미터에 주의해야 합니다. 이것이 출력된 숫자 값의 형식을 담당합니다. 이 예에서는 소수점 6자리로 값이 출력됩니다. 이 패러미터는 DoubleToString() 함수에서 포맷을 결정하는 것과 같습니다.

입력 시퀀스의 값이 너무 작거나 크면 과학적 형식을 사용하여 보다 명확하게 표시할 수 있습니다. 이렇게 하려면 해당 패러미터를 -5로 설정하십시오. vis4plot() 기능의 경우 기본적으로 -5 값이 설정됩니다.

시퀀스의 특성을 표시하기 위한 4개 차트의 방법의 명확성을 입증하기 위해서는 그러한 시퀀스의 생성기가 필요하다.


위-랜덤(Pseudo-Random) 시퀀스 제너레이터

클래스 RNDXor128 클래스는 위-랜덤 시퀀스를 생성하기 위한 것입니다.

아래에 해당 클래스를 설명하는 포함 파일의 소스 코드가 있습니다.

//-----------------------------------------------------------------------------------
//                                                                      RNDXor128.mqh
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#include <Object.mqh>
//-----------------------------------------------------------------------------------
// Generation of pseudo-random sequences. The Xorshift RNG algorithm 
// (George Marsaglia) with the 2**128 period of initial sequence is used.
//          uint rand_xor128()
//            {
//            static uint x=123456789,y=362436069,z=521288629,w=88675123;
//            uint t=(x^(x<<11));x=y;y=z;z=w;
//            return(w=(w^(w>>19))^(t^(t>>8)));
//            }
// Methods:
//  Rand()      - even distribution withing the range [0,UINT_MAX=4294967295].
//  Rand_01()   - even distribution within the range [0,1].
//  Rand_Norm() - normal distribution with zero mean and dispersion one.
//  Rand_Exp()  - exponential distribution with the parameter 1.0.
//  Rand_Laplace() - Laplace distribution with the parameter 1.0
//  Reset()     - resetting of all basic values to initial state.
//  SRand()     - setting new basic values of the generator.
//-----------------------------------------------------------------------------------
#define xor32  xx=xx^(xx<<13);xx=xx^(xx>>17);xx=xx^(xx<<5)
#define xor128 t=(x^(x<<11));x=y;y=z;z=w;w=(w^(w>>19))^(t^(t>>8))
#define inidat x=123456789;y=362436069;z=521288629;w=88675123;xx=2463534242

class RNDXor128:public CObject
  {
protected:
  uint      x,y,z,w,xx,t;
  uint      UINT_half;
public:
            RNDXor128()       {UINT_half=UINT_MAX>>1;inidat;};
  double    Rand()            {xor128;return((double)w);};
  int       Rand(double& a[],int n)
                              {int i;if(n<1)return(-1);
                               if(ArraySize(a)<n)return(-2);
                               for(i=0;i<n;i++){xor128;a[i]=(double)w;}
                               return(0);};
  double    Rand_01()         {xor128;return((double)w/UINT_MAX);};
  int       Rand_01(double& a[],int n)
                              {int i;if(n<1)return(-1);
                               if(ArraySize(a)<n)return(-2);
                               for(i=0;i<n;i++){xor128;a[i]=(double)w/UINT_MAX;}
                               return(0);};
  double    Rand_Norm()       {double v1,v2,s,sln;static double ra;static uint b=0;
                               if(b==w){b=0;return(ra);}
                               do{
                                 xor128;v1=(double)w/UINT_half-1.0;
                                 xor128;v2=(double)w/UINT_half-1.0;
                                 s=v1*v1+v2*v2;
                                 }
                               while(s>=1.0||s==0.0);
                               sln=MathLog(s);sln=MathSqrt((-sln-sln)/s);
                               ra=v2*sln;b=w;
                               return(v1*sln);};
  int       Rand_Norm(double& a[],int n)
                              {int i;if(n<1)return(-1);
                               if(ArraySize(a)<n)return(-2);
                               for(i=0;i<n;i++)a[i]=Rand_Norm();
                               return(0);};
  double    Rand_Exp()        {xor128;if(w==0)return(DBL_MAX);
                               return(-MathLog((double)w/UINT_MAX));};
  int       Rand_Exp(double& a[],int n)
                              {int i;if(n<1)return(-1);
                               if(ArraySize(a)<n)return(-2);
                               for(i=0;i<n;i++)a[i]=Rand_Exp();
                               return(0);};
  double    Rand_Laplace()    {double a;xor128;
                              a=(double)w/UINT_half;
                              if(w>UINT_half)
                                {a=2.0-a;
                                if(a==0.0)return(-DBL_MAX);
                                return(MathLog(a));}
                              else
                                {if(a==0.0)return(DBL_MAX);
                                return(-MathLog(a));}};
  int       Rand_Laplace(double& a[],int n)
                              {int i;if(n<1)return(-1);
                               if(ArraySize(a)<n)return(-2);
                               for(i=0;i<n;i++)a[i]=Rand_Laplace();
                               return(0);};
  void      Reset()           {inidat;};
  void      SRand(uint seed)  {int i;if(seed!=0)xx=seed;
                               for(i=0;i<16;i++){xor32;}
                               xor32;x=xx;xor32;y=xx;
                               xor32;z=xx;xor32;w=xx;
                               for(i=0;i<16;i++){xor128;}};
  int       SRand(uint xs,uint ys,uint zs,uint ws)
                              {int i;if(xs==0&&ys==0&&zs==0&&ws==0)return(-1);
                               x=xs;y=ys;z=zs;w=ws;
                               for(i=0;i<16;i++){xor128;}
                               return(0);};
  };
//-----------------------------------------------------------------------------------

랜덤 시퀀스를 생성하는 데 사용되는 알고리즘은 George Marsaglia의 "Xorshift RNG" 문서에 자세히 설명되어 있습니다(문서 끝에 있는 xorshift.zip 참조). RNDXor128 클래스의 메소드는 RNDXor128.mqh 파일에 설명되어 있습니다. 이 클래스를 사용하면 짝수, 정규 분포 또는 지수 분포(이중 지수 분포)를 사용하여 시퀀스를 가져올 수 있습니다.

RNDXor128 클래스의 인스턴스가 생성될 때 시퀀스의 기본 값이 초기 상태로 설정된다는 점에 유의해야 합니다. 따라서 RNDXor128을 사용하는 스크립트 또는 인디케이터를 새로 시작할 때마다 MathRand() 함수를 호출하는 것과는 대조적으로 동일한 시퀀스가 생성됩니다. MathSrand()를 호출한 후 MathRand()를 호출할 때와 동일합니다.


시퀀스 예제들

아래 예에서는 속성으로 서로 매우 다른 시퀀스를 분석할 때 얻은 결과를 확인할 수 있습니다.

예시 1. 균등 분포법에 따른 랜덤 시퀀스

#include "RNDXor128.mqh"
RNDXor128 Rnd;
//----------------------------------------------------------------------------
void OnStart()
  {
  int i;
  double dat[512];

  for(i=0;i<ArraySize(dat);i++) dat[i]=Rnd.Rand_01();
  ...  
  }

균등 분포

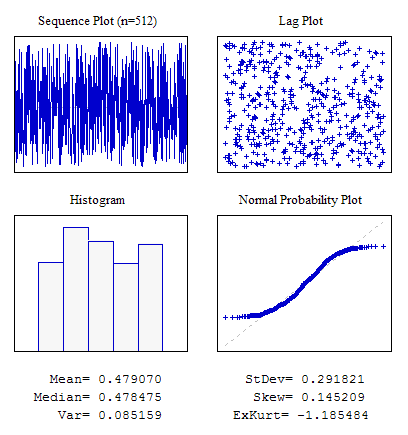
4번 그림. 균등 분포

예시 2. 정규 분포법에 따른 랜덤 시퀀스

#include "RNDXor128.mqh"
RNDXor128 Rnd;
//----------------------------------------------------------------------------
void OnStart()
  {
  int i;
  double dat[512];

  for(i=0;i<ArraySize(dat);i++) dat[i]=Rnd.Rand_Norm();
  ...  
  }

정규 분포

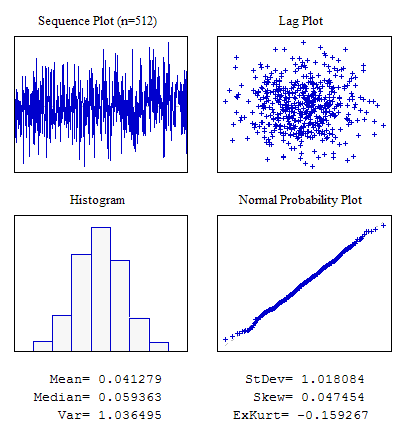
5번 그림. 정규 분포

예시 3. 지수 분포법에 따른 랜덤 시퀀스

#include "RNDXor128.mqh"
RNDXor128 Rnd;
//----------------------------------------------------------------------------
void OnStart()
  {
  int i;
  double dat[512];

  for(i=0;i<ArraySize(dat);i++) dat[i]=Rnd.Rand_Exp();
  ...  
  }

지수 분포

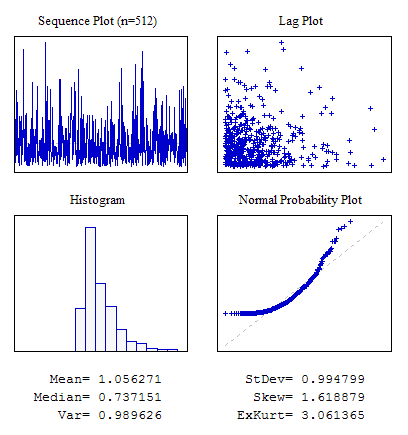
6번 그림. 지수 분포

예시 4. 라플라스 분포에 따른 랜덤 시퀀스

#include "RNDXor128.mqh"
RNDXor128 Rnd;
//----------------------------------------------------------------------------
void OnStart()
  {
  int i;
  double dat[512];

  for(i=0;i<ArraySize(dat);i++) dat[i]=Rnd.Rand_Laplace();
  ...  
  }

라플라스 분포

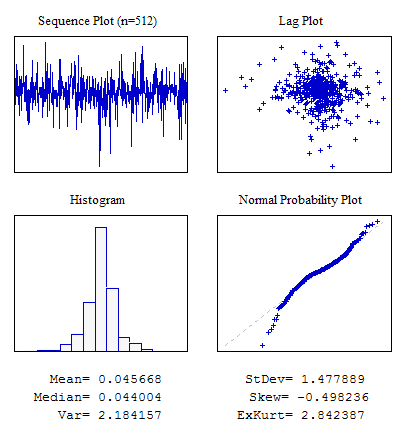
7번 그림. 라플라스 분포

Example 5. 사인 시퀀스

//----------------------------------------------------------------------------
void OnStart()
  {
  int i;
  double dat[512];

  for(i=0;i<ArraySize(dat);i++) dat[i]=MathSin(2*M_PI/4.37*i);
  ...  
  }

사인 시퀀스

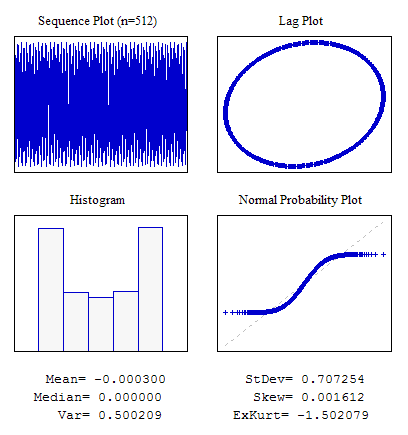
8번 그림. 사인 시퀀스

예시 6. 인접 인디케이션 간에 가시적 상관 관계가 있는 시퀀스.

#include "RNDXor128.mqh"
RNDXor128 Rnd;
//----------------------------------------------------------------------------
void OnStart()
  {
  int i;
  double dat[512],a;

  for(i=0;i<ArraySize(dat);i++) {a+=Rnd.Rand_Laplace();dat[i]=a;}
  ...  
  }

인접 인디케이션 간의 상관 관계

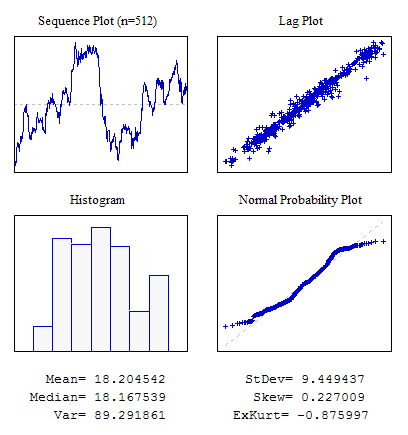
9번 그림. 인접 인디케이션 간의 상관 관계


마치며

모든 종류의 계산을 구현하는 프로그램 알고리즘의 개발은 항상 어려운 일입니다. 이는 변수를 반올림, 잘라내기, 오버플로우할 때 발생할 수 있는 실수를 최소화하기 위해 많은 요구 사항을 고려해야 하기 때문입니다.

이 문서에서 쓰일 예시를 작성하면서 프로그램 알고리즘 분석을 전혀 하지 않았습니다. 함수를 작성할 때, 수학적 알고리즘이 "직접" 구현되었습니다. 따라서 이 알고리즘들을 "중요한" 어플리케이션에서 사용하려면 안정성 및 정확성을 분석해야 합니다.

이 문서에서는 gnuplot 어플리케이션의 기능을 전혀 설명하지 않았습니다. 그 내용은 이 문서에서 다루는 내용을 아득히 넘어가기 때문입니다. 어쨌든, Gnuplot은 MetaTrader 5와 함께 사용할 수 있도록 조정될 수 있다는 것을 짚고 넘어가고자 합니다. 본 목적을 위하여 소스에 수정을 가미하고 다시 컴파일해야합니다. 뿐만 아니라, gnuplot과의 상호 작용은 프로그래밍 인터페이스를 통해 구성될 수 있기 때문에 파일을 사용하여 gnuplot에 명령을 전달하는 방법은 아마도 최적의 방법이 아닐 것입니다.


파일

  • erremove.mq5 – 샘플링에서 에러를 제거하는 스크립트 예제.
  • function_dstat.mq5 – 통계적 모수 계산용 함수.
  • function_dhist.mq5 - 히스토그램 값 계산용 함수.
  • function_drankit.mq5 – 정규 분포 스케일으로 차트를 그릴 때 쓰이는 값을 계산하는 함수.
  • s4plot.mq5 – 하나의 시트에 네개의 차트를 그리는 스크립트 예제.
  • RNDXor128.mqh – 랜덤 시퀀스 제너레이터 클래스.
  • xorshift.zip - 조지 마르사글리아. "Xorshift RNGs".

 

MetaQuotes 소프트웨어 사를 통해 러시아어가 번역됨.
원본 기고글: https://www.mql5.com/ru/articles/273

파일 첨부됨 |
ZIP파일 다운로드
erremove.mq5 (4.53 KB)
function_dhist.mq5 (1.21 KB)
function_drankit.mq5 (2.46 KB)
xorshift.zip (38.35 KB)
function_dstat.mq5 (1.35 KB)
s4plot.mq5 (10.52 KB)
rndxor128.mqh (12.01 KB)
경고: 이 자료들에 대한 모든 권한은 MetaQuotes(MetaQuotes Ltd.)에 있습니다. 이 자료들의 전부 또는 일부에 대한 복제 및 재출력은 금지됩니다.

이 작가의 다른 글

토론으로 가기
MetaTrader 5에서 자동 정리 기능 맵 (코호넨 맵) 이용하기 MetaTrader 5에서 자동 정리 기능 맵 (코호넨 맵) 이용하기
자체 구성 기능 맵(코호넨 맵)의 가장 흥미로운 측면 중 하나는 사람이 관리하지 않아도 스스로 데이터를 분류하는 법을 배운다는 것입니다. 기본적인 형태로 입력 데이터의 유사성 맵(클러스터링)을 생성합니다. SOM 맵은 고차원 데이터의 분류 및 시각화에 사용할 수 있습니다. In this article we will consider several simple applications of Kohonen maps.
소스 코드의 트레이싱, 디버깅, 및 구조 분석 소스 코드의 트레이싱, 디버깅, 및 구조 분석
실행된 코드의 구조 생성과 추적에 따른 전체 문제를 큰 어려움 없이 해결할 수 있습니다. MQL5 언어의 새로운 기능인 복잡한 유형의 데이터(구조 및 클래스)의 자동 생성과 로컬 범위를 벗어날 때 이러한 변수가 제거됨에 따라 MetaTrader 5에서 이러한 가능성이 대두되었습니다. 이 문서에서는 방법론에 대한 해석과 레디메이드 툴을 보여드리겠습니다.
Expert Advisor 최적화 시 커스텀 조건 만들기 Expert Advisor 최적화 시 커스텀 조건 만들기
MetaTrader 5 클라이언트 터미널은 Expert Advisor 패러미터 최적화 용도로 여러 선택지를 제공합니다. 전략 테스터에 포함된 최적화 기준 외에도 개발자에게 자신만의 기준을 만들 수 있는 기회가 주어집니다. 이를 통해 Expert Advisor를 테스트하고 최적화할 수 있는 가능성이 무궁무진해집니다. 본 문서에서 이러한 기준을 만드는 실제 방법(복잡하고 단순한 방법 모두)을 설명할 것입니다.
MQL5 에서의 통계적 확률 분산 MQL5 에서의 통계적 확률 분산
이 문서에서는 적용 통계에 사용되는 랜덤 변수의 확률 분포(정규 분포, 로그-정규 분포, 이항 분포, 로그 분포, 지수 분포, 코시 분포, 스튜던트 t 분포, 라플라스 분포, 푸아송 분포, 쌍곡 시컨트 분포, 베타 및 감마 분포)를 다룹니다. 또한 이러한 배포를 처리하기 위한 클래스도 제공됩니다.