Stime statistiche
121
0
Introduzione
Oggigiorno, è spesso possibile incontrare articoli e pubblicazioni scritti su argomenti legati all'econometria, alla previsione di serie di prezzi, alla scelta e alla stima dell'adeguatezza di un modello, ecc. Ma nella maggior parte dei casi, il ragionamento si basa sul presupposto che un lettore conosca i metodi delle statistiche matematiche e possa facilmente stimare i parametri statistici di una sequenza analizzata.
La stima dei parametri statistici di una sequenza è molto importante poiché la maggior parte dei modelli e metodi matematici si basa su ipotesi diverse. Ad esempio, normalità della legge di distribuzione o valore di dispersione o altri parametri. Pertanto, durante l'analisi e la previsione delle serie temporali abbiamo bisogno di uno strumento semplice e conveniente che consenta di stimare in modo rapido e chiaro i principali parametri statistici. In questo articolo, proveremo a creare uno strumento del genere.
L'articolo descrive brevemente i parametri statistici più semplici di una sequenza casuale e diversi metodi della sua analisi visiva. Offre l'implementazione di questi metodi in MQL5 e i metodi di visualizzazione del risultato dei calcoli utilizzando l'applicazione Gnuplot. In nessun modo questo articolo ha preteso di essere un manuale o un riferimento; per questo può contenere alcune familiarità accettate riguardo alla terminologia e alle definizioni.
Analisi dei parametri su un campione
Supponiamo che esista un processo stazionario esistente all'infinito nel tempo, che può essere rappresentato come una sequenza di campioni discreti. Chiamiamo questa sequenza di campioni popolazione generale. Una parte dei campioni selezionati dalla popolazione generale sarà chiamata campionamento dalla popolazione generale o campionamento di N campioni. Inoltre, supponiamo che non ci siano noti parametri veri, quindi li stimeremo sulla base di un campionamento finito.
Evitare gli outlier
Prima di iniziare la stima statistica dei parametri, è opportuno notare che l'accuratezza della stima può essere insufficiente se il campionamento contiene errori grossolani (outlier). C'è un'enorme influenza dei valori anomali sull'accuratezza delle stime se il campionamento ha un volume ridotto. I valori anomali sono i valori che divergono in modo anomalo dal centro della distribuzione. Tali deviazioni possono essere causate da diversi eventi difficilmente probabili ed errori comparsi durante la raccolta dei dati statistici e la formazione della sequenza.
È difficile decidere se filtrare o meno gli outlier, poiché nella maggior parte dei casi è impossibile rilevare chiaramente se un valore è un outlier o appartiene al processo analizzato. Quindi, se vengono rilevati valori anomali e si decide di filtrarli, sorge una domanda: cosa dovremmo fare con quei valori di errore? La variante più logica è escludere dal campionamento ciò che può aumentare l'accuratezza della stima delle caratteristiche statistiche; ma dovresti stare attento ad escludere i valori anomali dal campionamento quando lavori con sequenze temporali
Per avere la possibilità di escludere gli outlier da un campionamento o almeno di rilevarli, implementiamo l'algoritmo descritto nel libro "Statistics for Traders" scritto da S.V. Bulashev.
Secondo questo algoritmo, dobbiamo calcolare cinque valori di stima del centro di distribuzione:
- Mediana;
- Centro del 50% dell'intervallo interquartile (intervallo medioquartile, MQR);
- Media aritmetica dell'intero campionamento;
- Media aritmetica sull'intervallo interquartile del 50% (media interquartile, IQM);
- Centro dell'intervallo (midrange) - determinato come valore medio del valore massimo e minimo in un campionamento.
Quindi i risultati della stima del centro di distribuzione sono ordinati in ordine crescente; e, quindi, il valore medio o il terzo in ordine viene scelto come centro di distribuzione Xcen. Pertanto, la stima scelta sembra essere minimamente influenzata dagli outlier.
Inoltre, utilizzando la stima ottenuta del centro di distribuzione Xcen, calcoliamo la deviazione standard s, l'eccesso di K e il tasso di censura secondo la formula empirica:
dove N è il numero di campioni nel campionamento (volume del campionamento).
Quindi i valori che si trovano al di fuori dell'intervallo:
verranno conteggiati come outlier e quindi devono essere esclusi dal campionamento.
Questo metodo è descritto in dettaglio nel libro "Statistics for Traders", quindi passiamo direttamente all'implementazione dell'algoritmo. L'algoritmo che consente di rilevare ed escludere gli outlier è implementato nella funzione erremove().
Di seguito puoi trovare lo script scritto per testare questa funzione.
//---------------------------------------------------------------------------- // erremove.mq5 // Copyright 2011, MetaQuotes Software Corp. // https://www.mql5.com //---------------------------------------------------------------------------- #property copyright "Copyright 2011, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" #import "shell32.dll" bool ShellExecuteW(int hwnd,string lpOperation,string lpFile, string lpParameters,string lpDirectory,int nShowCmd); #import //---------------------------------------------------------------------------- // Script program start function //---------------------------------------------------------------------------- void OnStart() { int i; double dat[100]; double y[]; srand(1); for(i=0;i<ArraySize(dat);i++)dat[i]=rand()/16000.0; dat[25]=3; // Make Error !!! erremove(dat,y,1); } //---------------------------------------------------------------------------- int erremove(const double &x[],double &y[],int visual=1) { int i,m,n; double a[],b[5]; double dcen,kurt,sum2,sum4,gs,v,max,min; if(!ArrayIsDynamic(y)) // Error { Print("Function erremove() error!"); return(-1); } n=ArraySize(x); if(n<4) // Error { Print("Function erremove() error!"); return(-1); } ArrayResize(a,n); ArrayCopy(a,x); ArraySort(a); b[0]=(a[0]+a[n-1])/2.0; // Midrange m=(n-1)/2; b[1]=a[m]; // Median if((n&0x01)==0)b[1]=(b[1]+a[m+1])/2.0; m=n/4; b[2]=(a[m]+a[n-m-1])/2.0; // Midquartile range b[3]=0; for(i=m;i<n-m;i++)b[3]+=a[i]; // Interquartile mean(IQM) b[3]=b[3]/(n-2*m); b[4]=0; for(i=0;i<n;i++)b[4]+=a[i]; // Mean b[4]=b[4]/n; ArraySort(b); dcen=b[2]; // Distribution center sum2=0; sum4=0; for(i=0;i<n;i++) { a[i]=a[i]-dcen; v=a[i]*a[i]; sum2+=v; sum4+=v*v; } if(sum2<1.e-150)kurt=1.0; kurt=((n*n-2*n+3)*sum4/sum2/sum2-(6.0*n-9.0)/n)*(n-1.0)/(n-2.0)/(n-3.0); // Kurtosis if(kurt<1.0)kurt=1.0; gs=(1.55+0.8*MathLog10((double)n/10.0)*MathSqrt(kurt-1))*MathSqrt(sum2/(n-1)); max=dcen+gs; min=dcen-gs; m=0; for(i=0;i<n;i++)if(x[i]<=max&&x[i]>=min)a[m++]=x[i]; ArrayResize(y,m); ArrayCopy(y,a,0,0,m); if(visual==1)vis(x,dcen,min,max,n-m); return(n-m); } //---------------------------------------------------------------------------- void vis(const double &x[],double dcen,double min,double max,int numerr) { int i; double d,yma,ymi; string str; yma=x[0];ymi=x[0]; for(i=0;i<ArraySize(x);i++) { if(yma<x[i])yma=x[i]; if(ymi>x[i])ymi=x[i]; } if(yma<max)yma=max; if(ymi>min)ymi=min; d=(yma-ymi)/20.0; yma+=d;ymi-=d; str="unset key\n"; str+="set title 'Sequence and error levels (number of errors = "+ (string)numerr+")' font ',10'\n"; str+="set yrange ["+(string)ymi+":"+(string)yma+"]\n"; str+="set xrange [0:"+(string)ArraySize(x)+"]\n"; str+="plot "+(string)dcen+" lt rgb 'green',"; str+=(string)min+ " lt rgb 'red',"; str+=(string)max+ " lt rgb 'red',"; str+="'-' with line lt rgb 'dark-blue'\n"; for(i=0;i<ArraySize(x);i++)str+=(string)x[i]+"\n"; str+="e\n"; if(!saveScript(str)){Print("Create script file error");return;} if(!grPlot())Print("ShellExecuteW() error"); } //---------------------------------------------------------------------------- bool grPlot() { string pnam,param; pnam="GNUPlot\\binary\\wgnuplot.exe"; param="-p MQL5\\Files\\gplot.txt"; return(ShellExecuteW(NULL,"open",pnam,param,NULL,1)); } //---------------------------------------------------------------------------- bool saveScript(string scr1="",string scr2="") { int fhandle; fhandle=FileOpen("gplot.txt",FILE_WRITE|FILE_TXT|FILE_ANSI); if(fhandle==INVALID_HANDLE)return(false); FileWriteString(fhandle,"set terminal windows enhanced size 560,420 font 8\n"); FileWriteString(fhandle,scr1); if(scr2!="")FileWriteString(fhandle,scr2); FileClose(fhandle); return(true); } //----------------------------------------------------------------------------
Diamo uno sguardo dettagliato alla funzione erremove(). Come primo parametro della funzione passiamo l'indirizzo dell'array x[], dove sono memorizzati i valori del campionamento analizzato; il volume di campionamento non deve essere inferiore a quattro elementi. Si suppone che la dimensione dell'array x[] sia uguale alla dimensione del campionamento, ecco perché il valore N del volume del campionamento non viene superato. I dati che si trovano nell'array x[] non vengono modificati come risultato dell'esecuzione della funzione.
Il parametro successivo è l'indirizzo dell'array y[]. In caso di corretta esecuzione della funzione, questo array conterrà la sequenza di input con outlier esclusi. La dimensione dell'array y[] è inferiore alla dimensione dell'array x[] per il numero di valori esclusi dal campionamento. L'array y[] deve essere dichiarato dinamico, altrimenti sarà impossibile modificarne la dimensione nel corpo della funzione.
L'ultimo parametro (opzionale) è il flag responsabile della visualizzazione dei risultati di calcolo. Se il suo valore è uguale a uno (valore di default), allora prima della fine dell'esecuzione della funzione verrà disegnato il grafico che mostra le seguenti informazioni in una finestra separata: la sequenza di input, la linea del centro di distribuzione e i limiti di intervallo, valori al di fuori dei quali verranno considerati outlier.
Il metodo per disegnare i grafici verrà descritto in seguito. In caso di esito positivo, la funzione restituisce il numero di valori esclusi dal campionamento; in caso di errore restituisce -1. Se non vengono rilevati valori di errore (outlier), la funzione restituirà 0 e la sequenza nell'array y[] sarà la stessa di x[].
All'inizio della funzione, le informazioni vengono copiate dall'array x[] all'array a[], quindi vengono ordinate in ordine crescente e vengono effettuate cinque stime del centro di distribuzione.
Il centro dell'intervallo (midrange) è determinato come la somma dei valori estremi dell'array ordinato a[] diviso per due.
La mediana è calcolata per i volumi dispari del campionamento N come segue:
e per volumi pari del campionamento:
Considerando che gli indici dell'array ordinato a[] iniziano da zero, otteniamo:
m=(n-1)/2; median=a[m]; if((n&0x01)==0)b[1]=(median+a[m+1])/2.0;
Il centro dell'intervallo interquartile del 50% (intervallo medioquartile, MQR):
dove M=N/4 (divisione intera).
Per l'array ordinato a[] otteniamo:
m=n/4; MQR=(a[m]+a[n-m-1])/2.0; // Midquartile range
Medie aritmetiche dell'intervallo interquartile del 50% (media interquartile, IQM). Il 25% dei campioni viene tagliato da entrambi i lati del campionamento e il restante 50% viene utilizzato per il calcolo della media aritmetica:
dove M=N/4 (divisione intera).
m=n/4; IQM=0; for(i=m;i<n-m;i++)IQM+=a[i]; IQM=IQM/(n-2*m); // Interquartile mean(IQM)
La media aritmetica (mean) è determinata per l'intero campionamento.
Ciascuno dei valori determinati viene scritto nell'array b[], quindi l'array viene ordinato in ordine crescente. Un valore dell'elemento dell'array b[2] viene scelto come centro della distribuzione. Inoltre, utilizzando questo valore, calcoleremo le stime imparziali della media aritmetica e del coefficiente di eccesso; l'algoritmo di calcolo verrà descritto in seguito.
Le stime ottenute vengono utilizzate per il calcolo del coefficiente di censura e dei limiti dell'intervallo per il rilevamento degli outlier (le espressioni sono mostrate sopra). Alla fine, la sequenza con gli outlier esclusi viene formata nell'array y[] e le funzioni vis() vengono chiamate per disegnare il grafico. Diamo una breve occhiata al metodo di visualizzazione utilizzato in questo articolo.
Visualizzazione
Per visualizzare i risultati del calcolo, utilizzo l'applicazione freeware gnuplot destinata alla creazione di vari grafici 2D e 3D. Gnuplot ha la possibilità di visualizzare i grafici sullo schermo (in una finestra separata) o di scriverli su un file in diversi formati grafici. I comandi di tracciatura dei grafici possono essere eseguiti da un file di testo preparato in via preliminare. La pagina web ufficiale del progetto gnuplot è gnuplot.sourceforge.net. L'applicazione è multipiattaforma e viene distribuita sia come file di codice sorgente che come file binari compilati per una determinata piattaforma.
Gli esempi scritti per questo articolo sono stati testati con Windows XP SP3 e la versione 4.2.2 di gnuplot. Il file gp442win32.zip può essere scaricato da http://sourceforge.net/projects/gnuplot/files/gnuplot/4.4.2/. Non ho testato gli esempi con altre versioni e build di gnuplot.
Una volta scaricato l'archivio gp442win32.zip, decomprimilo. Di conseguenza, viene creata la cartella \gnuplot, che contiene l'applicazione, il file della guida, la documentazione e gli esempi. Per interagire con le applicazioni, inserisci l'intera cartella \gnuplot nella cartella principale del tuo client terminal MetaTrader 5.
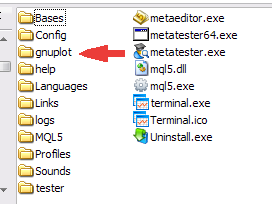
Figura 1. Posizionamento della cartella \gnuplot
Una volta spostata la cartella, è possibile modificare l'operatività dell'applicazione gnuplot. Per farlo, esegui il file \gnuplot\binary\wgnuplot.exe, quindi, quando appare il prompt dei comandi "gnuplot>", digita il comando "plot sin(x)". Di conseguenza, dovrebbe apparire una finestra con la funzione sin(x) disegnata. Inoltre, puoi provare gli esempi inclusi nella consegna dell'applicazione; per farlo, scegli la voce File\Demos e seleziona il file \gnuplot\demo\all.dem.
Ora, all'avvio dello script erremove.mq5, il grafico mostrato nella figura 2 verrà disegnato in una finestra separata:
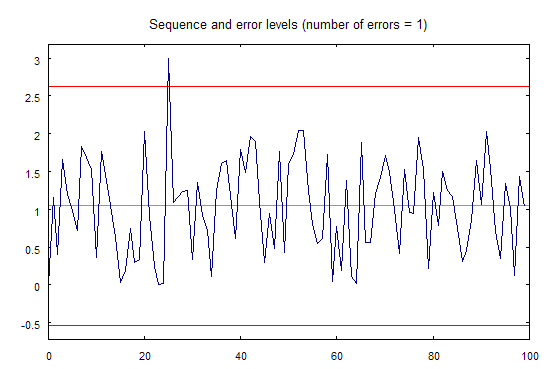
Figura 2. Il grafico che viene disegnato utilizzando lo script erremove.mq5.
Più avanti nell'articolo parleremo solo brevemente di alcune funzionalità dell'utilizzo di gnuplot, poiché le informazioni sul programma e sui suoi controlli possono essere facilmente trovate nella documentazione, fornita insieme ad esso, e in vari siti Web, come http://gnuplot.ikir.ru/.
Gli esempi di programmi scritti per questo articolo utilizzano un metodo di interazione più semplice con gnuplot per disegnare i grafici. All'inizio viene creato il file di testo gplot.txt; contiene i comandi di gnuplot e le informazioni da visualizzare. Quindi l'applicazione wgnuplot.exe viene avviata con il nome di quel file passato come argomento nella riga di comando. L'applicazione wgnuplot.exe viene chiamata utilizzando la funzione ShellExecuteW() importata dalla libreria di sistema shell32.dll; è il motivo per cui l'importazione di dll esterne deve essere consentita nel terminale client.
La versione di gnuplot data consente di disegnare i grafici in una finestra separata per due tipi di terminali: wxt e windows. Il terminale wxt utilizza gli algoritmi di antialiasing per il disegno dei grafici, cosa che permette di ottenere un'immagine di qualità superiore rispetto al terminale windows. Tuttavia, il terminale di Windows è stato utilizzato per scrivere gli esempi di questo articolo. Il motivo è che, quando si lavora con il terminale di Windows, il processo di sistema creato come risultato della chiamata "wgnuplot.exe -p MQL5\\Files\\gplot.txt" e l'apertura di una finestra del grafico viene automaticamente interrotto quando la finestra viene chiusa .
Se si sceglie il terminale wxt, quando si chiude la finestra del grafico il processo di sistema wgnuplot.exe non verrà chiuso automaticamente. Pertanto, se si utilizza il terminale wxt e si chiama wgnuplot.exe molte volte come descritto sopra, nel sistema potrebbero accumularsi più processi senza alcun segno di attività. Utilizzando la chiamata "wgnuplot.exe -p MQL5\\Files\\gplot.txt" e il terminale di Windows, è possibile evitare l'apertura di finestre aggiuntive indesiderate e la comparsa di processi di sistema non chiusi.
La finestra, dove viene visualizzato il grafico, è interattiva ed elabora gli eventi dei clic del mouse e della tastiera. Per ottenere le informazioni sui tasti di scelta rapida predefiniti, eseguire wgnuplot.exe, scegliere un tipo di terminale utilizzando il comando "set terminal windows" e tracciare qualsiasi grafico, ad esempio utilizzando il comando "plot sin(x)". Se la finestra del grafico è attiva (in primo piano), vedrai un suggerimento visualizzato nella finestra di testo di wgnuplot.exe non appena premi il pulsante "h".
Stima dei parametri
Dopo la breve conoscenza del metodo di disegno grafico, torniamo alla stima dei parametri della popolazione generale sulla base del suo campionamento finito. Supponendo che non siano noti parametri statistici della popolazione generale, utilizzeremo solo stime imparziali di questi parametri.
La stima dell'aspettativa matematica o media campionaria può essere considerata come il parametro principale che determina la distribuzione di una sequenza. La media campionaria viene calcolata utilizzando la seguente formula:
dove N è il numero di campioni nel campionamento.
Il valore medio è una stima del centro di distribuzione e viene utilizzato per il calcolo di altri parametri legati ai momenti centrali, cosa che rende questo parametro particolarmente importante. Oltre al valore medio, utilizzeremo la stima della dispersione (dispersione, varianza), la deviazione standard, il coefficiente di asimmetria (asimmetria) e il coefficiente di eccesso (curtosi) come parametri statistici.
dove m sta per i momenti centrali.
I momenti centrali sono caratteristiche numeriche di distribuzione di una popolazione generale.
Il secondo, terzo e quarto momento centrale selettivo sono determinati dalle seguenti espressioni:
Ma quei valori sono imparziali. Qui dovremmo menzionare la Statistica k e la Statistica h. In determinate condizioni, consentono di ottenere stime non distorte dei momenti centrali, quindi possono essere utilizzate per il calcolo di stime non distorte di dispersione, deviazione standard, asimmetria e curtosi.
Da notare che il calcolo del quarto momento nelle stime k e h viene eseguito in modi diversi. Come risultato, si ottengono espressioni diverse per la stima della curtosi quando si usa k o h. Ad esempio, in Microsoft Excel l'eccesso viene calcolato utilizzando la formula che corrisponde all'uso delle stime k, e nel libro "Statistics for Traders", la stima imparziale della curtosi viene eseguita utilizzando le stime h.
Scegliamo le stime h e poi, sostituendole al posto di 'm' nell'espressione data in precedenza, calcoleremo i parametri necessari.
Dispersione e Deviazione Standard:
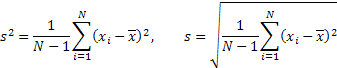
Asimmetria:
Curtosi:
Il coefficiente di eccesso (curtosi) calcolato secondo l'espressione data per la sequenza con legge di distribuzione normale è uguale a 3.
Occorre prestare attenzione che il valore ottenuto sottraendo 3 dal valore calcolato viene spesso utilizzato come valore di curtosi; quindi il valore ottenuto viene normalizzato rispetto alla normale legge di distribuzione. Nel primo caso, questo coefficiente è chiamato curtosi; nel secondo caso si parla di "curtosi in eccesso".
Il calcolo dei parametri secondo l'espressione data viene eseguito nella funzione dStat():
struct statParam { double mean; double median; double var; double stdev; double skew; double kurt; }; //---------------------------------------------------------------------------- int dStat(const double &x[],statParam &sP) { int i,m,n; double a,b,sum2,sum3,sum4,y[]; ZeroMemory(sP); // Reset sP n=ArraySize(x); if(n<4) // Error { Print("Function dStat() error!"); return(-1); } sP.kurt=1.0; ArrayResize(y,n); ArrayCopy(y,x); ArraySort(y); m=(n-1)/2; sP.median=y[m]; // Median if((n&0x01)==0)sP.median=(sP.median+y[m+1])/2.0; sP.mean=0; for(i=0;i<n;i++)sP.mean+=x[i]; sP.mean/=n; // Mean sum2=0;sum3=0;sum4=0; for(i=0;i<n;i++) { a=x[i]-sP.mean; b=a*a;sum2+=b; b=b*a;sum3+=b; b=b*a;sum4+=b; } if(sum2<1.e-150)return(1); sP.var=sum2/(n-1); // Variance sP.stdev=MathSqrt(sP.var); // Standard deviation sP.skew=n*sum3/(n-2)/sum2/sP.stdev; // Skewness sP.kurt=((n*n-2*n+3)*sum4/sum2/sum2-(6.0*n-9.0)/n)* (n-1.0)/(n-2.0)/(n-3.0); // Kurtosis return(1);Quando viene chiamato dStat(), l'indirizzo dell'array x[] viene passato alla funzione. Contiene i dati iniziali e il collegamento alla struttura statParam, che conterrà i valori calcolati dei parametri. In caso di errore quando ci sono meno di quattro elementi nell'array, la funzione restituisce -1.
Istogramma
Oltre ai parametri calcolati nella funzione dStat(), la legge di distribuzione della popolazione generale è molto interessante per noi. Per stimare visivamente la legge di distribuzione sul campionamento finito, possiamo disegnare un istogramma. Quando si disegna l'istogramma, l'intervallo di valori del campionamento è suddiviso in diverse sezioni simili. E quindi viene calcolato il numero di elementi in ciascuna sezione (frequenze di gruppo).
Inoltre, viene disegnato un diagramma a barre sulla base delle frequenze di gruppo. Si chiama istogramma. Dopo la normalizzazione alla larghezza dell'intervallo, l'istogramma rappresenterà una densità empirica di distribuzione di un valore casuale. Usiamo l'espressione empirica descritta nelle "Statistics for Traders" per determinare un numero ottimale di sezioni per disegnare l'istogramma:
dove L è il numero di sezioni richiesto, N è il volume di campionamento ed e è la curtosi.
Di seguito puoi trovare il dHist(), che determina il numero di sezioni, calcola il numero di elementi in ciascuna di esse e normalizza le frequenze di gruppo ottenute.
struct statParam { double mean; double median; double var; double stdev; double skew; double kurt; }; //---------------------------------------------------------------------------- int dHist(const double &x[],double &histo[],const statParam &sp) { int i,k,n,nbar; double a[],max,s,xmin; if(!ArrayIsDynamic(histo)) // Error { Print("Function dHist() error!"); return(-1); } n=ArraySize(x); if(n<4) // Error { Print("Function dHist() error!"); return(-1); } nbar=(sp.kurt+1.5)*MathPow(n,0.4)/6.0; if((nbar&0x01)==0)nbar--; if(nbar<5)nbar=5; // Number of bars ArrayResize(a,n); ArrayCopy(a,x); max=0.0; for(i=0;i<n;i++) { a[i]=(a[i]-sp.mean)/sp.stdev; // Normalization if(MathAbs(a[i])>max)max=MathAbs(a[i]); } xmin=-max; s=2.0*max*n/nbar; ArrayResize(histo,nbar+2); ArrayInitialize(histo,0.0); histo[0]=0.0;histo[nbar+1]=0.0; for(i=0;i<n;i++) { k=(a[i]-xmin)/max/2.0*nbar; if(k>(nbar-1))k=nbar-1; histo[k+1]++; } for(i=0;i<nbar;i++)histo[i+1]/=s; return(1); }
L'indirizzo dell'array x[], che contiene la sequenza iniziale, viene passato alla funzione. Il contenuto dell'array non viene modificato a seguito dell'esecuzione della funzione. Il parametro successivo è il collegamento all'array dinamico histo[], dove verranno memorizzati i valori calcolati. Il numero di elementi di quell'array corrisponderà al numero di sezioni utilizzate per il calcolo più due elementi.
Un elemento contenente valore zero viene aggiunto all'inizio e alla fine dell'array histo[]. L'ultimo parametro è l'indirizzo della struttura statParam, la quale deve contenere i valori precedentemente calcolati dei parametri in essa memorizzati. Nel caso in cui l'array histo[] passato alla funzione non sia un array dinamico o l'array di input x[] contenga meno di quattro elementi, la funzione interrompe la sua esecuzione e restituisce -1.
Dopo aver disegnato un istogramma dei valori ottenuti, puoi stimare visivamente se il campionamento corrisponde alla normale legge di distribuzione. Per una rappresentazione grafica più visiva della corrispondenza alla legge normale di distribuzione, possiamo disegnare un grafico con la scala di probabilità normale (Normal Probability Plot) oltre all'istogramma.
Grafico della probabilità normale
L'idea principale di disegnare un grafico di questo tipo è che l'asse X deve essere teso in modo che i valori visualizzati di una sequenza con distribuzione normale giacciano sulla stessa linea. In questo modo, l'ipotesi di normalità può essere verificata graficamente. Puoi trovare informazioni più dettagliate su questo tipo di grafici qui: "Normal probability plot" o "e-Handbook of Statistical Methods".
Per calcolare i valori richiesti e disegnare il grafico della probabilità normale, viene utilizzata la funzione dRankit() mostrata di seguito.
struct statParam { double mean; double median; double var; double stdev; double skew; double kurt; }; //---------------------------------------------------------------------------- int dRankit(const double &x[],double &resp[],double &xscale[],const statParam &sp) { int i,n; double np; if(!ArrayIsDynamic(resp)||!ArrayIsDynamic(xscale)) // Error { Print("Function dHist() error!"); return(-1); } n=ArraySize(x); if(n<4) // Error { Print("Function dHist() error!"); return(-1); } ArrayResize(resp,n); ArrayCopy(resp,x); ArraySort(resp); for(i=0;i<n;i++)resp[i]=(resp[i]-sp.mean)/sp.stdev; ArrayResize(xscale,n); xscale[n-1]=MathPow(0.5,1.0/n); xscale[0]=1-xscale[n-1]; np=n+0.365; for(i=1;i<(n-1);i++)xscale[i]=(i+1-0.3175)/np; for(i=0;i<n;i++)xscale[i]=ltqnorm(xscale[i]); return(1); } //---------------------------------------------------------------------------- double A1 = -3.969683028665376e+01, A2 = 2.209460984245205e+02, A3 = -2.759285104469687e+02, A4 = 1.383577518672690e+02, A5 = -3.066479806614716e+01, A6 = 2.506628277459239e+00; double B1 = -5.447609879822406e+01, B2 = 1.615858368580409e+02, B3 = -1.556989798598866e+02, B4 = 6.680131188771972e+01, B5 = -1.328068155288572e+01; double C1 = -7.784894002430293e-03, C2 = -3.223964580411365e-01, C3 = -2.400758277161838e+00, C4 = -2.549732539343734e+00, C5 = 4.374664141464968e+00, C6 = 2.938163982698783e+00; double D1 = 7.784695709041462e-03, D2 = 3.224671290700398e-01, D3 = 2.445134137142996e+00, D4 = 3.754408661907416e+00; //---------------------------------------------------------------------------- double ltqnorm(double p) { int s=1; double r,x,q=0; if(p<=0||p>=1){Print("Function ltqnorm() error!");return(0);} if((p>=0.02425)&&(p<=0.97575)) // Rational approximation for central region { q=p-0.5; r=q*q; x=(((((A1*r+A2)*r+A3)*r+A4)*r+A5)*r+A6)*q/(((((B1*r+B2)*r+B3)*r+B4)*r+B5)*r+1); return(x); } if(p<0.02425) // Rational approximation for lower region { q=sqrt(-2*log(p)); s=1; } else //if(p>0.97575) // Rational approximation for upper region { q = sqrt(-2*log(1-p)); s=-1; } x=s*(((((C1*q+C2)*q+C3)*q+C4)*q+C5)*q+C6)/((((D1*q+D2)*q+D3)*q+D4)*q+1); return(x); }
L'indirizzo dell'array x[] viene immesso nella funzione. L'array contiene la sequenza iniziale. I parametri successivi sono riferimenti agli array di output resp[] e xscale[]. Dopo l'esecuzione della funzione, negli array vengono scritti i valori utilizzati per disegnare il grafico rispettivamente sugli assi X e Y. Quindi l'indirizzo della struttura statParam viene passato alla funzione. Deve contenere i valori calcolati in precedenza dei parametri statistici della sequenza di input. In caso di errore la funzione restituisce -1.
Quando si formano i valori per l'asse X, viene chiamata la funzione ltqnorm(). Calcola la funzione integrale inversa della distribuzione normale. L'algoritmo utilizzato per il calcolo è tratto da "An algorithm for computing the inverse normal cumulative distribution function".
Quattro grafici
In precedenza ho citato la funzione dStat() dove vengono calcolati i valori dei parametri statistici. Ripetiamo brevemente il loro significato.
Dispersione (varianza): il valore medio dei quadrati di deviazione di un valore casuale dalla sua aspettativa matematica (valore medio). Il parametro che mostra quanto è grande la deviazione di un valore casuale dal suo centro di distribuzione. Maggiore è il valore di questo parametro, maggiore è la deviazione.
Deviazione standard: poiché la dispersione viene misurata come il quadrato di un valore casuale, la deviazione standard viene spesso utilizzata come caratteristica più evidente della dispersione. È uguale alla radice quadrata della dispersione.
Asimmetria: se disegniamo una curva di distribuzione di un valore casuale, l'asimmetria mostrerà quanto sia asimmetrica la curva di densità di probabilità rispetto al centro di distribuzione. Se il valore dell'asimmetria è maggiore di zero, la curva della densità di probabilità ha una pendenza a sinistra ripida e una pendenza a destra piatta. Se il valore dell'asimmetria è negativo, la pendenza sinistra è piatta e quella destra è ripida. Quando la curva della densità di probabilità è simmetrica al centro di distribuzione, l'asimmetria è uguale a zero.
Il coefficiente di eccesso (curtosi) descrive la nitidezza di un picco della curva di densità di probabilità e la pendenza delle pendenze delle code di distribuzione. Più acuto è il picco della curva vicino al centro di distribuzione, maggiore è il valore della curtosi.
Nonostante il fatto che i parametri statistici menzionati descrivano una sequenza in dettaglio, spesso è possibile caratterizzare una sequenza in modo più semplice, sulla base del risultato delle stime rappresentate in forma grafica. Ad esempio, un normale grafico di una sequenza può completare notevolmente una vista ottenuta durante l'analisi dei parametri statistici.
In precedenza nell'articolo ho citato le funzioni dHist() e dRankit() che consentono di preparare i dati per disegnare un istogramma o un grafico con la scala della probabilità normale. La visualizzazione dell'istogramma e del grafico di distribuzione normale insieme al grafico ordinario sullo stesso foglio consentono di determinare visivamente le principali caratteristiche della sequenza analizzata.
Questi tre grafici elencati dovrebbero essere integrati con un altro: il grafico con i valori correnti della sequenza sull'asse Y e i suoi valori precedenti sull'asse X. Tale grafico è chiamato "Lag Plot". Se c'è una forte correlazione tra indicazioni adiacenti, i valori di un campionamento si estenderanno in linea retta. E se non c'è correlazione tra indicazioni adiacenti, ad esempio quando si analizza una sequenza casuale, i valori saranno dispersi in tutto il grafico.
Per una rapida stima di un primo campionamento, suggerisco di disegnare quattro grafici su un unico foglio e di visualizzare su di esso i valori calcolati del parametro statistico. Questa non è un'idea nuova; qui puoi leggere di più sull'utilizzo dell'analisi dei quattro grafici menzionati: "4-Plot".
Alla fine dell'articolo c'è la sezione "File" contenente lo script s4plot.mq5, il quale disegna quei quattro grafici su un unico foglio. L'array dat[] viene creato all'interno della funzione OnStart() dello script. Contiene la sequenza iniziale. Vengono quindi richiamate di conseguenza le funzioni dStat(), dHist() e dRankit() per il calcolo dei dati necessari al disegno dei grafici. Successivamente viene chiamata la funzione vis4plot(). Crea un file di testo con i comandi gnuplot sulla base dei dati calcolati, quindi chiama l'applicazione per disegnare i grafici in una finestra separata.
Non ha senso mostrare l'intero codice dello script nell'articolo, poiché dStat(), dHist() e dRankit() sono stati descritti in precedenza, la funzione vis4plot(), che crea una sequenza di comandi gnuplot, non ha eventuali peculiarità significative e la descrizione dei comandi gnuplot esce dai limiti dell'oggetto dell'articolo. Oltre a ciò, puoi utilizzare un altro metodo per disegnare i grafici invece dell'applicazione gnuplot.
Quindi mostriamo solo una parte di s4plot.mq5, ovvero la sua funzione OnStart().
//---------------------------------------------------------------------------- // Script program start function //---------------------------------------------------------------------------- void OnStart() { int i; double dat[128],histo[],rankit[],xrankit[]; statParam sp; MathSrand(1); for(i=0;i<ArraySize(dat);i++) dat[i]=MathRand(); if(dStat(dat,sp)==-1)return; if(dHist(dat,histo,sp)==-1)return; if(dRankit(dat,rankit,xrankit,sp)==-1)return; vis4plot(dat,histo,rankit,xrankit,sp,6); }
In questo esempio, viene utilizzata una sequenza casuale per riempire l'array dat[] con i dati iniziali utilizzando la funzione MathRand(). L'esecuzione dello script dovrebbe comportare quanto segue:
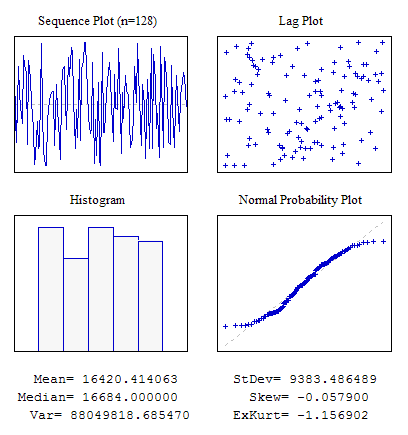
Figura 3. Quattro grafici. Script s4plot.mq5
Dovresti prestare attenzione all'ultimo parametro della funzione vis4plot(). È responsabile del formato dei valori numerici emessi. In questo esempio, i valori vengono emessi con sei cifre decimali. Questo parametro è uguale a quello che determina il formato nella funzione DoubleToString().
Se i valori della sequenza di input sono troppo piccoli o troppo grandi, puoi utilizzare il formato scientifico per una visualizzazione più ovvia. Per farlo, imposta quel parametro su -5, ad esempio. Il valore -5 è impostato come predefinito per la funzione vis4plot().
Per dimostrare l'ovvietà del metodo dei quattro grafici per la visualizzazione delle peculiarità di una sequenza, abbiamo bisogno di un generatore di tali sequenze.
Generatore di una sequenza pseudo-casuale
La classe RNDXor128 è destinata alla generazione di sequenze pseudo-casuali.
Di seguito, è riportato il codice sorgente del file include che descrive quella classe.
//----------------------------------------------------------------------------------- // RNDXor128.mqh // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #include <Object.mqh> //----------------------------------------------------------------------------------- // Generation of pseudo-random sequences. The Xorshift RNG algorithm // (George Marsaglia) with the 2**128 period of initial sequence is used. // uint rand_xor128() // { // static uint x=123456789,y=362436069,z=521288629,w=88675123; // uint t=(x^(x<<11));x=y;y=z;z=w; // return(w=(w^(w>>19))^(t^(t>>8))); // } // Methods: // Rand() - even distribution withing the range [0,UINT_MAX=4294967295]. // Rand_01() - even distribution within the range [0,1]. // Rand_Norm() - normal distribution with zero mean and dispersion one. // Rand_Exp() - exponential distribution with the parameter 1.0. // Rand_Laplace() - Laplace distribution with the parameter 1.0 // Reset() - resetting of all basic values to initial state. // SRand() - setting new basic values of the generator. //----------------------------------------------------------------------------------- #define xor32 xx=xx^(xx<<13);xx=xx^(xx>>17);xx=xx^(xx<<5) #define xor128 t=(x^(x<<11));x=y;y=z;z=w;w=(w^(w>>19))^(t^(t>>8)) #define inidat x=123456789;y=362436069;z=521288629;w=88675123;xx=2463534242 class RNDXor128:public CObject { protected: uint x,y,z,w,xx,t; uint UINT_half; public: RNDXor128() {UINT_half=UINT_MAX>>1;inidat;}; double Rand() {xor128;return((double)w);}; int Rand(double& a[],int n) {int i;if(n<1)return(-1); if(ArraySize(a)<n)return(-2); for(i=0;i<n;i++){xor128;a[i]=(double)w;} return(0);}; double Rand_01() {xor128;return((double)w/UINT_MAX);}; int Rand_01(double& a[],int n) {int i;if(n<1)return(-1); if(ArraySize(a)<n)return(-2); for(i=0;i<n;i++){xor128;a[i]=(double)w/UINT_MAX;} return(0);}; double Rand_Norm() {double v1,v2,s,sln;static double ra;static uint b=0; if(b==w){b=0;return(ra);} do{ xor128;v1=(double)w/UINT_half-1.0; xor128;v2=(double)w/UINT_half-1.0; s=v1*v1+v2*v2; } while(s>=1.0||s==0.0); sln=MathLog(s);sln=MathSqrt((-sln-sln)/s); ra=v2*sln;b=w; return(v1*sln);}; int Rand_Norm(double& a[],int n) {int i;if(n<1)return(-1); if(ArraySize(a)<n)return(-2); for(i=0;i<n;i++)a[i]=Rand_Norm(); return(0);}; double Rand_Exp() {xor128;if(w==0)return(DBL_MAX); return(-MathLog((double)w/UINT_MAX));}; int Rand_Exp(double& a[],int n) {int i;if(n<1)return(-1); if(ArraySize(a)<n)return(-2); for(i=0;i<n;i++)a[i]=Rand_Exp(); return(0);}; double Rand_Laplace() {double a;xor128; a=(double)w/UINT_half; if(w>UINT_half) {a=2.0-a; if(a==0.0)return(-DBL_MAX); return(MathLog(a));} else {if(a==0.0)return(DBL_MAX); return(-MathLog(a));}}; int Rand_Laplace(double& a[],int n) {int i;if(n<1)return(-1); if(ArraySize(a)<n)return(-2); for(i=0;i<n;i++)a[i]=Rand_Laplace(); return(0);}; void Reset() {inidat;}; void SRand(uint seed) {int i;if(seed!=0)xx=seed; for(i=0;i<16;i++){xor32;} xor32;x=xx;xor32;y=xx; xor32;z=xx;xor32;w=xx; for(i=0;i<16;i++){xor128;}}; int SRand(uint xs,uint ys,uint zs,uint ws) {int i;if(xs==0&&ys==0&&zs==0&&ws==0)return(-1); x=xs;y=ys;z=zs;w=ws; for(i=0;i<16;i++){xor128;} return(0);}; }; //-----------------------------------------------------------------------------------
L'algoritmo utilizzato per generare una sequenza casuale è descritto in dettaglio nell'articolo "Xorshift RNGs" di George Marsaglia (vedi xorshift.zip alla fine dell'articolo). I metodi della classe RNDXor128 sono descritti nel file RNDXor128.mqh. Utilizzando questa classe si possono ottenere sequenze con distribuzione pari, normale o esponenziale o con distribuzione di Laplace (doppio esponenziale).
È necessario prestare attenzione al fatto che, quando viene creata un'istanza della classe RNDXor128, i valori di base della sequenza vengono impostati sullo stato iniziale. Pertanto, contrariamente alla chiamata della funzione MathRand(), ad ogni nuovo inizio di uno script o di un indicatore che utilizza RNDXor128 verrà generata una stessa sequenza. Lo stesso di quando si chiama MathSrand() e poi MathRand().
Esempi di sequenza
Di seguito, a titolo di esempio, puoi trovare i risultati ottenuti analizzando sequenze estremamente diverse tra loro con le loro proprietà.
Esempio 1. Una sequenza casuale con la legge di distribuzione pari.
#include "RNDXor128.mqh" RNDXor128 Rnd; //---------------------------------------------------------------------------- void OnStart() { int i; double dat[512]; for(i=0;i<ArraySize(dat);i++) dat[i]=Rnd.Rand_01(); ... }
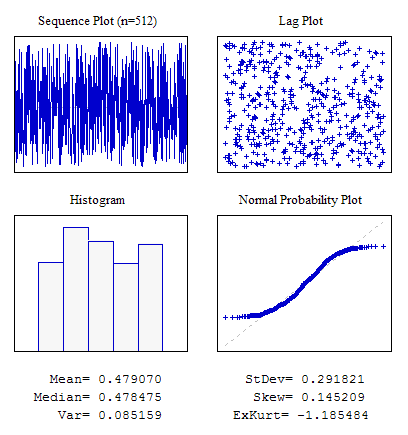
Figura 4. Distribuzione uniforme
Esempio 2. Una sequenza casuale con la normale legge di distribuzione.
#include "RNDXor128.mqh" RNDXor128 Rnd; //---------------------------------------------------------------------------- void OnStart() { int i; double dat[512]; for(i=0;i<ArraySize(dat);i++) dat[i]=Rnd.Rand_Norm(); ... }
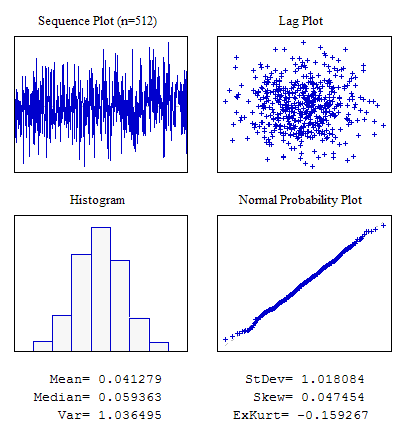
Figura 5. Distribuzione normale
Esempio 3. Una sequenza casuale con la legge esponenziale della distribuzione.
#include "RNDXor128.mqh" RNDXor128 Rnd; //---------------------------------------------------------------------------- void OnStart() { int i; double dat[512]; for(i=0;i<ArraySize(dat);i++) dat[i]=Rnd.Rand_Exp(); ... }
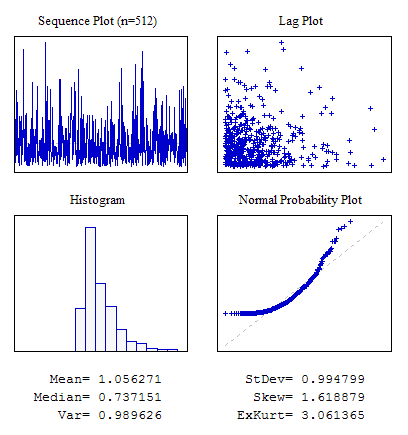
Figura 6. Distribuzione esponenziale
Esempio 4. Una sequenza casuale con distribuzione di Laplace.
#include "RNDXor128.mqh" RNDXor128 Rnd; //---------------------------------------------------------------------------- void OnStart() { int i; double dat[512]; for(i=0;i<ArraySize(dat);i++) dat[i]=Rnd.Rand_Laplace(); ... }
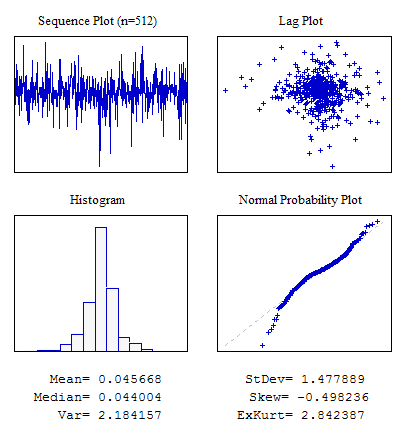
Figura 7. Distribuzione Laplace
Esempio 5. Sequenza sinusoidale
//---------------------------------------------------------------------------- void OnStart() { int i; double dat[512]; for(i=0;i<ArraySize(dat);i++) dat[i]=MathSin(2*M_PI/4.37*i); ... }
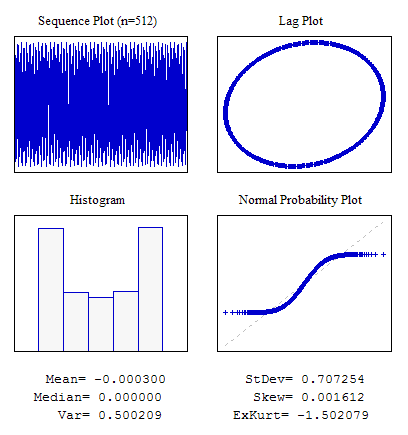
Figura 8. Sequenza sinusoidale
Esempio 6. Una sequenza con correlazione visibile tra indicazioni adiacenti.
#include "RNDXor128.mqh" RNDXor128 Rnd; //---------------------------------------------------------------------------- void OnStart() { int i; double dat[512],a; for(i=0;i<ArraySize(dat);i++) {a+=Rnd.Rand_Laplace();dat[i]=a;} ... }
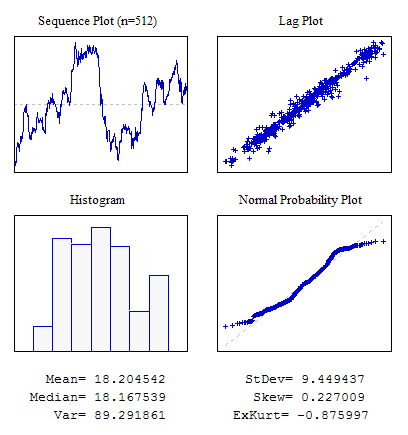
Figura 9. Correlazione tra indicazioni adiacenti
Conclusione
Lo sviluppo di algoritmi di programma che implementano qualsiasi tipo di calcolo è sempre un lavoro duro da fare. Il motivo è la necessità di considerare molti requisiti per ridurre al minimo gli errori che possono verificarsi durante l'arrotondamento, il troncamento e l'overflow delle variabili.
Durante la scrittura degli esempi per l'articolo non ho eseguito alcuna analisi degli algoritmi del programma. Durante la scrittura della funzione, gli algoritmi matematici sono stati implementati "direttamente. Quindi, se li utilizzerai in applicazioni "serie", devi analizzare la loro stabilità e precisione.
L'articolo non descrive affatto le caratteristiche dell'applicazione gnuplot. Queste domande vanno appena oltre lo scopo di questo articolo. Ad ogni modo, vorrei menzionare che gnuplot può essere adattato per l'utilizzo congiunto con MetaTrader 5. A tal fine, è necessario apportare alcune correzioni al codice sorgente e ricompilarlo. Inoltre, il modo di passare comandi a gnuplot utilizzando un file probabilmente non è un modo ottimale, poiché l'interazione con gnuplot può essere organizzata tramite un'interfaccia di programmazione.
File
- erremove.mq5 – esempio di script che esclude errori da un campionamento.
- function_dstat.mq5 – funzione per il calcolo dei parametri statistici.
- function_dhist.mq5 - funzione per il calcolo dei valori dell'istogramma.
- function_drankit.mq5 – funzione per il calcolo dei valori utilizzata quando si disegna un grafico con la scala della distribuzione normale.
- s4plot.mq5 – esempio di script che disegna quattro grafici su un unico foglio.
- RNDXor128.mqh – classe del generatore di una sequenza casuale.
- xorshift.zip - George Marsaglia. "Xorshift RNGs".
Tradotto dal russo da MetaQuotes Ltd.
Articolo originale: https://www.mql5.com/ru/articles/273
Utilizzo di feature map auto-organizzanti (mappe Kohonen) su MetaTrader 5
Tracciamento, debug e analisi strutturale del codice sorgente
Creazione di criteri personalizzati di ottimizzazione degli Expert Advisor
Distribuzioni statistiche di probabilità in MQL5
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Accetti la politica del sito e le condizioni d’uso