
统计估计
简介
如今,您经常能看到与计量经济学、价格序列预测、选择和估计模型的适当性等主题相关的文章和出版物。但在大多数情形下,推理基于以下假设,即读者精通数学统计方法且能够轻松估计所分析序列的统计参数。
对某个序列的统计参数进行估计非常重要,因为大多数数学模型和方法均基于不同的假设。例如,正态分布规律或离差值(或其他参数)就是这样。因此,在分析和预测时间序列时,我们需要一个简单方便的工具,用于快速清晰地估计主要统计参数。在本文中,我们将尝试创建一个这样的工具。
本文简要说明了一个随机序列的最简单统计参数,以及其可视分析的几种方法。本文还说明了如何在 MQL5 中实现这些方法,以及使用 Gnuplot 应用程序对计算结果进行可视化的方法。本文无意作为手册或参考资料使用,所以可能会包含某些普遍接受的术语和定义。
样本参数分析
假定在时间中存在一个无限存在的静止过程,该过程可被表示为一个离散样本序列。让我们将这个样本序列称为总体。从总体中选出的一部分样本被称为从总体得出的采样或对 N 个样本进行的采样。此外,假设我们不知道任何参数真实值,因此我们将依据有限采样的方法进行估计。
避免异常值
在开始参数的统计估计之前,我们应注意,如果采样包含过大误差(异常值),则估计的精度可能不够。如果采样量太少,则异常值会对估计精度产生较大影响。异常值指异常偏离分布中心的值。此类偏离可能是由于在采集统计数据和形成序列时出现的不同罕见事件和错误而造成的。
很难决定是否要筛选出异常值,因为在大多数情形下无法明确确定某个值是异常值还是属于所分析的过程。因此,如果检测到异常值并决定筛选出它们,就会出现一个问题 - 我们该如何处理这些误差值?最符合逻辑的做法就是将它们从采样中排除,这样可以提升统计特征的估计精度;但是在处理时间序列时,您应谨慎地从采样中排除异常值。
为了能够从采样中排除异常值,或至少检测到这些值,让我们来实现 S.V. Bulashev 所著《 Statistics for Traders》(面向交易者的统计)一书中所介绍的算法吧。
根据该算法,我们需要计算分布中心的五个估计值:
- 中值;
- 50% 四分位中心间距(中四分位距,MQR);
- 整个采样的算术平均值;
- 50% 四分位距的算术平均值(四分位距平均值,IQM);
- 间距的中心(中列数)- 确定为采样中最大值和最小值的平均值。
接下来按升序排列分布中心的估计结果;然后选择平均值(即序列中的第三个值)作为分布中心 Xcen。因此,所选择的估计值似乎受异常值的影响最小。
此外,使用得出的分布中心估计值 Xcen并根据以下经验公式可计算出标准方差 s、超量系数 K 和删减系数的值:
![]()
其中 N 是采样中样本的数量(采样量)。
接下来超出以下范围:
![]()
的值将被视为异常值,因此应从采样中排除。
在《Statistics for Traders》(面向交易者的统计)一书中详细介绍了这种方法,因此让我们直接开始算法的实现。允许检测和排除异常值的算法是在 erremove() 函数中实现的。
您可以在以下部分找到为测试此函数而编写的脚本。
//---------------------------------------------------------------------------- // erremove.mq5 // Copyright 2011, MetaQuotes Software Corp. // https://www.mql5.com //---------------------------------------------------------------------------- #property copyright "Copyright 2011, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" #import "shell32.dll" bool ShellExecuteW(int hwnd,string lpOperation,string lpFile, string lpParameters,string lpDirectory,int nShowCmd); #import //---------------------------------------------------------------------------- // Script program start function //---------------------------------------------------------------------------- void OnStart() { int i; double dat[100]; double y[]; srand(1); for(i=0;i<ArraySize(dat);i++)dat[i]=rand()/16000.0; dat[25]=3; // Make Error !!! erremove(dat,y,1); } //---------------------------------------------------------------------------- int erremove(const double &x[],double &y[],int visual=1) { int i,m,n; double a[],b[5]; double dcen,kurt,sum2,sum4,gs,v,max,min; if(!ArrayIsDynamic(y)) // Error { Print("Function erremove() error!"); return(-1); } n=ArraySize(x); if(n<4) // Error { Print("Function erremove() error!"); return(-1); } ArrayResize(a,n); ArrayCopy(a,x); ArraySort(a); b[0]=(a[0]+a[n-1])/2.0; // Midrange m=(n-1)/2; b[1]=a[m]; // Median if((n&0x01)==0)b[1]=(b[1]+a[m+1])/2.0; m=n/4; b[2]=(a[m]+a[n-m-1])/2.0; // Midquartile range b[3]=0; for(i=m;i<n-m;i++)b[3]+=a[i]; // Interquartile mean(IQM) b[3]=b[3]/(n-2*m); b[4]=0; for(i=0;i<n;i++)b[4]+=a[i]; // Mean b[4]=b[4]/n; ArraySort(b); dcen=b[2]; // Distribution center sum2=0; sum4=0; for(i=0;i<n;i++) { a[i]=a[i]-dcen; v=a[i]*a[i]; sum2+=v; sum4+=v*v; } if(sum2<1.e-150)kurt=1.0; kurt=((n*n-2*n+3)*sum4/sum2/sum2-(6.0*n-9.0)/n)*(n-1.0)/(n-2.0)/(n-3.0); // Kurtosis if(kurt<1.0)kurt=1.0; gs=(1.55+0.8*MathLog10((double)n/10.0)*MathSqrt(kurt-1))*MathSqrt(sum2/(n-1)); max=dcen+gs; min=dcen-gs; m=0; for(i=0;i<n;i++)if(x[i]<=max&&x[i]>=min)a[m++]=x[i]; ArrayResize(y,m); ArrayCopy(y,a,0,0,m); if(visual==1)vis(x,dcen,min,max,n-m); return(n-m); } //---------------------------------------------------------------------------- void vis(const double &x[],double dcen,double min,double max,int numerr) { int i; double d,yma,ymi; string str; yma=x[0];ymi=x[0]; for(i=0;i<ArraySize(x);i++) { if(yma<x[i])yma=x[i]; if(ymi>x[i])ymi=x[i]; } if(yma<max)yma=max; if(ymi>min)ymi=min; d=(yma-ymi)/20.0; yma+=d;ymi-=d; str="unset key\n"; str+="set title 'Sequence and error levels (number of errors = "+ (string)numerr+")' font ',10'\n"; str+="set yrange ["+(string)ymi+":"+(string)yma+"]\n"; str+="set xrange [0:"+(string)ArraySize(x)+"]\n"; str+="plot "+(string)dcen+" lt rgb 'green',"; str+=(string)min+ " lt rgb 'red',"; str+=(string)max+ " lt rgb 'red',"; str+="'-' with line lt rgb 'dark-blue'\n"; for(i=0;i<ArraySize(x);i++)str+=(string)x[i]+"\n"; str+="e\n"; if(!saveScript(str)){Print("Create script file error");return;} if(!grPlot())Print("ShellExecuteW() error"); } //---------------------------------------------------------------------------- bool grPlot() { string pnam,param; pnam="GNUPlot\\binary\\wgnuplot.exe"; param="-p MQL5\\Files\\gplot.txt"; return(ShellExecuteW(NULL,"open",pnam,param,NULL,1)); } //---------------------------------------------------------------------------- bool saveScript(string scr1="",string scr2="") { int fhandle; fhandle=FileOpen("gplot.txt",FILE_WRITE|FILE_TXT|FILE_ANSI); if(fhandle==INVALID_HANDLE)return(false); FileWriteString(fhandle,"set terminal windows enhanced size 560,420 font 8\n"); FileWriteString(fhandle,scr1); if(scr2!="")FileWriteString(fhandle,scr2); FileClose(fhandle); return(true); } //----------------------------------------------------------------------------
让我们详细研究下 erremove() 函数。作为函数的第一个参数,我们传递数组 x[] 的地址,并在该数组中存储所分析采样的值;采样量不得小于四个元素。假定数组 x[] 的大小等于采样大小,这也是不传递采样量中 N 值的原因。执行函数并不会导致数组 x[] 中存储的数据发生变化。
下一个参数是数组 y[] 的地址。如果成功执行了该函数,该数组将包含排除异常值之后的输入序列。数组 y[] 的大小比数组 x[] 的要小,其差值等于从采样中排除的值的数量。数组 y[] 必须被声明为动态数组,否则无法在函数主体中更改其大小。
最后一个(可选)参数是负责实现计算结果可视化的标志。如果其值等于 1(默认值),则在函数执行完毕前,在一个单独窗口中会显示含有以下信息的图表:输入序列、分布中心线和范围极限,超过该范围的值将被视为异常值。
以后将会介绍绘制图表的方法。如果成功执行,则函数会返回从采样中排除的值的数量;如果出现错误,则返回 -1。如果找不到偏差较大的值(异常值),则函数将返回 0,并且数组 y[] 中的序列将与 x[] 中的序列相同。
在函数的开头,信息会从数组 x[] 复制到数组 a[],然后按升序排序,接下来再计算分布中心的五个估计值。
区间的中心(中列数)等于排序后的数组 a[] 的极值之和再除以 2。
中值的计算分为两种,对于奇数采样量 N,采用以下等式:
![]()
对于偶数采样量,采用以下等式:
![]()
考虑到排序后数组 a[] 的索引从 0 开始,我们得到:
m=(n-1)/2; median=a[m]; if((n&0x01)==0)b[1]=(median+a[m+1])/2.0;
50% 四分位中心间距(中四分位矩,MQR):
![]()
其中 M=N/4(整除)。
对于排序后的数组 a[],我们得到:
m=n/4; MQR=(a[m]+a[n-m-1])/2.0; // Midquartile range
50% 四分位距的算术平均值(四分位距平均值,IQM)。从采样的两个极端值中去除了 25% 的样本,剩余的 50% 用于计算算术平均值:
![]()
其中 M=N/4(整除)。
m=n/4; IQM=0; for(i=m;i<n-m;i++)IQM+=a[i]; IQM=IQM/(n-2*m); // Interquartile mean(IQM)
算术平均值(平均值)通过整个采样来确定。
每一个确定的值都被写入 b[] 数组,然后按升序排列该数组。数组中的元素 b[2] 的值被选为分布中心。此外,我们还将使用该值来计算算术平均值和多余量系数的无偏估计值,并将在以后说明算法。
接下来使用得出的估计值来计算异常值的删减系数和范围限制(表达式如上所示)。最后,数组 y[] 中会生成排除了异常值的序列,并会调用 vis() 函数来绘制图形。让我们简单看下本文所用的可视化方法。
可视化
为了显示计算结果,我使用了免费应用程序 Gnuplot,该程序用于绘制各种 2D 和 3D 图形。Gnuplot 能够在屏幕上显示图表(在单独的窗口中)或以不同的图形格式将图表写入一个文件。可以从预备的文本文件中执行绘图命令。Gnuplot 项目的官方网页为 gnuplot.sourceforge.net。应用程序支持多个平台,并且作为源代码文件以及专为某个平台编译的二进制文件予以发布。
在 Windows XP SP3 中使用 4.2.2 版 Gnuplot 测试了专为本文编写的示例。可以在 http://sourceforge.net/projects/gnuplot/files/gnuplot/4.4.2/ 下载 gp442win32.zip 文件。我没有用其他版本 的 Gnuplot 测试这些示例。
下载 gp442win32.zip 档案之后,请将其解压缩。这样就创建了 \gnuplot 文件夹,该文件夹包含应用程序、帮助文件、说明文档和示例。要与应用程序互动,请将整个 \gnuplot 文件夹放到 MetaTrader 5 客户端的根文件夹中。
图 1. 文件夹 \gnuplot 的放置
移动完文件夹之后,您可以更改 Gnuplot 应用程序的可操作性。为此,执行文件 \gnuplot\binary\wgnuplot.exe,然后在 "gnuplot>" 命令提示符出现时键入 "plot sin(x)" 命令。结果,会出现一个在其中绘制有 sin(x) 函数的窗口。您还可以尝试包含在应用程序交付包中的示例;为此,请选择 File\Demos 菜单项,然后选择文件 \gnuplot\demo\all.dem。
现在,在您启动 erremove.mq5 脚本时,将会在一个单独的窗口中绘制图 2 所示的图形:
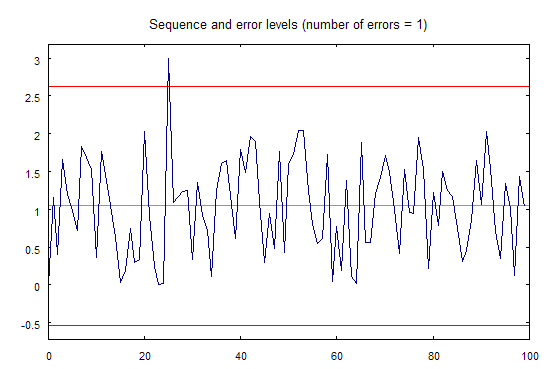
图 2. 使用 erremove.mq5 脚本绘制的图形。
此外,在本文中我们将很少讨论 Gnuplot 使用方面的一些特点,因为您可以在程序随附的说明文档和各个网站(例如 http://gnuplot.ikir.ru/)中轻松找到有关程序及其控制的信息。
为本文所写的程序示例使用与 Gnuplot 互动的最简单方法来绘制图表。首先,创建文本文件 gplot.txt;该文件包含 Gnuplot 命令以及要显示的信息。接下来启动 wgnuplot.exe 应用程序,并且该文件的名称作为命令行中的一个参数传递。使用从系统库文件 shell32.dll 导入的 ShellExecuteW() 函数来调用 wgnuplot.exe 应用程序;这就是为什么必须在客户端中允许导入外部 dll 文件的原因。
所提供的 Gnuplot 版本允许针对两类终端(wxt 和视窗)在一个单独窗口中绘制图表:wxt 终端使用抗锯齿算法来绘制图表,与窗口终端相比能够获得品质更高的画面。然而,在编写本文示例时使用了窗口终端。原因是在使用窗口终端时,通过调用 "wgnuplot.exe -p MQL5\\Files\\gplot.txt" 和打开图形窗口创建的系统进程在窗口关闭时会自动关闭。
如果选择 wxt 终端,则在关闭图表窗口时,系统进程 wgnuplot.exe 将不会自动关闭。因此,如果使用 wxt 客户端并如上所述多次调用 wgnuplot.exe,则可能在系统中累积起多个没有任何活动迹象的进程。使用 "wgnuplot.exe -p MQL5\\Files\\gplot.txt" 调用和窗口终端,便可以避免打开不必要的其他窗口以及出现未关闭的系统进程。
显示图表的窗口具有交互性,可处理鼠标单击事件和键盘事件。要获取默认热键的信息,请运行 wgnuplot.exe,使用 "set terminal windows" 命令选择一个终端类型,然后再绘制任何图表,例如使用 "plot sin(x)" 命令。如果图表窗口处于活动状态(突出显示),则只要按下 "h" 键即可在 wgnuplot.exe 的文本窗口中看到一个提示。
参数的估计
在快速了解图表绘制方法之后,让我们返回到依据总体有限采样进行的总体参数估计上来。假定不知道总体的统计参数,我们将仅使用这些参数的无偏估计值。
数学期望值的估计值或采样平均值可被视为确定序列分布的主要参数。使用以下公式计算采样平均值:
![]()
其中 N 是采样中样本的数量。
平均值是分布中心的估计值,用于计算与中心移动相关的其他参数,这使得该参数特别重要。除平均值以外,我们还使用离差(离差、方差)、标准方差、偏度系数(偏度)和超量系数(峰度)作为统计参数。
![]()
其中 m 是中心动差。
中心动差是总体分布的数字特征。
第二个、第三个和第四个选择性中心动差通过以下表达式确定:
![]()
但是这些值是无偏的。在这里,我们应提一下 k 统计量和 h 统计量。在某些条件下,它们能够允许获得中心动差的无偏估计值,因此可用于计算离差、标准方差、偏度和峰度的无偏估计值。
注意,在 k 和 h 估计中,第四动差的计算是以不同方式进行的。这样一来,在使用 k 或 h 评估峰度时便获得了不同表达式。例如,在 Microsoft Excel 中,使用对应于采用 k 估计的公式计算超出量,而在《Statistics for Traders》(面向交易者的统计)一书中,峰度的无偏估计则使用 h 估计值进行。
让我们选择 h 估计值,然后通过将其替换为先前给出的表达式中的 "m",就可以计算出所需的参数了。
离差和标准方差:
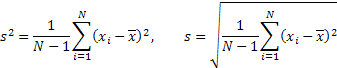
偏度:
![]()
峰度:
![]()
为遵守正态分布规律的序列给出了表达式,根据这一表达式计算出的超量系数(峰度)等于 3。
您应该注意到,从计算出来的值减去 3 后所得到的值经常被用作峰度值;因此,得到的值相对于正态分布规律实现了标准化。在第一种情形中,此系数被称为峰度;在第二种情形中,它被称为“超出峰度”。
在 dStat() 函数中根据给出表达式来计算参数:
struct statParam { double mean; double median; double var; double stdev; double skew; double kurt; }; //---------------------------------------------------------------------------- int dStat(const double &x[],statParam &sP) { int i,m,n; double a,b,sum2,sum3,sum4,y[]; ZeroMemory(sP); // Reset sP n=ArraySize(x); if(n<4) // Error { Print("Function dStat() error!"); return(-1); } sP.kurt=1.0; ArrayResize(y,n); ArrayCopy(y,x); ArraySort(y); m=(n-1)/2; sP.median=y[m]; // Median if((n&0x01)==0)sP.median=(sP.median+y[m+1])/2.0; sP.mean=0; for(i=0;i<n;i++)sP.mean+=x[i]; sP.mean/=n; // Mean sum2=0;sum3=0;sum4=0; for(i=0;i<n;i++) { a=x[i]-sP.mean; b=a*a;sum2+=b; b=b*a;sum3+=b; b=b*a;sum4+=b; } if(sum2<1.e-150)return(1); sP.var=sum2/(n-1); // Variance sP.stdev=MathSqrt(sP.var); // Standard deviation sP.skew=n*sum3/(n-2)/sum2/sP.stdev; // Skewness sP.kurt=((n*n-2*n+3)*sum4/sum2/sum2-(6.0*n-9.0)/n)* (n-1.0)/(n-2.0)/(n-3.0); // Kurtosis return(1);在调用 dStat() 时,数组 x[] 的地址被传递给函数。它包含初始数据以及到 statParam 结构的链接,该结构将包含计算出来的参数值。当发生数组少于四个元素的错误时,函数会返回 -1。
直方图
除了在 dStat() 函数中计算的参数以外,总体的分布规律也让我们产生了很大兴趣。为了以可视方式估计有限采样的分布规律,我们可以绘制一个直方图。在绘制直方图时,采样值范围被分为若干个类似段。然后会计算各段中的元素数量(组频)。
此外,也可根据组频绘制一个柱状图。它被称为直方图。在标准化到范围宽度以后,直方图将表示一个随机值的经验分布密度。让我们使用《Statistics for Traders》(面向交易者的统计)一书所介绍的经验表达式来确定绘制直方图的最佳分段数量:
![]()
其中 L 是所需的段数,N 是采样量,e 是峰度。
下面是 dHist() 函数,该函数用于确定段数,计算各段中的元素数量并对获得的组频进行标准化。
struct statParam { double mean; double median; double var; double stdev; double skew; double kurt; }; //---------------------------------------------------------------------------- int dHist(const double &x[],double &histo[],const statParam &sp) { int i,k,n,nbar; double a[],max,s,xmin; if(!ArrayIsDynamic(histo)) // Error { Print("Function dHist() error!"); return(-1); } n=ArraySize(x); if(n<4) // Error { Print("Function dHist() error!"); return(-1); } nbar=(sp.kurt+1.5)*MathPow(n,0.4)/6.0; if((nbar&0x01)==0)nbar--; if(nbar<5)nbar=5; // Number of bars ArrayResize(a,n); ArrayCopy(a,x); max=0.0; for(i=0;i<n;i++) { a[i]=(a[i]-sp.mean)/sp.stdev; // Normalization if(MathAbs(a[i])>max)max=MathAbs(a[i]); } xmin=-max; s=2.0*max*n/nbar; ArrayResize(histo,nbar+2); ArrayInitialize(histo,0.0); histo[0]=0.0;histo[nbar+1]=0.0; for(i=0;i<n;i++) { k=(a[i]-xmin)/max/2.0*nbar; if(k>(nbar-1))k=nbar-1; histo[k+1]++; } for(i=0;i<nbar;i++)histo[i+1]/=s; return(1); }
数组 x[] 的地址被传递合函数。它包含初始序列。函数的执行不会导致数组的内容发生变化。接下来的参数用作到动态数组 histo[] 的链接,将在该数组中存储计算出来的值。该数组的元素数量将等于计算所用段数再加上两个元素。
在数组 histo[] 的开头和结束各添加一个包含零值的元素。最后一个参数是 statParam 结构的地址,该结构应包含先前计算出来并存储在其中的参数值。如果传递给函数的数组 histo[] 不是一个动态数组,或者输入数组 x[] 包含的元素少于四个,则函数会停止执行并返回 -1。
一旦绘制了所获值的直方图,就可以按可视方式估计采样是否遵守正态分布规律。为了获得更加可视化的是否遵守正态分布规律的图示,除直方图以外,我们还可以绘制带有正态概率刻度的图形(正态概率图)。
正态概率图
绘制此类图形的主要目的是应当拉伸 X 轴,从而让遵守正态分布规律的序列的显示值位于同一直线上。如此一来,便可以通过图形方式来检查正态性假设。您可以通过以下链接查找有关此类图形的详细信息:"正态概率图" 或 "统计方法电子手册"。
为了计算绘制正态概率图所需的值,使用了以下函数 dRankit()。
struct statParam { double mean; double median; double var; double stdev; double skew; double kurt; }; //---------------------------------------------------------------------------- int dRankit(const double &x[],double &resp[],double &xscale[],const statParam &sp) { int i,n; double np; if(!ArrayIsDynamic(resp)||!ArrayIsDynamic(xscale)) // Error { Print("Function dHist() error!"); return(-1); } n=ArraySize(x); if(n<4) // Error { Print("Function dHist() error!"); return(-1); } ArrayResize(resp,n); ArrayCopy(resp,x); ArraySort(resp); for(i=0;i<n;i++)resp[i]=(resp[i]-sp.mean)/sp.stdev; ArrayResize(xscale,n); xscale[n-1]=MathPow(0.5,1.0/n); xscale[0]=1-xscale[n-1]; np=n+0.365; for(i=1;i<(n-1);i++)xscale[i]=(i+1-0.3175)/np; for(i=0;i<n;i++)xscale[i]=ltqnorm(xscale[i]); return(1); } //---------------------------------------------------------------------------- double A1 = -3.969683028665376e+01, A2 = 2.209460984245205e+02, A3 = -2.759285104469687e+02, A4 = 1.383577518672690e+02, A5 = -3.066479806614716e+01, A6 = 2.506628277459239e+00; double B1 = -5.447609879822406e+01, B2 = 1.615858368580409e+02, B3 = -1.556989798598866e+02, B4 = 6.680131188771972e+01, B5 = -1.328068155288572e+01; double C1 = -7.784894002430293e-03, C2 = -3.223964580411365e-01, C3 = -2.400758277161838e+00, C4 = -2.549732539343734e+00, C5 = 4.374664141464968e+00, C6 = 2.938163982698783e+00; double D1 = 7.784695709041462e-03, D2 = 3.224671290700398e-01, D3 = 2.445134137142996e+00, D4 = 3.754408661907416e+00; //---------------------------------------------------------------------------- double ltqnorm(double p) { int s=1; double r,x,q=0; if(p<=0||p>=1){Print("Function ltqnorm() error!");return(0);} if((p>=0.02425)&&(p<=0.97575)) // Rational approximation for central region { q=p-0.5; r=q*q; x=(((((A1*r+A2)*r+A3)*r+A4)*r+A5)*r+A6)*q/(((((B1*r+B2)*r+B3)*r+B4)*r+B5)*r+1); return(x); } if(p<0.02425) // Rational approximation for lower region { q=sqrt(-2*log(p)); s=1; } else //if(p>0.97575) // Rational approximation for upper region { q = sqrt(-2*log(1-p)); s=-1; } x=s*(((((C1*q+C2)*q+C3)*q+C4)*q+C5)*q+C6)/((((D1*q+D2)*q+D3)*q+D4)*q+1); return(x); }
数组 x[] 的地址被输入到函数中。该数组包含初始序列。接下来的参数是对输出数组 resp[] 和 xscale[] 的引用。在执行函数之后,用于在 X 轴和 Y 轴上绘制图表的值被分别写入数组。接下来 statParam 结构的地址被传递给函数。它应包含先前计算出来的输入序列的统计参数值。如果出错,函数会返回 -1。
在生成用于 X 轴的值时,应调用函数 ltqnorm()。它用于计算正态分布的逆向积分函数。算法来自 "An algorithm for computing the inverse normal cumulative distribution function"(用于计算逆向正态累积分布函数的一种算法)一文。
四张图表
先前我提到过 dStat() 函数,在该函数中可计算统计参数的值。让我们简要回顾一下它们的含义。
离差(方差) – 一个随机值与其数学期望值(平均值)之间偏差的平方的平均值。该参数显示一个随机值与其分布中心的偏差有多大。该参数的值越大,偏差就越大。
标准方差 – 因为离差是通过一个随机值的平方来计算的,所以标准方差通常被用作一个更明显的离差特征。它等于离差的平方根。
偏度 – 如果我们绘制一个随机值的分布曲线,偏度将显示概率密度曲线相对于分布中心的不对称程度。如果偏度值大于零,则概率密度曲线的左坡比较陡峭,右坡则比较平衡。如果偏度值是负数,则左坡平缓,右坡陡峭。当概率分布曲线与分布中心对称时,则偏度等于零。
超量系数(峰度) – 它描述了概率密度曲线峰值的锐度以及分布尾部坡度的陡峭程度。靠近分布中心的曲线峰部越尖锐,峰度值就越大。
尽管所提及的统计参数详细描述了一个序列,但您通常可以采用更简单的方式来描述一个序列的特征,其依据是以图形方式表示的估计结果。例如,一个普通的序列图能够大大充实在分析统计参数时所得出的观点。
在本文的前面,我已经提到过 dHist() 和 dRankit() 函数,它们允许为绘制直方图或带有正态概率刻度的图表准备数据。通过在同一张纸上显示直方图、正态分布图和普通图,您便能够直观地确定所分析序列的主要特征。
所列的这三张图表还应补充另一张图表,其中以 Y 轴表示序列的当前值,以 X 轴表示序列的先前值。此类图表被称为“滞后图”。如果相邻指示之间存在较强的相关性,则采样值会被拉成一条直线。如果相邻指示之间没有相关性,例如在分析一个随机序列时,则值将散布在整张图表上。
为了快速估计初始采样,建议在一张图纸上绘制四张图表并在其中显示计算出的统计参数值。这个想法并不新鲜;您可以通过以下链接阅读有关使用上述四张图表进行分析的文章:"4-Plot"。
本文末尾的“文件”部分包含脚本 s4plot.mq5,可使用该脚本在一张图纸上绘制这四张图表。在脚本的 OnStart() 函数内创建了数组 dat[]。该数组包含初始序列。然后依次调用 dStat()、dHist() 和 dRankit() 函数来计算绘制图表所需的数据。接下来调用 vis4plot() 函数。该函数会根据计算出的数据创建一个包含 Gnuplot 命令的文本文件,然后调用应用程序,用于在一个单独的窗口中绘制图表。
在本文中显示整个脚本代码没有意义,因为先前已经说明了 dStat()、dHist() 和 dRankit() 函数,创建 Gnuplot 命令序列的 vis4plot() 函数没有任何重要特征,并且 Gnuplot 命令的说明已超出了本文范畴。此外,您还可以不使用 Gnuplot 应用程序,而使用其他方法来绘制图表。
因此,让我们仅显示 s4plot.mq5 的一部分 - 其 OnStart() 函数。
//---------------------------------------------------------------------------- // Script program start function //---------------------------------------------------------------------------- void OnStart() { int i; double dat[128],histo[],rankit[],xrankit[]; statParam sp; MathSrand(1); for(i=0;i<ArraySize(dat);i++) dat[i]=MathRand(); if(dStat(dat,sp)==-1)return; if(dHist(dat,histo,sp)==-1)return; if(dRankit(dat,rankit,xrankit,sp)==-1)return; vis4plot(dat,histo,rankit,xrankit,sp,6); }
在本例中运用了 MathRand() 函数,使用一个随机序列来填充具有初始数据的 dat[] 数组。执行脚本后应返回以下结果:
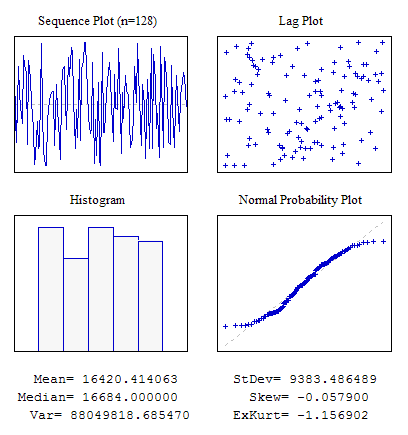
图 3. 四张图表。脚本 s4plot.mq5
您应留意 vis4plot() 函数的最后一个参数。它负责所输出数值的格式。在本例中,输出值具有六位小数。此参数与 DoubleToString() 函数中用于确定格式的参数相同。
如果输入序列的值太小或太大,您可以使用科学计数法实现更清晰的显示。例如,为实现此目的,可将该参数设置为 -5。值 -5 为 vis4plot() 函数的默认设置。
为了清晰说明用四张图表显示序列特征这一方法,我们需要用到此类序列的生成器。
伪随机序列生成器
类 RNDXor128 用于生成伪随机序列。
以下是描述该类的包含文件的源代码。
//----------------------------------------------------------------------------------- // RNDXor128.mqh // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #include <Object.mqh> //----------------------------------------------------------------------------------- // Generation of pseudo-random sequences. The Xorshift RNG algorithm // (George Marsaglia) with the 2**128 period of initial sequence is used. // uint rand_xor128() // { // static uint x=123456789,y=362436069,z=521288629,w=88675123; // uint t=(x^(x<<11));x=y;y=z;z=w; // return(w=(w^(w>>19))^(t^(t>>8))); // } // Methods: // Rand() - even distribution withing the range [0,UINT_MAX=4294967295]. // Rand_01() - even distribution within the range [0,1]. // Rand_Norm() - normal distribution with zero mean and dispersion one. // Rand_Exp() - exponential distribution with the parameter 1.0. // Rand_Laplace() - Laplace distribution with the parameter 1.0 // Reset() - resetting of all basic values to initial state. // SRand() - setting new basic values of the generator. //----------------------------------------------------------------------------------- #define xor32 xx=xx^(xx<<13);xx=xx^(xx>>17);xx=xx^(xx<<5) #define xor128 t=(x^(x<<11));x=y;y=z;z=w;w=(w^(w>>19))^(t^(t>>8)) #define inidat x=123456789;y=362436069;z=521288629;w=88675123;xx=2463534242 class RNDXor128:public CObject { protected: uint x,y,z,w,xx,t; uint UINT_half; public: RNDXor128() {UINT_half=UINT_MAX>>1;inidat;}; double Rand() {xor128;return((double)w);}; int Rand(double& a[],int n) {int i;if(n<1)return(-1); if(ArraySize(a)<n)return(-2); for(i=0;i<n;i++){xor128;a[i]=(double)w;} return(0);}; double Rand_01() {xor128;return((double)w/UINT_MAX);}; int Rand_01(double& a[],int n) {int i;if(n<1)return(-1); if(ArraySize(a)<n)return(-2); for(i=0;i<n;i++){xor128;a[i]=(double)w/UINT_MAX;} return(0);}; double Rand_Norm() {double v1,v2,s,sln;static double ra;static uint b=0; if(b==w){b=0;return(ra);} do{ xor128;v1=(double)w/UINT_half-1.0; xor128;v2=(double)w/UINT_half-1.0; s=v1*v1+v2*v2; } while(s>=1.0||s==0.0); sln=MathLog(s);sln=MathSqrt((-sln-sln)/s); ra=v2*sln;b=w; return(v1*sln);}; int Rand_Norm(double& a[],int n) {int i;if(n<1)return(-1); if(ArraySize(a)<n)return(-2); for(i=0;i<n;i++)a[i]=Rand_Norm(); return(0);}; double Rand_Exp() {xor128;if(w==0)return(DBL_MAX); return(-MathLog((double)w/UINT_MAX));}; int Rand_Exp(double& a[],int n) {int i;if(n<1)return(-1); if(ArraySize(a)<n)return(-2); for(i=0;i<n;i++)a[i]=Rand_Exp(); return(0);}; double Rand_Laplace() {double a;xor128; a=(double)w/UINT_half; if(w>UINT_half) {a=2.0-a; if(a==0.0)return(-DBL_MAX); return(MathLog(a));} else {if(a==0.0)return(DBL_MAX); return(-MathLog(a));}}; int Rand_Laplace(double& a[],int n) {int i;if(n<1)return(-1); if(ArraySize(a)<n)return(-2); for(i=0;i<n;i++)a[i]=Rand_Laplace(); return(0);}; void Reset() {inidat;}; void SRand(uint seed) {int i;if(seed!=0)xx=seed; for(i=0;i<16;i++){xor32;} xor32;x=xx;xor32;y=xx; xor32;z=xx;xor32;w=xx; for(i=0;i<16;i++){xor128;}}; int SRand(uint xs,uint ys,uint zs,uint ws) {int i;if(xs==0&&ys==0&&zs==0&&ws==0)return(-1); x=xs;y=ys;z=zs;w=ws; for(i=0;i<16;i++){xor128;} return(0);}; }; //-----------------------------------------------------------------------------------
在 George Marsaglia 所著的 "Xorshift RNGs" 一文中详细描述了用于生成伪随机序列的算法(见本文末尾的 xorshift.zip)。在文件 RNDXor128.mqh 中描述了 RNDXor128 类的方法。使用该类后,您就可以获得遵守均匀分布、正态分布、经验分布或拉普拉斯分布(双指数分布)规律的序列。
您应该会注意到,在创建 RNDXor128 类的一个实例时,序列的基值被设置为初始状态。因此,与每次启动使用 RNDXor128 的脚本或指标时调用 MathRand() 函数相比,将生成一个相同的序列。调用 MathSrand() 和 MathRand() 时也是如此。
序列示例
例如,您可以在下面找到在分析属性极其不同的序列时得到的结果。
示例 1.遵守均匀分布规律的随机序列。
#include "RNDXor128.mqh" RNDXor128 Rnd; //---------------------------------------------------------------------------- void OnStart() { int i; double dat[512]; for(i=0;i<ArraySize(dat);i++) dat[i]=Rnd.Rand_01(); ... }
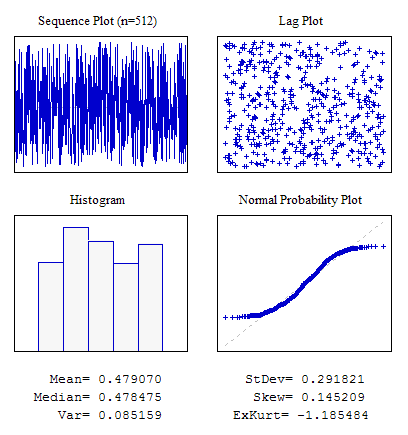
图 4. 均匀分布
示例 2.遵守正态分布规律的随机序列。
#include "RNDXor128.mqh" RNDXor128 Rnd; //---------------------------------------------------------------------------- void OnStart() { int i; double dat[512]; for(i=0;i<ArraySize(dat);i++) dat[i]=Rnd.Rand_Norm(); ... }
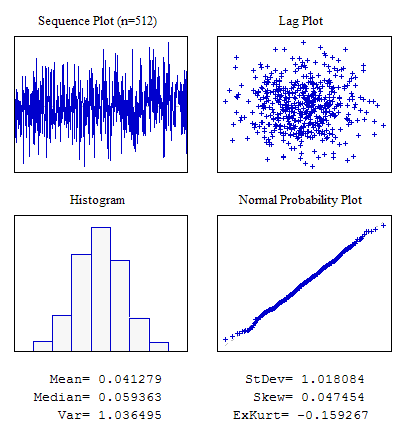
图 5. 正态分布
示例 3.遵守指数分布规律的随机序列。
#include "RNDXor128.mqh" RNDXor128 Rnd; //---------------------------------------------------------------------------- void OnStart() { int i; double dat[512]; for(i=0;i<ArraySize(dat);i++) dat[i]=Rnd.Rand_Exp(); ... }
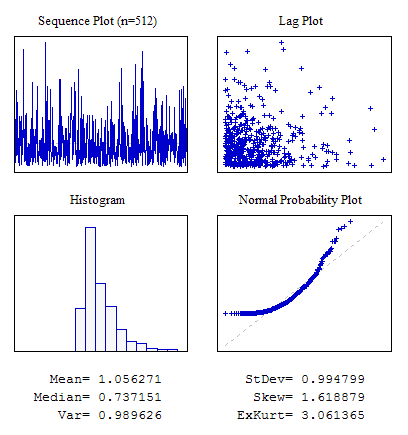
图 6. 指数分布
示例 4.遵守拉普拉斯分布规律的随机序列。
#include "RNDXor128.mqh" RNDXor128 Rnd; //---------------------------------------------------------------------------- void OnStart() { int i; double dat[512]; for(i=0;i<ArraySize(dat);i++) dat[i]=Rnd.Rand_Laplace(); ... }
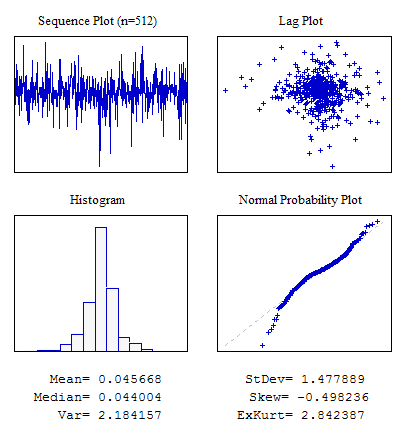
图 7. 拉普拉斯分布
示例 5.正弦序列
//---------------------------------------------------------------------------- void OnStart() { int i; double dat[512]; for(i=0;i<ArraySize(dat);i++) dat[i]=MathSin(2*M_PI/4.37*i); ... }
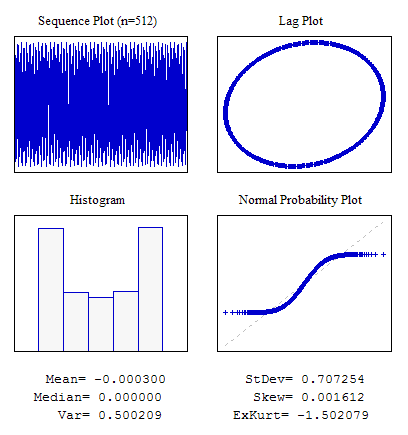
图 8. 正弦序列
示例 6.相邻指标之间具有明显相关性的序列。
#include "RNDXor128.mqh" RNDXor128 Rnd; //---------------------------------------------------------------------------- void OnStart() { int i; double dat[512],a; for(i=0;i<ArraySize(dat);i++) {a+=Rnd.Rand_Laplace();dat[i]=a;} ... }
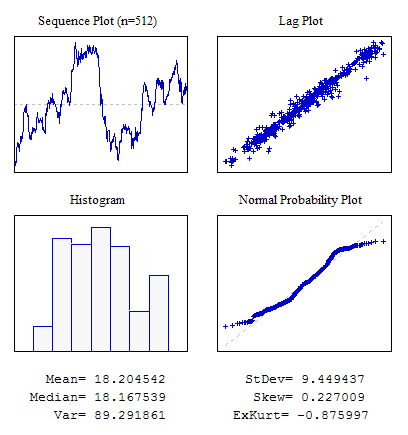
图 9. 相邻指示之间的相关性
总结
开发可实现任何类型计算的程序算法始终都是一项艰巨工作。原因在于必须考虑大量要求,以最大限度减少在对变量进行四舍五入、截断和溢流操作时可能出现的错误。
在编写本文的示例时,我没有对程序算法进行过任何分析。在编写函数时,数学算法是“直接”实现的。因此,如果您要在重要的应用程序中使用它们,则应分析其稳定性和精确度。
本文完全没有说明 Gnuplot 应用程序的特点。这些问题都不属于本文的范畴。不管怎样,我仍然愿意指出可以修改 Gnuplot 从而使其能与 MetaTrader 5 配合使用。为此,您需要在其源代码中进行某些修改并对其重新编译。此外,使用某个文件将命令传递给 Gnuplot 可能并非最佳做法,因为可以通过编程接口实现与 Gnuplot 的互动。
文件
- erremove.mq5 – 从采样中排除错误的脚本示例。
- function_dstat.mq5 – 用于计算统计参数的函数。
- function_dhist.mq5 - 用于计算直方图的值的函数。
- function_drankit.mq5 – 用于计算在绘制带有正态分布刻度的图表时所用值的函数。
- s4plot.mq5 – 在一张图纸上绘制四张图表的脚本示例。
- RNDXor128.mqh – 随机序列生成器类。
- xorshift.zip - George Marsaglia. 的"Xorshift RNGs"。
本文由MetaQuotes Ltd译自俄文
原文地址: https://www.mql5.com/ru/articles/273
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。
 在 MetaTrader 5 中使用自组织特征映射(Kohonen 映射)
在 MetaTrader 5 中使用自组织特征映射(Kohonen 映射)
 使用带 ENCOG 机器学习框架的 MetaTrader 5 指标进行时间序列预测
使用带 ENCOG 机器学习框架的 MetaTrader 5 指标进行时间序列预测
 创建 EA 交易优化的自定义标准
创建 EA 交易优化的自定义标准
 用于预测市场价格的通用回归模型
用于预测市场价格的通用回归模型
"消除异常值
在进行统计参数估计之前,应当注意的是,如果样本中存在严重错误(异常值),则估 计精度可能不足。当样本量较小时,异常值对估算精度的影响尤为明显。异常值是指异常偏离分布中心的值。造成这种偏差的原因可能是在收集统计数据和生成序列过程中发生的各种不可能事件和错误。
决定是否过滤离群值相当困难,因为在大多数情况下,无法明确确定给定值是离群值还是属于所考虑的过程。如果检测到离群值并决定对其进行过滤,那么问题就来了,如何处理这些错误值?最合理的做法是直接将它们从样本中剔除,这样对总体统计特征的估计精度可能会提高,但我们不应忘记,在处理时间序列 时,应该谨慎地从序列中剔除样本"。
最好还是不要这样做。
是的,所有数据都应该验证,是的,验证应该自动化。
但是,放弃数据源总比手动或自动篡改原始数据要好。
在现实生活中,以 "低概率 "为由接受或排除大风险是造成许多悲剧和灾难的原因。
维克多,就是这个问题。
你认为峰度 可以小于 1 吗?
如果是的话。
则等于-1。:-)
好文章!
维克多,就是这个问题。
你认为峰度 可以小于 1 吗?
如果是的话。
则等于-1。:-)
好文章!
很有可能,理论上峰度 不可能小于 1。对于由直线样本组成的序列,可能会得到一个等于 1 的值。例如,1,2,3,4,5。
至于文章中使用的算法是否会因为误差而导致峰度 值 小于 1,我就不得而知了。文章最后提到,尚未对系数计算算法的行为进行研究。
事实上,在计算无偏估计值时,峰度值可以小于 1。例如,对于输入序列 4,7,13,16。
感谢您的意见。我会进行修改。