Возможности Мастера MQL5, которые вам нужно знать (Часть 60): Обучение на основе вывода (Wasserstein-VAE) с использованием скользящей средней и стохастического осциллятора

Введение

При изучении паттернов, возникающих при сочетании скользящей средней и стохастического осциллятора, мы обратились к машинному обучению как к средству систематизации нашего подхода. В машинном обучении существует три основных метода обучения нейронных сетей: обучение с учителем, обучение с подкреплением и обучение на основе вывода. Исходя из того, что каждый из этих методов обучения может использоваться на разных этапах разработки модели/сети, мы доказываем, что модель может быть обогащена за счет включения всех этих методов.

Краткий обзор

Статья об обучении с учителем включала в себя моделирование характеристик состояний. Характеристики представляют собой паттерны скользящей средней и стохастического осциллятора. Состояния - прогнозируемые изменения цен, которые отстают от паттернов, и эти изменения предсказываются нашей моделью/сетью. Это иллюстрируется простой схемой ниже.

 

Использование термина "состояния" (states) для прогнозирования изменений цен является удачным решением, поскольку от обучения с учителем мы переходим к обучению с подкреплением. Как установлено в рамках обучения с подкреплением, состояния являются ключевой отправной точкой процесса обучения, что во многом напоминает схему ниже.

Существует ряд вариаций в обучении с подкреплением в зависимости от используемого алгоритма, но в большинстве случаев, в принципе, используются две нейронные сети. Первая представляет собой политику, которая показана в верхней из двух сетей на приведенной выше схеме, а вторая — сеть значений, которая представлена в нижней части.

Обучение с подкреплением может быть единственным методом обучения модели или системы, но, как мы указали в предыдущей статье, его следует чаще использовать для моделей, развернутых в реальных условиях. После этого баланс между исследованием и эксплуатацией станет более актуальным для обеспечения адаптации уже обученной модели к меняющимся рыночным условиям. Но что еще важнее, мы увидели, как решения о покупке или продаже могут дополнительно обрабатываться при выборе типа действий, необходимых для прогнозируемого состояния.

Вывод

Это приводит нас к выводу (inference), или тому, что также называют обучением без учителя (unsupervised-learning). В чем цель вывода? В начале я придерживался мнения, что это позволяет нам брать обученные нейронные сети/модели для конкретной ситуации и, с некоторыми незначительными корректировками и настройками, применять их в других условиях. Для трейдеров это означает обучение модели для пары EURUSD, а затем, с небольшими корректировками, перенос этих знаний, например, на пару EURJPY. Однако, как подтвердит большинство трейдеров, даже разработка неарбитражного советника, способного одновременно торговать более чем одним символом, — это сложный процесс с проблематичным соотношением риска и доходности.

Кроме того, вычислительные затраты на обучение различных моделей для нескольких валютных пар уже не так высоки, как раньше. Это во многом стало возможным благодаря более быстрым графическим процессорам и распространенности облачной инфраструктуры, которая делает вычисления доступными для множества пользователей. Таким образом, в теории эта ситуация должна привести к созданию множества моделей. Хотя стоимость хранения данных также снижается, особенно если учесть, что большие модели с миллионами параметров теперь хранятся как обычные файлы, я думаю, что вывод с помощью энкодеров доказывает необходимость сжатия этих знаний и их большей "возможности хранения".

Теперь, поскольку потребность в большем количестве или специальном хранилище практически отсутствует, учитывая его низкую стоимость, от этой идеи можно легко отказаться. Если учесть, что модель обучения с учителем уже обучена, а система обучения с подкреплением поддерживает ее в актуальном состоянии, то что же тогда даст вывод? Мы утверждаем, что не все данные представлены в виде непрерывных временных рядов. 

Если рассматривать случаи старых исторических данных, которые могут быть в чем-то похожи на текущие или развивающиеся события, то вывод может помочь в сопоставлении этих данных, минимизируя белый шум. Под "сопоставлением" мы подразумеваем схему, изображенную на рисунке ниже:

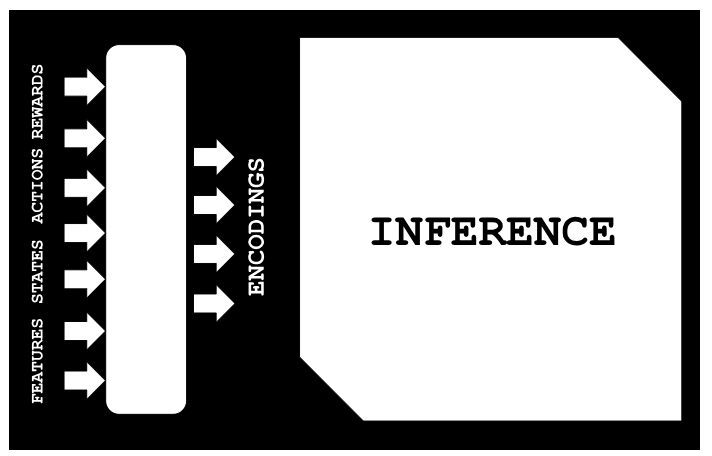
Таким образом, в ситуации, когда доступны параметры для исторических данных, ниже мы покажем, как без учителя (в данном случае с помощью линейной регрессии) мы можем вывести соответствующие состояния, действия и вознаграждения. Все это стало возможным благодаря тому, что мы обучили модель вариационного автоэнкодера сопоставлять признаки-состояния-действия-награды (features-states-actions-rewards, FSAR) со скрытым слоем, который мы называем кодировками (encodings). Используя наборы данных FSAR и кодировки, мы построили модель линейной регрессии, которая помогает нам заполнить недостающие данные в наборе данных FSAR. Это основное назначение модели, которое мы рассмотрим в этой статье.

Однако, если взглянуть на процесс обучения с учителем и процесс обучения с подкреплением, становится ясно, что с течением времени возрастает потребность в более целостной интеграции накопленных знаний. И хотя проведение еще одного этапа обучения с учителем в течение более длительного периода, а затем запуск обучения с подкреплением может быть одним из вариантов, обучение на основе вывода должно представлять собой более масштабируемую и целостную альтернативу.

Итак, подводя итог нашему введению, можно сказать, что вывод — это оценка скрытых переменных на основе наблюдаемых данных. В байесовских моделях вывод обычно представляет собой вычисление апостериорного распределения скрытых переменных при наличии наборов данных видимого слоя. Таким образом, с математической точки зрения процесс можно формально определить следующим образом:

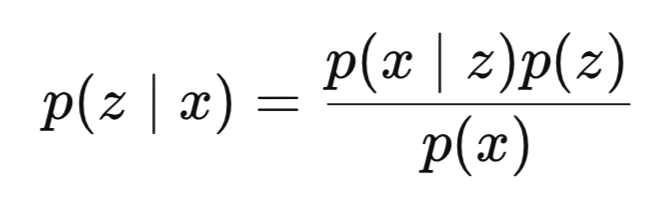
где:

• z — скрытая переменная или кодировка.
  
  
• x — наблюдаемые данные, в нашем случае - FSAR.
  
  
• p(z∣x) — апостериорная вероятность (то, что мы хотим узнать) или вероятность наблюдения z при условии, что x уже наблюдалось,
  
  
• p(x∣z) — вероятность увидеть x при предъявлении z
  
  
• p(z) — априорное распределение,
  
  
• p(x) — доказательство.

Зачастую P(x) трудно вычисляется.

Почему? Знаменатель p(x) включает в себя интегрирование по всем возможным скрытым переменным:

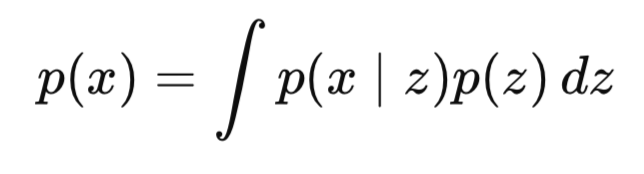
В многомерном пространстве, то есть по мере увеличения размера скрытой переменной, это, как правило, вычислительно невыполнимо.

Как же тогда могут помочь VAE? VAE преобразуют задачу приближенного вывода в задачу оптимизации. Это достигается за счет введения энкодера/сети вывода и декодера/генеративной сети. Кодировщик отвечает на вопрос q(z|x), который представляет собой обученное приближение к внешней области; в то время как сеть декодера отвечает на вопрос p(x|z), который представляет собой реконструкцию данных (в нашем случае FSAR) из скрытого кода (кодировки).

Однако ключевое нововведение VAE заключается в том, что вместо точного вычисления апостериорного распределения, VAE оптимизируется для оптимизация нижней границы доказательств (Evidence Lower Bound Optimization, ELBO). ELBO - объективная функция, которая используется для обучения VAE путем аппроксимации истинного распределения данных, обеспечивая при этом усвоение моделью значимых скрытых представлений и снижение уровня шума. Ключевая интуитивное решение:

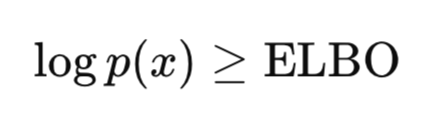
Как уже упоминалось выше, вычисление p(x) — очень сложная и трудноразрешимая задача; однако доказать, что p(x), и, соответственно, log p(x), больше заданного значения, вполне возможно и выполнимо. Поскольку наша цель — максимизировать p(x), то, максимизируя или повышая нижнюю границу, мы в конечном итоге также повышаем p(x). VAE обучается выявлять скрытую структуру на основе данных и проходит сквозное обучение с использованием градиентного спуска. Таким образом он демонстрирует амортизированный вывод и генеративное моделирование в рамках одной системы.

Почему VAE является ключевым элементом философии вывода? Потому что VAE учится выполнять вывод с помощью энкодера. Это означает, что вместо решения задачи вывода при каждом появлении нового набора данных используется общий энкодер. Это также называется амортизированным выводом. Это превосходный инструмент для оценки компромисса между точностью и регулярностью, а также для понимания в целом того, как скрытые переменные представляют генеративную структуру.

Для данной статьи мы применяем VAE, исследуя расстояние Вассерштейна вместо традиционной дивергенции Кульбака-Лейблера (KL-divergence) при сравнении распределений. Причины носят преимущественно исследовательский характер, поскольку в будущих статьях мы могли бы рассмотреть дивергенцию Кульбака-Лейблера. Однако высказывалось мнение, что такая дивергенция чрезмерно ограничивает латентное пространство, что, в свою очередь, может привести к последующему коллапсу. Во-вторых, утверждается, что расстояние Вассерштейна является более гибкой метрикой для сравнения распределений, особенно в ситуациях, когда рассматриваемые распределения практически не перекрываются.

Основная идея расстояния Вассерштейна заключается в измерении "стоимости" преобразования одного распределения вероятностей в другое. Поэтому его иногда называют метрикой землекопа. Выражается следующим уравнением:

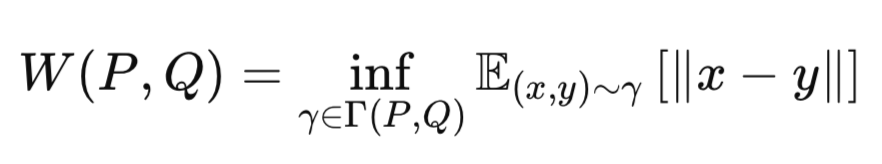
где:

• P - истинное распределение данных (например, гауссово априорное распределение p(z)).

• Q - приблизительное распределение (например, результаты энкодера q(z∣x)).

• γ - совместное распределение (связь) по P и Q.

• Γ(P,Q) - множество всех возможных связей между P и Q.

• ∥x−y∥ - метрика расстояния (например, евклидово расстояние).

• inf - инфимум (наибольшая нижняя граница, т.е. наименьшая возможная стоимость транспортировки).

Таким образом, расстояние Вассерштейна вычисляет минимальное количество "работы", необходимое для перемещения массы Q в соответствии с P. VAE на основе расстояния Вассерштейна (Wasserstein VAE) важен, поскольку он позволяет получать более четкие выборки и имеет более выразительные скрытые представления. Как правило, считается, что при обучении в определенных условиях достигается большая стабильность.

Существуют два основных распространенных варианта реализации алгоритма Wasserstein VAE. WVAE-MMD и WVAE-GAN. Первый метод использует максимальное среднее расхождение (Maximum-Mean-Discrepancy) для сравнения p(z) и q(z). Именно его мы будем использовать в этой статье. WVAE-GAN использует состязательные потери (adversarial loss) для выравнивания скрытых распределений. Возможно, мы рассмотрим этот вариант реализации в будущих статьях. Максимальное среднее расхождение описывается следующим уравнением:

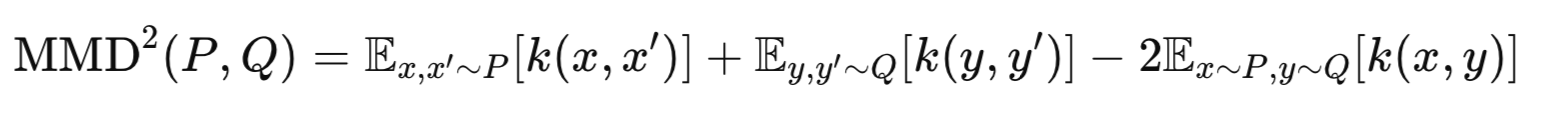
где:

• P - истинное априорное распределение (например, p(z)=N(0,I)).

• Q - распределение энкодера (например, q(z∣x)).

• k(⋅,⋅) - функция ядра (например, Gaussian RBF).

• x,x′ - два независимых образца из P.

• y,y′ - две независимые выборки из Q.

MMD сравнивает усредненные вложения P и Q в многомерном пространстве (воспроизводящее ядро гильбертова пространства). Чем ближе эти средние значения друг к другу, тем больше сходства в распределениях.

Реализация VAE

Мы начинаем с реализации наших моделей/сетей на Python, главным образом потому, что обучать их здесь удобнее, чем на чистом MQL5. В MQL5 существуют обходные пути, включающие использование OpenCL, которые могут уменьшить разрыв в производительности, однако мы еще не рассматривали их в рамках этой серии статей. Мы реализуем класс Wasserstein VAE на языке Python следующим образом:

class WassersteinVAEUnsupervised(nn.Module):
    def __init__(self, feature_dim, encoding_dim, k_neighbors=5):
        super().__init__()
        self.encoding_dim = encoding_dim
        self.k_neighbors = k_neighbors
        
        # Feature encoder
        self.feature_encoder = nn.Sequential(
            nn.Linear(feature_dim, 256),
            nn.ReLU(),
            nn.Linear(256, 128),
            nn.ReLU(),
            nn.Linear(128, encoding_dim * 2)  # mean and logvar
        )
        
        # Buffer for storing training references
        self.register_buffer('ref_encoding', torch.zeros(1, encoding_dim))
        self.register_buffer('ref_states', torch.zeros(1, 1))
        self.register_buffer('ref_actions', torch.zeros(1, 1))
        self.register_buffer('ref_rewards', torch.zeros(1, 1))
        self._references_loaded = False
    
    def encode(self, features):
        h = self.feature_encoder(features)
        z_mean, z_logvar = torch.chunk(h, 2, dim=1)
        return z_mean, z_logvar
    
    def reparameterize(self, mean, logvar):
        std = torch.exp(0.5 * logvar)
        eps = torch.randn_like(std)
        return mean + eps * std
    
    def update_references(self, encoding_vectors, states, actions, rewards):
        """Store reference data for unsupervised prediction"""
        self.ref_encoding = encoding_vectors.detach().clone()
        self.ref_states = states.detach().clone().unsqueeze(-1)
        self.ref_actions = actions.detach().clone().unsqueeze(-1)
        self.ref_rewards = rewards.detach().clone().unsqueeze(-1)
        self._references_loaded = True
    
    def knn_predict(self, z, ref_values):
        # z shape: [batch_size, encoding_dim]
        # ref_values shape: [ref_size, 1] or [ref_size]
        
        # Ensure ref_values is properly shaped
        ref_values = ref_values.view(-1)  # Flatten to [ref_size]
        
        # Calculate distances between z and reference encodings
        distances = torch.cdist(z, self.ref_encoding)  # [batch_size, ref_size]
        
        # Get top-k nearest neighbors
        _, indices = torch.topk(distances, k=self.k_neighbors, largest=False)  # [batch_size, k]
        
        # Gather corresponding reference values
        neighbor_values = torch.gather(
            ref_values.unsqueeze(0).expand(indices.size(0), -1),  # [batch_size, ref_size]
            1,
            indices
        )  # [batch_size, k]
        
        # Average the nearest values
        predictions = neighbor_values.mean(dim=1, keepdim=True)  # [batch_size, 1]
        
        return predictions
    
    def gaussian_predict(self, z, ref_values):
        # Input validation
        assert z.dim() == 2, "z must be 2D [batch, encoding]"
        assert ref_values.dim() == 2, "ref_values must be 2D"
        
        # Calculate distances (Euclidean)
        distances = torch.cdist(z, self.ref_encoding)  # [batch, ref_size]
        
        # Convert to similarities (Gaussian weights)
        weights = torch.softmax(-distances, dim=1)  # [batch, ref_size]
        
        # Prepare reference values
        ref_values = ref_values.squeeze(-1) if ref_values.size(1) == 1 else ref_values
        ref_values = ref_values.unsqueeze(0) if ref_values.dim() == 1 else ref_values
        
        # Ensure proper shapes
        ref_values = ref_values.view(-1, 1)  # Force [792, 1] shape
        
        # Calculate distances
        distances = torch.cdist(z, self.ref_encoding)  # [batch_size, 792]
        
        # Convert to weights
        weights = torch.softmax(-distances, dim=1)  # [batch_size, 792]
        
        # Matrix multiplication Weighted combination
        predictions = torch.matmul(weights, ref_values)  # [batch, 1]
        
        return predictions.unsqueeze(-1) if predictions.dim() == 1 else predictions
    
    def linear_predict(self, z, ref_values):
        """Linear regression prediction using normal equations"""
        # Add bias term
        X = torch.cat([self.ref_encoding, torch.ones_like(self.ref_encoding[:, :1])], dim=1)
        y = ref_values
        
        # Compute closed-form solution
        XtX = torch.matmul(X.T, X)
        Xty = torch.matmul(X.T, y)
        theta = torch.linalg.solve(XtX, Xty)
        
        # Predict with new z values
        X_new = torch.cat([z, torch.ones_like(z[:, :1])], dim=1)
        return torch.matmul(X_new, theta)

    def predict_from_encoding(self, z):
        if not self._references_loaded:
            raise RuntimeError("Reference data not loaded")
            
        # Validate reference shapes
        self.ref_states = self.ref_states.view(-1, 1)
        self.ref_actions = self.ref_actions.view(-1, 1)
        self.ref_rewards = self.ref_rewards.view(-1, 1)
        
        states = self.knn_predict(z, self.ref_states)
        actions = self.gaussian_predict(z, self.ref_actions)
        rewards = self.linear_predict(z, self.ref_rewards)
        
        return states, actions, rewards
    
    def forward(self, features, states=None, actions=None, rewards=None):
        z_mean, z_logvar = self.encode(features)
        z = self.reparameterize(z_mean, z_logvar)
        
        if states is not None and actions is not None and rewards is not None:
            return {
                'z': z,
                'z_mean': z_mean,
                'z_logvar': z_logvar
            }
        else:
            pred_states, pred_actions, pred_rewards = self.predict_from_encoding(z)
            return {
                'states': pred_states,
                'actions': pred_actions,
                'rewards': pred_rewards
            }

Представленная выше реализация Wasserstein VAE состоит, главным образом, из четырех элементов. Энкодер признаков, буфер опорных значений, методы прогнозирования и двухрежимный прямой проход. Кодировщик признаков представляет собой трехслойный многослойный перцептрон, задача которого — сжимать входные данные до параметров латентного пространства (z, z-среднее и z-логарифмическое значение). В буферах эталонных данных хранятся предварительно обученные входные данные модели, включающие признаки, состояния, действия и вознаграждения, а также их соответствующие кодировки. Перечисленные методы прогнозирования предназначены для предсказания состояний, действий и вознаграждений для неполного набора данных, представленного только в виде признаков. К таким методам относятся K-NN, взвешивание по Гауссу и линейная регрессия. Они работают в латентном пространстве, сопоставляя кодировки с недостающими точками данных состояний, действий и вознаграждений. Двухрежимный прямой проход обрабатывает как обучение, так и вывод результатов.

Ключевыми функциональными компонентами являются процесс кодирования, система отсчета, механизмы прогнозирования и поток вывода. В процессе кодирования входные данные — признаки, состояния, действия и вознаграждения — проходят через сеть кодировщика. Выходные данные разделяются на "кодировку" z, z-среднее значение и z-логарифмическое значение. Кроме того, в этом процессе прием репараметризации позволяет нам получать дифференцируемые выборки. В эталонной системе хранятся "замороженные" выходные данные вместе с соответствующими парами входных данных FSAR. Для этого требуется явная инициализация с помощью функции update_references().

Три механизма прогнозирования направлены на предсказание состояний, действий или вознаграждений. Наша модель работает на основе предположения, что характеристики всегда доступны в составе набора данных FSAR, однако бывают случаи, когда может отсутствовать только SAR (состояния-действия-вознаграждения). Метод кластеризации KNN отображает состояния, метод регрессии на основе гауссовых процессов — действия, а метод линейной регрессии — вознаграждения. Таким образом, процесс вывода кодирует входные признаки в латентное пространство, выбирает метод прогнозирования для каждого типа входных данных на основе упомянутых выше пар, а затем возвращает соответствующие оценки состояния/действия/вознаграждения.

Однако наш подход, описанный выше, можно было бы несколько улучшить. Изменения можно условно разделить на 3 категории. Улучшения архитектуры, совершенствование обучения или просто повышение надежности. Улучшения архитектуры могут включать в себя: добавление спектральной нормализации для обеспечения непрерывности по Липшицу; реализацию обучаемой температуры для взвешивания в гауссовском процессе; включение управления долговременной памятью (FIFO/обрезка); и добавление метода Монте-Карло для оценки неопределенности. Процесс обучения также можно улучшить, введя штраф за градиент для ограничений Вассерштейна; добавив регуляризацию латентного пространства (условия MMD/покрытия); внедрив адаптивный выбор метода прогнозирования; и добавив ансамблевое взвешивание методов прогнозирования.

Вопросы повышения устойчивости несколько неоднозначны, однако можно предпринять попытки с использованием следующих инструментов: возможности обнаружения отклонений от распределения; системы оценки качества эталонного набора данных; динамической регулировки размера окрестности; и масштабирования шума в зависимости от входных данных.

Реализация MMD-Loss

В качестве формы используемой Wasserstein VAE используется MMD-loss, а ниже представлены две функции потерь, применяемые в VAE:

def mmd_loss(y_true, y_pred, kernel_mul=2.0, kernel_num=5):
    """
    MMD loss using Gaussian RBF kernel.
    Args:
        y_true: Ground truth samples (shape: [batch_size, dim])
        y_pred: Predicted samples (shape: [batch_size, dim])
        kernel_mul: Multiplier for kernel bandwidths
        kernel_num: Number of kernels to use
    Returns:
        MMD loss (scalar)
    """
    batch_size = y_true.size(0)
    
    # Combine real and predicted samples
    xx = y_true
    yy = y_pred
    xy = torch.cat([xx, yy], dim=0)
    
    # Compute pairwise distances
    distances = torch.cdist(xy, xy, p=2)
    
    # Compute MMD using multiple RBF kernels
    loss = 0.0
    for sigma in [kernel_mul ** k for k in range(-kernel_num, kernel_num + 1)]:
        if sigma == 0:
            continue
        kernel_val = torch.exp(-distances ** 2 / (2 * sigma ** 2))
        k_xx = kernel_val[:batch_size, :batch_size]
        k_yy = kernel_val[batch_size:, batch_size:]
        k_xy = kernel_val[:batch_size, batch_size:]
        
        # MMD formula: E[k(x,x)] + E[k(y,y)] - 2*E[k(x,y)]
        loss += (k_xx.mean() + k_yy.mean() - 2 * k_xy.mean())
    
    return loss / (2 * kernel_num)

def compute_loss(predictions, batch):
    # Ensure shapes match (squeeze if needed)
    pred_states = predictions['states'].squeeze(-1)  # [B, 1] → [B]
    pred_actions = predictions['actions'].squeeze(-1)
    pred_rewards = predictions['rewards'].squeeze(-1)
    
    # MMD Loss (distributional matching)
    mmd_state = mmd_loss(batch['states'], pred_states)
    mmd_action = mmd_loss(batch['actions'], pred_actions)
    mmd_reward = mmd_loss(batch['rewards'], pred_rewards)
    
    # Combine losses (adjust weights as needed)
    total_loss = mmd_state + mmd_action + mmd_reward
    
    return {
        'loss': total_loss,
        'mmd_state': mmd_state,
        'mmd_action': mmd_action,
        'mmd_reward': mmd_reward
    }

Входными параметрами функции MMD-Loss являются y_true и y_pred. Они представляют собой сравнение эталонных и сгенерированных образцов. Размерность является ключевым моментом при сравнении. Входные параметры kernel_mul/kernel_num управляют шириной полосы пропускания ядра RBF и, следовательно, влияют на чувствительность к различным масштабам разностей распределения.

Комбинация образцов xy объединяет реальные и сгенерированные образцы для вычисления всех попарных расстояний за одну операцию. Это обеспечивает эффективное использование памяти и гарантирует согласованность вычислений расстояний. Для вычисления расстояния используется значение p=2 (евклидово расстояние), что является стандартом для MMD. Этот выбор напрямую влияет на чувствительность к различиям в распределении. Операция cdist является, с математической точки зрения, основной, поскольку MMD основана на попарных сравнениях.

Многоядерный подход использует геометрически разнесенные полосы пропускания (kernel_mul^k) для получения представления о характеристиках многомасштабного распределения. Это позволяет избежать ситуации, когда sigma=0, что приводит к делению на ноль. Каждое ядро вносит равный вклад в итоговую потерю за счет усреднения. В расчете MMD используется основная формула (k_xx + k_yy - 2k_xy), которая количественно определяет расхождения между распределениями. Операции усреднения позволяют получить оценки ожидаемых значений на основе конечных выборок, а нормализация по количеству ядер обеспечивает согласованность масштаба функции потерь в различных конфигурациях.

Улучшения в этой модели MMD можно внести за счет выбора ядра, где: можно реализовать адаптивный выбор полосы пропускания на основе выборочной статистики; можно провести эксперименты с ядрами, отличными от RBF, чтобы определить, какие ядра лучше всего подходят для каких типов данных; можно реализовать автоматическое определение релевантности для полос пропускания. Численную устойчивость также можно обеспечить путем: добавления небольшого числа эпсилон к знаменателю для обеспечения стабильности; реализации вычислений в логарифмической области для очень малых значений ядра; и ограничения экстремальных значений расстояния для предотвращения переполнения. Другие меры могут включать в себя повышение эффективности вычислений и интеграцию VAE. 

Для выполнения этого вывода нам необходим большой объем другого кода, который мы здесь явно не выделяем. Следует отметить, что генерация входных данных для FASR осуществляется путем запуска кода из двух предыдущих статей о скользящй средней и стохастическом осцилляторе. В статье об обучении с учителем представлены компоненты признаков и состояний нашего входного сигнала VAE, а в статье об обучении с подкреплением — код, описывающий действия и вознаграждения.

Реализация линейной регрессии

Для использования нашей модели вывода мы полагаемся исключительно на функции регрессии, которые отображают данные из латентного слоя на отсутствующие входные данные, а не на сеть VAE. Это противоречит тому, что мы делали в предыдущих статьях, где нам приходилось экспортировать обученную нами нейронную сеть в виде файла ONNX. 

Причина в том, что нас интересует дополнение входного набора данных для обученной нами VAE.

В дальнейшем мы будем располагать только данными о характеристиках. Таким образом, вопрос сводится к тому, каковы состояния, действия и вознаграждения, связанные с этими характеристиками. Для ответа на этот вопрос при инициализации нашего советника нам необходимо обучить модель линейной регрессии с использованием наборов данных, содержащих пары кодировок-признаков, кодировок-состояний, кодировок-действий и кодировок-вознаграждений. После обучения (или подгонки) нашей модели линейной регрессии, для каждой новой точки данных признаков мы будем сопоставлять ее с кодировкой, а затем использовать эту кодировку в той же модели для сопоставления с состояниями, действиями и вознаграждениями.

Этот процесс подбора связей для кодирования использует обучение без учителя. Наша линейная регрессия реализована в MQL5 следующим образом:

//+------------------------------------------------------------------+
// Linear Regressor (unchanged from previous implementation)         |
//+------------------------------------------------------------------+
class LinearRegressor
{
private:
   vector m_coefficients;
   double m_intercept;

   matrix m_coefficients_2d;
   vector m_intercept_2d;

public:
   void Fit(const matrix &X, const vector &y)
   {  int n = (int)X.Rows();
      int p = (int)X.Cols();
      matrix X_with_bias(n, p + 1);
      for(int i = 0; i < n; i++)
      {  for(int j = 0; j < p; j++)
            X_with_bias[i][j] = X[i][j];
         X_with_bias[i][p] = 1.0;
      }
      matrix Xt = X_with_bias.Transpose();
      matrix XtX = Xt.MatMul(X_with_bias);
      matrix XtX_inv = XtX.Inv();
      vector y_col = y;
      y_col.Resize(n, 1);
      vector beta = XtX_inv.MatMul(Xt.MatMul(y_col));
      m_coefficients = beta;
      m_coefficients.Resize(p);
      m_intercept = beta[p];
   }

   void Fit2d(const matrix &X, const matrix &Y)
   {  int n = (int)X.Rows();    // Number of samples
      int p = (int)X.Cols();    // Number of input features
      int k = (int)Y.Cols();    // Number of output encodings
      // Add bias term (column of 1s) to X
      matrix X_with_bias(n, p + 1);
      for(int i = 0; i < n; i++)
      {  for(int j = 0; j < p; j++)
            X_with_bias[i][j] = X[i][j];
         X_with_bias[i][p] = 1.0;
      }
      // Calculate coefficients using normal equation: (X'X)^-1 X'Y
      matrix Xt = X_with_bias.Transpose();
      matrix XtX = Xt.MatMul(X_with_bias);
      matrix XtX_inv = XtX.Inv();
      matrix beta = XtX_inv.MatMul(Xt.MatMul(Y));
      // Split coefficients and intercept
      m_coefficients_2d.Resize(p, k);  // Coefficients for each output encodings
      m_intercept_2d.Resize(k);        // Intercept for each input feature
      for(int j = 0; j < p; j++)
      {  for(int d = 0; d < k; d++)
         {  m_coefficients_2d[j][d] = beta[j][d];
         }
      }
      for(int d = 0; d < k; d++)
      {  m_intercept_2d[d] = beta[p][d];
      }
   }

   double Predict(const vector &x)
   {  return m_intercept + m_coefficients.Dot(x);
   }

   vector Predict2d(const vector &X) const
   {  int p = (int)X.Size();    // Number of input features
      int k = (int)m_intercept_2d.Size(); // Number of output encodings
      vector predictions(k);  // vector to store predictions
      for(int d = 0; d < k; d++)
      {  // Initialize with intercept for this output dimension
         predictions[d] = m_intercept_2d[d];
         // Add contribution from each feature
         for(int j = 0; j < p; j++)
         {  predictions[d] += m_coefficients_2d[j][d] * X[j];
         }
      }
      return predictions;
   }
};

Основная структура обеспечивает раздельное хранение коэффициентов для одномерной (для переменных m_coefficients/m_intercept) и двухмерной (для переменных m_coefficients_2d/m_intercept_2d) структуры. Для повышения эффективности пакетных операций используется матричная алгебра. Она реализует как одновыходные, так и многовыходные варианты регрессии. Ее методы подгонки используют уравнение нормального распределения путем прямого решения уравнения (X'X)^- 1X'y. Смещение обрабатывается путем добавления столбца из единиц к входным признакам. 2D-специализация класса также позволяет обрабатывать несколько выходных данных одновременно с помощью матричных операций.

Методы прогнозирования используют скалярное произведение, которое служит эффективной линейной комбинацией входных данных и весов. Обработка размерностей корректно выполняется как для сценариев с одним, так и с несколькими выходными данными, а управление памятью предварительно выделяет результирующий вектор для повышения эффективности. Для вызова и реализации прогнозов состояний, действий и вознаграждений мы используем псевдокласс Wasserstein VAE. На языке MQL5 это выглядит так:

//+------------------------------------------------------------------+
// Wasserstein VAE Predictors Implementation (unchanged)             |
//+------------------------------------------------------------------+
class WassersteinVAEPredictors
{
private:
   LinearRegressor m_feature_predictor;
   LinearRegressor m_state_predictor;
   LinearRegressor m_action_predictor;
   LinearRegressor m_reward_predictor;
   bool m_predictors_trained;

public:
   WassersteinVAEPredictors() : m_predictors_trained(false) {}

   void FitPredictors(const matrix &features,
                      const vector &states,
                      const vector &actions,
                      const vector &rewards,
                      const matrix &encodings)
   {  m_feature_predictor.Fit2d(features, encodings);
      m_state_predictor.Fit(encodings, states);
      m_action_predictor.Fit(encodings, actions);
      m_reward_predictor.Fit(encodings, rewards);
      m_predictors_trained = true;
   }

   void PredictFromFeatures(const vector &y, vector &z)
   {  if(!m_predictors_trained)
      {  Print("Error: Predictors not trained yet");
         return;
      }
      z = m_feature_predictor.Predict2d(y);
   }

   void PredictFromEncodings(const vector &z, double &state, double &action, double &reward)
   {  if(!m_predictors_trained)
      {  Print("Error: Predictors not trained yet");
         return;
      }
      state = m_state_predictor.Predict(z);
      action = m_action_predictor.Predict(z);
      reward = m_reward_predictor.Predict(z);
   }
};

Кроме того, в рамках нашего пользовательского класса сигналов мы теперь используем функцию Infer для обработки наших прогнозов. Это выглядит следующим образом:

//+------------------------------------------------------------------+
//| Inference Learning Forward Pass.                                 |
//+------------------------------------------------------------------+
vector CSignal_WVAE::Infer(int Index, ENUM_POSITION_TYPE T)
{  vectorf _f = Get(Index, m_time.GetData(X()), m_close, m_ma, m_ma_lag, m_sto);
   vector _features;
   _features.Init(_f.Size());
   _features.Fill(0.0);
   for(int i = 0; i < int(_f.Size()); i++)
   {  _features[i] = _f[i];
   }
// Make a prediction
   vector _encodings;
   _encodings.Init(__ENCODINGS);
   _encodings.Fill(0.0);
   double _state = 0.0, _action = 0.0, _reward = 0.0;
   if(Index == 1)
   {  m_vae_1.PredictFromFeatures(_features, _encodings);
      m_vae_1.PredictFromEncodings(_encodings, _state, _action, _reward);
   }
   else if(Index == 2)
   {  m_vae_2.PredictFromFeatures(_features, _encodings);
      m_vae_2.PredictFromEncodings(_encodings, _state, _action, _reward);
   }
   else if(Index == 5)
   {  m_vae_5.PredictFromFeatures(_features, _encodings);
      m_vae_5.PredictFromEncodings(_encodings, _state, _action, _reward);
   }
   vector _inference;
   _inference.Init(3);
   _inference[0] = _state;
   _inference[1] = _action;
   _inference[2] = _reward;
   //
   if(T == POSITION_TYPE_BUY)
   {  if(_state > 0.5)
      {  _inference[0] -= 0.5;
         _inference[0] *= 2.0;
         if(_action < 0.0)
         {  _inference[0] = 0.0;
         }
      }
      else
      {  _inference[0] = 0.0;
      }
   }
   else if(T == POSITION_TYPE_SELL)
   {  if(_state < 0.5)
      {  _inference[0] -= 0.5;
         _inference[0] *= -2.0;
         if(_action > 0.0)
         {  _inference[0] = 0.0;
         }
      }
      else
      {  _inference[0] = 0.0;
      }
   }
   return(_inference);
}

Новички могут ознакомиться со сборкой советника в Мастере здесь и здесь. Как было указано в предыдущей статье, из 10 исходных моделей только модели 1, 2 и 5 позволяли двигаться вперед. Таким образом, функции обработки условий на покупку и продажу для этого советника обрабатывают только эти три паттерна. Мы прогнозируем 3 значения. Состояния, действия и вознаграждения. Состояния ограничены диапазоном от 0 до 1. Действия также ограничены аналогичным диапазоном, в то время как вознаграждения находятся в диапазоне от -1 до +1. Любой, кто имеет некоторый опыт обучения и использования нейронных сетей, знает, что результаты тестирования или развертывания нейронных сетей после обучения с целевыми значениями, соответствующими установленным предельным значениям, не всегда попадают в ожидаемые пределы. Часто требуется некоторая форма нормализации данных после форвард-теста.

Мы здесь не проводим никакой нормализации, а просто обращаем на это внимание читателя, чтобы он учитывал это при внедрении обученной нейронной сети в производство. Мы загружаем в Python данные о ежедневных ценах EURUSD за 2 года, чтобы обучить VAE, который предоставляет нам набор данных, сопоставляющий признаки, состояния, действия и вознаграждения с кодировками. Этот набор данных, в свою очередь, аппроксимируется моделями линейной регрессии, которые затем используются для отображения состояний, действий и вознаграждений при предъявлении признаков. Из загруженных данных, обрабатываемых модулем Python в Meta Trader 5, 80% используется для обучения, а 20% остается для тестирования.

Данные охватывают период с 2023.01.01 по 2025.01.01. Таким образом, форвард-тест будет произведен примерно за 5 месяцев до 1 января 2025 года. Мы проводим тестирование в течение несколько более длительного периода, за 6 месяцев до 2024.07.01 по 2025.01.01, и получаем следующие отчеты:

Для паттерна 1:

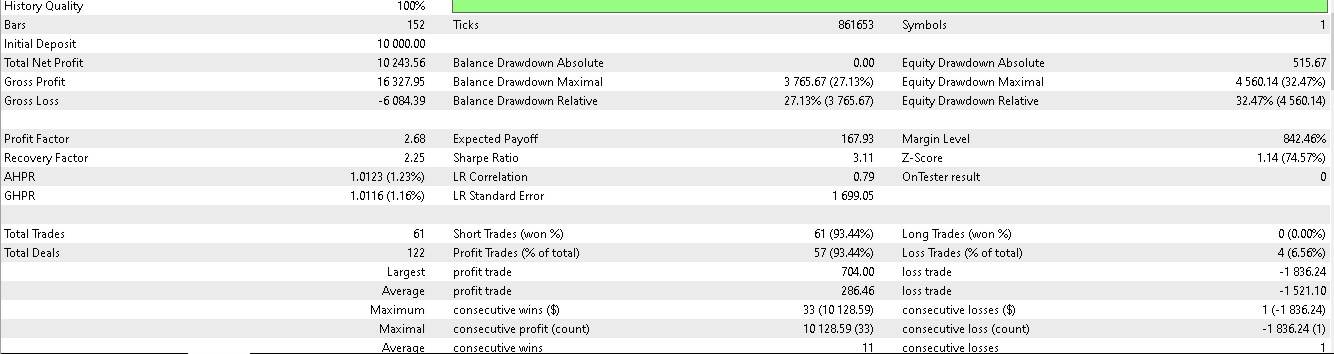
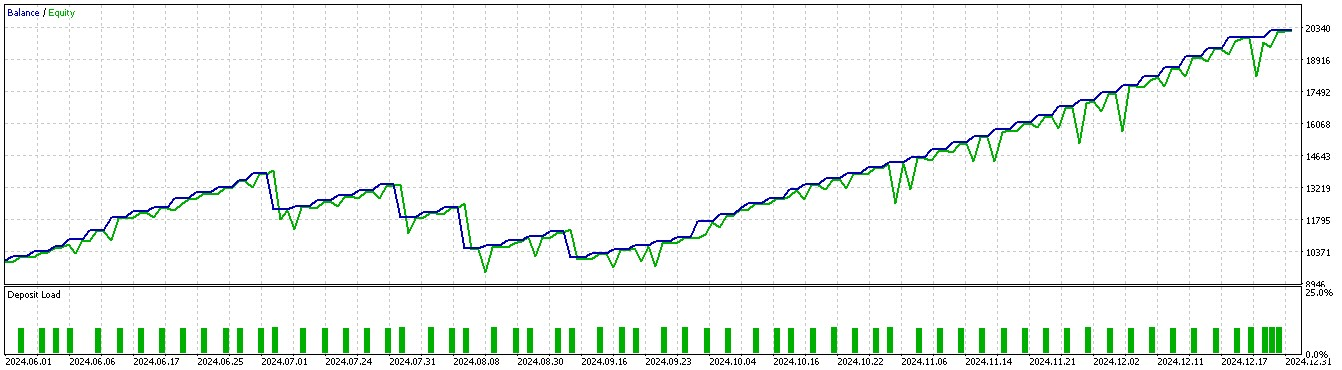
Для паттерна 2:

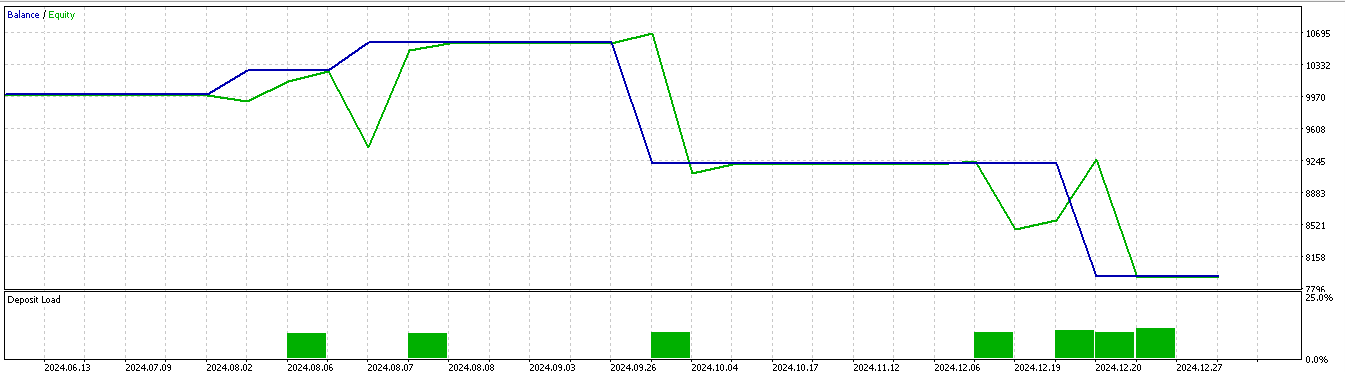
Для паттерна 5:

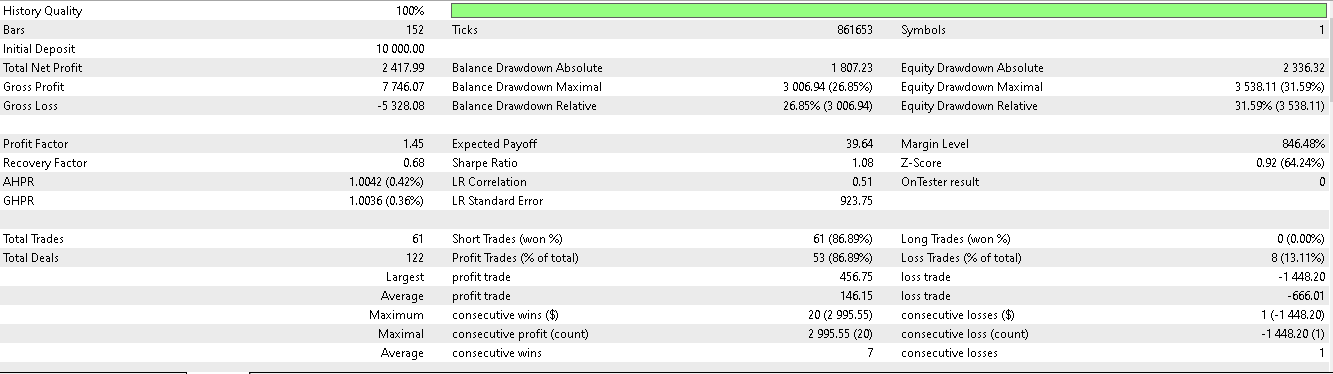
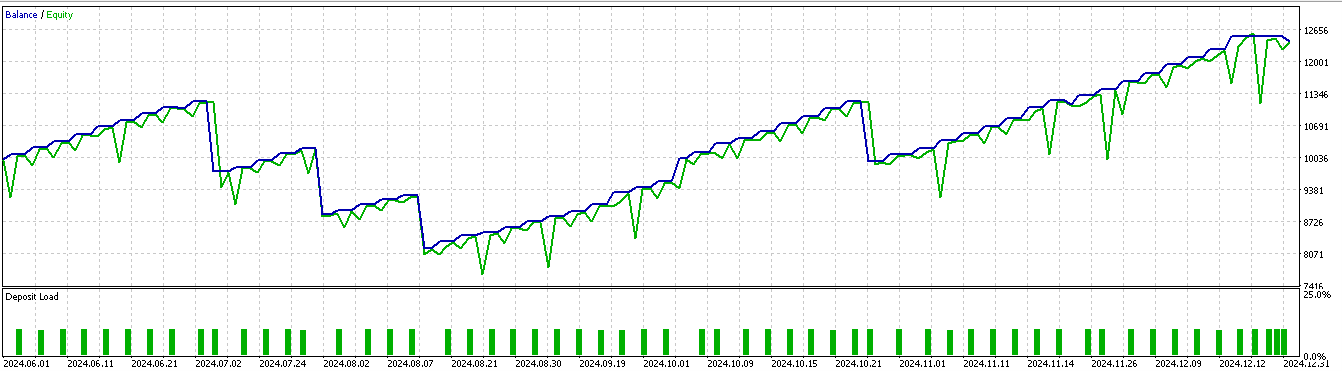
По всей видимости, только паттерны 1 и 5 способны извлечь выгоду из выводов, основанных на коротком двухлетнем периоде обучения/тестирования.

Заключение

В завершение нашего обзора паттернов скользящей средней и стохастического осциллятора, используемых в машинном обучении, рассмотрим пример их применения в процессе обучения на основе вывода. Мы представили возможный путь реализации обучения на основе вывода, исходя из аргумента, что после завершения обучения с учителем и внедрения обучения с подкреплением в реальную тестовую среду остается необходимость в более целостном подходе к сбору и "хранению" всех знаний, полученных как в процессе обучения с учителем, так и в процессе обучения с подкреплением. Я считаю, что обучение на основе вывода подходит для этой роли, особенно учитывая, что его метод обучения не дублирует то, что мы уже использовали в обучении с учителем и обучении с подкреплением.

Имя	Описание
wz_60.mq5	В заголовок включен советник, созданный мастером сборки, для отображения необходимых файлов сборки
SignalWZ_60.mqh	Файл класса сигнала
60_vae_1.onnx	Модель VAE ONNX для паттерна 1, не требуется для советника.
60_vae_2.onnx	Модель VAE ONNX для паттерна 2, аналогично
60_vae_5.onnx	Модель VAE ONNX для паттерна 5, то же самое