Теория категорий в MQL5 (Часть 18): Квадрат естественности

Введение

Теория категорий может показаться слишком субъективной для MQL5-трейдеров. До сих пор в этой серии статей мы использовали общесистемный подход, отдавая предпочтение морфизмам для прогнозирования и классификации финансовых данных.

Естественные преобразования , ключевое понятие теории категорий, часто воспринимается просто как сопоставление функторов. Этот взгляд, хотя и не ошибочный, может привести к некоторой путанице, если учесть, что функтор связывает два объекта, поскольку возникает вопрос, какие объекты связывает естественное преобразование? Короткий ответ — два объекта кодомена функторов. В этой статье мы попытаемся показать, что стоит за этим определением, а также включить экземпляр трейлинг-класса советника, который использует этот морфизм для прогнозирования изменений волатильности.

Мы используем две категории для использования в качестве примеров при иллюстрации естественных преобразований. Это минимальное число для пары функторов, используемых для определения естественного преобразования. Первый будет состоять из двух объектов, содержащих нормализованные значения индикаторов. Мы будем рассматривать индикаторы ATR и Bollinger Bands. Вторая категория, которая будет служить категорией кодомена, поскольку к ней будут вести два функтора, будет включать четыре объекта, фиксирующие диапазоны ценовых баров значений, которые мы хотим спрогнозировать.

Категории

Категория значений индикатора упоминается в нашей статье только для того, чтобы помочь понять изложенные здесь концепции. Она играет минимальную роль в прогнозировании интересующей нас волатильности, потому что для достижения этой цели мы в первую очередь будем полагаться на квадрат естественности (naturality square). Тем не менее, ее значение трудно переоценить. В Интернете не так много информации о квадрате естественности. Я советую ознакомиться с этим постом (на английском) для получения дополнительных сведений.

Итак, вернемся к нашей категории доменов. Как уже упоминалось, в ней есть два объекта: один со значениями ATR, а другой со значениями полос Боллинджера. Эти значения нормализованы таким образом, что объекты имеют фиксированную мощность (размер). Значения, представленные в каждом объекте, представляют собой соответствующие изменения значений индикатора. Эти изменения регистрируются с шагом 10% от минус 100% до плюс 100%, что означает, что мощность каждого объекта равна 21. Таким образом, они включают в себя следующие значения:

{

-100, -90, -80, -70, -60, -50, -40, -30, -20, -10,

 0,

 10, 20, 30, 40, 50, 60, 70, 80, 90, 100

}

Морфизм, связывающий эти объекты, идентичные элементам, будет объединять значения в зависимости от того, были ли они зарегистрированы в одно и то же время, тем самым актуализируя данные об изменениях в двух значениях индикатора.

Эти значения изменения индикатора могли быть взяты из любого другого индикатора, связанного с волатильностью. Принципы остаются прежними. Изменение значения индикатора делится на сумму абсолютных значений предыдущего и текущего показаний индикатора, чтобы получить десятичную дробь. Затем умножаем эту дробь на 10 и округляем до нуля. Затем она снова умножается на 10 и ей присваивается индекс в наших объектах, описанных выше, в зависимости от значения, которому она эквивалентна.

Категория диапазонов ценовых баров будет состоять из четырех объектов, которые будут в центре внимания квадрата естественности, используемого при составлении прогнозов. Поскольку наша категория предметной области (с изменениями индикатора) состоит из двух объектов, и у нас есть два функтора, ведущие от нее к этому кодомену, из этого следует, что каждый из этих функторов сопоставляется с объектом. Сопоставленные объекты не всегда должны быть разными, однако в нашем случае, чтобы помочь прояснить наши концепции, мы позволяем каждому объекту, отображаемому в категории домена, иметь свой собственный объект кодомена в категории ценовых диапазонов. Таким образом, 2 объекта, умноженные на 2 функтора, дадут 4 объекта конечной точки, членов нашей категории кодомена.

Поскольку у нас четыре объекта и мы не хотим дублирования, каждый объект будет регистрировать различный набор изменений диапазона ценовых баров. Чтобы помочь в этом, два функтора будут представлять разные дельты прогноза. Один функтор будет отображать диапазон ценового бара после одного бара, а другой функтор будет отображать изменения ценового диапазона после двух баров. Кроме того, сопоставления объекта ATR будут относиться к ценовым диапазонам на одном баре, тогда как сопоставления объекта полос Боллинджера будут относиться к ценовым диапазонам на двух барах. Ниже приведен листинг, реализующий всё, указанное выше:

      CElement<string> _e;
      for(int i=0;i<m_extra_training+1;i++)
      {
         double _a=((m_high.GetData(i+_x)-m_low.GetData(i+_x))-(m_high.GetData(i+_x+1)-m_low.GetData(i+_x+1)))/((m_high.GetData(i+_x)-m_low.GetData(i+_x))+(m_high.GetData(i+_x+1)-m_low.GetData(i+_x+1)));
         double _c=((m_high.GetData(i+_x)-m_low.GetData(i+_x))-(m_high.GetData(i+_x+2)-m_low.GetData(i+_x+2)))/((m_high.GetData(i+_x)-m_low.GetData(i+_x))+(m_high.GetData(i+_x+2)-m_low.GetData(i+_x+2)));
         double _b=((fmax(m_high.GetData(i+_x),m_high.GetData(i+_x+1))-fmin(m_low.GetData(i+_x),m_low.GetData(i+_x+1)))
                     -(fmax(m_high.GetData(i+_x+2),m_high.GetData(i+_x+3))-fmin(m_low.GetData(i+_x+2),m_low.GetData(i+_x+3))))
                     /((fmax(m_high.GetData(i+_x),m_high.GetData(i+_x+1))-fmin(m_low.GetData(i+_x),m_low.GetData(i+_x+1)))
                     +(fmax(m_high.GetData(i+_x+2),m_high.GetData(i+_x+3))-fmin(m_low.GetData(i+_x+2),m_low.GetData(i+_x+3))));
         double _d=((fmax(m_high.GetData(i+_x),m_high.GetData(i+_x+1))-fmin(m_low.GetData(i+_x),m_low.GetData(i+_x+1)))
                     -(fmax(m_high.GetData(i+_x+3),m_high.GetData(i+_x+4))-fmin(m_low.GetData(i+_x+3),m_low.GetData(i+_x+4))))
                     /((fmax(m_high.GetData(i+_x),m_high.GetData(i+_x+1))-fmin(m_low.GetData(i+_x),m_low.GetData(i+_x+1)))
                     +(fmax(m_high.GetData(i+_x+3),m_high.GetData(i+_x+4))-fmin(m_low.GetData(i+_x+3),m_low.GetData(i+_x+4))));
         
         ...
      }

Эти объекты будут иметь один размер, поскольку они регистрируют только текущие изменения. Морфизмы среди них будут перемещаться методом квадратной перестановки от проекции ценового диапазона с одним баром до прогноза ценового диапазона с двумя барами, на два ценовых бара вперед. Подробнее об этом мы узнаем, когда формально определим естественные преобразования ниже.

Взаимосвязь между диапазонами ценовых баров и полученными рыночными данными также показана в нашем источнике выше. Изменения, регистрируемые в каждом объекте, не нормализуются, как в случае со значениями индикатора, а скорее изменения в диапазоне делятся на сумму текущего и предыдущего диапазонов баров для получения неокругленного десятичного значения.

Функторы: Привязка значений индикатора к диапазонам ценовых баров

Функторы были представлены в нашей серии четыре статьи назад, но здесь они рассматриваются как пара двух категорий. Функторы полноты отображают не только объекты, но и морфизмы, поэтому, поскольку наша доменная категория значений индикаторов имеет два объекта и морфизм, это означает, что в нашей категории кодомена будет три выходные точки: две от объекта и одна от морфизма для каждого функтора. С двумя функторами это дает шесть конечных точек в нашем кодомене.

Сопоставление нормализованных целочисленных значений индикатора с изменениями диапазона десятичных ценовых баров (изменениями, которые регистрируются как дроби, а не как необработанные значения) можно выполнить с помощью многослойных перцептронов, рассмотренных в последних двух статьях. Существует множество других, еще не исследованных в этой серии, методов создания такого сопоставления, например, метод случайныйого леса например.

Эта иллюстрация предназначена только для полноты картины и понимания, что такое естественное преобразование и каковы все ее предпосылки. Когда трейдеры сталкиваются с новыми концепциями, наиболее важный вопрос для них - каково их применение и польза? Вот почему я заявил в начале, что для наших целей прогнозирования мы сосредоточимся на квадрате естественности, который определяется исключительно четырьмя объектами в категории кодомена. Таким образом, упоминание категории предметной области и ее объектов здесь просто помогает определить естественные преобразования и не помогает в нашем конкретном применении в этой статье.

Естественные преобразования: преодоление разрыва

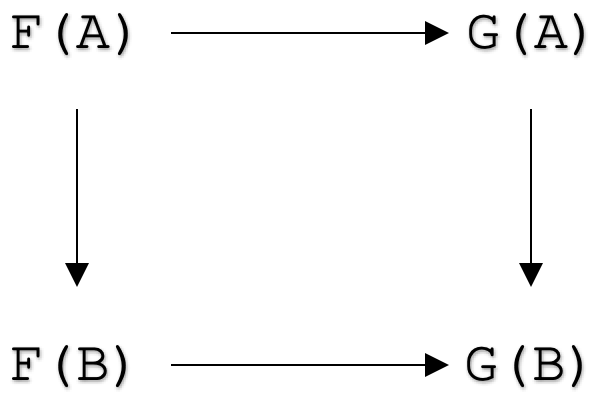
Теперь мы можем взглянуть на аксиомы естественных преобразований, чтобы перейти к их применению. Формально естественное преобразование между функторами

F: C --> D

и

G: C --> D

это семейство морфизмов

ηA: F(A) --> G(A)

для всех объектов А в категории С такова, что для всех морфизмов

f: A --> B

в категории С перемещает следующая диаграмма:

 

В Интернете можно найти немало материалов о естественных преобразованиях, но, тем не менее, может быть полезно взглянуть на более наглядное определение, ведущее к квадрату естественности. Для этого предположим, что у вас есть две категории C и D, причем категория C имеет два объекта X и Y, определенные следующим образом:

X = {5, 6, 7}

и

Y = {Q, R, S}

Предположим также, что у нас есть морфизм между этими объектами, f определен как:

f: X à Y

такие, что f(5) = S, f(6) = R и f(7) = R.

В этом примере два функтора F и G между категориями C и D будут выполнять две простые вещи. Подготовим список и список списков соответственно. Таким образом, функтор F, примененный к X, выведет:

[5, 6, 5, 7, 5, 6, 7, 7]

и аналогично функтор G (список списков) даст:

[[5, 6], [5, 7, 5, 6, 7], [7]]

Если мы применим эти функторы аналогично объекту Y, мы получим 4 объекта в категории кодомена D. Они представлены, как показано ниже:

Обратите внимание, что сейчас мы фокусируемся только на четырех объектах в категории D. Поскольку у нас есть два объекта в нашей доменной категории C, у нас также будет два естественных преобразования каждое по отношению к объекту в категории C. Они представлены ниже:

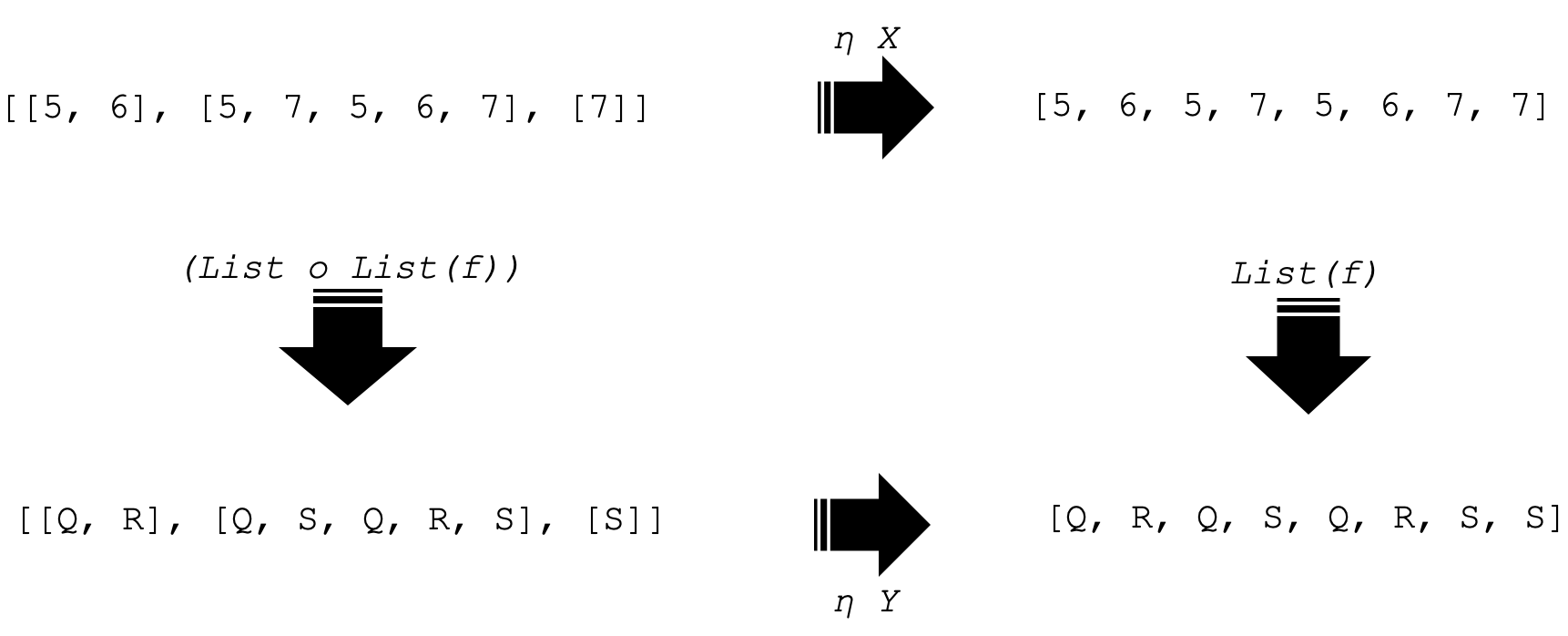
Изображение выше демонстрирует квадрат естественности. Стрелки указывают на перестановки. Две горизонтальные стрелки — это наши естественные преобразования (natural transformation, NT) по отношению к каждому объекту в C, а вертикальные стрелки — это выходные данные функтора при применении к морфизму f в категории C для функторов F и G.

Важность сохранения структуры и взаимоотношений — это ключевой аспект NT, который можно упустить из виду, но, несмотря на всю его простоту, он имеет решающее значение. Чтобы прояснить нашу точку зрения, давайте рассмотрим пример из кулинарии. Предположим, у нас есть два знаменитых повара, назовем их А и B. Каждый из них располагает уникальным способом приготовления одного и того же блюда из стандартного набора ингредиентов. Мы бы рассматривали ингредиенты как объект в более широкой категории типов ингредиентов, а два блюда, которые готовит каждый шеф-повар, также принадлежали бы другой, более широкой категории типов блюд. Естественная трансформация между двумя блюдами, приготовленными нашими поварами А и B, будет регистрировать ингредиенты и дополнительные приготовления, необходимые для изменения блюда, приготовленного шеф-поваром А, на блюдо, приготовленное шеф-поваром B. При таком подходе мы регистрируем больше информации и можем проверить и посмотреть, понадобится ли, скажем, блюду шеф-повара C аналогичная NT, чтобы соответствовать блюду шеф-повара B, а если нет, то в какой степени? Но помимо сравнения, использование NT для получения блюда от шеф-повара B потребует рецепт шеф-повара А, стили и методы приготовления. Это означает, что они должны быть сохранены. Такое сохранение важно также и как средство разработки новых рецептов или даже проверки существующих с учетом чьих-либо ограничений в диете.

Применение: Прогнозирование волатильности

Теперь мы можем рассмотреть возможные применения в прогнозировании. В этой серии мы много рассматривали прогнозирование изменения диапазона ценовых баров. Мы используем этот прогноз, чтобы определить, во-первых, нужно ли нам корректировать трейлинг-стоп на открытых позициях, а во-вторых, насколько нам нужно его корректировать.

Реализация квадрата естественности в качестве ключевого инструмента в этой задаче будет осуществляться с помощью многослойных перцептронов (multi-layer perceptron, MLP), как это было в наших последних двух статьях, с той разницей, что здесь эти MLP составлены вокруг квадратной перестановки (square commutation). Это позволяет нам проверить наши прогнозы, поскольку любые два этапа могут дать прогноз. Четыре угла квадрата отражают разные прогнозы в какой-то момент будущего изменения диапазона наших ценовых баров. По мере продвижения к углу D мы больше смотрим в будущее, причем угол А прогнозирует изменение диапазона только для следующего бара. Это означает, что если мы сможем обучить MLP, которые связывают все четыре угла, используя изменение диапазона для самого последнего ценового бара, мы сможем делать прогнозы намного дальше, за пределы одного бара.

Шаги, необходимые для применения наших NT для получения прогноза, показаны в приведенном ниже списке:

//+------------------------------------------------------------------+
//| NATURAL TRANSFORMATION CLASS                                     |
//+------------------------------------------------------------------+
class CTransformation
   {
      protected:
      
      public:
      
      CDomain<string>               domain;  //codomain object of first functor
      CDomain<string>               codomain;//codomain object of second functor
      
      uint                          hidden_size;
      CMultilayerPerceptron         transformer;
      CMLPBase                      init;
      
      void                          Transform(CDomain<string> &D,CDomain<string> &C)
                                    {
                                       domain=D;
                                       codomain=C;
                                       
                                       int _inputs=D.Cardinality(),_outputs=C.Cardinality();
                                       
                                       if(_inputs>0 && _outputs>0)
                                       {
                                          init.MLPCreate1(_inputs,hidden_size+fmax(_inputs,_outputs),_outputs,transformer);
                                       }
                                    }
      
      //
      void                          Let()
                                    {
                                       this.codomain.Let();
                                       this.domain.Let();
                                    };
      
                                    CTransformation(void){ hidden_size=1; };
                                    ~CTransformation(void){};
   };

Во-первых, у нас есть класс NT, указанный выше. Что касается случайного определения, мы могли бы ожидать, что оно будет включать экземпляр двух функторов, которые оно связывает. Это применимо, но значительно увеличит объем кода. Ключевым моментом в NT являются две области, отображаемые функторами. Именно они и выделены.

//+------------------------------------------------------------------+
//| NATURALITY CLASS                                                 |
//+------------------------------------------------------------------+
class CNaturalitySquare
   {
      protected:
      
      public:
      
      CDomain<string>               A,B,C,D;
      
      CTransformation               AB;
      
      uint                          hidden_size_bd;
      CMultilayerPerceptron         BD;
      
      uint                          hidden_size_ac;
      CMultilayerPerceptron         AC;
      
      CTransformation               CD;
      
      CMLPBase                      init;
      
      
                                    CNaturalitySquare(void){};
                                    ~CNaturalitySquare(void){};
   };

Квадрат естественности, диаграмма которого показана выше, также будет иметь свой класс, представленный экземплярами класса NT. Его четыре угла, выраженные буквами A, B, C и D, являются объектами, захваченными доменным классом, и только два из его морфизмов будут прямыми MLP, тогда как два других распознаются как NT.

Практическая реализация на MQL5

Практическая реализация в MQL5, учитывая наше использование MLP, неизбежно столкнется с проблемами, прежде всего, с тем, как мы обучаем и храним то, что мы узнали (веса сети). В этой статье, в отличие от двух последних, веса от обучения вообще не сохраняются, что означает, что на каждом новом столбце генерируется и обучается новый экземпляр каждого из четырех MLP. Это реализовано с помощью функции обновления, как показано ниже:

//+------------------------------------------------------------------+
//| Refresh function for naturality square.                          |
//+------------------------------------------------------------------+
double CTrailingCT::Refresh()
   {
      double _refresh=0.0;
      
      m_high.Refresh(-1);
      m_low.Refresh(-1);
      
      int _x=StartIndex();
      
      // atr domains capture 1 bar ranges       
      // bands' domains capture 2 bar ranges    
      // 1 functors capture ranges after 1 bar  
      // 2 functors capture ranges after 2 bars 
      
      int _info_ab=0,_info_bd=0,_info_ac=0,_info_cd=0;
      CMLPReport _report_ab,_report_bd,_report_ac,_report_cd;
      CMatrixDouble _xy_ab;_xy_ab.Resize(m_extra_training+1,1+1);
      CMatrixDouble _xy_bd;_xy_bd.Resize(m_extra_training+1,1+1);
      CMatrixDouble _xy_ac;_xy_ac.Resize(m_extra_training+1,1+1);
      CMatrixDouble _xy_cd;_xy_cd.Resize(m_extra_training+1,1+1);
      
      CElement<string> _e;
      for(int i=0;i<m_extra_training+1;i++)
      {
         ...
         
         if(i<m_extra_training+1)
         {
            _xy_ab[i].Set(0,_a);//in
            _xy_ab[i].Set(1,_b);//out
            
            _xy_bd[i].Set(0,_b);//in
            _xy_bd[i].Set(1,_d);//out
            
            _xy_ac[i].Set(0,_a);//in
            _xy_ac[i].Set(1,_c);//out
            
            _xy_cd[i].Set(0,_c);//in
            _xy_cd[i].Set(1,_d);//out
         }
      }
      
      m_train.MLPTrainLM(m_naturality_square.AB.transformer,_xy_ab,m_extra_training+1,m_decay,m_restarts,_info_ab,_report_ab);
     
      ...

      //
      if(_info_ab>0 && _info_bd>0 && _info_ac>0 && _info_cd>0)
      {
         ...
      }
      
      return(_refresh);
   }

Приведенная выше функция обновления обучает MLP, инициализированные со случайными весами, только на последнем ценовом баре. Этого явно будет недостаточно для других торговых систем или реализаций общего кода, однако входной параметр m_extra_training, нулевое значение по умолчанию которого поддерживается для наших целей тестирования, может быть скорректирован в сторону увеличения, чтобы обеспечить более полное тестирование перед составлением прогнозов.

Использование параметра для дополнительного обучения неизбежно создаст перегрузку производительности эксперта и фактически указывает на то, почему в этой статье вообще избегалось считывание и запись весов во время обучения.

Преимущества и ограничения

Если мы проведем тесты по EURUSD на дневном временном интервале с 2022.08.01 по 2023.08.01, один из наших лучших прогонов даст следующий результат:

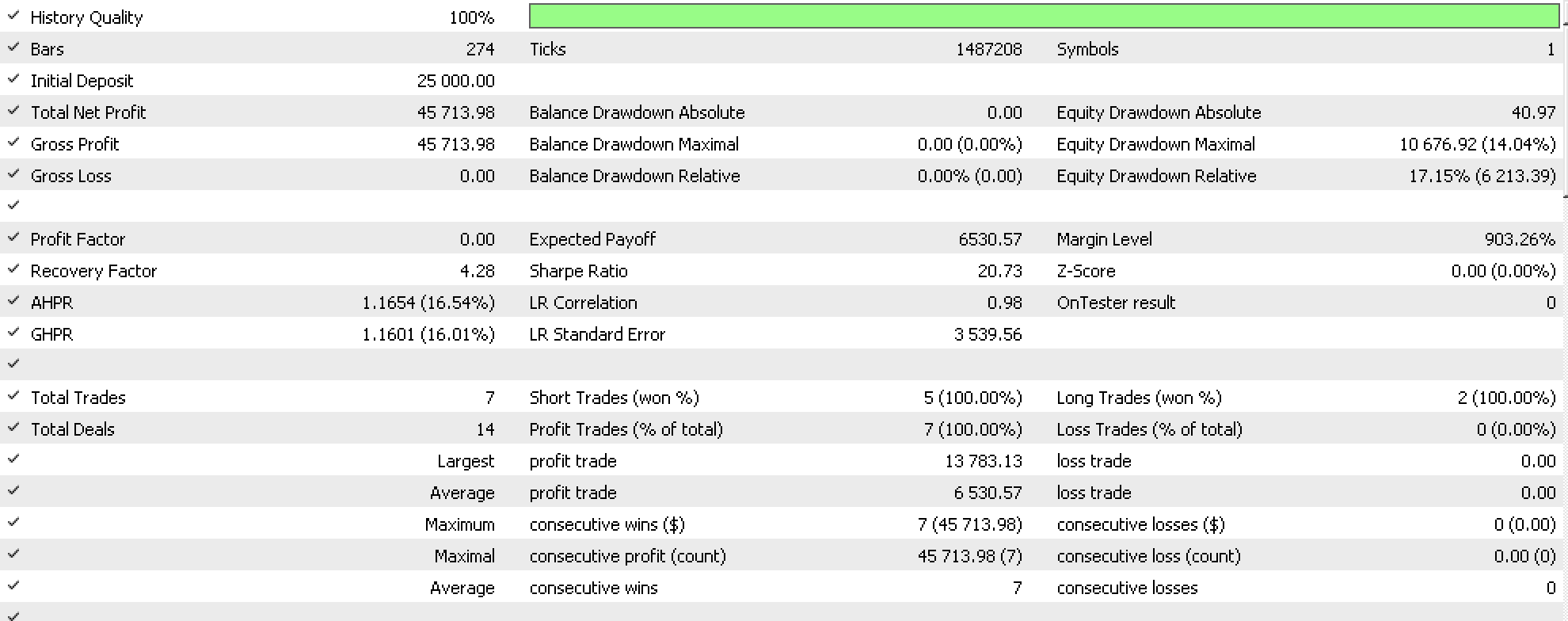
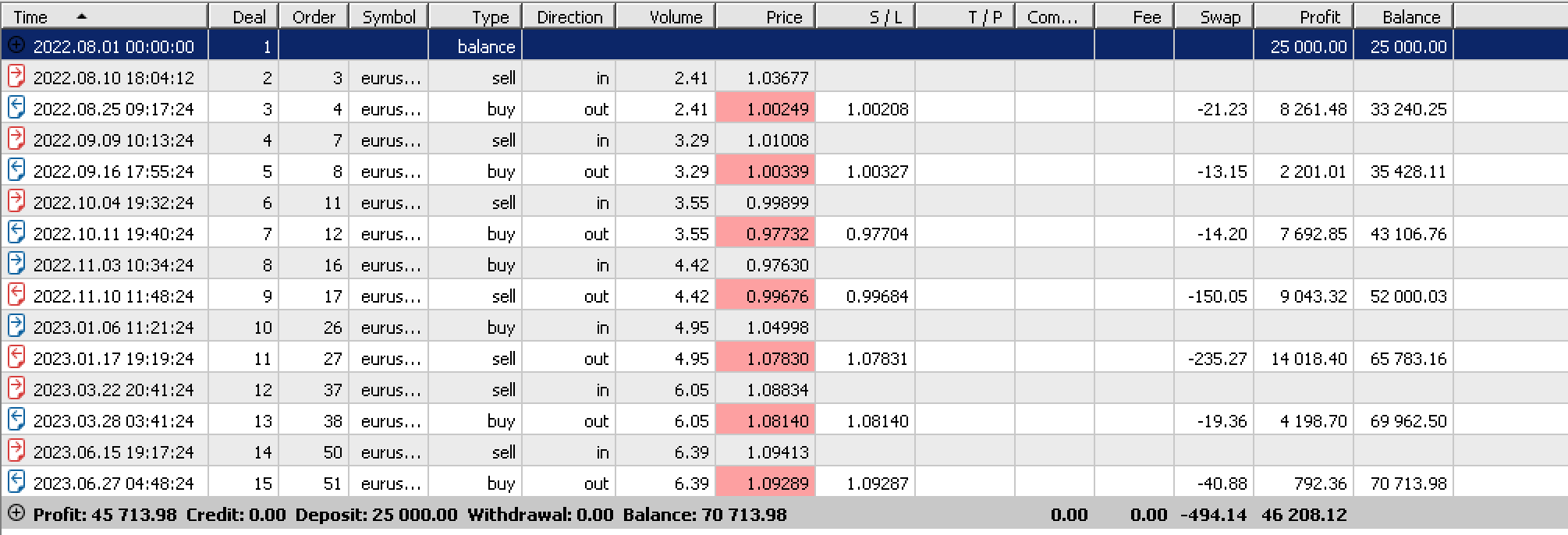
Если мы запустим тесты с теми же настройками в неоптимизированный период (в нашем случае за годичный период до нашего диапазона тестирования), мы получаем отрицательные результаты, которые не отражают производительность, полученную в приведенном выше отчете. Как можно видеть, вся прибыль была получена при срабатывании стоп-лоссов.

По сравнению с подходами, которые мы использовали ранее в этой серии для прогнозирования волатильности, этот подход, безусловно, требует больших ресурсов и явно требует изменений в способе определения наших четырех объектов в квадрате естественности, чтобы обеспечить возможность движения вперед в течение неоптимизированных периодов.

Заключение

Подводя итог, ключевая концепция, изложенная здесь, — это естественные преобразования. Они важны для связывания категорий путем фиксации разницы между параллельной парой функторов, соединяющих категории. Рассматренные здесь примеры использования касались прогнозирования волатильности с использованием квадрата естественности, однако другие возможные приложения включают генерацию сигналов входа и выхода, а также определение размера позиции. Кроме того, может быть полезно упомянуть, что в этой статье и на протяжении всей этой серии мы не проводили никаких предварительных прогонов с полученными оптимизированными настройками. Так что, скорее всего, они не смогут работать "из коробки" (то есть в том виде, в котором предоставлен код), но смогут после внесения изменений, например, путем объединения изложенных идей с другими стратегиями, которые может применять читатель. Вот почему использование мастер-классов MQL5 оказывается полезным, поскольку оно легко позволяет это сделать.

Ссылки

Ссылки на статьи в Википедии и на сайте stackexchange.com.

Примечания к приложениям

Поместие файл SignalCT_16_.mqh в папку MQL5\include\Expert\Signal\, а файл ct_16.mqh - в MQL5\include\.

Возможно, вам также будут полезны рекомендации, приведенные здесь, о том, как собрать советник с помощью Мастера. Как указано в статье, я не использовал трейлинг-стоп и фиксированную маржу для управления капиталом. Обе составляющие являются частью библиотеки MQL5. Как всегда, цель статьи – не представить вам Грааль, а скорее, предложить идею, которую вы можете адаптировать к собственной стратегии.