
Эксперименты с нейросетями (Часть 5): Нормализация входных параметров для передачи в нейросеть
Введение
Добрый день, уважаемые пользователи сообщества MQL5. Немного поразмыслив над результатами наших предыдущих экспериментов, возникла задача, как улучшить показатели обучения, а в итоге и прибыльности советников, которые мы разработали ранее.
Сегодня мы поговорим о важности сигнала. А именно, передачи данных в нейросеть для анализа и прогнозирования будущих результатов. Запомните — это очень важная составляющая нейросети. Скорее сказать, самая важная из всех. Я хочу донести к своим читателям важность понимания сигналов, что бы вы избежали досадных недоразумений, типа "я использовал самую продвинутую библиотеку, и она не работает". В прошлых статьях мы применили некоторые интересные методы, сегодня попробуем, передать данные индикатора нормализовав его значения.
От меня как всегда подробное не очень заумное объяснение. Думаю, все смогут разобраться.
Важность нормализации входных параметров для передачи в нейросеть
Нормализация входных параметров является важным шагом в процессе подготовки данных для обучения нейронных сетей. Этот процесс позволяет привести входные данные к определенному диапазону значений, что помогает улучшить стабильность и скорость сходимости обучения.
В этой статье мы рассмотрим, почему нормализация является важным этапом в обучении нейронных сетей и какие методы нормализации могут быть использованы.
Нормализация входных параметров - что это значит?
Нормализация входных параметров заключается в преобразовании входных данных, чтобы они имели определенный диапазон значений. Часто применяются два основных метода нормализации: нормализация по среднему и стандартному отклонению (z-нормализация), и нормализация по минимуму и максимуму (мин-макс нормализация).
Z-нормализация использует среднее значение и стандартное отклонение для центрирования и масштабирования данных. Для этого каждое значение вычитается из среднего значения и делится на стандартное отклонение. Мин-макс нормализация использует минимальное и максимальное значения для масштабирования данных в заданный диапазон.
Почему нормализация входных параметров важна?
Нормализация входных параметров важна для улучшения стабильности и скорости сходимости обучения. Если входные данные не нормализованы, то некоторые параметры могут иметь большой диапазон значений, что может привести к проблемам в обучении нейронной сети. Например, градиенты могут стать слишком большими или маленькими, что приведет к проблемам в оптимизации и ухудшению точности предсказаний.
Нормализация также позволяет ускорить процесс обучения, поскольку сходимость алгоритма оптимизации может быть улучшена. Правильно нормализованные данные также могут помочь в избежании проблемы переобучения, что может возникнуть, если входные данные не имеют хорошей репрезентативности.
Какие методы нормализации могут быть использованы?
Методы нормализации могут варьироваться в зависимости от типа данных и задачи, которую мы пытаемся решить. Например, для изображений часто используются методы нормализации, такие как нормализация по среднему и стандартному отклонению (z-нормализация) и нормализация по минимуму и максимуму (мин-макс нормализация). Однако, для других типов данных, таких как звуковые сигналы или текстовые данные, может быть более эффективным использование других методов нормализации.
Для звуковых сигналов, например, часто используется нормализация по максимальной амплитуде, где все значения сигнала масштабируются в диапазон от -1 до 1. Для текстовых данных может быть полезной нормализация по количеству слов или символов в предложении.
Кроме того, в некоторых случаях может быть полезной нормализация не только входных данных, но и целевых переменных. Например, в задачах регрессии, где целевая переменная имеет большой диапазон значений, может быть полезной нормализация целевой переменной, чтобы улучшить стабильность обучения и точность предсказаний.
Нормализация входных параметров является важным шагом в процессе подготовки данных для обучения нейронных сетей. Этот процесс позволяет привести входные данные к определенному диапазону значений, что помогает улучшить стабильность и скорость сходимости обучения. В зависимости от типа данных и задачи, которую мы пытаемся решить, могут быть использованы различные методы нормализации. Кроме того, в некоторых случаях может быть полезной нормализация не только входных данных, но и целевых переменных.
Методы нормализации
Min-Max нормализация
В машинном обучении, нормализация является важным этапом предварительной обработки данных, которая позволяет улучшить стабильность и скорость сходимости обучения. Одним из наиболее распространенных методов нормализации является Min-Max нормализация, которая позволяет привести значения данных к диапазону от 0 до 1. В этой статье мы рассмотрим, как можно использовать Min-Max нормализацию для временных рядов.
Временные ряды являются последовательностью значений, измеренных в разные моменты времени. Примерами временных рядов могут служить данные о температуре, ценах на акции или количество продаж товаров. Временные ряды могут быть использованы для прогнозирования будущих значений, анализа трендов и паттернов или выявления аномалий.
Временные ряды могут иметь разный диапазон значений и изменения во времени могут быть неоднородными. Например, цены на акции могут иметь большой диапазон значений и колебаться в зависимости от сезонности, новостей и других факторов. Для эффективного анализа и прогнозирования временных рядов необходимо привести значения к определенному диапазону.
Метод Min-Max нормализации приводит значения к диапазону от 0 до 1 путем масштабирования значений в соответствии с минимальным и максимальным значениями. Формула для Min-Max нормализации выглядит следующим образом:
x_norm = (x - x_min) / (x_max - x_min)
где x - значение данных, x_min - минимальное значение во всем наборе данных, x_max - максимальное значение во всем наборе данных, x_norm - нормализованное значение.
Применение метода Min-Max нормализации к временным рядам может помочь привести данные к общему диапазону значений и упростить анализ. Например, если мы имеем данные о температуре, которые колеблются в диапазоне от -30 до +30 градусов, мы можем применить Min-Max нормализацию, чтобы привести значения к диапазону от 0 до 1. Это позволит нам сравнивать значения в разные периоды времени и выявлять тренды и аномалии.
Однако, при применении Min-Max нормализации к временным рядам необходимо учитывать особенности данного метода и его влияние на данные. Во-первых, применение Min-Max нормализации может привести к потере информации о распределении значений внутри диапазона. Например, если в наборе данных присутствуют выбросы или экстремальные значения, то они будут приведены к 0 или 1 и потеряются в анализе. В этом случае можно использовать альтернативные методы нормализации, например, Z-score нормализацию.
Во-вторых, при использовании Min-Max нормализации необходимо учитывать динамику изменений данных. Если данные имеют неравномерную динамику изменений, то нормализация может привести к искажению временных паттернов и аномалий. В этом случае можно применить локальную нормализацию, где минимальное и максимальное значения определяются для каждой группы данных внутри определенного периода времени.
В-третьих, при использовании Min-Max нормализации необходимо учитывать влияние выборки на результаты анализа. Если выборка наблюдений не сбалансирована или содержит выбросы, то нормализация может привести к ошибочным выводам. В этом случае можно использовать альтернативные методы обработки данных, например, удаление выбросов или сглаживание данных.
В заключение, метод Min-Max нормализации является одним из наиболее распространенных методов нормализации в машинном обучении и может быть эффективно применен к временным рядам для приведения значений к общему диапазону. Однако, при использовании данного метода необходимо учитывать особенности данных и применять дополнительные методы обработки, чтобы избежать искажений в анализе и прогнозировании временных рядов.
Пример:
int OnInit() { // объявляем и инициализируем массив double data_array[] = {1.2, 2.3, 3.4, 4.5, 5.6}; // находим минимальное и максимальное значение в массиве double min_value = ArrayMinimum(data_array, 0, ArraySize(data_array)-1); double max_value = ArrayMaximum(data_array, 0, ArraySize(data_array)-1); // создаем массив для хранения результата нормализации double norm_array[ArraySize(data_array)]; // нормализуем массив for(int i = 0; i < ArraySize(data_array); i++) { norm_array[i] = (data_array[i] - min_value) / (max_value - min_value); } // выводим результат for(int i = 0; i < ArraySize(data_array)-1; i++) { Print("Исходный массив: ", data_array[i]); Print("Результат Min-Max нормализации: ", norm_array[i]); } return(INIT_SUCCEEDED); }
Этот код создает массив data_array , содержащий пять чисел с плавающей запятой. Затем он находит минимальное и максимальное значение в массиве при помощи функций ArrayMinimum() и ArrayMaximum() , создает новый массив norm_array для хранения результата нормализации и заполняет его, вычисляя для каждого элемента (data_array[i] - min_value) / (max_value - min_value) . Наконец, результат выводится на экран при помощи функции Print() .
Результат:
2023.04.07 13:22:32.937 11111111111111 (EURUSD,H1) Исходный массив: 1.2 2023.04.07 13:22:32.937 11111111111111 (EURUSD,H1) Результат Min-Max нормализации: 0.39999999999999997 2023.04.07 13:22:32.937 11111111111111 (EURUSD,H1) Исходный массив: 2.3 2023.04.07 13:22:32.937 11111111111111 (EURUSD,H1) Результат Min-Max нормализации: 0.7666666666666666 2023.04.07 13:22:32.937 11111111111111 (EURUSD,H1) Исходный массив: 3.4 2023.04.07 13:22:32.937 11111111111111 (EURUSD,H1) Результат Min-Max нормализации: 1.1333333333333333 2023.04.07 13:22:32.937 11111111111111 (EURUSD,H1) Исходный массив: 4.5 2023.04.07 13:22:32.937 11111111111111 (EURUSD,H1) Результат Min-Max нормализации: 1.5
Z-нормализация
Временные ряды являются важным инструментом в анализе данных, особенно в экономике, финансах, метеорологии, науке о материалах и других областях. Одним из основных методов предварительной обработки временных рядов является Z-нормализация, которая может помочь улучшить качество анализа данных.
Z-нормализация - это метод центрирования и масштабирования временных рядов. Она заключается в преобразовании временного ряда таким образом, чтобы среднее значение временного ряда было равно нулю, а стандартное отклонение было равно единице. Это может быть полезным для сравнения временных рядов между собой, а также для устранения влияния сезонности и трендов.
Процесс Z-нормализации временных рядов включает в себя следующие шаги:
- Вычислите среднее значение временного ряда.
- Вычислите стандартное отклонение временного ряда.
- Для каждого элемента временного ряда вычислите разницу между его значением и средним значением временного ряда.
- Разделите каждую разницу на стандартное отклонение.
Полученные значения будут иметь среднее значение, равное нулю, и стандартное отклонение, равное единице.
Преимущества Z-нормализации:
- Улучшение качества анализа данных. Z-нормализация может помочь устранить влияние сезонности и трендов, что может улучшить качество анализа данных.
- Легкость использования. Z-нормализация проста в использовании и может быть применена к различным типам временных рядов.
- Полезность для сравнения временных рядов. Z-нормализация позволяет сравнивать временные ряды между собой, так как она устраняет влияние различных масштабов и единиц измерения.
Однако Z-нормализация также имеет некоторые ограничения:
- Не подходит для временных рядов с экстремальными значениями. Если временный ряд содержит экстремальные значения, Z-нормализация может привести к искаженным результатам.
- Не подходит для нестационарных временных рядов. Если временный ряд нестационарный (т.е. имеет тренд или сезонность), то Z-нормализация может устранить эти характеристики, что может привести к некорректному анализу данных.
- Не гарантирует нормальность распределения. Z-нормализация может помочь привести распределение временного ряда к нормальному, но не гарантирует, что распределение будет именно нормальным.
Несмотря на эти ограничения, Z-нормализация является важным методом предварительной обработки временных рядов, который может помочь улучшить качество анализа данных. Он может быть использован в различных областях, включая экономику, финансы, метеорологию и науку о материалах.
Например, в экономике и финансах Z-нормализация может быть использована для сравнения производительности различных активов или портфелей, а также для анализа риска и волатильности.
В метеорологии Z-нормализация может помочь устранить влияние сезонности и трендов на анализ погодных данных, таких как температура или осадки.
В науке о материалах Z-нормализация может быть использована для анализа временных рядов свойств материалов, таких как термическое расширение или магнитные свойства.
В заключение, Z-нормализация является важным методом предварительной обработки временных рядов, который может помочь улучшить качество анализа данных в различных областях. Несмотря на некоторые ограничения, Z-нормализация проста в использовании и может быть применена к различным типам временных рядов.
Пример:
int OnInit() { // объявляем и инициализируем массив double data_array[] = {1.2, 2.3, 3.4, 4.5, 5.6}; // находим среднее значение и стандартное отклонение в массиве double mean_value = ArrayAverage(data_array, 0, ArraySize(data_array)-1); double std_value = ArrayStdDev(data_array, 0, ArraySize(data_array)-1); // создаем массив для хранения результата нормализации double norm_array[ArraySize(data_array)]; // нормализуем массив for(int i = 0; i < ArraySize(data_array); i++) { norm_array[i] = (data_array[i] - mean_value) / std_value; } // выводим результат for(int i = 0; i < ArraySize(data_array)-1; i++) { Print("Исходный массив: ", data_array[i]); Print("Результат Z-нормализации: ", norm_array[i]); } return(INIT_SUCCEEDED); } double ArrayAverage(double &array[], int start_pos=0, int count=-1) { double sum = 0.0; int size = ArraySize(array); // Определение индекса последнего элемента int end_pos = count < 0 ? size - 1 : start_pos + count - 1; end_pos = end_pos >= size ? size - 1 : end_pos; // Вычисление суммы элементов for(int i = start_pos; i <= end_pos; i++) { sum += array[i]; } // Вычисление среднего значения double avg = sum / (end_pos - start_pos + 1); return (avg); } double ArrayStdDev(double &array[], int start_pos=0, int count=-1) { double mean = ArrayAverage(array, start_pos, count); double sum = 0.0; int size = ArraySize(array); // Определение индекса последнего элемента int end_pos = count < 0 ? size - 1 : start_pos + count - 1; end_pos = end_pos >= size ? size - 1 : end_pos; // Вычисление суммы квадратов отклонений от среднего for(int i = start_pos; i <= end_pos; i++) { sum += MathPow(array[i] - mean, 2); } // Вычисление стандартного отклонения double std_dev = MathSqrt(sum / (end_pos - start_pos + 1)); return (std_dev); }
Этот код создает массив data_array , содержащий пять чисел с плавающей запятой. Затем он находит среднее значение и стандартное отклонение в массиве при помощи функций ArrayAverage() и ArrayStdDev() , создает новый массив norm_array для хранения результата нормализации и заполняет его, вычисляя для каждого элемента (data_array[i] - mean_value) / std_value . Наконец, результат выводится на экран при помощи функции Print() .
Результат:
2023.04.07 13:51:57.501 11111111111111 (EURUSD,H1) Исходный массив: 1.2 2023.04.07 13:51:57.501 11111111111111 (EURUSD,H1) Результат Z-нормализации: -1.3416407864998738 2023.04.07 13:51:57.501 11111111111111 (EURUSD,H1) Исходный массив: 2.3 2023.04.07 13:51:57.501 11111111111111 (EURUSD,H1) Результат Z-нормализации: -0.4472135954999581 2023.04.07 13:51:57.501 11111111111111 (EURUSD,H1) Исходный массив: 3.4 2023.04.07 13:51:57.501 11111111111111 (EURUSD,H1) Результат Z-нормализации: 0.44721359549995776 2023.04.07 13:51:57.501 11111111111111 (EURUSD,H1) Исходный массив: 4.5 2023.04.07 13:51:57.501 11111111111111 (EURUSD,H1) Результат Z-нормализации: 1.3416407864998736
Дифференцирование
Дифференцирование временных рядов является важным методом анализа данных, который позволяет убрать из ряда тренд и/или сезонность, делая его более стационарным. В этой статье мы рассмотрим, что такое дифференцирование, как его применять и какие преимущества это может дать.
Что такое дифференцирование временных рядов?
Дифференцирование - это процесс нахождения разностей между последовательными значениями временного ряда. Количество разностей, которые нужно найти, зависит от степени стационарности, которую вы хотите достичь. Обычно достаточно одной или двух разностей для устранения тренда или сезонности. Один разностный шаг выглядит следующим образом:
y'(t) = y(t) - y(t-1)
где y'(t) - разность между текущим значением ряда и предыдущим значением.
Если ряд нестационарен, то после дифференцирования его значения становятся более случайными, без видимых трендов или сезонности. Это может помочь выделить более явные особенности временного ряда, такие как циклы или изменчивость.
Как применять дифференцирование временных рядов?
Для дифференцирования временного ряда следуйте этим шагам:
- Определите, является ли ряд нестационарным. Если в ряду есть тренд или сезонность, то он нестационарный.
- Определите, насколько разностей вам нужно для получения стационарности. Если вы хотите убрать только тренд, то достаточно одной разности. Если вы хотите убрать сезонность, то может потребоваться две или более разностей.
- Примените разностное преобразование к ряду. Используйте формулу y'(t) = y(t) - y(t-1), чтобы найти первую разность. Если вам нужно найти вторую разность, примените формулу к y'(t).
- Проверьте, является ли ряд стационарным. Для этого можно использовать статистические тесты на стационарность, такие как тест Дики-Фуллера.
- Если ряд нестационарный, повторите процесс дифференцирования, пока ряд не станет стационарным.
Какие преимущества дает дифференцирование временных рядов?
Дифференцирование временных рядов может дать несколько преимуществ:
- Улучшение прогнозирования: Когда временной ряд стационарен, прогнозирование становится проще, потому что статистические свойства ряда не меняются со временем.
- Устранение тренда: При дифференцировании ряда удаляется линейный тренд, что делает ряд более стационарным и улучшает его анализ.
- Устранение сезонности: При использовании нескольких разностных шагов можно удалить сезонность из временного ряда, что делает его более стационарным.
- Удаление шума: При дифференцировании ряда удалаются низкочастотные компоненты (тренд и сезонность), что может помочь убрать шум, вносимый этими компонентами.
- Улучшение интерпретации: Когда ряд стационарен, его можно анализировать с помощью классических статистических методов, что делает интерпретацию данных более простой и понятной.
Однако дифференцирование также может иметь недостатки. Например, если вы дифференцируете ряд слишком много раз, он может потерять важные сигналы, что приведет к неверным выводам. Кроме того, дифференцирование может вводить дополнительный шум в ряд.
Дифференцирование временных рядов - это полезный метод анализа данных, который позволяет убрать из ряда тренд и/или сезонность, делая его более стационарным. Это улучшает прогнозирование, удаляет шум и улучшает интерпретацию данных. Однако дифференцирование также может иметь недостатки, поэтому его следует использовать с осторожностью и в сочетании с другими методами анализа данных.
Пример:
int OnInit() { // объявляем и инициализируем массив double data_array[] = {1.2, 2.3, 3.4, 4.5, 5.6}; // создаем массив для хранения результата дифференцирования double diff_array[ArraySize(data_array)]; // дифференцируем массив for(int i = 0; i < ArraySize(data_array)-1; i++) { diff_array[i] = data_array[i+1] - data_array[i]; } // выводим результат for(int i = 0; i < ArraySize(data_array)-1; i++) { Print("Исходный массив: ", data_array[i]); Print("Результат дифференцирования: ", diff_array[i]); } return(INIT_SUCCEEDED); }
Этот код создает массив data_array , содержащий пять чисел с плавающей запятой. Затем он создает новый массив diff_array для хранения результата дифференцирования и заполняет его, вычитая каждый элемент i+1 из элемента i в data_array . Наконец, результат выводится на экран при помощи функции Print() .
Результат:
2023.04.07 13:13:50.650 11111111111111 (EURUSD,H1) Исходный массив: 1.2 2023.04.07 13:13:50.650 11111111111111 (EURUSD,H1) Результат дифференцирования: 1.0999999999999999 2023.04.07 13:13:50.650 11111111111111 (EURUSD,H1) Исходный массив: 2.3 2023.04.07 13:13:50.650 11111111111111 (EURUSD,H1) Результат дифференцирования: 1.1 2023.04.07 13:13:50.650 11111111111111 (EURUSD,H1) Исходный массив: 3.4 2023.04.07 13:13:50.650 11111111111111 (EURUSD,H1) Результат дифференцирования: 1.1 2023.04.07 13:13:50.650 11111111111111 (EURUSD,H1) Исходный массив: 4.5 2023.04.07 13:13:50.650 11111111111111 (EURUSD,H1) Результат дифференцирования: 1.0999999999999996
Логарифмическое преобразование
Логарифмическое преобразование временных рядов - это метод преобразования данных, который используется для улучшения свойств ряда перед анализом и моделированием. Этот метод особенно полезен, когда данные имеют высокую изменчивость или исходные значения находятся в широком диапазоне.
Что такое логарифмическое преобразование?
Логарифмическое преобразование - это процесс применения логарифмической функции к каждому значению во временном ряде. Логарифмическая функция используется для сжатия значений ряда, особенно если они находятся в широком диапазоне. Применение логарифма позволяет снизить изменчивость ряда, так как он сглаживает пики и провалы в данных, делая их менее выраженными.
Когда логарифмическое преобразование является полезным?
Логарифмическое преобразование может быть полезным в следующих ситуациях:
- Когда данные имеют высокую изменчивость: Если данные имеют высокую изменчивость, то логарифмическое преобразование может сгладить их и сделать их более предсказуемыми.
- Когда данные находятся в широком диапазоне: Если данные находятся в широком диапазоне, то логарифмическое преобразование может сжать их и улучшить их интерпретацию.
- Когда данные имеют экспоненциальный тренд: Если данные имеют экспоненциальный тренд, то логарифмическое преобразование может сделать его линейным, что облегчает анализ и моделирование.
- Когда данные не соответствуют нормальному распределению: Если данные не соответствуют нормальному распределению, то логарифмическое преобразование может сделать их более нормальными.
Пример применения логарифмического преобразования:
Допустим, у нас есть временной ряд, который представляет ежедневные продажи магазина за несколько лет. Поскольку продажи могут быть очень переменными и неоднородными, мы можем применить логарифмическое преобразование, чтобы сгладить данные и сделать их более предсказуемыми.
Продолжая наш пример, мы можем применить логарифмическое преобразование к нашему временному ряду продаж. Для этого мы применим логарифмическую функцию к каждому значению в нашем ряду.
Например, если мы имеем ряд продаж {100, 200, 300, 400}, мы можем применить логарифмическое преобразование, чтобы получить {log(100), log(200), log(300), log(400)} или просто {2, 2.3, 2.5, 2.6}, используя натуральный логарифм.
Как мы можем видеть из примера, логарифмическое преобразование сжало значения ряда, что сделало его более удобным для анализа и моделирования. Это позволяет нам лучше понимать тенденции в продажах и сделать более точные прогнозы.
Однако, не стоит забывать, что логарифмическое преобразование не является универсальным методом и не всегда подходит для всех типов данных. Кроме того, при применении логарифмического преобразования следует быть осторожным и не забывать вернуться к исходному масштабу данных при необходимости.
В заключение, логарифмическое преобразование - это полезный метод преобразования временных рядов, который позволяет улучшить их свойства перед анализом и моделированием. Он может быть особенно полезен для данных с высокой изменчивостью или находящихся в широком диапазоне. Однако, при его использовании необходимо помнить о его ограничениях и правильно интерпретировать результаты.
Пример:
int OnInit() { // объявляем и инициализируем массив double data_array[] = {1.2, 2.3, 3.4, 4.5, 5.6}; // создаем массив для хранения результата нормализации double norm_array[ArraySize(data_array)]; // нормализуем массив LogTransform(data_array, norm_array); // выводим результат for(int i = 0; i < ArraySize(data_array)-1; i++) { Print("Исходный массив: ", data_array[i]); Print("Результат логарифмического преобразования: ", norm_array[i]); } return(INIT_SUCCEEDED); } void LogTransform(double& array1[], double& array2[]) { int size = ArraySize(array1); for(int i = 0; i < size; i++) { array2[i] = MathLog10(array1[i]); } }
Функция LogTransform() используется для логарифмического преобразования массива данных array1 и сохранения результата в массив array2 .
Алгоритм работает следующим образом: функция MathLog10() используется для преобразования каждого элемента массива array1 в логарифм по основанию 10, и результат сохраняется в соответствующем элементе массива array2 .
Обратите внимание, что функция LogTransform() принимает массивы данных по ссылке (через & ), что означает, что изменения, внесенные в массив array2 внутри функции, будут отражены в оригинальном массиве, переданном в качестве аргумента при вызове функции.
Результат:
2023.04.07 14:21:22.374 11111111111111 (EURUSD,H1) Исходный массив: 1.2 2023.04.07 14:21:22.374 11111111111111 (EURUSD,H1) Результат логарифмического преобразования: 0.07918124604762482 2023.04.07 14:21:22.374 11111111111111 (EURUSD,H1) Исходный массив: 2.3 2023.04.07 14:21:22.374 11111111111111 (EURUSD,H1) Результат логарифмического преобразования: 0.36172783601759284 2023.04.07 14:21:22.374 11111111111111 (EURUSD,H1) Исходный массив: 3.4 2023.04.07 14:21:22.374 11111111111111 (EURUSD,H1) Результат логарифмического преобразования: 0.5314789170422551 2023.04.07 14:21:22.374 11111111111111 (EURUSD,H1) Исходный массив: 4.5 2023.04.07 14:21:22.374 11111111111111 (EURUSD,H1) Результат логарифмического преобразования: 0.6532125137753437
Дополнительные методы обработки, что бы избежать искажений в анализе и прогнозировании временных рядов.
Временные ряды широко используются для анализа и прогнозирования в различных областях, таких как экономика, финансы, наука о климате и т.д. Однако, данные, получаемые из реального мира, часто содержат искажения, такие как выбросы, пропущенные значения или шум, которые могут повлиять на точность анализа и прогнозирования временных рядов. В этой статье мы рассмотрим дополнительные методы обработки, которые помогут избежать искажений в анализе и прогнозировании временных рядов.
Удаление выбросов
Выбросы - это значения, которые сильно отличаются от остальных значений в ряде. Они могут быть вызваны ошибками измерения, ошибками ввода данных или непредвиденными событиями, такими как кризисы или аварии. Удаление выбросов из временного ряда может улучшить качество анализа и прогнозирования.
Язык MQL5 предоставляет несколько функций для удаления выбросов. Например, функция iqr() может использоваться для определения межквартильного диапазона и вычисления границ выбросов. Функция MODE_OUTLIERS может использоваться для определения выбросов на основе значения уровня принятия решений. Эти функции могут быть использованы в комбинации с другими функциями для удаления выбросов.
Пример:
void RemoveOutliers(double& array[]) { int size = ArraySize(array); double mean = ArrayAverage(array); double stddev = ArrayStdDev(array, mean); for(int i = 0; i < size; i++) { if(MathAbs(array[i] - mean) > 2 * stddev) { array[i] = mean; } } } double ArrayAverage(double &array[], int start_pos=0, int count=-1) { double sum = 0.0; int size = ArraySize(array); // Определение индекса последнего элемента int end_pos = count < 0 ? size - 1 : start_pos + count - 1; end_pos = end_pos >= size ? size - 1 : end_pos; // Вычисление суммы элементов for(int i = start_pos; i <= end_pos; i++) { sum += array[i]; } // Вычисление среднего значения double avg = sum / (end_pos - start_pos + 1); return (avg); } double ArrayStdDev(double &array[], int start_pos=0, int count=-1) { double mean = ArrayAverage(array, start_pos, count); double sum = 0.0; int size = ArraySize(array); // Определение индекса последнего элемента int end_pos = count < 0 ? size - 1 : start_pos + count - 1; end_pos = end_pos >= size ? size - 1 : end_pos; // Вычисление суммы квадратов отклонений от среднего for(int i = start_pos; i <= end_pos; i++) { sum += MathPow(array[i] - mean, 2); } // Вычисление стандартного отклонения double std_dev = MathSqrt(sum / (end_pos - start_pos + 1)); return (std_dev); }
Функция RemoveOutliers() использует среднее значение и стандартное отклонение для определения выбросов в массиве array . Если элемент массива находится за пределами диапазона двух стандартных отклонений от среднего значения, он считается выбросом и заменяется на среднее значение.
Обратите внимание, что функция RemoveOutliers() также принимает массив данных по ссылке (через & ), что означает, что изменения, внесенные в массив внутри функции, будут отражены в оригинальном массиве, переданном в качестве аргумента при вызове функции.
Сглаживание данных
Сглаживание данных - это процесс удаления шума из временного ряда. Шум может быть вызван случайными флуктуациями или непредвиденными событиями. Сглаживание данных позволяет снизить влияние шума на анализ и прогнозирование временных рядов.
Язык MQL5 предоставляет несколько функций для сглаживания данных. Например, функция iMA() может использоваться для вычисления скользящего среднего. Это позволяет сгладить данные, уменьшить шум и обнаружить тренды. Функция iRSI() может использоваться для вычисления относительной силы индекса, который также может использоваться для сглаживания данных и выявления трендов.
Пример:
void SmoothData(double& array[], int period) { int size = ArraySize(array); double smoothed[size]; double weight = 1.0 / period; for(int i = 0; i < size; i++) { double sum = 0.0; for(int j = i - period + 1; j <= i; j++) { if(j >= 0 && j < size) { sum += array[j]; } } smoothed[i] = sum * weight; } ArrayCopy(smoothed, array, 0, 0, size); }
Эта функция использует простое скользящее среднее для сглаживания данных в массиве array . Переменная period указывает количество элементов, используемых для расчета среднего значения в каждой точке.
Внутри функции создается новый массив smoothed , куда сохраняются сглаженные данные. Затем в цикле проходим по каждому элементу массива array и вычисляем среднее значение для периода, определенного переменной period .
Наконец, массив smoothed копируется обратно в массив array с помощью функции ArrayCopy() . Обратите внимание, что функция SmoothData() также принимает массив данных по ссылке (через & ), что означает, что изменения, внесенные в массив внутри функции, будут отражены в оригинальном массиве, переданном в качестве аргумента при вызове функции.
Пропущенные значения
Пропущенные значения - это значения, которые отсутствуют в временном ряду. Они могут быть вызваны ошибками ввода данных или проблемами в процессе сбора данных. Пропущенные значения могут оказать значительное влияние на анализ и прогнозирование временных рядов. При обработке пропущенных значений необходимо решить, как их заполнять. Язык MQL5 предоставляет несколько функций для обработки пропущенных значений.
Функция iBarShift() может использоваться для поиска индекса бара, соответствующего определенной дате. Если значение временного ряда отсутствует для определенной даты, можно использовать значение с предыдущего бара или заполнить его средним значением временного ряда за определенный период времени.
Пример:
void FillMissingValues(double& array[]) { int size = ArraySize(array); double last_valid = 0.0; for(int i = 0; i < size; i++) { if(IsNaN(array[i])) { array[i] = last_valid; } else { last_valid = array[i]; } } }
Эта функция использует метод "заполнения" - он заменяет все пропущенные значения предыдущим действительным значением в массиве array . Для этого мы создаем переменную last_valid , которая хранит последнее действительное значение в массиве, и проходим по каждому элементу массива. Если текущее значение является пропущенным ( NaN ), мы заменяем его на last_valid . Если значение не является пропущенным, мы сохраняем его в last_valid и продолжаем итерацию.
Обратите внимание, что функция FillMissingValues() также принимает массив данных по ссылке (через & ), что означает, что изменения, внесенные в массив внутри функции, будут отражены в оригинальном массиве, переданном в качестве аргумента при вызове функции.
Интерполяция
Интерполяция - это метод заполнения пропущенных значений, который предполагает, что пропущенные значения между двумя известными значениями можно вычислить с использованием некоторой функции. В MQL5 можно использовать функцию MathSpline() для интерполяции значений.
Конечно, есть и другие методы обработки данных, которые могут помочь улучшить анализ и прогнозирование временных рядов. Например, декомпозиция временных рядов может помочь выделить тренды, циклы и сезонные компоненты. Кластерный анализ и анализ факторов могут помочь идентифицировать факторы, которые влияют на временные ряды.
В заключение, использование дополнительных методов обработки данных может значительно улучшить анализ и прогнозирование временных рядов. Язык MQL5 предоставляет различные функции для обработки данных, которые могут быть использованы для удаления выбросов, сглаживания данных и обработки пропущенных значений. Кроме того, существуют и другие методы обработки данных, которые могут быть применены для улучшения анализа и прогнозирования временных рядов.
Пример:
double Interpolate(double& array[], double x) { int size = ArraySize(array); int i = 0; // Находим два ближайших элемента в массиве while(i < size && array[i] < x) { i++; } if(i == 0 || i == size) { // x находится за пределами диапазона массива return 0.0; } // Вычисляем веса для интерполяции double x0 = array[i-1]; double x1 = array[i]; double w1 = (x - x0) / (x1 - x0); double w0 = 1.0 - w1; // Интерполируем значение return w0 * array[i-1] + w1 * array[i]; }
Функция Interpolate принимает два аргумента: ссылку на массив с числами с плавающей запятой и значение x , которое нужно интерполировать. Алгоритм интерполяции заключается в нахождении двух ближайших элементов в массиве, вычислении весов для интерполяции и последующем вычислении интерполированного значения. Если значение x находится за пределами диапазона массива, функция вернет 0.
Обратите внимание, что функция Interpolate также принимает массив данных по ссылке (через & ), что означает, что изменения, внесенные в массив внутри функции, будут отражены в оригинальном массиве, переданном в качестве аргумента при вызове функции.
Виды сигналов наиболее предпочтительны для передачи в нейросеть
Сигналы являются ключевым элементом для работы нейронных сетей. Они представляют собой данные, которые передаются в нейросеть для обработки и анализа. Выбор подходящего типа сигнала для передачи в нейросеть может значительно повлиять на ее эффективность и точность. В этой статье мы рассмотрим наиболее предпочтительные виды сигналов для передачи в нейросеть.
Числовые сигналы
Числовые сигналы являются наиболее распространенным типом сигналов, используемых в нейросетях. Они представляют собой числовые значения, которые могут быть обработаны и анализированы нейросетью. Числовые сигналы могут быть как дискретными, так и непрерывными. Дискретные сигналы имеют конечное количество значений, в то время как непрерывные сигналы представляют собой бесконечное количество значений.
Изображения
Изображения также являются популярным типом сигналов, используемых в нейросетях. Они представляют собой графические изображения, которые могут быть обработаны нейросетью. Изображения могут быть как черно-белыми, так и цветными. Для передачи изображений в нейросеть они должны быть преобразованы в числовой формат.
Текстовые сигналы
Текстовые сигналы также могут быть использованы для передачи данных в нейросеть. Они представляют собой текстовые строки, которые могут быть обработаны и анализированы нейросетью. Текстовые сигналы могут быть как на естественных языках, так и на специальных языках программирования.
Аудиосигналы
Аудиосигналы также могут быть использованы для передачи данных в нейросеть. Они представляют собой звуковые сигналы, которые могут быть обработаны и анализированы нейросетью. Аудиосигналы могут быть как голосовыми, так и музыкальными.
Видеосигналы
Видеосигналы представляют собой последовательность изображений, которые могут быть обработаны и анализированы нейросетью
Сенсорные сигналы
Сенсорные сигналы являются важным типом сигналов для передачи в нейросеть в задачах машинного зрения и робототехники. Они могут включать в себя данные от датчиков, таких как гироскопы, акселерометры, датчики расстояния и другие. Эти данные могут быть использованы для обучения нейросети, чтобы она могла анализировать и реагировать на окружающую среду.
Графические сигналы
Графические сигналы представляют собой векторные или растровые изображения, которые могут быть обработаны и анализированы нейросетью. Они могут быть использованы для задач, связанных с графикой и дизайном, таких как распознавание символов и форм, создание автоматических рисунков и т.д.
Временные ряды
Временные ряды представляют собой последовательность чисел, которые измеряются во времени. Они могут быть использованы для задач, связанных с прогнозированием, предсказанием трендов и анализом временных данных. Нейросети могут использоваться для обработки временных рядов, чтобы выявить скрытые паттерны и предсказать будущие значения.
Как выбрать подходящий тип сигнала для передачи в нейросеть?
Выбор подходящего типа сигнала для передачи в нейросеть зависит от конкретной задачи и доступных данных. Некоторые задачи могут требовать использования нескольких типов сигналов одновременно. Например, задача распознавания речи может включать в себя использование аудиосигналов и текстовых сигналов одновременно.
При выборе типа сигнала для передачи в нейросеть, необходимо учитывать его характеристики, такие как размер, разрешение, формат и т.д. Кроме того, необходимо обеспечить соответствующую предобработку данных, такую как нормализация, фильтрация и т.д., чтобы обеспечить оптимальное качество и точность обработки данных нейросетью.
В заключение, выбор подходящего типа сигнала для передачи в нейросеть является важным шагом для достижения оптимальных результатов в задачах машинного обучения. Различные типы сигналов могут использоваться для обучения нейросетей в зависимости от конкретной задачи и доступных данных. Правильный выбор типа сигнала и соответствующей предобработки данных может помочь обеспечить оптимальную точность и качество работы нейросети.
Однако, необходимо также учитывать ограничения вычислительной мощности и доступности данных. Некоторые типы сигналов могут быть более сложными для обработки нейросетью, что может требовать большей вычислительной мощности и большего количества данных для обучения. Поэтому, необходимо балансировать между качеством и доступностью данных при выборе типа сигнала для обучения нейросети.
В целом, выбор подходящего типа сигнала для передачи в нейросеть является важным шагом для достижения оптимальных результатов в задачах машинного обучения. Нейросети могут обрабатывать различные типы сигналов, такие как аудио, видео, текст, сенсорные данные, графические данные и временные ряды. Правильный выбор типа сигнала и соответствующей предобработки данных может помочь обеспечить оптимальную точность и качество работы нейросети в конкретной задаче.
Практика
На практике сегодня рассмотрим несколько советников на базе нашего любимого перцептрона. Передавать будем значения индикатора Accelerator Oscillator. Передадим значение индикатора на 4 свечах и применим описанные выше методы нормализации. Для чистоты эксперимента сравним результаты советников с преобразованием и без них. В советнике без преобразования передадим значения индикатора напрямую.
Тут я предоставлю все параметры для оптимизации и форвард тестирования, чтобы дальше в тексте не повторяться:
- Рынок Forex;
- Валютная пара EURUSD;
- Период H1;
- СтопЛосс 300 и ТейкПрофит 600;
- Режим оптимизации и тестирования «Только цены открытия» и «Максимум комплексного критерия». Очень важно использовать режим «Максимум комплексного критерия» он показал более стабильные и прибыльные результаты по сравнению с «Максимальная прибыльность»;
- Диапазон оптимизации 3 года. С 2019.04.06 по 2022.04.06 . 3 года не является, каким-то критерием. Вы можете попробовать больше или меньше самостоятельно;
- Диапазон форвард тестирования 1 год. С 2022.04.06 по 2023.04.06 . Проверяем все на основе алгоритма изложенного в моей статье (Эксперименты с нейросетями (Часть 3): Практическое применение). То есть одновременная торговля несколькими лучшими результатами оптимизации;
- Проводить оптимизацию мы будем теперь 40 раз. Увеличим в 2 раза по сравнению с предыдущими тестами и посмотрим на результаты.
- Во всех форвард тестированиях использовалось 40 результатов оптимизации одновременно. Величина увеличена по сравнению с предыдущими тестами в моих статьях в 2 раза;
- Оптимизация советников с перцептроном «Быстрая (генетический алгоритм)»;
- Начальный депозит 10000 единиц;
- Плече 1:500.
Для оптимизации я использую небольшую программу автокликер, которую я написал на Delphi. Здесь я не могу ее выложить, но всем, кому понадобится, я отправлю в личных сообщениях, если Вы мне напишете. Работает это так:
- Вводим необходимое количество оптимизаций.
- Наводим курсор мышки на кнопку Старт в оптимизаторе стратегий.
- Идем заниматься своими делами.
Оптимизация закончится по истечению указанных циклов и программа закроется. Автокликер реагирует на изменение цвета кнопки Старт. Ниже на скриншоте как выглядит программа.
Советник perceptron AC 4 SL TP:
Данные индикатора передаем на прямую без использования нормализации.
Результаты оптимизации:

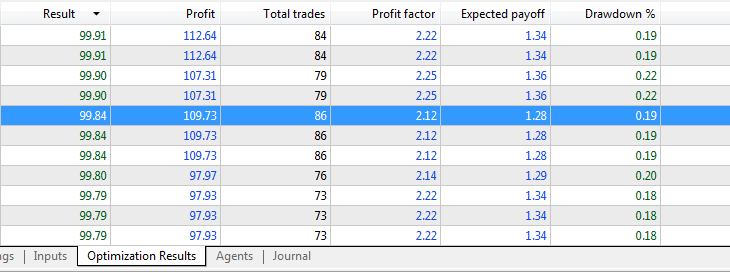
Результаты форвард тестирования:
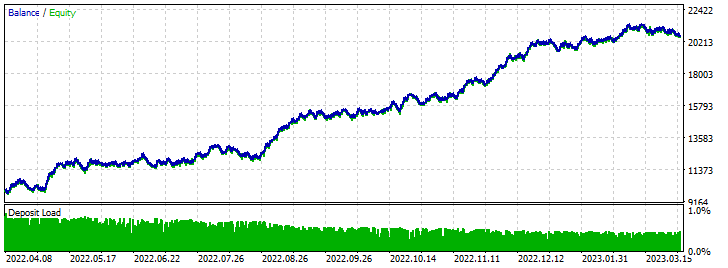
Советник perceptron AC 4 (Differentiation) SL TP:
Данные индикатора передаем с использованием Min-Max нормализации.
Результаты оптимизации:
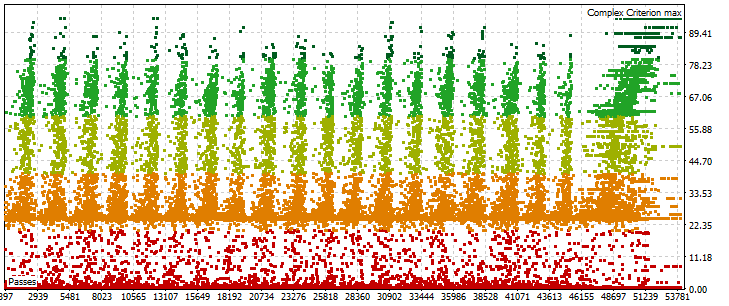
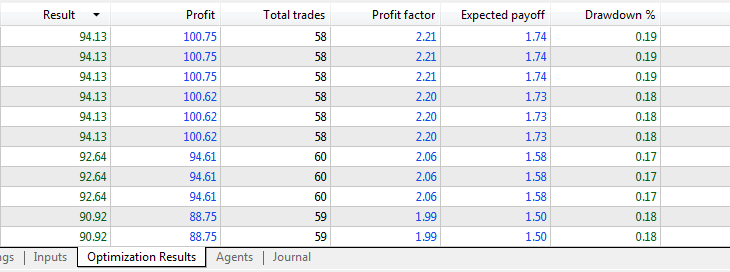
Результаты форвард тестирования:
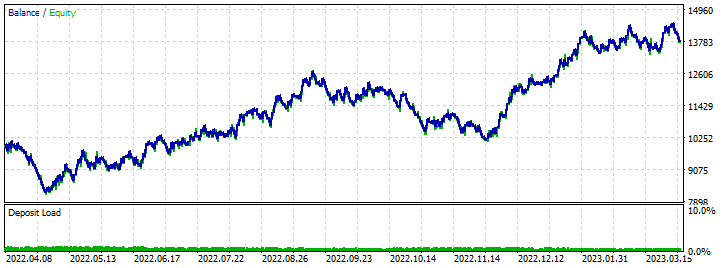
Заключение
Список файлов во вложении:
- perceptron AC 4 SL TP - opt - советник на перцептроне для оптимизации на индикаторе AC без использования нормализации;
- perceptron AC 4 SL TP - trade - оптимизированный советник на перцептроне на индикаторе AC без использования нормализации;
- perceptron AC 4 (Differentiation) SL TP - opt - советник на перцептроне для оптимизации на индикаторе AC c использованием дифференцирования для нормализации;
- perceptron AC 4 (Differentiation) SL TP - trade - оптимизированный советник на перцептроне на индикаторе AC c использованием дифференцирования для нормализации;
Нормализация позволяет уменьшить влияние выбросов в данных, что может помочь в предотвращении переобучения модели. Правильно нормализованные данные позволяют сети лучше "понимать" взаимосвязи между параметрами, что ведет к более точным предсказаниям и улучшению качества модели.
В статье мы рассмотрели несколько методов нормализации, но это не единственные способы обработки данных для улучшения обучения нейронных сетей. Каждый конкретный случай требует индивидуального подхода, и метод нормализации должен быть выбран в зависимости от характеристик данных и конкретной задачи.
В целом, нормализация входных параметров является важным шагом в процессе обучения нейронных сетей. Неправильно обработанные данные могут привести к плохим результатам и отрицательно повлиять на работу модели. Правильно нормализованные данные могут улучшить стабильность и скорость сходимости обучения, а также привести к более точным предсказаниям и улучшению качества модели.
Спасибо за внимание, друзья, и до встречи!
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Какой процент статьи сгенерирован НС?
По моим ощущениям - 80%.