MQL5 Wizard Techniques you should know (Part 54): Reinforcement Learning with hybrid SAC and Tensors
Introduction
Soft Actor Critic (SAC) is one of the algorithms used in Reinforcement Learning when training a neural network. To recap, reinforcement learning is a budding method of training in machine learning, alongside supervised learning and unsupervised learning.
Replay Buffer
The replay buffer is a very important component of SAC off-policy algorithm in Reinforcement Learning given that it keeps past-experiences of state, action, reward, next state, and the done-flag (for logging if an episode complete or ongoing) into sample mini batches for training. Its main purpose is to de-correlate various experiences, such that the agent is able to learn from a more diverse set of experiences, which tends to improve learning-stability and sample-efficiency.
In implementing SAC, we can use the MQL5 language, but the networks created would not be as efficient to train as those created in Python with open-source libraries like TensorFlow or PyTorch. And therefore, as we saw in the last reinforcement learning article where python was used to model a rudimentary SAC Network, we continue with Python but this time looking to explore and harness its Tensor graphs. There are, in principle, two ways of implementing a replay buffer in Python. The manual approach or the Tensor-based approach.
With the manual approach, basic python data structures like lists or NumPy arrays are engaged. However, with the Tensor-based method deep learning frameworks like TensorFlow or PyTorch are employed with this approach being more efficient for GPU acceleration due to the Seamless integration with neural network training pipelines. In the manual approach, the replay buffer is made with ‘NumPy’ arrays, which is simple and effective for small-scale problems. This could be handles as follows:
import numpy as np class ReplayBuffer: def __init__(self, max_size, state_dim, action_dim): self.max_size = max_size self.states = np.zeros((max_size, state_dim), dtype=np.float32) self.actions = np.zeros((max_size, action_dim), dtype=np.float32) self.rewards = np.zeros(max_size, dtype=np.float32) self.next_states = np.zeros((max_size, state_dim), dtype=np.float32) self.dones = np.zeros(max_size, dtype=np.float32) self.ptr = 0 self.size = 0 def add(self, state, action, reward, next_state, done): ... def sample(self, batch_size): idx = np.random.randint(0, self.size, size=batch_size) return ( self.states[idx], ... self.dones[idx], )
While this approach is relatively straightforward to implement, and is also very similar to what we did use in the prior SAC article, it may not scale well for larger problems or GPU acceleration.
With the Tensor-based method, the replay buffer is coded with either PyTorch or TensorFlow. The latter, in my experience (so far) seems a bit problematic. I was able to set up a GPU to run with TensorFlow, but the specific nature of the whole chain of drivers and versions of attendant software libraries that need to be present for a specific version of not just TensorFlow but also Python when using a particular GPU, is certainly overwhelming.
I tried PyTorch later, and maybe it was thanks to my earlier experience with TensorFlow, but the process was much smoother. The PyTorch integration of neural network training with GPU acceleration is so seamless, a dataset of almost a million rows when fed to a fairly complex 10-million parameter network, can have a single epoch run in about 4 minutes on a very basic NVIDIA T4. We can perform a rudimentary implementation in Python as follows:
import torch class ReplayBuffer: def __init__(self, max_size, state_dim, action_dim): self.max_size = max_size self.states = torch.zeros((max_size, state_dim), dtype=torch.float32) ... self.ptr = 0 self.size = 0 def add(self, state, action, reward, next_state, done): self.states[self.ptr] = torch.tensor(state, dtype=torch.float32) self.actions[self.ptr] = torch.tensor(action, dtype=torch.float32) self.rewards[self.ptr] = torch.tensor(reward, dtype=torch.float32) self.next_states[self.ptr] = torch.tensor(next_state, dtype=torch.float32) self.dones[self.ptr] = torch.tensor(done, dtype=torch.float32) self.ptr = (self.ptr + 1) % self.max_size self.size = min(self.size + 1, self.max_size) def sample(self, batch_size): idx = torch.randint(0, self.size, (batch_size,)) return ( self.states[idx], self.actions[idx], self.rewards[idx], self.next_states[idx], self.dones[idx], )
This method is very efficient since it integrates directly with PyTorch's autograd and optimization pipelines. So to sum up the comparison between manual and tensor, the manual approach Pros are simplicity in implementation, with no dependency on deep learning frameworks. The Cons, on the other hand, are limited scalability and no GPU acceleration. With the tensor-based approach the pros are seamless integration with neural networks, GPU acceleration and large-scale problems while Cons would be some decent familiarity/ knowledge of TensorFlow/PyTorch complex implementations.
As a rule, therefore, one should pick their approach while considering the scale of their problem and hardware availability; with tensor-based methods being favoured for large-scale problems or GPU training. Furthermore, if your environment has variable sized states like with images, then the tensor-based method would be suited. In addition, SAC can be enhanced with Prioritized Experience Replay (PER) where the replay buffer sampling is based on the relative importance of each state in the buffer by measuring the Temporal Difference Error or other key metrics. PER implementation is easier with tensor-based replay buffers, since it allows efficient priority updates and sampling.
As with any code listing, before deployment it is always a good idea to perform some testing and Debugging and with a replay buffer, this can be realised via the addition of dummy data and verifying that the sampling works correctly. In addition, one should ensure that the replay buffer handles edge cases like being empty or being full. Python-Assertions or unit tests can be used to validate the functionality. Once the replay buffer is ready, what follows next is integration to the SAC training loop by storing experiences after each training step and then sampling mini batches for updates.
Often one is looking for a balance when setting the replay buffer size because it should be large enough to store a diverse set of experiences but not too large that it slows down the sampling process. The replay buffer can be optimized for speed and memory by using efficient data structures like PyTorch tensors; avoiding unnecessary copying of data; and pre-allocating memory for the buffer. Profiling the replay buffer can help identify and address performance bottlenecks.
So to sum up, a well implemented SAC buffer is essential for the success of SAC and many off-policy algorithms. It ensures stable and efficient training via the provision of diverse, de-correlated experiences.
Critic Network
In SAC algorithms, the critic-network estimates the Q-value (or state action value, or the next action for the actor to take) when presented with the current environment state and the actor's choice of the next action. SAC engages 2 such critic-networks to reduce overestimation bias and also improve the learning stability. As a neural network that takes as input 2 clamped data sets of actor-network's probability distribution of actions and ‘coordinates’ of environment states therefore, the choice of using NumPy or Tensors will depend on the problem size (as defined by network size and volume of data to use in training) and also the hardware availability.
With a manual non tensor implementation of critic-networks, NumPy comes in handy for matrix operations and gradient updates. In cases where networks have less than 5 layers with sizes not over 15 each or for education & illustration purposes, this could be a workable solution. With this approach, forward and backward propagation passes are implemented manually, which could be error-prone and not as efficient when scaling up to large training data sets. This is what a manual python implementation could look like:
import numpy as np class CriticNetwork: def __init__(self, state_dim, action_dim, hidden_dim=256): self.state_dim = state_dim self.action_dim = action_dim self.hidden_dim = hidden_dim # Initialize weights and biases self.W1 = np.random.randn(state_dim + action_dim, hidden_dim) self.b1 = np.zeros(hidden_dim) self.W2 = np.random.randn(hidden_dim, hidden_dim) self.b2 = np.zeros(hidden_dim) self.W3 = np.random.randn(hidden_dim, 1) self.b3 = np.zeros(1) def forward(self, state, action): x = np.concatenate([state, action], axis=-1) x = np.maximum(0, x @ self.W1 + self.b1) # ReLU activation x = np.maximum(0, x @ self.W2 + self.b2) # ReLU activation q_value = x @ self.W3 + self.b3 return q_value def update(self, states, actions, targets, learning_rate=1e-3): # Manual gradient descent (simplified) q_values = self.forward(states, actions) error = q_values - targets # Backpropagation and weight updates (not shown for brevity)
As already noted, this approach is not scalable for large networks or datasets and lacks GPU acceleration. If, on the other hand, we elect to use Tensors, with PyTorch, we would be able to harness automatic differentiation and GPU acceleration. These properties do bode well for large scale problems and production level implementations. A very basic coding example of this could be as follows:
import torch import torch.nn as nn import torch.nn.functional as F class CriticNetwork(nn.Module): def __init__(self, state_dim, action_dim, hidden_dim=256): super(CriticNetwork, self).__init__() self.fc1 = nn.Linear(state_dim + action_dim, hidden_dim) self.fc2 = nn.Linear(hidden_dim, hidden_dim) self.fc3 = nn.Linear(hidden_dim, 1) def forward(self, state, action): x = torch.cat([state, action], dim=-1) x = F.relu(self.fc1(x)) x = F.relu(self.fc2(x)) q_value = self.fc3(x) return q_value
PyTorch in particular comes with a few crucial libraries, namely ‘torch.optim’ for handling network optimization and ‘torch.nn’ for setting the network architecture. This is all accomplished in a highly scalable and efficient approach.
So, while a manual approach is doable as shown in the sample listing above, and it offers the pros of simplicity and not having to rely on deep learning frameworks, its inability to scale or even properly harness GPUs, is a hindrance to adoption.
Using tensors in critic networks would also present similar pros and cons covered above with the replay buffer which broadly implies as already concluded that the manual approach is often suited in situations where the problems being solved are very small, and it is important to illustrate or ‘teach’ the intricacies of neural networks. In practice, though, Tensors are more practical for the reasons already shared.
SAC networks, if we recall, use two critic-networks (often referred to as Q1 and Q2) to mitigate overestimation bias. The target Q value is therefore determined as the minimum of the two Q-values produced by the networks. To illustrate, the critic networks, like part of the output of the actor-network, do produce a vector with estimated rewards for taking each of the available actions.
So, naturally within each such vector, the index/ action with the highest value would forecast the highest reward. The principal purpose of the critic networks is to conservatively determine the gradient for back propagating the actor network.
During the actor network update, the gradient of the objective function is computed and back propagated through the actor network from the minimum of the two Q-values. The minimum choice ensures the actor is optimized to choose actions that are robust to the over estimation errors in the critics.
These critic-networks that provide the gradient to the objective function that updates the actor network also need to be trained. But since they are estimating future rewards from actions, how is their training target established? The answer is for the critic updates, SAC does not directly use the minimum of the two Q-values. Instead, an update is performed for each critic (Q1 and Q2) using the soft Bellman-Equation derived target.
class DoubleCriticNetwork(nn.Module): def __init__(self, state_dim, action_dim, hidden_dim=256): super(DoubleCriticNetwork, self).__init__() self.Q1 = CriticNetwork(state_dim, action_dim, hidden_dim) self.Q2 = CriticNetwork(state_dim, action_dim, hidden_dim) def forward(self, state, action): q1 = self.Q1(state, action) q2 = self.Q2(state, action) return q1, q2
In addition, Target-networks in SAC, are another separate set of networks (one for each critic Q1 & Q2) that are used to compute the target Q-values that are key in back propagation of these critic-networks. They themselves get updated slowly via polyak averaging, so as to have stability during training. The use of target networks stems from the need to provide a stable target for the Bellman-Equation without which, it is argued, Q-value estimates of the critic-networks would diverge or oscillate due to the feedback loop between the Q-values and the targets.
for target_param, param in zip(target_critic.parameters(), critic.parameters()): target_param.data.copy_(tau * param.data + (1 - tau) * target_param.data) ``` where `tau` is the polyak averaging coefficient (e.g., 0.005).
The loss function for the critics would then be the mean-squared error (MSE) between the predicted Q-value and the target Q-value, as established by the Bellman-Equation with the help of the aforementioned target networks.
target_q_value = reward + (1 - done) * gamma * min(Q1_target(next_state, next_action), Q2_target(next_state, next_action)) ``` where `gamma` is the discount factor.
So to train the critics, a mini batch would be sampled from the replay buffer, and the target Q-value computed. With this, the critic networks would be updated by gradient descent. An optimizer such as Adam can be used to make the training more efficient.
optimizer = torch.optim.Adam(critic.parameters(), lr=learning_rate)
Debugging and testing can be performed by feeding dummy inputs and verifying output shape and values. One should ensure the network can overfit to a small data set. As already mentioned, python assertions can be used in validating input data. The critic networks are integrated in the SAC training loop by computing Q-values, updating the critic-loss, and synchronizing the target networks. It is important to ensure the critic network is updated in tandem with the actor and value networks, which is why Tensors and particularly the use of GPUs is a big deal here.
A few extra optimization tips could be adopted for the critic networks as well, and firstly these include batch normalization or layer normalization. Secondly, experimenting with different activation functions like ReLU or Leaky could yield different results depending on the tested data and nature of the network that is employed. Also, hyperparameters like learning rate and network depth can be fine-tuned. Monitoring of the critic loss during training is important to detect issues like overfitting and instability.
To conclude, the critic network is a crucial component of SAC, instrumental for estimating Q-values plus guiding actor's policy updates. A well implemented critic-network ensures stable and efficient learning.
Value Networks
This network that is also referred to as the state-value function is an optional part of SAC that we could elect to use. Its purpose is to estimate the expected cumulative reward of a state under the current policy by using the soft value function. While the use of a value network is ‘optional’ it carries quite a few advantages if implemented properly. Firstly because it explicitly incorporates entropy, the soft value function encourages the policy to explore more efficiently and effectively. The Soft value function action tends to provide a smoother target for training, which can help with stabilizing the learning process.
This stability is very beneficial when faced with high dimensioned input data (when input data vector is large in size >10) or the action spaces are continuous in nature (e.g. an action option of (0.14, 0.67, 1.51) as opposed to (buy, sell, hold)) or when data environments are faced with multiple local optima (scenario where many different network weight configurations appear to give decent results when each configuration is training on separate data sets or environments, but none of these weight configurations is able to generalise or maintain their performance on wider datasets).
To sum up value networks in SAC, they are used to estimate the expected return of a state independent of any action, which helps reduce variances in the Q-value estimates by providing a soft target. The arguments for using tensors vs manual are very similar to those given for the critic-network above. Most modern SAC networks do not implement the value network, but instead dwell on the extra 2 target networks to assist in setting the training targets for the 2 critic-networks.
Besides using a single value network above to moderate the critic network training targets, we could also use 2 value networks. In this scenario, a value network and a value target network are also both used to estimate the value function, which predicts the expected return (cumulative reward) from any given state. The target value network in particular is used to stabilize training, not just in this case but also with Deep-QN networks. Being a copy of the value network, it is updated less frequently, and provides a stable target for training.
Actor Network
This is the principle network, and it is also referred to as the policy network. It takes as input environment states and outputs two vectors, mean and standard deviation, that serve as parameters of a probability distribution over actions which can be used to sample stochastically. The 2 critic-networks, their attendant target networks, and the value-network if used all serve to aid the back propagation and training of this network.
Being a network, we should benefit from tensor use significantly, given the central role it plays in SAC. Also since all aforementioned networks are attendant to the training of this network, the actor network, then the use of GPUs to parallelize and allow concurrent training of these multiple networks is something that one should seek to explore since it brings a lot of efficiencies.
import torch import torch.nn as nn import torch.nn.functional as F import torch.distributions as dist class ActorNetwork(nn.Module): def __init__(self, state_dim, action_dim, hidden_dim=256): super(ActorNetwork, self).__init__() self.fc1 = nn.Linear(state_dim, hidden_dim) self.fc2 = nn.Linear(hidden_dim, hidden_dim) self.fc_mean = nn.Linear(hidden_dim, action_dim) self.fc_log_std = nn.Linear(hidden_dim, action_dim) def forward(self, state): x = F.relu(self.fc1(state)) x = F.relu(self.fc2(x)) mean = self.fc_mean(x) log_std = self.fc_log_std(x) return mean, log_std def sample_action(self, state): mean, log_std = self.forward(state) std = torch.exp(log_std) normal = dist.Normal(mean, std) action = normal.rsample() # Reparameterization trick return torch.tanh(action), normal.log_prob(action).sum(dim=-1, keepdim=True)
The actor network as we have already noted in the last SAC article outputs two key ‘vectors’ of data; the mean, and the standard deviation of a Gaussian distribution. These two are put together to determine the next action in a Stochastic manner, which is important for exploration and optimization in continuous action spaces. The mean stands for the centre of the action spread or distribution, while the standard deviation controls the spread or randomness of the distribution. These two define a Gaussian distribution from which actions can be selected. The Python code below helps accomplish this.
import torch def select_action(mean, log_std): """ Given the SAC actor's output (mean and log_std), this function selects an action index. Args: mean (torch.Tensor): Mean of the action distribution, shape (n_actions,) log_std (torch.Tensor): Log standard deviation, shape (n_actions,) Returns: int: The index of the selected action. """ std = log_std.exp() # Convert log standard deviation back to standard deviation .... return selected_index # Example inputs mean = torch.tensor([0.2, -0.5, 1.0, 0.3]) # Example mean values for 4 actions log_std = torch.tensor([-1.0, -0.7, -0.2, -0.5]) # Example log std values # Select action action_index = select_action(mean, log_std) print("Selected Action Index:", action_index)
In practice, though, we would have to run this function in MQL5 because after training the model in Python it would be exported as an ONNX file and as an ONNX it's outputs on any forward pass would be similar to what was used in Python when training. So since these two outputs would be received in MQL5, this action selection function therefore would also have to be in MQL5.
These two outputs define a Gaussian or Normal distribution from which actions are chosen. The choosing of the actions is done stochastically to encourage exploration so that the agent does not always choose the same action for a given state. When back propagating, for efficiency, reparameterization is used so that gradients are able to flow through the sampling process.
Also, from our Python function above since most action in real-world applications have a scope or are bounded, SAC applies the Tanh function to squash sampled actions to be in the -1 to +1 range. This ensures the action stays within a manageable range while preserving the stochastic nature of the process.
Agent
The agent in SAC, which we represent as the agent class in Python here, combines policy optimization (actor network) with the value function approximation (the pairing of the 2 critic networks the value network and the target value network). The agent should be highly sample efficient and be able to handle continuous action spaces. This is since it brings together not just these networks but also the replay buffer with the goal of learning an ‘optimal policy’ or suitable weights and biases for the actor network.
Given the high-level overview nature of the agent, it perhaps goes without saying that tensors would be essential if the network training is to be performed with some efficiency. Below is a python run down of how this could be done:
import torch import torch.nn.functional as F import torch.optim as optim class SACAgent: def __init__(self, state_dim, action_dim, hidden_dim=256, replay_buffer_size=1e6, batch_size=256, gamma=0.99, tau=0.005, alpha=0.2): self.state_dim = state_dim ... self.alpha = alpha # Initialize networks and replay buffer self.actor = ActorNetwork(state_dim, action_dim, hidden_dim) .... self.value_optimizer = optim.Adam(self.value_network.parameters(), lr=3e-4) def select_action(self, state): state = torch.FloatTensor(state).unsqueeze(0) action, _ = self.actor.sample_action(state) return action.detach().numpy()[0] def update(self): # Sample a batch from the replay buffer states, actions, rewards, next_states, dones = self.replay_buffer.sample(self.batch_size) # Convert to tensors states = torch.FloatTensor(states) ... dones = torch.FloatTensor(dones).unsqueeze(1) # Update value network target_value = self.target_value_network(next_states) ... # Update critic networks q1_value = self.critic1(states, actions) ... self.critic2_optimizer.step() # Update actor network new_actions, log_probs = self.actor.sample_action(states) ... self.actor_optimizer.step() # Update target networks for target_param, param in zip(self.target_value_network.parameters(), self.value_network.parameters()): target_param.data.copy_(self.tau * param.data + (1 - self.tau) * target_param.data)
Since we are using tensors, with PyTorch, it is important to emphasize that the manual assignment of a GPU device, if it is available, goes a long way in ensuring that the tensors are running/ executing as efficiently as possible.
Environment
The environment is where the training and target/action data-sets get defined. It essentially defines the problem the agent is trying to solve by providing state, reward and termination signal to the agent, based on its actions. The environment can be implemented manually (i.e. from 1st principles) or by inheritance by using libraries like OpenAI's Gym for standardized environments. A tensor-based environment could be implemented as follows:
import torch class TensorEnvironment: def __init__(self): self.state_space = 4 # Example: state dimension self.action_space = 2 # Example: action dimension self.state = torch.zeros(self.state_space) # Initial state def reset(self): self.state = torch.randn(self.state_space) # Reset to a random state return self.state def step(self, action): # Define transition dynamics and reward function next_state = self.state + action # Simple transition ... self.state = next_state return next_state, reward, done, {} def render(self): print(f"State: {self.state}")
One would then use a loop to collect experiences and update the agent periodically:
for episode in range(num_episodes): state = env.reset() episode_reward = 0 for step in range(max_steps): action = agent.select_action(state) next_state, reward, done, _ = env.step(action) agent.replay_buffer.add(state, action, reward, next_state, done) state = next_state episode_reward += reward if len(agent.replay_buffer) > batch_size: agent.update() if done: break print(f"Episode {episode}, Reward: {episode_reward}")
Wizard assembly and testing
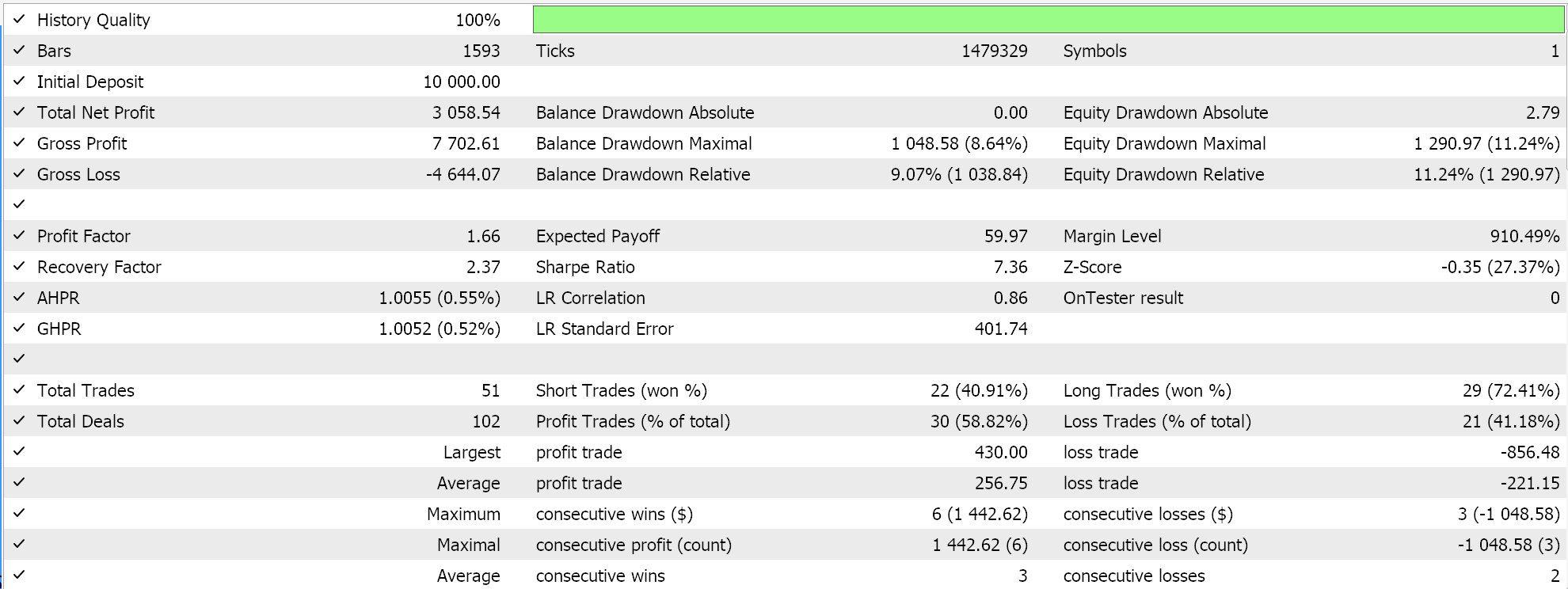
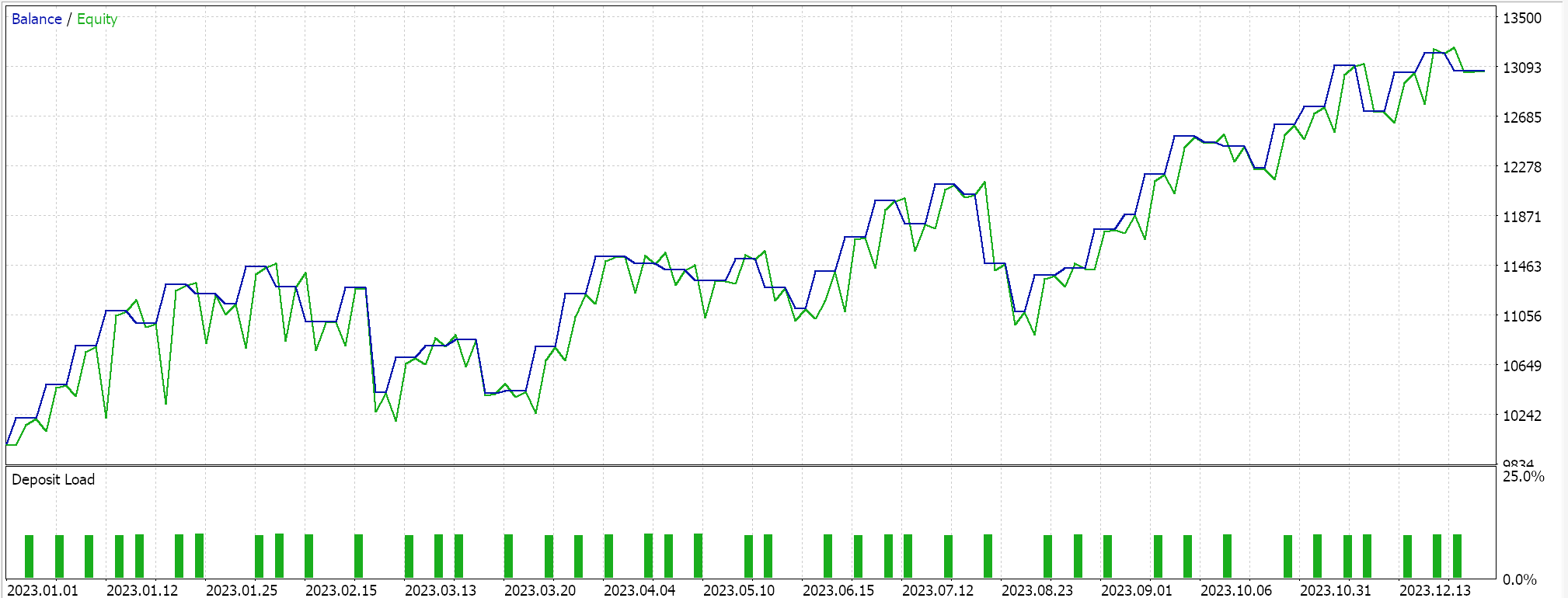
We test out our tensor-based hybrid SAC that besides having an actor network and 2 critic networks uses a value network and a target value network in the place of the 2 target networks (that train the critics). We use EUR USD pair on the 4-hour time frame for the year 2023.
Both TensorFlow and PyTorch allow not just training of models, but also their cross validation. TensorFlow allows passing validation x and y data values to its fit function, while PyTorch essentially allows the same in passing this data to a data_loader. A test run in MQL5 compiled Expert Advisor that does not perform a cross validation (or inference) gives us the following results for EUR USD over 2023:
We use, as in the last SAC article, ONNX to export the model from python and import it into MQL5. We have been dealing with 5 neural networks and yet only one is making the forecasts we need as the other 4 help in just back propagating. The network we need and export is the actor network. This network, though, outputs not one but 2 vectors, as already mentioned. The mean and the standard deviation. Therefore, before we can use the ONNX model in MQL5, we need to accurately define the output shapes of this model. The input shape is straight forward. We set the shapes in MQL5 as follows:
//+------------------------------------------------------------------+ //| Validation arch protected data. | //+------------------------------------------------------------------+ bool CSignalSAC::ValidationSettings(void) { if(!CExpertSignal::ValidationSettings()) return(false); //--- initial data checks if(m_period != PERIOD_H4) { Print(" time frame should be H4 "); return(false); } if(m_actor_handle == INVALID_HANDLE) { Print("Actor OnnxCreateFromBuffer error ", GetLastError()); return(false); } // Set input shapes const long _actor_in_shape[] = {1, __STATES}; // Set output shapes const long _actor_out_shape[] = {1, __ACTIONS}; if(!OnnxSetInputShape(m_actor_handle, ONNX_DEFAULT, _actor_in_shape)) { Print("Actor OnnxSetInputShape error ", GetLastError()); return(false); } if(!OnnxSetOutputShape(m_actor_handle, 0, _actor_out_shape)) { Print("Actor OnnxSetOutputShape error ", GetLastError()); return(false); } if(!OnnxSetOutputShape(m_actor_handle, 1, _actor_out_shape)) { Print("Actor OnnxSetOutputShape error ", GetLastError()); return(false); } //read best weights //--- ok return(true); }This is handled in the validation function of our custom signal class, since the ONNX model will not run unless these shapes are accurately defined. New readers can find guides on how to assemble an Expert Advisor from a custom signal *.*mqh file here and here.
Conclusion
We have implemented a Soft Actor Critic reinforcement learning algorithm in Python with the aid of tensors. Tensors are crucial in machine learning because they deliver huge efficiency gains when training models, an aspect that is very important especially for traders. The size of training datasets and the need for more intricately designed networks tends to lead to slower training processes. This set back is therefore addressed not just by using tensors, but also by harnessing the power of GPUs.
| Name | Description |
|---|---|
| hybrid_sac.mq5 | Wizard assembled Expert Advisor with Header showing used files |
| SignlWZ_54.mqh | Custom Signal Class File |
| model.onnx | ONNX Network File |
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
 Deconstructing examples of trading strategies in the client terminal
Deconstructing examples of trading strategies in the client terminal
 Building a Keltner Channel Indicator with Custom Canvas Graphics in MQL5
Building a Keltner Channel Indicator with Custom Canvas Graphics in MQL5
 From Basic to Intermediate: Variables (III)
From Basic to Intermediate: Variables (III)
 Mastering JSON: Create Your Own JSON Reader from Scratch in MQL5
Mastering JSON: Create Your Own JSON Reader from Scratch in MQL5
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use