ニューラルネットワークの実践：擬似逆行列(II)

はじめに

ニューラルネットワークに関する新しい記事へようこそ。 

前回の記事「ニューラルネットワークの実践：擬似逆行列(I)」では、MQL5ライブラリに用意されている関数を使用して疑似逆行列を求める方法を紹介しました。しかし、多くのプログラミング言語と同様に、MQL5ライブラリの関数も行列やそれに類する構造を前提とした計算をおこないます。

本記事では、行列の積や、行列の可逆性を判断するために重要な行列式を求めるための因数分解について扱います。しかし、疑似逆行列の値を導き出すためには、もう1つの因数分解を実装する必要があります。それが「行列の逆行列を求める」ための因数分解です。この因数分解は逆行列を生成することから成ります。

では、転置行列はどうでしょうか。前回の記事では、転置行列を用いた行列の積をシミュレートするための因数分解について説明しました。そのため、この操作自体は問題なく実行できます。

ただし、本記事では逆行列の計算方法について詳しく説明することはしません。これは、その計算が特に難解であるからではなく、本連載の目的が、特定の機能の実装方法を詳述するのではなく、教育的な内容を提供することにあるためです。そのため、本記事では異なるアプローチを取ります。行列の逆行列を計算するために必要な一般的な因数分解に焦点を当てる代わりに、最初から使用してきたデータを使用して擬似逆行列の因数分解について詳しく説明します。つまり、一般的な方法を提示するのではなく、専門的なアプローチを採用します。このようにすることで、単なる一般的な因数分解を学ぶよりも、なぜこの計算が必要なのかをより深く理解できるようになります。そして何よりも、特定の目的に特化した手法を用いることで、計算をより効率的に実行できることが分かるでしょう。では、この概念をさらに掘り下げるために、新たなテーマへ進みましょう。

特化できるのに一般化する理由

このセクションのタイトルは、一見すると議論を呼ぶ表現かもしれません。または、一部の読者にとってはすぐには理解しがたいものかもしれません。多くのプログラマーは、できるだけ汎用的なソリューションを開発しようとします。汎用性が高いほど、より幅広い用途に適用できるため、効率的なツールが作れると考えるからです。そのため、あらゆる場面で使えるようにと、一般化を追求します。しかし、こうした一般化が、不要なオーバーヘッド（計算負荷）を生む場合があります。もし特化した方法で同じ目的をより効率的に達成できるなら、わざわざ一般化する必要があるでしょうか。その場合、一般化は何のメリットももたらしません。

もしこの考え方が腑に落ちない場合は、次の問いについて考えてみてください。この点を説明するために、例を挙げて説明しましょう。次の質問について考えてみましょう。

コンピューターとは何でしょうか。また、コンピューターにはなぜこれほど多くのコンポーネントが含まれているのでしょうか。新しいハードウェアのイノベーションがソフトウェア ソリューションに取って代わることが多いのはなぜでしょうか。

1990年以降に生まれた方や過去の技術に触れたことがない方は、これからお話しすることは少し驚かれるかもしれません。1970年代から1980年代初頭にかけて、コンピュータは現在とは大きく異なるものでした。例えば、当時のビデオゲームはすべてハードウェアのみで実装されていました。それらは、トランジスタ、抵抗、コンデンサなどの電子部品を組み合わせて作られていました。ソフトウェアベースのゲームは存在しませんでした。すべてがハードウェアで実装されました。ここで、少し想像してみてください。電子部品だけを使って、「PONG」のような単純なゲームを作ることを。当時のエンジニアたちは信じられないほど優秀でした。

しかし、トランジスタ、抵抗、コンデンサといった個別の部品を使用することで、システムは動作が遅くなり、シンプルな設計に留めざるを得ませんでした。ところが、Z80や6502プロセッサのような最初の組み立てキットが登場すると、状況は一変しました。これらのプロセッサ（現在でも入手可能）により、計算をハードウェアで実装するよりも、ソフトウェアとしてプログラムする方がはるかに簡単で高速になったのです。こうしてソフトウェア時代の幕が開かれました。では、これがニューラルネットワークや現在の実装とどう関係しているのでしょうか。焦らずに、親愛なる読者の皆さん。これから説明していきます。

比較的複雑なタスクであっても、単純な命令を組み合わせることでプログラムできるようになったため、コンピューターは非常に汎用性の高いものとなりました。多くのイノベーションはまずソフトウェアとして誕生します。というのも、ソフトウェアは開発や改良のスピードが速いからです。そして、ある機能が十分に洗練されると、さらなる効率向上のためにハードウェアとして実装されることがあります。この進化の過程は、特にGPUに顕著に見られます。GPUの多くの機能は、最初はソフトウェア上で開発され、その後、時間をかけて最適化されたのちにハードウェアとして組み込まれるのです。ここで、議論の本題に戻りましょう。一般化は可能ですが、それによって生じる非効率性は開発段階ではなく、主に実行時に現れます。汎用的な実装は、実行時に予期せぬエラーが発生しないよう、追加のテストが必要になることが多いのです。一方で、特化したアプローチはエラーが発生しにくく、より高速な実行のために最適化することができます。

データベース内のたった4つの値を扱うだけなのに、なぜこれが重要なのかと思うかもしれません。ですが、読者の皆さん、その理由はここにあります。多くの場合、私たちはまず小さなデータセットで動作するシステムを作り、そこから徐々に拡張しながら、より大量のデータを扱えるようにしていきます。しかし、やがて実行時間が非効率になってしまいます。すると、以前はソフトウェアでおこなっていた同じ計算を、より効率的に実行するために、ハードウェアの特化が必要になってくるのです。こうして、新しいハードウェア技術が誕生していくのです。

ハードウェア開発の動向を追っている方なら、専門技術へのシフトが進んでいることに気づいているかもしれません。しかし、なぜそうなるのでしょうか。それは、ソフトウェアベースのソリューションが、最終的にはハードウェアベースのソリューションに比べてコスト効率が悪くなるためです。ニューラルネットワークの計算を高速化すると宣伝されている新しいGPUを急いで購入する前に、まずは既存のハードウェアをどのように最適化できるかを理解することが重要です。そのためには、汎用的な計算ではなく、特化した計算が求められます。そこで本記事では、擬似逆行列の計算最適化に焦点を当てることにしました。一般的な計算を用いて擬似逆行列の因数分解を説明するのではなく、より専門的な計算の実装に取り組みます。ただし、ここでの目的は学習であり、計算性能の最適化を目指すわけではない点に注意してください。ここで言う「最適化」とは、計算手法の実装に関するものであり、計算能力を最大限に引き出し、専用ハードウェアで因数分解をおこなうようなレベルには達しません。しかし、まさにこうした過程を経て、新しいハードウェア技術が誕生していくのです。

ニューラルネットワークの計算機能を備えたGPUやCPUについては、これまで多くの議論が交わされてきました。しかし、本当にそのアプローチが必要なのでしょうか。この問いに答えるには、まずソフトウェアの観点から何が起こっているのかを理解することが重要です。では次のトピックへ進み、ソフトウェア面でどのような実装が行われるのかを見ていきましょう。

擬似逆行列：提案されたアプローチ

ここまでで、重要なポイントはご理解いただけたかと思います。では、次のことを考えてみましょう。私たちのデータベースでは、それぞれの情報をX座標とY座標を持つ2次元プロットとして視覚化できます。この視覚化により、データポイント間の数学的な関係を明確にすることが可能になります。本連載の初めから、私たちはこの関係を明らかにする手段として線形回帰を取り上げてきました。前回の記事では、スカラー計算を用いて傾きと切片を求める方法を解説し、それによって以下の式を導き出しました。

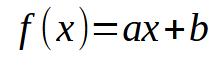
この場合、求めるべき値はaとbです。しかし、もう1つの方法として行列分解を利用するアプローチもあります。具体的には、疑似逆行列を実装する必要があります。その計算方法を以下に示します。

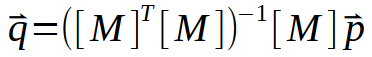
ここで、定数aとbの値はベクトルqに含まれています。qを求めるには、行列Mを一連の因数分解をおこなう必要があります。しかし、最も興味深いのは、その過程が次の図に示されている点です。

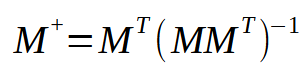
この図はまさに私たちが実装すべき内容を表しています。これは擬似逆行列で何が起こるかを示しています。結果として得られる行列には「擬似逆行列」という特別な名前が付けられていることに注意してください。上の図から分かるように、この行列はベクトルpと掛け合わされ、ベクトルqを生成します。このベクトルqが、私たちが得たい結果です。

前回の記事やこの記事の冒頭で触れたように、擬似逆関数はライブラリに実装されており、そのために行列が使用されます。しかし、ここでは行列を使う代わりに、それに似たものである「配列」を使用します。したがって、この時点で直面する問題は、配列を行列に変換するか、配列に対して擬似逆を実装するかという選択肢になります。計算がどのように実装されているのかを示したいので、今回は2番目のアプローチ、すなわち擬似逆行列の実装を選びます。関連する計算は以下の通りです。

01. //+------------------------------------------------------------------+
02. matrix __PInv(const double &A[])
03. {
04.     double M[], T[4], Det;
05. 
06.     ArrayResize(M, A.Size() * 2);
07.     M[0] = M[1] = 0;
08.     M[3] = (double)A.Size();
09.     for (uint c = 0; c < M[3]; c++)
10.     {
11.         M[0] += (A[c] * A[c]);
12.         M[2] = (M[1] += A[c]);
13.     }
14.     Det = (M[0] * M[3]) - (M[1] * M[2]);
15.     T[0] = M[3] / Det;
16.     T[1] = T[2] = -(M[1] / Det);
17.     T[3] = M[0] / Det;
18.     ZeroMemory(M);
19.     for (uint c = 0; c < A.Size(); c++)
20.     {
21.         M[(c * 2) + 0] = (A[c] * T[0]) + T[1];
22.         M[(c * 2) + 1] = (A[c] * T[2]) + T[3];
23.     }
24. 
25.     matrix Ret;
26.     Ret.Init(A.Size(), 2);
27.     for (uint c = 0; c < A.Size(); c++)
28.     {
29.         Ret[c][0] = M[(c * 2) + 0];
30.         Ret[c][1] = M[(c * 2) + 1];
31.     }
32. 
33.     return Ret;
34. }
35. //+------------------------------------------------------------------+

上記のコードフラグメントは、私たちがおこなうべき作業をすべて実行します。一見すると少し複雑に見えるかもしれませんが、実際には非常にシンプルで効率的です。本質的には、さまざまなdouble型の値を保持する配列を扱っています。他の型を使用することもできますが、読者の皆さんは、この時点からdouble型の使用に慣れ始めることが重要です。その理由はすぐに明らかになるでしょう。すべての因数分解手順が完了すると、最終的にはdouble型の値を含む行列が得られます。

さて、注意深く見てください。私たちが扱っている配列は単純なものですが、これを2列の行列として扱います。では、なぜこれが可能なのでしょうか。このコードをどのように使用するのかを説明する前に、この点を理解しましょう。

6行目では、配列内の要素数と同じ数の行を持つ行列を作成しますが、列数は2に設定されます。これは、内部に1列しか持たない配列とは異なります。7行目と8行目では、行列Mを非常に特別な方法で初期化します。この点を理解するためには、以下の画像を見てください。

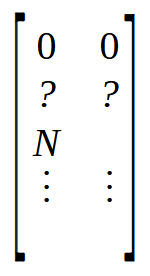
最初の2つの位置はゼロに設定され、その後に疑問符でマークされた他の2つの位置が続くことに注意してください。これは、それらの正確な値がまだわかっていないためです。すぐに、Nでマークされた位置があります。この値Nは配列のサイズを表します。しかし、なぜ配列のサイズを行列に配置するのでしょうか。理由は簡単です。関数を使用して同じ値を探すよりも、既知の位置にある値にアクセスする方が高速だからです。行列の先頭に4つの空き位置が必要なので、配列のサイズをNというラベルの付いた位置に配置します。これが7行目と8行目でおこなわれていることです。

さて、前の画像に示されているように、最初に実行する必要があるステップは、行列とその転置行列との乗算です。しかし、ここでは行列は存在しません。私たちが持っているのは配列、より正確にはベクトルです。では、どうやって掛け算をおこなうのでしょうか。実はとても簡単です。これを実現するには、9行目のループを使います。しかし、このループは一体何をしているのでしょうか。一見すると少し不思議に思えるかもしれませんが、次の画像を見て、何がおこなわれているのかを理解しましょう。

配列は基本的に値の集合であり、ここではa0からanまで表されます。よく考えてみると、配列として見るのではなく、データの構成に応じて、1列の行列または1行の行列として考えることができます。ここで、1列の行列と1行の別の行列の間で演算を実行すると、行列ではなくスカラー値が取得されます。擬似逆行列の公式では、まず行列とその転置行列を掛け合わせる必要があることに注意してください。ただし、上記の配列を暗黙的に行列として考えることができます。下の画像をご覧ください。

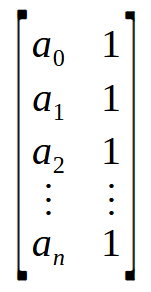
まったく、これで必要な行列ができました。n×2の行列にその転置行列を掛け合わせると、2×2の行列が得られます。つまり、配列、より正確にはベクトルを 2×2の行列に変換することに成功しました。これは、まさに 9 行目の for ループがおこなっていることです。行列にその転置行列を掛け、その結果を 6 行目で宣言された行列の先頭に配置します。

次に、先ほど作成した行列の逆行列を求める必要があります。2×2行列の場合、逆行列を計算する最も速く簡単な方法は行列式を使うことです。ここで重要な事実は、逆行列や行列式を見つける汎用的な方法が必要ないということです。また、行列に転置を掛ける汎用的な方法も必要ありません。すべてを単純な2×2の行列に縮小したことで、これらすべてを直接処理でき、タスクがはるかにシンプルかつ高速になります。したがって、行列式を計算するには14行目を使用します。これで逆行列を計算できます。この逆行列の計算は、汎用的に実装すると遅くなりますが、私たちが選んだ方法により非常に速く計算できます。15行目から17行目では、配列を介して得られた行列の逆行列を生成します。この時点で、ほぼすべてが準備完了です。次におこなうべきは、18行目で行列Mをクリアすることです。さて、ここで注意が必要です。行列Tには逆行列が含まれ、配列Aには擬似逆行列に因数分解するための値が含まれています。残るのは、一方の行列をもう一方で掛け、その結果を行列Mに配置することだけです。ここで重要なのは、行列Tが2×2であるのに対し、配列Aはn×2行列として扱えることです。この掛け算によって、擬似逆行列の値を含むn×2の行列が得られます。

この因数分解は19行目のループで実行されます。そして、21行目と22行目でその値を行列Mに配置します。これで、擬似逆行列の結果が得られます。ここで説明したプロセスは、GPU機能を活用して非常に大規模なデータベースの線形回帰を計算するためにOpenCLブロックに移植できます。場合によっては、CPUを使うと計算に数分かかることがありますが、タスクをGPUに送信することで計算速度が大幅に向上します。これは、この記事の最初に説明した最適化の一環です。

あとは、配列Mの結果を行列に配置するだけです。これは25行目から31行目でおこなわれます。M内に格納された内容が、すでに望ましい結果を表しています。添付ファイルにコードを掲載するので、すべてがどのように動作するかを確認し、前回の記事に記載された内容と比較することができます。しかし、すべてが完璧というわけではありません。関数内でテストをおこなっていないことに注意してください。これは、関数が教育的な目的のものである一方、目指しているのはそれをハードウェアに実装できるものに近づけることだからです。その場合、テストは別の方法で実行され、処理時間を節約できます。

さて、これでは重要な質問に答えていません。このPInv（擬似逆行列）関数は、どのようにして線形回帰の結果を非常に速く生成できるのでしょうか。この質問に答えるために、次のトピックに進みましょう。

最高速度

前のセクションでは、配列に基づいて擬似逆行列の計算をおこなう方法について説明しました。しかし、このプロセスをさらに加速することができます。擬似逆関数のみを返すのではなく、線形回帰の値を返すことが可能です。これを実現するためには、前のセクションのコードにいくつかの調整を加える必要があります。これらの変更により、線形方程式の因数を求めるために、GPUまたは専用CPUのフルスピードを活用できるようになります。求められる係数は傾きと切片です。更新されたコードの一部は以下の通りです。

01. //+------------------------------------------------------------------+
02. void Straight_Function(const double &Infos[], double &Ret[])
03. {
04.     double M[], T[4], Det;
05.     uint n = (uint)(Infos.Size() / 2);
06. 
07.     if (!ArrayIsDynamic(Ret))
08.     {
09.         Print("Response array must be of the dynamic type...");
10.         Det = (1 / MathAbs(0));
11.     }
12.     ArrayResize(M, Infos.Size());
13.     M[0] = M[1] = 0;
14.     M[3] = (double)(n);
15.     for (uint c = 0; c < n; c++)
16.     {
17.         M[0] += (Infos[c * 2] * Infos[c * 2]);
18.         M[2] = (M[1] += Infos[c * 2]);
19.     }
20.     Det = (M[0] * M[3]) - (M[1] * M[2]);
21.     T[0] = M[3] / Det;
22.     T[1] = T[2] = -(M[1] / Det);
23.     T[3] = M[0] / Det;
24.     ZeroMemory(M);
25.     for (uint c = 0; c < n; c++)
26.     {
27.         M[(c * 2) + 0] = (Infos[c * 2] * T[0]) + T[1];
28.         M[(c * 2) + 1] = (Infos[c * 2] * T[2]) + T[3];
29.     }
30.     ArrayResize(Ret, 2);
31.     ZeroMemory(Ret);
32.     for (uint c = 0; c < n; c++)
33.     {
34.         Ret[0] += (Infos[(c * 2) + 1] * M[(c * 2) + 0]);
35.         Ret[1] += (Infos[(c * 2) + 1] * M[(c * 2) + 1]);
36.     }
37. }
38. //+------------------------------------------------------------------+

上記のコードでは、すでにチェックが実行されていることに注意してください。このチェックは、返された配列が動的型であるかどうかを確認します。それ以外の場合、アプリケーションを終了する必要があります。終了処理は10行目でおこなわれます。前回の記事では、この行の意味について説明しました（必要に応じて、詳細については前回の記事を参照してください）。それ以外では、コードの大部分は30行目までは前のセクションで説明した内容とほぼ同じように機能し続けますが、30行目以降は異なる方向に進みます。しかし、少し立ち止まってみましょう。このコードを見ると、特に転置行列を行列、あるいは配列に掛け合わせる方法や、逆行列を元の行列に掛け合わせて擬似逆行列を計算する方法が不自然に思えるかもしれません。

このコードの断片に見られるものの意味は何でしょうか。非常に複雑に見えるものは、実は単なる「点の行列」に過ぎません。より理解を深めるために、下の画像を参照してください。

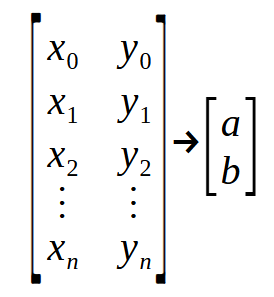
1つの「行列」が入力され、別の「行列」が出力されることに注意してください。2行目の宣言では、パラメータInfosは画像に表示される最初の行列を表し、Retは2番目の行列を表します。値aとbは、直線の方程式を構築するために決定しようとしている係数です。さて、よく注意してください。左側の行列の各行はグラフ上の点を表します。偶数インデックスの値は、前に説明した関数で使用される値に対応します。一方、奇数インデックスの値は、この記事の冒頭で述べた式のベクトル、つまりベクトルpを表します。

このトピックの冒頭で説明した関数は、グラフ上のすべてのポイントを取得し、線形回帰方程式を返します。これを実現するには、データを何らかの方法で分ける必要があります。これをおこなう方法は、偶数値と奇数値を整理することです。このため、このコードは前のセクションのコードとは大きく異なって見えるかもしれません。ただし、少なくとも30行目までは同じように機能します。その時点で、以前のコードには見られなかった操作がおこなわれます。ここでは、行列Mに格納されている擬似逆行列の結果を取得し、それをInfosパラメータの奇数インデックス位置にあるベクトルで乗算します。これにより、直線または線形回帰の方程式を定義するために必要な定数で構成されるRetベクトルが生成されます。

前の記事のPInv関数によって返された値を使用して同じ操作を実行すると、このフラグメントに示されているものと同じ結果が得られます。唯一の違いは、この特定の実装は、専用のニューラルネットワーク計算ユニットなどのハードウェアベースでの実行に適したように設計されている点です。これにより、プロセッサに新しいテクノロジが統合され、メーカーは特定のプロセッサや回路に人工知能やニューラルネットワーク機能が組み込まれていると主張できるようになります。しかし、これは革命的でも画期的でもありません。単に、以前はソフトウェアで実行されていたものをハードウェアで実装し、汎用システムを特殊なシステムに変換するだけです。

最終的な考察

親愛なる読者および愛好家の皆様。これまで説明してきた内容から、現段階でニューラルネットワークと人工知能について知るべきことはすべてカバーできたと思います。ただし、これまで私たちが扱ってきたのはニューラルネットワークそのものではなく、単一のニューロンの使い方と構築方法でした。というのも、私たちはまだ1つの計算しか実行していないからです。ニューラルネットワークでは、同じ計算を繰り返しおこないますが、そのスケールは大きくなります。すぐには実感しづらいかもしれませんが、ニューラルネットワークは単なるグラフ構造の実装に過ぎません。各ノードはニューロンや線形回帰関数を表し、計算結果に応じて特定の経路がたどられます。

おそらく、この視点はあまり刺激的に感じられないかもしれませんし、些細に思えるかもしれません。それでも、これが現実です。メディアや知識のない人々がどれだけ魔法のように描写しようとも、ニューラルネットワークには特別な魔力や幻想的な要素は何もありません。機械によるすべての作業は、単純な数学的計算に過ぎません。これらの計算を理解すれば、ニューラルネットワークの本質を理解できるようになります。さらに、これを通して生物の行動をシミュレートする方法についても洞察を得ることができます。生物が有機的な機械であるからではありませんが、ある意味ではそう言うこともできるかもしれません。しかし、それはまた別の話です。

私が尊敬する読者の皆様に望んでいるのは、これまでに探求してきた単一のニューロンの概念を理解することによって、ニューラルネットワークの本質を最も単純なレベルで把握していただくことです。

今後の記事では、単一のニューロンを小さなネットワークに組み込み、それが何かを学習できるようにする方法について説明します。なお、私は意図的にこれらの概念を金融市場に適用することを避けているので、将来的にもそのような内容を期待しないでください。私の目標は、皆さんがニューラルネットワークが何であり、どのように学習するのかを理解し、学び、そして自分の経験を通じて説明できるようにすることです。そのためには、理解しやすいシンプルなシステムで実験をおこなうことが必要です。

このトピックの続きを楽しみにしていてください。皆さんと共有できる興味深い内容、探求する価値のあるテーマを思いついておきます。それまでは、添付された資料を活用して、単一のニューロンがどのように機能するかを学んでみてください。