グラフ理論：ダイクストラ法を取引に適用する

はじめに

本記事では、最短経路問題を効率的に解くことで知られるグラフ理論の基本手法、ダイクストラ法の実装について解説します。もともとはルーティングやネットワーク最適化に応用される手法ですが、今回は価格変動を重み付きグラフとしてモデル化することで金融市場に応用します。ここで、ノードは価格水準や時間区間を表し、エッジはノード間の移動コスト（あるいは移動確率）を表します。

このアプローチの目的は、ダイクストラ法を利用して次の価格データの到来を予測し、現時点から将来の価格までの「最短経路」を特定することです。市場の動きをグラフとして捉えることで、価格が最も通りやすい経路を見つけ出し、取引判断を最小コスト・最小リスクに基づいて最適化することができます。

グラフ理論は複雑な市場構造を分析する強力な枠組みを提供し、ダイクストラ法はその中を体系的に探索する方法を与えます。価格変動をボラティリティや価格差などの重みを持つエッジとして解釈することで、リスクを最小化したり効率を最大化した最適経路を算出できます。

予測される価格配列は、現価格から将来の価格水準までの最短距離として機能し、トレーダーにトレンドを事前に見極めるためのデータ駆動型手法を提供します。この方法は、アルゴリズムトレーディングと計算数学を結びつけ、古典的なグラフアルゴリズムが金融時系列データに潜む機会をどのように発見できるかを示しています。

ダイクストラの基本概念

用語	本記事での解釈
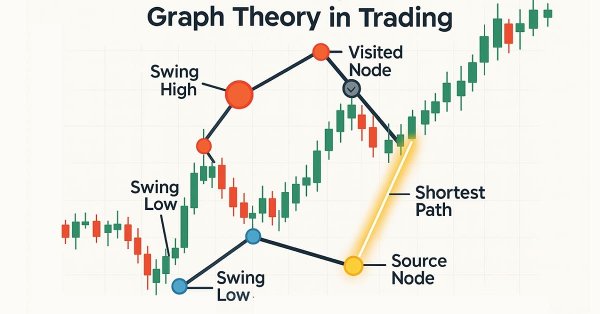
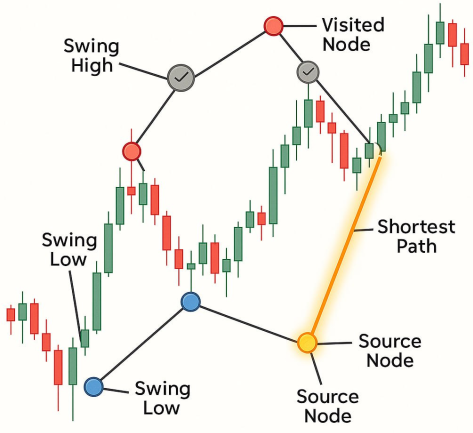
グラフ：ノードとエッジの集合。	グラフ： チャート上のスイングハイとスイングローで形成される構造。各スイングポイントがノードとなり、それらの間の価格の移動経路がエッジとして表される。
重さ：ノード間を移動するコスト	重さ：価格があるスイングポイントから別のスイングポイントに移動する際のコスト（または必要な労力）。価格差の絶対値などで表すことができる。
始点：アルゴリズムの出発点	始点：直近の有効なスイングポイント（価格がまだ反転していない最新の高値または安値）。ここを出発点として、最短経路の計算を開始する。
訪問済み集合：処理済みのノード集合	訪問済み集合：アルゴリズムがすでに評価を終え、再訪することのないすべてのスイングポイント。取引の観点では、価格によってすでに突破された、またはすでに到達したスイングポイントを指す。
距離表：各ノードまでの最短距離を記録する表	距離表：各ノードを、始点から到達するまでの最小「コスト（距離）」値に対応付けるマッピング。取引の観点では、現在の価格位置から他のスイングポイントまで、どれだけ低コスト（もしくは容易）に価格が移動できるかを示す。

ステップバイステップのプロセス

1. 初期化

• 始点の距離を0に設定する。
• 他のすべてのノードの距離を無限大に設定する。
• 常に「現在わかっている最小距離のノード」を選択できるよう、優先度付きキュー（または最小ヒープ）を作成する。

2. 最も近い未訪問ノードを訪問する

• 始点から処理を開始する。
• 各隣接ノードについて次を計算する。

  new_distance = distance_to_current + edge_weight

  このnew_distanceが既存の距離より小さい場合、その距離を更新する。

3. 現在のノードを訪問済みにする。

• 処理が完了したノードは再訪しない。

4. 繰り返し：

• 次に距離が最も短い未訪問ノードを選択して訪問を続ける。
• すべてのノードを訪問するか、最短経路が確定するまでこの手順を繰り返す。

while unvisited nodes remain:
    select node with the smallest tentative distance
    for each neighbor:
        if new path to neighbor is shorter:
            update the shortest distance
    mark current node as visited

導入手順

//+------------------------------------------------------------------+
//|                                               Dijkstars Algo.mq5 |
//|                                  Copyright 2025, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2025, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property strict
#include <Trade/Trade.mqh>
CTrade trade;

まず、trade.mqhファイルをインクルードします。これにより、MQL5に標準で用意されている取引機能にアクセスできるようになり、CTradeクラスを通じて取引操作をプログラムで実行できます。 CTradeクラスは、ポジションの発注、変更、決済といった一連の取引処理をおこなうためのメソッドを提供します。このファイルをインクルードした後、CTradeのインスタンスとしてtradeを作成します。このtradeオブジェクトを通じて、Buy()、Sell()、PositionOpen()などのメソッドを呼び出し、エキスパートアドバイザー(EA)内で自動的に注文を送信することが可能になります。この初期設定は、EAが自動的に売買注文を実行できるようにするための基礎となります。

// Input Parameters
input int    TakeProfit   = 1000;     
input int   StopLoss = 385;
input double  In_Lot = 0.01;
input int    LeftBars    = 3;
input int    RightBars   = 3;
input int    MaxSwings   = 50;
input double Lots        = 0.1;
input double PointBuffer = 10;
input int    Slippage    = 5;
ENUM_TIMEFRAMES TimeFrame;

このセクションでは、EAの入力パラメータを定義します。これにより、トレーダーはEAの設定画面から主要な取引条件を自由にカスタマイズすることができます。TakeProfitとStopLossは、それぞれテイクプロフィット(TP)とストップロス(SL)の目標値（ポイント単位）を設定します。In_LotおよびLotsは、取引数量（ロットサイズ）を指定するために使用されます。LeftBarsとRightBarsは、左右のバーと比較して高値または安値を特定することでスイングハイやスイングローを検出する際に用いられます。MaxSwingsはEAが追跡するスイングポイントの最大数を制限し、pointBufferはSLやTPに安全マージンを加えるためのバッファ距離を指定します。Slippageは注文実行時に許容される最大価格乖離を定義し、TimeFrameはEAが分析をおこなうチャートの時間足を指定します。

// Node Structure
struct SwingPoint {
   int index;
   datetime time;
   double price;
   bool isHigh;
   bool visited;
   double distance;
   bool   used;
   int previous;
};

この構造体は、ダイクストラ法を応用した取引システムにおけるSwingPointの設計図を定義しています。スイングポイントは、グラフ理論上の「ノード」に相当し、各スイングの主要情報を保持します。

• Index：スイングが検出されたバーのインデックス番号を示します。
• Time：そのバーの正確なタイムスタンプです。
• Price：スイング時点の高値または安値を保持します。
• IsHigh：スイングハイであればtrue、スイングローであればfalseを示します。
• Visited：アルゴリズムがすでに処理を完了したノードを追跡するためのフラグです。
• Distance ：ダイクストラの最短経路計算における、始点からこのノードまでの累積コストを格納します。
• Used：このスイングポイントがすでに取引判断に使用されたかどうかを示します。
• Previous：最短経路上でこのノードに到達する直前のノードを記録します。

SwingPoint swingPoints[];

//+------------------------------------------------------------------+
//| OnInit                                                           |
//+------------------------------------------------------------------+
int OnInit() {
   Print("Dijkstra Swing EA initialized");
   return INIT_SUCCEEDED;
}

ここでは、チャート上で検出されたすべてのスイングハイおよびスイングローを保持するために、動的配列swingPoints[]が宣言されています。各要素は先ほど定義したSwingPoint構造体であり、この配列は価格アクションをグラフ構造として表現するノード群としてEA全体で利用されます。OnInit()関数内では、EAの初期化処理がおこなわれます。ターミナルに「Dijkstra Swing EA initialized successfully」というメッセージを出力し、最後にINIT_SUCCEEDEDを返すことで、EAの起動が正常に完了したことをMetaTraderに通知します。

//+------------------------------------------------------------------+
//| Detect swing highs and lows                                      |
//+------------------------------------------------------------------+
void DetectSwings(int left, int right) {
   ArrayResize(swingPoints, 0);

   int totalBars = Bars(_Symbol, PERIOD_CURRENT) - right;
   for (int i = left; i < totalBars; i++) {
      bool isHigh = true, isLow = true;
      double high = High(i), low = Low(i);

      for (int j = 1; j <= left; j++) {
         if (High(i - j) >= high) isHigh = false;
         if (Low(i - j) <= low) isLow = false;
      }
      for (int j = 1; j <= right; j++) {
         if (High(i + j) >= high) isHigh = false;
         if (Low(i + j) <= low) isLow = false;
      }

      if (isHigh || isLow) {
         int idx = ArraySize(swingPoints);
         ArrayResize(swingPoints, idx + 1);
         swingPoints[idx].index = i;
         swingPoints[idx].time = Time(i);
         swingPoints[idx].price = isHigh ? high : low;
         swingPoints[idx].isHigh = isHigh;
         swingPoints[idx].visited = false;
         swingPoints[idx].distance = DBL_MAX;
         swingPoints[idx].previous = -1;

         if (idx >= MaxSwings) break;
      }
   }
}

この関数DetectSwings()は、チャート上のスイングハイおよびスイングローを検出する役割を持ちます。検出ロジックは、各ローソク足の高値・安値をその前後のバーと比較することで、局所的な頂点または谷を特定するというものです。処理の冒頭で、ArrayResizeを用いてswingPoints配列を初期化し、呼び出しごとにクリーンな検出をおこないます。その後、バーをleftから「totalBars - right」までループし、各バーがスイングハイまたはスイングローの条件を満たすかを確認します。

スイングハイの判定では、対象バーの高値が直前のleft本および直後のright本の高値よりすべて高いかを比較します。スイングローの場合は逆に、安値が前後のバーの安値よりすべて低いかを確認します。どちらかの条件を満たした場合、そのバーは有効なスイングポイントと見なされます。この局所比較により、価格の重要な転換点（山と谷）のみを抽出します。

スイングポイントが検出されると、その情報はSwingPoints[]配列に格納されます。各スイングポイントには、バーのインデックス、時刻、価格、そしてスイングハイかスイングローか(IsHigh)といったすべての関連情報が含まれます。また、経路探索の初期化として、visited（訪問済みフラグ）、distance（距離）、previous（前のノード）といった値がデフォルトで設定されます。この構造は、後にダイクストラ法を用いてスイング間の経路確率を評価するための基盤となります。ループ処理は、検出されたスイングの数がMaxSwingsに達した時点で早期に終了し、過剰なメモリ使用やパフォーマンス低下を防ぎます。

//+------------------------------------------------------------------+
//| Apply Dijkstra's algorithm                                       |
//+------------------------------------------------------------------+
void ApplyDijkstra() {
   if (ArraySize(swingPoints) == 0) return;

   swingPoints[0].distance = 0;

   for (int i = 0; i < ArraySize(swingPoints); i++) {
      int u = -1;
      double minDist = DBL_MAX;

      for (int j = 0; j < ArraySize(swingPoints); j++) {
         if (!swingPoints[j].visited && swingPoints[j].distance < minDist) {
            minDist = swingPoints[j].distance;
            u = j;
         }
      }

      if (u == -1) break;

      swingPoints[u].visited = true;

      for (int v = 0; v < ArraySize(swingPoints); v++) {
         if (!swingPoints[v].visited) {
            double cost = MathAbs(swingPoints[u].price - swingPoints[v].price);
            if (swingPoints[u].distance + cost < swingPoints[v].distance) {
               swingPoints[v].distance = swingPoints[u].distance + cost;
               swingPoints[v].previous = u;
            }
         }
      }
   }
}

この関数では、ダイクストラ法を実装し、最初のスイングポイントから他のすべてのスイングポイントへの最短経路を計算します。スイングハイやスイングロー間の価格変動を重み付きグラフとして扱います。まず、スイングポイントが存在するかを確認し、配列が空であれば関数は即座に終了します。その後、最初のノード（出発点）のdistanceを0に設定し、経路探索における始点であることを示します。

アルゴリズムはループに入り、各反復で、未訪問のスイングポイントのうち、既知のdistanceが最も小さいノード(u)を選択します。このノードは訪問済みとしてマークされ、アルゴリズムはその未訪問の隣接ノードをすべて評価します。それぞれの隣接ノード(v)に対して、uからvへの移動コスト（重み）を、両者の絶対価格差を基に計算します。もしuを経由してvに到達する累積コストが、現在記録されている距離よりも小さい場合、vのdistanceを更新し、uをpreviousノードとして記録します。

この処理は、到達可能なすべてのスイングポイントが訪問されるか、もはや未訪問のノードが残っていない場合まで続きます。関数終了時には、各スイングポイントはソースからの最短累積コストと、最適経路上の前のノードへのポインタを保持しています。この情報により、EAは最近の市場構造を通じて最も効率的な経路をたどり、価格が次に再訪する可能性の高いスイングポイントを特定できます。これがスマートな取引シグナル生成の基盤となります。

//+------------------------------------------------------------------+
//| Visualize Swing Points and Connections                           |
//+------------------------------------------------------------------+
void VisualizeSwings() {
   for (int i = 0; i < ArraySize(swingPoints); i++) {
      string objName = "Swing_" + IntegerToString(i);
      ObjectDelete(0, objName);

      ObjectCreate(0, objName, OBJ_ARROW, 0, swingPoints[i].time, swingPoints[i].price);
      ObjectSetInteger(0, objName, OBJPROP_ARROWCODE, swingPoints[i].isHigh ? 233 : 234);
      ObjectSetInteger(0, objName, OBJPROP_COLOR, swingPoints[i].isHigh ? clrRed : clrBlue);
   }

   for (int i = 1; i < ArraySize(swingPoints); i++) {
      int prev = swingPoints[i].previous;
      if (prev != -1) {
         string lineName = "Line_" + IntegerToString(i);
         ObjectDelete(0, lineName);

         ObjectCreate(0, lineName, OBJ_TREND, 0,
                      swingPoints[prev].time, swingPoints[prev].price,
                      swingPoints[i].time, swingPoints[i].price);
         ObjectSetInteger(0, lineName, OBJPROP_COLOR, clrGray);
         ObjectSetInteger(0, lineName, OBJPROP_WIDTH, 1);
      }
   }
}

VisualizeSwings()関数は、検出されたスイングポイントとそれらの間の接続をチャート上に描画する役割を持ち、トレーダーがEAの構造やロジックを視覚的に確認できるようにします。最初のforループでは、swingPoints[]配列を順に処理し、各スイングに対応する矢印オブジェクトを作成します。新しいオブジェクトを作成する前に、同名の既存オブジェクトは削除され、チャートの混雑を防ぎます。矢印には明確な色が割り当てられています。スイングハイは赤(arrow code 233)、スイングローは青(arrow code 234)で描かれ、視覚的に区別しやすくなっています。

次のforループでは、各スイングポイントとその対応するpreviousノード（ダイクストラ法で決定された）との間に線を引きます。これらの線は、潜在的な取引パスを評価するための最短経路接続を表しています。既存の同名線オブジェクトは描画前に削除されます。線はOBJ_TRENDを用いて描かれ、グレーで標準幅に設定され、視覚的に整った構造を維持します。

この可視化により、EAがどのスイングポイントを特定し、それらがどのように接続され、ダイクストラ法に基づいてどの経路が選ばれたかを確認でき、意思決定の検証に役立ちます。特にバックテストや実取引中に、EAが意図どおりに市場構造を分析しているかを確認する際に有用です。

double High(int index){return (iHigh(_Symbol, _Period, index));}
double Low(int index){return (iLow(_Symbol, _Period, index));}
datetime Time(int index){return (iTime(_Symbol, _Period, index));}

これらのヘルパー関数High()、Low()、Time()は、組み込みのMQL5関数iHigh()、iLow()、iTime()の簡易ラッパーです。指定したindexのバーに対して、現在の銘柄・時間足の高値、安値、バーの時間を簡単に取得できます。これらのショートハンドを使うことで、スイング検出や可視化時にバーのデータに繰り返しアクセスする際、コードがより簡潔で読みやすくなります。

//+------------------------------------------------------------------+
//|                          Filter and mark                         |
//+------------------------------------------------------------------+
void FilterAndMarkValidSwings(SwingPoint &points[]) {
   int count = ArraySize(points);
   if(count < 2) return;

   for(int i = 0; i < count; i++) {
      if(points[i].used) continue;

      bool isValid = true;
      double swingPrice = points[i].price;
      int swingIndex = points[i].index;

      // Scan forward in time from the swing point
      for(int j = swingIndex - 1; j >= 0; j--) {
         double high = iHigh(_Symbol, TimeFrame, j);
         double low  = iLow(_Symbol, TimeFrame, j);

         // Invalidate swing high if price went higher later
         if(points[i].isHigh && high > swingPrice) {
            isValid = false;
            break;
         }

         // Invalidate swing low if price went lower later
         if(!points[i].isHigh && low < swingPrice) {
            isValid = false;
            break;
         }
      }

      if(isValid) {
         points[i].used = true;

         // Draw object on chart
         string objName = points[i].isHigh ? 
            StringFormat("SwingHigh_%d", TimeToString(iTime(_Symbol, TimeFrame, swingIndex))) :
            StringFormat("SwingLow_%d", TimeToString(iTime(_Symbol, TimeFrame, swingIndex)));

         color swingColor = points[i].isHigh ? clrRed : clrBlue;

         ObjectCreate(0, objName, OBJ_HLINE, 0, 0, swingPrice);
         ObjectSetInteger(0, objName, OBJPROP_COLOR, swingColor);
         ObjectSetInteger(0, objName, OBJPROP_STYLE, STYLE_DASH);
         ObjectSetInteger(0, objName, OBJPROP_WIDTH, 1);
      }
   }
}

FilterAndMarkValidSwings()関数は、スイングポイントのリストを精査し、将来の価格変動によって無効化されていない有効なポイントを特定します。SwingPoints配列の参照を受け取り、配列内を順に処理し、すでにusedとしてマークされたポイントはスキップします。各候補スイングについては、まず有効と仮定し、その後、形成後に価格がそのスイングを超えたかどうかを過去の価格データに基づいて検証します。

有効性の判定では、スイングのインデックスから過去のバーを逆向きにスキャンします。スイングハイの場合は、後続のどのローソク足の高値もそれを上回ったかどうかを確認し、スイングローの場合は、後続のどのローソク足の安値もそれを下回ったかどうかを確認します。この条件に該当する場合、そのスイングポイントは価格に「突破」されたため無効と見なされ、以降の計算には使用されません。条件に該当しなければ、そのスイングポイントは有効であると判断され、usedとしてフラグが立てられます。

有効なスイングごとに、チャート上に水平線を描画して視覚的にマークします。線は破線で描かれ、スイングハイは赤、スイング安値は青に設定されます。オブジェクト名はスイングの種類と検出されたバーの時間を組み合わせて付けられます。この視覚的なフィードバックにより、トレーダーはEAがどのスイングポイントを強く有効と見なしているかを即座に確認でき、分析や取引中にロジックを信頼し、デバッグしやすくなります。

//+------------------------------------------------------------------+
//|                        Cleaning up old swings                    |
//+------------------------------------------------------------------+
void CleanOldSwingObjects(int keepBars = 100) {
   datetime oldestDate = iTime(_Symbol, TimeFrame, keepBars);
   int total = ObjectsTotal(0);

   for(int i = total - 1; i >= 0; i--) {
      string name = ObjectName(0, i);
      if(StringFind(name, "SwingHigh_") == 0 || StringFind(name, "SwingLow_") == 0) {
         datetime swingTime = (datetime)ObjectGetInteger(0, name, OBJPROP_TIME);
         if(swingTime < oldestDate) {
            ObjectDelete(0, name);
         }
      }
   }
}

この関数は、チャート上の古くなったスイング関連のビジュアル要素を削除して、表示の明瞭さとパフォーマンスを維持する役割を持っています。keepBarsパラメータを用いて「古い」オブジェクトの閾値を決定します。これは、keepBars本前のバーのタイムスタンプを取得し、それ以前に作成されたスイングオブジェクトを古いものとして扱います。関数はチャート上の全てのグラフィカルオブジェクトを逆順でループし、その名前が「SwingHigh_」または「SwingLow_」で始まるかを確認して、スイングマーカーであるかを判別します。

各スイングオブジェクトについて、作成時間を取得し、カットオフタイムスタンプ(oldestDate)と比較します。オブジェクトの時間が古ければ、ObjectDelete()を使ってチャートから削除されます。この処理により、チャートには最新かつ関連性のあるスイングポイントのみが表示され、不要な情報で煩雑にならないように保たれます。また、長期間のヒストリーデータやライブ市場で多数のスイングが蓄積される場合でも、パフォーマンス低下を防ぐ効果があります。

//+------------------------------------------------------------------+
//| Generate Signal & Trade                                          |
//+------------------------------------------------------------------+
void GenerateSignalAndTrade() {
   if (ArraySize(swingPoints) < 2) return;

   int last = ArraySize(swingPoints) - 1;
   int prev = swingPoints[last].previous;
   if (prev == -1) return;

   double entry = swingPoints[last].price;
   double reference = swingPoints[prev].price;
   double sl, tp;
   bool isBuy = entry > reference, isSell = entry < reference;

   SetSLTP(entry, reference, isBuy, sl, tp);

   if (PositionSelect(_Symbol)) return;

   if (isBuy)
      ExecuteTrade(ORDER_TYPE_BUY);
   else if(isSell)
      ExecuteTrade(ORDER_TYPE_SELL); 
}

GenerateSignalAndTrade()関数は、ダイクストラ法によってスイングポイント間で算出された直近のパスの方向に基づき、売買シグナルを生成する役割を持ちます。まず、比較対象となるスイングポイントが最低2つ存在すること、そして最新のスイングポイントに有効なpreviousノードがあることを確認します。次に、最新スイングとその直前に接続されたスイングの価格を取得し、両者の価格関係を基に取引方向を決定します。最新価格が直前の価格より高ければ買いシグナル、低ければ売りシグナルとなります。

方向が決まった後、関数はSetSLTP()を用いてストップロス(SL)およびテイクプロフィット(TP)のレベルを計算します。これらはスイングポイント間の距離に基づいて設定されます。取引を実行する前に、同じシンボルで既にポジションが開かれていないかを確認し、重複を避けます。最後にExecuteTrade()を使って適切な注文タイプで取引を発注します。このロジックにより、有効なスイングポイント間で構造的に裏付けされた明確な方向性が確認された場合のみ、取引が実行されるようになっています。

//+------------------------------------------------------------------+
//| Calculate SL and TP based on distance to previous node           |
//+------------------------------------------------------------------+
void SetSLTP(double entry, double ref, bool isBuy, double &sl, double &tp) {
   double distance = MathAbs(entry - ref) + PointBuffer * _Point;
   if (isBuy) {
      sl = entry - distance;
      tp = entry + distance;
   } else {
      sl = entry + distance;
      tp = entry - distance;
   }
}

SetSLTP()関数は、取引のストップロス(SL)およびテイクプロフィット(TP)レベルを、現在のエントリー価格と基準価格（通常は直前のスイングポイント）の距離に基づいて計算します。まず、両価格間の絶対差を求め、安全のために少量のバッファ（ポイント単位）を加えます。買いの場合は、ストップロスをエントリー価格の下に、テイクプロフィットを上に設定し、売りの場合は逆にストップロスを上に、テイクプロフィットを下に設定します。これにより、リスクとリワードがスイング構造を中心に対称的に配置され、EAが価格の動きに沿って構造に基づいた意味のあるSLとTPを設定できるようになります。

//+------------------------------------------------------------------+
//| Execute trade with risk parameters                               |
//+------------------------------------------------------------------+
void ExecuteTrade(ENUM_ORDER_TYPE tradeType){

   double point = SymbolInfoDouble(_Symbol, SYMBOL_POINT);
   double price = (tradeType == ORDER_TYPE_BUY) ? SymbolInfoDouble(_Symbol, SYMBOL_ASK) :
                                                  SymbolInfoDouble(_Symbol, SYMBOL_BID);

   // Convert StopLoss and TakeProfit from pips to actual price distances
   double sl_distance = StopLoss * point;
   double tp_distance = TakeProfit * point;
   
   double sl = (tradeType == ORDER_TYPE_BUY) ? price - sl_distance :
                                               price + sl_distance;
   
   double tp = (tradeType == ORDER_TYPE_BUY) ? price + tp_distance :
                                               price - tp_distance;

   trade.PositionOpen(_Symbol, tradeType, In_Lot, price, sl, tp, NULL);
}

ExecuteTrade()関数は、あらかじめ設定されたリスクパラメータに基づいて取引注文を実行する役割を持ちます。まず、現在の市場価格を取得します。買い注文の場合はAsk価格、売り注文の場合はBid価格を使用します。次に、入力値（stopLossとTakeProfit）をポイント単位から実際の価格差に換算してストップロスとテイクプロフィットのレベルを計算します。取引の種類に応じて、ストップロスとテイクプロフィットをエントリー価格の上または下に適切に配置します。

最後に、CTradeクラスのPositionOpen()メソッドを用いて、計算されたパラメータ（ロットサイズ、方向、エントリー価格、SL、TP、コメントなし）で取引を実行します。これにより、市場の方向にかかわらず、一貫したリスク管理フレームワークに従った取引が可能になります。

//+------------------------------------------------------------------+
//| OnTick                                                           |
//+------------------------------------------------------------------+
void OnTick() {
   static datetime lastBarTime = 0;
   datetime currentBarTime = iTime(_Symbol, _Period, 0);

   if (currentBarTime != lastBarTime) {
      lastBarTime = currentBarTime;

      DetectSwings(LeftBars, RightBars);
      ApplyDijkstra();
      VisualizeSwings();
      GenerateSignalAndTrade();
      FilterAndMarkValidSwings(swingPoints);
      CleanOldSwingObjects();

   }
}

OnTick()関数はEAのメイン実行ループであり、毎回のティック到来時に呼び出されます。重複処理を避けるため、lastBarTimeというstatic変数を用いて、新しいバーが形成されたかどうかを現在のバーの始値時刻と比較して検出します。新しいバーが形成された場合、lastBarTimeを更新し、以下の主要な処理を実行します。まず、DetectSwingsにより新しいスイングハイとスイングローを検出し、次にApplyDijkstraでスイング間の最適経路を算出します。VisualiseSwingsでチャート上にスイングとその接続線を描画し、GenerateSignalAndTradeにより経路の方向に基づいた取引シグナルを生成し、実行します。さらにFilterAndMarkValidSwingsで無効化されたスイングを除外し、CleanOldSwingObjectsで古いオブジェクトを削除してチャートを整理します。

この構造により、EAは市場構造を効率的かつ論理的に処理することが可能になります。

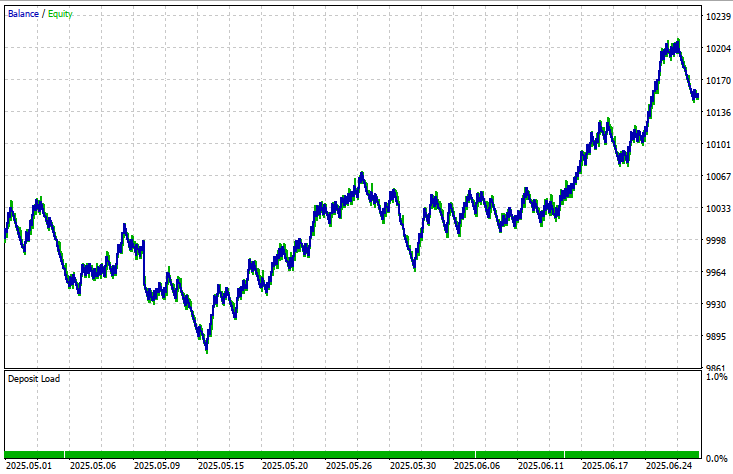
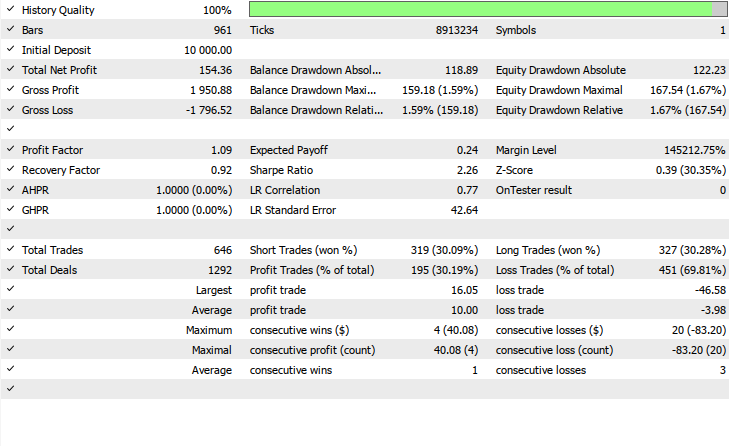
バックテスト結果

バックテストは1時間足(H1)で、2025年5月1日から2025年6月20日までの2か月間の期間で実施され、以下の入力設定が使用されました。

• テイクプロフィット(TP) = 1000ポイント
• ストップロス = 385
• 入力ロット = 0.01
• 左のバー = 3
• 右のバー = 3
• 最大スイング = 50
• ポイントバッファ = 10.0
• スリッページ = 5

結論

まとめると、本記事では、スイングハイとスイングローをグラフのノードとして扱い、ダイクストラ法を応用して金融市場の構造を解釈する完全なMQL5 EAを構築しました。システムは新しいバーごとに重要なスイングポイントを検出し、価格がすでに突破した無効なポイントを除外したうえで、有効なスイングを経路探索アルゴリズム上の頂点として扱います。次に、スイング間の価格差を辺の重みとして用い、市場構造上で最も効率的な経路を計算し、価格が進む最も可能性の高い方向を特定します。

この解析に基づき、EAは方向性のあるエントリーシグナルを生成し、スイングポイント間の距離に応じて適切に計算されたストップロスとテイクプロフィットを設定して取引を実行します。検出されたスイングポイントや計算された経路は矢印やトレンドラインでチャート上に可視化され、不要なオブジェクトはクリアされることでチャートは常に整理され更新された状態が保たれます。

結論として、このEAは従来のインジケーター中心の取引を超え、グラフベースのアルゴリズムをプライスアクション分析に統合することで、より構造的で論理的な取引判断を可能にしています。エントリーを市場スイングのジオメトリに沿わせ、各ノードは有効な場合にのみ一度使用される仕組みにより、価格が自然にサポートやレジスタンスを通過する動きを模倣しています。また、検出・検証・経路探索・実行・可視化の各機能がモジュール化されているため、戦略の改良、拡張、バックテストが容易におこなえます。本プロジェクトは、プライスアクションをナビゲート可能なネットワークとして扱い、データ構造理論と市場の振る舞いを組み合わせた、スマートで適応的な取引システムの基盤を提供します。