
重构经典策略(第五部分):基于USDZAR的多品种分析
引言
将人工智能整合到交易策略中的方法不胜枚举,但不幸的是,在决定将资金投入哪种策略之前,我们无法评估每一种方法。 今天,我们重新审视一种流行的多品种分析交易策略,以确定是否可以使用人工智能改进这一策略。我们将为您提供所需的信息,以便您能够做出明智的决策,判断这一策略是否适合您的投资者概况。
交易策略概览
采用多品种分析的交易策略主要基于一篮子交易品种之间的相关性。相关性是两个变量之间线性依赖程度的度量。然而,相关性常常被误认为是两个变量之间关系的标志,而事实并非总是如此。
全球交易者利用他们对相关资产的基本理解来指导投资决策、衡量风险水平,甚至将其作为退出信号。例如,我们以 USDZAR 货币对为例。美国政府是世界上主要的石油出口国之一,而南非政府则是世界上最大的黄金出口国。
由于这些商品对两国国内生产总值的贡献比例相当大,人们自然可以预期这些商品的价格水平可能会解释 USDZAR 货币对的部分变化。因此,如果石油在现货市场的表现优于黄金,我们可能会预期美元比兰特更强,反之亦然。
方法论概述
为了评估这种关系,我们使用在 MQL5 中编写的脚本从我们的 MetaTrader 5 终端导出了所有市场数据。我们使用两组可能的输入数据来训练各种模型:
- USDZAR 的 OHLC 常规报价。
- 石油和黄金价格的组合。
从收集到的数据来看,石油与 USDZAR 货币对的相关性似乎比黄金更强。
由于我们的数据处于不同的尺度,我们在训练之前对数据进行了标准化和归一化处理。我们进行了10折交叉验证,但未进行随机打乱,以比较不同输入集之间的准确度。
我们的研究结果表明,第一组可能产生的误差最低。表现最佳的模型是使用常规 OHLC 数据的线性回归模型。然而,在第二组中,表现最佳的模型是 KNeigborsRegressor 算法。
我们成功地进行了超参数调整,使用随机搜索对模型的 5 个参数进行了 500 次迭代。我们通过将定制模型的误差水平与默认模型在验证集上的误差水平进行比较来测试过拟合情况,该验证集在优化过程中被保留了下来。在对两个模型使用相同训练集进行训练后,我们的定制模型在验证集上的表现优于默认模型。
最后,我们将定制模型导出为 ONNX 格式,并将其集成到我们的EA中。
数据提取
我编写了一个方便的脚本,帮助从您的 MetaTrader 5 终端提取所需数据,只需将脚本拖放到您想要的品种上,它就会为您提取数据,并将其存放到路径:“\MetaTrader 5\MQL5\Files..”下。
//+------------------------------------------------------------------+ //| ProjectName | //| Copyright 2020, CompanyName | //| http://www.companyname.net | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com/en/users/gamuchiraindawa" #property version "1.00" #property script_show_inputs //---Amount of data requested input int size = 100000; //How much data should we fetch? //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void OnStart() { //---File name string file_name = "Market Data " + Symbol() + ".csv"; //---Write to file int file_handle=FileOpen(file_name,FILE_WRITE|FILE_ANSI|FILE_CSV,","); for(int i= size;i>=0;i--) { if(i == size) { FileWrite(file_handle,"Time","Open","High","Low","Close"); } else { FileWrite(file_handle,iTime(Symbol(),PERIOD_CURRENT,i), iOpen(Symbol(),PERIOD_CURRENT,i), iHigh(Symbol(),PERIOD_CURRENT,i), iLow(Symbol(),PERIOD_CURRENT,i), iClose(Symbol(),PERIOD_CURRENT,i)); } } } //+------------------------------------------------------------------+
在Python中进行数据分析的探索
我们从导入标准库开始。
#Libraries import pandas as pd import numpy as np import seaborn as sns
现在,让我们读取之前提取的数据。
#Dollar VS Rand USDZAR = pd.read_csv("/home/volatily/market_data/Market Data USDZAR.csv") #US Oil USOIL = pd.read_csv("/home/volatily/market_data/Market Data US Oil.csv") #SA Gold SAGOLD = pd.read_csv("/home/volatily/market_data/Market Data XAUUSD.csv")
检查数据。
USOIL
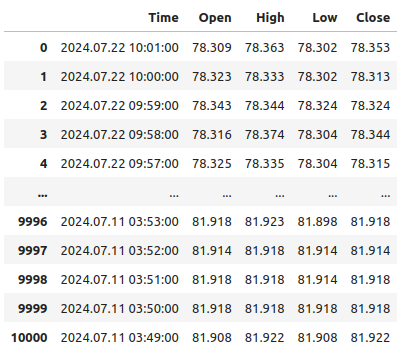
图1:我们的数据是按时间倒序排列的。
注意,我们的时间戳是从接近现在开始,然后逐渐回溯到过去,这对于机器学习任务来说是不理想的。让我们将数据的顺序反转过来,以便我们能够对未来进行预测,而不是对过去进行预测。
#Format the data USDZAR = USDZAR[::-1] USOIL = USOIL[::-1] SAGOLD = SAGOLD[::-1]
在可以合并数据集之前,让我们首先确保它们都使用日期列作为索引。通过这样做,可以确保我们只选择所有数据集共有的日期,并且以正确的时序顺序排列。
#Set the indexes USOIL = USOIL.set_index("Time") SAGOLD = SAGOLD.set_index("Time") USDZAR = USDZAR.set_index("Time")
合并数据集。
#Merge the dataframes merged_df = pd.merge(USOIL,SAGOLD,how="inner",left_index=True,right_index=True,suffixes=(" US OIL"," SA GOLD")) merged_df = pd.merge(merged_df,USDZAR,how="inner",left_index=True,right_index=True)
定义预测时间范围。
#Define the forecast horizon look_ahead = 10
目标将是 USDZAR 货币对的未来收盘价,我们还将包括一个二元目标,以便于可视化。
#Label the data merged_df["Target"] = merged_df["Close"].shift(-look_ahead) merged_df["Binary Target"] = 0 merged_df.loc[merged_df["Close"] < merged_df["Target"],"Binary Target"] = 1
删除任何空行。
#Drop empty rows
merged_df.dropna(inplace=True)
观察相关性水平。
#Let's observe the correlation levels merged_df.corr()
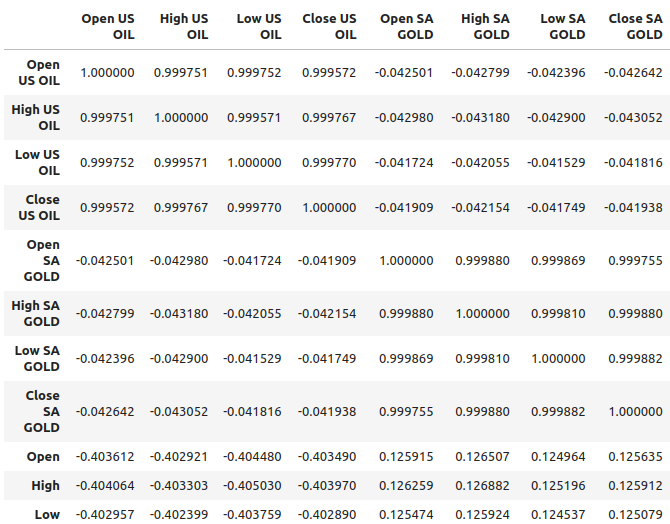
图2:我们数据集中的相关性水平
石油似乎与 USDZAR 货币对显示出相对较强的相关性水平,大约为 -0.4,而黄金与该货币对的相关性水平相对较弱,大约为 0.1。重要的是要记住,相关性并不总是意味着变量之间存在关系,有时相关性结果是由于一个共同的原因同时影响了这两个变量。
例如,历史上,黄金与美元之间的关系是相反的。每当美元贬值时,交易者就会将资金从美元中撤出,转而投资黄金。这在历史上导致了每当美元表现不佳时,黄金价格就会上涨。所以在这个简单的例子中,共同的原因就是那些同时参与这两个市场的交易者。
散点图有助于我们可视化两个变量之间的关系,因此我们创建了一个石油价格与黄金价格的散点图,并根据 USDZAR 的价格水平是升值(红色)还是贬值(绿色)来对点进行着色。正如人们可以看到的,数据中并没有明显的分离状态。事实上,我们创建的任何散点图都没有显示出强烈的关系。
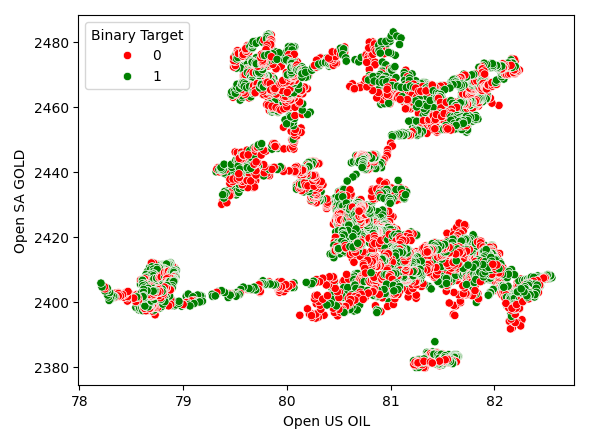
图3:黄金价格与石油价格的散点图
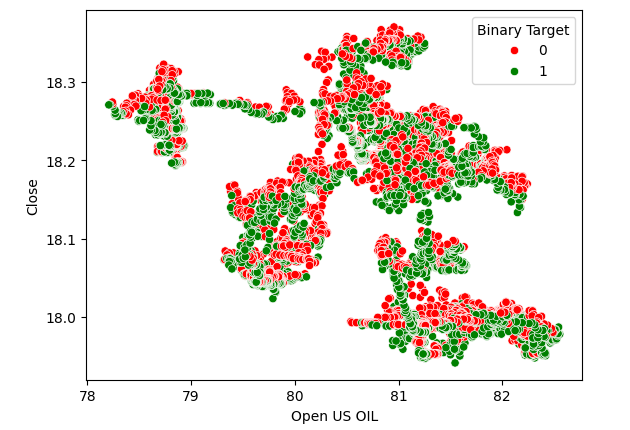
图4:石油价格与 USDZAR 收盘价的散点图
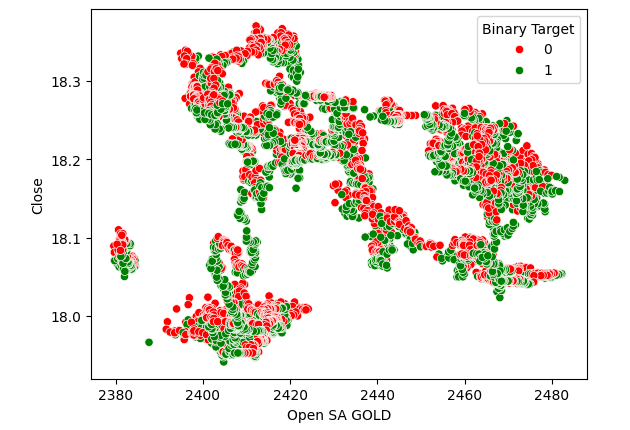
图5:黄金价格与 USDZAR 收盘价的散点图
相关性建模
让我们重新设置数据集的索引以便我们可以进行交叉验证。
#Reset the index
merged_df.reset_index(inplace=True)
现在,我们将导入我们需要用来建模数据中关系的库。
#Import the libraries we need from sklearn.linear_model import LinearRegression from sklearn.linear_model import Lasso from sklearn.ensemble import GradientBoostingRegressor from sklearn.ensemble import RandomForestRegressor from sklearn.ensemble import AdaBoostRegressor from sklearn.ensemble import BaggingRegressor from sklearn.neighbors import KNeighborsRegressor from sklearn.svm import LinearSVR from sklearn.neural_network import MLPRegressor from sklearn.model_selection import TimeSeriesSplit from sklearn.metrics import root_mean_squared_error from sklearn.preprocessing import RobustScaler
定义预测变量和目标变量。
#Define the predictors normal_predictors = ["Open","High","Low","Close"] oil_gold_predictors = ["Open US OIL","High US OIL","Low US OIL","Close US OIL","Open SA GOLD","High SA GOLD","Low SA GOLD","Close SA GOLD"] target = "Target"
数据标准化。
#Scale the data all_predictors = normal_predictors + oil_gold_predictors scaler = RobustScaler() scaled_data = pd.DataFrame(scaler.fit_transform(merged_df.loc[:,all_predictors]),columns=all_predictors,index=np.arange(0,merged_df.shape[0]))
初始化模型。
#Now prepare the models models = [ LinearRegression(), Lasso(), GradientBoostingRegressor(), RandomForestRegressor(), AdaBoostRegressor(), BaggingRegressor(), KNeighborsRegressor(), LinearSVR(), MLPRegressor(hidden_layer_sizes=(10,5),early_stopping=True), MLPRegressor(hidden_layer_sizes=(50,15),early_stopping=True) ] columns = [ "Linear Regression", "Lasso", "Gradient Boosting Regressor", "Random Forest Regressor", "AdaBoost Regressor", "Bagging Regressor", "KNeighbors Regressor", "Linear SVR", "Small Neural Network", "Large Neural Network" ]
实例化时间序列交叉验证对象。
#Prepare the time-series split object splits = 10 tscv = TimeSeriesSplit(n_splits=splits,gap=look_ahead)
创建一个数据帧来存储我们的误差水平。
#Prepare the dataframes to store the error levels normal_error = pd.DataFrame(columns=columns,index=np.arange(0,splits)) new_error = pd.DataFrame(columns=columns,index=np.arange(0,splits))
现在我们将使用嵌套的for循环来执行交叉验证。第一个循环遍历我们的模型列表,而第二个循环对每个模型进行交叉验证,并存储误差水平。
#First we iterate over all the models we have available for j in np.arange(0,len(models)): #Now we have to perform cross validation with each model for i,(train,test) in enumerate(tscv.split(scaled_data)): #Get the data X_train = scaled_data.loc[train[0]:train[-1],oil_gold_predictors] X_test = scaled_data.loc[test[0]:test[-1],oil_gold_predictors] y_train = merged_df.loc[train[0]:train[-1],target] y_test = merged_df.loc[test[0]:test[-1],target] #Fit the model models[j].fit(X_train,y_train) #Measure the error new_error.iloc[i,j] = root_mean_squared_error(y_test,models[j].predict(X_test))
这些误差水平是使用普通模型输入得到的。
normal_error
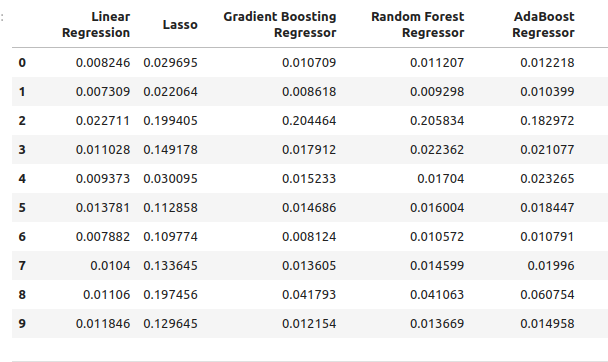
图6:使用 OHLC 预测变量进行预测时的误差水平
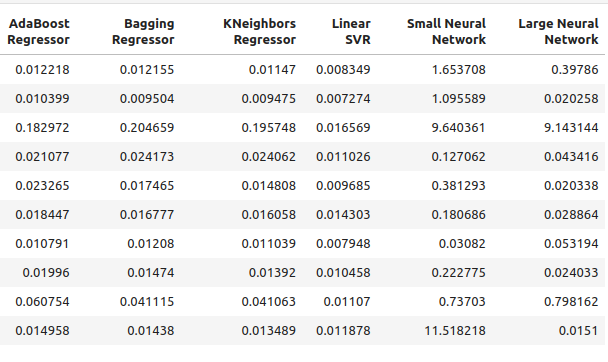
图7:使用 OHLC 预测变量进行预测时的误差水平 II
现在我们来看一下仅使用石油和黄金价格时的误差水平。
new_error
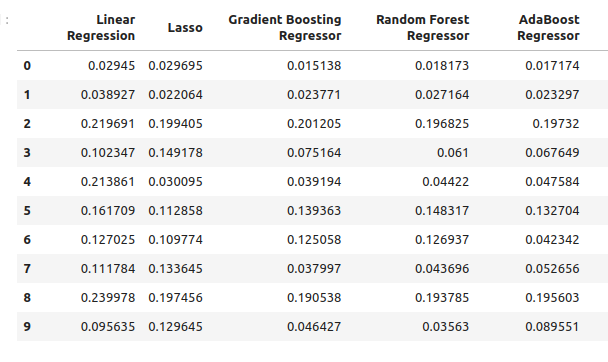
图8:使用石油和黄金价格进行预测时的准确率水平。
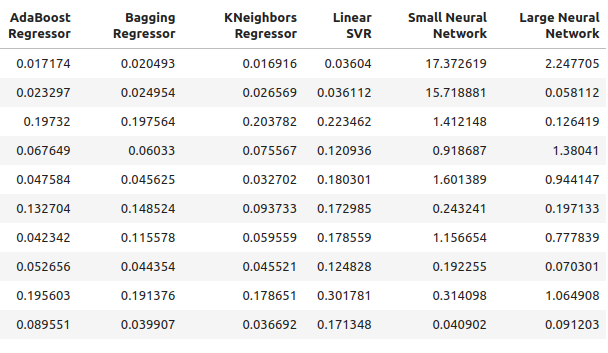
图9:使用石油和黄金价格进行预测时的准确率水平 II
让我们看看使用普通预测变量时每个模型的平均表现。
#Let's see our average performance on the normal dataset
for i in (np.arange(0,normal_error.shape[0])):
print(f"{models[i]} normal error {((normal_error.iloc[:,i].mean()))}")
Lasso() normal error 0.11138143304314707
GradientBoostingRegressor() normal error 0.03472997520534606
RandomForestRegressor() normal error 0.03616484012058101
AdaBoostRegressor() normal error 0.037484107657877755
BaggingRegressor() normal error 0.03670486223028821
KNeighborsRegressor() normal error 0.035113189373409175
LinearSVR() normal error 0.01085610361276552
MLPRegressor(early_stopping=True, hidden_layer_sizes=(10, 5)) normal error 2.558754334716706
MLPRegressor(early_stopping=True, hidden_layer_sizes=(50, 15)) normal error 1.0544369296125597
现在我们将评估使用新的预测变量时的平均表现。
#Let's see our average performance on the new dataset
for i in (np.arange(0,normal_error.shape[0])):
print(f"{models[i]} normal error {((new_error.iloc[:,i].mean()))}")
Lasso() normal error 0.11138143304314707
GradientBoostingRegressor() normal error 0.0893855335909897
RandomForestRegressor() normal error 0.08957454602573789
AdaBoostRegressor() normal error 0.08658796789785872
BaggingRegressor() normal error 0.08887059320664067
KNeighborsRegressor() normal error 0.07696901077705855
LinearSVR() normal error 0.15463529064256165
MLPRegressor(early_stopping=True, hidden_layer_sizes=(10, 5)) normal error 3.8970873719426784
MLPRegressor(early_stopping=True, hidden_layer_sizes=(50, 15)) normal error 0.6958177634524169
我们来观察预测准确率的变化。
#Let's see our average performance on the normal dataset
for i in (np.arange(0,normal_error.shape[0])):
print(f"{models[i]} changed by {((normal_error.iloc[:,i].mean()-new_error.iloc[:,i].mean()))/normal_error.iloc[:,i].mean()}%") Lasso() changed by 0.0%
GradientBoostingRegressor() changed by -1.573728690057642%
RandomForestRegressor() changed by -1.4768406476311784%
AdaBoostRegressor() changed by -1.3099914419240863%
BaggingRegressor() changed by -1.421221271695885%
KNeighborsRegressor() changed by -1.1920256220116057%
LinearSVR() changed by -13.244087580439862%
MLPRegressor(early_stopping=True, hidden_layer_sizes=(10, 5)) changed by -0.5230408480672479%
MLPRegressor(early_stopping=True, hidden_layer_sizes=(50, 15)) changed by 0.34010489967561475%
特征选择
在石油和黄金预测变量中表现最佳的模型是 KNeighbors 回归器,让我们看看哪些特征对它来说最重要。
#Our best performing model was the KNeighbors Regressor #Let us perform feature selection to test how stable the relationship is from mlxtend.feature_selection import SequentialFeatureSelector as SFS
创建模型的一个新实例。
#Let us select our best model
model = KNeighborsRegressor()
我们将使用逐步向前选择法来识别对我们模型最重要的特征。现在我们将一次性让模型访问所有预测变量。
#Create the sequential selector object sfs1 = SFS( model, k_features=(1,len(all_predictors)), forward=True, scoring="neg_mean_squared_error", cv=10, n_jobs=-1 )
拟合序列特征选择器。
#Fit the sequential selector sfs1 = sfs1.fit(scaled_data.loc[:,all_predictors],merged_df.loc[:,"Target"])
观察算法所选择的最佳特征可能会让我们得出结论:石油和黄金价格在预测 USDZAR 时并没有多大用处,因为我们的算法只选择了3个特征,它们是 USDZAR 的开盘价、最低价和收盘价的报价。
#Now let us see which predictors were selected
sfs1.k_feature_names_
超参数优调
让我们尝试使用 scikit-learn 的 RandomizedSearchCV 模块来进行超参数调整。该算法帮助我们采样一个可能过于庞大而无法完全采样的响应面。当我们使用具有众多参数的模型时,输入的总组合数会以极快的速度增长。因此,当我们处理具有许多可能值的众多参数时,更倾向于使用随机搜索算法。
该算法在结果的准确性与计算时间之间提供了一种权衡。这种权衡是通过调整我们允许的迭代次数来控制的。请注意,由于该算法的随机性,可能难以完全复现本文中展示的结果。
导入 scikit-learn 模块。
#Now we will load the libraries we need
from sklearn.model_selection import RandomizedSearchCV
准备专门的训练集和测试集。
#Let us see if we can tune the model #First we will create train test splits train_X = scaled_data.loc[:(scaled_data.shape[0]//2),:] train_y = merged_df.loc[:(merged_df.shape[0]//2),"Target"] test_X = scaled_data.loc[(scaled_data.shape[0]//2):,:] test_y = merged_df.loc[(merged_df.shape[0]//2):,"Target"]
为了进行参数调整,我们需要传递一个实现 scikit-learn 接口的估计器,随后传递一个字典,其中的键对应于估计器的参数,而值对应于每个参数允许的输入范围。在此基础上,我们指定要执行 5 折交叉验证,然后我们需要指定评分指标为负均方误差。
#Create the tuning object rs = RandomizedSearchCV(KNeighborsRegressor(n_jobs=-1),{ "n_neighbors": [1,2,3,4,5,8,10,16,20,30,60,100], "weights":["uniform","distance"], "leaf_size":[1,2,3,4,5,10,15,20,40,60,90], "algorithm":["ball_tree","kd_tree"], "p":[1,2,3,4,5,6,7,8] },cv=5,n_iter=500,return_train_score=False,scoring="neg_mean_squared_error")
在训练集上进行参数调整。
#Let's perform the hyperparameter tuning rs.fit(train_X,train_y)
查看我们获得的结果,从最好到最差。
#Let's store the results from our hyperparameter tuning tuning_results = pd.DataFrame(rs.cv_results_) tuning_results.loc[:,["param_n_neighbors","param_weights","param_leaf_size","param_algorithm","param_p","mean_test_score"]].sort_values(by="mean_test_score",ascending=False)
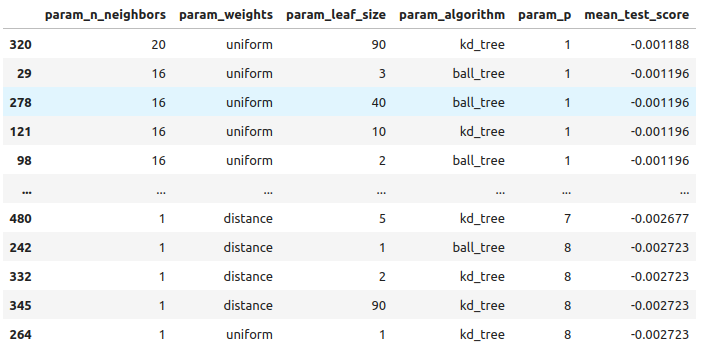
图10:模型调整的最佳结果
这些是我们找到的最佳参数。
#The best parameters we came across
rs.best_params_
'p': 1,
'n_neighbors': 4,
'leaf_size': 15,
'algorithm': 'ball_tree'}
检查过拟合
让我们准备好比较我们定制的模型和默认模型。两个模型将在相同的训练集上进行训练。如果默认模型在验证集上的表现优于我们定制的模型,那么这可能是一个信号,表明我们对训练数据进行了过拟合。然而,如果我们的定制模型表现更好,那么这可能表明我们成功地调整了模型参数而没有过拟合。
#Create instances of the default model and the custmoized model default_model = KNeighborsRegressor() customized_model = KNeighborsRegressor(p=rs.best_params_["p"],weights=rs.best_params_["weights"],n_neighbors=rs.best_params_["n_neighbors"],leaf_size=rs.best_params_["leaf_size"],algorithm=rs.best_params_["algorithm"])
让我们来检测默认模型的准确率。
#Measure the accuracy of the default model default_model.fit(train_X,train_y) root_mean_squared_error(test_y,default_model.predict(test_X))
现在检测定制模型的准确率。
#Measure the accuracy of the customized model
customized_model.fit(train_X,train_y)
root_mean_squared_error(test_y,customized_model.predict(test_X)) 看起来我们在没有过拟合的情况下很好地调整了模型!现在,让我们准备好将我们的定制模型导出为ONNX格式。
导出为ONNX格式
Open Neural Network Exchange(ONNX)是一个用于构建和部署机器学习模型的互操作性框架,它以一种与语言无关的方式工作。通过使用ONNX,我们的机器学习模型可以在任何支持ONNX API的编程语言中轻松使用。在本文撰写时,ONNX API正由世界上最大的公司组成的联盟开发和维护。
Import the libraries we need #Let's prepare to export the customized model to ONNX format import onnx from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType
我们需要确保我们的数据经过了缩放和标准化处理,并且这种处理方式可以在MetaTrader 5终端中重现。因此,我们将执行一个标准变换,我们以后可以在终端中随时执行这个操作。我们将减去每一列的平均值,这将使数据居中。然后,我们将每个值除以其所在列的标准差,这将帮助我们的模型更好地理解不同量纲变量之间的变化。
#Train the model on all the data we have #But before doing that we need to first scale the data in a way we can repeat in MQL5 scale_factors = pd.DataFrame(columns=all_predictors,index=["mean","standard deviation"]) for i in np.arange(0,len(all_predictors)): scale_factors.iloc[0,i] = merged_df.loc[:,all_predictors[i]].mean() scale_factors.iloc[1,i] = merged_df.loc[:,all_predictors[i]].std() scale_factors

图12:将用于缩放和标准化数据的一些值,并未把所有列都显示出来
现在,让我们进行归一化和标准化。
for i in all_predictors:
merged_df.loc[:,i] = (merged_df.loc[:,i] - merged_df.loc[:,i].mean()) / merged_df.loc[:,i].std()
现在来看看我们的数据。
merged_df
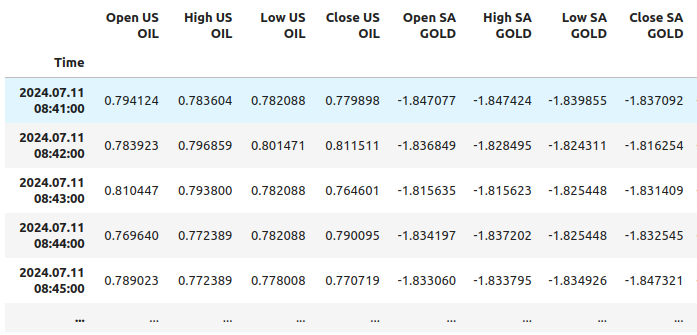
图11:缩放后的数据示例,并未把所有列都显示出来
初始化我们的定制模型。
customized_model = KNeighborsRegressor(p=rs.best_params_["p"],weights=rs.best_params_["weights"],n_neighbors=rs.best_params_["n_neighbors"],leaf_size=rs.best_params_["leaf_size"],algorithm=rs.best_params_["algorithm"]) customized_model.fit(merged_df.loc[:,all_predictors],merged_df.loc[:,"Target"])
定义模型的输入参数格式。
#Define the input shape and type initial_type = [("float_tensor_type",FloatTensorType([1,train_X.shape[1]]))]
创建ONNX表示。
#Create an ONNX representation
onnx_model = convert_sklearn(customized_model,initial_types=initial_type)
保存ONNX模型。
#Store the ONNX model onnx_model_name = "USDZAR_FLOAT_M1.onnx" onnx.save_model(onnx_model,onnx_model_name)
可视化ONNX模型。
Netron 是一个开源的机器学习模型可视化工具。Netron 不仅支持 ONNX,还支持许多其他框架,例如 Keras。我们将使用 Netron 来确保 ONNX 模型具有我们预期的输入和输出格式。
导入 Netron 模块。
#Let's visualize the model in netron import netron
现在我们可以使用 Netron 来可视化这个模型。
#Run netron
netron.start(onnx_model_name)
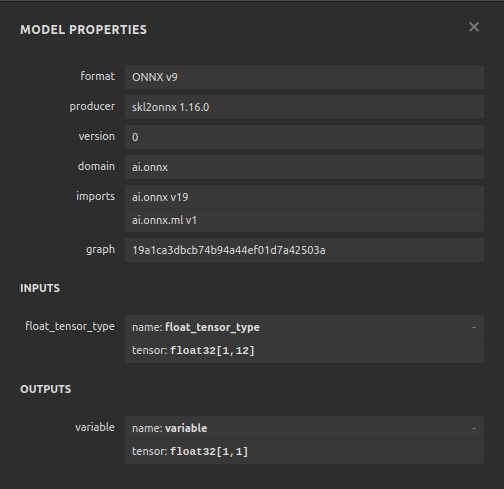
图12:我们ONNX模型的规格
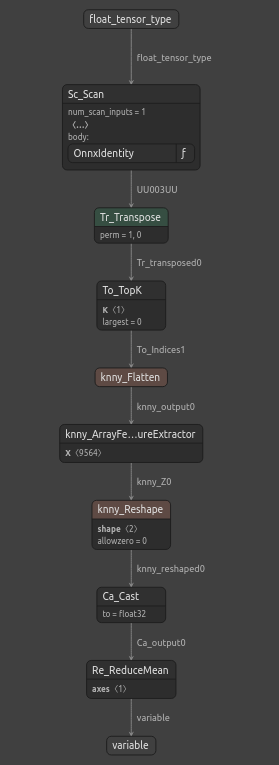
图13:我们ONNX模型的结构
我们的ONNX模型符合预期,输入和输出的格式准确地处于我们期望的位置。现在我们可以继续构建基于ONNX模型的EA了。
在MQL5中的实现
现在可以开始构建我们的EA,让我们首先将ONNX模型集成到应用程序中。通过将ONNX文件指定为资源,ONNX文件将被包含在编译后的程序中,该程序带有.ex5扩展名。
//+------------------------------------------------------------------+ //| USDZAR.mq5 | //| Gamuchirai Zororo Ndawana | //| https://www.mql5.com/en/gamuchiraindawa | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com/en/gamuchiraindawa" #property version "1.00" //+-----------------------------------------------------------------+ //| Require the ONNX file | //+-----------------------------------------------------------------+ #resource "\\Files\\USDZAR_FLOAT_M1.onnx" as const uchar onnx_model_buffer[];
现在我们导入交易库。
//+-----------------------------------------------------------------+ //| Libraries we need | //+-----------------------------------------------------------------+ #include <Trade/Trade.mqh> CTrade Trade;
定义用户可编辑的输入参数。
//+------------------------------------------------------------------+ //| Inputs | //+------------------------------------------------------------------+ double input sl_width = 0.4; //How tight should our stop loss be? int input lot_multiple = 10; //How many times bigger than minimum lot should we enter? double input max_risk = 10; //After how much profit/loss should we close?
现在我们还需要定义一些全局变量。
//+------------------------------------------------------------------+ //| Global Variables | //+------------------------------------------------------------------+ long onnx_model; //Our onnx model double mean_values[12],std_values[12]; //The scaling factors we used for our data vector model_inputs = vector::Zeros(12); //Our model's inputs vector model_forecast = vector::Zeros(1); //Our model's output double bid,ask; //Market prices double minimum_volume; //Smallest lot size double state = 0; //0 means we have no positions, 1 means we have buy position, 2 means we have sell position.
现在,让我们定义一些辅助函数,以便于我们重复执行某些任务。首先,让我们控制风险水平。如果总盈亏超过了我们设定的风险水平,将自动平仓。
//+------------------------------------------------------------------+ //| Check if we have reached our risk level | //+------------------------------------------------------------------+ void check_risk_level(void) { //--- Check if we have surpassed our maximum risk level if(MathAbs(PositionGetDouble(POSITION_PROFIT)) > max_risk) { //--- We should close our positions Trade.PositionClose("USDZAR"); } }
既然我们已经集成了人工智能系统,让我们用它来检测反转。如果我们的系统预测价格将对我们不利,我们将关闭头寸,并提醒终端用户已检测到潜在的反转。
//+------------------------------------------------------------------+ //| Check if there is a reversal may be coming | //+------------------------------------------------------------------+ void check_reversal(void) { if(((state == 1) && (model_forecast[0] < iClose("USDZAR",PERIOD_M1,0))) ||((state == 2) && (model_forecast[0] > iClose("USDZAR",PERIOD_M1,0)))) { //--- There may be a reversal coming Trade.PositionClose("USDZAR"); //--- Give the user feedback Alert("Potential reversal detected"); } }
现在我们需要一个函数来寻找入场机会。如果我们的模型预测与更高时间框架上的价格水平变化一致,我们才会认为该入场时机是有效的。
//+------------------------------------------------------------------+ //| Find an entry opportunity | //+------------------------------------------------------------------+ void find_entry(void) { //---Check for the change in price on higher timeframes if(iClose("USDZAR",PERIOD_D1,0) > iClose("USDZAR",PERIOD_D1,21)) { //--- We're looking for buy oppurtunities if(model_forecast[0] > iClose("USDZAR",PERIOD_M1,0)) { //--- Open the position Trade.Buy(minimum_volume,"USDZAR",ask,(ask - sl_width),(ask + sl_width),"USDZAR AI"); //--- Update the system state state = 1; } } //---Check for the change in price on higher timeframes else if(iClose("USDZAR",PERIOD_D1,0) < iClose("USDZAR",PERIOD_D1,21)) { //--- We're looking for sell oppurtunities if(model_forecast[0] < iClose("USDZAR",PERIOD_M1,0)) { //--- Open sell position Trade.Sell(minimum_volume,"USDZAR",bid,(bid + sl_width),(bid - sl_width),"USDZAR AI"); //--- Update the system state state = 2; } } }
现在我们需要一个函数从模型中获取预测。要做到这一点,我们首先需要获取当前市场价格,然后通过减去均值并除以标准差来转换它们。
//+------------------------------------------------------------------+ //| Obtain a forecast from our model | //+------------------------------------------------------------------+ void model_predict(void) { //Let's fetch our model's inputs //--- USDZAR model_inputs[0] = ((iOpen("USDZAR",PERIOD_M1,0) - mean_values[0]) / std_values[0]); model_inputs[1] = ((iHigh("USDZAR",PERIOD_M1,0) - mean_values[1]) / std_values[1]); model_inputs[2] = ((iLow("USDZAR",PERIOD_M1,0) - mean_values[2]) / std_values[2]); model_inputs[3] = ((iClose("USDZAR",PERIOD_M1,0) - mean_values[3]) / std_values[3]); //--- XTI OIL US model_inputs[4] = ((iOpen("XTIUSD",PERIOD_M1,0) - mean_values[4]) / std_values[4]); model_inputs[5] = ((iHigh("XTIUSD",PERIOD_M1,0) - mean_values[5]) / std_values[5]); model_inputs[6] = ((iLow("XTIUSD",PERIOD_M1,0) - mean_values[6]) / std_values[6]); model_inputs[7] = ((iClose("XTIUSD",PERIOD_M1,0) - mean_values[7]) / std_values[7]); //--- GOLD SA model_inputs[8] = ((iOpen("XAUUSD",PERIOD_M1,0) - mean_values[8]) / std_values[8]); model_inputs[9] = ((iHigh("XAUUSD",PERIOD_M1,0) - mean_values[9]) / std_values[9]); model_inputs[10] = ((iLow("XAUUSD",PERIOD_M1,0) - mean_values[10]) / std_values[10]); model_inputs[11] = ((iClose("XAUUSD",PERIOD_M1,0) - mean_values[11]) / std_values[11]); //--- Get a prediction OnnxRun(onnx_model,ONNX_DEFAULT,model_inputs,model_forecast); }
既然我们正在分析多个交易品种,就需要将它们添加到市场观察窗口中。
//+------------------------------------------------------------------+ //| Load the symbols we need and add them to the market watch | //+------------------------------------------------------------------+ void load_symbols(void) { SymbolSelect("XAUUSD",true); SymbolSelect("XTIUSD",true); SymbolSelect("USDZAR",true); }
我们需要一个负责加载我们缩放因子的函数,即每列的均值和标准差。
//+------------------------------------------------------------------+ //| Load the scale values | //+------------------------------------------------------------------+ void load_scale_values(void) { //--- Mean //--- USDZAR mean_values[0] = 18.14360511919699; mean_values[1] = 18.145737421580925; mean_values[2] = 18.141568574864074; mean_values[3] = 18.14362306984525; //--- XTI US OIL mean_values[4] = 80.76956702216644; mean_values[5] = 80.7864452112087; mean_values[6] = 80.75236177331661; mean_values[7] = 80.76923546633206; //--- GOLD SA mean_values[8] = 2430.5180384776245; mean_values[9] = 2430.878959640318; mean_values[10] = 2430.1509598494354; mean_values[11] = 2430.5204140526976; //--- Standard Deviation //--- USDZAR std_values[0] = 0.11301636249300206; std_values[1] = 0.11318116432297631; std_values[2] = 0.11288670156099372; std_values[3] = 0.11301994613848391; //--- XTI US OIL std_values[4] = 0.9802409859148413; std_values[5] = 0.9807944310705999; std_values[6] = 0.9802449355481064; std_values[7] = 0.9805961626626833; //--- GOLD SA std_values[8] = 26.397404261230328; std_values[9] = 26.414599597905003; std_values[10] = 26.377605644853944; std_values[11] = 26.395208330942864; }
最后,我们需要一个负责加载我们ONNX文件的函数。
//+------------------------------------------------------------------+ //| Load the onnx file from buffer | //+------------------------------------------------------------------+ bool load_onnx_file(void) { //--- Create the model from the buffer onnx_model = OnnxCreateFromBuffer(onnx_model_buffer,ONNX_DEFAULT); //--- The input size for our onnx model ulong input_shape [] = {1,12}; //--- Check if we have the right input size if(!OnnxSetInputShape(onnx_model,0,input_shape)) { Comment("Incorrect input shape, the model has input shape ",OnnxGetInputCount(onnx_model)); return(false); } //--- The output size for our onnx model ulong output_shape [] = {1,1}; //--- Check if we have the right output size if(!OnnxSetOutputShape(onnx_model,0,output_shape)) { Comment("Incorrect output shape, the model has output shape ",OnnxGetOutputCount(onnx_model)); return(false); } //--- Everything went fine return(true); } //+------------------------------------------------------------------+
现在我们已经定义了这些辅助函数,我们可以在EA中开始使用它们了。首先,让我们定义应用程序首次加载时的行为。我们将从加载ONNX模型开始,准备好缩放值,然后我们将获取市场数据。
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- Load the onnx file if(!load_onnx_file()) { return(INIT_FAILED); } //--- Load our scaling values load_scale_values(); //--- Add the symbols we need to the market watch load_symbols(); //--- The smallest lotsize we can use minimum_volume = SymbolInfoDouble("USDZAR",SYMBOL_VOLUME_MIN) * lot_multiple; //--- Everything went fine return(INIT_SUCCEEDED); }
每当我们的程序被停用时,需要释放不再使用的资源。
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- Release the resources we used for our onnx model OnnxRelease(onnx_model); //--- Remove the expert advisor ExpertRemove(); }
最后,每当价格发生变化时,我们需要从模型中获取新的预测,获取最新的市场价格,然后要么开立新的头寸,要么管理我们当前已经持有的头寸。
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- We always need a forecast from our model model_predict(); //--- Fetch market prices bid = SymbolInfoDouble("USDZAR",SYMBOL_BID); ask = SymbolInfoDouble("USDZAR",SYMBOL_ASK); //--- If we have no open positions, find an entry if(PositionsTotal() == 0) { //--- Find an entry find_entry(); //--- Reset the system state state = 0; } //--- If we have open postitions, manage them else { //--- Check for a reveral warning from our AI check_reversal(); //--- Check if we have not reached our max risk levels check_risk_level(); } }
将所有这些整合在一起,我们现在可以观察我们的程序在运行。
图17:我们的EA
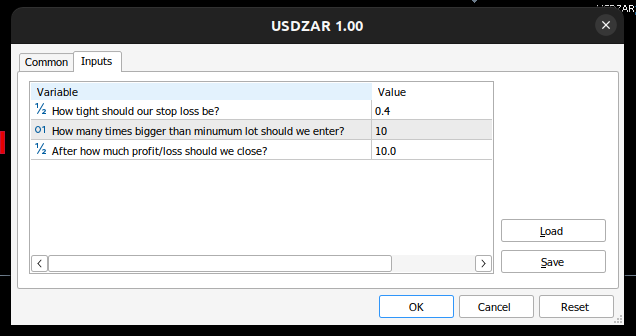
图14:EA的输入参数
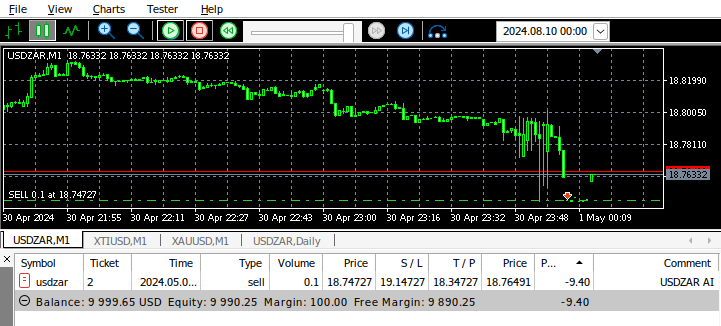
图15:我们的程序在运行
结论
在本文中,我们展示了如何构建一个由人工智能驱动的多交易品种EA。尽管我们使用常规的 OHLC 数据获得了较低的误差水平,但这并不一定意味着 MetaTrader 5 终端中的所有交易品种都是一样的。可能存在一组不同的交易品种组合,其误差水平可能比 USDZAR 的 OHLC 报价更低。
本文由MetaQuotes Ltd译自英文
原文地址: https://www.mql5.com/en/articles/15570
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。
 创建 MQL5-Telegram 集成 EA 交易 (第二部分):从 MQL5 发送信号到 Telegram
创建 MQL5-Telegram 集成 EA 交易 (第二部分):从 MQL5 发送信号到 Telegram
 重塑经典策略(第四部分):标普500指数与美国国债
重塑经典策略(第四部分):标普500指数与美国国债
 使用 SMA 和 EMA 自动优化止盈和指标参数的示例
使用 SMA 和 EMA 自动优化止盈和指标参数的示例
 交易中的神经网络:时空神经网络(STNN)
交易中的神经网络:时空神经网络(STNN)
太棒了,又一次出色的演练。感谢您提供的工作手册,我们现在有了一个测试自己相关性的模板。非常感谢