行列分解：より実用的なモデリング

はじめに

こんにちは、皆さん。また、教訓的な内容を特集した私の新しい記事へようこそ。

前回の「行列分解：基本事項」稿では、読者の皆さんに一般的な計算における行列の使用方法について簡単に説明しました。ただし、その際には計算のプロセスを理解してもらうことに重点を置いたため、行列の適切なモデリングにはあまり注意を払っていませんでした。

行と列ではなく列のみが指定されているため、行列モデリングが少し奇妙であることに気付かなかったかもしれません。行列分解を実行するコードを読むと、これは非常に奇妙に見えます。行と列がリストされていることを期待していた場合、因数分解しようとしたときに混乱する可能性があります。

さらに、この行列モデリング方法は最適ではありません。これは、この方法で行列をモデル化すると、いくつかの制限に遭遇し、より適切な方法でモデル化がおこなわれていれば必要のない他のメソッドや関数を使用せざるを得なくなるためです。

この手順は複雑ではありませんが、正しく使用するには十分な理解が必要なので、前回の記事では詳細には触れませんでした。この記事では、行列のモデル化に関する誤った考えを避け、正しい因数分解を確実におこなうために、すべてをより冷静に、急がずに検討します。

行列は、その性質上、追加の実装作業が最小限で済むため、特定の種類の計算を実行するのに適した方法です。ただし、まったく同じ理由で、行列で何かを実装するときは細心の注意を払う必要があります。従来のモデリングとは異なり、行列で何かを誤ってモデリングすると、奇妙な結果が得られるか、開発されたコードの保守に大きな困難が生じることになります。

行列のモデリングにおける注意

なぜ前回の記事のモデリングが奇妙に感じられるのか、疑問に思う方もいるかもしれません。それには理由があります。おそらく、その記事で説明された内容はすべて理解できたことでしょう。しかし、もう一度、前回の記事で行列をモデリングしたコードの一部を見てみましょう。これにより、私が皆さんに伝えたいことがさらに明確になるかもしれません。以下がそのコードです。

20. //+------------------------------------------------------------------+
21. void Arrow(const int x, const int y, const ushort angle, const uchar size = 100)
22. {
23.     double M_1[2][2] = {
24.                            cos(_ToRadians(angle)), sin(_ToRadians(angle)),
25.                           -sin(_ToRadians(angle)), cos(_ToRadians(angle))
26.                         },
27.            M_2[][2]  =  {
28.                            0.0,  0.0,
29.                            1.5, -.75,
30.                            1.0,  0.0,
31.                            1.5,  .75
32.                         },
33.            M_3[M_2.Size() / 2][2];

動作はするものの、フラグメントからは問題が非常にわかりにくく、理解が難しいことがわかります。コードで多次元配列を記述する場合は、次の構成を使用することをお勧めします。

ラベル[Dimension_01][Dimension_02]....[Dimension_N];

コードは一般的にはシンプルに見えますが、この表記法を行列分解の分野に適用すると理解が難しくなります。行列を扱う際、多次元配列をこの方法で表現すると混乱が生じるためです。その理由はすぐに明らかになります。簡潔に説明するために、この概念を2次元システム、つまり行と列に限定して考えますが、実際の行列には任意の数の次元を含めることが可能です。2次元行列に簡略化すると、表記法は次のようになります。

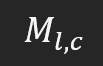
これは何を意味するのでしょうか。文字「M」は行列の名前を表し、「l」は行数、「c」は列数を示します。一般的に、行列要素を参照する際には、同じ表記法を使用します。

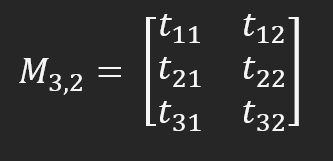
行列Mは、行と列のシステムを使用してアクセスできる6つの要素から構成されています。ただし、前の画像をよく見てください。どのように見えますか。経験によっては異なる見え方をするかもしれませんが、プログラミング用語ではこれは2次元配列です。しかし、このアプローチでは、行列が静的に見えます。行列は動的なエンティティであり、計算内容に応じて様々な方法で読み取ることが可能です。対角線で読み取る必要がある場合もあれば、列ごと、あるいは行ごとに読み取る必要がある場合もあります。したがって、行列を多次元配列として捉えると、動的なものが静的なものに変わり、一部の行列計算の実装が複雑になります。

しかし、ここで私たちが学ぶのはプログラミングの基礎ではありません。読者の皆さんに、行列を本来の動的なエンティティとして維持しながら、最も効果的に視覚化する方法をお見せしたいと思います。

したがって、行列を配列として考えること自体は間違いではありません。しかし、問題はそれを多次元配列として考えるときに発生します。理想的には、行列は次元数が固定されていない1次元配列として考えるべきです。この点は一見奇妙に思えるかもしれませんが、実際の問題は言語によるものです。現在、いくつかの概念を説明するのに適切な用語や表現が不足しています。

アイザック・ニュートンが初めて計算を説明した際に直面した困難を思い出してください。適切な用語が存在しなかったため、彼は多くの問題に苦しんだことでしょう。しかし、質問に戻りましょう。

行列を配列として表現する方法はすでに存在します。しかし、ここで最初の問題が発生します。それは、配列内の要素をどのように並べ替えるかということです。この問題を理解していない場合、行列の因数分解に関する他の関連事項も把握できていないことになります。要素の順序は、因数分解コードの実装方法に大きく影響します。結果はどちらの場合も同じですが、正しい結果を得るには、配列内での遷移が多少必要になることがあります。これは、コンピュータのメモリが線形であるためです。要素を t11、t12、t21、t22、t31、t32​の順で配置した場合、特定の計算を実行するために異なる順序で要素にアクセスする必要があり、ジャンプを強いられることになります。これは、どの状況でも必ず発生します。

通常、配列の要素を並べ替える場合は、行ごとに処理しますが、列ごとに読み取ることも可能です。自分の好みに応じて自由に並べ替えられます。

この作業が完了すると、プログラミングとは関係なく行列分解に関する別の小さな問題が発生しますが、ここでは詳細には触れません。理由は簡単です。この問題への対処方法は、行列の実装方法や使用する行列の種類によって異なるためです。発生する可能性のある問題の解決策を実装し、因数分解を正しく実行するためには、書籍や数学文献を学ぶことをお勧めします。ただし、コードは開発の最も簡単な部分であり、最も難しいのは因数分解がどのように実行されるかを理解することです。前の図に示した行列式の計算を例に挙げれば、これは正方行列ではなく、この場合の行列式の構築は正方行列の場合とは異なります。特定のケースごとに特別なアプローチが必要になるため、数学的な部分についてはしっかりと学習することが重要です。

混乱

さて、これですべてが説明されたので、コーディング段階に進むことができます。前回の記事で説明した例を続けましょう。これは非常に実用的で理解しやすいものです。さらに、この例では、状況によっては行列計算を使用することの別の利点を簡単に示しています。コードがどのようなものであったかを思い出してみましょう。これがそのコードです。

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. #property indicator_chart_window
04. #property indicator_plots 0
05. //+------------------------------------------------------------------+
06. #include <Canvas\Canvas.mqh>
07. //+------------------------------------------------------------------+
08. CCanvas canvas;
09. //+------------------------------------------------------------------+
10. #define _ToRadians(A) (A * (M_PI / 180.0))
11. //+------------------------------------------------------------------+
12. void MatrixA_x_MatrixB(const double &A[][], const double &B[][], double &R[][], const int nDim)
13. {
14.     for (int c = 0, size = (int)(B.Size() / nDim); c < size; c++)
15.     {
16.         R[c][0] = (A[0][0] * B[c][0]) + (A[0][1] * B[c][1]);
17.         R[c][1] = (A[1][0] * B[c][0]) + (A[1][1] * B[c][1]);
18.     }
19. }
20. //+------------------------------------------------------------------+
21. void Arrow(const int x, const int y, const ushort angle, const uchar size = 100)
22. {
23.     double M_1[2][2]{
24.                         cos(_ToRadians(angle)), sin(_ToRadians(angle)),
25.                         -sin(_ToRadians(angle)), cos(_ToRadians(angle))
26.                     },
27.            M_2[][2] {
28.                         0.0,  0.0,
29.                         1.5, -.75,
30.                         1.0,  0.0,
31.                         1.5,  .75
32.                     },
33.            M_3[M_2.Size() / 2][2];
34. 
35.     int dx[M_2.Size() / 2], dy[M_2.Size() / 2];
36.     
37.     MatrixA_x_MatrixB(M_1, M_2, M_3, 2);
38.     ZeroMemory(M_1);
39.     M_1[0][0] = M_1[1][1] = size;
40.     MatrixA_x_MatrixB(M_1, M_3, M_2, 2);
41. 
42.     for (int c = 0; c < (int)M_2.Size() / 2; c++)
43.     {
44.         dx[c] = x + (int) M_2[c][0];
45.         dy[c] = y + (int) M_2[c][1];
46.     }
47. 
48.     canvas.FillPolygon(dx, dy, ColorToARGB(clrPurple, 255));
49.     canvas.FillCircle(x, y, 5, ColorToARGB(clrRed, 255));
50. }
51. //+------------------------------------------------------------------+
52. int OnInit()
53. {    
54.     int px, py;
55.     
56.     px = (int)ChartGetInteger(0, CHART_WIDTH_IN_PIXELS, 0);
57.     py = (int)ChartGetInteger(0, CHART_HEIGHT_IN_PIXELS, 0);
58. 
59.     canvas.CreateBitmapLabel("BL", 0, 0, px, py, COLOR_FORMAT_ARGB_NORMALIZE);
60.     canvas.Erase(ColorToARGB(clrWhite, 255));
61.         
62.     Arrow(px / 2, py / 2, 160);
63. 
64.     canvas.Update(true);
65.     
66.     return INIT_SUCCEEDED;
67. }
68. //+------------------------------------------------------------------+
69. int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[])
70. {
71.     return rates_total;
72. }
73. //+------------------------------------------------------------------+
74. void OnDeinit(const int reason)
75. {
76.     canvas.Destroy();
77. }
78. //+------------------------------------------------------------------+

このコードは前回の記事で説明されており、その付録にも掲載されているため、ここでは繰り返しません。デモ コードで実際に何かを実行するArrowプロシージャとMatrixA_x_MatrixBプロシージャのみに焦点を当てましょう。

まず、配列の作成方法を変更します。この変更は見た目以上に単純で微妙なものになりますが、開始方法が変わる点に注意してください。

上記のコードに示されているM_1配列から始めましょう。それが何であるかを理解するために調べてみてください。

ここで注目すべき点があります。これは前のセクションで説明したトピックと正確に関連しています。行23では、2行2列の配列または行列M_1を宣言しています。この場合、非常にシンプルです。同じことが配列または行列M_2にも当てはまります。配列または行列M_2には行数の定義はありませんが、列数は定義されており、その数は2です。ここまでは疑問や問題はありません。コード内の新しい行はそれぞれ行列の新しい行に対応し、その行の新しい列はそれぞれ行列の新しい列となるため、何をしているのか非常に簡単に理解できます。全体として、非常にシンプルです。ただし、MatrixA_x_MatrixBプロシージャのコードには問題があります。問題を特定できますか。できませんか。それともできますか。おそらく、問題に気付いても理解できないかもしれません。

実際の問題は、行列の乗算をおこなうMatrixA_x_MatrixBプロシージャにあります。ここでおこなっていることは非常に単純であり、コードの実装には影響しません。ただし、問題が存在し、作業の進行を遅らせているため、解決する必要があります。より複雑な乗算を実装する必要があるとすぐに、これが大きな障害となります。

もし問題に気付かなかった場合は、変数Bに注目してください。これは、別の行列を乗算するための行列です。問題をよりわかりやすくするために、行列Aには2つの列があるため、行列Bを1列2行に減らしてみましょう。乗算を実行するには、下の図に示すようにする必要があります。

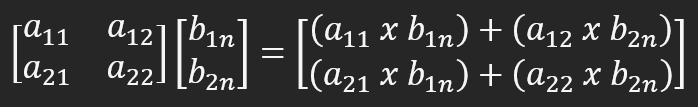
これで正しい結果が得られます。これは、行列を乗算または因数分解するときに起こることと全く同じです。詳細については、この問題を調べることをお勧めします。どちらの場合も、乗算は列の行ごとに実行され、列に残る値になります。これは、2番目の因数が列であるために発生します。乗算が列で実行される場合、結果の値は行の形式で配置する必要があります。

これまで述べてきたことは混乱を招くように思われるかもしれませんが、実際にはこれが行列乗算を実行するためのルールです。別のプログラマーがコードを分析しても、すべてが正しく行われているとはわからないかもしれません。これは、上の図に示されている計算を実行する必要がある16行目と17行目に見られる問題です。しかし、行列Aでは行単位の計算を使用し、行列Bでも行単位の計算を使用します。この単純な例では正しいデータが提供されますが、これが私たちを混乱させる要因となります。

それで、どうなるのでしょうか。すべてがうまくいっているなら、そのままにしておけばいいと思うかもしれません。しかし、それは重要ではありません。ある時点で、より大きな行列を処理したり、わずかに異なるケースをカバーしたりするためにコードを改善する必要が生じた場合、比較的単純なものを機能させようとすることで、問題がはるかに複雑になることがあります。したがって、混乱を避けるためには、そのようなことは適切におこなう必要があります。この問題を解決するには、このモデルを少し異なるモデルに置き換える必要があります。最初はすべてが混乱しているように見えるかもしれませんが、上の図に示されているように、正しいものになります。

混乱を避けるために、新しいトピックでこれをおこなう方法を見てみましょう。

物事を簡単にする

ここでおこなうことは複雑に思えるかもしれませんが、正しく慎重におこなえばそれほど難しくはありません。面倒に感じるかもしれませんが、かなり簡単な方法で実行できます。下の図をご覧ください。

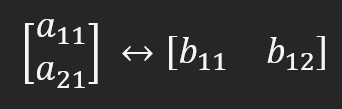
この表現は、両方の行列が等しいことを示しています。左側に要素Aを持つ行列が行行列であるため、これを右側に要素Bを持つ行列（この場合は列行列）に変換する際には、多くの変更をおこなう必要はなく、場合によってはスピンやインデックスの変更のみで済みます。ただし、行行列を列行列に変換したり、その逆を行ったり、行列を因数分解したりするには、これを複数回実行する必要がある場合があります。この例が正しいためには、a11はb11に等しく、a21はb12に等しくなければなりません。

場合によっては、大きな変更を加えなくても、行構造を列の1つに変換できるインデックスを変更するだけで済むことに気づくかもしれません。しかし、これを正しくおこなう方法は、各特定のケースによって異なります。したがって、関連する数学の書籍から行列因数分解の実行方法を学ぶことが重要です。

さて、前のトピックで見たコードに戻りましょう。まず、プレゼンテーションを修正し、以下のようにコードを変更します。

20. //+------------------------------------------------------------------+
21. void Arrow(const int x, const int y, const ushort angle, const uchar size = 100)
22. {
23.     double  M_1[]= {
24.                        cos(_ToRadians(angle)), sin(_ToRadians(angle)),
25.                        -sin(_ToRadians(angle)), cos(_ToRadians(angle))
26.                    },
27.             M_2[]= {
28.                        0.0,  0.0,
29.                        1.5, -.75,
30.                        1.0,  0.0,
31.                        1.5,  .75
32.                    },
33.            M_3[M_2.Size()];

配列にインデックスがなくなったことに注意してください。行列構造は、コードに示されているように作成されます。つまり、行は行、列は列として扱われます。ただし、M_3などの動的配列には注意が必要です。これらの行列の要素にアクセスする際に実行時エラーを回避するためには、割り当てられた長さを正しく定義することが重要です。

これが最初の部分です。この後、MatrixA_x_MatrixBプロシージャでは、計算の実行方法が理解できなくなります。また、42行目のループ（前のトピックのコードを参照）では、データを正しくデコードできなくなります。

まず、MatrixA_x_MatrixB手順で実行された計算を修正し、次にプロットを修正します。ただし、続行する前に、行列M_1は対称で正方形であるため、実質的に変更されていないことに留意してください。これは、行と列の両方で読み取ることができるケースの1つです。

コードの大部分が変更されるため、新しいコードを見てみましょう。これにより、全体の動作が説明しやすくなると思います。

09. //+------------------------------------------------------------------+
10. #define _ToRadians(A) (A * (M_PI / 180.0))
11. //+------------------------------------------------------------------+
12. void MatrixA_x_MatrixB(const double &A[], const ushort Rows, const double &B[], double &R[])
13. {
14.     uint Lines = (uint)(A.Size() / Rows);
15. 
16.     for (uint cbl = 0; cbl < B.Size(); cbl += Rows)
17.         for (uint car = 0; car < Rows; car++)
18.         {
19.             R[car + cbl] = 0;
20.             for (uint cal = 0; cal < Lines; cal++)
21.                 R[car + cbl] += (A[(cal * Rows) + car] * B[cal + cbl]);
22.         }
23. }
24. //+------------------------------------------------------------------+
25. void Plot(const int x, const int y, const double &A[])
26. {
27.     int dx[], dy[];
28. 
29.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
30.     {
31.         ArrayResize(dx, c0 + 1, A.Size());
32.         ArrayResize(dy, c0 + 1, A.Size());
33.         dx[c0] = x + (int)(A[c1++]);
34.         dy[c0] = y + (int)(A[c1++]);
35.     }
36. 
37.     canvas.FillPolygon(dx, dy, ColorToARGB(clrPurple, 255));
38.     canvas.FillCircle(x, y, 5, ColorToARGB(clrRed, 255));
39. 
40.     ArrayFree(dx);
41.     ArrayFree(dy);
42. }
43. //+------------------------------------------------------------------+
44. void Arrow(const int x, const int y, const ushort angle, const uchar size = 100)
45. {
46.     double  M_1[]={
47.                      cos(_ToRadians(angle)), sin(_ToRadians(angle)),
48.                      -sin(_ToRadians(angle)), cos(_ToRadians(angle))
49.                   },
50.             M_2[]={
51.                      0.0,  0.0,
52.                      1.5, -.75,
53.                      1.0,  0.0,
54.                      1.5,  .75
55.                   },
56.            M_3[M_2.Size()];
57.     
58.     MatrixA_x_MatrixB(M_1, 2, M_2, M_3);
59.     ZeroMemory(M_1);
60.     M_1[0] = M_1[3] = size;
61.     MatrixA_x_MatrixB(M_1, 2, M_3, M_2);
62.     Plot(x, y, M_2);
63. }
64. //+------------------------------------------------------------------+

今ではすべてがずっと複雑になっているように思えるかもしれません。このような混乱は本当に必要なのでしょうか。落ち着いてください。親愛なる読者の皆さん。このコードは複雑でも混乱でもありません。実際には非常にシンプルで明確です。さらに、非常に柔軟性があります。その理由を説明しましょう。

このフラグメントでは、2つの行列の乗算が正しくおこなわれています。この場合、行内列モデルを実装し、乗算の結果として新しい行を取得しました。21行目で正確に乗算がおこなわれています。12行目で実行される手順は非常に複雑に思えるかもしれませんが、実際にはそうではありません。これらの変数は、配列内の特定のインデックスに正しくアクセスできるように存在しています。

1つの行列の行数が他の行列の列数と等しいことを確認するテストがないため、この手順を使用する場合は、実行時エラーを回避するために注意が必要です。

行列Aは列に整理され、行列Bは行に整理され、その結果が行に整理された行列Rに格納されます。これは58行目と61行目で発生します。まず、58行目を見てみましょう。渡される最初の行列は列行列M_1です。2番目の行列として、動的で行に整理された行列M_2を渡します。この順序を58行目で変更すると、計算値にエラーが発生します。2×3が3×2と異なるのは奇妙に思えるかもしれませんが、行列に関しては因子の順序が結果に影響します。ただし、これは前に行われたことと似ています。もちろん、呼び出しの2番目の引数は、最初の行列の列数を指定します。ここでの目標は教育的なものであり、行列B（この場合はM_2）を行列A（M_1）で乗算できるかどうかを確認しません。構造は変更せず、おそらく行列M_2の行数を増やすだけで、MatrixA_x_MatrixBの因数分解には影響しないと想定しています。

59行目と60行目については、前回の記事で既に説明しました。また、61行目でおこなわれることは58行目でおこなわれることと同じであるため、説明はすでに行われたと仮定できます。ただし、62行目には25行目のプロシージャを呼び出す新しい呼び出しがあります。25行目は、他のオブジェクトやイメージを画面に直接プロットするために使用できます。このプロシージャに行型行列を渡すだけで済みます。各行は、描画する画像の頂点を表します。行列内のポイントは2次元画面にプロットされるため、最初の列がX、2番目の列がYの順序でなければなりません。したがって、3Dで何かを描画する場合でも、Z次元の頂点がXY平面に投影されるように、行列内で何らかの計算を行う必要があります。物事を分離したり、行列のサイズを気にする必要はありません。Plotメソッドがこれをおこないます。27行目で2つの動的配列を宣言していることに注意してください。29行目では、多くの人が慣れているループの書き方とは異なる興味深いforループを作成します。このループには2つの変数があります。1つはループによって制御され、もう1つはコード内にあります。変数c0は、dxとdyのインデックスを正しくインスタンス化し、必要に応じてさらにメモリを割り当てようとするループによって管理されます。これは31行目と32行目でおこなわれます。これは非効率的に思えるかもしれませんが、MQL5のドキュメントを見ると、まったくそうではないことがわかります。

一方、変数c1はコード内で管理されます。これを理解するために、33行目と34行目でc1に何が起こるかを見てみましょう。各反復で1ずつ増加します。ただし、forループを終了するタイミングを決定するのはc1です。ループの終了条件については、29行目をご覧ください。

ここでは、配列または行列Aが正しく構成されているかどうかをチェックしません。1行に2つの列がない場合、このforループのどこかの時点で、範囲外の位置にアクセスしようとしたことを示す実行時エラーが生成されます。したがって、行列Aを作成するときは注意が必要です。

最後に、37行目を使用してCCanvasクラスのメソッドを呼び出します。これは、チャートに行列の形状をプロットするためにおこなわれます。38行目は、プロットを開始するポイントの位置を示しています。すべてがうまくいけば、以下の画像が表示されます。

そしてもちろん、40行目と41行目では、割り当てられたメモリをオペレーティングシステムに返し、使用しなくなったリソースを解放します。

最終的な検討事項

過去2回の記事では、多くの人が難しいと感じる行列の因数分解について取り上げました。ここで紹介した内容は、計算における行列の使用に関するすべての側面や利点を網羅しているわけではありません。しかし、行列を計算する方法を理解することの重要性を強調したいと思います。ゲームやベクター画像エディターなどの3Dプログラムでは、このタイプの因数分解が利用されています。また、一見単純なプログラム（例えばラスター画像処理プログラム）でも、システムパフォーマンスを最適化するために行列計算が重要な役割を果たしています。

これらの2つの記事では、できるだけ簡単に理解できるように説明することを心がけました。多くのプログラミング初心者が特定の知識を学ぶ必要を無視していることに気づいたからです。しばしば、彼らは舞台裏で何が起こっているかを理解せずに、ライブラリやその他の高度なソフトウェアを使用しています。

ここでは、プロセスをできるだけ単純化しました。2つの行列を乗算するという1つの操作に焦点を当て、その単純さを示しました。また、MatrixA_x_MatrixBプロシージャで行われる作業をGPUではなくCPUを使用しておこなう方法に焦点を当てました。ただし、一般的には行列分解はCPUではなくGPUで実行され、正しいプログラミングにはOpenCLが使用されます。

ある意味で、行列計算の可能性は一部の人々が考えているよりもはるかに広いことを示すことができたと思います。記事で紹介した資料をじっくりと読み解いていただき、行列因数分解が基礎となるさまざまなトピックについての理解を深めていただければ幸いです。

最後に、2つの行列の乗算は特定の問題を解決するためにおこなわれるものであり、これは本や学校で伝統的に教えられている方法とは異なります。この因数分解モデルは一般的には使えないため、注意が必要です。このモデルは、オブジェクトを回転させるという特定の問題を解決することにのみ適しています。