MetaTrader 5 / 例
English Русский Español Deutsch Português
preview
行列分解：基本

行列分解：基本

MetaTrader 5 — 例 | 9 9月 2024, 10:38
63 0
Daniel Jose
Daniel Jose

はじめに

皆さん、教育的な内容の私の新しい記事へようこそ。

今回は行列の計算についてお話します。読者の皆さん、内容が純粋に数学的で複雑すぎるだろうと思ってこの記事を読むのをやめないでください。多くの人が考えていることに反し、優れたプログラマーは自分だけが理解できる巨大なプログラムを書くわけでも、流行のプログラミング言語を使ってコードを書くわけでもありません。本物の優秀なプログラマーは、コンピューターとは、どのように計算を実行すべきかを指示できる計算機に過ぎないことを理解しています。具体的に何を作るかは問題ではありません。数学的なコードを含まないシンプルなテキストエディタでも構いません。しかし、これは単なる幻想に過ぎません。実際には、テキストエディタでさえ、そのコードにはかなりの量の数学が含まれています。

基本的にプログラミングでは、分解（お好みなら「計算」ということもできます）をおこなうには2つの方法があります。第一の方法は、スカラー形式で計算することです。つまり、言語が提供する関数を使って、以下のように数式を書くのです。


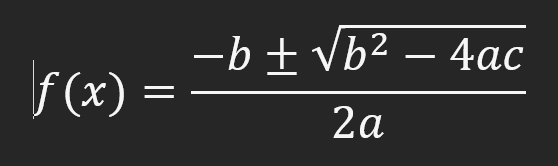
この誰でもわかる公式を使えば、二次関数の根を計算することができます。どのプログラミング言語でも、その言語で利用可能な関数やリソースを使用して簡単に書くことができます。しかし、計算をおこなうには別の方法があります。行列です。一部の人は好んでベクトルと呼びますが、この記事では、物事を表すのに行列を使うので、「行列」と呼ぶことにします。このタイプの分解は次のようになります。


プログラミングを始めたばかりの愛好家の中には、これをコードでどう書けばいいのかわからない人もいます。結局、同じ結果を得るために行列表記をスカラー表記に変換してしまうのです。

問題は、それが正しいか正しくないかではありません。得られた結果が正しければ、さほど問題ではありません。この場合、この行列は何かがある点を中心に回転することを示しています。この記事では、読者の皆さんに、MQL5やその他の言語を使って、この行列形式をスカラー形式に変換することなく、コードに直接書き込む方法を紹介したいと思います。これが難しいと思っている人は多いです。実際、すべては見かけよりずっとシンプルです。では、この記事に従って、その方法を学んでください。


スカラー形式の代わりに行列を使う理由

コードの書き方を見る前に、分解を実装するためにどのような方法を選べばよいかを考えてみましょう。

プログラミング言語に関する情報を検索すれば、スカラー形式のコードの書き方に行き当たるのは明らかです。その理由は、行列形式を使用してコードを書くのは少し分かりにくいからです。これを理解するために、上に示した行列や他の行列をコード行として書いてみましょう。何かぎこちないのがわかるでしょう。コードは奇妙に見えるし、あまり意味がありません。スカラー形式であれば、コードはより理解しやすくなります。このため、分解のコードを行列形式で書いている人を見かけることはありません。

しかし、いくつかの分解は、スカラー等価物よりも行列形式で書く方がはるかに簡単です。例えば、多次元配列として簡単に表現できる大量のデータを処理する必要がある場合です。これを理解するために、まずベクター画像について考えてみましょう。ピクセル単位の画面を描く代わりに、ベクターを使用します。これによって、回転、拡大縮小、剪断変形、その他の操作を、行列を使った極めて簡単な方法でおこなうことができます。言い換えれば、行列を使う計算コードを書くということです。スカラー形式でも同じ変換が可能ですが、行列を使った方がはるかにシンプルになります。

ベクターグラフィックスが十分に複雑に思えないなら、3Dオブジェクトについて考えてみましょう。行列の分解がなぜ面白いのか、お分かりいただけたでしょうか。

3Dオブジェクトでは、行列を使った変換の方がはるかに簡単です。スカラー方式で同じことをするのは非常に難しく、時間がかかります。それは可能ですが、あまりに難しいのでやる気をなくしてしまいます。冒頭で述べたような公式を使って、3Dオブジェクトの正投影をおこなう必要性について考えてみましょう。このようなことを実装するのは悪夢です。しかし、行列を使用するコードを作成する場合、3Dオブジェクトの複雑さは重要ではありません。

これはビデオカードや3Dモデリングプログラムで使われているものです。実際、あなたが気づかないだけで、計算には行列が使われています。では、分解のコードを書くときに、ある形式を使うべきときと、別の形式を使うべきときがあるのでしょうか。これは経験と知識によります。1つの方法を強制するような厳格なルールはありません。しかし、可能な限り速く、シンプルで効率的にするために、両方の方法をプログラムする方法を知っておくことは重要です。

スカラー形式は広く使われており、文字通りプログラムされているので、ここでは行列形式のコードの書き方だけに焦点を当てます。よりシンプルに理解しやすくするため、具体的なトピックに分けて説明します。さっそく始めましょう。


スカラー手法

ここでは、非常にシンプルで明確なことがわかるでしょう。この記事はあくまでも教育目的であることをお忘れなく。特定の何かをプログラミングするためのものではありません。

まず、MQL5で小さなプログラムを作ってみましょう。これから説明することは、他の言語にも応用できます。それはすべて、あなたがどれだけ言葉を知っているかにかかっています。以下に示す非常にシンプルなコードから始めましょう。

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. #property indicator_chart_window
04. #property indicator_plots 0
05. //+------------------------------------------------------------------+
06. #include <Canvas\Canvas.mqh>
07. //+------------------------------------------------------------------+
08. CCanvas canvas;
09. //+------------------------------------------------------------------+
10. int OnInit()
11. {
12.     
13.     int px, py;
14.     
15.     px = (int)ChartGetInteger(0, CHART_WIDTH_IN_PIXELS, 0);
16.     py = (int)ChartGetInteger(0, CHART_HEIGHT_IN_PIXELS, 0);
17. 
18.     canvas.CreateBitmapLabel("BL", 0, 0, px, py, COLOR_FORMAT_ARGB_NORMALIZE);
19.     canvas.Erase(ColorToARGB(clrWhite, 255));
20.         
21.     canvas.Update(true);
22.     
23.     return INIT_SUCCEEDED;
24. }
25. //+------------------------------------------------------------------+
26. int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[])
27. {
28.     return rates_total;
29. }
30. //+------------------------------------------------------------------+
31. void OnDeinit(const int reason)
32. {
33.     canvas.Destroy();
34. }
35. //+------------------------------------------------------------------+

見ての通り、このコードは指標です。他のものを使用することもできますが、この指標はいくつかの理由でより興味深いものになります。この指標を使用していくつかの機能を実装でき、MetaTrader 5からの特定の呼び出しを傍受できるからです。

このコードは非常にシンプルで、ほとんど何もしません。単にチャートウィンドウを白や、使いたい色に変えるだけです。生成されるコードをできるだけ単純化するために、6行目ではMQL5標準ライブラリを使用していることに注意してください。この行で、コンパイラにCanvas.mqhヘッダーファイルを追加するように指示します。Canvas.mqhヘッダーファイルは、MetaTrader 5をインストールするときにデフォルトで作成されます。これで、この記事で取り上げる内容を大幅に簡略化できます。そして、8行目でグローバル変数を宣言して、CCanvasクラスにアクセスできるようにしています。クラスについて話すのだから、特定の方法で使わなければなりません。1つ重要なことがあります。私は通常、クラスをポインタとして使うのが好きですが、なぜこんなことをするのかと疑問に思う人も多いでしょう。できるだけ単純化するために、誰もが普通に使うように、つまり、何かを参照するための単純な変数としてクラスを使うことにします。

そこで、15行目と16行目では、指標を配置するチャートウィンドウのサイズを固定しています。ウィンドウは作りません。これは3行目に示されています。指標は何も追跡しないので、コンパイラの警告メッセージを避けることができます。これには4行目を使用します。この指標をサブウィンドウに適用すると、15行目と16行目に表示される情報は異なります。

18行目では、Canvasクラスに、何かを描きたい領域を作りたいことを伝えています。このエリアは、左上隅（2つ目と3つ目のパラメータ）から左下隅（次の2つのパラメータ）まで続いています。最初のパラメータは、CCanvasクラスによって生成されたオブジェクトの名前です。最後のパラメータは、この領域でどのような組み合わせで描画するかを指定します。これらの描画モードについてのより詳細な情報は、ドキュメントを参照してください。アルファを色として持つモデルを使用します。つまり、選択された領域で描くものすべてに透明度を作り出すことができます。

次のステップは、その部分をきれいにすることです。これは19行目でおこなわれ、その直後の21行目でメモリ内の情報を画面に表示することが指示されています。CCanvasを使って領域に配置した情報は、作成と同時に画面に表示されるわけではないことを理解しておくことが重要です。すべての描画はまずメモリ上でおこなわれます。これらは21行目が実行されるまで画面に表示されません。とてもシンプルです。さて、基本を押さえたところで、画面にプロットするものを見てみましょう。これは以下のコードに示されています。

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. #property indicator_chart_window
04. #property indicator_plots 0
05. //+------------------------------------------------------------------+
06. #include <Canvas\Canvas.mqh>
07. //+------------------------------------------------------------------+
08. CCanvas canvas;
09. //+------------------------------------------------------------------+
10. #define _ToRadians(A) (A * (M_PI / 180.0))
11. //+------------------------------------------------------------------+
12. void Arrow(const int x, const int y, const ushort angle)
13. {
14.     int ax[] = {0, 150, 100, 150},
15.         ay[] = {0, -75,   0,  75};
16.     int dx[ax.Size()], dy[ax.Size()];
17.     
18.     for (int c = 0; c < (int)ax.Size(); c++)
19.     {
20.         dx[c] = (int)((ax[c] * cos(_ToRadians(angle))) + (ay[c] * sin(_ToRadians(angle)))) + x;
21.         dy[c] = (int)((ax[c] * (-sin(_ToRadians(angle)))) + (ay[c] * cos(_ToRadians(angle)))) + y;
22.     }
23. 
24.     canvas.FillPolygon(dx, dy, ColorToARGB(clrBlue, 255));
25.     canvas.FillCircle(x, y, 5, ColorToARGB(clrRed, 255));
26. }
27. //+------------------------------------------------------------------+
28. int OnInit()
29. {    
30.     int px, py;
31.     
32.     px = (int)ChartGetInteger(0, CHART_WIDTH_IN_PIXELS, 0);
33.     py = (int)ChartGetInteger(0, CHART_HEIGHT_IN_PIXELS, 0);
34. 
35.     canvas.CreateBitmapLabel("BL", 0, 0, px, py, COLOR_FORMAT_ARGB_NORMALIZE);
36.     canvas.Erase(ColorToARGB(clrWhite, 255));
37.         
38.     Arrow(px / 2, py / 2, 60);
39. 
40.     canvas.Update(true);
41.     
42.     return INIT_SUCCEEDED;
43. }
44. //+------------------------------------------------------------------+
45. int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[])
46. {
47.     return rates_total;
48. }
49. //+------------------------------------------------------------------+
50. void OnDeinit(const int reason)
51. {
52.     canvas.Destroy();
53. }
54. //+------------------------------------------------------------------+

ここでは、記事の冒頭で示された公式をスカラー変換していることに注意してください。行列表記法を使用します。つまり、オブジェクトを回転させるのです。しかし、このオブジェクトは何なのでしょうか。これを理解するために、次の画像をご覧ください。これは、MetaTrader 5でコードを実行したときに表示されるものです。


回転させるオブジェクトは矢印です。しかし、このコードを見て、矢印がどこでプロットされているかわかるでしょうか。ARROW関数を呼び出している38行目をご覧ください。ARROWは12行目にあります。明らかに、矢印は12行目の関数内のどこかにあるはずです。どこでしょうか。矢印は14行目と15行目で定義されています。この矢印をプロットするために2つの配列を持っていることに注意してください。ここでは、それを非常にシンプルな方法で描いています。ここからが最も興味深いところです。

この矢印は絶対的に定義されています。つまり、現実世界で表現されるようにプロットするのですが、仮想的に表現することもできます。整数値の代わりに浮動小数点値を使うこともできます。したがって、矢印をプロットした値に任意のスカラーを掛けることで、その大きさを決定することができますが、複雑にしないために、ここではこれをおこないませんでした。読者の皆さんが行列分解の実装方法を理解できるように、できるだけシンプルにします。

16行目には多くの人を混乱させるような記述があります。しかし、そのように書かれている理由は簡単です。オブジェクトの描画に何点使うか事前にわからないし、24行目で描画するために中間配列が必要なので、アプリケーションにメモリを確保するように指示する必要があります。16行目のフォームを使って、コンパイラに、点を描画するのに必要なだけの領域を確保するように指示します。つまり、使用するのは動的配列ですが、静的に割り当てられています。もし、このようなコードの書き方をしなければ、Arrow関数と同じコードを以下のコードのように組み立てて作らなければなりません。

11. //+------------------------------------------------------------------+
12. void Arrow(const int x, const int y, const ushort angle)
13. {
14.     int ax[] = {0, 150, 100, 150},
15.         ay[] = {0, -75,   0,  75};
16.     int dx[], dy[];
17.     
18.     ArrayResize(dx, ax.Size());
19.     ArrayResize(dy, ax.Size());
20.     
21.     for (int c = 0; c < (int)ax.Size(); c++)
22.     {
23.         dx[c] = (int)((ax[c] * cos(_ToRadians(angle))) + (ay[c] * sin(_ToRadians(angle)))) + x;
24.         dy[c] = (int)((ax[c] * (-sin(_ToRadians(angle)))) + (ay[c] * cos(_ToRadians(angle)))) + y;
25.     }
26. 
27.     canvas.FillPolygon(dx, dy, ColorToARGB(clrBlue, 255));
28.     canvas.FillCircle(x, y, 5, ColorToARGB(clrRed, 255));
29. 
30.     ArrayFree(dx);
31.     ArrayFree(dy);
32. }
33. //+------------------------------------------------------------------+

16行目で、動的配列の表示をしていることに注目してください。このタイプの配列は、実行中に使用されるスペースを定義します。以下の変更が必要です。コードの18行目と19行目では、プログラムが実行中に異常終了しないように、必要なスペースを確保しなければなりません。また、このコードでは、30行目と31行目で割り当てたメモリをオペレーティングシステムに返さなければなりません。これは良いプログラミング方法だと考えられています。多くのプログラマーに割り当てられたリソースを返さない傾向がありますが、これではアプリケーションがリソースを消費してしまいます。しかし、スニペットとメインコードの間に見られる小さな違い以外は、すべて同じように機能します。

メインコードに戻りましょう。18行目のループは、回転させたい形状の一部であるすべての点を通過します。

では、面白いものに注目してください。形状を回転させ、ある場所に移動させます。具体的には、X点とY点（この場合は画面の中心）に移動させます。38行目では、位置と回転角度（60度）を定義しています。

すべての三角関数はデフォルトで度ではなくラジアン単位の値を使うので、度をラジアンに変換する必要があります。これはまさに10行目の定義でおこなわれていることです。この方法なら、多くの場合非常に混乱を招く可能性があるラジアンで値を表すよりも、図形をどの程度回転させる必要があるかを示す方が自然になります。

そこで、配列の各点について、以下の式を適用します。


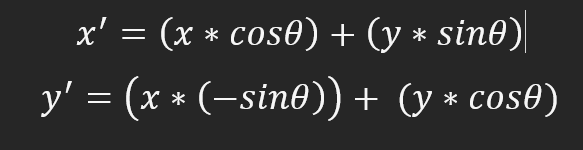
画像は反時計回りに回転し、0度が時計の9時の位置に対応するようになります。わかりやすく言うと、90度は6時間、180度は3時間、270度は12時間です。回転は反時計回りであることを忘れないでください。この動作を変更するには、計算方法を変更する必要があります。複雑なことは何もありません。すべてがシンプルです。時計回りの回転を評価するには、計算式を以下のように変更する必要があります。


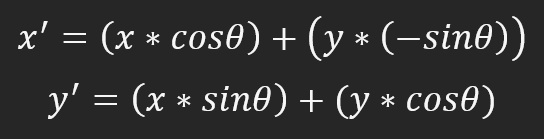
すべてが極めてシンプルです。この場合、3時方向は0度、6時方向は90度、9時方向は180度、12時方向は270度の角度となります。角度の値をゼロから180度に変えただけのように見えますが、それ以上のことをしています。回転方向が反時計回りから時計回りに変わっています。

しかし、私が見せたかったのはそういうことではありません。これはただの興味深い点です。私が示したいことを本当に説明するために、まず、誰もが通常使う形ですべてを提示しましょう。多くの場合、その方がシンプルで簡単だからです。だたし、これはどんな状況にも簡単に適応できるものではありません。

この記事の主な焦点はこのことではなく、モデリング行列の計算にあるので、ここではこのことについて詳しく触れないことにします。プログラマーが一般的にどのようにこれらの問題を解決するのかを見てみましょう。最も簡単な方法は、興味のあるものを仮想単位に変換することです。まずすべての計算をおこない、その結果をグラフィック単位に変換します。仮想単位を使用して何かを作成する場合、整数ではなく浮動値（通常はdouble型）を使用します。つまり、前と同じコードは次のようになります。

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. #property indicator_chart_window
04. #property indicator_plots 0
05. //+------------------------------------------------------------------+
06. #include <Canvas\Canvas.mqh>
07. //+------------------------------------------------------------------+
08. CCanvas canvas;
09. //+------------------------------------------------------------------+
10. #define _ToRadians(A) (A * (M_PI / 180.0))
11. //+------------------------------------------------------------------+
12. void Arrow(const int x, const int y, const ushort angle, const uchar size = 100)
13. {
14.     double ax[] = {0.0,  1.5, 1.0, 1.5},
15.            ay[] = {0.0, -.75, 0.0, .75};
16.     int dx[ax.Size()], dy[ax.Size()];
17.     
18.     for (int c = 0; c < (int)ax.Size(); c++)
19.     {
20.         ax[c] *= size;
21.         ay[c] *= size;
22.         dx[c] = (int) ((ax[c] * cos(_ToRadians(angle))) + (ay[c] * sin(_ToRadians(angle)))) + x;
23.         dy[c] = (int) ((ax[c] *(-sin(_ToRadians(angle)))) + (ay[c] * cos(_ToRadians(angle)))) + y;
24.     }
25. 
26.     canvas.FillPolygon(dx, dy, ColorToARGB(clrGreen, 255));
27.     canvas.FillCircle(x, y, 5, ColorToARGB(clrRed, 255));
28. }
29. //+------------------------------------------------------------------+
30. int OnInit()
31. {    
32.     int px, py;
33.     
34.     px = (int)ChartGetInteger(0, CHART_WIDTH_IN_PIXELS, 0);
35.     py = (int)ChartGetInteger(0, CHART_HEIGHT_IN_PIXELS, 0);
36. 
37.     canvas.CreateBitmapLabel("BL", 0, 0, px, py, COLOR_FORMAT_ARGB_NORMALIZE);
38.     canvas.Erase(ColorToARGB(clrWhite, 255));
39.         
40.     Arrow(px / 2, py / 2, 60);
41. 
42.     canvas.Update(true);
43.     
44.     return INIT_SUCCEEDED;
45. }
46. //+------------------------------------------------------------------+
47. int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[])
48. {
49.     return rates_total;
50. }
51. //+------------------------------------------------------------------+
52. void OnDeinit(const int reason)
53. {
54.     canvas.Destroy();
55. }
56. //+------------------------------------------------------------------+

作成したオブジェクトを拡大できるようになった以外は、ほとんど何も変わっていません。これは20行目と21行目でおこなわれます。オブジェクトは14行目と15行目で作成されます。すべてのコードに変更はありません。しかし、この単純な変更は、アプリケーションを他のシナリオに移植するのに役立ちます。例えば、ユーザーがチャートのサイズを変更した場合、12行目のsizeパラメータだけを変更することで、オブジェクトを一定の比率に保つことができます。

しかし、これが行列を扱う上でどのように役立つのか、私にはまだ理解できません。こんなふうにできるのなら、なぜ複雑にするのでしょうか。さて、行列を使ってこのようなことをするのが本当に難しいかどうか見てみましょう。そのために新しいトピックを始めます。


行列分解の使用

この記事の目的は読者を教育することなので、できるだけシンプルに物事を進めたいと思います。したがって、私たちが必要とする材料、つまりこの特殊なケースにおける行列の乗算を実証するために必要なものだけを実装します。しかし、読者の皆さんは、これだけでも行列とスカラーの乗算を実行するのに十分であることがおわかりでしょう。行列分解を実装する際に多くの人が直面する最大の課題は、スカラーの分解と異なり、因子の順序が結果に影響を与えるため、行列の場合はその点に注意が必要だということです。前のトピックと同じコードを行列を使うとどうなるでしょうか。以下は、行列を使って分解をおこなうコードです。
01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. #property indicator_chart_window
04. #property indicator_plots 0
05. //+------------------------------------------------------------------+
06. #include <Canvas\Canvas.mqh>
07. //+------------------------------------------------------------------+
08. CCanvas canvas;
09. //+------------------------------------------------------------------+
10. #define _ToRadians(A) (A * (M_PI / 180.0))
11. //+------------------------------------------------------------------+
12. void MatrixA_x_MatrixB(const double &A[][], const double &B[][], double &R[][], const int nDim)
13. {
14.     for (int c = 0, size = (int)(B.Size() / nDim); c < size; c++)
15.     {
16.         R[c][0] = (A[0][0] * B[c][0]) + (A[0][1] * B[c][1]);
17.         R[c][1] = (A[1][0] * B[c][0]) + (A[1][1] * B[c][1]);
18.     }
19. }
20. //+------------------------------------------------------------------+
21. void Arrow(const int x, const int y, const ushort angle, const uchar size = 100)
22. {
23.     double M_1[2][2]{
24.                         cos(_ToRadians(angle)), sin(_ToRadians(angle)),
25.                         -sin(_ToRadians(angle)), cos(_ToRadians(angle))
26.                     },
27.            M_2[][2] {
28.                         0.0,  0.0,
29.                         1.5, -.75,
30.                         1.0,  0.0,
31.                         1.5,  .75
32.                     },
33.            M_3[M_2.Size() / 2][2];
34. 
35.     int dx[M_2.Size() / 2], dy[M_2.Size() / 2];
36.     
37.     MatrixA_x_MatrixB(M_1, M_2, M_3, 2);
38.     ZeroMemory(M_1);
39.     M_1[0][0] = M_1[1][1] = size;
40.     MatrixA_x_MatrixB(M_1, M_3, M_2, 2);
41. 
42.     for (int c = 0; c < (int)M_2.Size() / 2; c++)
43.     {
44.         dx[c] = x + (int) M_2[c][0];
45.         dy[c] = y + (int) M_2[c][1];
46.     }
47. 
48.     canvas.FillPolygon(dx, dy, ColorToARGB(clrPurple, 255));
49.     canvas.FillCircle(x, y, 5, ColorToARGB(clrRed, 255));
50. }
51. //+------------------------------------------------------------------+
52. int OnInit()
53. {    
54.     int px, py;
55.     
56.     px = (int)ChartGetInteger(0, CHART_WIDTH_IN_PIXELS, 0);
57.     py = (int)ChartGetInteger(0, CHART_HEIGHT_IN_PIXELS, 0);
58. 
59.     canvas.CreateBitmapLabel("BL", 0, 0, px, py, COLOR_FORMAT_ARGB_NORMALIZE);
60.     canvas.Erase(ColorToARGB(clrWhite, 255));
61.         
62.     Arrow(px / 2, py / 2, 160);
63. 
64.     canvas.Update(true);
65.     
66.     return INIT_SUCCEEDED;
67. }
68. //+------------------------------------------------------------------+
69. int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[])
70. {
71.     return rates_total;
72. }
73. //+------------------------------------------------------------------+
74. void OnDeinit(const int reason)
75. {
76.     canvas.Destroy();
77. }
78. //+------------------------------------------------------------------+

読者の皆さんが理解できるように、特別な修正を加えることなく、できるだけシンプルなコードにしました。通常、行列計算を使った分解を書くときは少し違ったやり方をするのですが、これについては細かい説明が必要なので、今後の記事で説明することにしましょう。この詳細をさらに説明しなければなりません。簡単なことのように思えるかもしれませんが、きちんと対処しなければ、底なし沼にはまることになります。しかし、このクレイジーなコードはいったい何をするのでしょうか。するのは前のトピックと同じことですが、ここでは行列の乗算を使って同じ計算をおこないます。このコードは非常に複雑に見えるかもしれませんが、そうではなく、前のコードよりずっとシンプルなのです。ある行列に別の行列を掛け合わせる方法を理解すれば、すべてがずっと簡単になります。ただし、乗算は期待通りにはいきません。言い換えれば、コードを修正する必要がある場合、いくつかのことをさせてくれないのです。しかし、すでに言ったように、このバージョンはデモンストレーションのためだけのものです。正しい選択肢は次回の記事で紹介します。しかし、分解は少々奇妙な方法でおこなわれたとしても、期待通りの結果をもたらします。

これを使う前に、この詳細を知っておく必要があります。しかし、もしあなたがすでに行列分解の仕組みをある程度理解していれば、あとはずっと理解しやすくなるでしょう。12行目は、行列の分解を実行するコードを実装していることに注意してください。簡単なものです。基本的には、最初の行列に2番目の行列を掛け、その結果を3番目の行列に入れます。乗算はある行列の列と別の行列の行に対しておこなわれるので、分解はかなり簡単です。ここでは従う必要のあるルールがいくつかあります。例えば、一方の行列の行数と他方の行列の列数は等しくなければなりません。これは行列に関する基本的な数学なので、どのように進めればいいのか、なぜそのようにする必要があるのかがわからない場合は、まずそれを理解するようにしてください。行列Aには列を置き、行列Bには行を置きます。ここでの場合、以下のようなものが得られます。

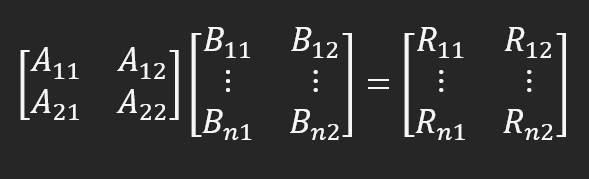
一見、とても分かりにくいように見えるかもしれませんが、とてもシンプルなことです。要素Aの行列に要素Bの行列を掛け合わせ、その結果、要素Rの行列が得られます。
R11 = (A11 x B11) + (A12 x B12);  R12 = (A21 x B11) + (A22 x B12) R21 = (A11 x B21) + (A12 x B22);  R22 = (A21 x B21) + (A22 x B22) R31 = (A11 x B31) + (A12 x B32);  R32 = (A21 x B31) + (A22 x B32)
などなど。これは、計算がスカラーであった場合におこなわれることです。これはまさに12行目のプロシージャがおこなっていることです。計算の組み立てにもっと自由度を持たせることが重要だと思います。これを理解するために、21行目の関数を見てみましょう。ここでは5つの行列が定義されています。もっと少なくてもいいです。最初に整理しておきましょう。将来的には、もっと直感的で理解しやすい方法でこれをモデル化する方法を検討するかもしれませんが、このモデルでもまだ理解するのはかなり簡単です。23行目と33行目の間に行列を描き、計算に使用します。さて、35行目で、画面上の矢印を表現するために使うものを宣言します。37行目から40行目にかけて、必要な計算をおこないます。これからやることはとても面白いです。実用的な観点からも、分解の自由という観点からもです。37行目では、まず行列M_1に行列M_2を掛け、その結果を行列M_3に入れます。この乗算は何を意味するのでしょうか。画像が回転します。しかし、M_2行列にあるスケールはまだモデルで使用されているため、まだ画面に表示することはできません。画像を正しい縮尺で表現するには、もう1つ計算が必要です。しかし、まず38行目で行列M_1の内容をクリアし、その直後の39行目で画像のスケールを変更する方法を指定しています。今のところいくつかの新しいオプションがありますが、スケーリングにのみ焦点を当てるつもりです。40行目では、すでに回転されているオブジェクトデータに、使用したいスケールをすでに含む新しい行列を掛け合わせます。これを以下に示します。

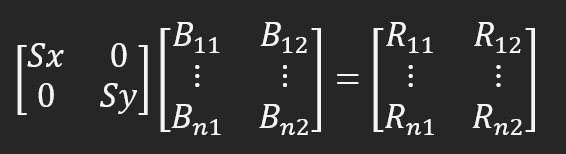
ここでSxはX軸に沿った新しい寸法、SyはY軸に沿った新しい寸法です。両方の値をSizeに設定しているので、オブジェクトをズームしているかのような変化が起こります。これが、もっと多くのことができると言った理由です。FillPolygon関数はこの行列構造を扱う方法を知らないので、FillPolygonが矢印をプロットできるようにデータを分割する必要があります。48行目にforループがあり、結果は前のトピックと同じです。


最終的な検討事項

この記事では、行列計算のかなり簡単な方法を紹介しました。私は興味深いものを提示すると同時に、この計算がどのようにおこなわれるのかを最もシンプルな方法で説明する方法を見つけようとしましたが、本稿で検討した行列モデルは、すべての可能なタイプの分解を実行するのに最適なものではありません。そこで近々、行列を表現するためのより適切なモデルについての新しい記事を発表する予定です。また、この新しいデータ分解法を使えるように説明します。では、次回お会いしましょう。


MetaQuotes Ltdによりポルトガル語から翻訳されました。
元の記事: https://www.mql5.com/pt/articles/13646

添付されたファイル |
ZIPをダウンロード
App1.mq5 (1.87 KB)
App2.mq5 (1.97 KB)
App3.mq5 (2.62 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
リプレイシステムの開発（第4４回）：Chart Tradeプロジェクト（III） リプレイシステムの開発（第4４回）：Chart Tradeプロジェクト（III）
前回の記事では、OBJ_CHARTで使用するテンプレートデータの操作方法について解説しました。ただし、あの記事ではトピックの概要に焦点を当て、詳細な部分には触れていませんでした。これは、説明をよりシンプルにするために、非常に簡略化された手法を用いたからです。物事は一見シンプルに見えることが多いですが、実際にはそうではないケースもあり、全体を正確に理解するためには、まず最も基本的な部分をしっかり押さえる必要があります。
MQL5でのもみ合いレンジブレイクアウト戦略に基づくエキスパートアドバイザー(EA)の開発 MQL5でのもみ合いレンジブレイクアウト戦略に基づくエキスパートアドバイザー(EA)の開発
この記事では、もみ合い期間後の価格ブレイクアウトを活用したエキスパートアドバイザー(EA)の作成手順を説明します。トレーダーは、もみ合いレンジを特定し、ブレイクアウトレベルを設定することで、この戦略に基づいて取引判断を自動化できます。EAは、誤ったブレイクアウトを回避しつつ、明確なエントリポイントとエグジットポイントを提供することを目的としています。
DoEasy - サービス関数（第2回）：はらみ線パターン DoEasy - サービス関数（第2回）：はらみ線パターン
今回は、引き続きDoEasyライブラリの価格パターンを見ていきましょう。また、プライスアクションフォーメーションのはらみ線パターンクラスも作成します。
MQL5入門（第8回）：初心者のためのEA構築ガイド(II) MQL5入門（第8回）：初心者のためのEA構築ガイド(II)
この記事では、MQL5フォーラムでよく見られる初心者からの質問を取り上げ、実践的な解決策を紹介します。売買やローソク足の価格取得、取引限度額の設定、取引期間や利益/損失の閾値の管理といった基本的なタスクを自動売買で実行する方法を学びます。MQL5でのこれらの概念の理解と実装を強化するため、ステップごとのガイダンスも提供します。