MQL5の圏論（第4回）：スパン、実験、合成

はじめに

前回は、圏論が、積、余積、普遍性の概念によって、複雑なシステムでどのように活用できるかを見て、金融やアルゴリズム取引への応用例も紹介しました。ここでは、スパン、実験、合成について深く掘り下げていきます。これらの概念が、システムに関する推論をよりニュアンス豊かで柔軟なものにし、より洗練された取引戦略を開発するためにどのように活用されるかを見ていきます。金融市場の基本構造を圏論の観点から理解することで、トレーダーは金融商品の挙動について新たな洞察を得、より洗練されたポートフォリオを構築し、より効果的なリスク管理戦略を開発することができます。全体として、金融における圏論の適用は、金融市場に対する私たちの考え方に革命をもたらし、トレーダーがより多くの情報に基づいた意思決定をおこなえるようにする可能性を秘めています。

スパン、実験、合成

圏論において、スパン（英語）は、3つのオブジェクトとそれらの間の2つの射を関係づける構成です。具体的には、スパンとは、以下のような形の図です。

 

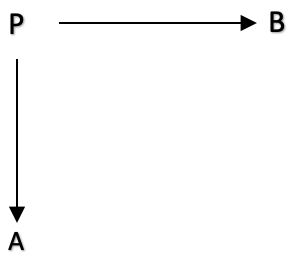
この非常に基本的な図は、下の1本の線でも表すことができます：

A<--- f --- P --- g --->B

ここで、A、B、Pは圏における始域であり、f:PからA、およびg::PからBは、圏における射です。射f:PからA、およびg::PからBをスパンの脚と呼びます。

スパンPは、A-B間の2つの異なる経路や視点を、一方はfを経由し、他方はgを経由して関連付ける方法と考えることができます。脚f、gはそれぞれA、Bでこれらのパスを接続し、2つのパスの比較や合成を可能にします。

まず、理論から説明し、MQL5での応用を考えてみましょう。

スパンは、圏内の2つの異なる射を比較する方法を提供するため、圏論において重要です。2つの射f:A → Bとg:A → Cの2つの射が与えられた場合、BからCへのスパンは、B ← A → Cの形の図です。ここで、2つの矢印は射fとgを表します。スパンは、圏論における限界と余極限の定義によく使われます。例えば、ある圏における図式の極限は、その図式上の普遍的な錐として定義することができます。錐とは、極限オブジェクトから、ある条件を満たす図式の各オブジェクトまでのスパンです。

スパンは、関係するオブジェクトが射のペアによって関連付けられる制限の一種である引き戻しの定義にも役立ちます。圏において2つの射f:A → Bとg:A → Cが与えられた場合、fとgの引き戻しは、オブジェクトPとともに、、f⊖p1=g⊖p2であり、Pはこの性質に関して普遍であるような2つの射p1:P → Bとp2:P→Cです。引き戻しは、代数幾何学、位相幾何学、コンピュータサイエンスなど、数学と科学の多くの分野で重要な役割を担っています。

圏論におけるもう1つの重要な概念は実験であり、これは2つの平行な射とその共領域を結ぶ第3の射からなる図です。実験とは、ある圏の物体を変形させる2つの異なる方法を比較する方法と考えることができます。例えば、2つの射f:A → Bとg:A → Cが与えられている場合、BからCへの実験とは、A→B⟶D←Cの形の図で、矢印はそれぞれ射f、g、hを表します。実験では、スパンと同様に極限や余極限を定義することができます。また、同じ終域を持つ2つの異なる射を識別するために使用できる余極限の一種である余等化子を定義するのにも有効です。

合成(は、2つ以上の射の合成から生じる、圏論の基本的な概念です。圏において2つの射f:A → Bとg:B→Cが与えられている場合、それらの合成は射g ∘ f:A → Cです。これは、fに続いてgを適用することで得られます。合成は結合的であり、任意の3つの射f、g、hに対して (h ∘ g) ∘ f = h ∘ (g ∘ f)であることを意味します。この性質は、一度に多くの射を合成することを可能にし、ある公理を満たすオブジェクトと射の集まりである圏という概念を定義するために使われます。

ここでは、圏論におけるスパン、実験、合成の金融や取引における即興的な10の応用例を紹介します。

1. スパンは、金融デリバティブの原資産と、そのペイオフを再現するために使用するヘッジ手段をモデル化することができます。スパンの普遍性は、デリバティブの価格を決定するのに役立ちます。
2. リスクを最小化しリターンを最大化する方法で異なる資産クラスを組み合わせることによる合成による効率的なポートフォリオ構築。これは、合成の普遍性を利用することで導き出すことができます。
3. スパンは、金融機関がさまざまな市場要因にさらされるリスクエクスポージャーをモデル化することができます。これは、金融機関の資産と関連する市場指数を結ぶスパンを構築することで実現できます。
4. 実験では、さまざまな市場条件下で、さまざまな取引アルゴリズムの性能をテストすることができます。これは、市場行動を模倣した実験を構築し、模擬データでアルゴリズムの性能を測定することでシミュレーションすることができます。
5. 金融システムの挙動を拡大したスケールでモデル化するには、始域の合成が役立ちます。例えば、SP500の様々なセクターが異なる長いサイクルでどのように相関しているかを見るための応用が可能です。
6. スパンは、よりシンプルな商品の組み合わせを使って、特定の金融商品の複製をモデル化することができます。これは、既存の金融商品との相関が少ないなど、望ましい性質を持つ新しい金融商品を設計する際に有効です。
7. 実験では、特定の戦略のパフォーマンスをコントロールグループと比較することで、取引戦略をテストすることができます。これは、もう一度、実験の普遍性を利用して実現することができます。
8. また、実験では、さまざまな市場のマイクロストラクチャー設計の効率性を検証することができます。これは、さまざまなタイプの市場参加者の行動をシミュレートする実験を構築し、その結果得られる市場の成果を測定することで実現することができます。
9. 合成は、金融機関の総合的なリスクエクスポージャーをモデル化することができます。これは、金融機関のさまざまなビジネスラインの合成を構築し、その相互依存性を分析することによっておこなうことができます。
10. スパンは、異なる財務データソース間の関係をモデル化することができます。異種のデータソースから有用な特徴を抽出することができる機械学習アルゴリズムを設計することができます。

この考え方の応用として、ある証券のロング取引ポジションの利益と、その証券の移動平均とATRという2つの変数の間に関係があるかどうかを調べるというスパンの「実験」を説明することができます。この「実験」は、頂点、2つの始域、それらの間の射を含む図として表現することができます。

例えば、移動平均の始域とATRの始域をそれぞれ表すA、Bという2つの始域を含む圏Cがあるとします。そしてこの圏には、ロングポジションの利益を表し、頂点として機能する始域Pも存在します。

続いて、ロングポジションフロートPを始域AおよびBの観測値にそれぞれ対応付ける、2つの射f:P -> Aとg:P -> Bを定義できます。これらの射は、観測値のロギングを表しています。

  この図式的表現によって、より抽象的で形式的な方法で実験を分析し、圏論の概念とツールを適用して推論することができます。

「実験」をおこなうために、現在のチャート銘柄、例えばEURUSDに0.1ロットの買い注文を開き、新しいバーごとに現在のフロート、MA、ATRを記録します。観測されたデータに基づいて、データ間に相関関係があるかどうかを確認し、ロングポジションの理想的なトレーリングストップシステムを考え出すのに利用することができます。ここで使用したMAとATRの指標は、読者がより適切と考えるものに簡単に置き換えることができます。これらはあくまで説明のために選んだものです。

 

3月1日にEURUSDの1時間足でこの実験をおこなった場合、これがデータの一部となります。

 

P:(フロート/プロフィット)	A:ATR	B:MA
-6.60000	0.00203	1.12138
-14.90000	0.00181	1.12136
-18.80000	0.00175	1.12140
-24.20000	0.00157	1.12125
-29.00000	0.00146	1.12100
-24.30000	0.00127	1.12078

 

 

2つの始域データセットA、Bのそれぞれとポジションの利益との遅行相関をおこなえば、それぞれの始域がポジションのネガティブドローダウンを予測できるかどうかを設定することができるのです。この情報は、ロングポジションの既存のストップロスを設定または移動する際に役立ちます。

 

これらのスパンがストップロスの定義に役立つもう一つの方法は、それぞれの形態fとgを介した末端領域AとBのそれぞれが、ロングポジションの理想的なストップロスがどの程度であるべきかの共積（和）を形成すると仮定することです。これらの射は、要するに入力を受けて出力を提供する関数です。この場合、各端末始域はその指標値を入力として提供し、各関数f、gは出力double値を提供することになります。

 

このdouble値を合計すると、余積に相当する、理想的なストップロス価格が得られます。射の出力（損切り価格）が射の指標入力と線形関係にあるとするならば、これらの式は暗黙の了解となります。

ここで、xa ⊆ Aで、ma and cは線形関係の傾きとy切片の係数です。同様に、B始域についても

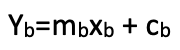
この仮説は、理想的な損切りデルタと指標値の間に直線的な関係があることを想定しています。もしこの関係が曲線であれば、上記の方程式は2次方程式となり、より多くの係数と指数を持つことになります。しかし、よりシンプルなオプションとして、以下のようなコーディングが可能です。

 

double _sl=((m_ma.Main(_index)*m_slope_ma)+(m_intercept_ma*m_symbol.Point()))+((m_atr.Main(_index)*m_slope_atr)+(m_intercept_atr*m_symbol.Point()));
      

 

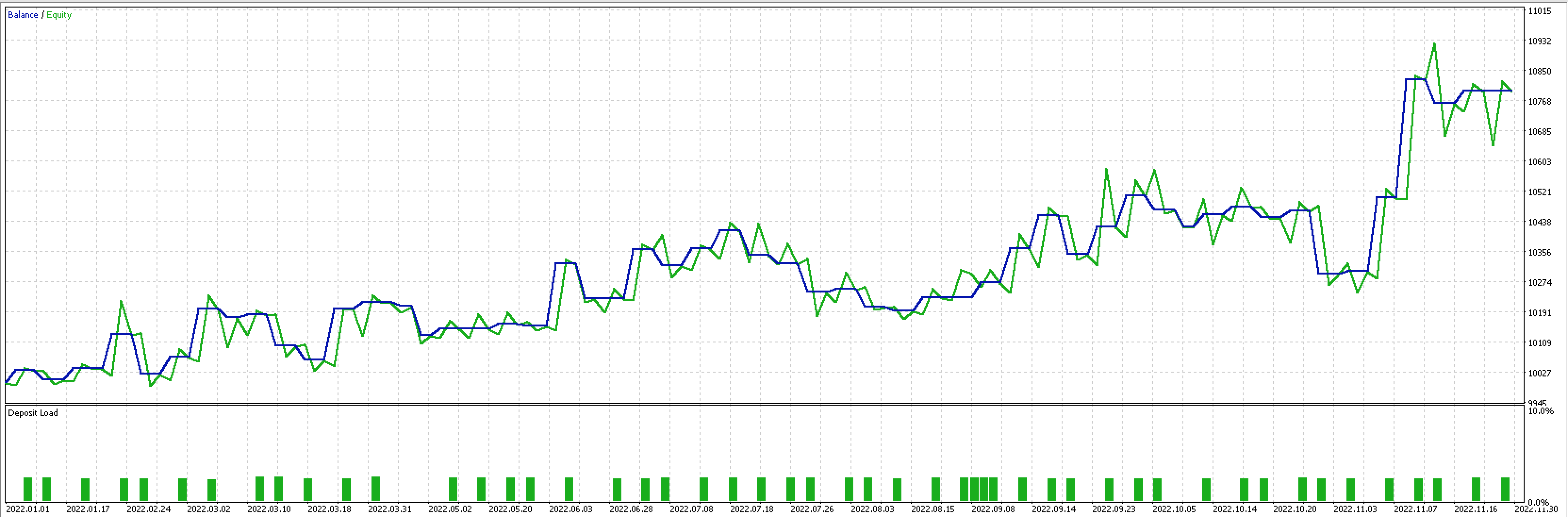
MQL5に搭載されているエキスパートトレーリングクラスを利用して、理想の損切りデルタを利用した独自のトレーリングクラスを構築する場合、A始域とB始域の係数mとcをこのトレーリングクラスの入力とすることができます。過去1年間、EURUSDの1時間足で、当社のシグナルを組み込みの「signalRSI.mqh」クラスでテストすると、以下のようなレポートと曲線が得られました。

 

 

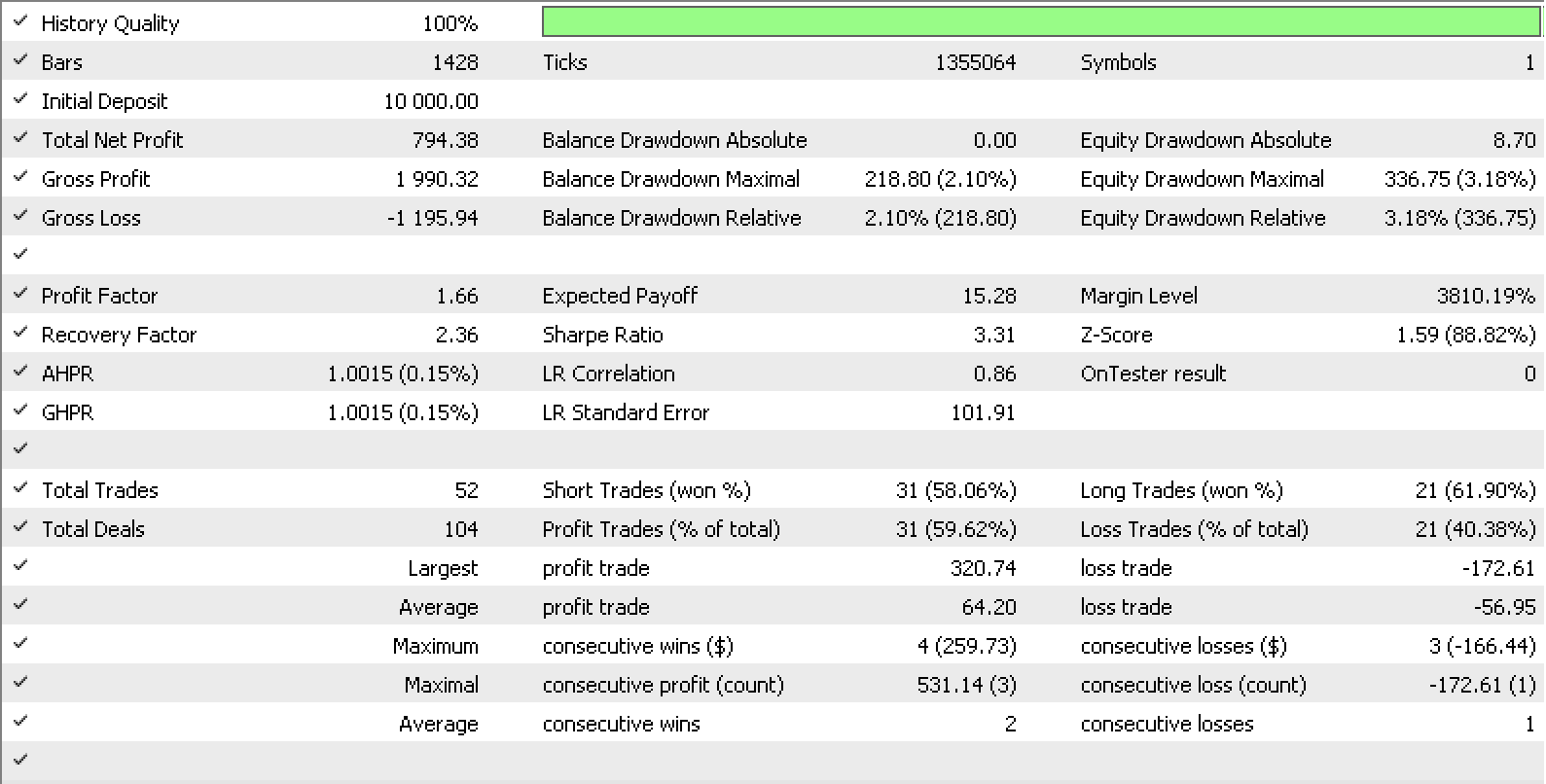
ここで示した考え方は、合成スパンを視野に入れると、さらに発展する可能性があります。

合成スパンは、スパンのスパンです。私たちの場合、指標の数値が少し遅れている、という言い方もできます。このわずかなタイムラグが、トレーリングストップの価格の正確性を低下させている可能性があります。これを解決するために、始域A、Bをスパンとして構成し直すことが考えられます。AはA'とCの積に、BはCとB'の積に変更されることになります。

   

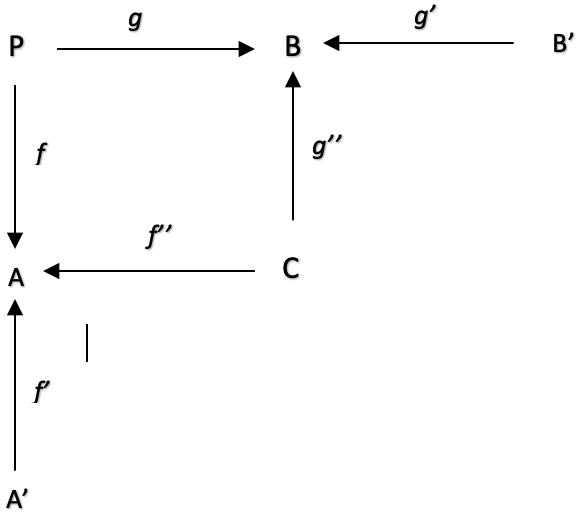
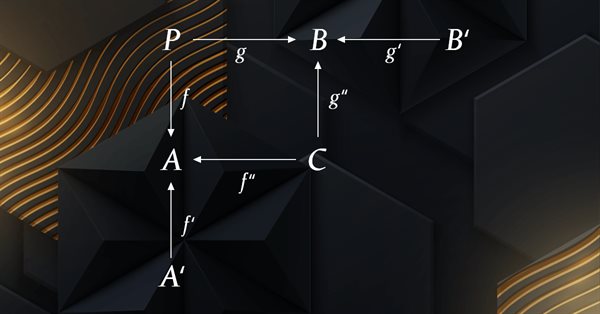
部分始域A'、C、B'にマッピングする複合スパンは、始域AとBのオブザーバブル間のデータと関係のより詳細なビューを提供することで、トレーリングストップ システムを微調整して、射fPからA、g:PからB、f':A'からA、f'':CからA、g'':CからB、g':B'からBを最適化するのに役立ちます。

 

A、Bを再構成すると、AはA'とCの積、BはCとB'の積として捉えることになります。PはA、Bの和ですが、これらは積となります。ATRは一定期間の平均的な価格変動幅であるため、数学的には期間長さの逆数とその期間中の価格変動幅の合計の積に相当し、期間長さの逆数をA'、価格の合計をCとします。逆に言えば、MAは、期間の逆数と最近の価格の和の積に相当します。ですから、この場合もスパンAで行っているのと同じ商品手配をしています。

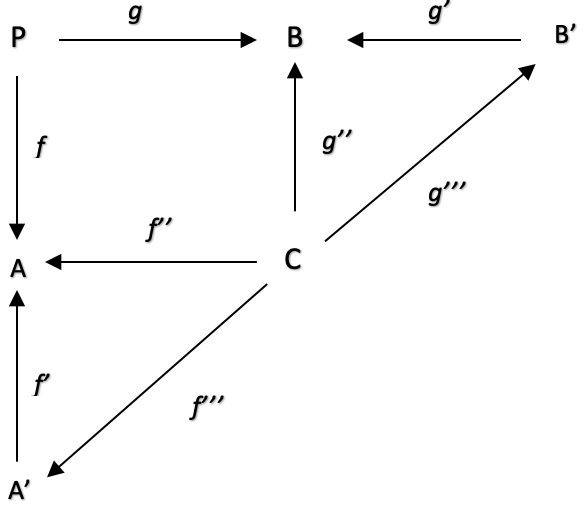
Cの領域は価格と表示されていますが、少し衒学的に言えば、ATR（A）に利用される価格は一定期間のトゥルーレンジ値の合計であり、MAに与えられる価格は単に現在の終値の合計である点で矛盾しているように思えます。

 

そこで、始域間の射に注目し、始域の中にあるものを解き明かさないという圏論の不文律が役に立つのです。これを使えば、上図のように簡単に図を組み立てることができるだけでなく、不変性を簡単に特定することができるからです。この普遍性が、最適化や欠損値の解決に一般的に使用される他の数多くの数学的手法と、ここでの方法を異なるものにしています。

私たちが考えるに、始域Cは価格を表しています。その始域がどのように価格帯と近い価格を処理するかは、この記事の範囲外であり、実際、ここでの目的では最終的な結果に影響することはありません。

しかし、普遍性を見る前に、データをこれらの部分始域に分解することで、異なる観測データ間のパターンや相関関係を特定することが容易になり、射fとgだけでなく、f'、f''、g'、g''も最適化できることに留意する必要があります。

もう一度簡単に説明すると、追加された端子領域A'、C、B'の関係は線形であり、上記の式形式がそのまま適用されます。

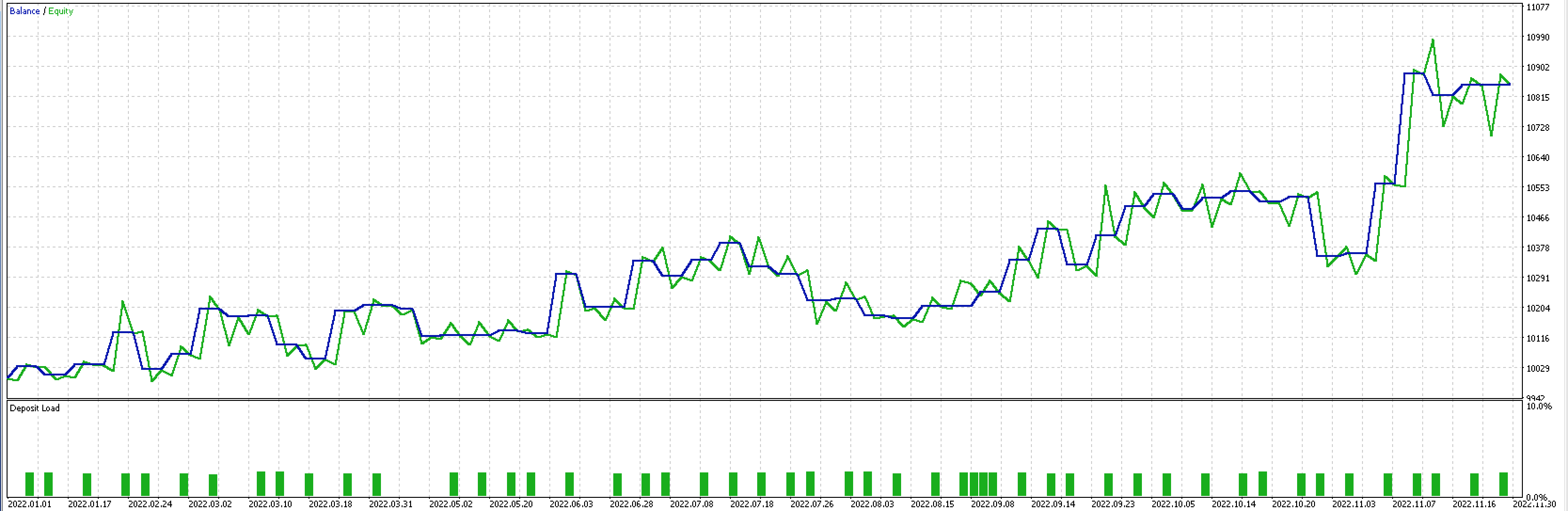
上記のように、射の数が3倍になったので、より多くの入力でテストを実行すると、次のようなレポートとテスト曲線が得られます。

 

 

 

 

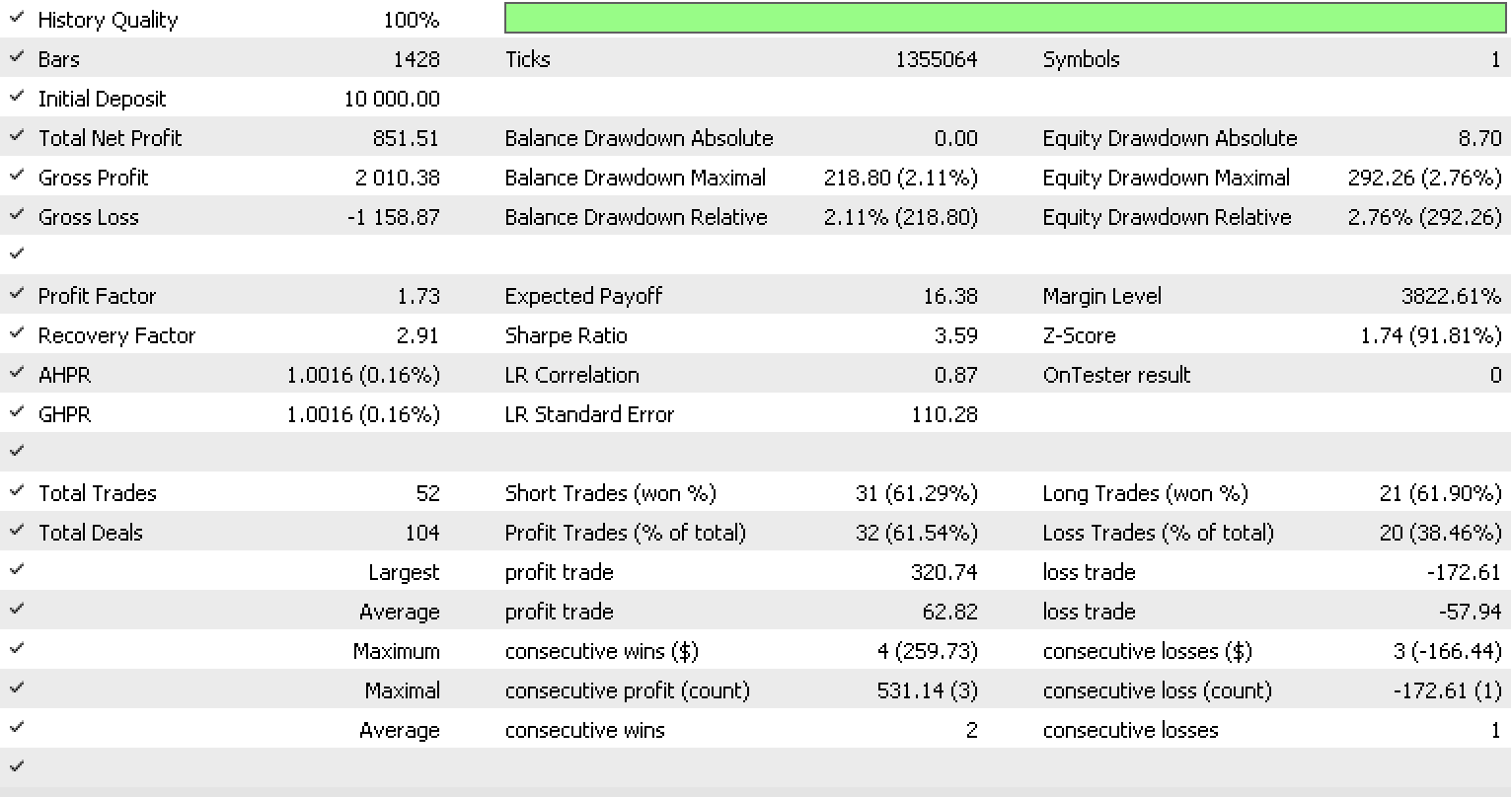
トレーリングシステムの全体的な性能の向上が明らかです。しかし、これは入力パラメーターの数が前回の3倍に増えたことによるオーバーフィッティングの可能性があります。

普遍的の概念に戻ると、複合スパンはこの概念の2つの候補を提示しています。まず、領域Aspanにおいて、領域A'と領域C,が末端であるため、A'とCの間に普遍的な射が暗示されます。

これらの形態に、CからA'、CからB'へのそれぞれf''、g''のラベルを付けると、価格とATRに選ばれた期間の間に関係があることを意味します。同様に、価格とMA指標の期間にも関係があるでしょう。

上記の射の仮説のように、価格と指標期間の関係は、上記の単純な式に固執する線形になることもあれば、最も高い指数を選んで2次方程式を採用する曲線になることもあります。

しかし、線形関係にこだわり、前回のトレーリングクラスのバージョンに基づき、（f'''とg'''を除く）すべての射の定数を一定（変更せず、常にデフォルト値を使用）にしておけば、同じ期間に比較テストを行い、以前のトレーリングクラスと比較してどのように機能するかを確認できます。

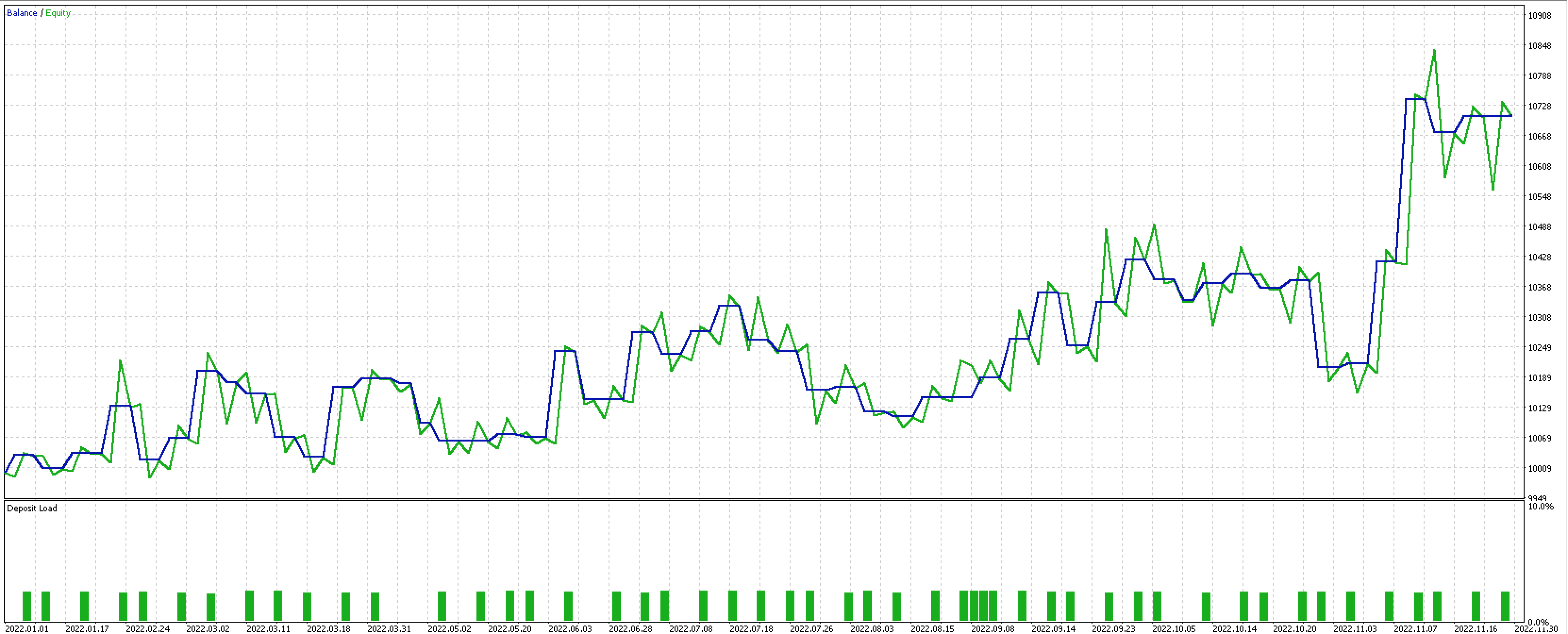
これがテスト結果です。

 

 

 

3つのレポートの中でベストな結果ではありませんが、より少ない入力で、普遍性の原則を用いながら、パフォーマンスを発揮することができたということは、より長期的な視点で検討する価値のあるアイデアであると言えるのではないでしょうか。いつものように、ここに掲載されているすべてのコードは、聖杯や完全な取引システムではないので、読者は、その一部を使用する前に、自分自身の研究と勤勉をおこなうことを強くお勧めします。

結論

最後に、圏論におけるスパン、実験、合成が、出口取引戦略の設定にどのように利用できるかを見てきました。スパンとは、ここでは始域として表現されているアイデアや概念、システムの組を構成するセル単位のことです。このペアリングは、本質的にこのスパンの普遍性である実験を提供します。合成は、そのスパンを他のスパンで補強し、より洞察力のあるシステムや手法を生み出すもので、今回の例では、取引システムの出口戦略を微調整するのに役立ちました。