MQL5 中的范畴论 (第 4 部分)：跨度、实验、及合成

概述

在上一篇文章中，我们看到了范畴论如何通过其乘积、余积和通用性质的概念在复杂系统中发挥作用，分享了其在金融和算法交易中的应用示例。 在此，我们将深入研究跨度、实验、及合成。 我们将看到这些概念如何提供一种更细致和灵活的系统推理方式，以及如何运用它们来开发更复杂的交易策略。 以范畴论的角度了解金融市场的底层结构，交易者可以得到对金融产品行为的新见解，构建更复杂的投资组合，并制定更有效的风险管理策略。 总体而言，范畴论在金融中的应用有可能彻底改变我们对金融市场的思考方式，并令交易者能够做出更明智的决策。

跨度、实验、及合成

在范畴论中，跨度（span）是将三个对象和它们之间的两个态射联系起来的构造。 具体来说，跨度是形状的关系示图：

 

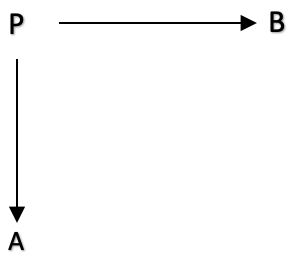
这个非常基本的示图也可以用下面的一行表示：

A<--- f --- P --- g --->B

其中 A、B 和 P 是类别中的域，f：P 到 A 和 g：P 到 B 是类别中的态射。 态射 f：P 到 A 和 g：P 到 B，称为跨度的腿。

跨度 P，可被认为是在 A 和 B 之间关联方式的两条不同路径或视角，一条经由 f，另一条经由 g。 支腿 f 和 g 是分别连接 A 和 B 处的路径，并允许比较和组合这两条路径。

我们先回顾一下理论，然后再深入探讨于 MQL5 内可能的应用。

跨度在范畴论中很重要，因为它们提供了一种比较范畴中两种不同态射的方法。 给定两个态射 f：A → B 和 g：A → C，从 B 到 C 的范围是形式 B ← A → C 的示图，其中两个箭头表示态射 f 和 g。 跨度通常用于定义范畴论中的极限和共极限。 例如，可以将范畴中逻辑示意图的极限定义为该示图上的通用圆锥体，其中圆锥体是从极限对象到关系图中满足特定条件的每个对象的跨度。

跨度在定义回拉时也很有用，其是一种限制类型，其中所涉及的对象通过一对态射相关。 给定两个态射 f：A → B 和 g：A → C 在一个范畴中，f 和 g 的回拉是一个对象 P，以及两个态射 p1：P → B 和 p2：P → C，使得 f ∘ p1 = g ∘ p2 和 P 在这个性质上是共通的。 回拉在数学和科学的许多领域都很重要，包括代数几何、拓扑学、和计算机科学。

范畴论中的另一个重要概念是实验，它是由两个平行态射和连接它们的协域的第三个态射组成的示图。 实验可以被认为是一种范畴论里变换对象的两种不同比较方法之一。 例如，给定两个态射 f：A → B 和 g：A → C，从 B 到 C 的实验是形式 A → B ⟶ D ← C 的示图，其中箭头分别表示态射 f、g 和 h。 实验可用于以类似于跨度的方式定义极限和余限，并且它们也可用于定义协均衡器，其是一种可用于识别具有相同协域的两个不同态射的余限。

合成是范畴论中的基本概念，它由两个或多个态射组合而成。 给定两个态射 f：A → B 和 g：B → C，它们的合成是态射 g ∘ f：A → C，它是通过应用 f 后跟 g 获得的。 合成性质是结合，针对任何三个态射 f、g 和 h，这意味着（h ∘ g）∘ f = h ∘（g ∘ f）。 此性质允许一次组合多个态射，且用于定义范畴的概念，其为满足某些公理的对象和态射的集合。

以下是跨度、实验和合成在金融和交易范畴论中的十个即兴应用：

1. 跨度可以模拟金融衍生品的基础资产，以及用于复现其收益的对冲工具。 跨度的通用性质将有助于定义衍生品的价格。
2. 通过组合不同的资产类别，以最小化风险和最大化回报的方式，通过合成来有效地构建投资组合。 这可以通过使用合成物的通用性质来指导。
3. 跨度可以针对金融机构应对不同市场因素的风险承受能力建模。 这可以通过构造一个将机构资产与相关市场指数联系起来的跨度来达成。
4. 实验可以测试不同交易算法在不同市场条件下的性能。 这可以通过构造模拟市场行为的实验，并测量算法在模拟数据上的性能来模拟。
5. 按缩小的比例针对金融系统的行为进行建模是域合成能提供帮助的事情。 举例，研究 SP500 如何在各个不同的较长周期分区中相互关联。
6. 跨度可以使用更简单的工具合成来针对特定金融产品的复现建模。 这对于设计具有理想性质（例如与现有金融产品的相关性较小）的新型金融产品时很有用。
7. 实验可以通过比较特定策略与对照组的表现来测试交易策略。 这可以使用实验的普遍性再次实现。
8. 实验还可以测试不同市场微观结构设计的效率。 通过构造一个模拟不同类型市场参与者行为的实验，并衡量由此产生的市场结果，即可做到这一点。
9. 合成材料可以针对金融机构的整体风险承受能力建模。 这可以通过构造机构各种业务线的组合，并分析它们的相互依赖性来完成。
10. 跨度可以针对不同财务数据源之间的关系进行建模。 据其可以设计机器学习算法，能从不同的数据源中提取有用的特征。

为了描述这个概念的应用，我们可以讲述一个跨度“实验”，它涉及发现一个证券的多头持仓利润与一对其它变量（即证券的移动平均线和平均真实范围）之间是否存在关系。 这个“实验”可以表示为一个示图，涉及一个顶点、两个域和它们之间的态射。

假设我们有一个范畴 C，其中包含两个域 A 和 B，分别表示移动平均线的域和平均真实范围的域。 在这个范畴中，我们还有一个域 P，代表多头持仓利润，并充当我们的顶点。

然后，我们可以继续定义两个态射 f：P -> A 和 g：P -> B，它们将多头持仓浮动盈利 P 分别映射到其在域 A 和 B 中的可观察量。 这些态射表示可观察量的日志记录。

  这种示图表示令我们能够以更抽象和正式的方式分析实验，并应用范畴论的概念和工具来推导它。

为了执行“实验”，我们在当前图表品种上打立一笔买入订单，比如 EURUSD，0.1 手，然后在每根新柱线上记录当前的浮动盈利、MA 和 ATR。 根据观察到的数据，我们可以看到数据之间是否存在任何相关性，然后可据其为多头持仓提出理想的尾随停止系统。 这里所用的 MA 和 ATR 指标可以很容易地以读者认为更合适的指标代替。 我选择这些只是为了说明。

 

如果我们在 3 月 1 日的小时时间帧内基于 EURUSD 进行此实验，我们将得到一些数据。

 

P: (浮动盈利)	A: ATR	B: MA
-6.60000	0.00203	1.12138
-14.90000	0.00181	1.12136
-18.80000	0.00175	1.12140
-24.20000	0.00157	1.12125
-29.00000	0.00146	1.12100
-24.30000	0.00127	1.12078

 

 

如果我们在两个域数据集 A 和 B 中的每一个与持仓利润之间进行滞后相关性，这可以帮助设置这些域中的每一个是否可以预测持仓的负向回撤。 此信息将有助于设置或移动多头持仓的现有止损。

 

这些跨度可有助于定义止损的另一种方式是，如果我们假设每个终端域 A 和 B，通过它们各自的态射 f & g 来形成多头持仓的理想止损应该相距多远的共积（总和）。 这些态射本质上是接受输入，并提供输出的函数。 在这种情况下，每个终端域将提供其指标值作为输入，每个函数 f 和 g 将提供双精度值的输出。

 

将这些双精度值相加，相当于一个共积，将给我们理想的止损价格。 如果我们认为态射的输出（止损价格）与态射的指标输入具有线性关系，那么这些方程是隐含的。

其中 xa ⊆ A 和 ma 和 ca 是线性关系的斜率和 y-截距系数。 与其类似，对于 B 域

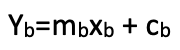
该假设适用于理想止损增量，和指标值之间的线性关系。 如果这种关系是一条曲线，那么上述方程就是二次的，且拥有更多的系数和指数。 但是，我们更简单的选项可以按如下所示进行编码。

 

double _sl=((m_ma.Main(_index)*m_slope_ma)+(m_intercept_ma*m_symbol.Point()))+((m_atr.Main(_index)*m_slope_atr)+(m_intercept_atr*m_symbol.Point()));
      

 

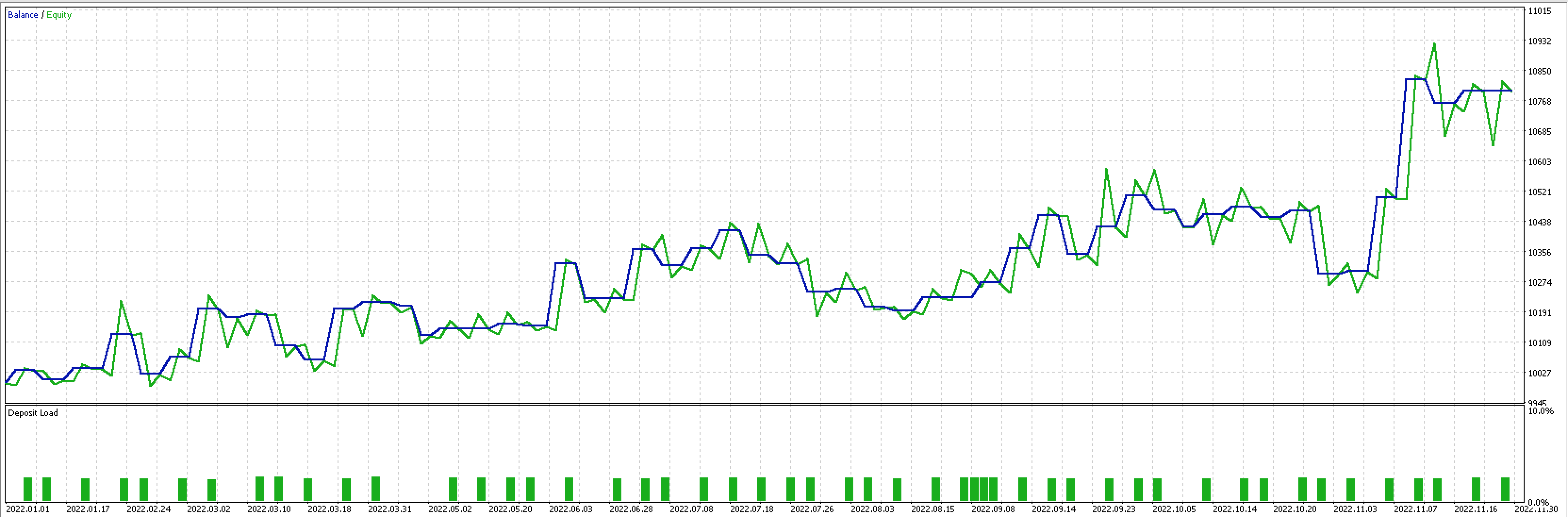
如果，我们基于 MQL5 内置的智能尾随类构建自己的尾随类，并采用我们的理想止损增量，那么 A 域和 B 域的系数 m 和 c 都可以作为此尾随类的输入。 测试基于过去一年的数据，对于 EURUSD 的小时数据，我们的信号作为内置的 “signalRSI.mqh” 类，为我们给出下面所示的报告和曲线。

 

 

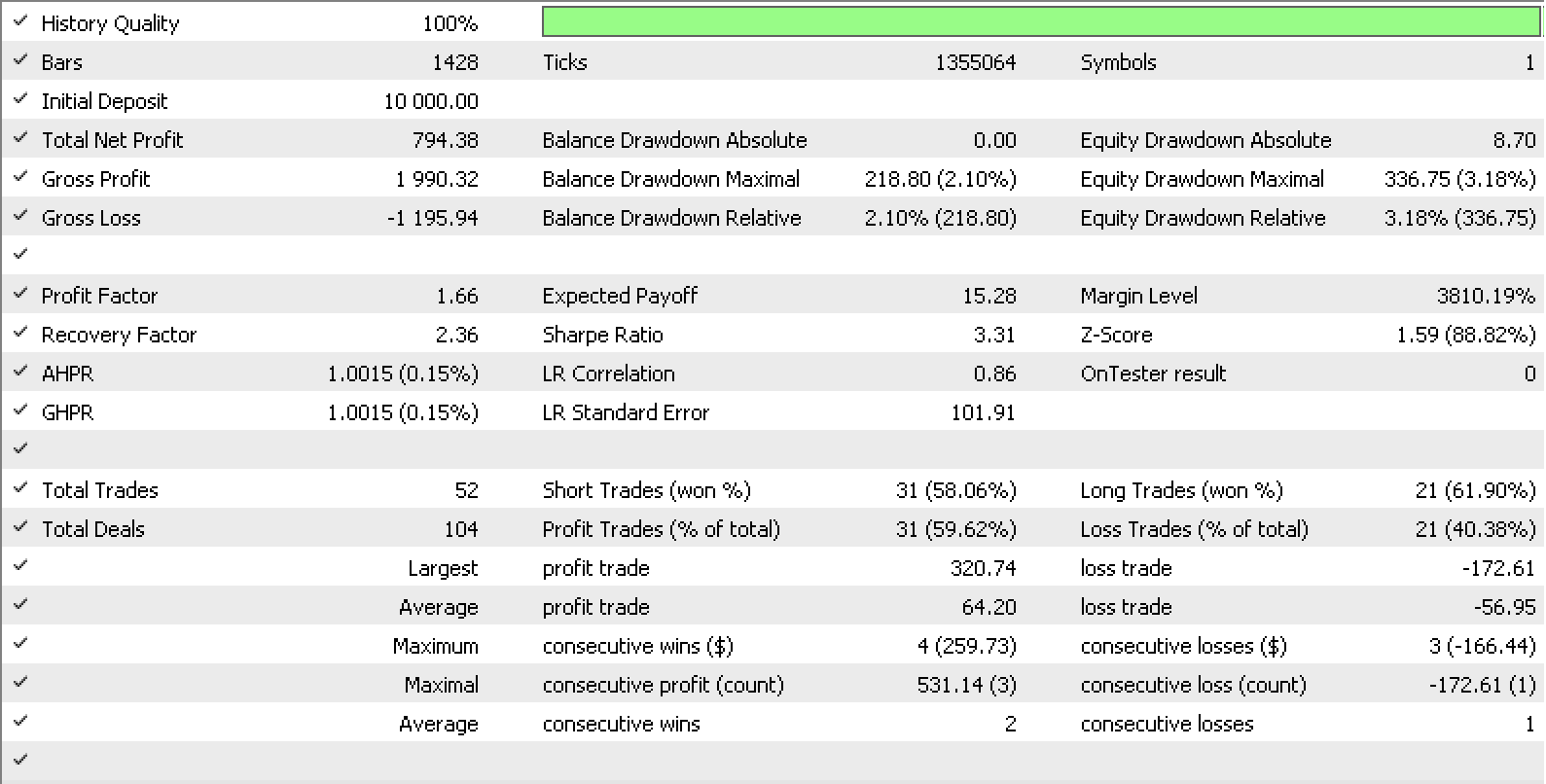
如果我们看一下合成跨度，这里指出的思路可以进一步发展。

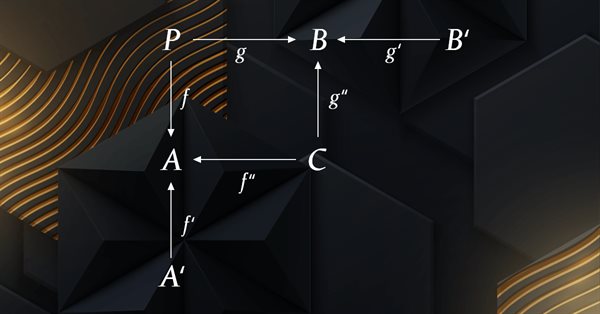
合成跨度是跨度的跨度。 在我们的例子中，我们可以得以证实，指标值有些滞后。 这种略微的滞后可能导致我们的尾随停止价格不太精确。 为了定位这个问题，我们可以将域 A 和 B 重新构建为跨度。 A 将更改为 A' 和 C 的乘积，而 B 将更改为 C 和 B' 的乘积。

   

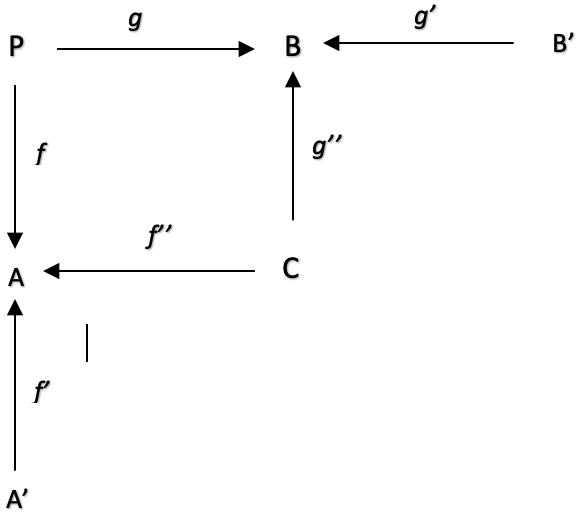
映射到子域 A'、C 和 B' 的合成跨度可以帮助优化态射 f：P 到 A、g：P 到 B、f'：A' 到 A、f''：C 到 A、g''：C 到 B，以及 g'：B' 到 B，通过提供域 A 和 B 中可观察量之间的更精细的数据视图和关系，微调我们的尾随停止系统。

 

在重新构成 A 和 B 时，我们现在将它们视为 A' & C 的乘积，B 的 C & B'。请记住，P 是 A 和 B 的总和，但这些将是乘积。 我们知道 ATR 是设定区间内价格的平均真实范围，因此它在数学上等价于周期长度的倒数与该长度上的价格范围总和之间的乘积，覆盖该长度上的价格范围的总和意味着我们的周期长度倒数为 A'，价格总和为 C。 相反，MA 相当于一个周期的倒数和最近价格的总和的乘积。 故此，在这种情况下，我们也有与跨度 A 相同的乘积分配。

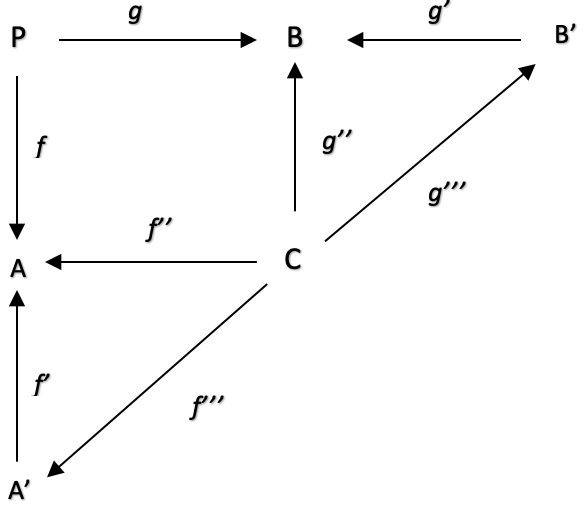
域 C 被标记为价格，若是我们有点迂腐，这似乎是矛盾的，因为应用于 ATR（A） 的价格是一段时间内真实范围值的总和，而给定 MA 的价格只是累加当前收盘价。

 

这就是范畴论不成文规则派上用场的地方，即关注域之间的态射，而并不解封域内是什么。 因为这一点，我们不仅可以如上所示那样轻松地组装我们的示图，而且还可以轻松识别可能的通用性质。 通用性质令我们的方示与其它通常用于优化或求解缺失值的众多数学方法区分开来。

就我们而言，域 C 代表价格。 该域如何处理价格范围与收盘价不在本文的讨论范围内，事实上，就我们的目的而言，不会影响最终结果。

然而，在我们查看相应的通用性质之前，需要注意的是，通过将数据分解为这些子域，可以更轻松地识别不同可观察量之间的形态和相关性，这不仅可以帮助优化态射 f 和 g，还可以优化 f'、f''、g' 和 g''。

再一次为简洁起见，我们可以将添加的终端域 A'、C 和 B' 之间的关系视为线性关系，这意味着上述方程格式仍然适用。

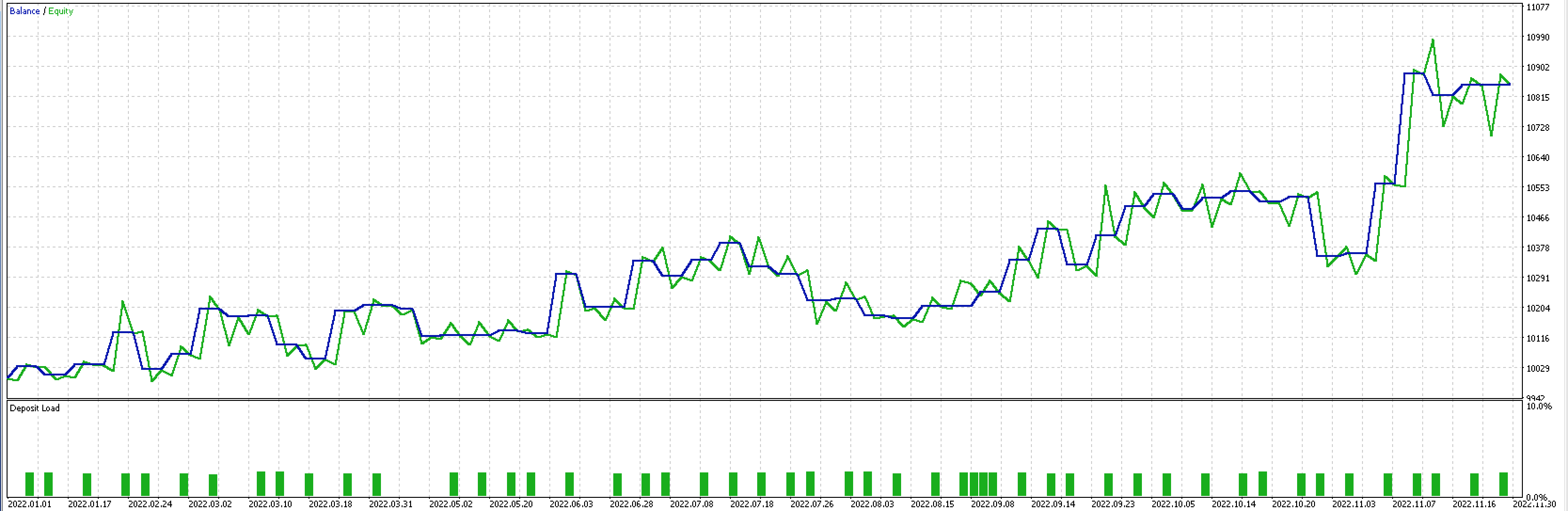
如果如上所述，我们现在采用更多输入运行测试，因为态射的数量增加了两倍，我们会得到以下报告和测试曲线。

 

 

 

 

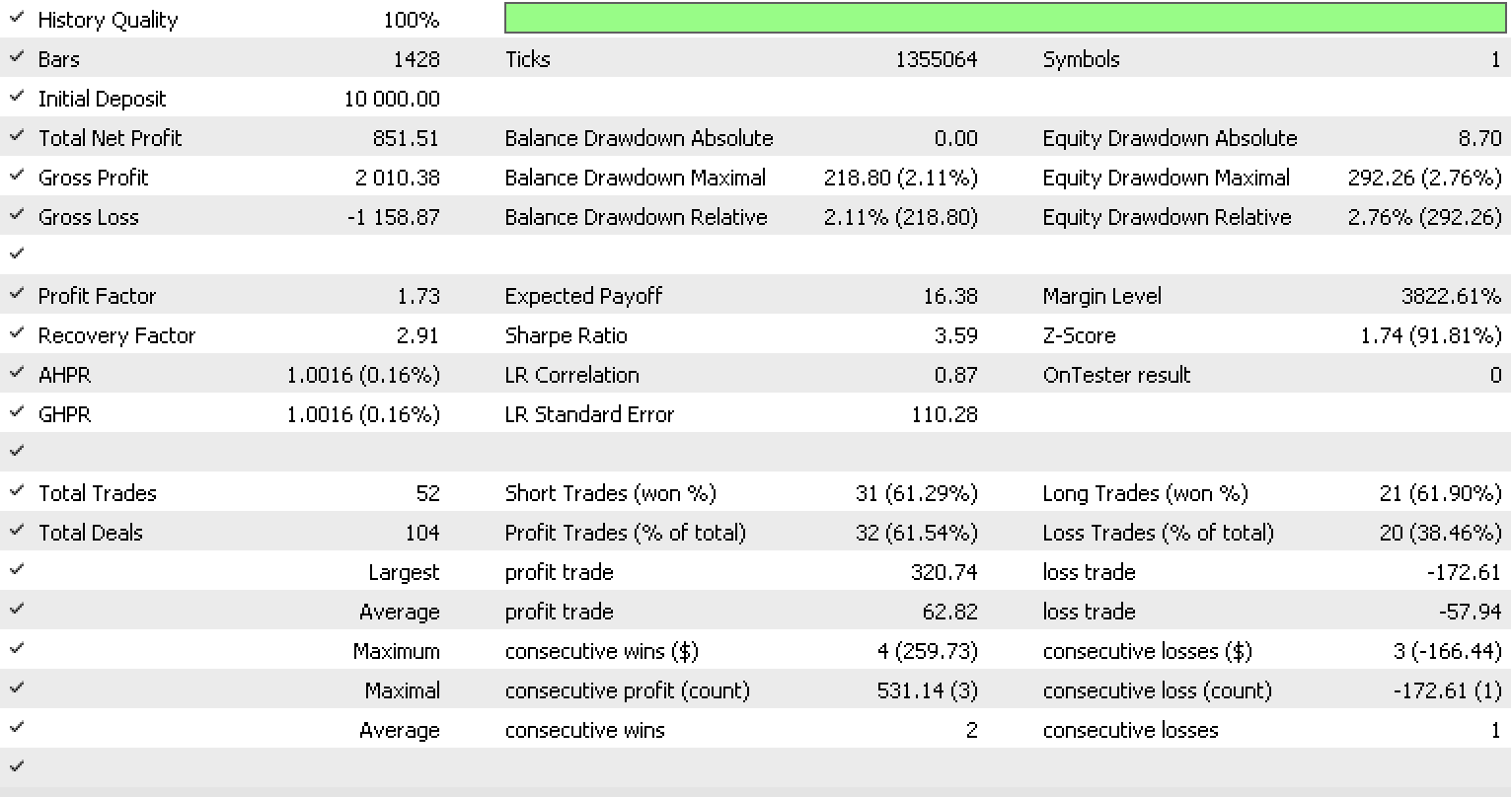
尾随系统的整体性能明显提高。 然而，这可能是由于过度拟合，因为输入参数的数量比之前的测试增加了 3 倍。

回到通用性质的概念，我们的合成跨度确实为我们提供了这个概念的两个候选者。 首先，在域 A 跨度中，由于域 A' 和域 C 是终端，因此在 A' 和 C 之间隐含了一个通用态射。

如果我们将这些态射分别标记为 C 到 A' 和 C 到 B' 的 f''' 和 g'''，我们是在暗示价格与 ATR 选择的周期之间存在关系。 同样，价格和 MA 指标的周期之间也存在关系。

正如上述态射中的假设一样，价格和指标周期之间的关系可以是线性的，这意味着我们可以坚持上面的简单方程格式，也可以是曲线，这意味着我们需选择最高指数，并采用二次方程。

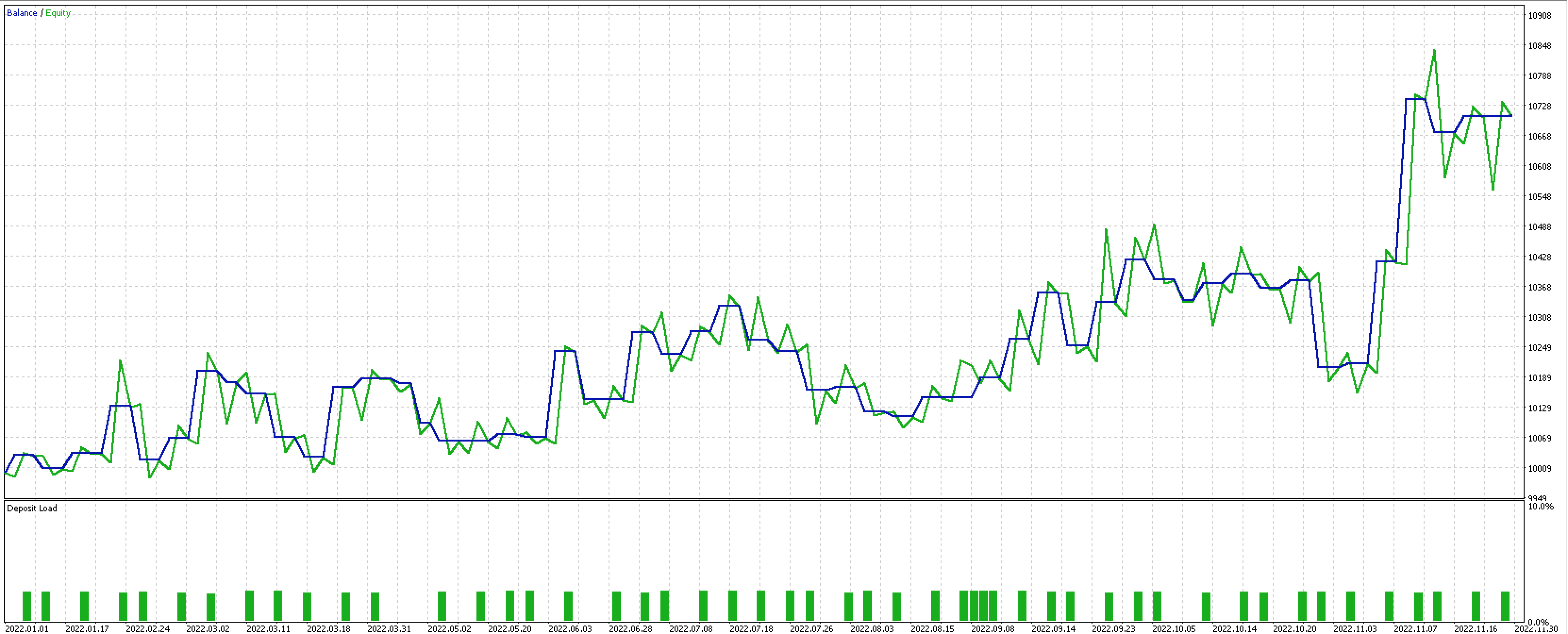
然而，如果我们坚持线性关系，并在我们最后一个版本的尾随类的基础上，我们将常量保留为所有态射（除了 f''' 和 g'''）常量（不变且始终使用默认值），我们可以在同一时间段内运行比较测试，看看它与我们以前的尾随类相比表现如何。

这是测试结果。

 

 

 

结果不是三份报告中最好的，但性能水平只有少量输入，同时按照通用性质原则是否意味着这可能是一个值得在更长时期内研究的思路？ 与往常一样，这里发布的所有代码都不是圣杯或完整的交易系统，因此敦促读者在使用其中的任何部分之前一定要自行研究和尽职调查。

结束语

总之，我们已经看到了如何运用范畴论中的跨度、实验以及合成来设置离场交易策略。 跨度是一对思想/戒律或系统的单元单元，在这里表示为域。 这种配对确实提供了实验，这些实验本质上是这个跨度的通用性质。 合成采用跨度，并据其它跨度来增加，以便提出更有洞察力的系统和方法，在我们的例子中，这些系统和方法对于微调交易系统的离场策略很有用。