
Calcolo delle caratteristiche integrali delle emissioni degli indicatori
Introduzione
Le emissioni degli indicatori rappresentano una direzione nuova e piuttosto promettente nello studio delle serie temporali. Si caratterizza per il fatto che l'analisi non è focalizzata sugli indicatori in quanto tali ma sulle loro emissioni nel futuro o nel passato in base alle quali possiamo effettivamente fare una previsione del contesto di mercato:
- livelli di supporto e resistenza in futuro;
- direzione del trend (movimento dei prezzi);
- forza di movimento accumulata nel passato.
Il mio precedente articolo intitolato "Disegno delle emissioni dell'indicatore in MQL5" trattava dell'algoritmo di disegno delle emissioni e ne specificava le caratteristiche chiave. Lascia che ti rinfreschi la memoria:
L'emissione è un insieme di punti situati alle intersezioni di linee peculiari degli indicatori in esame.
I punti di emissione, a loro volta, presentano alcune peculiarità:
- I punti di emissione dello stesso tipo tendono a raggrupparsi.
- I cluster di punti densi possono attrarre o, al contrario, respingere il prezzo.
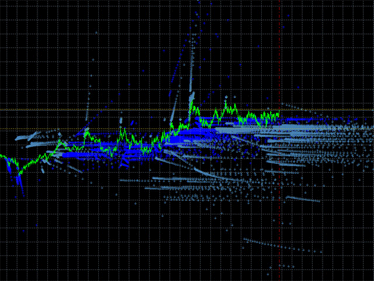
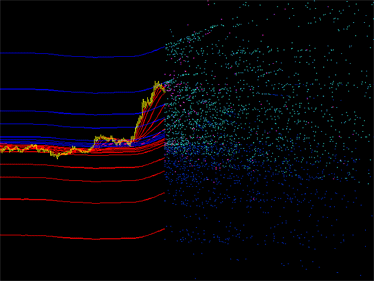
Galleria emissioni:
 |  |
|---|---|
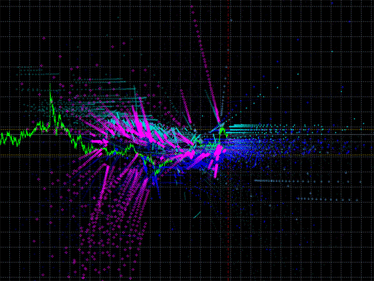 | 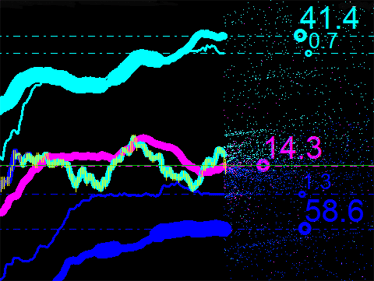 |
Fig. 1. Esempi di grafici di emissione degli indicatori. A sinistra: emissione dell'indicatore DCMV. A destra: emissione degli indicatori iMA e indicatori iEnvelopes.
Nell'illustrazione del calcolo delle caratteristiche integrali delle emissioni, prenderemo gli inviluppi di media mobile (Envelopes) e le medie mobili (Moving Average) stessi con i seguenti parametri di input:
//--- external variable for storing averaging period of the iEnvelopes indicator input int ma_period=140; // averaging period of the iEnvelopes indicator //--- array for storing deviations of the iEnvelopes indicator double ENV[]={0.01,0.0165,0.0273,0.0452,0.0747,01234,0.204,0.3373,0.5576,0.9217,1.5237}; //--- array for storing iMA indicator periods int MA[]={4,7,11,19,31,51,85};
Quindi, cercheremo intersezioni di linee peculiari degli indicatori selezionati. Il numero di linee e le loro caratteristiche (periodi medi e deviazioni) sono scelti a caso. L'emissione può infatti essere tracciata utilizzando qualsiasi insieme di parametri per questi indicatori (purché si intersechino nello spazio).
Ora che abbiamo scelto gli indicatori, procediamo alla creazione di un Expert Advisor che fungerà da programma di base per l'analisi delle emissioni. Avremo bisogno di ottenere i dati calcolati dagli indicatori tecnici iMA e iEnvelopes. Propongo di utilizzare un metodo descritto nella Guida all'uso degli indicatori tecnici negli Expert Advisor.
Per tracciare le linee di cui dobbiamo trovare le intersezioni, abbiamo solo bisogno di impostare due punti per ciascuna delle linee. Pertanto, è sufficiente ottenere i valori dell'indicatore solo per due barre (es. corrente e precedente). Il prezzo sulla barra precedente è statico, mentre il prezzo sulla barra attuale è dinamico e quindi nuovi punti continuano a essere generati ad ogni nuovo tick. Ecco il codice:
//+------------------------------------------------------------------+ //| emission_of_MA_envelope.mq5 | //| Copyright 2013, DC2008 | //| https://www.mql5.com/ru/users/DC2008 | //+------------------------------------------------------------------+ #property copyright "Copyright 2013, DC2008" #property link "https://www.mql5.com/ru/users/DC2008" #property version "1.00" //--- #include <GetIndicatorBuffers.mqh> #include <Emission.mqh> //--- external variable for storing averaging period of the iEnvelopes indicator input int ma_period=140; // averaging period of the iEnvelopes indicator //--- array for storing deviations of the iEnvelopes indicator double ENV[]={0.01,0.0165,0.0273,0.0452,0.0747,01234,0.204,0.3373,0.5576,0.9217,1.5237}; //--- array for storing the iMA indicator periods int MA[]={4,7,11,19,31,51,85}; //--- array for storing pointers to the iMA and iEnvelopes indicators int handle_MA[]; int handle_Envelopes[]; //--- market data datetime T[],prevTimeBar=0; double H[],L[]; #define HL(a, b) (a+b)/2 //--- class instances CEmission EnvMa(0,300); PointEmission pEmission; //--- drawing styles for points of emission #define COLOR_UPPER C'51,255,255' #define COLOR_LOWER C'0,51,255' #define COLOR_MA C'255,51,255' color colorPoint[]={COLOR_UPPER,COLOR_LOWER,COLOR_MA}; CodeColor styleUpper={158,COLOR_UPPER,SMALL}; CodeColor styleLower={158,COLOR_LOWER,SMALL}; CodeColor styleMA={158,COLOR_MA,SMALL}; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { ArraySetAsSeries(T,true); ArraySetAsSeries(H,true); ArraySetAsSeries(L,true); //--- int size=ArraySize(MA); ArrayResize(handle_MA,size); //--- create a pointer to the object - the iMA indicator for(int i=0; i<size; i++) { handle_MA[i]=iMA(NULL,0,MA[i],0,MODE_SMA,PRICE_MEDIAN); //--- if an error occurs when creating the object, print the message if(handle_MA[i]<0) { Print("The iMA object[",MA[i],"] has not been created: Error = ",GetLastError()); //--- forced program termination return(-1); } } //--- size=ArraySize(ENV); ArrayResize(handle_Envelopes,size); //--- create a pointer to the object - the iEnvelopes indicator for(int i=0; i<size; i++) { handle_Envelopes[i]=iEnvelopes(NULL,0,ma_period,0,MODE_SMA,PRICE_MEDIAN,ENV[i]); //--- if an error occurs when creating the object, print the message if(handle_Envelopes[i]<0) { Print("The iEnvelopes object[",ENV[i],"] has not been created: Error = ",GetLastError()); //--- forced program termination return(-1); } } //--- return(0); } //+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- } //+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- market data CopyTime(NULL,0,0,2,T); CopyHigh(NULL,0,0,2,H); CopyLow(NULL,0,0,2,L); //--- fill the declared arrays with current values from all indicator buffers string name; uint GTC=GetTickCount(); //---- indicator buffers double ibMA[],ibMA1[]; // arrays for the iMA indicator double ibEnvelopesUpper[]; // array for the iEnvelopes indicator (UPPER_LINE) double ibEnvelopesLower[]; // array for the iEnvelopes indicator (LOWER_LINE) for(int i=ArraySize(handle_MA)-1; i>=0; i--) { if(!CopyBufferAsSeries(handle_MA[i],0,0,2,true,ibMA)) return; //--- for(int j=ArraySize(handle_Envelopes)-1; j>=0; j--) { if(!GetEnvelopesBuffers(handle_Envelopes[j],0,2,ibEnvelopesUpper,ibEnvelopesLower,true)) return; //--- find the intersection point of the iEnvelopes(UPPER_LINE) and iMA indicators pEmission=EnvMa.CalcPoint(ibEnvelopesUpper[1],ibEnvelopesUpper[0],ibMA[1],ibMA[0],T[0]); if(pEmission.real) // if the intersection point is found, draw it in the chart { name="iEnvelopes(UPPER_LINE)"+(string)j+"=iMA"+(string)i+(string)GTC; EnvMa.CreatePoint(name,pEmission,styleUpper); } //--- find the intersection point of the iEnvelopes(LOWER_LINE) and iMA indicators pEmission=EnvMa.CalcPoint(ibEnvelopesLower[1],ibEnvelopesLower[0],ibMA[1],ibMA[0],T[0]); if(pEmission.real) // if the intersection point is found, draw it in the chart { name="iEnvelopes(LOWER_LINE)"+(string)j+"=iMA"+(string)i+(string)GTC; EnvMa.CreatePoint(name,pEmission,styleLower); } } //--- for(int j=ArraySize(handle_MA)-1; j>=0; j--) { if(i!=j) { if(!CopyBufferAsSeries(handle_MA[j],0,0,2,true,ibMA1)) return; //--- find the intersection point of the iMA and iMA indicators pEmission=EnvMa.CalcPoint(ibMA1[1],ibMA1[0],ibMA[1],ibMA[0],T[0]); if(pEmission.real) // if the intersection point is found, draw it in the chart { name="iMA"+(string)j+"=iMA"+(string)i+(string)GTC; EnvMa.CreatePoint(name,pEmission,styleMA); } } } } //--- deletion of the graphical objects of emission not to stuff the chart if(T[0]>prevTimeBar) // delete once per bar { int total=ObjectsTotal(0,0,-1); prevTimeBar=T[0]; for(int obj=total-1;obj>=0;obj--) { string obj_name=ObjectName(0,obj,0,OBJ_TEXT); datetime obj_time=(datetime)ObjectGetInteger(0,obj_name,OBJPROP_TIME); if(obj_time<T[0]) ObjectDelete(0,obj_name); } Comment("Emission © DC2008 Objects = ",total); } //--- }
Non mi soffermerò su ogni dettaglio di questo Expert Advisor. La cosa principale da notare qui è che per tracciare l'emissione, usiamo un'istanza di classe CEmission responsabile del calcolo e della visualizzazione dei punti di intersezione di due linee qualsiasi.
//+------------------------------------------------------------------+ //| Emission.mqh | //| Copyright 2013, DC2008 | //| https://www.mql5.com/ru/users/DC2008 | //+------------------------------------------------------------------+ #property copyright "Copyright 2013, DC2008" #property link "https://www.mql5.com/ru/users/DC2008" #property version "1.00" #define BIG 7 // point size #define SMALL 3 // point size //+------------------------------------------------------------------+ //| pMABB structure | //+------------------------------------------------------------------+ struct PointEmission { double x; // X-coordinate of the time point double y; // Y-coordinate of the price point datetime t; // t-coordinate of the point's time bool real; // whether the point exists }; //+------------------------------------------------------------------+ //| CodeColor structure | //+------------------------------------------------------------------+ struct CodeColor { long Code; // point symbol code color Color; // point color int Width; // point size }; //+------------------------------------------------------------------+ //| Base class for emissions | //+------------------------------------------------------------------+ class CEmission { private: int sec; int lim_Left; // limiting range of visibility in bars int lim_Right; // limiting range of visibility in bars public: PointEmission CalcPoint(double y1, // Y-coordinate of straight line 1 on bar [1] double y0, // Y-coordinate of straight line 1 on bar [0] double yy1, // Y-coordinate of straight line 2 on bar [1] double yy0, // Y-coordinate of straight line 2 on bar [0] datetime t0 // t-coordinate of the current bar Time[0] ); bool CreatePoint(string name, // point name PointEmission &point, // coordinates of the point CodeColor &style); // point drawing style CEmission(int limitLeft,int limitRight); ~CEmission(); }; //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ CEmission::CEmission(int limitLeft,int limitRight) { sec=PeriodSeconds(); lim_Left=limitLeft; lim_Right=limitRight; } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ CEmission::~CEmission() { } //+------------------------------------------------------------------+ //| The CalcPoint method of the CEmission class | //+------------------------------------------------------------------+ PointEmission CEmission::CalcPoint(double y1, // Y-coordinate of straight line 1 on bar [1] double y0, // Y-coordinate of straight line 1 on bar [0] double yy1,// Y-coordinate of straight line 2 on bar [1] double yy0,// Y-coordinate of straight line 2 on bar [0] datetime t0 // t-coordinate of the current bar Time[0] ) { PointEmission point={NULL,NULL,NULL,false}; double y0y1=y0-y1; double y1yy1=y1-yy1; double yy0yy1=yy0-yy1; double del0=yy0yy1-y0y1; if(MathAbs(del0)>0) { point.x=y1yy1/del0; if(point.x<lim_Left || point.x>lim_Right) return(point); point.y=y1+y0y1*y1yy1/del0; if(point.y<0) return(point); point.t=t0+(int)(point.x*sec); point.real=true; return(point); } return(point); } //+------------------------------------------------------------------+ //| The CreatePoint method of the CEmission class | //+------------------------------------------------------------------+ bool CEmission::CreatePoint(string name, // point name PointEmission &point, // coordinates of the point CodeColor &style) // point drawing style { if(ObjectCreate(0,name,OBJ_TEXT,0,0,0)) { ObjectSetString(0,name,OBJPROP_FONT,"Wingdings"); ObjectSetInteger(0,name,OBJPROP_ANCHOR,ANCHOR_CENTER); ObjectSetInteger(0,name,OBJPROP_FONTSIZE,style.Width); ObjectSetString(0,name,OBJPROP_TEXT,CharToString((uchar)style.Code)); ObjectSetDouble(0,name,OBJPROP_PRICE,point.y); ObjectSetInteger(0,name,OBJPROP_TIME,point.t); ObjectSetInteger(0,name,OBJPROP_COLOR,style.Color); return(true); } return(false); }
Va notato che i punti di emissione sono rappresentati mediante oggetti grafici come Testo. Prima di tutto, deriva dal fatto che le ancore degli oggetti dovrebbero essere allineate al centro del simbolo. In secondo luogo, è possibile variare le dimensioni dell'oggetto in un'ampia gamma. Queste proprietà puntuali offrono un grande potenziale per ottenere emissioni complesse.
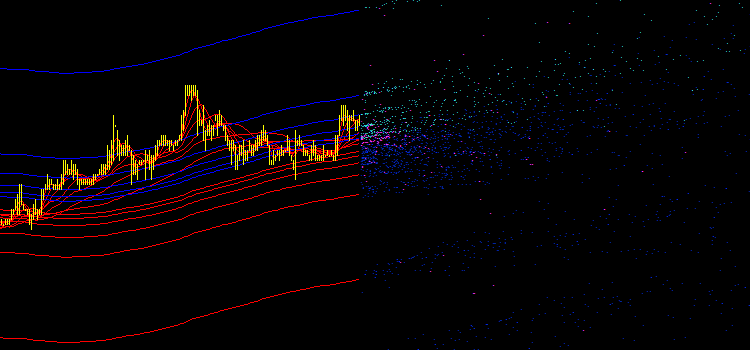
Fig. 2. Emissione originale degli indicatori iMA e iEnvelopes
Caratteristiche Integrali delle Emissioni
Quindi, dopo aver posizionato l'Expert Advisor proposto sul grafico, abbiamo ottenuto molti punti in diversi colori (vedi Fig. 2):
- Aqua - intersezioni di iMA e iEnvelopes, buffer UPPER_LINE.
- Blu - intersezioni di iMA e iEnvelopes, buffer LOWER_LINE.
- Magenta - intersezioni di iMA e iMA.
Questo caos non può essere utilizzato nel trading automatico. Abbiamo bisogno di segnali, livelli e altre caratteristiche quantitative del mercato, mentre qui otteniamo solo immagini visive per la meditazione e la chiromanzia e nessun numero.
Le caratteristiche integrali delle emissioni servono a generalizzare i dati ottenuti come risultato delle emissioni degli indicatori.
La necessità di caratteristiche integrali delle emissioni è anche guidata dal fatto che offrono opportunità per ricerche di mercato utilizzando nuovi tipi di indicatori: canali integrali, linee, livelli, segnali, ecc. Per determinare i valori di emissione più tipici, inizieremo in piccolo e calcoleremo il prezzo medio per ogni tipo di punto per tracciare ulteriormente linee orizzontali attraverso di essi come mostrato di seguito:
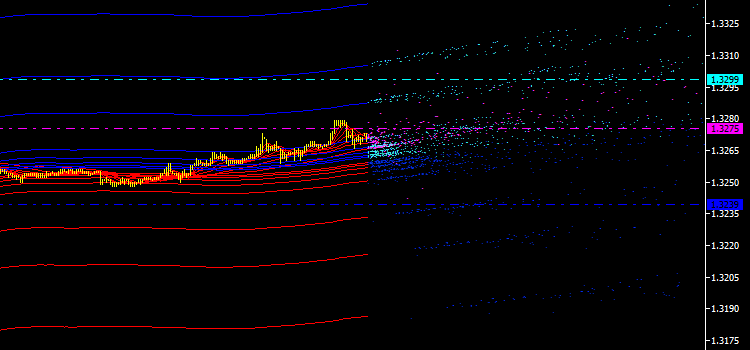
Fig. 3. Linee orizzontali del prezzo medio per ogni tipo di punto
A tal fine, aggiungeremo alcuni blocchi di codice aggiuntivi al codice esistente. Alla sezione dati:
//--- arrays for calculation and display of integral characteristics of emissions #define NUMBER_TYPES_POINT 3 double sum[NUMBER_TYPES_POINT],sumprev[NUMBER_TYPES_POINT]; datetime sum_time[NUMBER_TYPES_POINT]; int n[NUMBER_TYPES_POINT],W[NUMBER_TYPES_POINT]; color colorLine[]={clrAqua,clrBlue,clrMagenta};
Al modulo OnTick():
//--- calculation of integral characteristics of emissions ArrayInitialize(n,0); ArrayInitialize(sum,0.0); ArrayInitialize(sum_time,0.0); for(int obj=total-1;obj>=0;obj--) { string obj_name=ObjectName(0,obj,0,OBJ_TEXT); datetime obj_time=(datetime)ObjectGetInteger(0,obj_name,OBJPROP_TIME); if(obj_time>T[0]) { color obj_color=(color)ObjectGetInteger(0,obj_name,OBJPROP_COLOR); double obj_price=ObjectGetDouble(0,obj_name,OBJPROP_PRICE); for(int i=ArraySize(n)-1; i>=0; i--) if(obj_color==colorPoint[i]) { n[i]++; sum[i]+=obj_price; sum_time[i]+=obj_time; } } } //--- displaying integral characteristics of emissions for(int i=ArraySize(n)-1; i>=0; i--) { if(n[i]>0) { name="H.line."+(string)i; ObjectCreate(0,name,OBJ_HLINE,0,0,0,0); ObjectSetInteger(0,name,OBJPROP_COLOR,colorLine[i]); ObjectSetInteger(0,name,OBJPROP_STYLE,STYLE_DASHDOT); ObjectSetInteger(0,name,OBJPROP_WIDTH,1); ObjectSetDouble(0,name,OBJPROP_PRICE,sum[i]/n[i]); } }
Andiamo avanti. Calcoliamo ora il valore del tempo medio per ogni set di punti e segniamolo sulla riga corrispondente del prezzo medio (vedi Fig. 4). Abbiamo così ottenuto le prime caratteristiche quantitative di emissioni mai statiche, sempre in movimento nello spazio.
Il grafico mostra solo le loro posizioni momentanee. Dobbiamo in qualche modo mantenerli fissi nella storia per poterli studiare in seguito. Finora non è ancora chiaro come ciò possa essere fatto e dobbiamo dargli un'attenta considerazione... Nel frattempo, apporteremo ulteriori miglioramenti e visualizzeremo il numero di punti coinvolti nel calcolo accanto ai marker nel grafico. Questi sono una sorta di pesi delle caratteristiche ottenute che saranno utili anche in ulteriori analisi.
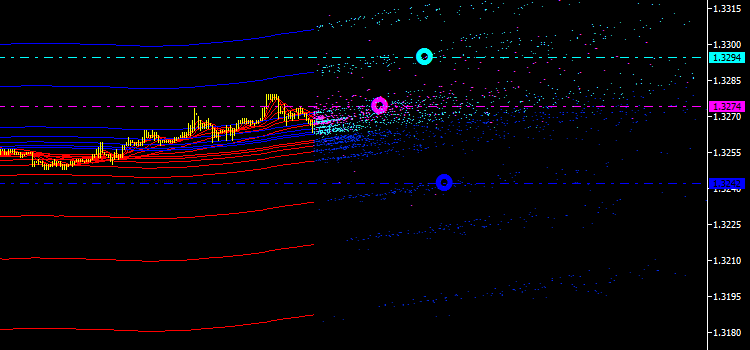
Fig. 4. Indicatori nei punti di intersezione del prezzo medio e del tempo medio
Tuttavia, per comodità dell'analisi, useremo i loro rapporti percentuali. Poiché i principali punti di emissione sono quelli risultanti dalle intersezioni degli indicatori iMA e iEnvelopes, considereremo la loro somma pari al 100%. Vediamo cosa abbiamo adesso:
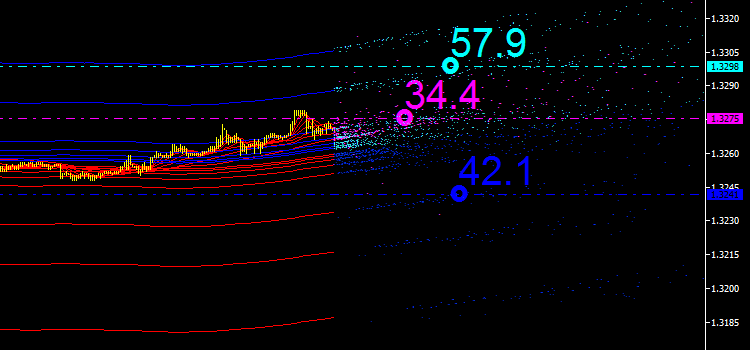
Fig. 5. Rapporto percentuale per ogni tipo di punto di emissione
Se sommiamo i tre valori, daranno più del 100% in totale. Il valore di 34,4 visualizzato in magenta è proprietà dei punti di intersezione di iMA e iMA in un determinato momento, ovvero l'indicatore si è incrociato, ma con dati di input diversi. In questo caso si tratta di un valore di riferimento e si potrebbe pensare in seguito al modo in cui può essere utilizzato nell'analisi di mercato.
Tuttavia, un altro problema sorge quando otteniamo rapporti percentuali sul numero di punti: come possiamo fissare anche i valori percentuali delle caratteristiche di emissione nella storia, tanto più che anch'essi variano?!
Analisi grafica
Sebbene ora abbiamo le caratteristiche integrali delle emissioni, non siamo ancora abbastanza vicini all'analisi e allo sviluppo di una strategia commerciale basata sui dati ottenuti. Tuttavia, un lettore attento deve aver già individuato una soluzione a questo problema (vedi Fig. 1). La soluzione è la seguente: Propongo di disegnare curve integrali utilizzando spessori diversi che sarebbero proporzionali al rapporto percentuale dei principali punti di emissione.
La porzione corrente della curva verrà tracciata lungo la linea del prezzo medio tra la barra attuale e quella precedente, tenendo presente che queste coordinate sono di fatto prese dal futuro. È una sorta di principale canale integrale di emissioni di indicatori. So che suona davvero molto confuso... E devi pensare se dovresti continuare a leggere. Ma spero che questo diventi sempre più interessante man mano che procediamo.
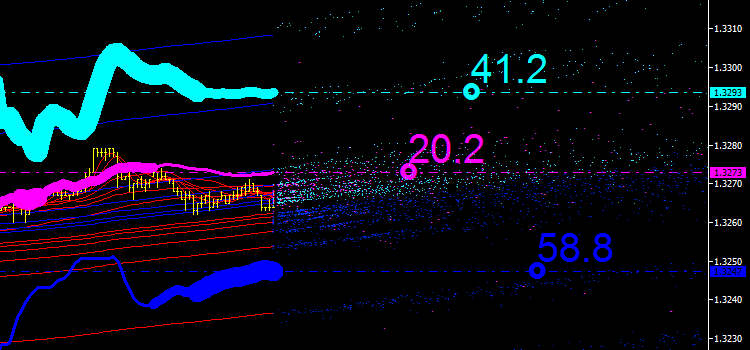
Fig. 6. Canale integrale delle emissioni degli indicatori
Quindi sembra che abbiamo trovato un uso per l'emissione "iMA & iMA" (visualizzata in magenta nel grafico). E abbiamo ottenuto un nuovo indicatore: la media mobile integrata.
Ora torniamo al codice dell'Expert Advisor per vedere quali modifiche sono avvenute nel modulo OnTick():
//--- displaying integral characteristics of emissions ArrayInitialize(W,10); W[ArrayMaximum(n)]=20; W[ArrayMinimum(n)]=3; for(int i=ArraySize(n)-1; i>=0; i--) { if(n[i]>0) { //--- horizontal lines of mean prices name="H.line."+(string)i; ObjectCreate(0,name,OBJ_HLINE,0,0,0,0); ObjectSetInteger(0,name,OBJPROP_COLOR,colorLine[i]); ObjectSetInteger(0,name,OBJPROP_STYLE,STYLE_DASHDOT); ObjectSetInteger(0,name,OBJPROP_WIDTH,1); ObjectSetDouble(0,name,OBJPROP_PRICE,sum[i]/n[i]); //--- markers name="P."+(string)i; ObjectCreate(0,name,OBJ_TEXT,0,0,0); ObjectSetString(0,name,OBJPROP_FONT,"Wingdings"); ObjectSetInteger(0,name,OBJPROP_ANCHOR,ANCHOR_CENTER); ObjectSetInteger(0,name,OBJPROP_FONTSIZE,17); ObjectSetString(0,name,OBJPROP_TEXT,CharToString(163)); ObjectSetInteger(0,name,OBJPROP_COLOR,colorLine[i]); ObjectSetDouble(0,name,OBJPROP_PRICE,sum[i]/n[i]); ObjectSetInteger(0,name,OBJPROP_TIME,sum_time[i]/n[i]); //--- integral curves name="T"+(string)i+".line"+(string)T[1]; ObjectCreate(0,name,OBJ_TREND,0,0,0); ObjectSetInteger(0,name,OBJPROP_COLOR,colorLine[i]); ObjectSetInteger(0,name,OBJPROP_WIDTH,W[i]); if(sumprev[i]>0) { ObjectSetDouble(0,name,OBJPROP_PRICE,0,sumprev[i]); ObjectSetInteger(0,name,OBJPROP_TIME,0,T[1]); ObjectSetDouble(0,name,OBJPROP_PRICE,1,(sum[i]/n[i])); ObjectSetInteger(0,name,OBJPROP_TIME,1,T[0]); } //--- numerical values of integral characteristics name="Text"+(string)i+".control"; ObjectCreate(0,name,OBJ_TEXT,0,0,0); ObjectSetInteger(0,name,OBJPROP_ANCHOR,ANCHOR_LEFT_LOWER); ObjectSetInteger(0,name,OBJPROP_FONTSIZE,30); ObjectSetInteger(0,name,OBJPROP_COLOR,colorLine[i]); string str=DoubleToString((double)n[i]/(double)(n[0]+n[1])*100,1); ObjectSetString(0,name,OBJPROP_TEXT,str); ObjectSetDouble(0,name,OBJPROP_PRICE,0,(sum[i]/n[i])); ObjectSetInteger(0,name,OBJPROP_TIME,0,sum_time[i]/n[i]); } }
Continuiamo la nostra analisi grafica. Ma manca qualcosa... Sembra che abbiamo perso un'altra importante caratteristica di emissione. Le curve integrali sono state tracciate solo sulla base dei prezzi medi. Tuttavia dobbiamo considerare la coordinata del tempo medio. Dai un'occhiata alla figura sottostante e presta particolare attenzione ai limiti del canale:
- La linea dell'acqua è il limite superiore del canale.
- La linea blu è il limite inferiore del canale.
Dobbiamo identificare l'indicatore più vicino nel tempo alla barra zero.
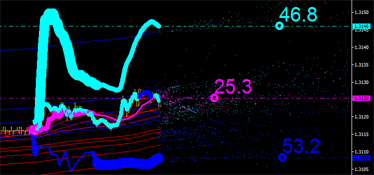 | 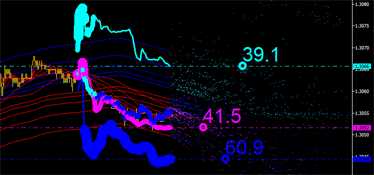 |
|---|
Fig. 7. Caratteristiche integrali costanti nel tempo. Sinistra: limite superiore iniziale del canale. A destra: limite inferiore iniziale del canale.
Questo problema può essere risolto come segue: aggiungiamo la linea del prezzo (PRICE_MEDIAN) al grafico dei prezzi e facciamo cambiare colore alla linea a seconda del colore del marker (acqua o blu) che è più vicino all'ultima barra (vedi Fig. 7). Inoltre, inseriamo il seguente blocco di codice nel codice esistente:
//--- if(n[ArrayMinimum(n)]>0) { datetime d[2]; for(int j=0;j<2;j++) { d[j]=sum_time[j]/n[j]; } int i=ArrayMinimum(d); name="Price.line"+(string)T[1]; ObjectCreate(0,name,OBJ_TREND,0,0,0); ObjectSetInteger(0,name,OBJPROP_WIDTH,8); ObjectSetDouble(0,name,OBJPROP_PRICE,0,HL(H[1],L[1])); ObjectSetInteger(0,name,OBJPROP_TIME,0,T[1]); ObjectSetDouble(0,name,OBJPROP_PRICE,1,HL(H[0],L[0])); ObjectSetInteger(0,name,OBJPROP_TIME,1,T[0]); ObjectSetInteger(0,name,OBJPROP_COLOR,colorLine1[i]); } //---
Ora preparati per il passaggio successivo. E se provassimo a tracciare le emissioni in base alle caratteristiche integrali delle emissioni originali, tipo delle emissioni di secondo ordine? Dopotutto, anche quelle linee si intersecano tra loro e dovrebbero, di conseguenza, avere punti di emissione. Vediamo cosa può venirne fuori. Migliora il blocco di codice precedente aggiungendo le seguenti righe di codice:
//--- emissions of integral characteristics of the original emissions pEmission=EnvMa.CalcPoint(sumprev[0],sum[0]/n[0],sumprev[2],sum[2]/n[2],T[0]); if(pEmission.real) // if the intersection point is found, draw it in the chart { name="test/up"+(string)GTC; EnvMa.CreatePoint(name,pEmission,styleUpper2); } pEmission=EnvMa.CalcPoint(sumprev[1],sum[1]/n[1],sumprev[2],sum[2]/n[2],T[0]); if(pEmission.real) // if the intersection point is found, draw it in the chart { name="test/dn"+(string)GTC; EnvMa.CreatePoint(name,pEmission,styleLower2); }
E inserisci le seguenti righe nella sezione dati:
#define COLOR_2_UPPER C'102,255,255' #define COLOR_2_LOWER C'51,102,255' CodeColor styleUpper2={178,COLOR_2_UPPER,BIG}; CodeColor styleLower2={178,COLOR_2_LOWER,BIG};
Puoi controllare i risultati nella figura sottostante. Possiamo vedere nuovi punti che per ora non suggeriscono nulla.
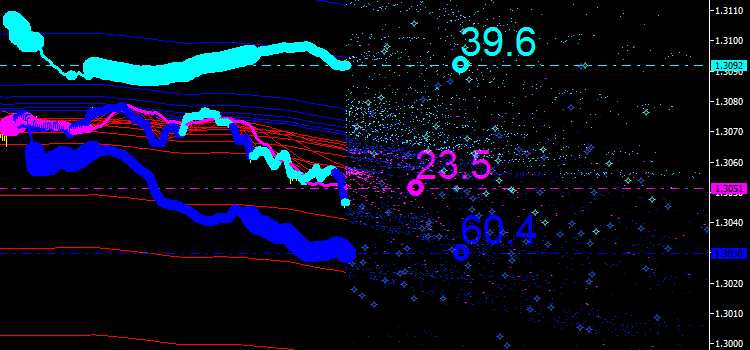
Fig. 8. Emissioni di linee integrali
Le caratteristiche integrali possono ovviamente essere calcolate anche per nuovi punti (vedi Fig. 9) con le loro emissioni riportate nel grafico e così via fino a quando non diventa irrealizzabile!
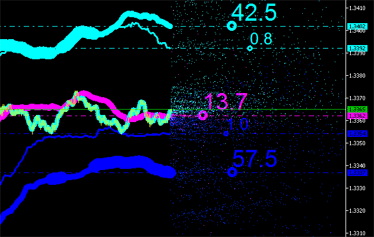 | 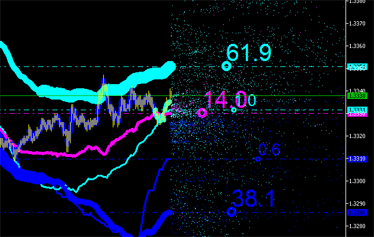 |
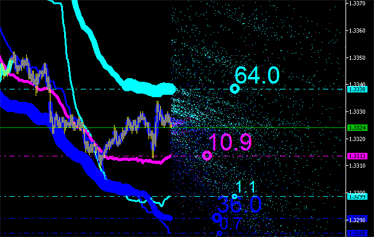 | 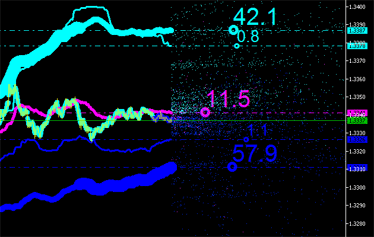 |
Fig. 9. Caratteristiche integrali delle emissioni
Quindi abbiamo tracciato tutto ciò di cui avevamo bisogno e ottenuto le caratteristiche integrali delle emissioni. Possiamo ora procedere alla loro analisi e allo sviluppo di una strategia di trading. Ma sembra ancora impossibile! Cosa ci sta bloccando adesso?
Serie temporale delle emissioni
L'analisi grafica ci consente di studiare le caratteristiche integrali delle emissioni, ma è troppo dispendiosa in termini di risorse. Se proviamo a eseguire il codice proposto nella modalità visiva del tester di strategia, la velocità del test scenderà presto a zero! Ciò è dovuto al gran numero di oggetti grafici nel grafico.
Quindi si vorrebbe naturalmente sbarazzarsi di tutta quell'abbondanza di punti e lasciare solo le curve integrali. Per risolvere questo problema, utilizzeremo array speciali (buffer).
Le serie temporali delle emissioni sono array appositamente organizzati in cui vengono accumulate le informazioni sulle emissioni.
Differiscono dalle serie temporali standard in quanto i dati che contengono non sono sequenziati in base all'ora, anche se l'ora è il campo chiave.
Fig. 10. Serie temporale delle caratteristiche di emissione
Questi array sono disposti in modo tale che i nuovi elementi vengano memorizzati in celle vuote o in celle piene di vecchi valori. A questo scopo utilizzeremo la classe CTimeEmission. Ecco come è implementato nel codice:
//+------------------------------------------------------------------+ //| TimeEmission.mqh | //| Copyright 2013, DC2008 | //| https://www.mql5.com/ru/users/DC2008 | //+------------------------------------------------------------------+ #property copyright "Copyright 2013, DC2008" #property link "https://www.mql5.com/ru/users/DC2008" #property version "1.00" //--- #include <Emission.mqh> #define ARRMAX 64 #define ARRDELTA 8 //+------------------------------------------------------------------+ //| pIntegral structure | //+------------------------------------------------------------------+ struct pIntegral { double y; // Y-coordinate of the price point (mean price of the points with the same time) datetime t; // t-coordinate of the point's time int n; // n-number of points with the same time }; //+------------------------------------------------------------------+ //| Base class for time series of emissions | //+------------------------------------------------------------------+ class CTimeEmission { private: pIntegral time_series_Emission[]; // time series of emission int size_ts; // number of elements in time series datetime t[1]; public: //--- method of writing new elements to time series of emission void Write(PointEmission &point); //--- method of reading integral characteristics of emissions pIntegral Read(); CTimeEmission(); ~CTimeEmission(); }; //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ CTimeEmission::CTimeEmission() { ArrayResize(time_series_Emission,ARRMAX,ARRMAX); size_ts=ArraySize(time_series_Emission); for(int i=size_ts-1; i>=0; i--) time_series_Emission[i].t=0; } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ CTimeEmission::~CTimeEmission() { } //+------------------------------------------------------------------+ //| The Write method of the CTimeEmission class | //+------------------------------------------------------------------+ void CTimeEmission::Write(PointEmission &point) { CopyTime(NULL,0,0,1,t); size_ts=ArraySize(time_series_Emission); for(int k=0;k<size_ts;k++) { if(time_series_Emission[k].t<t[0]) // find the first empty cell { if(k>size_ts-ARRDELTA) { // increase the array size, if necessary int narr=ArrayResize(time_series_Emission,size_ts+ARRMAX,ARRMAX); for(int l=size_ts-1;l<narr;l++) time_series_Emission[l].t=0; } time_series_Emission[k].y=point.y; time_series_Emission[k].t=point.t; time_series_Emission[k].n=1; return; } if(time_series_Emission[k].t==point.t) // find the first similar cell { time_series_Emission[k].y=(time_series_Emission[k].y*time_series_Emission[k].n+point.y)/(time_series_Emission[k].n+1); time_series_Emission[k].n++; return; } } } //+------------------------------------------------------------------+ //| The Read method of the CTimeEmission class | //+------------------------------------------------------------------+ pIntegral CTimeEmission::Read() { CopyTime(NULL,0,0,1,t); pIntegral property_Emission={0.0,0,0}; size_ts=ArraySize(time_series_Emission); for(int k=0;k<size_ts;k++) { if(time_series_Emission[k].t>=t[0]) { property_Emission.y+=time_series_Emission[k].y*time_series_Emission[k].n; property_Emission.t+=(time_series_Emission[k].t-t[0])*time_series_Emission[k].n; property_Emission.n+=time_series_Emission[k].n; } } if(property_Emission.n>0) { property_Emission.y=property_Emission.y/property_Emission.n; property_Emission.t=property_Emission.t/property_Emission.n+t[0]; } return(property_Emission); }
Qui possiamo vedere l'implementazione di due metodi di classe: scrivere i punti di emissione in serie temporali e leggere i valori delle caratteristiche integrali delle emissioni.
Calcolo parsimonioso delle caratteristiche integrali
Ora che abbiamo le serie temporali delle emissioni, possiamo iniziare a creare un algoritmo parsimonioso per il calcolo delle caratteristiche integrali per sviluppare ulteriormente una strategia di trading. Aggiorniamo l'Expert Advisor originale:
//+------------------------------------------------------------------+ //| emission_of_MA_envelope_ts.mq5 | //| Copyright 2013, DC2008 | //| https://www.mql5.com/ru/users/DC2008 | //+------------------------------------------------------------------+ #property copyright "Copyright 2013, DC2008" #property link "https://www.mql5.com/ru/users/DC2008" #property version "1.00" //--- #include <GetIndicatorBuffers.mqh> #include <Emission.mqh> #include <TimeEmission.mqh> //--- number of point types #define NUMBER_TYPES_POINT 3 //--- array for storing the iMA indicator periods int MA[]={4,7,11,19,31,51,85}; //--- external variable for storing averaging period of the iEnvelopes indicator input int ma_period=140; // averaging period of the iEnvelopes indicator //--- array for storing deviations of the iEnvelopes indicator double ENV[]={0.01,0.0165,0.0273,0.0452,0.0747,01234,0.204,0.3373,0.5576,0.9217,1.5237}; //--- array for storing pointers to the iMA indicator int handle_MA[]; //--- array for storing pointers to the iEnvelopes indicator int handle_Envelopes[]; //--- market data datetime T[],prevTimeBar=0; double H[],L[]; #define HL(a, b) (a+b)/2 //--- class instances CEmission EnvMa(0,200); PointEmission pEmission; CTimeEmission tsMA[NUMBER_TYPES_POINT]; pIntegral integral[NUMBER_TYPES_POINT]; //--- drawing styles for points of emission #define DEL 500 //--- arrays for calculation and display of integral characteristics of emissions double sumprev[NUMBER_TYPES_POINT]; int n[NUMBER_TYPES_POINT],W[NUMBER_TYPES_POINT]; color colorLine[]={clrAqua,clrBlue,clrMagenta}; int fontPoint[]={30,30,30}; int fontMarker[]={16,16,16}; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { ArraySetAsSeries(T,true); ArraySetAsSeries(H,true); ArraySetAsSeries(L,true); ArrayInitialize(sumprev,0.0); //--- int size=ArraySize(MA); ArrayResize(handle_MA,size); //--- create a pointer to the object - the iMA indicator for(int i=0; i<size; i++) { handle_MA[i]=iMA(NULL,0,MA[i],0,MODE_SMA,PRICE_MEDIAN); //--- if an error occurs when creating the object, print the message if(handle_MA[i]<0) { Print("The iMA object[",MA[i],"] has not been created: Error = ",GetLastError()); //--- forced program termination return(-1); } } //+------------------------------------------------------------------+ size=ArraySize(ENV); ArrayResize(handle_Envelopes,size); //--- create a pointer to the object - the iEnvelopes indicator for(int i=0; i<size; i++) { handle_Envelopes[i]=iEnvelopes(NULL,0,ma_period,0,MODE_SMA,PRICE_MEDIAN,ENV[i]); //--- if an error occurs when creating the object, print the message if(handle_Envelopes[i]<0) { Print("The iEnvelopes object[",ENV[i],"] has not been created: Error = ",GetLastError()); //--- forced program termination return(-1); } } //--- return(0); } //+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- } //+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- market data CopyTime(NULL,0,0,2,T); CopyHigh(NULL,0,0,2,H); CopyLow(NULL,0,0,2,L); //--- fill the declared arrays with current values from all indicator buffers string name; uint GTC=GetTickCount(); //---- indicator buffers double ibMA[],ibMA1[]; // arrays for the iMA indicator double ibEnvelopesUpper[]; // array for the iEnvelopes indicator (UPPER_LINE) double ibEnvelopesLower[]; // array for the iEnvelopes indicator (LOWER_LINE) for(int i=ArraySize(handle_MA)-1; i>=0; i--) { if(!CopyBufferAsSeries(handle_MA[i],0,0,2,true,ibMA)) return; //--- for(int j=ArraySize(handle_Envelopes)-1; j>=0; j--) { if(!GetEnvelopesBuffers(handle_Envelopes[j],0,2,ibEnvelopesUpper,ibEnvelopesLower,true)) return; //--- find the intersection point of the iEnvelopes(UPPER_LINE) and iMA indicators pEmission=EnvMa.CalcPoint(ibEnvelopesUpper[1],ibEnvelopesUpper[0],ibMA[1],ibMA[0],T[0]); if(pEmission.real) // if the intersection point is found, add it to the time series of emission tsMA[0].Write(pEmission); //--- find the intersection point of the iEnvelopes(LOWER_LINE) and iMA indicators pEmission=EnvMa.CalcPoint(ibEnvelopesLower[1],ibEnvelopesLower[0],ibMA[1],ibMA[0],T[0]); if(pEmission.real) // if the intersection point is found, add it to the time series of emission tsMA[1].Write(pEmission); } //--- for(int j=ArraySize(handle_MA)-1; j>=0; j--) { if(i!=j) { if(!CopyBufferAsSeries(handle_MA[j],0,0,2,true,ibMA1)) return; //--- find the intersection point of the iMA and iMA indicators pEmission=EnvMa.CalcPoint(ibMA1[1],ibMA1[0],ibMA[1],ibMA[0],T[0]); if(pEmission.real) // if the intersection point is found, add it to the time series of emission tsMA[2].Write(pEmission); } } } //--- deletion of the graphical objects of emission not to stuff the chart if(T[0]>prevTimeBar) { prevTimeBar=T[0]; //--- for(int i=ArraySize(n)-1; i>=0; i--) sumprev[i]=integral[i].y; //--- for(int obj=ObjectsTotal(0,0,-1)-1;obj>=0;obj--) { string obj_name=ObjectName(0,obj,0,OBJ_TREND); datetime obj_time=(datetime)ObjectGetInteger(0,obj_name,OBJPROP_TIME); if(obj_time<T[0]-DEL*PeriodSeconds()) ObjectDelete(0,obj_name); } Comment("Emission © DC2008 Graphical objects = ",ObjectsTotal(0,0,-1)); } //--- calculation of integral characteristics of emission for(int i=ArraySize(n)-1; i>=0; i--) integral[i]=tsMA[i].Read(); //--- displaying integral characteristics of emission ArrayInitialize(W,5); if(integral[0].n>integral[1].n) { W[0]=20; W[1]=10; } else { W[0]=10; W[1]=20; } for(int i=ArraySize(n)-1; i>=0; i--) { //--- horizontal lines of mean prices name="H.line."+(string)i; ObjectCreate(0,name,OBJ_HLINE,0,0,0,0); ObjectSetInteger(0,name,OBJPROP_COLOR,colorLine[i]); ObjectSetInteger(0,name,OBJPROP_STYLE,STYLE_DASHDOT); ObjectSetInteger(0,name,OBJPROP_WIDTH,1); ObjectSetDouble(0,name,OBJPROP_PRICE,integral[i].y); //--- markers name="P."+(string)i; ObjectCreate(0,name,OBJ_TEXT,0,0,0); ObjectSetString(0,name,OBJPROP_FONT,"Wingdings"); ObjectSetInteger(0,name,OBJPROP_ANCHOR,ANCHOR_CENTER); ObjectSetInteger(0,name,OBJPROP_FONTSIZE,fontMarker[i]); ObjectSetString(0,name,OBJPROP_TEXT,CharToString(163)); ObjectSetInteger(0,name,OBJPROP_COLOR,colorLine[i]); ObjectSetDouble(0,name,OBJPROP_PRICE,integral[i].y); ObjectSetInteger(0,name,OBJPROP_TIME,integral[i].t); //--- integral curves name="T"+(string)i+".line"+(string)T[1]; ObjectCreate(0,name,OBJ_TREND,0,0,0); ObjectSetInteger(0,name,OBJPROP_COLOR,colorLine[i]); ObjectSetInteger(0,name,OBJPROP_WIDTH,W[i]); if(sumprev[i]>0) { ObjectSetDouble(0,name,OBJPROP_PRICE,0,sumprev[i]); ObjectSetInteger(0,name,OBJPROP_TIME,0,T[1]); ObjectSetDouble(0,name,OBJPROP_PRICE,1,integral[i].y); ObjectSetInteger(0,name,OBJPROP_TIME,1,T[0]); } //--- numerical values of integral characteristics if(integral[0].n+integral[1].n>0) { name="Text"+(string)i+".control"; ObjectCreate(0,name,OBJ_TEXT,0,0,0); ObjectSetInteger(0,name,OBJPROP_ANCHOR,ANCHOR_LEFT_LOWER); ObjectSetInteger(0,name,OBJPROP_FONTSIZE,fontPoint[i]); ObjectSetInteger(0,name,OBJPROP_COLOR,colorLine[i]); string str=DoubleToString((double)integral[i].n/(double)(integral[0].n+integral[1].n)*100,1); ObjectSetString(0,name,OBJPROP_TEXT,str); ObjectSetDouble(0,name,OBJPROP_PRICE,0,integral[i].y); ObjectSetInteger(0,name,OBJPROP_TIME,0,integral[i].t); } } }
Il codice si è accorciato, mentre la velocità di calcolo è aumentata. Ora puoi testare e ottimizzare i tuoi robot di trading senza visualizzazione!
Uso delle caratteristiche integrali nel trading
Le caratteristiche integrali possono essere utilizzate come generatore di segnali per:
- svolta del canale,
- intersezione tra loro o il prezzo,
- cambiare direzione.
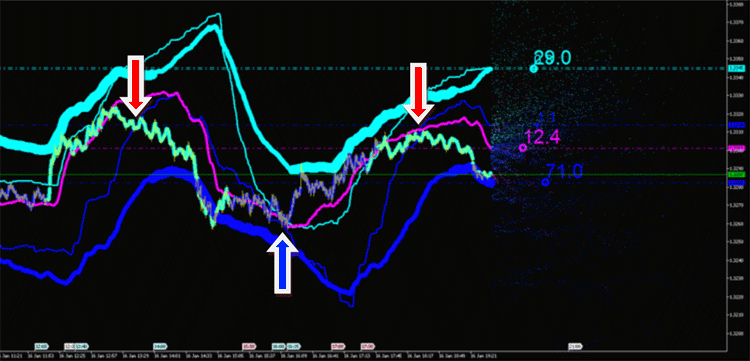
Fig. 11. Segnali di scambio agli incroci delle caratteristiche integrali delle emissioni
Conclusione
- Il calcolo delle caratteristiche integrali delle emissioni degli indicatori fornisce nuovi strumenti e metodi per l'analisi di mercato (serie temporali).
- Utilizzando le serie temporali, siamo riusciti ad aumentare la velocità dei calcoli delle caratteristiche integrali.
- E ci ha aperto la possibilità di sviluppare strategie di trading automatizzate che utilizzano le emissioni.
Tradotto dal russo da MetaQuotes Ltd.
Articolo originale: https://www.mql5.com/ru/articles/610
Avvertimento: Tutti i diritti su questi materiali sono riservati a MetaQuotes Ltd. La copia o la ristampa di questi materiali in tutto o in parte sono proibite.
Questo articolo è stato scritto da un utente del sito e riflette le sue opinioni personali. MetaQuotes Ltd non è responsabile dell'accuratezza delle informazioni presentate, né di eventuali conseguenze derivanti dall'utilizzo delle soluzioni, strategie o raccomandazioni descritte.
 Informazioni generali sui segnali di trading per MetaTrader 4 e MetaTrader 5
Informazioni generali sui segnali di trading per MetaTrader 4 e MetaTrader 5
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Accetti la politica del sito e le condizioni d’uso
Eccone uno...
Guarda il video
Video sull'argomento
Video sulle emissioni
DC2008, puoi dirmi cosa sono le linee in più (blu con valore 0,8 e blu con valore 1,1)?