Un nuevo enfoque para los criterios personalizados en las optimizaciones (Parte 1): Ejemplos de funciones de activación

Introducción

La búsqueda de la optimización ideal para encontrar la combinación adecuada de parámetros continúa. El foro está repleto de métodos sugeridos para persuadir al Optimizador de MetaTrader de que devuelva y clasifique los distintos pases para permitir que un desarrollador elija una combinación (o combinaciones) de parámetros que sean estables. La introducción de empresas de Prop Trading (o empresas de fondeo) en el panorama, con sus rigurosos límites, comprensiblemente mucho más estrictos de lo que podría exigir un operador privado, ha hecho que esto sea aún más difícil.

La capacidad de definir un criterio personalizado, e incluso utilizar el criterio complejo con su metodología opaca, ha introducido la posibilidad de reducir el análisis sintáctico o, al menos, el análisis de los resultados en Excel, Python, R o en software propietario, para obtener la mejor permutación de parámetros.

El problema es que todavía no es raro ver el uso de return(0) en criterios personalizados publicados. Esto conlleva peligros reales o potenciales, entre ellos la posibilidad de descartar resultados (apenas) no deseados o, lo que es peor, desviar el proceso de optimización genética de vías potencialmente productivas.

En un intento por volver a algunos principios básicos, tras realizar algunos experimentos muy empíricos, traté de encontrar algunas ecuaciones de curvas. Para ello, consulté la publicación «Activation Functions in Neural Networks» y adopté y modifiqué algunas para utilizarlas aquí. Además, tras haberlos aclarado, he sugerido algunos métodos para ponerlos en práctica.

El plan para esta serie de artículos es el siguiente:

1. Introducción y funciones de activación estándar con código MQL5
2. Modificaciones, escalado y ponderación, y ejemplos reales.
3. Una herramienta para explorar diferentes curvas, escalas y ponderaciones.
4. Cualquier otro punto que surja...

Estado actual del uso de criterios personalizados

Dos colaboradores, por quienes siento un gran respeto, hicieron algunas observaciones excelentes para ilustrar el problema, con inquietudes sobre el uso de return(0) y los resultados devueltos por el criterio complejo. Alain Verleyen, moderador del foro, informa que una operación que arroja una pérdida de 6000 obtiene una puntuación más alta que otra que arroja un beneficio de 1736 con más operaciones (y una puntuación considerablemente mejor en cuanto a factor de beneficio, RF, ratio de Sharpe y drawdown). Alain dice: «El críptico «criterio complejo» da algunos resultados extraños». Yo iría más allá y diría que sin duda debe generar dudas significativas sobre la metodología que hay detrás del criterio complejo. Si, como comenta Muhammad Fahad más adelante en el mismo hilo, y estoy seguro de que tiene razón, «los resultados de saldo negativo no son especialmente malos para la optimización, sino que desempeñan un papel crucial en la evaluación que la generación futura hace de lo malo y lo peor mientras se cruzan los genes», la obtención de una puntuación tan positiva podría desviar al optimizador genético.

Hace mucho, mucho tiempo que no utilizo MT4, pero recuerdo vagamente la posibilidad de introducir restricciones para determinadas estadísticas de resultados. En MQL5, a primera vista, parece que no hay otra forma de hacerlo que utilizar el instrumento muy contundente de return(0) en un criterio personalizado, cuyas posibles desventajas ya se han mencionado. Se me ocurre que si podemos obtener un valor de retorno muy cercano a 1 cuando la ratio o métrica está en o por encima de nuestro mínimo deseado, en o por debajo de nuestro máximo deseado, o incluso en o cerca de un objetivo específico, y luego multiplicando los valores de cada métrica/ratio entre sí y multiplicando el resultado por 100, podríamos estar en el buen camino...

¿Por qué buscar inspiración en las redes neuronales?

1.- Optimización genética como red neuronal... 

Independientemente de si el algoritmo genético tiene una red neuronal detrás, el proceso lógico parece ser el mismo: probar una combinación paramétrica, puntuarla (según el criterio de optimización seleccionado), conservar las selecciones potencialmente rentables para su mejora posterior y descartar el resto. Esto se repite hasta que la mejora en la puntuación seleccionada se estabiliza.

2.- Valles, gradientes explosivos, ponderación, normalización y selección manual. 

El problema de la superficie de error no convexa es bien conocido en el aprendizaje automático. Del mismo modo, parece que en la optimización genética podríamos acabar en mínimos locales o puntos de inflexión, desviados por las instrucciones return(0) que provocan el descarte de «conocimiento» por parte del algoritmo genético.

El procesamiento de diversas métricas para formar un criterio personalizado también requiere mucha reflexión. Mis primeros intentos fueron muy rudimentarios, ya que utilicé diversos factores para la división y la multiplicación, por no mencionar los factores exponenciales, lo que dio lugar a puntuaciones que rozaban lo absurdamente alto (gradiente explosivo). El complejo algoritmo de puntuación del criterio utiliza claramente una función para limitar la puntuación entre 0 y 100, lo que sugiere el uso de una función de tipo sigmoide o logística.

La necesidad de aplicar ponderaciones a los componentes individuales de un criterio personalizado es evidente: necesitamos utilizar ponderaciones para determinar la prioridad de los distintos componentes y normalizar tanto las entradas, para ajustar la sensibilidad de nuestro modelo, como las salidas, para permitir la comparación entre modelos. En un próximo artículo analizaremos la ponderación y la normalización.

Cuando analizamos los resultados de una optimización, ya sea manualmente o en una hoja de cálculo, podemos ordenarlos según diversas medidas de rendimiento, filtrar los resultados y, de forma rápida y casi inconsciente, seleccionar conjuntos de parámetros por el color de las métricas clave. Aquí simplemente estamos volviendo a aplicar los procesos descritos, que son en sí mismos un intento de imitar nuestro propio procesamiento intelectual del resultado completo.

Funciones de activación en redes neuronales

Me llama la atención que las funciones que estaba buscando eran similares a las que encontré hace uno o dos años cuando estaba estudiando las funciones de activación en redes neuronales.

Las funciones de activación en las redes neuronales se pueden clasificar, en términos generales, en tres tipos: binarias, lineales y no lineales:

• Las funciones binarias clasifican los valores en una de dos clases devolviendo 1 o 0. No son especialmente útiles en nuestro caso de uso.
• Las funciones lineales devuelven transformaciones mediante simples operaciones de suma, multiplicación, resta o división, o una combinación de las mismas. Tampoco son de gran ayuda en nuestro caso de uso.
• Las funciones no lineales devuelven curvas de resultados que están restringidas en los extremos de x, pero permiten discriminar los valores de x a través de un rango centrado en 0. Este rango y centro se pueden modificar mediante el uso de compensaciones.

Cabe señalar que el uso de

return(0);

así como el retorno sin restricciones del producto de numerosas medidas de resultado, de lo cual soy culpable, y que sigo viendo en los foros, son métodos que replican los problemas asociados con estas dos primeras clases; por otro lado, las funciones no lineales tienden a estar restringidas para evitar gradientes explosivos, mientras mantienen un gradiente de -∞ a ∞.

A modo de explicación, recapitularé algunos de los ejemplos estándar. Analizaremos ReLU, Softplus, Sigmoid y Tanh, junto con, en el próximo artículo, mis propias modificaciones: Flipped ReLU, Point ReLU, Flipped Sigmoid, Point Sigmoid, Flipped Tanh y Point Tanh.

a) Función de activación ReLU

El objetivo de esta función es devolver cero cuando x es <= 0 y x si x > 0, o, en notación matemática, f(x) = max(0,x). La línea obtenida se ilustra a continuación, y la función MQL5 se puede definir así:

double ReLU(double x) {
   return(MathMax(0, x));
}

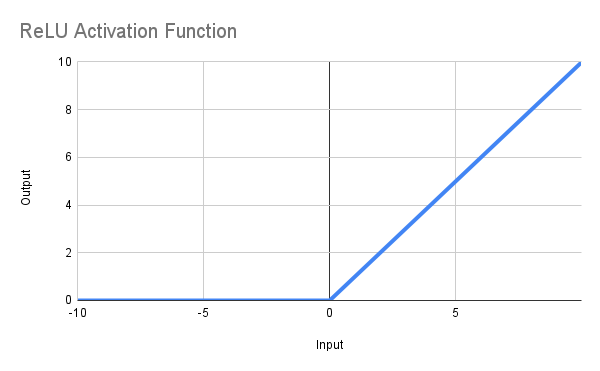
Hasta ahora todo bien, dirás, pero quiero fijar un valor mínimo para el factor de recuperación de 5 o superior... Bueno, simplemente cambia el código a *:

input double MinRF = 5.0;

double RF = TesterStatistics(STAT_RECOVERY_FACTOR);
double DeviationRF = RF - MinRF;

double ReLU(double x) {
   return(MathMax(0, x));
}

double ScoreRF = ReLU(DeviationRF);

Desplazando así la línea hacia la derecha, partiendo de 0 en RF = 5,0, tal y como se ilustra:

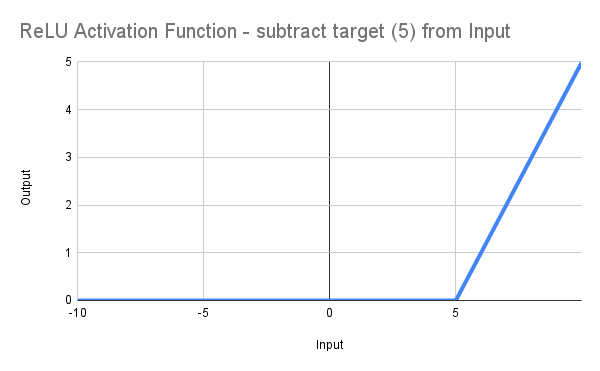
Esto, por supuesto, no es mucho más avanzado que escribir *:

input double MinRF = 5.0;

double RF = TesterStatistics(STAT_RECOVERY_FACTOR);
double ScoreRF = (RF - MinRF);

Pero nos da un punto de partida...

* Hay otro problema, y es que el valor objetivo, 5, en realidad devolverá 0 y solo los valores >5 devolverán un valor distinto de cero. No pretendo dedicar tiempo a este tema, ya que los diversos problemas que presenta esta función impiden que siga siendo útil en nuestro caso de uso.

Problemas

Pronto queda claro que aún tenemos dos problemas, ambos derivados de la simplicidad inherente de nuestro código. Dije anteriormente:

«Esto, por supuesto, no es mucho más avanzado que escribir

input double MinRF = 5.0;
double RF = TesterStatistics(STAT_RECOVERY_FACTOR);


double ScoreRF = (RF - MinRF);

Pero nos da un punto de partida...»

Los problemas son bien conocidos en las redes neuronales:

• ReLU moribundo: La principal debilidad de ReLU es que las neuronas pueden «morir» permanentemente cuando solo producen ceros. Esto ocurre cuando las entradas muy negativas crean gradientes cero, lo que hace que estas neuronas se vuelvan inactivas y no puedan seguir aprendiendo. Esto también se conoce como el problema del gradiente desaparecido.

• Salida sin restricciones: Las salidas ReLU pueden crecer infinitamente para entradas positivas, a diferencia de las funciones Sigmoid o Tanh, que tienen límites superiores incorporados. Esta falta de una restricción superior puede provocar en ocasiones problemas de explosión del gradiente durante el entrenamiento de redes neuronales profundas. Esto también se conoce como el problema del gradiente explosivo.

El segundo problema se aborda en estadística normalizando los valores en una ventana de observación, pero este método no está disponible para nosotros dentro de los límites del optimizador.

Por lo tanto, necesitamos una solución que

1. genere restricciones matemáticas, proporcionando una normalización automatizada; y
2. ofrezcan cierto grado de linealidad, en lugar de devolver 0, en una parte significativa de la muestra.

b) Función de activación Softplus

No pretendo entrar en detalles aquí, pero lo menciono de pasada como una etapa entre ReLU y las funciones superiores. Está bien descrito en Geeksforgeeks y simplemente publicaré la siguiente imagen, fórmula y código. Debe quedar claro que, al abordar el problema del ReLU moribundo, el problema de salida sin restricciones continúa. Además, hay una transición suave entre la cola muy poco profunda y la pendiente derecha. Esto introduce la necesidad de considerar una compensación de corrección, un concepto al que volveremos más adelante:

La fórmula es Softplus(x) = ln(1 + e^x) y el código MQL5 es

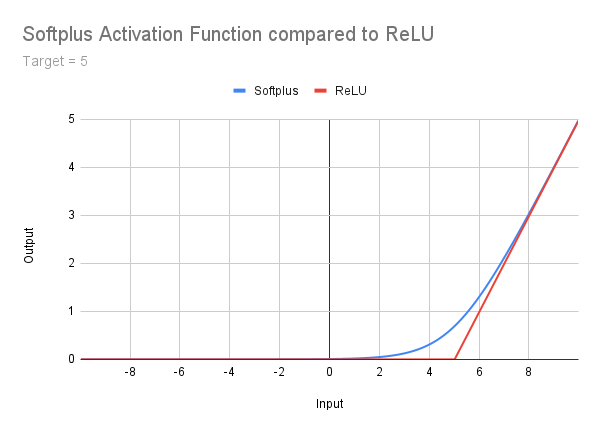
double Softplus(double x) {
   return(MathLog(1 + MathExp(x)));
}

Disfruta leyendo si lo deseas, pero ahora llegamos a las funciones que nos dan resultados restringidos entre 0 y 1.

c) Función de activación sigmoidea

La función sigmoide se expresa matemáticamente como f(x) = 𝛔(x) = 1 / (1 + e^(-x)). Es idéntica a la derivada de la función Softplus y se puede codificar en MQL5 de la siguiente manera:

double Sigmoid(double x) {
   return(1 / (1 + MathExp(-x)));
}

Al observar la curva (abajo), se aprecia inmediatamente que

1. está restringido entre 0 y 1, resolviendo así nuestro problema de salida sin restricciones;

2. aunque es difícil apreciarlo a esta escala, se mantiene un gradiente variable, que nunca llega a cero, desde -∞ hasta ∞; y 

3. La curva sin desplazamiento obtiene una puntuación de 0,5 con un valor de 0.

Para abordar el punto 3), de modo que nos acerquemos al punto 1 cuando x == nuestro valor umbral (objetivo), es necesario desplazar la curva hacia la izquierda, no solo por nuestro valor umbral, sino también por una corrección que se consigue prácticamente utilizando un valor de corrección >= 5. 

Por lo tanto, la implementación en MQL5 es:

input double MinRF = 5.0;
sinput double SigCorrection = 5;

double RF = TesterStatistics(STAT_RECOVERY_FACTOR);
double DeviationRF = RF - MinRF;

double CorrectedSigmoid(double x) {
   return(1 / (1 + MathExp(-(x - SigCorrection))));
}

double ScoreRF = CorrectedSigmoid(DeviationRF);

A continuación se ilustra la curva de la función sigmoidea sin corregir para un objetivo de 5, junto con la derivada (multiplicada por 4) que se analizará a continuación.

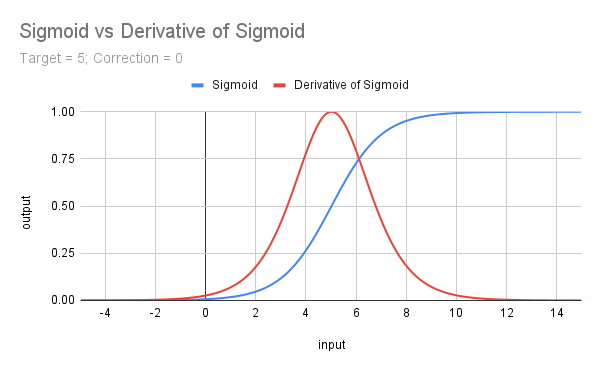
d) Derivada de la sigmoide (𝛔')

Esto nos da una forma agradable, centrada y maximizada en x = 0... Representa la pendiente de la función sigmoide, y la fórmula es f(x) = 𝛔(x) - 𝛔^2(x) o 𝛔(x) * (1 - 𝛔(x)). 

La función adolece potencialmente (al igual que todas las no funciones que consideraremos) del problema del gradiente desaparecido, un riesgo que puede mitigarse con el simple recurso de multiplicarla por 4 (ya que 𝛔’(x) = 0,25), lo que además, de manera útil, vuelve a restringir el resultado entre 0 y 1. El centrado en un valor de x nos permite apuntar a un punto o, más correctamente, a un rango centrado en un punto.

En MQL5 podemos hacerlo así:

input double TargetTrades = 100;

double Trades = TesterStatistics(STAT_TRADES);
double DeviationTrades = Trades - TargetTrades;

double Sigmoid(double x) {
   return(1 / (1 + MathExp(-x)));
}

double Deriv4Sigmoid(double x) {
   return(4 * (Sigmoid(x) * (1 - Sigmoid(x))));
}

double ScoreTrades = Deriv4Sigmoid(DeviationTrades);

Nota: Dado que nuestros resultados para la función sigmoide, su derivada (multiplicada por 4) y la siguiente función Tanh y su derivada, ambas reescaladas entre 0 y 1, están todos restringidos entre 0 y 1, no necesitamos proporcionar ningún escalar adicional en la producción. Por supuesto, podemos multiplicarlos por cualquier factor para normalizarlos o darles prioridad sobre cualquier otro índice de optimización que podamos incluir en nuestro criterio personalizado final. Veamos esto en el próximo artículo.

Nos queda por explorar una última función estándar, y esa es Tanh...

e) Tangente hiperbólica o Tanh

Tanh es la última de nuestras funciones de activación que vamos a explorar en nuestra búsqueda de utilidad en los criterios personalizados. Seguiré un patrón similar con menos explicaciones que antes, pero aplicando los mismos principios.

El siguiente gráfico muestra la gráfica de Tanh con su derivada.

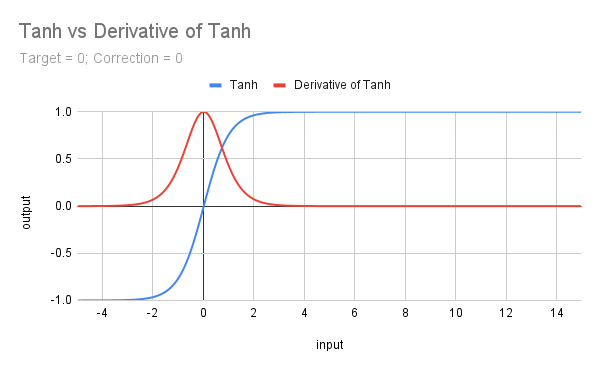
La fórmula para Tanh es f(x) = (e^x - e^(-x))/(e^x + e^(-x)) y en MQL5 tiene su propia función, por lo que es fácil de codificar. Por supuesto, tenemos que manejar valores objetivo y factores de corrección, pero aún así nos facilita la vida:

input double MinRF = 5.0;
sinput double TanhCorrection = 2.5; // Anything between 2 and 3 would be reasonable (see last figure)

double RF = TesterStatistics(STAT_RECOVERY_FACTOR);
double DeviationRF = RF - MinRF;

double CorrectedRSTanh(double x) {
   return((MathTanh(x  + TanhCorrection) + 1) / 2);  // rescaled and corrected
}

double ScoreRF = CorrectedRSTanh(DeviationRF);

El código anterior reescala la función subyacente para limitarla entre 0 y 1 (sumando 1 y dividiendo por 2). También introduce un factor de corrección y un objetivo, y la curva resultante se muestra en el siguiente gráfico que ilustra la derivada de Tanh. No debe pasar desapercibido para nadie que Tanh tiene una forma similar al sigmoide, y que ambas son derivadas entre sí; exploraremos estas similitudes en el próximo artículo.

f) Derivada de Tanh

La fórmula matemática para la derivada de Tanh es f(x) = 1 - Tanh^2(x).

En MQL5 podemos hacerlo así:

input double TargetTrades = 100;

double Trades = TesterStatistics(STAT_TRADES);
double DeviationTrades = Trades - TargetTrades;

double DerivTanh(double x) {
   return(1 - MathPow(x, 2));

}double ScoreTrades = DerivTanh(DeviationTrades);

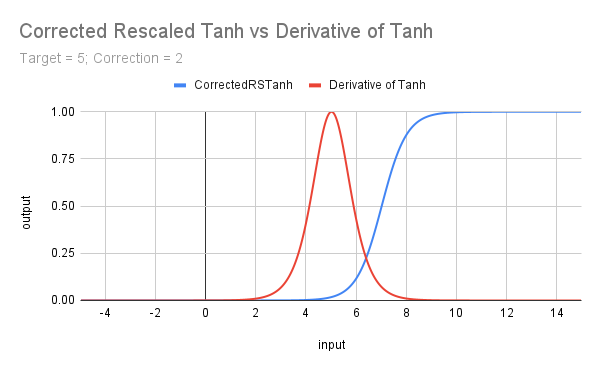
El siguiente gráfico muestra el efecto de reescalar la función Tanh, corrigiéndola para aproximar el despegue desde 0 con el valor objetivo (umbral) de x, e introduciendo un objetivo tanto para Tanh como para la derivada de Tanh.

Resumen y próximos pasos

En este artículo, hemos analizado brevemente la relación entre el aprendizaje automático, por un lado, y el proceso de optimización con «posprocesamiento» (ya sea genético o completo), además del posprocesamiento manual o con Excel, por otro. Hemos comenzado a analizar cómo los distintos tipos de funciones de activación pueden perfeccionar los criterios personalizados y cómo codificarlos.

Los problemas de los gradientes que desaparecen y explotan en ReLU y Softplus nos han llevado a centrar nuestra atención en funciones con curvas como la de la función sigmoide y también la de su derivada. Hemos visto cómo esto nos permite favorecer, en nuestra puntuación, rangos de enlace único (es decir, x > t) o rangos de doble enlace (t1 < x < t2), al tiempo que se elimina el problema de los gradientes explosivos y se mitiga el de los gradientes que desaparecen.

Hemos analizado el uso de compensaciones correccionales y compensaciones objetivo para ayudar a garantizar que se preste atención a los rangos de valores de atributos deseados.

En el próximo artículo, veremos algunas modificaciones de esta lista de funciones estándar con atributos similares, pero no idénticos. También exploraremos la idea de escalado y ponderación antes de ver ejemplos del uso de diferentes funciones en los criterios personalizados.