优化中自定义准则的新方法（第一部分）：激活函数示例

概述

寻找理想的优化方法以确定正确参数组合的探索仍在继续。论坛上充斥着各种建议的方法，旨在说服MetaTrader优化器返回并对各种优化结果进行排序，以便开发者能够选择稳定的一种（或多种）参数组合。随着自营交易公司的加入，设定更严格的界限（其严苛程度远超普通个人交易者的需求），使得这一挑战愈发严峻。

自定义准则的定义能力，甚至利用其不透明方法论的复合准则，使得减少在Excel、Python、R或专有软件中对结果进行解析或至少分析的工作量成为可能，从而获得最优的参数排列组合。

其问题在于，在已发布的自定义准则中，使用“return(0)”的情况仍屡见不鲜。这样存在实际或潜在的危险，包括可能丢弃（勉强）不符合要求的结果，或者更糟的是，使遗传优化过程偏离潜在的有效路径。

在试图重现一些基本原理的过程中，我进行了一些符合实证的实验，尝试寻找一些曲线方程。为此，我查阅了《神经网络中的激活函数》一文，并对其中的一些函数进行了改编，以便在此处使用。此外，在阐明这些函数后，我还提出了一些将其付诸实践的方法。

本系列文章的结构如下：

1. 引言及标准激活函数（附MQL5代码）
2. 修改、缩放、加权及实际案例
3. 探索不同曲线、缩放和加权的工具
4. 其他可能出现的问题……

自定义准则的当前使用情况

两位我极为敬重的论坛贡献者，提出了一些绝佳观点来阐明问题，他们对于在自定义准则中使用“return(0)”以及复合准则所返回的结果感到担忧。论坛版主阿兰·韦莱恩（Alain Verleyen）反馈 ，有一组参数结果亏损6000，但其得分却高于另一组盈利1736且交易次数更多（且在盈利因子、风险回报比、夏普比率以及回撤方面表现均大幅优于前者）的参数。阿兰说：“神秘的‘复合准则’给出了一些奇怪的结果。”我则更进一步认为，这无疑会让人对复合准则背后的方法论产生重大质疑。正如穆罕默德·法哈德（Muhammad Fahad）在同一帖子的后续部分所评论的那样——我确信他说得没错——“负余额结果对于优化而言并非特别糟糕，在基因交叉过程中，它们对于后代判断优劣起着至关重要的作用”，而如此高的正向得分可能会误导遗传优化器。

我使用MT4已是很久很久以前的事了，但我依稀记得当时可以为某些结果统计数据设置约束条件。在MQL5中，乍一看，除了在自定义准则中使用极为粗暴的“return(0)”方法外，似乎无法实现这一点，而“return(0)”的潜在弊端此前已提及。我突发奇想，如果当比率或指标达到或高于期望的最小值、达到或低于期望的最大值，甚至达到或接近特定目标时，我们能得到一个非常接近1的返回值，然后将每个指标/比率的值相乘，再将结果乘以100，或许我们就能有所突破……

为什么要从神经网络中寻找灵感？

1.遗传优化与神经网络类似…… 

无论遗传算法背后是否有神经网络支撑，其逻辑过程似乎都是相同的——尝试一组参数组合，根据所选的优化准则对其进行评分，保留可能盈利的选项以进一步优化，并舍弃其余选项。这一过程不断重复，直至所选分数不再提升。

2.低谷、梯度爆炸、加权、归一化与手动选择 

在机器学习领域，非凸误差曲面问题广为人知。类似地，在遗传优化中，我们似乎也可能最终陷入局部最小值或鞍点，这是由于“return(0)”语句误导了遗传算法，使其丢弃了“认知”。

将各种指标处理以形成自定义准则也需要深思熟虑……我早期的尝试非常简单，使用了各种除法和乘法因子，更不用说指数因子了，结果导致分数高得离谱（梯度爆炸）……显然，复合准则分数算法使用了一种函数将分数限制在0到100之间，提示其使用了Sigmoid或逻辑型函数。

显然，应该对自定义准则的各个组成部分应用权重：我们需要利用权重来确定各个组成部分的优先级，同时对输入和输出进行标准化处理，以调整模型的敏感度，并便于对不同模型进行比较。我们将在之后的文章中探讨加权和标准化问题。

当我们手动或在电子表格中查看优化运行结果时，我们可能会根据各种输出指标进行排序，筛选结果，并快速、几乎下意识地根据关键指标的颜色来选择参数集。这里，我们只是重新运用前述流程，而这些流程本身正是试图模仿我们自身对于完整结果进行思维处理的方式。

神经网络中的激活函数

我突然意识到，我一直在寻找的函数，与一两年前我研究神经网络中的激活函数时遇到的那些颇为相似。

神经网络中的激活函数大致可分为三类：二元函数、线性函数和非线性函数：

• 二元函数通过返回1或0将值分类为两类中的一种。这类函数在我们的应用场景中不太有用；
• 线性函数通过简单的加法、乘法、减法或除法或这些运算的组合进行变换后返回结果。它们在我们的应用场景中同样帮助不大。
• 非线性函数返回的曲线在x的极值处受到限制，但允许在以0为中心的一定范围内对x的值进行区分。这个范围和中心可以通过使用偏移量进行调整。

应当说明的是，使用

return(0);

正如不受限制地返回众多结果乘积（我曾犯过这样的错误，而且在论坛上仍能看到有人这么做），两种方法都会重现与前两类相关的问题；另一方面，非线性函数往往受到限制以防止梯度爆炸，同时保持从-∞到∞的梯度范围。

为了解释清楚，我将回顾一些标准示例。我们将探讨修正线性单元（ReLU）函数、Softplus函数、Sigmoid函数和双曲正切（Tanh）函数，并在下一篇文章中介绍我自己的改进版本，包括翻转修正线性单元（Flipped ReLU）、点修正线性单元（Point ReLU）、翻转Sigmoid（Flipped Sigmoid）、点Sigmoid（Point Sigmoid）、翻转双曲正切（Flipped Tanh）和点双曲正切（Point Tanh）。

a) ReLU激活函数

该函数的作用是，当x小于等于0时返回0，当x大于0时返回x，用数学符号表示为f(x) = max(0,x)。所得的直线如下图所示，MQL5函数可以这样定义：

double ReLU(double x) {
   return(MathMax(0, x));
}

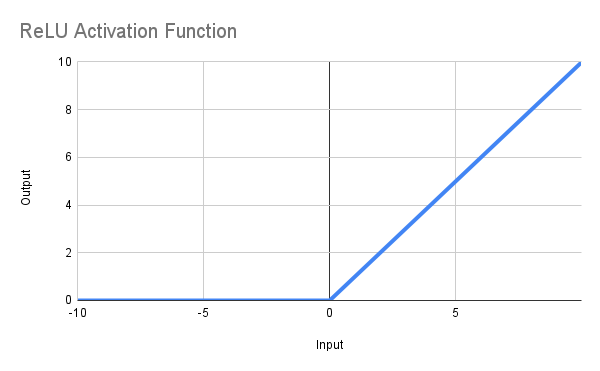
到目前为止，您可能会说进展还算顺利，但我想将恢复因子（RF）的目标最小值设定为5或更高……嗯，只需将代码简单修改* ：

input double MinRF = 5.0;

double RF = TesterStatistics(STAT_RECOVERY_FACTOR);
double DeviationRF = RF - MinRF;

double ReLU(double x) {
   return(MathMax(0, x));
}

double ScoreRF = ReLU(DeviationRF);

如此一来，曲线便会向右平移，在RF等于5.0时从0开始，如下图所示：

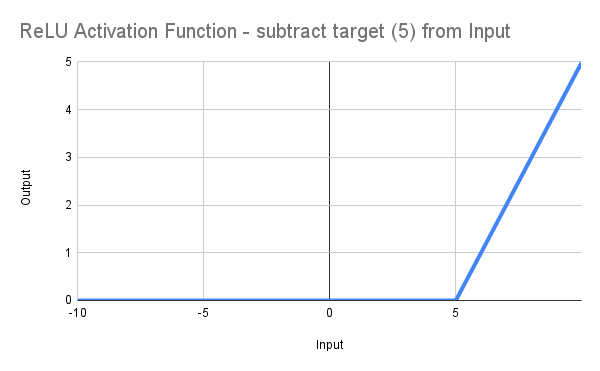
当然，这并不比编写*更高级

input double MinRF = 5.0;

double RF = TesterStatistics(STAT_RECOVERY_FACTOR);
double ScoreRF = (RF - MinRF);

但是，这给了我们一个起点……

*还存在另一个问题，即目标值5实际上会返回0，只有大于5的值才会返回非零值。我不打算在这个问题上花费时间，因为该函数存在的其它各种问题，使其在我们的应用场景中不再具有进一步的使用价值。

问题

很快又会发现，我们仍然面临两个问题，这两个问题都是代码固有的简单性所导致的……我之前说过：

当然，这并不比编写更高级

input double MinRF = 5.0;
double RF = TesterStatistics(STAT_RECOVERY_FACTOR);


double ScoreRF = (RF - MinRF);

但是，这给了我们一个起点……

这些问题在神经网络领域广为人知：

• “死亡”修正线性单元（Dying ReLU）：ReLU的主要弱点在于，当神经元仅输出0时，它们可能会永久“死亡”。这种情况发生在强负输入产生零梯度时，导致这些神经元失去活性，无法继续学习。因此也被称为梯度消失问题。

• 无约束输出：与具有内置上限的Sigmoid或Tanh函数不同，ReLU对于正输入的输出可以无限增大。这种缺乏上限约束的情况有时会在深度神经网络的训练过程中引发梯度爆炸情况。这也被称为梯度爆炸问题。

第二个问题在统计学中，可以通过在观测窗口内对数值进行标准化处理，但在优化器的限制范围内，我们无法采用这种方法。

因此，我们需要一种解决方案，该方案能够

1. 从数学上生成约束条件，实现自动标准化；并且
2. 在样本的很大一部分范围内提供一定程度的线性特性，而不是返回0……

b) Softplus激活函数

我无意在此深入探讨Softplus激活函数的细节，只是顺带提及，将其作为ReLU与更高级函数之间的一个过渡阶段。Geeksforgeeks网站对其有详尽地描述，我在此仅贴出下图、公式及代码。显而易见，尽管Softplus激活函数解决了“死亡”修正线性单元问题，但无约束输出问题依然存在。此外，Softplus函数在极浅的尾部与右侧斜坡之间过渡平滑。这就引发了引入校正偏移量的需求——我们稍后将再探讨这一概念：

其公式为Softplus（x）=ln（1+e^x），MQL5代码为

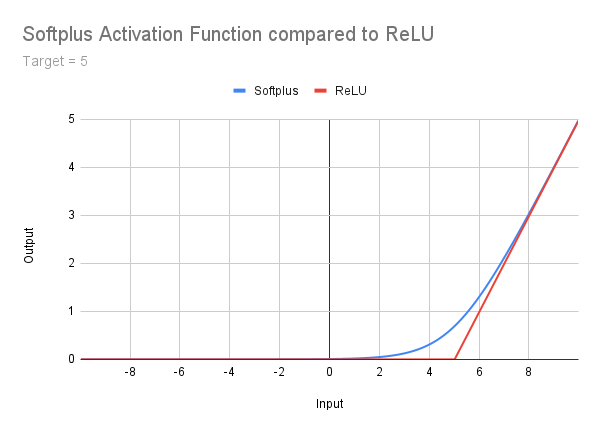
double Softplus(double x) {
   return(MathLog(1 + MathExp(x)));
}

如果您有兴趣，不妨自行深入了解，但是现在让我们来探讨那些能给出0到1之间约束结果的函数……

c) Sigmoid激活函数

Sigmoid函数的数学表达式为f(x) = 𝛔(x) = 1 / (1 + e^(-x))。它与Softplus函数的导数相同，在MQL5中的代码编写方式如下：

double Sigmoid(double x) {
   return(1 / (1 + MathExp(-x)));
}

观察下图中的曲线，可以立刻发现：

1. 该函数的输出被约束在0和1之间，从而解决了我们之前提到的无约束输出问题；

2. 尽管在这个范围内不太直观，但从-∞到∞，曲线始终保持变化的梯度，且梯度永远不会变为0；并且 

3. 未平移的曲线在输入值为0时，输出值为0.5。

为了解决第3点问题，使得当x等于我们的阈值（目标）值时，输出接近1，有必要将曲线向左平移，平移量不仅包括我们的阈值，还需通过一个校正量进行调整，实际中使用的校正值需大于等于5。 

因此，在MQL5中的实现方式如下：

input double MinRF = 5.0;
sinput double SigCorrection = 5;

double RF = TesterStatistics(STAT_RECOVERY_FACTOR);
double DeviationRF = RF - MinRF;

double CorrectedSigmoid(double x) {
   return(1 / (1 + MathExp(-(x - SigCorrection))));
}

double ScoreRF = CorrectedSigmoid(DeviationRF);

下图展示了针对目标值5未校正的Sigmoid函数曲线，以及其导数（乘以4后的结果，后续将进行讨论）。

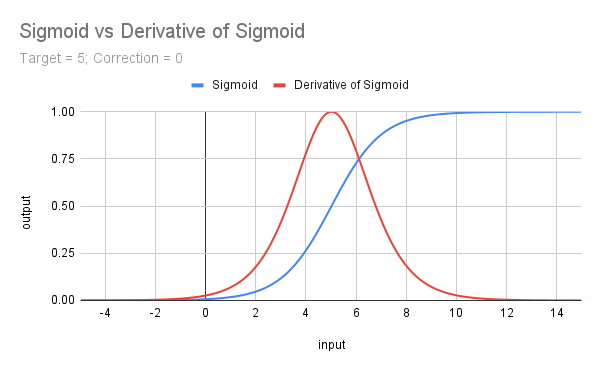
d) Sigmoid函数的导数（𝛔'）

其为我们呈现出优美的形状，该形状以x = 0为中心，并在该点达到最大值……它代表了Sigmoid函数的斜率，其公式为f(x) = 𝛔(x) - 𝛔^2(x) or 𝛔(x) * (1 - 𝛔(x))。 

该函数（如同我们即将探讨的所有非线性函数一样）可能存在梯度消失问题，不过，通过一个简单的办法——将其乘以4（因为 𝛔’(x) = 0.25），可以降低这种风险。而且，这样做还有一个好处，就是再次将结果约束在0和1之间。以某个x值为中心，使我们能够瞄准一个点，或者更准确地说，瞄准以该点为中心的一个范围。

在MQL5中的实现如下：

input double TargetTrades = 100;

double Trades = TesterStatistics(STAT_TRADES);
double DeviationTrades = Trades - TargetTrades;

double Sigmoid(double x) {
   return(1 / (1 + MathExp(-x)));
}

double Deriv4Sigmoid(double x) {
   return(4 * (Sigmoid(x) * (1 - Sigmoid(x))));
}

double ScoreTrades = Deriv4Sigmoid(DeviationTrades);

请注意：由于Sigmoid函数、其导数（乘以4后）以及接下来的Tanh函数及其导数（均重新缩放至0到1之间）的结果都被约束在0和1之间，因此在实际应用中，我们无需再提供额外的缩放因子。当然，我们可以乘以任何系数，将它们标准化到特定范围，或者在我们最终自定义的准则可能包含的其他优化比率中，赋予它们高优先级。我们将在下一篇文章中详细探讨这一点。

我们还有一个最后要探讨的标准函数，那就是Tanh……

e) Tanh函数

Tanh是我们为在自定义准则中寻找实用功能而探索的最后一个激活函数。接下来我将采用与之前类似的模式进行介绍，解释会比之前简略，但是应用的原则是相同的。

下图展示了Tanh及其导数的曲线图：

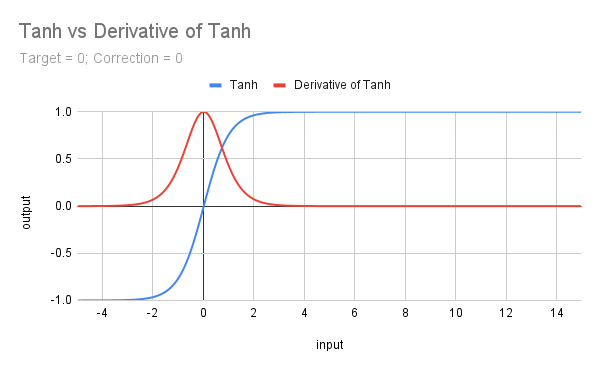
Tanh的公式为f(x) = (e^x - e^(-x))/(e^x + e^(-x)) ，在MQL5中它有对应的内置函数，因此编码实现非常直接。当然，我们仍需处理目标值和校正因子，但却能大大简化我们的工作。

input double MinRF = 5.0;
sinput double TanhCorrection = 2.5; // Anything between 2 and 3 would be reasonable (see last figure)

double RF = TesterStatistics(STAT_RECOVERY_FACTOR);
double DeviationRF = RF - MinRF;

double CorrectedRSTanh(double x) {
   return((MathTanh(x  + TanhCorrection) + 1) / 2);  // rescaled and corrected
}

double ScoreRF = CorrectedRSTanh(DeviationRF);

上述代码通过对基础函数加1再除以2的方式，将其输出范围重新缩放至0到1之间。另外，还引入了校正因子和目标值，所得曲线展示在接下来描绘Tanh导数的图表中。想必大家都注意到了，Tanh与Sigmoid函数形状相似，它们的导数之间也存在相似性；我们将在下一篇文章中深入探讨这些相似之处。

f)Tanh的导数

Tanh导数的数学公式为f(x) = 1 - Tanh^2(x)。

在MQL5中的实现如下：

input double TargetTrades = 100;

double Trades = TesterStatistics(STAT_TRADES);
double DeviationTrades = Trades - TargetTrades;

double DerivTanh(double x) {
   return(1 - MathPow(x, 2));

}double ScoreTrades = DerivTanh(DeviationTrades);

接下来的图表展示了对Tanh进行重新缩放并校正后的效果，校正目的是使其在目标（阈值）值x处近似从0开始上升，同时为Tanh及其导数都引入目标值设定。

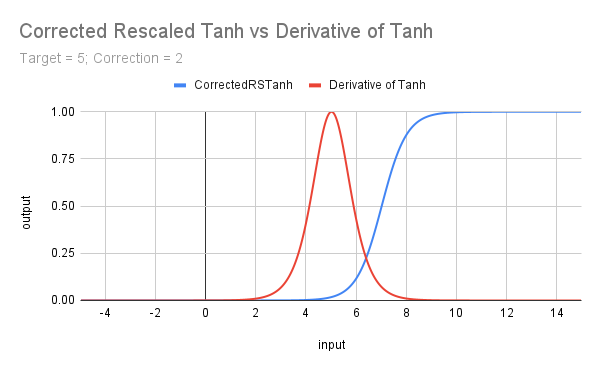
总结与下一步计划

在本文中，我们简要探讨了机器学习与优化过程（无论是基于遗传算法还是全局优化算法，并辅以Excel或手动后处理）之间的关系。我们开始研究各种激活函数如何优化自定义准则，以及如何在代码中实现这些函数。

ReLU和Softplus函数存在的梯度消失和梯度爆炸问题，促使我们将注意力转向具有类似Sigmoid函数及其导数曲线的函数。我们已经看到，这些函数如何有助于在评分中更倾向于单边界范围（即x > t）或双边界范围（t1 < x < t2），同时消除梯度爆炸问题，并缓解梯度消失问题。

我们还研究了如何利用校正偏移量和目标偏移量，以确保聚焦于期望的属性值范围。

在下一篇文章中，我们将探讨对上述标准函数进行一些修改，使得修改后的函数具有相似但不完全相同的特性。我们还将探讨缩放和加权的概念，并研究在自定义准则中使用不同函数的实例。