Ingeniería de características con Python y MQL5 (Parte III): El ángulo del precio (2) Coordenadas polares

El interés abierto por transformar los cambios en los niveles de precios en cambios en los ángulos no ha disminuido. Como ya hemos comentado en nuestro artículo anterior de esta serie, hay muchos retos que superar para convertir con éxito los cambios en los niveles de precios en un ángulo que represente ese cambio.

Una de las limitaciones más citadas en los debates comunitarios y en las publicaciones de los foros es la falta de significado interpretable detrás de dichos cálculos. Los miembros experimentados de la comunidad suelen explicar que existe un ángulo entre dos líneas, por lo que intentar calcular el ángulo formado por un cambio en el precio no tiene ningún significado físico en el mundo real. 

La falta de interpretación en el mundo real es solo uno de los muchos retos que deben superar los operadores interesados en calcular el ángulo creado por los cambios en los niveles de precios. En nuestro artículo anterior, intentamos resolver este problema sustituyendo el tiempo del eje x, con el fin de que el ángulo formado fuera una relación entre los niveles de precios y tuviera algún significado interpretable. Durante nuestra exploración, observamos que es muy fácil encontrar nuestro conjunto de datos plagado de valores «infinitos» después de realizar esta transformación. Los lectores interesados en refrescar rápidamente lo que observamos anteriormente pueden encontrar un enlace rápido al artículo aquí.

Dadas las numerosas dificultades que surgen al intentar transformar los cambios en los niveles de precios en un cambio correspondiente en el ángulo y la falta de un significado definido en el mundo real, la información organizada sobre el tema es limitada. 

Abordaremos el problema de la conversión de precios a ángulos desde una perspectiva totalmente nueva. En esta ocasión, utilizaremos un enfoque matemáticamente más sofisticado y robusto en comparación con las herramientas que creamos en nuestro primer intento. Los lectores que ya estén familiarizados con las coordenadas polares pueden pasar directamente a la sección «Introducción a MQL5» para ver cómo se implementan estas herramientas matemáticas en MQL5. 

De lo contrario, ahora procederemos a comprender qué son las coordenadas polares y desarrollaremos una intuición sobre cómo podemos aplicarlas para calcular el ángulo formado por los cambios de precio en nuestra terminal MetaTrader 5 y utilizar estas señales para operar. Es decir:

1. La solución que proponemos tiene un significado físico en el mundo real.
2. También resolveremos el problema que experimentamos anteriormente con valores infinitos o indefinidos.

¿Qué son las coordenadas polares y para qué pueden ser útiles?

Cada vez que utilizamos la tecnología GPS o incluso simples aplicaciones de hojas de cálculo, estamos empleando una tecnología conocida como coordenadas cartesianas. Se trata de un sistema matemático para representar puntos en un plano, normalmente con dos ejes perpendiculares. 

Cualquier punto del sistema cartesiano se representa como un par de coordenadas (x, y). Donde x representa la distancia horizontal desde el origen y y representa la distancia vertical desde el origen. 

Si queremos estudiar procesos que tienen componentes periódicos o algún tipo de movimiento circular, las coordenadas polares son más adecuadas para ello que las coordenadas cartesianas. Las coordenadas polares son un sistema completamente diferente que se utiliza para representar puntos en un plano utilizando una distancia desde un punto de referencia y un ángulo desde una dirección de referencia, que aumenta en sentido antihorario.  

Los mercados financieros tienden a mostrar patrones que se repiten de forma casi periódica. Por lo tanto, pueden representarse como coordenadas polares. Parece que el ángulo que los operadores desean calcular a partir de los cambios en los niveles de precios se puede obtener de forma natural representando los niveles de precios como pares polares. 

Las coordenadas polares se representan como un par (r, theta) en el que:

• R: Representa la distancia radial desde el punto de referencia (origen).
• Theta: Representa el ángulo medido desde la dirección de referencia.

Utilizando las funciones trigonométricas implementadas en la API de matrices y vectores de MQL5, podemos convertir sin problemas los cambios de precio en un ángulo que representa dicho cambio. 

Para lograr nuestro objetivo, primero debemos familiarizarnos con la terminología que utilizaremos a lo largo de nuestra discusión de hoy. Primero, debemos definir nuestras entradas x e y que se convertirán. Para nuestra discusión, definiremos x como el precio de apertura del símbolo, e y como el precio de cierre.

Figura 1: Definición de nuestros puntos cartesianos que se convertirán en puntos polares.

Ahora que hemos definido nuestras entradas x e y, necesitamos calcular el primer elemento del par polar, la distancia radial desde el origen, r. 

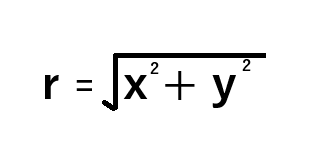
Figura 2: La fórmula cerrada para calcular r, a partir de x e y.

Cuando se representan geométricamente, podemos imaginar las coordenadas polares como la descripción de un círculo. El ángulo formado entre r y x es theta. Por lo tanto, las coordenadas polares simplemente proponen que usar r y theta es tan informativo como usar x e y directamente. Cuando x e y se visualizan como se muestra en la figura 3, entonces la distancia radial, r, se calcula aplicando el teorema de Pitágoras a los lados x e y.

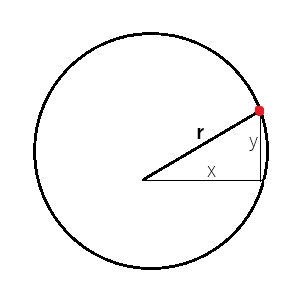
Figura 3: Las coordenadas polares pueden visualizarse como la descripción de un punto en un círculo.

El ángulo entre r y x, theta, satisface nuestro deseo de significado en el mundo real. En este sencillo ejemplo, theta se correlaciona con la dirección de la tendencia que se forma a partir de los cambios en el precio de apertura y cierre. El valor de Theta se obtiene calculando la tangente inversa del precio de cierre dividido por el precio de apertura, como se muestra en la figura a continuación.

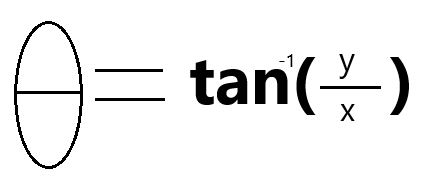
Figura 4: Cálculo de theta a partir de nuestros precios de apertura x y cierre y.

Dadas unas coordenadas polares cualesquiera (r, theta), podemos convertirlas fácilmente a sus niveles de precio originales utilizando las dos fórmulas siguientes:

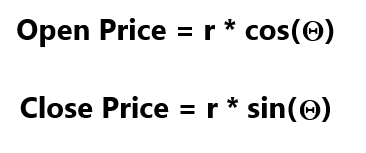
Figura 5: Cómo convertir coordenadas polares de nuevo a coordenadas cartesianas.

Hasta ahora hemos analizado 4 fórmulas, pero solo las últimas 3 contienen theta. La primera fórmula que utilizamos para calcular r no tiene relación con theta. Las últimas tres fórmulas que hemos analizado contienen theta y se pueden diferenciar fácilmente. Las derivadas de estas funciones trigonométricas son resultados bien conocidos que se pueden encontrar fácilmente en línea o en cualquier libro de texto de cálculo elemental. 

Utilizaremos estas 3 derivadas como entradas adicionales para entrenar a nuestra computadora a aprender la relación entre los cambios en los ángulos y sus correspondientes cambios en los niveles de precios.

Primeros pasos en MQL5

Comencemos. Primero necesitamos crear un script en MQL5 que obtenga datos históricos del mercado de nuestro terminal MetaTrader 5 y que también realice las transformaciones para darnos los ángulos que se están creando.

Primero debemos definir el nombre del archivo CSV que estamos creando y luego especificar cuántas barras de datos vamos a obtener. Dado que el número de barras a obtener puede variar según su bróker, hemos configurado este parámetro como una entrada para el script.

#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs

//---File name
string file_name = _Symbol + " " + " Polar Coordinates.csv";

//---Amount of data requested
input int size = 100;
int size_fetch = size + 100;

Cuando se ejecute nuestro script, crearemos un gestor de archivos para escribir los niveles de precios y sus correspondientes cambios de ángulo.

void OnStart()
  {
      //---Write to file
       int file_handle=FileOpen(file_name,FILE_WRITE|FILE_ANSI|FILE_CSV,",");
       
    for(int i=size;i>0;i--){
      if(i == size){
            FileWrite(file_handle,"Time","Open","High","Low","Close","R","Theta","X Derivatie","Y Derivative","Theta Derivative");
      }
      
      else{

Procedamos a calcular r utilizando la fórmula que analizamos en la figura 2.

double r = MathSqrt(MathPow(iOpen(_Symbol,PERIOD_CURRENT,i),2) + MathPow(iClose(_Symbol,PERIOD_CURRENT,i),2));

Theta se calcula mediante la tangente inversa de la razón entre y y x. Esto está implementado para nosotros en la API de MQL5.

double theta = MathArctan2(iClose(_Symbol,PERIOD_CURRENT,i),iOpen(_Symbol,PERIOD_CURRENT,i));

Recuerde que la fórmula para calcular x (Precio de apertura) se proporciona en la figura 5 anterior. Podemos diferenciar esta fórmula con respecto a theta para calcular la primera derivada del precio de apertura. La derivada de cos(), como ya sabes, es -sin().

double derivative_x = r * (-(MathSin(theta)));

También podemos calcular la derivada de y, ya que conocemos la derivada de las funciones trigonométricas.

double derivative_y = r * MathCos(theta);

Por último, conocemos la primera derivada de theta. Sin embargo, la función trigonométrica no está implementada directamente en la API de MQL5; en su lugar, utilizaremos una identidad matemática para sustituirla usando las funciones MQL5 apropiadas.

double derivative_theta = (1/MathPow(MathCos(theta),2));

Ahora que hemos calculado nuestros ángulos, podemos proceder a escribir nuestros datos.

           FileWrite(file_handle,iTime(_Symbol,PERIOD_CURRENT,i),
                                 iOpen(_Symbol,PERIOD_CURRENT,i),
                                 iHigh(_Symbol,PERIOD_CURRENT,i),
                                 iLow(_Symbol,PERIOD_CURRENT,i),
                                 iClose(_Symbol,PERIOD_CURRENT,i),
                                 r,
                                 theta,
                                 derivative_x,
                                 derivative_y,
                                 derivative_y
                                 );
      } 
    }
    
    FileClose(file_handle);
  }
//+---------

Analizando nuestros datos

Ahora que nuestros datos están escritos en formato CSV, usémoslos para entrenar a nuestra computadora a operar con los ángulos formados. Utilizaremos algunas bibliotecas de Python para acelerar nuestro proceso de desarrollo.

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

Etiquete los datos para indicar si los niveles de precios aumentaron al día siguiente o si disminuyeron al día siguiente.

data = pd.read_csv("EURUSD  Polar Coordinates.csv")
data["UP DOWN"] = 0
data.loc[data["Close"] < data["Close"].shift(-1),"UP DOWN"] = 1
data

Esta es la señal de trading que estamos buscando. Tenga en cuenta que siempre que R y Theta aumentan en nuestro conjunto de datos original, los niveles de precios nunca disminuyen. Esta llamada a Pandas no devuelve nada, y esto demuestra el significado en el mundo real que respalda a las parejas polares. Conocer los valores futuros de R y Theta es tan útil como conocer el nivel de precios futuro.

data.loc[(data["R"] < data["R"].shift(-1)) & (data['Theta'] < data['Theta'].shift(-1)) & (data['Close'] > data['Close'].shift(-1))

Del mismo modo, si realizamos la misma consulta pero en la dirección opuesta, es decir, si buscamos instancias en las que R y Theta aumentaron, pero el precio futuro disminuyó, nuevamente encontraremos que pandas devuelve 0 instancias.

data.loc[(data["R"] > data["R"].shift(-1)) & (data['Theta'] > data['Theta'].shift(-1)) & (data['Close'] < data['Close'].shift(-1))]

Por lo tanto, nuestras señales de negociación se generarán siempre que nuestro ordenador prevea que los valores futuros de R y Theta serán mayores que sus valores actuales. A continuación, podemos visualizar nuestros datos de precios como puntos en un círculo polar. Como podemos observar en la figura 6, los datos siguen siendo difíciles de separar de manera efectiva.

data['Theta_rescaled'] = (data['Theta'] - data['Theta'].min()) / (data['Theta'].max() - data['Theta'].min()) * (2 * np.pi)
data['R_rescaled'] = (data['R'] - data['R'].min()) / (data['R'].max() - data['R'].min()) 

# Create the polar plot
fig, ax = plt.subplots(subplot_kw={'projection': 'polar'})

# Plot data points on the polar axis
ax.scatter(data['Theta_rescaled'], data['R_rescaled'],c=data["UP DOWN"], cmap='viridis', edgecolor='black', s=100)

# Add plot labels
ax.set_title("Polar Plot of OHLC Points")
plt.colorbar(plt.cm.ScalarMappable(cmap='viridis'), ax=ax, label='1(UP) | O(DOWN)')

plt.show()

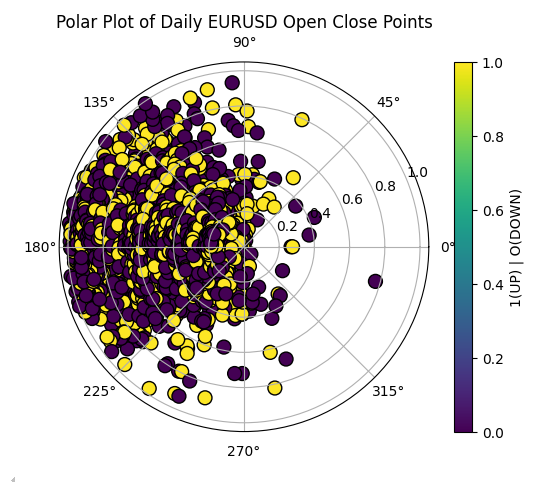
Figura 6: Visualización de nuestros datos de precios como puntos polares en un círculo polar.

Comprobemos rápidamente si alguno de nuestros valores es nulo.

data.isna().any()

Figura 7: Comprobando si alguno de nuestros valores es nulo.

Modelado de datos

Todos nuestros valores están definidos, estupendo. También necesitamos etiquetar los datos. Recordemos que nuestro objetivo es el valor futuro de theta y r.

LOOK_AHEAD = 1
data['R Target'] = data['R'].shift(-LOOK_AHEAD)
data['Theta Target'] = data['Theta'].shift(-LOOK_AHEAD)
data.dropna(inplace=True)
data.reset_index(drop=True,inplace=True)

Tenga en cuenta que queremos descartar los datos de los últimos 2 años para poder utilizarlos como prueba para nuestra aplicación.

#Let's entirely drop off the last 2 years of data
_ = data.iloc[-((365 * 2) + 230):,:]
data = data.iloc[:-((365 * 2) + 230),:]
data

Figura 8: Nuestro conjunto de datos tras eliminar los datos de los últimos 2 años.

Ahora vamos a entrenar al ordenador utilizando los datos disponibles. Utilizaremos un árbol de decisión con refuerzo de gradiente como modelo preferido porque son particularmente buenos para aprender efectos de interacción.

from sklearn.ensemble import GradientBoostingRegressor
from sklearn.model_selection import train_test_split,TimeSeriesSplit,cross_val_score

Ahora definamos nuestro objeto de división de series temporales.

tscv = TimeSeriesSplit(n_splits=5,gap=LOOK_AHEAD)

Defina las entradas y los objetivos.

X = data.columns[1:-5]
y = data.columns[-2:]

Divide los datos en dos mitades: una para entrenamiento y otra para prueba.

train , test = train_test_split(data,test_size=0.5,shuffle=False)

Ahora prepara el entrenamiento y prueba las divisiones.

train_X = train.loc[:,X]
train_y = train.loc[:,y]

test_X = test.loc[:,X]
test_y = test.loc[:,y]

Es necesario estandarizar las divisiones de entrenamiento y prueba.

mean_scores = train_X.mean()
std_scores = train_X.std()

Escalar los datos.

train_X = ((train_X - mean_scores) / std_scores)
test_X = ((test_X - mean_scores) / std_scores)

Inicializar el modelo.

model = GradientBoostingRegressor()

Prepare una tabla para almacenar los resultados.

results = pd.DataFrame(index=["Train","Test"],columns=["GBR"])

Ajustar el modelo para predecir R.

results.iloc[0,0] = np.mean(np.abs(cross_val_score(model,train_X,train_y["R Target"],cv=tscv)))
results.iloc[1,0] = np.mean(np.abs(cross_val_score(model,test_X,test_y["R Target"],cv=tscv)))
results

GBR
Entrenamiento	0.76686
Prueba	0.89129

Ajustar el modelo para predecir Theta.

results.iloc[0,0] = np.mean(np.abs(cross_val_score(model,train_X,train_y["Theta Target"],cv=tscv)))
results.iloc[1,0] = np.mean(np.abs(cross_val_score(model,test_X,test_y["Theta Target"],cv=tscv)))
results

GBR
Entrenamiento	0.368166
Prueba	0.110126

Exportar a ONNX

Carguemos las bibliotecas que necesitamos.

import onnx
import skl2onnx 
from skl2onnx.common.data_types import FloatTensorType

Inicializar los modelos.

r_model = GradientBoostingRegressor()
theta_model = GradientBoostingRegressor()

Almacene las puntuaciones de estandarización global para todo el conjunto de datos en formato CSV.

mean_scores = data.loc[:,X].mean()
std_scores = data.loc[:,X].std()

mean_scores.to_csv("EURUSD Polar Coordinates Mean.csv")
std_scores.to_csv("EURUSD Polar Coordinates Std.csv")

Normalizar todo el conjunto de datos.

data[X] = ((data.loc[:,X] - mean_scores) / std_scores)

Ajustar los modelos a los datos escalados.

r_model.fit(data.loc[:,X],data.loc[:,'R Target'])
theta_model.fit(data.loc[:,X],data.loc[:,'Theta Target'])

Define la forma de entrada.

initial_types = [("float_input",FloatTensorType([1,len(X)]))]

Prepare los prototipos ONNX para guardarlos.

r_model_proto = skl2onnx.convert_sklearn(r_model,initial_types=initial_types,target_opset=12)
theta_model_proto = skl2onnx.convert_sklearn(theta_model,initial_types=initial_types,target_opset=12)

Guarda los archivos ONNX.

onnx.save(r_model_proto,"EURUSD D1 R Model.onnx")
onnx.save(theta_model_proto,"EURUSD D1 Theta Model.onnx")

Primeros pasos en MQL5

Ya estamos listos para construir nuestra aplicación de trading.

//+------------------------------------------------------------------+
//|                                              EURUSD Polar EA.mq5 |
//|                                               Gamuchirai Ndawana |
//|                    https://www.mql5.com/en/users/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Ndawana"
#property link      "https://www.mql5.com/en/users/gamuchiraindawa"
#property version   "1.00"

//+------------------------------------------------------------------+
//| System Constants                                                 |
//+------------------------------------------------------------------+
#define ONNX_INPUTS 9                                              //The total number of inputs for our onnx model
#define ONNX_OUTPUTS 1                                             //The total number of outputs for our onnx model
#define TF_1  PERIOD_D1                                            //The system's primary time frame
#define TRADING_VOLUME 0.1                                         //The system's trading volume

Cargue los modelos ONNX como recursos del sistema.

//+------------------------------------------------------------------+
//| System Resources                                                 |
//+------------------------------------------------------------------+
#resource "\\Files\\EURUSD D1 R Model.onnx" as uchar r_model_buffer[];
#resource "\\Files\\EURUSD D1 Theta Model.onnx" as uchar theta_model_buffer[];

Definamos nuestras variables globales. Utilizaremos algunas de estas variables para estandarizar nuestros datos, almacenar las predicciones de nuestro modelo ONNX y mucho más.

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+
double mean_values[] = {1.1884188643844635,1.1920754015799868,1.1847545720868993,1.1883860236998025,1.6806588395310122,0.7853854898794739,-1.1883860236998025,1.1884188643844635,1.1884188643844635};
double std_values[]  = {0.09123896995032886,0.09116171300874902,0.0912656190371797,0.09120265318308786,0.1289537623737421,0.0021932437785043796,0.09120265318308786,0.09123896995032886,0.09123896995032886};
double current_r,current_theta;
long r_model,theta_model;
vectorf r_model_output = vectorf::Zeros(ONNX_OUTPUTS);
vectorf theta_model_output = vectorf::Zeros(ONNX_OUTPUTS);
double bid,ask;
int ma_o_handler,ma_c_handler,state;
double ma_o_buffer[],ma_c_buffer[];

Cargar la biblioteca de comercio.

//+------------------------------------------------------------------+
//| Library                                                          |
//+------------------------------------------------------------------+
#include <Trade/Trade.mqh>
CTrade Trade;

Nuestra aplicación de negociación se compone principalmente de controladores de eventos. Durante cada etapa del ciclo de vida de la aplicación, llamaremos a funciones específicas para realizar tareas que correspondan a nuestro objetivo en ese momento. Así pues, durante la inicialización, configuraremos nuestros indicadores técnicos y, cuando haya nuevos precios disponibles, actualizaremos nuestras lecturas a partir de esos indicadores.

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---
   if(!setup())
     {
      Comment("Failed To Load Corretly");
      return(INIT_FAILED);
     }

   Comment("Started");
//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//---
   OnnxRelease(r_model);
   OnnxRelease(theta_model);
  }
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//---
   update();
  }
//+------------------------------------------------------------------+

Obtención de una predicción a partir de nuestro modelo ONNX. Tenga en cuenta que convertimos todos los datos de entrada del modelo al tipo float para garantizar que el modelo reciba datos con el formato y tamaño correctos, según lo esperado.

//+------------------------------------------------------------------+
//| Get a prediction from our models                                 |
//+------------------------------------------------------------------+
void get_model_prediction(void)
  {
//Define theta and r
   double o = iOpen(_Symbol,PERIOD_CURRENT,1);
   double h = iHigh(_Symbol,PERIOD_CURRENT,1);
   double l = iLow(_Symbol,PERIOD_CURRENT,1);
   double c = iClose(_Symbol,PERIOD_CURRENT,1);
   current_r = MathSqrt(MathPow(o,2) + MathPow(c,2));
   current_theta = MathArctan2(c,o);

   vectorf model_inputs =
     {
      (float) o,
      (float) h,
      (float) l,
      (float) c,
      (float) current_r,
      (float) current_theta,
      (float)(current_r * (-(MathSin(current_theta)))),
      (float)(current_r * MathCos(current_theta)),
      (float)(1/MathPow(MathCos(current_theta),2))
     };

//Standardize the model inputs
   for(int i = 0; i < ONNX_INPUTS;i++)
     {
      model_inputs[i] = (float)((model_inputs[i] - mean_values[i]) / std_values[i]);
     }

//Get a prediction from our model
   OnnxRun(r_model,ONNX_DATA_TYPE_FLOAT,model_inputs,r_model_output);
   OnnxRun(theta_model,ONNX_DATA_TYPE_FLOAT,model_inputs,theta_model_output);

//Give our prediction
   Comment(StringFormat("R: %f \nTheta: %f\nR Forecast: %f\nTheta Forecast: %f",current_r,current_theta,r_model_output[0],theta_model_output[0]));
  }

Actualice el sistema cada vez que se ofrezcan nuevos precios.

//+------------------------------------------------------------------+
//| Update system state                                              |
//+------------------------------------------------------------------+
void update(void)
  {
   static datetime time_stamp;
   datetime current_time = iTime(_Symbol,TF_1,0);

   bid = SymbolInfoDouble(_Symbol,SYMBOL_BID);
   ask = SymbolInfoDouble(_Symbol,SYMBOL_ASK);
   if(current_time != time_stamp)
     {
      CopyBuffer(ma_o_handler,0,0,1,ma_o_buffer);
      CopyBuffer(ma_c_handler,0,0,1,ma_c_buffer);
      time_stamp = current_time;
      get_model_prediction();
      manage_account();
      if(PositionsTotal() == 0)
         get_signal();
     }
  }

Gestionar la cuenta. Si estamos perdiendo dinero en una operación, preferimos cerrarla rápidamente. De lo contrario, si hemos iniciado una operación, pero las medias móviles se cruzan de una forma que socava nuestra confianza en esa posición, la cerraremos inmediatamente.

//+------------------------------------------------------------------+
//| Manage the open positions we have in the market                  |
//+------------------------------------------------------------------+
void manage_account()
  {
   if(AccountInfoDouble(ACCOUNT_BALANCE) < AccountInfoDouble(ACCOUNT_EQUITY))
     {
      while(PositionsTotal() > 0)
         Trade.PositionClose(Symbol());
     }

   if(state == 1)
     {
      if(ma_c_buffer[0] < ma_o_buffer[0])
         Trade.PositionClose(Symbol());
     }

   if(state == -1)
     {
      if(ma_c_buffer[0] > ma_o_buffer[0])
         Trade.PositionClose(Symbol());
     }
  }

Configure las variables del sistema, como los indicadores técnicos y los modelos ONNX.

//+------------------------------------------------------------------+
//| Setup system variables                                           |
//+------------------------------------------------------------------+
bool setup(void)
  {
   ma_o_handler = iMA(Symbol(),TF_1,50,0,MODE_SMA,PRICE_CLOSE);
   ma_c_handler = iMA(Symbol(),TF_1,10,0,MODE_SMA,PRICE_CLOSE);

   r_model = OnnxCreateFromBuffer(r_model_buffer,ONNX_DEFAULT);
   theta_model = OnnxCreateFromBuffer(theta_model_buffer,ONNX_DEFAULT);

   if(r_model == INVALID_HANDLE)
      return(false);
   if(theta_model == INVALID_HANDLE)
      return(false);

   ulong input_shape[] = {1,ONNX_INPUTS};
   ulong output_shape[] = {1,ONNX_OUTPUTS};

   if(!OnnxSetInputShape(r_model,0,input_shape))
      return(false);
   if(!OnnxSetInputShape(theta_model,0,input_shape))
      return(false);

   if(!OnnxSetOutputShape(r_model,0,output_shape))
      return(false);
   if(!OnnxSetOutputShape(theta_model,0,output_shape))
      return(false);

   return(true);
  }

Comprueba si tenemos una señal de trading. Comprobaremos principalmente la orientación de nuestra estrategia de cruce de medias móviles. Después, comprobaremos nuestras expectativas según los modelos ONNX. Por lo tanto, si el cruce de la media móvil nos da un sentimiento bajista, pero nuestros modelos r y theta ONNX nos dan un sentimiento alcista, no abriremos ninguna posición hasta que los dos sistemas estén de acuerdo.

//+------------------------------------------------------------------+
//| Check if we have a trading signal                                |
//+------------------------------------------------------------------+
void get_signal(void)
  {
   if(ma_c_buffer[0] > ma_o_buffer[0])
     {
      if((r_model_output[0] < current_r) && (theta_model_output[0] < current_theta))
        {
         return;
        }
        
      if((r_model_output[0] > current_r) && (theta_model_output[0] > current_theta))
        {
         Trade.Buy(TRADING_VOLUME * 2,Symbol(),ask,0,0);
         Trade.Buy(TRADING_VOLUME * 2,Symbol(),ask,0,0);
         state = 1;
         return;
        }
        
      Trade.Buy(TRADING_VOLUME,Symbol(),ask,0,0);
      state = 1;
      return;
     }

   if(ma_c_buffer[0] < ma_o_buffer[0])
     {
      if((r_model_output[0] > current_r) && (theta_model_output[0] > current_theta))
        {
         return;
        }

     if((r_model_output[0] < current_r) && (theta_model_output[0] < current_theta))
        {
         
         Trade.Sell(TRADING_VOLUME * 2,Symbol(),bid,0,0);
         Trade.Sell(TRADING_VOLUME * 2,Symbol(),bid,0,0);
         state = -1;
         return;
        }

      Trade.Sell(TRADING_VOLUME,Symbol(),bid,0,0);
      state = -1;
      return;
     }
  }

Elimine las constantes del sistema que no estamos utilizando.

//+------------------------------------------------------------------+
//| Undefine system variables we don't need                          |
//+------------------------------------------------------------------+
#undef ONNX_INPUTS
#undef ONNX_OUTPUTS
#undef TF_1
//+------------------------------------------------------------------+

Probando el sistema

Ahora comencemos a probar nuestro sistema. Recordemos que durante la fase de preparación de datos, descartamos los datos a partir del 1 de enero de 2022, de modo que nuestra prueba retrospectiva refleje el rendimiento que podría tener nuestra estrategia con datos que nunca ha visto antes.

Figura 9: Nuestra configuración de pruebas retrospectivas.

Ahora especifique la configuración inicial de la cuenta. 

Figura 10: Nuestro segundo conjunto de ajustes para nuestra crucial prueba retrospectiva con datos fuera de muestra.

Podemos observar la curva de capital de las señales de negociación producidas por nuestro nuevo sistema. Nuestra estrategia comenzó con un saldo de 5000 dólares y finalizó con un saldo de alrededor de 7000 dólares; estos son buenos resultados y nos animan a seguir explorando y redefiniendo nuestra estrategia.

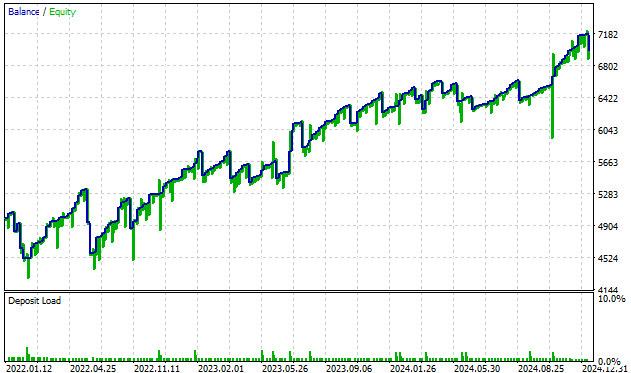
Figura 11: Resultados de las pruebas retrospectivas obtenidos al operar con las señales generadas por nuestras transformaciones angulares.

Analicemos nuestros resultados en detalle. Nuestra estrategia tuvo una precisión del 88% en datos fuera de la muestra. Esta información es alentadora y puede proporcionar al lector un buen punto de partida para desarrollar sus propias aplicaciones, ampliando la funcionalidad y las capacidades del terminal MetaTrader 5 que hemos demostrado en esta aplicación. O bien, el lector puede considerar utilizar nuestro marco como guía y reemplazar por completo nuestra estrategia comercial con la suya propia.

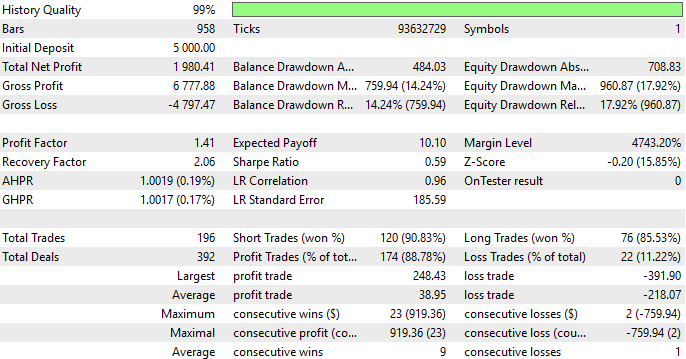
Figura 12: Análisis detallado de los resultados de nuestra prueba retrospectiva.

Conclusión

La solución que le hemos proporcionado hoy le ha demostrado cómo aprovechar la ventaja potencial que se obtiene al convertir de manera significativa los cambios en los niveles de precios en cambios en los ángulos. Nuestro procedimiento le proporciona un marco sencillo y elegante para abordar esta cuestión, lo que le permite obtener la mejor combinación de lógica comercial y lógica matemática. Además, a diferencia de los participantes ocasionales del mercado que se obsesionan con predecir el precio directamente, ahora usted dispone de objetivos alternativos que son tan útiles como conocer el precio en sí mismo, pero que son más fáciles de predecir de forma consistente que el precio en sí.

Archivo adjunto	Descripción
Polar Fetch Data	Nuestro script personalizado para obtener nuestros datos de precios y transformarlos en coordenadas polares.
EURUSD Polar EA	El Asesor Experto que opera con las señales generadas a partir de los cambios de ángulo detectados.
EURUSD D1 R Model	El modelo ONNX es responsable de predecir nuestros valores futuros de R.
EURUSD D1 Theta Model	El modelo ONNX es responsable de predecir nuestros valores futuros de Theta.
EURUSD Polar Coordinates	El Notebook Jupyter que utilizamos para analizar los datos que obtuvimos con nuestro script MQL5.