Características del Wizard MQL5 que debe conocer (Parte 08): Perceptrones

Introducción

La clase de señales de asesores del Wizard MQL5 contiene muchos ejemplos en la carpeta Include\Expert\Signal. Cada uno de ellos puede usarse de forma independiente, o bien combinarse al crear un asesor en el Wizard. En este artículo, crearemos y usaremos uno de estos archivos en un asesor. Este enfoque, además de minimizar el esfuerzo de codificación previa, permite probar más de una señal en un solo asesor asignando un peso a cada señal utilizada.

Las clases de perceptrón Alglib se representan como interfaces de red extensas e interconectadas en el archivo Include\Math\Alglib\dataanalysis.mqh. Resulta sencillo confundirse a primera vista, pero aquí trataremos algunas clases importantes que esperamos que faciliten la navegación por esta zona.

El propósito principal del uso de estas clases Alglib para el desarrollo de asesores será el mismo que en el uso del Wizard MQL5, la prueba de ideas. ¿Cómo podemos determinar si la idea x o el conjunto de entradas merecen nuestros esfuerzos para continuar desarrollando el sistema comercial? El artículo nos ayudará a responder a esa pregunta.

Antes de empezar, quizá resulte útil explicar con mayor detalle por qué los perceptrones, y quizá las redes neuronales en general, están ganando popularidad. Si nos centramos en las finanzas y los mercados, podemos ver que, debido a las limitaciones del análisis tradicional, topamos con muchos problemas para predecir las acciones del mercado.

Estos problemas existen porque los mercados son sistemas muy complejos y a menudo dinámicos en los que influyen más factores de los que aparecen en las noticias (información pública). En la mayoría de los casos, la relación entre las distintas variables del mercado no es lineal, y resulta muy variable. Los métodos de análisis tradicionales basados en linealidad pueden no ser capaces de captar y considerar eficazmente estas complejidades. Ejemplos de estos métodos pueden incluir enfoques tales como la correlación, el ACP o la regresión lineal. Aunque todas estas tácticas son muy sensatas, cada vez resultan más irrelevantes. Además, los datos del mercado contienen mucho ruido, ya que los movimientos del mercado están influidos no solo por el sentimiento de los inversores, sino también por los sesgos de comportamiento de los consumidores. Así, el análisis técnico tradicional se ve limitado por su dependencia de los datos históricos, sin considerar debidamente la dinámica del mercado al completo. En cambio, el análisis fundamental, que adopta una visión a largo plazo, es propenso a asumir riesgos a corto plazo, especialmente en lo referente a los movimientos de los precios. Aunque quienes se basan en el análisis fundamental no suelen recurrir al apalancamiento, la mayoría estaría de acuerdo en que supone un componente importante para equilibrar los activos gestionados y, por tanto, el riesgo a largo plazo. No obstante, el apalancamiento no puede utilizarse sin considerar los movimientos de precios a corto plazo.

Las nuevas alternativas a estos dos enfoques tradicionales son la economía conductual y las técnicas de inteligencia artificial basadas en redes neuronales. Nos centraremos en la segunda opción.

Recientemente, los mercados financieros se han visto sacudidos por la aplicación de la tecnología de inteligencia artificial con el lanzamiento de ChatGPT. Por ejemplo, muchas de las grandes empresas han entrado en esta carrera. A este respecto, merece la pena mencionar BloombergGPT y EinsteinGPT de Salesforce. Sin embargo, en este artículo no hablaremos de GPT, sino de una versión muy simplificada del mismo: los perceptrones.

No obstante, el creciente interés por las técnicas de inteligencia artificial para la ejecución de pronósticos se debe en parte a la gran cantidad de datos financieros que se recopilan y almacenan en volúmenes cada vez mayores. ¿Recuerda los tiempos en que a los analistas técnicos solo les importaba el precio de cierre diario de los valores? Hoy en día, todo el mundo conoce los precios OHLC de una barra de un minuto, eso por no hablar de los ticks, cuya frecuencia varía de un bróker a otro.

Esta sobrecarga de datos se produce al mismo tiempo que aumenta la potencia de cálculo gracias a la competencia entre los fabricantes de chips. No hace mucho se anunció que NVIDIA pronto se convertirá en el mayor vendedor de chips del mundo, gracias en gran parte a la creciente demanda de GPU, que ahora están de moda debido a la proliferación de GPT. Así, el aumento del almacenamiento de datos y la capacidad de cálculo provocará un mayor uso del trading algorítmico. Y aunque el trading algorítmico puede realizarse utilizando el análisis técnico y fundamental tradicional, las técnicas de inteligencia artificial con uso de redes neuronales están ganando cada vez más atención.

Las redes neuronales suelen ser mejores procesando grandes cantidades de datos e identificando patrones complejos no lineales. Suelen conseguirlo adaptándose a un entorno cambiante usando el aprendizaje profundo, una red multicapa en la que ciertas capas ocultas están especializadas en determinadas tareas, de modo que la predicción en entornos típicamente turbulentos/cambiantes resulta su mejor aplicación. Además de las finanzas, pueden analizar datos no estructurados, como artículos de noticias o publicaciones en redes sociales, valorar el sentimiento del mercado, la eficacia de los ensayos clínicos de medicamentos y aplicarse en muchos otros ámbitos.

Resumen de las clases del perceptrón Alglib

Como ya hemos mencionado, la jerarquía de clases de perceptrones de Alglib es una extensa biblioteca de clases que implementan redes neuronales, desde perceptrones simples (que analizaremos en este artículo) hasta conjuntos, que, siendo sinónimos de los transformadores, suponen pilas de redes neuronales. Como solo analizaremos la red neuronal más simple, llamada perceptrón, solo consideraremos las clases CMLPBase, CMLPTrain, CMLPTrainer y CMultilayerPerceptron. Usaremos otras clases de ayuda menores, como una clase para gestionar los informes o una clase para ayudar a normalizar los conjuntos de datos, pero destacaremos las principales.

La clase CMLPBase se usa para inicializar la red, definiendo el número de capas ocultas que tendrá la red, así como el número de neuronas en cada capa. La clase CMLPTrain inicializa la clase entrenador, estableciendo la cantidad de datos de entrada que admitirá la red y la cantidad de sus datos de salida. También rellena el entrenador con el conjunto de datos de entrenamiento, que deberá estar en forma de matriz, donde las primeras columnas contendrán las variables independientes, mientras que la última columna contendrá el regresor o clasificador dependiendo del tipo de red utilizada. En nuestro caso será un clasificador, ya que los perceptrones suelen producir una salida lógica. La clase CMLPTrainer se usa en el entrenamiento al llamar a la función MLPTrainNetwork de la clase CMLPTrain. Existen métodos de aprendizaje alternativos muy interesantes, como la agregación de carga inicial (boot-strap-aggregating), llamada por la función MLPEBaggedLM, pero solo pueden utilizarse con conjuntos (pilas de redes). Además, para entrenar la red pueden usarse algoritmos como el de parada anticipada, el LBFGS y el Levenberg-Marquadt.

Los métodos utilizados por estas clases abarcan el recorrido típico de las redes neuronales, desde la carga de los datos de entrenamiento hasta la realización del entrenamiento propiamente dicho y, por último, el paso al conjunto de datos actual para la predicción.

Así, las clases estarán escritas de la forma que funciona una red neuronal. En tiempo de ejecución, los datos de entrada pasarán por la red empezando por la primera capa, que en estas clases se denomina capa de entrada, siguiendo por las capas ocultas y, por último, por la capa de salida. Además, la activación de valores suele realizarse en cada neurona, y es precisamente esta activación la que permite a las redes procesar relaciones complejas más allá de las lineales, actuando como un filtro que permite a los valores seleccionados pasar al siguiente nivel. Este proceso es iterativo pero relativamente sencillo, ya que casi siempre consiste en multiplicar y sumar, y el resultado de la capa de salida dependerá principalmente de los pesos y las compensaciones de cada nivel. Así pues, son estos pesos y desplazamientos los que constituyen la esencia de las redes neuronales, y el proceso de ajustarlos no solo resulta exigente desde el punto de vista computacional, sino que también ha dado lugar al desarrollo de diferentes enfoques, ya que no es tan sencillo como una simple pasada. Este método funciona mejor en distintos tipos de redes porque las redes neuronales tienen muchas aplicaciones.

Así, la función de conexión directa para redes en AlgLib se llamará MLPProcess. Tiene variedades, pero el principio de funcionamiento es el mismo: toma los datos de entrada en un vector o array y ofrece los valores de la capa de salida, normalmente también en un vector o array. Hay redes con una sola neurona en la capa de salida, y en tales casos existirá una sobrecarga de esta función que retornará un único valor en lugar de un array.

Debemos señalar que, aunque codifiquemos y utilicemos un perceptrón de una sola capa oculta, nuestra clase de referencia se denominará perceptrón multicapa porque es escalable, ya que el número de capas ocultas para cualquier red inicializada se puede establecer durante la ejecución, y oscila entre 0 y 2.

Si intentamos aproximarnos un poco al funcionamiento de una conexión directa típica, podemos fijarnos en la función MLPInternalProcessVector. Una de las primeras acciones de dicha función será normalizar la cadena de datos de entrada para que todos los valores de este array de entrada estén más relacionados.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CBdSS::DSNormalize(CMatrixDouble &xy,const int npoints,
                        const int nvars,int &info,CRowDouble &means,
                        CRowDouble &sigmas)
  {
//--- function call
   DSNormalizeC(xy,npoints,nvars,info,means,sigmas);
//--- calculation
   for(int j=0; j<nvars; j++)
     {
      //--- change values
      for(int i=0; i<npoints; i++)
         xy.Set(i,j,(xy.Get(i,j)-means[j])/sigmas[j]);
     }
  }

Para ello, resulta imprescindible usar el valor medio y la desviación típica (sigma) de cada columna del vector de entrada para obtener valores en el intervalo 0 - 1. Por ello, los valores medios y sigmas deberán determinarse manualmente a partir de los conjuntos de datos de entrenamiento y asignarse después a las redes. Ya existen funciones que pueden realizar cálculos similares en el mismo archivo DSNormalize de Alglib, como mostramos a continuación:

//+------------------------------------------------------------------+
//| Normalize                                                        |
//+------------------------------------------------------------------+
void CBdSS::DSNormalize(CMatrixDouble &xy,const int npoints,
                        const int nvars,int &info,double &means[],
                        double &sigmas[])
  {
   CRowDouble Means,Sigmas;
   DSNormalize(xy,npoints,nvars,info,Means,Sigmas);
   Means.ToArray(means);
   Sigmas.ToArray(sigmas);
  }

También cabe destacar el array m_structinfo, que se utiliza para almacenar información clave sobre la red, como el número total de neuronas, el tipo de activación usado, el número total de pesos, el número de neuronas de la capa de entrada y el número de neuronas de la capa de salida.

Una vez normalizados, los datos pasan por la red y cada neurona de cada nivel puede tener su propia función de activación. Esta configuración puede definirse usando la función MLPSetNeuronInfo, que puede utilizarse fácilmente como ventaja al construir una red.

La alimentación directa del perceptrón resulta relativamente sencilla en comparación con el entrenamiento y el ajuste de los pesos de la red. Alglib ofrece principalmente dos enfoques de entrenamiento, el algoritmo Levenberg-Marquardt y el LBFGS.

Cuando se busca una solución de mínimos cuadrados no lineal, el algoritmo de Levenberg-Marquardt combina la velocidad del algoritmo de Gauss-Newton y la flexibilidad del algoritmo de descenso de gradiente en puntos de alta curvatura de la solución. Para ello, utiliza una matriz de Hesse para registrar la curvatura de la superficie como estimación de la proximidad a la solución. Sus aplicaciones se encuentran principalmente en las redes neuronales, donde resulta eficaz para tratar superficies de error no convexas, especialmente en situaciones en las que intervienen conjuntos de datos pequeños con arquitecturas de red relativamente simples, ya que calcular la matriz de Hesse requiere bastante trabajo.

El LBFGS (algoritmo Broyden-Fletcher-Goldfarb-Shanno con memoria limitada), en lugar de calcular la matriz de Hesse, la aproxima usando una memoria limitada mediante el registro de las actualizaciones más recientes de los pesos de la red, lo que hace que, en general, sea muy eficiente en el cálculo y la gestión de la memoria. Como tal, resulta más adecuado para situaciones con grandes conjuntos de datos y una arquitectura de red relativamente compleja.

Una comparación de las propiedades de convergencia de estos dos métodos sugiere que resulta preferible el algoritmo de Levenberg-Marquardt, ya que puede encontrar rápidamente una solución precisa incluso en situaciones en las que la suposición inicial estaba lejos de la verdad (por ejemplo, cuando la red se inicializa con pesos aleatorios). Además, a diferencia del descenso por gradiente, es menos propenso a atascarse en los mínimos locales. Esto lo hace un poco más fiable, en parte debido al uso del factor lambda de amortiguación Por otro lado, el LBFGS se ve más afectado por la suposición inicial (en nuestro caso, los pesos iniciales de la red) y debería converger más lentamente o estancarse en mínimos locales.

Ejemplar de la clase de señal del asesor

Encontrará más información sobre los perceptrones aquí Veamos la implementación de un ejemplar en código. La creación de un asesor usando el Wizard MQL5 requiere el conocimiento de tres clases típicas que definen un asesor basado en el Wizard, a saber: la clase de señal (que es el tema de nuestro enfoque en este artículo), la clase de trailing (que determina cómo se establecen los stop loss para las posiciones abiertas), y la clase de gestión de capital (que ayuda a establecer el tamaño de los lotes comerciales). Esto ya lo hemos tratado en artículos anteriores. Las tres clases deberán definirse y seleccionarse en el Wizard durante el montaje. Aunque la clase de gestión de capital ofrece un volumen de operaciones de tamaño optimizado, se podría utilizar una cuarta clase de Wizard que estudie cómo de seguro es para un asesor colocar varias órdenes dentro de una misma posición: basándose en la historia comercial o en algunos datos de indicadores, pero este no es el tema de este artículo.

Para implementar un ejemplar de las clases de perceptrón de Alglib como un perceptrón de una sola capa, deberemos empezar declarando ejemplares de nuestras clases clave en la interfaz de nuestra clase de señal de asesor personalizada. En los archivos de clase de las señales, siempre tenemos las funciones LongCondition y ShortCondition. Otro método importante que necesitaremos además de las funciones de inicialización y validación es una función para calcular o procesar la señal del perceptrón.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class CSignalPerceptron          : public CExpertSignal
  {
protected:
   
   int                           m_hidden;                              // 
   int                           m_features;                            // 
   int                           m_hidden_1_size;                       //
   int                           m_hidden_2_size;                       //  
   int                           m_training_points;                     //
   int                           m_training_restarts;                   //
   int                           m_activation_type;                     // 
   double                        m_hidden_1_bias;                       //
   double                        m_hidden_2_bias;                       //
   double                        m_output_bias;                         //

public:

...

protected:

   CBdSS                         m_norm;
   CMLPBase                      m_base;
   CMLPTrain                     m_train;
   CMatrixDouble                 m_xy;
   CMLPReport                    m_report;
   CMLPTrainer                   m_trainer;
   CMultilayerPerceptron         m_network;
   
   bool                          m_in_training;
      
   int                           m_inputs;
   int                           m_outputs;
   
   double                        m_last_long_y;
   double                        m_last_short_y;
   
   bool                          ReadWeights();
   bool                          WriteWeights(CRowDouble &Export);
   
   void                          Process(double &Y);
  };

La función de validación sirve en realidad como nuestra función de inicialización en este ejemplar de la clase de señal de asesor. Tenemos una función de inicialización incorporada, pero la validación nos vendrá mejor. En primer lugar, asignaremos el número de entradas y salidas de nuestro perceptrón. El número de entradas se puede optimizar, por lo que se leerá del parámetro, pero el número de salidas, al tratarse de una clasificación y no de una regresión, deberá ser al menos de 2.

Para ello, por simplicidad, fijaremos el número de salidas en 2. A continuación, redimensionaremos la matriz de datos de entrenamiento para que tenga las filas correspondientes al número de puntos de entrenamiento que consideraremos en cada columna al procesar la dirección. Sus columnas deberán corresponderse con la suma del número de entradas y salidas. Una salida igual a 2 supondrá el entrenamiento de dos coeficientes de peso para las direcciones alcistas y bajistas, y de hecho la pasada directa devolverá de forma similar dos probabilidades, una para una posición larga y otra para una posición corta: ambas sumarán uno. Después de ello, crearemos un entrenador, estableciendo el número de entradas y salidas para él.

   m_train.MLPCreateTrainerCls(m_inputs,m_outputs,m_trainer);

A continuación crearemos la red, y dependiendo del número de capas ocultas elegidas utilizaremos diferentes funciones para ello, en este caso, además, cada función permitirá definir el número de neuronas de entrada, el número de neuronas en cada capa oculta (si se utilizan) y finalmente el número de neuronas en la capa de salida.

   if(m_hidden==0)
   {
      m_base.MLPCreateC0(m_inputs,m_outputs,m_network);
   }
   else if(m_hidden==1)
   {
      m_base.MLPCreateC1(m_inputs,m_hidden_1_size,m_outputs,m_network);
   }
   else if(m_hidden==2)
   {
      m_base.MLPCreateC2(m_inputs,m_hidden_1_size,m_hidden_2_size,m_outputs,m_network);
   }
   else if(m_hidden>2||m_hidden<0)
   {
      printf(__FUNCSIG__+" invalid number of hidden layers should be 0, 1, or 2. ");
      return(false);
   }

Por último, configuraremos las funciones de activación de las capas oculta y de salida, así como en el desplazamiento de las capas. Las clases Alglib resultan bastante versátiles, por lo que las funciones de activación y desplazamiento podrán personalizarse no solo para cada capa, sino también para cada neurona. En este artículo, sin embargo, nos fijaremos en algo simplista.

Además de inicializar y comprobar nuestra red, necesitaremos disponer de los medios necesarios para explorar los pesos ideales de la red usando un sistema que permita almacenarlos y leerlos cuando sea necesario. Aquí podríamos considerar varios enfoques diferentes, pero nosotros utilizaremos simplemente la escritura de un archivo en el array de pesos de la red después de pasar una prueba cuando el criterio de prueba del asesor supere la prueba anterior. En la siguiente ejecución, nuestra red se inicializará leyendo estos pesos, y estos mejorarán con cada entrenamiento posterior. Las funciones WriteWeights y ReadWeights se encargarán, respectivamente, de escribir los pesos en un archivo y de leerlos.

Por último, la función Process se ejecutará en cada nueva barra para entrenar nuestra red con nuevos datos y, a continuación, procesar la señal actual, que se denominará variable Y. Aquí deberemos considerar algunas cosas: en primer lugar, la matriz de datos de prueba m_xy deberá normalizarse por columnas para que cada valor de la matriz esté comprendido entre -1,0 y +1,0. Como hemos mencionado antes, esto se podrá hacer utilizando otras funciones en las clases Alglib, y estas se encontrarán en el mismo archivo que las clases del perceptrón. Obviamente, podremos personalizar este enfoque para hacerlo más adecuado a una situación concreta, pero para nuestros propósitos se utilizarán las funciones incorporadas.

      //normalise data
      CRowDouble _means,_sigmas;
      m_norm.DSNormalize(m_xy,m_training_points,m_inputs,_info,_means,_sigmas);

En segundo lugar, el entrenamiento de la red se realizará usando dos funciones dependiendo de si iniciamos el proceso de entrenamiento o ya hemos realizado una ejecución del entrenamiento. Una vez empecemos el entrenamiento, podremos guardar los pesos de la pasada anterior y seguir entrenando con ellos para no tener que estar constantemente jugando con pesos aleatorios. La función de entrenamiento por defecto siempre aleatorizará los pesos, y si la utilizáramos, ¡aleatorizaríamos nuestros pesos en cada nueva barra!

      m_train.MLPSetDataset(m_trainer,m_xy,m_training_points);
      //
      if(!m_in_training)
      {
         m_train.MLPStartTraining(m_trainer,m_network,false);
         m_in_training=true;
      }
      else if(m_in_training)
      {
         while(m_train.MLPContinueTraining(m_trainer,m_network))
         {
            //
         }
      }

Gracias al Wizard, la integración de esta clase de señal completa con las clases de trailing y gestión de capital en el asesor se realizará sin problemas en 6 pasos, que se han reducido a cinco en las capturas de pantalla de la sección "Montaje y prueba". Tras ejecutarlos, deberíamos obtener un asesor con los siguientes archivos de inclusión:

//+------------------------------------------------------------------+
//| Include                                                          |
//+------------------------------------------------------------------+
#include <Expert\Expert.mqh>
//--- available signals
#include <Expert\Signal\My\SignalPerceptron.mqh>
//--- available trailing
#include <Expert\Trailing\TrailingNone.mqh>
//--- available money management
#include <Expert\Money\MoneyFixedMargin.mqh>

Montaje y prueba del asesor

Vamos a construir un asesor basado en nuestra clase de señal personalizada utilizando el Wizard. Es bastante sencillo (mire las capturas de pantalla).

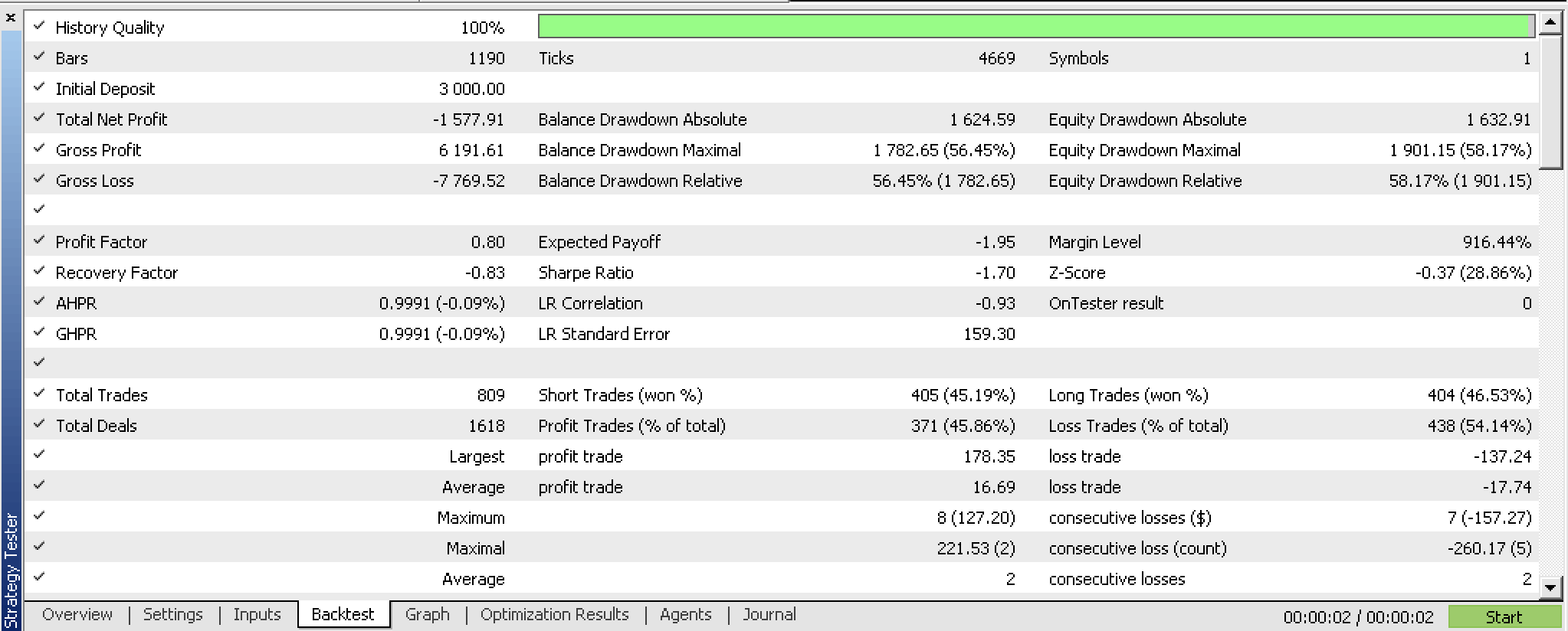
Si probamos nuestro asesor compilado antes de cualquier optimización, obtendremos el siguiente informe:

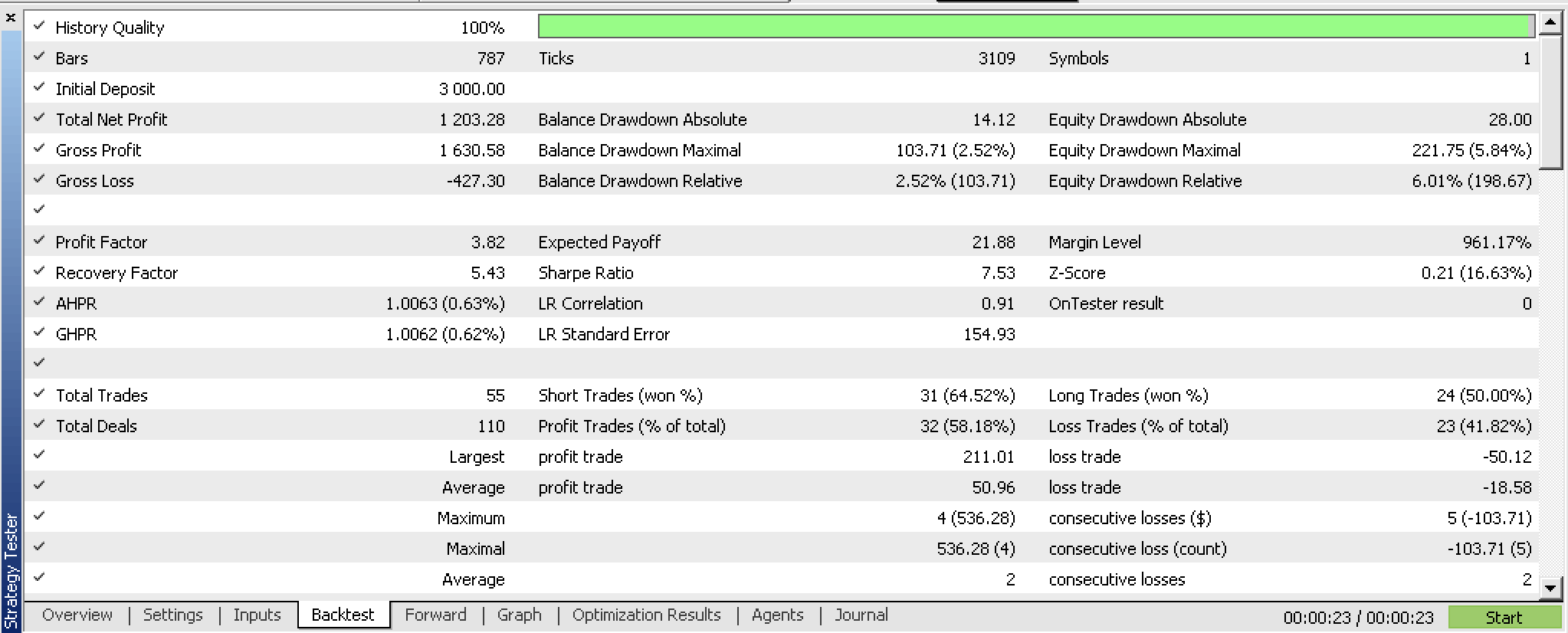
Si optimizamos nuestro asesor con una ventana de prueba forward, obtendremos los siguientes resultados:

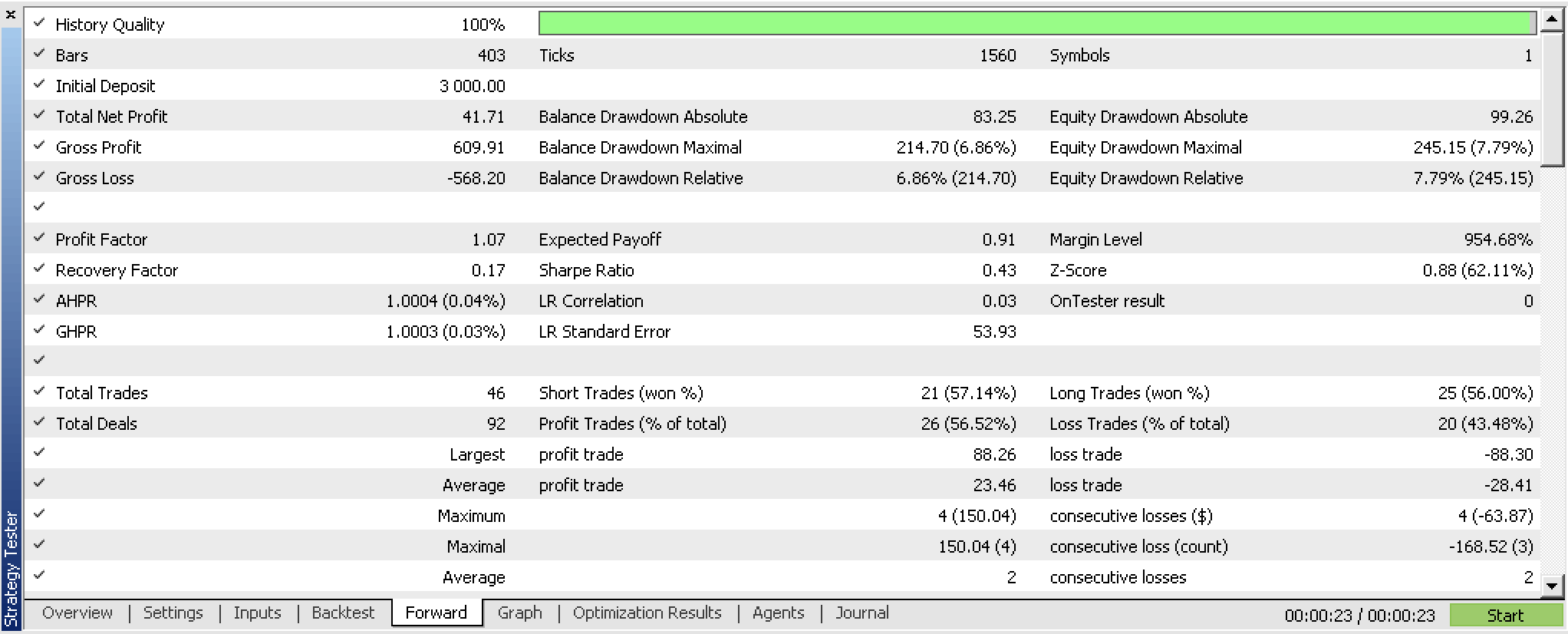
Hemos entrenado nuestro perceptrón y exportado sus pesos basándonos en los criterios de optimización de nuestro asesor. Una forma más breve de hacerlo sería utilizar las funciones de comprobación cruzada incorporadas o incluso utilizar algo más sencillo como el valor del error cuadrático medio del informe si no se utiliza el bagging. En ambos casos, conservaremos los pesos que tienen más probabilidades de coincidir con los clasificadores de entrenamiento. A juzgar por nuestras pruebas, la red muestra resultados prometedores, pero como siempre, no debemos olvidarnos de ser más minuciosos en las pruebas durante periodos de tiempo más largos utilizando los datos de ticks de nuestro bróker.

Conclusión

Hoy hemos visto cómo los perceptrones pueden implementarse con un código mínimo gracias a las clases de código de Alglib. Asimismo, hemos destacado algunos pasos preliminares, como la normalización del conjunto de datos, que deben darse antes de que los perceptrones merezcan ser probados y estudiados. Además, hemos mostrado medidas adicionales que merece la pena considerar cuando los perceptrones están listos para la prueba. Todos estos pasos y medidas adicionales, como la exportación de parámetros personalizables, se realizan con la ayuda de código auxiliar de las clases Alglib.

Así pues, las ventajas de uso de las clases Alglib consisten, en primer lugar, en minimizar la cantidad de código y el tiempo necesarios para crear el sistema bajo prueba. Pero existen inconvenientes, sobre todo en lo que respecta a la personalización. Por ejemplo, nuestros perceptrones no pueden tener más de dos capas ocultas. Y en escenarios en los que se modelan conjuntos de datos complejos, esto puede suponer un cuello de botella.