LibMatrix: Librería de Álgebra Matrix (Parte uno)

Introducción

En la escritura de los sistemas de trading complejos es esencial la aplicación de varias ramas de las matemáticas. Una de esas ramas es el álgebra lineal.

Actualmente no hay disponibles muchas librerías en MQL4 que implemente varios métodos de álgebra lineal (particularmente, la teoría de matrices y determinantes).

Este artículo describe la librería LibMatrix en MQL4 que incluye la implementación de las operaciones de matrix más comunes.

Matrix es una gama rectangular finita rellena con varios objetos matemáticos (por ejemplo, números).

Cuatro meses después de haberlo escrito en C++, el código por completo se volvió a escribir en MQL4 con algunas modificaciones.

1. Estructura de la estructura

Primero consideremos algunas peculiaridades del trabajo con matrices en la librería propuesta.

Antes que nada, las matrices se almacenan en gamas de una dimensión. Tiene que ver con el hecho de que, aunque las características que ofrece MQL4 para la creación de gamas multidimensionales, sólo es posible cambiar el tamaño de la primera dimensión. Para almacenar una matrix de N filas y M columnas, se necesita una gama N*M unidimensional. La matrix se almacena en una gama fila a fila, es decir, los primeros elementos de una fila en una gama de datos van seguidos por los elementos de la segunda fila, etc.

Segundo, cuando se crea la librería, se decidió no almacenar la información adicional en el tamaño de matrix en una gama de datos, ya que los tamaños son valores enteros, mientras que los elementos son números reales (almacenar los tamaños como números reales podría afectar mucho al funcionamiento de la librería).

Por lo que una matrix en el formato procesado por la librería propuesta consiste en tres variables: una gama unidimensional del tipo doble y dos valores enteros (es decir, del tipo int) para almacenar información en el número de filas y columnas de matrix.

La librería consiste en dos archivos: LibMatrix.mqh y LibMatrix.mq4. El primer archivo es para que se incluya como se requiere. Contiene prototipos de funciones que se pueden importar desde la librería. El segundo archivo contiene implementaciones de la función (código de programa). Eso es de lo que vamos a hablar un poco más adelante.

Las funciones implementadas en la librería se pueden dividir en varios grupos:

• funciones matemáticas generales (MathLerp, MathInRangeRandom, MathDoublesEqual)
• funciones auxiliares para trabajar con matrices (MatrIndiciesToOffset, MatrCopy, MatrSetSize, MatrResize)
• funciones para trabajar con filas y columnas (MatrSwapRows, MatrSwapCols, MatrCopyRow, MatrCopyCol, MatrRowIsZero, MatrColIsZero)
• funciones para comprobación general de condiciones (MatrIsSquare, MatrIsElemOnMainDiagonal, MatrCompatiblityCheckAdd, MatrCompatiblityCheckMul)
• funciones de inicio de contenido (MatrLoadZero, MatrLoadIdentity, MatrLoadInRangeRandom)
• funciones para comprobar las condiciones por tipo de contenido (MatrIsZero, MatrIsDiagonal, MatrIsIdentity, MatrIsSymmetric, MatrIsAntisymmetric, MatrEqual)
• funciones para aumento de operaciones teniendo en cuenta los elementos (MatrAddScalar, MatrSubScalar, MatrMulByScalar, MatrDivByScalar)
• funciones para operaciones matrix básicas (MatrAddMatr, MatrSubMatr, MatrMulMatr, MatrTrace, MatrTranspose)
• otras funciones (MatrGaussianElimination, MatrGJBatchSolve, MatrMinor, MatrAlgebraicComplement, MatrInvertUsingMinors, MatrInvertUsingGJ, MatrDet, MatrDetTriang, MatrRank, MatrRankTriang, MatrComputeConnectedMatr, MatrLerpMatr)
• funciones de entrada/salida (MatrPrint, FileWriteMatr, FileReadMatr)

Vamos a mirar más atentamente cada grupo.

2. Descripción de funciones

2.1. Funciones matemáticas generales

Primero se considera el grupo de funciones matemáticas generales. Incluye funciones que no están directamente asociadas con los matrices pero que se utilizan en la librería.

double MathLerp(double rangeLowLimit, double rangeHighLimit, double balance);

Esta función realiza una interpolación lineal entre dos valores, utilizando la siguiente fórmula: rangeLowLimit + balance * (rangeHighLimit - rangeLowLimit). El parámetro de balance debería estar dentro del rango [0:1].

double MathInRangeRandom(double rangeLowLimit, double rangeHighLimit);

Esta función devuelve números aleatorios distribuidos uniformemente desde el rango [rangeLowLimit;rangeHighLimit]. La función estándar MathRand se utiliza para generación.

bool MathDoublesEqual(double value1, double value2, double tolerance);

Esta función se utiliza para comprar dos valores, value1 y value2, de los de tipo doble con la precisión específica (tolerance). Se requiere el uso aproximado de comparaciones por la posible pérdida de precisión. El valor del parámetro de tolerance no debería ser negativo (como valor por defecto, puede utilizar la constante DEFAULT_TOLERANCE definida en la librería).

2.2. Funciones auxiliares para trabajar con matrices

Procedamos al grupo de las funciones auxiliares para trabajar con matrices. Este grupo cubre las funciones destinadas a la simplificación de operaciones relacionado con las matrices de empaquetado en gamas de una dimensión.

int MatrIndiciesToOffset(int row, int col, int numRows, int numCols)

Esta función calcula el intervalo de un elemento con respecto al principio de la gama en la que se empaqueta la matrix. Entre los parámetros que recibe, esta el número de la fila (row) y la columna (col) en la intersección en la que se encuentra el elemento, así como el tamaño de la matrix (numRows: número de filas de matrix; numCols: número de columnas de matrix). Los valores de row y col deben estar entre los rangos: [0;numRows-1] y [0;numCols-1] respectivamente.

void MatrCopy(double& src[], double& dst[]);

Esta función copia todos los elementos de la matrix scr a la matrix dst. Las gamas de datos de matrix son el único parámetro superado. Cuando se completa la copia, el tamaño de la matrix dst se vuelve igual al tamaño de la matrix scr.

void MatrSetSize(double& matr[], int numRows, int numCols);

Esta función cambia el tamaño de la gama de datos de matr para que se pueda almacenar una matrix de numRows filas y numCols columnas. No se garantiza la integridad de los datos de matrix. Los parámetros de numRows y numCols deberían ser sólo positivos.

void MatrResize(double& matr[], int numRowsOld, int numColsOld, int numRowsNew, int numColsNew);

Esta función cambia el tamaño de la gama de datos matr de la matrix existente. Los parámetros numRowsOld y numColsOld deben ser iguales al tamaño inicial de matrix. El nuevo tamaño lo establecen los parámetros de numRowsNew y numColsNew. La integridad de los datos de matrix están garantizados con el nuevo tamaño, excepto en el caso en el que disminuyan una o ambas matrix. Se inician a cero nuevos elementos.

2.3. Funciones para trabajar con filas y columnas

Echemos un vistazo a las funciones para trabajar con filas y columnas.

void MatrSwapRows(double& matr[], int numRows, int numCols, int row1, int row2);

Esta función intercambia el contenido de las filas row1 y row2 con la matrix matr de filas numRows y columnas numCols. Los valores de los parámetros row1 y row2 deberían estar dentro del rango [0;numRows-1].

void MatrSwapCols(double& matr[], int numRows, int numCols, int col1, int col2);

Esta función intercambia el contenido de las columnas col1 y col2. Los valores de los parámetros col1 y col2 deberían estar dentro del rango [0;numCols-1].

void MatrCopyRow(double& matr[], int numRows, int numCols, int rowToCopy, int rowToReplace);

Esta función copia el contenido de la fila rowToCopy a la fila rowToReplace. Los valores de los parámetros rowToCopy y rowToReplace deberían estar dentro del rango [0;numRows-1].

void MatrCopyCol(double& matr[], int numRows, int numCols, int colToCopy, int colToReplace);

Esta función copia el contenido de la columna colToCopy a la columna colToReplace. Los valores de los parámetros colToCopy y colToReplace deberían estar dentro del rango [0;numCols-1].

bool MatrRowIsZero(double& matr[], int numRows, int numCols, int row, double tolerance);

Esta función comprueba si la fila row es inválida con el grado de precisión tolerance. Si la fila es inválida, el valor devuelto será true.

bool MatrColIsZero(double& matr[], int numRows, int numCols, int col, double tolerance);

Esta función comprueba si la columna col es inválida con el grado de precisión tolerance. Si la fila es inválida, el valor devuelto será true.

2.4. Funciones para comprobación general de condiciones

El grupo de funciones para comprobación general de condiciones está diseñado para mejorar el código de legibilidad.

bool MatrIsSquare(int numRows, int numCols);

Esta función comprueba si el número de filas numRows y columnas numCols es cuadrado (es decir, comprueba si numRows=numCols). Devuelve true para matrices cuadradas.

bool MatrIsElemOnMainDiagonal(int row, int col);

Esta función comprueba si el elemento con los índices [row][col] está en la diagonal principal de matrix. Devuelve true para los elementos en la diagonal principal.

bool MatrCompatiblityCheckAdd(int numRows1, int numCols1, int numRows2, int numCols2);

Esta función comprueba la compatibilidad de dos matrices con fines de operaciones de adición. Las dimensiones se comprueban teniendo en cuenta los pares de equidad (numRows1=numRows2 y numCols1=numCols2); devuelve true en caso de equidad.

bool MatrCompatiblityCheckMul(int numRows1, int numCols1, int numRows2, int numCols2);

Esta función comprueba la compatibilidad de dos matrices con fines de multiplicación. Comprueba si el número de columnas en la primera matrix (numRows1 por la matrix de numCols1) es igual al número de filas de la segunda matrix (numRows2 por la matrix de numCols2). La multiplicación es posible si devuelve true.

2.5. Funciones de inicio de contenido de matrix

El grupo de funciones de inicio de contenido de matrix está destinado a cargar los matrices utilizados con más frecuencia (es decir, matrices inválidos y de identidad). Como la memoria no está asignada, se debería llamar a las funciones MatrSetSize o MartrResize antes de llamar al grupo de funciones.

void MatrLoadZero(double& matr[], int numRows, int numCols);

Esta función inicia la gama de datos matr a ceros, pues crea una matrix inválida de filas numRows y columnas numCols.

void MatrLoadIdentity(double& matr[], int numRows, int numCols);

Esta función inicia todos los elementos de la gama de datos matr a ceros, excepto aquellos que están en la diagonal principal de matrix. La matrix indicada de filas numRows y columnas numCols debería ser cuadrada.

void MatrLoadInRangeRandom(double& matr[], int numRows, int numCols, double rangeLowLimit, double rangeHighLimit);

Esta función inicia la gama de datos de la matrix matr a números aleatorios desde el rango [rangeLowLimit;rangeHighLimit] (los números aleatorios se general utilizando la función MathInRangeRandom).

2.6. Funciones para comprobar las condiciones por tipo

Vamos a hablar del grupo de funciones para comprobar condiciones por tipo. Las funciones de este grupo realizan una comparación con el grado de tolerancia de precisión (este valor de parámetro no debe ser negativo) y devuelve true si la condición a considerar es true.

bool MatrIsZero(double& matr[], int numRows, int numCols, double tolerance);

Esta función comprueba el matrix es inválida.

bool MatrIsDiagonal(double& matr[], int numRows, int numCols, double tolerance);

Esta función comprueba el matrix es diagonal. Se considerará que la matrix es diagonal si es cuadrada y si todos sus elementos fuera de la diagonal principal son cero.

bool MatrIsIdentity(double& matr[], int numRows, int numCols, double tolerance);

Esta función comprueba la matrix es identidad.

bool MatrIsSymmetric(double& matr[], int numRows, int numCols, double tolerance);

Esta función comprueba si la matrix es simétrica (por ejemplo a[i][j]=a[j][i] es true para cualquier i y j).

bool MatrIsAntisymmetric(double& matr[], int numRows, int numCols, double tolerance);

Esta función comprueba si la matrix está inclinada simétrica/antisimétrica (por ejemplo a[i][j]=-a[j][i] es true para cualquier i y j y a[k][k]=0 es true para cualquier k).

bool MatrEqual(double& matr1[], double& matr2[], int numRows, int numCols, double tolerance);

Esta función comprueba, teniendo en cuenta los elementos, la equidad entre matrices con las mismas dimensiones.

2.7. Funciones para aumento de operaciones teniendo en cuenta los elementos

Procedamos al grupo de las funciones para aumento de operaciones teniendo en cuenta los elementos. Este grupo es peculiar porque los resultados no se colocan en la gama inicial de la matrix mtr, sino en la nueva gama de result. Sin embargo, si la misma gama sobrepasa los parámetros de result y matr, los resultados se colocarán en la matrix inicial.

void MatrAddScalar(double& matr[], int numRows, int numCols, double scalar, double& result[]);

Esta función añade el valor para el aumento a cada uno de los elementos de la matrix.

void MatrSubScalar(double& matr[], int numRows, int numCols, double scalar, double& result[]);

Esta función sustrae el valor para el aumento a cada uno de los elementos de la matrix.

void MatrMulByScalar(double& matr[], int numRows, int numCols, double scalar, double& result[]);

Esta función divide cada elemento de la matrix por el valor del aumento.

void MatrDivByScalar(double& matr[], int numRows, int numCols, double scalar, double& result[]);

Esta función divide cada elemento de la matrix por el valor del aumento.

2.8. Funciones para operaciones matrix básicas

El grupo de funciones para operaciones matrix básicas consiste en funciones para realizar acciones elementales: cálculos de suma, producto y trazo, así como operaciones de transposición. El resultado del funcionamiento de la función (excepto para MatrTrace) se devuelve al result de la gama.

void MatrAddMatr(double& matr1[], double& matr2[], int numRows, int numCols, double& result[]);

Esta función añade hasta dos matrices con las mismas dimensiones.

void MatrSubMatr(double& matr1[], double& matr2[], int numRows, int numCols, double& result[]);

Esta función sustrae la matrix matr2 de la matrix matr1. Las matrices deberían ser del mismo tamaño.

void MatrMulMatr(
      double& matr1[], int numRows1, int numCols1,
      double& matr2[], int numRows2, int numCols2,
      double& result[], int& numRowsRes, int& numColsRes);

Esta función multiplica la matrix matr2 entre la matrix matr1. Los matrices deberían ser compatibles para su multiplicación, por ejemplo, el número de columnas (numCols1) en la primera matrix debería ser igual al número de filas (numRows2) en la segunda matrix. El tamaño de la matrix resultante se devuelve en referencias variables que se sobrepasan en los parámetros numRowsRes y numColsRes.

double MatrTrace(double& matr[], int numRows, int numCols);

Esta función calcula el trazo de la matrix (la suma de los elementos diagonales). La matrix debe ser cuadrada.

void MatrTranspose(double& matr[], int numRows, int numCols, double& result[], int& numRowsRes, int& numColsRes);

Esta función traslada la matrix (cambia columnas con filas). El nuevo tamaño de la matrix se devuelve en referencias variables que se sobrepasan en los parámetros numRowsRes y numColsRes.

2.9. Otras funciones

El grupo de otras funciones ofrece las posibilidades para la inversión de matrix, cálculo de rangos y determinantes, etc.

int MatrGaussianElimination(double& matr[], int numRows, int numCols, double& result[], double tolerance);

Esta función representa la implementación de la eliminación Gaugasiana con la giratoria. La matrix matr inicial de filas numRows y de columnas numCols se reduce a una forma trapezoidal (triangular), y los resultados se colocan en la gama result.

El valor devuelto es el número de filas independientes de la matrix (es decir, su rango). Como los cálculos pueden llevar al redondeo erróneo de las funciones, es necesario sobrepasar un parámetro de valor de tolerancia no negativa que defina el grado de precisión de la comparación.

bool MatrGJBatchSolve(
      double& matr[], int numRows, int numCols,
      double& rhs[], int numRowsRHS, int numColsRHS,
      double& roots[], int& numRowsRoots, int& numColsRoots,
      double tolerance
      );

Esta función representa la implementación de la eliminación Gauss-Jordan, destinada a la resolución de sets de varios sistemas de ecuación con el mismo sistema matrix.

El sistema matrix común se sobrepasa en los parámetros matr (gama de datos), numRows y numCols (dimensiones) También se sobrepasa como un matrix un set de vectores del lado derecho (el parámetro rhs), en el que cada columna representa el lado derecho del sistema bajo consideración.

En otras palabras, el parámetro numRowsRHS contiene el número de ecuaciones en el sistema (número de filas en el sistema matrix), mientras que el parámetro numColsRHS contiene el número de los vectores del lado derecho (número de sistemas a resolver).

Los resultados se devuelven en forma de matrix roots de filas numRowsRoots y columnas numColsRoots. La solución para cada sistema de ecuaciones se coloca en la columna matrix y responde a la solución del sistema de dicho sistema y la columna con el número relevante de la matrix rhs. La función devuelve true si se ha encontrado la solución para el set de sistemas de ecuaciones.

void MatrMinor(
      double& matr[], int numRows, int numCols,
      int rowToExclude, int colToExclude,
      double& result[], int& numRowsRes, int& numColsRes);

Esta función encuentra el matrix menor en la intersección de la fila rowToExcude y la columna colToExclude. Los elementos de matrix resultantes se devuelven en la gama result, mientras que las dimensiones se devuelven en referencias variables que se sobrepasan en los parámetros numRowsRes y numColsRes.

double MatrAlgebraicComplement(double& matr[], int numRows, int numCols, int elemRow, int elemCol, double tolerance);

Esta función calcula el cofactor algebraico (menos con un signo) para el elemento que está en la intersección de la fila elemRow y la columna elemCol. Para calcular el determinante, se utiliza la eliminación Gaussiana (en forma de función MatrGaussianElimination) con el grado de precisión establecida por el parámetro tolerance.

bool MatrInvertUsingMinors(double& matr[], int numRows, int numCols, double& result[], double tolerance);

Esta función calcula la el inverso del cuadrado matr de matrix utilizando una unión matrix (generada de cofactores algebraicos de los elementos matrix correspondientes). Una complejidad asintótica del algoritmo utilizado: O(N^5). La unión matrix se calcula utilizando la función MatrAlgebraicComplement (que emplea la eliminación Gaussiana) y por este motivo la función necesita sobrepasar un valor de parámetro de tolerance no negativa que defina el grado de precisión. Los elementos de la matrix resultante se colocan en la gama result. Si el inverso de la matrix se calcula satisfactoriamente (el determinante es diferente a cero), la función devuelve true.

bool MatrInvertUsingGJ(double& matr[], int numRows, int numCols, double& result[], double tolerance);

Esta función calcula el inverso de dicha matrix mrt cuadrada adjuntando un matrix de identidad, es decir, resolviendo los sistemas N (N=numRows=numCols) de ecuaciones lineales utilizando la función MatrGJBatchSolve (el matrix del lado derecho es identidad; el grado de precisión se establece por un valor de parámetro tolerance no negativo). Una complejidad asintótica del algoritmo utilizado: O(N^3). Los elementos de la matrix resultante se colocan en la gama result. Si el inverso de la matrix se calcula satisfactoriamente (el determinante es diferente a cero), la función devuelve true.

double MatrDet(double& matr[], int numRows, int numCols, double tolerance);

Esta función calcula el determinante de la matrix mtr cuadrada a través de la reducción a una forma trapezoidal (triangular). Para este propósito, se utiliza la eliminación con un grado de precisión de tolerance (este parámetro no debe ser negativo). Una complejidad asintótica del algoritmo: O(N^3).

double MatrDetTriang(double& matr[], int numRows, int numCols);

Esta función calcula el determinante de la matrix matr triangular.

double MatrRank(double& matr[], int numRows, int numCols, double tolerance);

Esta función calcula el rango de la matrix mtr cuadrada a través de la reducción a una forma trapezoidal (triangular). Para este propósito, se utiliza la eliminación con un grado de precisión de tolerance (este parámetro no debe ser negativo). Una complejidad asintótica del algoritmo: O(N^3).

double MatrRankTriang(double& matr[], int numRows, int numCols, double tolerance);

Esta función calcula el rango de la matrix matr triangular. La matrix debería reducirse a una de forma trapezoidal (triangular) fila por fila (por ejemplo, llamando a la función MatrGaussianElimination). El valor no negativo de tolerance establece el grado de precisión del cálculo de la primera fila inválida.

void MatrComputeConnectedMatr(double& matr[], int numRows, int numCols, double& result[], double tolerance);

Esta función calcula una unión matrix para el cuadrado matrix mtr. Los elementos de la matrix resultante se colocan en la gama result. El valor no negativo define el grado de precisión en el cálculo de los cofactores algebraicos.

void MatrLerpMatr(double& matr1[], double& matr2[], int numRows, int numCols, double balance, double& result[]);

Esta función realiza una interpolación teniendo en cuenta los elementos entre las matrices matr1 y matr2 del mismo tamaño. El parámetro de balance representa el coeficiente de la interpolación lineal y debería estar en el rango [0:1]. Los elementos de la matrix resultante se devuelven en la gama result.

2.10. Funciones entrada/salida

El grupo de funciones entrada/salida está destinado a guardar/cargar matrices, así como a la escritura de la salida depurada de una matrix en el log.

void MatrPrint(double& matr[], int numRows, int numCols);

Esta función está destinada a la escritura de la salida depurada del log (pestaña del Asesor Experto en el panel de la Terminal). Saca matrix fila a fila teniendo en cuenta que el log se muestra en la terminal en orden inverso (es decir, aparecen nuevas entradas al principio; la función imprime filas de matrix desde el fina para la comodidad del análisis visual de las matrices en el log).

void FileWriteMatr(double& matr[], int numRows, int numCols, int handle);

Esta función guarda una matrix (con sus dimensiones) en el archivo que gestiona su paso en el parámetro handle. El archivo se debe abrir en el modo FILE_BIN|FILE_WRITE.

void FileReadMatr(double& matr[], int& numRows, int& numCols, int handle);

Esta función carga un matrix desde un archivo. Primero, se leen las dimensiones de matrix a las referencias variables que sobrepasan en los parámetros numRows y numCols. Se vuelve a establecer el tamaño de la gama matr según al tamaño de matrix que sigue la carga de contenido de la gama matr del archivo. El control del archivo del que se leen los datos se pasa al parámetro handle; el archivo debe abrirse en modo FILE_BIN|FILE_READ.

Ahora que el lector está familiarizado con las descripciones de la función, se puede procedes a la resolución de problemas prácticos utilizando la librería.

3. Ejemplo de uso

Vamos a echar un visitado a un ejemplo de creación de una regresión polinomial en una serie de valores de precio utilizando la librería propuesta.

El proceso de creación de una regresión polinominal consiste en encontrar los coeficientes polinominales f(x)=a[0]+a[1]*x+...+a[degree]*x^degree del grado grado. Esto se realiza resolviendo un sistema de ecuaciones algebraicas lineales en las que los elementos del sistema matrix A[degree+1][degree+1] se definen de la siguiente manera: A[i][j]=(x[0]^(i+j)+x[1]^(i+j)+...+x[numPoints]^(i+j))/numPoints mientras los elementos del vector del lado derecho B[degree+1][1] se definen utilizando la siguiente fórmula: B[i]=(y[0]*x[0]^i+y[1]*x[1]^i+...+y[numPoints]*x[numPoints]^i)/numPoints

Para resolver la tarea a mano, hay un script (el archivo LibMatrixEx.mq4 en el archivo adjunto) que cree una polinomia y la muestre en el intervalo inicial y a su derecha (es decir, extrapolación). Los valores de polinomia en el intervalo de extrapolación se puede usar para predecir la dirección del movimiento del precio.

El script se controla utilizando tres líneas verticales: dos de ellas están destinadas a seleccionar el intervalo a analizar y el tercero establece el punto más derecho hasta el que se muestra la polinomia.

Para permitir el funcionamiento del script, necesita llevarlo al gráfico y establecer los parámetros necesarios: delay: tasa actualizada del gráfico (en ms); degree: grado de polinomia; linesMargin: distancia inicial entre las líneas de control; linesWidht: anchura del gráfico polinomio. También puede seleccionar los colores de las líneas de control verticales (parámetros colVLineInt y colVLineExt) y las líneas del gráfico (parámetros colInt y colExt)

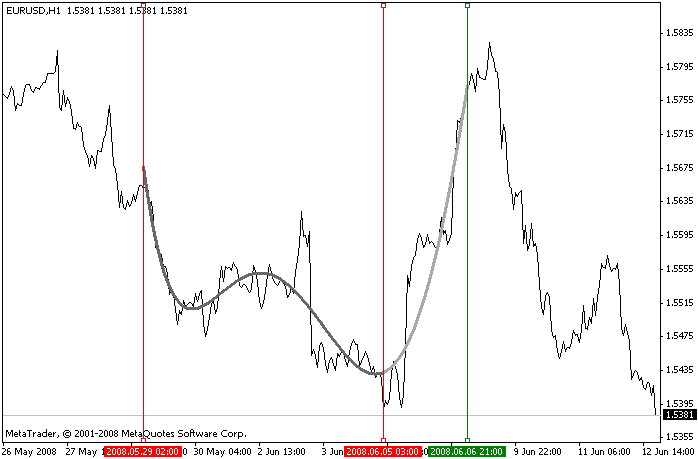
Ejemplo de funcionamiento del script

Vamos a revisar la función clave del script que lidia con matrices.

// creating polynomial regression
bool Regression(double& x[], double& y[], int numPoints, int polyDegree, double& poly[]) {
   // create system matrix
   double A[];
   int numRowsA = polyDegree + 1;
   int numColsA = polyDegree + 1;
   MatrSetSize(A, numRowsA, numColsA);
   // fill the matrix
   for (int row = 0; row < numRowsA; row++) {
      for (int col = 0; col < numColsA; col++) {
         int offset = MatrIndiciesToOffset(row, col, numRowsA, numColsA);
         A[offset] = SXY(x, y, numPoints, row + col, 0);
      }
   }
   // create a right hand side vector
   double B[];
   int numRowsB = polyDegree + 1;
   int numColsB = 1;
   MatrSetSize(B, numRowsB, numColsB);
   // fill the right hand side vector
   for (row = 0; row < numRowsB; row++) {
      offset = MatrIndiciesToOffset(row, 0, numRowsB, numColsB);
      B[offset] = SXY(x, y, numPoints, row, 1);
   }
   // solve a system of linear algebraic equations
   int numRowsX, numColsX;
   bool status =
      MatrGJBatchSolve(
         A, numRowsA, numColsA,
         B, numRowsB, numColsB,
         poly, numRowsX, numColsX,
         DEFAULT_TOLERANCE
      );
   if (!status) {
      Print("Error solving the system");
   }
   return (status);
}

La función se encarga de 5 argumentos. Los dos primeros son las gamas x e y que están destinadas a la resolución de las coordinadas de los puntos a través de los que se traza la polinomia. El número de puntos se traspasa en el parámetro numPoints. El cuarto argumento establece el grado de polinomia bajo consideración (debe ser menos que el número de puntos al menos por 1). El quinto argumento es la referencia a la gama que recibe los coeficientes polinominales.

Al principio de la función, se crea el matrix A, se cambia el tamaño y se rellena utilizando las fórmulas anteriores. Para hacer referencia a los elementos matrix a través de índices bidimensionales, utilizamos la función MatrIndiciesToOffset que calcula el intervalo de una dimensión con respecto al principio de la gama.

El vector columna B se rellena de forma similar. Esto va seguido de la llamada de la función MatrGJBatchSolve, que resuelve el sistema creado, encontrando los coeficientes polinominales.

El resto del código que comprueba las posiciones y salidas de la línea, la polinomia no debe suponer ninguna dificultad al lector.

Conclusión

El artículo ha introducido la librería para trabajar con matrices y trata la implementación de la función y sus peculiaridades.

El uso de la librería se ha demostrado a través del ejemplo de creación de una regresión polinominal en una serie de velas de valores de cierre de precio.

El código se comprobado detenidamente, pero puede tener errores. Si encuentra un error, por favor, hágamelo saber.