LibMatrix:矩阵代数库(第一部分)

MetaTrader 4 — 示例 | 11 四月 2016, 15:29

2 338

Evgeniy Logunov

简介

在编写复杂的自动交易系统的过程中，应用数学的各个分支是必不可少的。其中一种分支为线性代数。

在 MQL4 中，目前没有广泛公开的能够实现各种线性代数方法（尤其是矩阵和行列式）的库。

本文介绍了 MQL4 中的 LibMatrix 库，此库包含最常见的矩阵运算的实现。

矩阵是一个填充有一些数学对象（例如数字）的有限矩形数字。

在用 C++ 编写的四个月后，在 MQL4 中重新编写了整个代码，并进行了一些修改。

1.库结构

我们先来考虑在建议的库中处理矩阵的一些独特特性。

首先，所有矩阵都存储在一维数组中。这与以下事实有关：尽管 MQL4 提供创建多维数组的功能，但只能更改第一维度的大小。要存储一个由 N 行和 M 列组成的矩阵，我们需要一个 N*M 的一维数组。将此矩阵逐行装入数组中，即数据数组中的第二行元素跟在第一行元素的后面，以此类推。

其次，在创建库时，决定不在数据数组中存储有关矩阵大小的附加信息，因为大小为整数值，而元素为实数（将大小存储为实数会严重影响此库的运算）。

因此，采用已由建议库进行处理的格式的矩阵包含三个变量：double 类型的一维数组，以及两个用于存储矩阵行数和列数信息的整数变量（例如 int 类型）。

此库包含两个文件：LibMatrix.mqh 和 LibMatrix.mq4。根据需要，纳入第一个文件。它包含可从此库导入的函数原型。第二个文件包含函数实现（程序代码）。这就是我们下面要进一步讨论的内容。

此库中实现的函数可分成以下几组：

一般数学函数（MathLerp、MathInRangeRandom、MathDoublesEqual）
用于处理矩阵的辅助函数（MatrIndiciesToOffset、MatrCopy, MatrSetSize、MatrResize）
用于处理行和列的函数（MatrSwapRows、MatrSwapCols、MatrCopyRow、MatrCopyCol, MatrRowIsZero、MatrColIsZero）
用于常规检查条件的函数（MatrIsSquare、MatrIsElemOnMainDiagonal、MatrCompatiblityCheckAdd、MatrCompatiblityCheckMul）
内容初始化函数（MatrLoadZero、MatrLoadIdentity、MatrLoadInRangeRandom）
用于按内容类型检查条件的函数（MatrIsZero、MatrIsDiagonal、MatrIsIdentity、MatrIsSymmetric、MatrIsAntisymmetric、MatrEqual）
用于元素级标量运算的函数（MatrAddScalar、MatrSubScalar、MatrMulByScalar、MatrDivByScalar）
用于基本矩阵运算的函数（MatrAddMatr、MatrSubMatr、MatrMulMatr、MatrTrace、MatrTranspose）
其他函数（MatrGaussianElimination、MatrGJBatchSolve、MatrMinor、MatrAlgebraicComplement、MatrInvertUsingMinors、MatrInvertUsingGJ、MatrDet、MatrDetTriang、MatrRank、MatrRankTriang、MatrComputeConnectedMatr、MatrLerpMatr）
输入/输出函数（MatrPrint、FileWriteMatr、FileReadMatr）

我们来近距离了解各个组。

2.函数说明

2.1.一般数学函数

我们首先来考虑一般数学函数组：它包括并不与矩阵直接相关但却在此库中使用的函数。

double MathLerp(double rangeLowLimit, double rangeHighLimit, double balance);

此函数使用以下公式在两个值之间执行线性插值：rangeLowLimit + balance * (rangeHighLimit - rangeLowLimit)。Balance 参数值应在范围 [0;1] 内。

double MathInRangeRandom(double rangeLowLimit, double rangeHighLimit);

此函数返回均匀分布的随机数字，范围为 [rangeLowLimit;rangeHighLimit]。标准 MathRand 函数用于生成。

bool MathDoublesEqual(double value1, double value2, double tolerance);

此函数用于比较 double 类型的具有指定精确度的 (tolerance) 的两个值：value1 和 value2。由于准确性可能会降低，需要使用近似比较。tolerance 参数值不应为负数（您可以使用库中定义的 DEFAULT_TOLERANCE 常量作为默认值）。

2.2.用于处理矩阵的辅助函数

我们来继续讨论用于处理矩阵的辅助函数组。此组包括用于简化有关在一维数组中打包矩阵的操作的函数。

int MatrIndiciesToOffset(int row, int col, int numRows, int numCols)

此函数计算元素相对于已打包矩阵的数组的开头部分的偏移量。在这些参数中，它接收元素所处的交叉点处的行号 (row) 和列号 (col)，以及最大大小（numRows - 矩阵行数，numCols - 矩阵列数）。row 和 col 值应分别位于范围 [0;numRows-1] 和 [0;numCols-1] 以内。

void MatrCopy(double& src[], double& dst[]);

此函数将 src 矩阵的所有元素复制到 dst 矩阵中。矩阵数据数组是唯一传递的参数。完成 dst 矩阵复制后，矩阵大小将等于 src 矩阵大小。

void MatrSetSize(double& matr[], int numRows, int numCols);

此函数更改 matr 数据数组的大小，以便它能够存储由 numRows 行和 numCols 列组成的矩阵。不保证矩阵数据完整性。numRows 和 numCols 参数值应严格为正数。

void MatrResize(double& matr[], int numRowsOld, int numColsOld, int numRowsNew, int numColsNew);

此函数更改现有矩阵的 matr 数据数组的大小。numRowsOld 和 numColsOld 参数必须等于初始矩阵大小。新的大小由 numRowsNew 和 numColsNew 参数设置。对于新的大小，保证矩阵数据完整性，除非当一个或两个矩阵尺寸减小时。新的元素将被初始化为零。

2.3.用于处理行和列的函数

我们来看看用于处理行和列的函数。

void MatrSwapRows(double& matr[], int numRows, int numCols, int row1, int row2);

此函数互换由 numRows 行和 numCols 列组成的 matr 矩阵中的 row1 行和 row2 行的内容。Row1 和 row2 参数值应位于范围 [0;numRows-1] 以内。

void MatrSwapCols(double& matr[], int numRows, int numCols, int col1, int col2);

此函数互换 col1 和 col2 列的内容。Col1 和 col2 参数值应位于范围 [0;numCols-1] 以内。

void MatrCopyRow(double& matr[], int numRows, int numCols, int rowToCopy, int rowToReplace);

此函数应将 rowToCopy 行的内容复制到 rowToReplace 行中。rowToCopy 和 rowToReplace 参数值应在范围 [0;numRows-1] 内。

void MatrCopyCol(double& matr[], int numRows, int numCols, int colToCopy, int colToReplace);

此函数应将 colToCopy 列的内容复制到 colToReplace 列中。colToCopy 和 colToReplace 参数值应位于范围 [0;numCols-1] 以内。

bool MatrRowIsZero(double& matr[], int numRows, int numCols, int row, double tolerance);

此函数检查 row 行是否没有准确性的 tolerance 度。如果此行没有，则返回的值将为 true。

bool MatrColIsZero(double& matr[], int numRows, int numCols, int col, double tolerance);

此函数检查 col 列是否没有准确性的 tolerance 度。如果此列没有，则返回的值将为 true。

2.4.用于常规检查条件的函数

用于常规检查条件的函数组旨在提高代码可读性。

bool MatrIsSquare(int numRows, int numCols);

此函数检查由 numRows 行和 numCols 列组成的矩阵是否为正方形（即它检查是否 numRows=numCols）。如果是正方形矩阵，它将返回 true。

bool MatrIsElemOnMainDiagonal(int row, int col);

此函数检查带 [row][col] 指数的元素是否位于矩阵的主对角线上。如果元素位于主对角线上，此函数将返回 true。

bool MatrCompatiblityCheckAdd(int numRows1, int numCols1, int numRows2, int numCols2);

此函数检查两个用于类似加法运算的矩阵的兼容性。成对地检查尺寸是否相等（numRows1=numRows2 和 numCols1=numCols2）；如果相等，将返回 true。

bool MatrCompatiblityCheckMul(int numRows1, int numCols1, int numRows2, int numCols2);

此函数检查两个用于乘法运算的矩阵的兼容性。它检查第一个矩阵（numRows1 x numCols1 的矩阵）中的列数是否等于第二个矩阵（numRows2 x numCols2 的矩阵）中的行数。如果返回了 true，可执行乘法运算。

2.5.矩阵内容初始化函数

矩阵内容初始化函数组用于加载常用矩阵（例如空矩阵和单位矩阵）。由于未分配内存，MatrSetSize 或 MatrResize 函数应在调用组函数之前进行调用。

void MatrLoadZero(double& matr[], int numRows, int numCols);

此函数将 matr 数据数组初始化为零，应创建一个由 numRows 行和 numCols 列组成的空矩阵。

void MatrLoadIdentity(double& matr[], int numRows, int numCols);

此函数将 matr 数据数组的所有元素初始化为零，矩阵主对角线上的元素除外。由 numRows 行和 numCols 列组成的已初始化矩阵应为正方形。

void MatrLoadInRangeRandom(double& matr[], int numRows, int numCols, double rangeLowLimit, double rangeHighLimit);

此函数将 matr 矩阵的数据数组初始化为 [rangeLowLimit;rangeHighLimit] 范围以内的随机数字（随机数字使用 MathInRangeRandom 函数生成）。

2.6.用于按内容类型检查条件的函数

现在，我们来考虑按内容类型检查条件的函数组。此组函数执行精确性 tolerance 度的比较（此参数不能为负数），如果考虑的条件是真的，将返回 true。

bool MatrIsZero(double& matr[], int numRows, int numCols, double tolerance);

此函数检查矩阵是否为空。

bool MatrIsDiagonal(double& matr[], int numRows, int numCols, double tolerance);

此函数检查矩阵是否是对角的。如果矩阵为正方形且主对角线以外的所有元素都为零，则认为此矩阵是对角的。

bool MatrIsIdentity(double& matr[], int numRows, int numCols, double tolerance);

此函数检查矩阵是否为单位矩阵。

bool MatrIsSymmetric(double& matr[], int numRows, int numCols, double tolerance);

此函数检查矩阵是否对称（即，对于任何 i 和 j，a[i][j]=a[j][i] 为真）。

bool MatrIsAntisymmetric(double& matr[], int numRows, int numCols, double tolerance);

此函数检查矩阵是否斜对称/反对称（即，对于任何 i 和 j，a[i][j]=a[j][i] 为真；对于任何 k，a[k][k]=0 为真）。

bool MatrEqual(double& matr1[], double& matr2[], int numRows, int numCols, double tolerance);

此函数在相同尺寸的矩阵之间检查在元素级上是否相等。

2.7.用于元素级标量运算的函数

我们来继续讨论用于元素级标量原酸的函数组。此组的独特特性是，函数结果不是放置在matr 矩阵的初始数组中，而是放置在新的 result 矩阵中。然而，如果同一数组同时作为 result 和 matr 参数传递，则结果将放置在初始矩阵中。

void MatrAddScalar(double& matr[], int numRows, int numCols, double scalar, double& result[]);

此函数将 scalar 值加到每个矩阵元素上。

void MatrSubScalar(double& matr[], int numRows, int numCols, double scalar, double& result[]);

此函数从每个矩阵函数中减去 scalar 值。

void MatrMulByScalar(double& matr[], int numRows, int numCols, double scalar, double& result[]);

此函数将每个矩阵元素与 scalar 值相乘。

void MatrDivByScalar(double& matr[], int numRows, int numCols, double scalar, double& result[]);

此函数将每个矩阵元素除以 scalar 值。

2.8.用于基本矩阵运算的函数

用于基本矩阵运算的函数组包含用于执行基本运算 - 计算总和、乘积和轨迹，以及调换运算的函数。函数运算的结果（MatrTrace 除外）将返回到 result 数组中。

void MatrAddMatr(double& matr1[], double& matr2[], int numRows, int numCols, double& result[]);

此函数将两个具有相同尺寸的矩阵加起来。

void MatrSubMatr(double& matr1[], double& matr2[], int numRows, int numCols, double& result[]);

此函数从 matr1 矩阵中减去 matr2 矩阵。两个矩阵的大小应相等。

void MatrMulMatr(
      double& matr1[], int numRows1, int numCols1,
      double& matr2[], int numRows2, int numCols2,
      double& result[], int& numRowsRes, int& numColsRes);

此函数将 matr1 矩阵与 matr2 矩阵相乘。两个矩阵应相互兼容进行乘法运算，即，第一个矩阵中的列数 (numCols1) 应等于第二个矩阵中的行数 (numRows2)。产生矩阵的大小将返回在将在 numRowsRes 和 numColsRes 参数中传递其引用的变量中。

double MatrTrace(double& matr[], int numRows, int numCols);

此函数计算矩阵轨迹（对角元素的总和）。矩阵必须是正方形的。

void MatrTranspose(double& matr[], int numRows, int numCols, double& result[], int& numRowsRes, int& numColsRes);

此函数调换矩阵（互换列与行）。新矩阵的大小将返回在将在 numRowsRes 和 numColsRes 参数中传递其引用的变量中。

2.9.其他函数

其他函数组提供矩阵求逆、计算等级和行列式等的可能性。

int MatrGaussianElimination(double& matr[], int numRows, int numCols, double& result[], double tolerance);

此函数表示包含换轴的高斯消去法的实现。由 numRows 行和 numCols 列组成的初始 matr 矩阵被缩减为一个梯形（三角形）形态，同时结果放置在 result 数组中。

返回的值为矩阵的线性独立行的数量（即等级）。由于计算会导致函数四舍五入误差，因此，需要传递用于定义比较的精确度的非负 tolerance 值。

bool MatrGJBatchSolve(
      double& matr[], int numRows, int numCols,
      double& rhs[], int numRowsRHS, int numColsRHS,
      double& roots[], int& numRowsRoots, int& numColsRoots,
      double tolerance
      );

此函数表示高斯-约当消去法的实现，此法用于求解多个具有同一个系统矩阵的方程组的集合。

普通系统矩阵将在 matr（数据数组）、numRows 和 numCols（尺寸）函数中进行传递。右侧一组向量也将作为矩阵（rhs）进行传递，其中每列表示右侧正在考虑的系统。

换言之，numRowsRHS 参数包含系统中的方程数量（系统矩阵中的行数），numColsRHS 参数包含右侧向量的数量（要求解的方程组数量）。

结果将以由 numRowsRoots 行和 numColsRoots 列组成的 roots 矩阵的形式返回。每个方程组的解将放置在矩阵列中，并对应于给定系统矩阵的方程组的解，此矩阵列包含 rhs 矩阵中的相关数字。如果找到了方程组的解，此函数将返回 true。

void MatrMinor(
      double& matr[], int numRows, int numCols,
      int rowToExclude, int colToExclude,
      double& result[], int& numRowsRes, int& numColsRes);

此函数查找位于 rowToExclude 行和 colToExclude 列的相交处的矩阵的子式。产生矩阵的元素将返回在 result 数组中，而尺寸将返回在将在 numRowsRes 和 numColsRes 参数中传递其引用的变量中。

double MatrAlgebraicComplement(double& matr[], int numRows, int numCols, int elemRow, int elemCol, double tolerance);

此函数计算位于 elemRow 行和 elemCol 列的相交处的元素的代数余子式（带位置符号的子式）。为了计算行列式，我们使用了高斯消去法（以 MatrGaussianElimination 函数形式）以及 tolerance 参数设置的精确度。

bool MatrInvertUsingMinors(double& matr[], int numRows, int numCols, double& result[], double tolerance);

此函数使用联合矩阵计算正方形 matr 矩阵的逆（从相应矩阵元素的代数余子式生成）。使用算法的渐近复杂性：O(N^5)。使用 MatrAlgebraicComplement 函数（进而使用高斯消去法）计算联合矩阵，因此，此函数需要传递一个定义精确度的非负 tolerance 参数值。产生矩阵的元素将被放置在 result 数组中。如果成功地计算了矩阵的逆（行列式不为零），此函数将返回 true。

bool MatrInvertUsingGJ(double& matr[], int numRows, int numCols, double& result[], double tolerance);

此函数通过以下方式计算给定的正方形 matr 矩阵的逆：邻接单位矩阵，即通过使用 MatrGJBatchSolve 函数对 N (N=numRows=numCols) 线性方程组求解（右侧矩阵为单位矩阵；精确度由非负 tolerance 参数值设置）。使用算法的渐近复杂性：O(N^3)。产生矩阵的元素将被放置在 result 数组中。如果成功地计算了矩阵的逆（行列式不为零），此函数将返回 true。

double MatrDet(double& matr[], int numRows, int numCols, double tolerance);

此函数通过将正方形 matr 矩阵缩减为梯形（三角形）形态来计算此矩阵的行列式。为此，我们使用了高斯消去法以及精确性的 tolerance 度（此参数必须为非负数）。算法的渐近复杂性：O(N^3)。

double MatrDetTriang(double& matr[], int numRows, int numCols);

此函数计算三角形 matr 矩阵的行列式。

double MatrRank(double& matr[], int numRows, int numCols, double tolerance);

此函数通过将 matr 矩阵缩减为梯形（三角形）形态来计算此矩阵的等级。为此，我们使用了高斯消去法以及精确性的 tolerance 度（此参数必须为非负数）。算法的渐近复杂性：O(N^3)。

double MatrRankTriang(double& matr[], int numRows, int numCols, double tolerance);

此函数计算 matr 矩阵的等级。应以逐行的形式将此矩阵缩减为梯形（三角形）形态（例如，通过调用 MatrGaussianElimination 函数）。非负 tolerance 值设置第一个空行计算的精确度。

void MatrComputeConnectedMatr(double& matr[], int numRows, int numCols, double& result[], double tolerance);

此函数计算正方形 matr 矩阵的联合矩阵。产生矩阵的元素将被放置在 result 数组中。非负 tolerance 值定义在计算代数余子式过程中的准确度。

void MatrLerpMatr(double& matr1[], double& matr2[], int numRows, int numCols, double balance, double& result[]);

此函数在相同大小的 matr1 和 matr2 矩阵中执行元素级的线性插值。Balance 参数表示线性插值系数，应在范围 [0;1] 以内。产生矩阵的元素将被返回在 result 数组中。

2.10.输入/输出函数

输入-输出函数组用于保存/加载矩阵以及将矩阵的调试输出写入日志中。

void MatrPrint(double& matr[], int numRows, int numCols);

此函数用于将调试输出写入到日志中（终端面板中的 Expert Advisor 选项卡）。考虑到日志在终端中以相反的顺序显示，此函数将逐行输出矩阵（即，新的条目显示在顶部，函数从结尾处开始打印矩阵行，以便在日志中对矩阵进行直观分析）。

void FileWriteMatr(double& matr[], int numRows, int numCols, int handle);

此函数将矩阵（包括其尺寸）保存到将在 handle 参数中传递其手柄的文件中。此文件应在 FILE_BIN|FILE_WRITE 模式下打开。

void FileReadMatr(double& matr[], int& numRows, int& numCols, int handle);

此函数从文件加载矩阵。首先，矩阵尺寸将读取到将在 numRows 和 numCols 参数中传递其引用的变量中。然后，根据矩阵大小调整 matr 数组大小，然后从文件加载 matr 数组的内容。从中读取数据的文件的句柄在 handle 参数进行传递；此文件应在 FILE_BIN|FILE_READ 模式下打开。

既然读者熟悉函数说明，我们继续使用库来解决实际问题。

3.使用用例

我们来看看使用建议的库针对一系列价格值创建多项式回归的示例。

创建多项式回归的过程包括找到 degree 次数的多项式系数 f(x)=a[0]+a[1]*x+...+a[degree]*x^degree。此操作通过对线性代数方程组求解执行，在此方程组中，方程组矩阵 A[degree+1][degree+1] 的元素定义如下：A[i][j]=(x[0]^(i+j)+x[1]^(i+j)+...+x[numPoints]^(i+j))/numPoints，而右侧向量 B[degree+1][1] 的元素使用以下公式定义：B[i]=(y[0]*x[0]^i+y[1]*x[1]^i+...+y[numPoints]*x[numPoints]^i)/numPoints。

要解决手头的任务，我们有一个脚本（随附档案中的 LibMatrixEx.mq4 文件），此脚本用于创建一个多项式并在初始时间间隔上偏右显示此多项式（即外推）。有关外推时间间隔的多项式值可用于预测价格变动的方向。

此脚本使用三条垂直线进行控制：两条垂直线用于选择要分析的时间间隔，第三条线用于设置显示多项式的最右侧点。

要使此脚本运行，您需要将其拖到图表上并设置所需参数：delay - 图表刷新率（单位：ms)，degree - 多项式次数，linesMargin - 控制线之间的初始距离，linesWidth - 多项式图表的线宽。您还可以为垂直控制线（colVLineInt 和 colVLineExt 参数）和图表线条（colInt 和 colExt 参数）选择颜色。

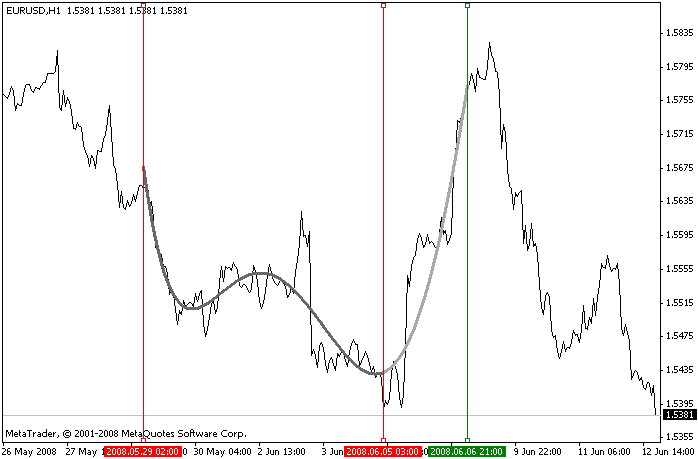
脚本操作示例

我们来查看用于处理矩阵的脚本的关键函数。

// creating polynomial regression bool Regression(double& x[], double& y[], int numPoints, int polyDegree, double& poly[]) {
   // create system matrix    double A[];
   int numRowsA = polyDegree + 1;
   int numColsA = polyDegree + 1;
   MatrSetSize(A, numRowsA, numColsA);
   // fill the matrix    for (int row = 0; row < numRowsA; row++) {
      for (int col = 0; col < numColsA; col++) {
         int offset = MatrIndiciesToOffset(row, col, numRowsA, numColsA);
         A[offset] = SXY(x, y, numPoints, row + col, 0);
      }
   }
   // create a right hand side vector    double B[];
   int numRowsB = polyDegree + 1;
   int numColsB = 1;
   MatrSetSize(B, numRowsB, numColsB);
   // fill the right hand side vector    for (row = 0; row < numRowsB; row++) {
      offset = MatrIndiciesToOffset(row, 0, numRowsB, numColsB);
      B[offset] = SXY(x, y, numPoints, row, 1);
   }
   // solve a system of linear algebraic equations    int numRowsX, numColsX;
   bool status =
      MatrGJBatchSolve(
         A, numRowsA, numColsA,
         B, numRowsB, numColsB,
         poly, numRowsX, numColsX,
         DEFAULT_TOLERANCE
      );
   if (!status) {
      Print("Error solving the system");
   }
   return (status); }