LibMatrix: Library of Matrix Algebra (Part One)

Introduction

Application of various branches of mathematics is essential in writing complex automated trading systems. One of such branches is linear algebra.

There are currently no extensive publicly available libraries in MQL4 that implement various methods of linear algebra (particularly, the theory of matrices and determinants).

This article describes the LibMatrix library in MQL4 that includes the implementation of the most common matrix operations.

Matrix is a finite rectangular array filled with some mathematical objects (e.g. numbers).

Four months after being written in C++ the entire code was rewritten in MQL4 with some modifications.

1. Library Structure

Let's first consider some peculiarities of working with matrices in the proposed library.

First of all, matrices are stored in one-dimensional arrays. It has to do with the fact that even though MQL4 offers features for creating multi-dimensional arrays, it is only possible to change the size of the first dimension. To store a matrix of N rows and M columns, we need a one-dimensional N*M array. The matrix is packed into an array row by row, i.e. the first row elements in a data array are followed by the second row elements and so on.

Second, when creating the library it was decided not to store additional information on matrix size in a data array as sizes are integer values, while elements are real numbers (storing sizes as real numbers could dramatically affect the operation of the library).

So a matrix in the format processed by the proposed library consists of three variables: a one-dimensional array of the double type and two integer variables (e.g. of the int type) for storing information on the number of matrix rows and columns.

The library consists of two files: LibMatrix.mqh and LibMatrix.mq4. The first file is to be included as required. It contains function prototypes that can be imported from the library. The second file contains function implementations (program code). That is what we are going to talk about further below.

The functions implemented in the library can be divided into several groups:

• general mathematical functions (MathLerp, MathInRangeRandom, MathDoublesEqual)
• auxiliary functions for working with matrices (MatrIndiciesToOffset, MatrCopy, MatrSetSize, MatrResize)
• functions for working with rows and columns (MatrSwapRows, MatrSwapCols, MatrCopyRow, MatrCopyCol, MatrRowIsZero, MatrColIsZero)
• functions for general check of conditions (MatrIsSquare, MatrIsElemOnMainDiagonal, MatrCompatiblityCheckAdd, MatrCompatiblityCheckMul)
• content initialization functions (MatrLoadZero, MatrLoadIdentity, MatrLoadInRangeRandom)
• functions for checking conditions by content type (MatrIsZero, MatrIsDiagonal, MatrIsIdentity, MatrIsSymmetric, MatrIsAntisymmetric, MatrEqual)
• functions for element-wise scalar operations (MatrAddScalar, MatrSubScalar, MatrMulByScalar, MatrDivByScalar)
• functions for basic matrix operations (MatrAddMatr, MatrSubMatr, MatrMulMatr, MatrTrace, MatrTranspose)
• other functions (MatrGaussianElimination, MatrGJBatchSolve, MatrMinor, MatrAlgebraicComplement, MatrInvertUsingMinors, MatrInvertUsingGJ, MatrDet, MatrDetTriang, MatrRank, MatrRankTriang, MatrComputeConnectedMatr, MatrLerpMatr)
• input/output functions (MatrPrint, FileWriteMatr, FileReadMatr)

Let's have a closer look at each of the groups.

2. Function Descriptions

2.1. General Mathematical Functions

We will first consider the group of general mathematical functions. It includes functions that are not directly associated with matrices but are used in the library.

double MathLerp(double rangeLowLimit, double rangeHighLimit, double balance);

This function performs linear interpolation between two values using the following formula: rangeLowLimit + balance * (rangeHighLimit - rangeLowLimit). The balance parameter value should be within the range [0;1].

double MathInRangeRandom(double rangeLowLimit, double rangeHighLimit);

This function returns uniformly distributed random numbers from the range [rangeLowLimit;rangeHighLimit]. The standard MathRand function is used for generation.

bool MathDoublesEqual(double value1, double value2, double tolerance);

This function is used to compare two values, value1 and value2, of the double type with the specified accuracy (tolerance). Use of approximate comparisons is required due to possible loss of accuracy. The tolerance parameter value should not be negative (as the default value, you can use the DEFAULT_TOLERANCE constant defined in the library).

2.2. Auxiliary Functions for Working with Matrices

Let's proceed to the group of auxiliary functions for working with matrices. This group covers functions intended for simplification of operations related to packing matrices in one-dimensional arrays.

int MatrIndiciesToOffset(int row, int col, int numRows, int numCols)

This function calculates the offset of an element with respect to the beginning of the array in which the matrix is packed. Among the parameters it receives are the number of the row (row) and the column (col) at the intersection of which the element lies, as well as the matrix size (numRows - number of matrix rows, numCols - number of matrix columns). The row and col values should lie within the ranges [0;numRows-1] and [0;numCols-1], respectively.

void MatrCopy(double& src[], double& dst[]);

This function copies all elements of the src matrix to the dst matrix. Matrix data arrays are the only parameters passed. Upon completion of copying the dst matrix size becomes equal to the src matrix size.

void MatrSetSize(double& matr[], int numRows, int numCols);

This function changes the size of the matr data array so that it can store a matrix of numRows rows and numCols columns. Matrix data integrity is not guaranteed. The numRows and numCols parameter values should be strictly positive.

void MatrResize(double& matr[], int numRowsOld, int numColsOld, int numRowsNew, int numColsNew);

This function changes the size of the matr data array of the existing matrix. The numRowsOld and numColsOld parameters must be equal to the initial matrix size. New size is set by the numRowsNew and numColsNew parameters. Matrix data integrity is guaranteed subject to new size, except for the cases where one or both matrix dimensions are decreased. New elements are initialized to zeros.

2.3. Functions for Working with Rows and Columns

Let's have a look at the functions for working with matrix rows and columns.

void MatrSwapRows(double& matr[], int numRows, int numCols, int row1, int row2);

This function swaps the content of the row1 and row2 rows for the matr matrix consisting of numRows rows and numCols columns. The row1 and row2 parameter values should lie within the range [0;numRows-1].

void MatrSwapCols(double& matr[], int numRows, int numCols, int col1, int col2);

This function swaps the content of the col1 and col2 columns. The col1 and col2 parameter values should lie within the range [0;numCols-1].

void MatrCopyRow(double& matr[], int numRows, int numCols, int rowToCopy, int rowToReplace);

This function copies the content of the rowToCopy row to the rowToReplace row. The rowToCopy and rowToReplace parameter values should be within the range [0;numRows-1].

void MatrCopyCol(double& matr[], int numRows, int numCols, int colToCopy, int colToReplace);

This function copies the content of the colToCopy column to the colToReplace column. The colToCopy and colToReplace parameter values should lie within the range [0;numCols-1].

bool MatrRowIsZero(double& matr[], int numRows, int numCols, int row, double tolerance);

This function checks whether the row row is null with the tolerance degree of accuracy. If the row is null, the returned value will be true.

bool MatrColIsZero(double& matr[], int numRows, int numCols, int col, double tolerance);

This function checks whether the col column is null with the tolerance degree of accuracy. If the column is null, the returned value will be true.

2.4. Functions for General Check of Conditions

The group of functions for general check of conditions is intended for improvement of the code readability.

bool MatrIsSquare(int numRows, int numCols);

This function checks whether the matrix of numRows rows and numCols columns is square (i.e. it checks whether numRows=numCols). It returns true for square matrices.

bool MatrIsElemOnMainDiagonal(int row, int col);

This function checks whether the element with the [row][col] indices is on the main diagonal of the matrix. It returns true for the elements on the main diagonal.

bool MatrCompatiblityCheckAdd(int numRows1, int numCols1, int numRows2, int numCols2);

This function checks compatibility of two matrices for purposes of addition-like operations. Dimensions are checked pairwise for equality (numRows1=numRows2 and numCols1=numCols2); true is returned in case of equality.

bool MatrCompatiblityCheckMul(int numRows1, int numCols1, int numRows2, int numCols2);

This function checks compatibility of two matrices for purposes of multiplication. It checks whether the number of columns in the first matrix (numRows1 by numCols1 matrix) is equal to the number of rows in the second matrix (numRows2 by numCols2 matrix). Multiplication is possible if true is returned.

2.5. Matrix Content Initialization Functions

The group of matrix content initialization functions is intended for loading frequently used matrices (e.g. null and identity matrices). Since memory is not allocated, the MatrSetSize or MatrResize functions should be called before calling the group functions.

void MatrLoadZero(double& matr[], int numRows, int numCols);

This function initializes the matr data array to zeros thus creating a null matrix of numRows rows and numCols columns.

void MatrLoadIdentity(double& matr[], int numRows, int numCols);

This function initializes all elements of the matr data array to zeros, except for those that are on the main diagonal of the matrix. The initialized matrix of numRows rows and numCols columns should be square.

void MatrLoadInRangeRandom(double& matr[], int numRows, int numCols, double rangeLowLimit, double rangeHighLimit);

This function initializes the data array of the matr matrix to random numbers from the range [rangeLowLimit;rangeHighLimit] (random numbers are generated using the MathInRangeRandom function).

2.6. Functions for Checking Conditions by Content Type

Let's now consider the group of functions for checking conditions by content type. The functions of this group perform a comparison with the tolerance degree of accuracy (this parameter value must not be negative) and return true if the condition under consideration is true.

bool MatrIsZero(double& matr[], int numRows, int numCols, double tolerance);

This function checks if the matrix is null.

bool MatrIsDiagonal(double& matr[], int numRows, int numCols, double tolerance);

This function checks if the matrix is diagonal. The matrix will be considered diagonal if it is square and all its elements outside the main diagonal are zero.

bool MatrIsIdentity(double& matr[], int numRows, int numCols, double tolerance);

This function checks if the matrix is identity.

bool MatrIsSymmetric(double& matr[], int numRows, int numCols, double tolerance);

This function checks if the matrix is symmetric (i.e. a[i][j]=a[j][i] is true for any i and j).

bool MatrIsAntisymmetric(double& matr[], int numRows, int numCols, double tolerance);

This function checks if the matrix is skew-symmetric/antisymmetric (i.e. a[i][j]=-a[j][i] is true for any i and j and a[k][k]=0 is true for any k).

bool MatrEqual(double& matr1[], double& matr2[], int numRows, int numCols, double tolerance);

This function checks element-wise equality between matrices with the same dimensions.

2.7. Functions for Element-wise Scalar Operations

Let's proceed to the group of functions for element-wise scalar operations. This group is peculiar in that function results are not placed in the initial array of the matr matrix but rather into the new result array. However, if the same array is passed as both the result and matr parameters, the results will be placed to the initial matrix.

void MatrAddScalar(double& matr[], int numRows, int numCols, double scalar, double& result[]);

This function adds the scalar value to each matrix element.

void MatrSubScalar(double& matr[], int numRows, int numCols, double scalar, double& result[]);

This function subtracts the scalar value from each matrix element.

void MatrMulByScalar(double& matr[], int numRows, int numCols, double scalar, double& result[]);

This function multiplies each matrix element by the scalar value.

void MatrDivByScalar(double& matr[], int numRows, int numCols, double scalar, double& result[]);

This function divides each matrix element by the scalar value.

2.8. Functions for Basic Matrix Operations

The group of functions for basic matrix operations consists of functions for performing elementary actions - calculations of sum, product and trace, as well as transposition operations. The results of function operation (except for MatrTrace) are returned to the result array.

void MatrAddMatr(double& matr1[], double& matr2[], int numRows, int numCols, double& result[]);

This function adds up two matrices with the same dimensions.

void MatrSubMatr(double& matr1[], double& matr2[], int numRows, int numCols, double& result[]);

This function subtracts the matr2 matrix from the matr1 matrix. The matrices should be of equal size.

void MatrMulMatr(
      double& matr1[], int numRows1, int numCols1,
      double& matr2[], int numRows2, int numCols2,
      double& result[], int& numRowsRes, int& numColsRes);

This function multiplies the matr1 matrix by the matr2 matrix. The matrices should be compatible for multiplication, i.e. the number of columns (numCols1) in the first matrix should be equal to the number of rows (numRows2) in the second matrix. The size of the resulting matrix is returned in variables references to which are passed in the numRowsRes and numColsRes parameters.

double MatrTrace(double& matr[], int numRows, int numCols);

This function calculates the matrix trace (sum of the diagonal elements). The matrix must be square.

void MatrTranspose(double& matr[], int numRows, int numCols, double& result[], int& numRowsRes, int& numColsRes);

This function transposes the matrix (swaps columns with rows). The new matrix size is returned in variables references to which are passed in the numRowsRes and numColsRes parameters.

2.9. Other Functions

The group of other function offers possibilities for matrix inversion, calculation of ranks and determinants, etc.

int MatrGaussianElimination(double& matr[], int numRows, int numCols, double& result[], double tolerance);

This function represents the implementation of Gaussian elimination with pivoting. The initial matr matrix of numRows rows and numCols columns is reduced to a trapezoidal (triangular) form, with the results being placed in the result array.

The returned value is the number of linearly independent rows of the matrix (i.e. its rank). Since calculations can lead to function rounding errors, it is required to pass a non-negative tolerance parameter value that defines the degree of accuracy of the comparison.

bool MatrGJBatchSolve(
      double& matr[], int numRows, int numCols,
      double& rhs[], int numRowsRHS, int numColsRHS,
      double& roots[], int& numRowsRoots, int& numColsRoots,
      double tolerance
      );

This function represents the implementation of Gauss-Jordan elimination intended for solving sets of several equation systems with one and the same system matrix.

The common system matrix is passed in the matr (data array), numRows and numCols (dimensions) parameters. A set of right hand side vectors is also passed as a matrix (the rhs parameter), where each column represents a right hand side of the system under consideration.

In other words, the numRowsRHS parameter contains the number of equations in the system (number of rows in the system matrix), while the numColsRHS parameter contains the number of right hand side vectors (number of systems to be solved).

The results are returned in the form of the roots matrix of numRowsRoots rows and numColsRoots columns. The solution for each system of equations is placed in the matrix column and corresponds to the solution for the system of the given system matrix and the column with the relevant number from the rhs matrix. The function returns true if the solution for the set of equation systems has been found.

void MatrMinor(
      double& matr[], int numRows, int numCols,
      int rowToExclude, int colToExclude,
      double& result[], int& numRowsRes, int& numColsRes);

This function finds the minor of the matrix lying at the intersection of the rowToExclude row and the colToExclude column. The resulting matrix elements are returned in the result array, while the dimensions are returned in variables references to which are passed in the numRowsRes and numColsRes parameters.

double MatrAlgebraicComplement(double& matr[], int numRows, int numCols, int elemRow, int elemCol, double tolerance);

This function calculates the algebraic cofactor (minor with a place sign) for the element lying at the intersection of the elemRow row and elemCol column. To calculate the determinant, we use Gaussian elimination (in the form of the MatrGaussianElimination function) with the degree of accuracy set by the tolerance parameter.

bool MatrInvertUsingMinors(double& matr[], int numRows, int numCols, double& result[], double tolerance);

This function calculates the inverse of the square matr matrix using a union matrix (generated from algebraic cofactors of the corresponding matrix elements). Asymptotic complexity of the employed algorithm: O(N^5). The union matrix is calculated using the MatrAlgebraicComplement function (which in turn employs Gaussian elimination) and for this reason the function needs to be passed a non-negative tolerance parameter value that defines the degree of accuracy. The elements of the resulting matrix are placed in the result array. If the inverse of the matrix is successfully calculated (the determinant is other than zero), the function returns true.

bool MatrInvertUsingGJ(double& matr[], int numRows, int numCols, double& result[], double tolerance);

This function calculates the inverse of the given square matr matrix by adjoining an identity matrix, i.e. by solving N (N=numRows=numCols) systems of linear equations using the MatrGJBatchSolve function (the matrix of right hand sides is identity; the degree of accuracy is set by a non-negative tolerance parameter value). Asymptotic complexity of the employed algorithm: O(N^3). The elements of the resulting matrix are placed in the result array. If the inverse of the matrix is successfully calculated (the determinant is other than zero), the function returns true.

double MatrDet(double& matr[], int numRows, int numCols, double tolerance);

This function calculates the determinant of the square matr matrix by reducing it to a trapezoidal (triangular) form. For this purpose, we use Gaussian elimination with tolerance degree of accuracy (this parameter must be non-negative). Asymptotic complexity of the algorithm: O(N^3).

double MatrDetTriang(double& matr[], int numRows, int numCols);

This function calculates the determinant of the triangular matr matrix.

double MatrRank(double& matr[], int numRows, int numCols, double tolerance);

This function calculates the rank of the matr matrix by reducing it to a trapezoidal (triangular) form. For this purpose, we use Gaussian elimination with tolerance degree of accuracy (this parameter must be non-negative). Asymptotic complexity of the algorithm: O(N^3).

double MatrRankTriang(double& matr[], int numRows, int numCols, double tolerance);

This function calculates the rank of the matr matrix. The matrix should be reduced to a trapezoidal (triangular) form row by row (e.g. by calling the MatrGaussianElimination function). The non-negative tolerance value sets the degree of accuracy of the first null row calculation.

void MatrComputeConnectedMatr(double& matr[], int numRows, int numCols, double& result[], double tolerance);

This function calculates a union matrix for the square matr matrix. The elements of the resulting matrix are placed in the result array. The non-negative tolerance value defines the degree of accuracy in calculating algebraic cofactors.

void MatrLerpMatr(double& matr1[], double& matr2[], int numRows, int numCols, double balance, double& result[]);

This function performs element-wise linear interpolation between the matr1 and matr2 matrices of the same size. The balance parameter represents the linear interpolation coefficient and should lie within the range [0;1]. The elements of the resulting matrix are returned in the result array.

2.10. Input/Output Functions

The group of input-output functions is intended for saving/loading matrices, as well as writing the debugging output of a matrix to the log.

void MatrPrint(double& matr[], int numRows, int numCols);

This function is intended for writing the debugging output to the log (Expert Advisors tab in the Terminal panel). It outputs the matrix row by row taking into consideration that the log is displayed in the terminal in the inverse order (i.e. new entries appear at the top; the function prints matrix rows starting from the end for the convenience of visual analysis of matrices in the log).

void FileWriteMatr(double& matr[], int numRows, int numCols, int handle);

This function saves a matrix (including its dimensions) to the file whose handle is passed in the handle parameter. The file should be open in the FILE_BIN|FILE_WRITE mode.

void FileReadMatr(double& matr[], int& numRows, int& numCols, int handle);

This function loads a matrix from a file. First, matrix dimensions are read to the variables references to which are passed in the numRows and numCols parameters. The matr array is then resized according to the matrix size which is followed by loading the content of the matr array from the file. The handle of the file from which the data is read is passed in the handle parameter; the file should be open in the FILE_BIN|FILE_READ mode.

Now that the reader has become familiar with the function descriptions, we can proceed to solving practical issues using the library.

3. Example of Use

Let's have a look at an example of creating a polynomial regression on a series of price values using the proposed library.

The process of creating a polynomial regression consists in finding polynomial coefficients f(x)=a[0]+a[1]*x+...+a[degree]*x^degree of the degree degree. This is carried out by solving a system of linear algebraic equations where elements of the system matrix A[degree+1][degree+1] are defined as follows: A[i][j]=(x[0]^(i+j)+x[1]^(i+j)+...+x[numPoints]^(i+j))/numPoints, while elements of the right-hand side vector B[degree+1][1] are defined using the following formula: B[i]=(y[0]*x[0]^i+y[1]*x[1]^i+...+y[numPoints]*x[numPoints]^i)/numPoints.

To solve the task at hand, we have a script (the LibMatrixEx.mq4 file in the attached archive) that creates a polynomial and displays it on the initial interval and to its right (i.e. extrapolation). Polynomial values on the extrapolation interval can be used to predict the direction of the price movement.

The script is controlled using three vertical lines: two of them are intended for selecting the interval to be analyzed and the third one sets the rightmost point up to which the polynomial is displayed.

To enable the operation of the script, you need to drag it onto the chart and set the required parameters: delay - chart refresh rate (in ms), degree - degree of polynomial, linesMargin - initial distance between the control lines, linesWidth - line width of the polynomial chart. You can also select colors for the vertical control lines (colVLineInt and colVLineExt parameters) and chart lines (colInt and colExt parameters).

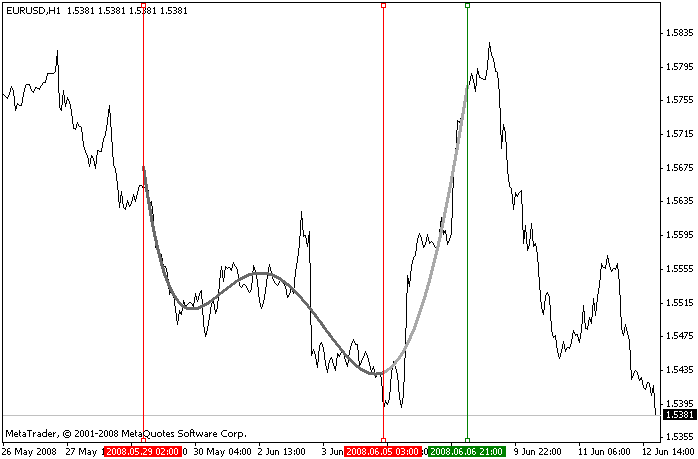
Script operation example

Let's review the key function of the script that deals with matrices.

// creating polynomial regression
bool Regression(double& x[], double& y[], int numPoints, int polyDegree, double& poly[]) {
   // create system matrix
   double A[];
   int numRowsA = polyDegree + 1;
   int numColsA = polyDegree + 1;
   MatrSetSize(A, numRowsA, numColsA);
   // fill the matrix
   for (int row = 0; row < numRowsA; row++) {
      for (int col = 0; col < numColsA; col++) {
         int offset = MatrIndiciesToOffset(row, col, numRowsA, numColsA);
         A[offset] = SXY(x, y, numPoints, row + col, 0);
      }
   }
   // create a right hand side vector
   double B[];
   int numRowsB = polyDegree + 1;
   int numColsB = 1;
   MatrSetSize(B, numRowsB, numColsB);
   // fill the right hand side vector
   for (row = 0; row < numRowsB; row++) {
      offset = MatrIndiciesToOffset(row, 0, numRowsB, numColsB);
      B[offset] = SXY(x, y, numPoints, row, 1);
   }
   // solve a system of linear algebraic equations
   int numRowsX, numColsX;
   bool status =
      MatrGJBatchSolve(
         A, numRowsA, numColsA,
         B, numRowsB, numColsB,
         poly, numRowsX, numColsX,
         DEFAULT_TOLERANCE
      );
   if (!status) {
      Print("Error solving the system");
   }
   return (status);
}

The function takes on 5 arguments. The first two are x and y arrays that are intended for storing the coordinates of the points through which the polynomial is plotted. The number of the points is passed in the numPoints parameter. The fourth argument sets the degree of the polynomial under consideration (it must be less than the number of points by at least 1). The fifth argument is the reference to the array that receives polynomial coefficients.

At the beginning of the function, the A matrix is created, resized and filled using the above formulas. To reference the matrix elements through two-dimensional indices, we use the MatrIndiciesToOffset function that calculates one-dimensional offset with respect to the beginning of the array.

The vector-column B is then filled in a similar way. This is followed by a call of the MatrGJBatchSolve function that solves the created system, thus finding the polynomial coefficients.

The rest of the code that checks line positions and outputs the polynomial should not be of any difficulty to the reader.

Conclusion

The article has introduced the library for working with matrices and discussed the implemented functions and their peculiarities.

The use of the library has been demonstrated by the example of creating a polynomial regression on a series of candlestick closing price values.

The code has been carefully checked but there might be errors. If you happen to find an error, please let me know.