Библиотека матричной алгебры LibMatrix (часть первая)

Введение

Использование различных разделов математики является неотъемлемой частью написания сложных автоматических торговых систем. Одним из таких разделов является линейная алгебра.

В настоящее время на языке MQL4 не существует обширных и публично доступных библиотек, реализующих различные методы линейной алгебры (в частности, теории матриц и определителей).

Данная статья описывает библиотеку LibMatrix на языке MQL4, включающую реализации наиболее широко используемых матричных операций.

Матрицей называется конечная прямоугольная таблица, заполненная некоторыми математическими объектами (например, числами).

Изначально весь код был написан на языке C++ и примерно через 4 месяца после этого переписан на MQL4 с некоторыми изменениями.

1. Состав библиотеки

Для начала рассмотрим некоторые особенности работы с матрицами в предлагаемой библиотеке.

Во-первых, для хранения матриц используются одномерные массивы. Это связано с тем, что язык MQL4 предоставляет возможность создания многомерных массивов, однако изменение размерности возможно лишь для первого измерения. Для хранения матрицы из N строк и M столбцов выделяется одномерный массив данных размерности N*M. Упаковка матрицы в массив осуществляется по строкам, т.е. сначала в массиве данных идут элементы первой строки, потом второй и так далее.

Во-вторых, при создании библиотеки было принято решение не помещать дополнительную информацию о размерностях матрицы в массив данных, т.к. размерности - это целые числа, а элементы являются вещественными (хранение размерностей в качестве вещественных чисел могло бы серьёзно снизить скорость работы библиотеки).

Таким образом, матрица в формате обрабатываемом предлагаемой библиотекой состоит из трёх переменных: одномерного массива типа double и двух целочисленных переменных (например, типа int) для хранения сведений о количестве строк и столбцов матрицы.

Библиотека состоит из двух файлов: LibMatrix.mqh и LibMatrix.mq4. Первый файл предназначен для подключения по месту требования. Он содержит прототипы функций, которые можно импортировать из библиотеки. Второй файл содержит реализации (программный код) функций. Именно о его содержимом в дальнейшем будет идти речь.

Функции, реализуемые в библиотеке, можно разделить на несколько групп:

• общие математические (MathLerp, MathInRangeRandom, MathDoublesEqual)
• вспомогательные для работы с матрицами (MatrIndiciesToOffset, MatrCopy, MatrSetSize, MatrResize)
• работа со строками и столбцами (MatrSwapRows, MatrSwapCols, MatrCopyRow, MatrCopyCol, MatrRowIsZero, MatrColIsZero)
• общая проверка условий (MatrIsSquare, MatrIsElemOnMainDiagonal, MatrCompatiblityCheckAdd, MatrCompatiblityCheckMul)
• инициализация содержимого (MatrLoadZero, MatrLoadIdentity, MatrLoadInRangeRandom)
• проверка условий по типу содержимого (MatrIsZero, MatrIsDiagonal, MatrIsIdentity, MatrIsSymmetric, MatrIsAntisymmetric, MatrEqual)
• поэлементные скалярные операции (MatrAddScalar, MatrSubScalar, MatrMulByScalar, MatrDivByScalar)
• простые матричные операции (MatrAddMatr, MatrSubMatr, MatrMulMatr, MatrTrace, MatrTranspose)
• прочие (MatrGaussianElimination, MatrGJBatchSolve, MatrMinor, MatrAlgebraicComplement, MatrInvertUsingMinors, MatrInvertUsingGJ, MatrDet, MatrDetTriang, MatrRank, MatrRankTriang, MatrComputeConnectedMatr, MatrLerpMatr)
• ввод-вывод (MatrPrint, FileWriteMatr, FileReadMatr)

Рассмотрим каждую из групп более подробно.

2. Описания функций

2.1. Общие математические функции

Для начала рассмотрим группу общих математических функций. В неё включены функции, не имеющие непосредственного отношения к матрицам, однако применяемые в библиотеке.

double MathLerp(double rangeLowLimit, double rangeHighLimit, double balance);

Функция выполняет линейную интерполяцию между двумя величинами по формуле rangeLowLimit + balance * (rangeHighLimit - rangeLowLimit). Значение параметра balance, должно находиться в диапазоне [0;1].

double MathInRangeRandom(double rangeLowLimit, double rangeHighLimit);

Функция возвращает равномерно распределенные случайные числа из диапазона [rangeLowLimit;rangeHighLimit]. Для генерации используется стандартная функция MathRand.

bool MathDoublesEqual(double value1, double value2, double tolerance);

Функция используется для сравнения двух значений, value1 и value2, типа double с заданной точностью (tolerance). Использование приближенных сравнений необходимо по причине возможных потерь точности при вычислениях. Значение параметра tolerance должно быть неотрицательным (в качестве значения по умолчанию можно использовать константу DEFAULT_TOLERANCE, определённую в библиотеке).

2.2. Вспомогательные функции для работы с матрицами

Перейдём к рассмотрению группы вспомогательных функций для работы с матрицами. В эту группу объединены функции, предназначенные для упрощения выполнения операций, связанных со способом упаковки матриц в одномерные массивы.

int MatrIndiciesToOffset(int row, int col, int numRows, int numCols)

Функция вычисляет смещение элемента относительно начала массива, в который упакована матрица. В качестве параметров передаются номера строки (row) и столбца (col), на пересечении которых расположен элемент, а также размерности матрицы (numRows - количество строк матрицы, numCols - количество столбцов матрицы). Значения параметров row и col должны лежать в диапазонах [0;numRows-1] и [0;numCols-1], соответственно.

void MatrCopy(double& src[], double& dst[]);

Функция выполняет копирование всех элементов матрицы src в матрицу dst. В качестве параметров передаются лишь массивы данных матриц; размерности матрицы dst по завершении копирования становятся равными размерностям матрицы src.

void MatrSetSize(double& matr[], int numRows, int numCols);

Функция изменяет размерность массива данных matr таким образом, чтобы в нём можно было хранить матрицу из numRows строк и numCols столбцов. Сохранность содержимого матрицы не гарантируется. Значения параметров numRows и numCols должны быть строго положительными.

void MatrResize(double& matr[], int numRowsOld, int numColsOld, int numRowsNew, int numColsNew);

Функция изменяет размерность массива данных matr существующей матрицы. Параметры numRowsOld и numColsOld должны быть равны исходным размерностям матрицы. Новые размерности задаются параметрами numRowsNew и numColsNew. Гарантируется сохранность содержимого матрицы с учётом новых размерностей за исключением случая, когда одна либо обе размерности матрицы уменьшаются. Новые элементы инициализируются нулями.

2.3. Работа со строками и столбцами

Рассмотрим группу функций для работы со строками и столбцами матриц.

void MatrSwapRows(double& matr[], int numRows, int numCols, int row1, int row2);

Функция меняет местами содержимое двух строк row1 и row2 для матрицы matr, состоящей из numRows строк и numCols столбцов. Значения параметров row1 и row2 должны лежать в промежутке [0;numRows-1].

void MatrSwapCols(double& matr[], int numRows, int numCols, int col1, int col2);

Функция меняет местами содержимое двух столбцов col1 и col2. Значения параметров col1 и col2 должны лежать в промежутке [0;numCols-1].

void MatrCopyRow(double& matr[], int numRows, int numCols, int rowToCopy, int rowToReplace);

Функция копирует содержимое строки rowToCopy в строку rowToReplace. Значения параметров rowToCopy и rowToReplace должны лежать в промежутке [0;numRows-1].

void MatrCopyCol(double& matr[], int numRows, int numCols, int colToCopy, int colToReplace);

Функция копирует содержимое столбца colToCopy в столбец colToReplace. Значения параметров colToCopy и colToReplace должны лежать в промежутке [0;numCols-1].

bool MatrRowIsZero(double& matr[], int numRows, int numCols, int row, double tolerance);

Функция проверяет является ли строка row нулевой с точностью tolerance. Если строка является нулевой - возвращаемое значение true.

bool MatrColIsZero(double& matr[], int numRows, int numCols, int col, double tolerance);

Функция проверяет, является ли столбец col нулевым с точностью tolerance. Если столбец является нулевым - возвращаемое значение true.

2.4. Общая проверка условий

Группа функций для общей проверки условий предназначена для улучшения читаемости кода.

bool MatrIsSquare(int numRows, int numCols);

Функция проверяет, является ли матрица с размерностями numRows и numCols квадратной (т.е. проверяется соблюдение условия numRows=numCols). Возвращает true для квадратных матриц.

bool MatrIsElemOnMainDiagonal(int row, int col);

Функция проверяет, принадлежит ли элемент с индексами [row][col] главной диагонали матрицы. Возвращает true для элементов главной диагонали.

bool MatrCompatiblityCheckAdd(int numRows1, int numCols1, int numRows2, int numCols2);

Функция проверяет совместимость двух матриц для выполнения операций типа сложения. Проверяется попарное равенство размерностей (numRows1=numRows2 и numCols1=numCols2); в случае равенства возвращает true.

bool MatrCompatiblityCheckMul(int numRows1, int numCols1, int numRows2, int numCols2);

Функция проверяет совместимость двух матриц для операции умножения. Проверяется равенство количества столбцов первой матрицы (с размерностями numRows1 и numCols1) количеству строк второй матрицы (с размерностями numRows2 и numCols2). Возвращает true если умножение возможно.

2.5. Инициализация содержимого матриц

Группа функций инициализации содержимого матриц предназначена для загрузки часто используемых матриц (например, нулевых и единичных). Выделение памяти не выполняется, поэтому вызовам функций группы должен предшествовать вызов функции MatrSetSize или MatrResize.

void MatrLoadZero(double& matr[], int numRows, int numCols);

Функция инициализирует массив данных matr нулями, тем самым создавая нулевую матрицу из numRows строк и numCols столбцов.

void MatrLoadIdentity(double& matr[], int numRows, int numCols);

Функция инициализирует нулями все элементы массива данных matr за исключением тех, что стоят на главной диагонали матрицы. Инициализируемая матрицы из numRows строк и numCols столбцов должна быть квадратной.

void MatrLoadInRangeRandom(double& matr[], int numRows, int numCols, double rangeLowLimit, double rangeHighLimit);

Функция инициализирует массив данных матрицы matr случайными числами из диапазона [rangeLowLimit;rangeHighLimit] (для генерации случайных чисел применяется функция MathInRangeRandom).

2.6. Функции проверки условий по типу содержимого

Рассмотрим группу функций проверки условий по типу содержимого. Функции этой группы выполняют сравнение с точностью tolerance (значение этого параметра должно быть неотрицательным) и возвращают true если проверяемое условие истинно.

bool MatrIsZero(double& matr[], int numRows, int numCols, double tolerance);

Функция проверяет, является ли матрица нулевой.

bool MatrIsDiagonal(double& matr[], int numRows, int numCols, double tolerance);

Функция проверяет, является ли матрица диагональной. Матрица будет считаться диагональной, если она квадратная и все элементы вне главной диагонали равны нулю.

bool MatrIsIdentity(double& matr[], int numRows, int numCols, double tolerance);

Функция проверяет, является ли матрица единичной.

bool MatrIsSymmetric(double& matr[], int numRows, int numCols, double tolerance);

Функция проверяет, является ли матрица симметричной (т.е. для любых индексов i и j выполняется a[i][j]=a[j][i]).

bool MatrIsAntisymmetric(double& matr[], int numRows, int numCols, double tolerance);

Функция проверяет, является ли матрица кососимметричной/антисимметричной (т.е. для любых индексов i и j выполняется a[i][j]=-a[j][i] и для любого k выполняется a[k][k]=0).

bool MatrEqual(double& matr1[], double& matr2[], int numRows, int numCols, double tolerance);

Функция проверяет поэлементное равенство матриц с одинаковыми размерностями.

2.7. Поэлементные скалярные операции

Перейдём к рассмотрению группы функций поэлементных скалярных операций. Особенностью данной группы является то, что результат работы функции помещается не в исходный массив матрицы matr, а в новый массив result. Тем не менее, если в качестве параметра result передать тот же самый массив, что и в качестве параметра matr - результат будет помещён в исходную матрицу.

void MatrAddScalar(double& matr[], int numRows, int numCols, double scalar, double& result[]);

Функция прибавляет величину scalar к каждому элементу матрицы.

void MatrSubScalar(double& matr[], int numRows, int numCols, double scalar, double& result[]);

Функция вычитает величину scalar из каждого элемента матрицы.

void MatrMulByScalar(double& matr[], int numRows, int numCols, double scalar, double& result[]);

Функция умножает каждый элемент матрицы на величину scalar.

void MatrDivByScalar(double& matr[], int numRows, int numCols, double scalar, double& result[]);

Функция делит каждый элемент матрицы на величину scalar.

2.8. Простые матричные операции

Группа простых матричных операций предоставляет функции для выполнения простейших действий - вычисления сумм, произведений, следа и выполнения транспонирования. Результат работы функций (кроме MatrTrace) возвращается в массив result.

void MatrAddMatr(double& matr1[], double& matr2[], int numRows, int numCols, double& result[]);

Функция складывает две матрицы с одинаковыми размерностями.

void MatrSubMatr(double& matr1[], double& matr2[], int numRows, int numCols, double& result[]);

Функция вычитает матрицу matr2 из матрицы matr1. Матрицы должны иметь одинаковые размерности.

void MatrMulMatr(
      double& matr1[], int numRows1, int numCols1,
      double& matr2[], int numRows2, int numCols2,
      double& result[], int& numRowsRes, int& numColsRes);

Функция умножает матрицу matr1 на матрицу matr2. Матрицы должны быть совместимыми для умножения, т.к. количество столбцов (numCols1) первой матрицы должно быть равно количеству строк (numRows2) второй матрицы. Размерности результатирующей матрицы возвращаются в переменных, ссылки на которые передаются в параметрах numRowsRes и numColsRes.

double MatrTrace(double& matr[], int numRows, int numCols);

Функция вычисляет след матрицы (сумму диагональных элементов). Матрица должна быть квадратной.

void MatrTranspose(double& matr[], int numRows, int numCols, double& result[], int& numRowsRes, int& numColsRes);

Функция выполняет транспонирование матрицы (меняет местами столбцы и строки). Размерности новой матрицы возвращаются в переменных, ссылки на которые передаются в параметрах numRowsRes и numColsRes.

2.9. Прочие функции

Группа прочих функций предоставляет возможности для обращения матриц, вычисления рангов и определителей и т.д.

int MatrGaussianElimination(double& matr[], int numRows, int numCols, double& result[], double tolerance);

Функция является реализацией метода Гаусса с выбором ведущего элемента. Исходная матрица matr, состоящая из numRows строк и numCols столбцов, приводится к трапецеидальному (треугольному) виду и результат помещается в массив result.

Возвращаемое значение является количеством линейно-независимых строк матрицы (т.е. её рангом). Т.к. вычисления могут приводить к ошибкам округления функции, требуется передавать неотрицательный параметр tolerance, задающий точность сравнения.

bool MatrGJBatchSolve(
      double& matr[], int numRows, int numCols,
      double& rhs[], int numRowsRHS, int numColsRHS,
      double& roots[], int& numRowsRoots, int& numColsRoots,
      double tolerance
      );

Функция является реализацией метода Жордана-Гаусса (Gauss-Jordan reduction), предназначенной для решения наборов из нескольких систем уравнений с одной и той же матрицей системы.

Общая матрица системы передается в параметрах matr (массив данных), numRows и numCols (размерности). Набор векторов правых частей также передаётся в виде матрицы (параметр rhs), каждый столбец которой представляет собой правую часть решаемой системы.

Т.е. параметр numRowsRHS содержит количество уравнений в системе (количество строк матрицы системы), а параметр numColsRHS содержит количество векторов правых частей (количество систем, которые нужно решить).

Результат возвращается в виде матрицы roots из numRowsRoots строк и numColsRoots столбцов, причём решение каждой системы уравнений помещается в столбце матрицы и соответствует решению системы из заданной матрицы системы и столбца с соответствующим номером из матрицы rhs. Функция возвращает true, если решение набора систем уравнений было найдено.

void MatrMinor(
      double& matr[], int numRows, int numCols,
      int rowToExclude, int colToExclude,
      double& result[], int& numRowsRes, int& numColsRes);

Функция извлекает минор элемента матрицы, стоящий на пересечении строки rowToExclude и столбца colToExclude. Элементы результатирующей матрицы возвращаются в массиве result; размерности возвращаются в переменных, ссылки на которые передаются в параметрах numRowsRes и numColsRes.

double MatrAlgebraicComplement(double& matr[], int numRows, int numCols, int elemRow, int elemCol, double tolerance);

Функция вычисляет алгебраическое дополнение (определитель минора со знаком) для элемента, стоящего на пересечении строки elemRow и столбца elemCol. Для вычисления определителя используется метод Гаусса (в виде функции MatrGaussianElimination) с точностью, задаваемой параметром tolerance.

bool MatrInvertUsingMinors(double& matr[], int numRows, int numCols, double& result[], double tolerance);

Функция выполняет обращение квадратной матрицы matr, используя союзную матрицу (формируется из алгебраических дополнений соответствующих элементов матрицы). Асимптотическая сложность используемого алгоритма - O(N^5). Для вычисления союзной матрицы используется функция MatrAlgebraicComplement (которая в свою очередь использует метод Гаусса), в связи с этим в функцию необходимо передавать неотрицательный параметр tolerance, задающий точность. Элементы результатирующей матрицы помещаются в массив result. В случае успешного вычисления обратной матрицы (определитель отличен от нуля) функция возвращает true.

bool MatrInvertUsingGJ(double& matr[], int numRows, int numCols, double& result[], double tolerance);

Функция вычисляет обратную матрицу для заданной квадратной матрицы matr путём приписывания единичной матрицы, т.е. решая N (N=numRows=numCols) систем линейных уравнений при помощи функции MatrGJBatchSolve (матрица правых частей является единичной; точность задаётся неотрицательной параметром tolerance). Асимптотическая сложность используемого алгоритма - O(N^3). Элементы результатирующей матрицы помещаются в массив result. В случае успешного вычисления обратной матрицы (определитель отличен от нуля) функция возвращает true.

double MatrDet(double& matr[], int numRows, int numCols, double tolerance);

Функция вычисляет определитель квадратной матрицы matr при помощи приведения её к трапецеидальному (треугольному) виду. Используется метод Гаусса с точностью tolerance (этот параметр должен быть неотрицательным). Асимптотическая сложность алгоритма - O(N^3).

double MatrDetTriang(double& matr[], int numRows, int numCols);

Функция вычисляет определитель треугольной матрицы matr.

double MatrRank(double& matr[], int numRows, int numCols, double tolerance);

Функция вычисляет ранг матрицы matr при помощи приведения её к трапецеидальному (треугольному) виду. Используется метод Гаусса с точностью tolerance (этот параметр должен быть неотрицательным). Асимптотическая сложность алгоритма - O(N^3).

double MatrRankTriang(double& matr[], int numRows, int numCols, double tolerance);

Функция вычисляет ранг матрицы matr. Матрица должна быть приведена к трапецеидальному (треугольному) виду построчно (например, при помощи вызова функции MatrGaussianElimination). Неотрицательный параметр tolerance задаёт точность поиска первой нулевой строки.

void MatrComputeConnectedMatr(double& matr[], int numRows, int numCols, double& result[], double tolerance);

Функция вычисляет союзную матрицу для квадратной матрицы matr. Элементы результатирующей матрицы помещаются в массив result. Неотрицательный параметр tolerance определяет точность, используемую при вычислении алгебраических дополнений.

void MatrLerpMatr(double& matr1[], double& matr2[], int numRows, int numCols, double balance, double& result[]);

Функция выполняет поэлементную линейную интерполяцию между матрицами matr1 и matr2 одинаковой размерности. Параметр balance является коэффициентом для линейной интерполяции и должен находиться в пределах [0;1]. Элементы результатирующей матрицы возвращаются в массиве result.

2.10. Функции ввода-вывода

Группа функций ввода-вывода предназначена для сохранения/загрузки матриц, а также для выполнения отладочной печати матрицы в лог.

void MatrPrint(double& matr[], int numRows, int numCols);

Функция предназначена для выполнения отладочной печати в лог (панель "Терминал", вкладка "Эксперты"). Матрица выводится построчно с учётом того, что лог в терминале отображается в обратном порядке (т.е. новые записи появляются сверху; функция печатает строки матрицы начиная с конца для удобства визуального анализа матриц в логе).

void FileWriteMatr(double& matr[], int numRows, int numCols, int handle);

Функция сохраняет матрицу (включая размерности) в файл, хэндл которого передаётся в параметре handle. Файл должен быть открыт в режиме FILE_BIN|FILE_WRITE.

void FileReadMatr(double& matr[], int& numRows, int& numCols, int handle);

Функция загружает матрицу из файла. Сначала в переменные, ссылки на которые переданы в параметрах numRows и numCols считываются размерности матрицы, затем размер массива matr изменяется в соответствии с размерностями матрицы, после чего производится загрузка содержимого массива matr из файла. Хэндл файла из которого производится чтение передаётся в параметре handle; файл должен быть открыт в режиме FILE_BIN|FILE_READ.

Теперь, когда читатель ознакомился с описаниями функций, можно перейти к решению практических задач при помощи библиотеки.

3. Пример использования

Рассмотрим пример построения полиномиальной регрессии по ряду цен при помощи предлагаемой библиотеки.

Построение полиномиальной регрессии заключается в нахождении коэффициентов полинома f(x)=a[0]+a[1]*x+...+a[degree]*x^degree степени degree, осуществляемое при помощи решения системы линейных алгебраических уравнений, в которой элементы матрицы системы A[degree+1][degree+1] определяются следующим образом: A[i][j]=(x[0]^(i+j)+x[1]^(i+j)+...+x[numPoints]^(i+j))/numPoints, а элементы вектора правой части B[degree+1][1] определяются по формуле: B[i]=(y[0]*x[0]^i+y[1]*x[1]^i+...+y[numPoints]*x[numPoints]^i)/numPoints.

Для решения поставленной задачи был написан скрипт (файл LibMatrixEx.mq4 в прилагаемом архиве), выполняющий построение полинома, его отображение на исходном промежутке и справа от него (т.е. выполняет экстраполяцию). Значения полинома на промежутке экстраполяции могут быть использованы для прогнозирования направления движения цены.

Управление скриптом осуществляется при помощи трёх вертикальных линий: две предназначены для выбора анализируемого промежутка, третья - для выбора крайней правой точки, до которой осуществляется отображение полинома.

Для работы скрипт следует перетащить на график и задать необходимые параметры: delay - периодичность (в миллисекундах) обновления графика, degree - степень полинома, linesMargin - начальное расстояние между управляющими линиями, linesWidth - толщина линий графика полинома. Также предоставляется возможность выбора цветов линий: управляющих вертикальных (параметры colVLineInt и colVLineExt) и линий графика (параметры colInt и colExt).

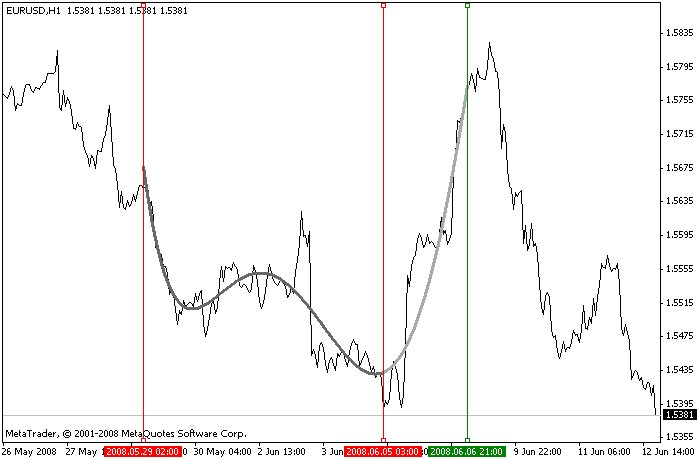
Пример работы скрипта

Рассмотрим ключевую функцию скрипта, осуществляющую работу с матрицами.

// построение полиномиальной регрессии
bool Regression(double& x[], double& y[], int numPoints, int polyDegree, double& poly[]) {
   // создаём матрицу системы
   double A[];
   int numRowsA = polyDegree + 1;
   int numColsA = polyDegree + 1;
   MatrSetSize(A, numRowsA, numColsA);
   // заполняем матрицу
   for (int row = 0; row < numRowsA; row++) {
      for (int col = 0; col < numColsA; col++) {
         int offset = MatrIndiciesToOffset(row, col, numRowsA, numColsA);
         A[offset] = SXY(x, y, numPoints, row + col, 0);
      }
   }
   // создаём вектор правых частей
   double B[];
   int numRowsB = polyDegree + 1;
   int numColsB = 1;
   MatrSetSize(B, numRowsB, numColsB);
   // заполняем вектор правых частей
   for (row = 0; row < numRowsB; row++) {
      offset = MatrIndiciesToOffset(row, 0, numRowsB, numColsB);
      B[offset] = SXY(x, y, numPoints, row, 1);
   }
   // решаем СЛАУ
   int numRowsX, numColsX;
   bool status =
      MatrGJBatchSolve(
         A, numRowsA, numColsA,
         B, numRowsB, numColsB,
         poly, numRowsX, numColsX,
         DEFAULT_TOLERANCE
      );
   if (!status) {
      Print("Произошла ошибка при решении системы");
   }
   return (status);
}

Функция принимает 5 аргументов. Первые два - массивы x и y - предназначены для хранения координат точек, по которым производится построение полинома. Количество точек передается в аргументе numPoints. Четвертый аргумент задаёт степень искомого полинома (она должна быть меньше количества точек по крайней мере на 1). Пятый аргумент - ссылка на массив, получающий коэффициенты полинома.

В начале функции производится создание матрицы A, изменение её размеров и заполнение по приведённым выше формулам. Для обращения к элементам матрицы через двухмерные индексы используется функция MatrIndiciesToOffset, производящая вычисление одномерного смещения относительно начала массива.

Далее аналогично производится заполнение вектора-столбца B. Последующий вызов функции MatrGJBatchSolve решает построенную систему, тем самым находя коэффициенты полинома.

Прочий код, осуществляющий проверку положений линий и вывод полинома не должен вызвать у читателя затруднений при разборе.

Заключение

Предложена библиотека для работы с матрицами, рассмотрены реализованные функции и их особенности.

Продемонстрировано применение библиотеки на примере построения полиномиальной регрессии по ряду цен закрытия свечей.

Код был тщательно проверен, однако автор не исключает наличие в нём ошибок. Если вы обнаружите ошибку, пожалуйста, сообщите о ней.