LibMatrix: Bibliothek der Matrix Algebra (Teil Eins)

Einführung

Die Anwendung der verschiedenen Zweige der Mathematik ist beim Schreiben von komplexen automatisierten Handelssystemen von wesentlicher Bedeutung. Einer dieser Zweige ist die lineare Algebra.

Es gibt aktuell keine umfangreichen öffentlich verfügbaren Bibliotheken in MQL4, die verschiedene Methoden der linearen Algebra umsetzen (insbesondere die Theorie der Matrizen und Determinanten).

Dieser Artikel beschreibt die LibMatrix Bibliothek in MQL4, die die Umsetzung der gebräuchlichsten Matrix-Operationen umfasst.

Matrix ist ein endliches rechteckiges Array, gefüllt mit einigen mathematischen Objekten (z.B. Zahlen).

Vier Monate nach dem Verfassen in C++, wurde der gesamte Code in MQL4 mit einigen Änderungen neu geschrieben.

1. Bibliotheksstruktur

Lassen Sie uns zunächst einige Besonderheiten der Arbeit mít Matrizen in der vorgeschlagenen Bibliothek betrachten.

Erstens, Matrizen werden in eindimensionalen Arrays gespeichert. Es hat mit der Tatsache zu tun, dass, obwohl MQL4 Funktionen zum Erstellen mehrdimensionaler Arrays bietet, es nur möglich ist die Größe der erste Dimension zu ändern. Um eine Matrix aus N Zeilen und M Spalten zu speichern, benötigen wir ein eindimensionales N*M Array. Die Matrix wird Zeile für Zeile in ein Array gepackt, d.h. die ersten Zeilenelemente in einem Datenarray werden gefolgt von den zweiten Zeilenelementen, und so weiter.

Zweitens, bei der Erstellung der Bibliothek wurde beschlossen keine zusätzlichen Informationen über die Matrixgröße zu speichern, da Größen Integer- (Ganzzahl) Werte sind, während Elemente reale Zahlen sind (speichern von Größen als reale Zahlenkönnte den Betrieb der Bibliothek dramatisch beeinflussen).

So besteht eine in dem Format durch die vorgeschlagene Bibliothek verarbeitete Matrix aus drei Variablen: ein eindimensionales Array des double Typ und zwei Integer Variablen Interger Variablentype and two integer variables (z.B. des int Typ) zum Speichern von Informationen auf der Anzahl an Zeilen und Spalten.

Die Bibliothek besteht aus zwei Dateien: LibMatrix.mqh und LibMatrix.mq4. Die erste Datei wird nach Bedarf eingefügt. Sie enthält Funktion Prototypen, die aus der Bibliothek importiert werden können. Die zweite Datei enthält Funktion-Umsetzungen (Programmcode). Das ist es, worüber wir im Folgenden weiter sprechen werden.

Die in der Bibliothek umgesetzten Funktionen können in mehrere Gruppen unterteilt werden:

• Allgemein mathematische Funktionen (MathLerp, MathInRangeRandom, MathDoublesEqual)
• Hilfsfunktionen für die Arbeit mit Matrizen (MatrIndiciesToOffset, MatrCopy, MatrSetSize, MatrResize)
• Funktionen für die Arbeit mit Zeilen und Spalten (MatrSwapRows, MatrSwapCols, MatrCopyRow, MatrCopyCol, MatrRowIsZero, MatrColIsZero)
• Funktionen für die allgemeine Prüfung von Bedingungen (MatrIsSquare, MatrIsElemOnMainDiagonal, MatrCompatiblityCheckAdd, MatrCompatiblityCheckMul)
• Inhalt-Initialisierungsfunktionen (MatrLoadZero, MatrLoadIdentity, MatrLoadInRangeRandom)
• Funktionen zum Prüfen von Bedingungen nach Inhaltsart (MatrIsZero, MatrIsDiagonal, MatrIsIdentity, MatrIsSymmetric, MatrIsAntisymmetric, MatrEqual)
• Funktionen für elementweise skalare Operationen (MatrAddScalar, MatrSubScalar, MatrMulByScalar, MatrDivByScalar)
• Funktionen für grundlegende Matrix-Operationen (MatrAddMatr, MatrSubMatr, MatrMulMatr, MatrTrace, MatrTranspose)
• andere Funktionen (MatrGaussianElimination, MatrGJBatchSolve, MatrMinor, MatrAlgebraicComplement, MatrInvertUsingMinors, MatrInvertUsingGJ, MatrDet, MatrDetTriang, MatrRank, MatrRankTriang, MatrComputeConnectedMatr, MatrLerpMatr)
• Eingabe/Ausgabe Funktionen (MatrPrint, FileWriteMatr, FileReadMatr)

Werfen wir einen näheren Blick auf jede der Gruppen.

2. Funktion Beschreibungen

2.1. Allgemeine Mathematische Funktionen

Als erstes werden wir die Gruppe der allgemeinen mathematischen Funktionen betrachten. Sie enthält Funktionen die nicht direkt mit Matrizen verbunden sind, aber in der Bibliothek verwendet werden.

double MathLerp(double rangeLowLimit, double rangeHighLimit, double balance);

Diese Funktion führt lineare Interpolation zwischen zwei Werten mit der folgenden Formel aus: rangeLowLimit + balance * (rangeHighLimit - rangeLowLimit). Der balance Parameter Wert muss innerhalb des Bereichs [0;1] sein.

double MathInRangeRandom(double rangeLowLimit, double rangeHighLimit);

Diese Funktion gibt gleichmäßig verteilte Zufallszahlen zurück aus dem Bereich [rangeLowLimit;rangeHighLimit]. Die Standard MathRand Funktion wird für zum Generieren verwendet.

bool MathDoublesEqual(double value1, double value2, double tolerance);

Diese Funktion wird zum Vergleichen von zwei Werten verwendet, value1 und value2 des double Typs mit der angegebenen Genauigkeit (Toleranz). Die Verwendung des Annäherungsvergleichs ist erforderlich, aufgrund des möglichen Verlusts an Genauigkeit. Der tolerance Parameterwert darf nicht negativ sein (wie der Standardwert, können Sie die in der Bibliothek definierte DEFAULT_TOLERANCE Konstante verwenden).

2.2. Hilfsfunktionen für die Arbeit mit Matrizen

Gehen wir weiter zu der Gruppe der Hilfsfunktionen für die Arbeit mit Matrizen. Diese Gruppe deckt Funktionen ab, die gedacht sind zur Vereinfachung von Operationen in Bezug auf das Packen von Matrizen in eindimensionale Arrays.

int MatrIndiciesToOffset(int row, int col, int numRows, int numCols)

Diese Funktion berechnet den Versatz eines Elements in Bezug auf den Anfang des Arrays, in dem das Element gepackt ist. Unter den Parametern die sie erhält, sind die Nummern der Zeilen (row) und der Spalten (col) am Schnittpunkt, an dem das Element liegt, sowie die Matrixgröße (numRows - Anzahl der Matrixzeilen, numCols - Anzahl der Matrixspalten). Die row und col Werte müssen innerhalb der Bereiche [0;numRows-1] und [0;numCols-1] liegen.

void MatrCopy(double& src[], double& dst[]);

Diese Funktion kopiert alle Elemente der src Matrix zu der dst Matrix. Matrix Datenarrays sind die einzigen übergebenen Parameter. Nach Abschluss des Kopiervorgangs wird die dst Matrixgröße gleich zu der src Matrixgröße.

void MatrSetSize(double& matr[], int numRows, int numCols);

Diese Funktion ändert die Größe des matr Datenarray, so dass es eine Matrix von numRows Zeilen und numCols Spalten speichern kann. Die Matrix Datenintegrität ist nicht garantiert. Die numRows und numCols Parameterwerte müssen strikt positiv sein.

void MatrResize(double& matr[], int numRowsOld, int numColsOld, int numRowsNew, int numColsNew);

Diese Funktion ändert die Größe des matr Datenarray der bestehenden Matrix. Die numRowsOld und numColsOld Parameter müssen gleich zu der ursprünglichen Matrixgröße sein. Die neue Größe wird festgelegt durch die numRowsNew und numColsNew Parameter. Die Matrix Datenintegrität ist garantiert gemäß der neuen Größe, ausgenommen für die Fälle, in denen eine oder beide Matrix-Dimensionen verringert werden. Neue Werte werden auf Nullen initialisiert.

2.3. Funktionen für die Arbeit mit Zeilen und Spalten

Sehen wir uns die Funktionen an für die Arbeit mit Zeilen und Spalten.

void MatrSwapRows(double& matr[], int numRows, int numCols, int row1, int row2);

Diese Funktion tauscht den Inhalt der row1 und row2 Zeilen für die matr Matrix bestehend aus numRows Zeilen und numCols Spalten. Die row1 und row2 Parameterwerte müssen innerhalb des Bereichs [0;numRows-1] liegen.

void MatrSwapCols(double& matr[], int numRows, int numCols, int col1, int col2);

Diese Funktion tauscht den Inhalt der col1 und col2 Spalten. Die col1 und col2 Parameterwerte müssen innerhalb des Bereichs [0;numCols-1] liegen.

void MatrCopyRow(double& matr[], int numRows, int numCols, int rowToCopy, int rowToReplace);

Diese Funktion kopiert den Inhalt der rowToCopy Zeile zu der rowToReplace Zeile. Die rowToCopy und rowToReplace Parameterwerte müssen innerhalb des Bereichs [0;numRows-1] liegen.

void MatrCopyCol(double& matr[], int numRows, int numCols, int colToCopy, int colToReplace);

Diese Funktion kopiert den Inhalt der colToCopy Spalte zu der colToReplace Spalte. Die colToCopy und colToReplace Parameterwerte müssen innerhalb des Bereichs [0;numCols-1] liegen.

bool MatrRowIsZero(double& matr[], int numRows, int numCols, int row, double tolerance);

Diese Funktion prüft ob die row Zeile Null ist mit dem tolerance Grad an Genauigkeit. Wenn die Zeile Null ist, ist der zurückgegebene Wert true.

bool MatrColIsZero(double& matr[], int numRows, int numCols, int col, double tolerance);

Diese Funktion prüft ob die col Spalte Null ist mit dem tolerance Grad an Genauigkeit. Wenn die Spalte Null ist, ist der zurückgegebene Wert true.

2.4. Funktionen für die allgemeine Prüfung von Bedingungen

Die Gruppe der Funktionen zur allgemeinen Prüfung von Bedingungen, ist gedacht für die Verbesserung der Code-Lesbarkeit.

bool MatrIsSquare(int numRows, int numCols);

Diese Funktion prüft ob die Matrix der numRows Zeilen und numCols Spalten quadratisch sind (d.h. sie prüft ob numRows=numCols). Sie gibt true zurück für quadratische Matrizen.

bool MatrIsElemOnMainDiagonal(int row, int col);

Diese Funktion prüft ob das Element mit den [row][col] Indizes auf der Hauptdiagonalen der Matrix liegt. Sie gibt true zurück für die Elemente auf der Hauptdiagonalen.

bool MatrCompatiblityCheckAdd(int numRows1, int numCols1, int numRows2, int numCols2);

Die Funktion prüft die Kompatibilität von zwei Matrizen zu Zwecken von Ergänzung-ähnlichen Vorgängen. Dimensionen werden paarweise auf Gleichheit geprüft (numRows1=numRows2 and numCols1=numCols2); Bei Gleichheit wird true zurückgegeben.

bool MatrCompatiblityCheckMul(int numRows1, int numCols1, int numRows2, int numCols2);

Die Funktion prüft die Kompatibilität von zwei Matrizen zu Zwecken der Multiplikation. Sie prüft ob die Anzahl der Spalten in der ersten Matrix (numRows1 mal numCols1 Matrix) gleich ist zu der Anzahl an Zeilen in der zweiten Matrix (numRows2 mal numCols2 Matrix). Multiplikation ist möglich wenn true zurückgegeben wird.

2.5. Matrix Inhalt Initialisierungsfunktionen

Die Gruppe der Matrix Inhalt Initialisierungsfunktionen ist für das Laden häufig genutzter Matrizen gedacht (z.B. Null und Identität-Matrizen). Da kein Speicher zugewiesen ist, müssen die MatrSetSize oder MatrResize Funktionen aufgerufen werden, vor dem Aufruf der Gruppenfunktionen.

void MatrLoadZero(double& matr[], int numRows, int numCols);

Diese Funktion initialisiert das matr Datenarray zu Nullen, so eine Null-Matrix der numRows Zeilen und numCols Spalten erzeugend.

void MatrLoadIdentity(double& matr[], int numRows, int numCols);

Diese Funktion initialisiert alle Elemente des matr Datenarray zu Nullen, ausgenommen diejenigen, die auf der Hauptdiagonalen der Matrix liegen. Die initialisierte Matrix numRows Zeilen und numCols Spalten muss quadratisch sein.

void MatrLoadInRangeRandom(double& matr[], int numRows, int numCols, double rangeLowLimit, double rangeHighLimit);

Diese Funktion initialisiert das Datenarray der matr Matrix zu Zufallszahlen aus dem Bereich [rangeLowLimit;rangeHighLimit] (Zufallszahlen werden mit der MathInRangeRandom Funktion generiert).

2.6. Funktionen zum Prüfen von Bedingungen nach Inhaltsart

Betrachten wir die Gruppe der Funktionen zum Prüfen von Bedingungen nach Inhaltsart. Die Funktionen dieser Gruppe führen einen Vergleich durch mit dem tolerance Grad an Genauigkeit (dieser Parameterwert darf nicht negativ sein) und gibt true zurück, wenn die Bedingung unter Berücksichtigung zutrifft.

bool MatrIsZero(double& matr[], int numRows, int numCols, double tolerance);

Diese Funktion prüft ob die Matrix Null ist.

bool MatrIsDiagonal(double& matr[], int numRows, int numCols, double tolerance);

Diese Funktion prüft ob die Funktion diagonal ist. Die Matrix wird als diagonal angesehen, wenn sie quadratisch ist und alle Elemente außerhalb der Hauptdiagonalen Null sind.

bool MatrIsSymmetric(double& matr[], int numRows, int numCols, double tolerance);

Diese Funktion prüft ob die Matrix ein neutrales Element ist (engl.identity).

bool MatrIsIdentity(double& matr[], int numRows, int numCols, double tolerance);

Diese Funktion prüft ob die Matrix symmetrisch ist (d.h. a[i][j]=a[j][i] trifft zu für jedes i Und j).

bool MatrIsAntisymmetric(double& matr[], int numRows, int numCols, double tolerance);

Diese Funktion prüft ob die Matrix schiefsymmetrisch/antisymmetrisch ist (d.h. a[i][j]=-a[j][i] is true for any i and j and a[k][k]=0 trifft zu für jedes k).

bool MatrEqual(double& matr1[], double& matr2[], int numRows, int numCols, double tolerance);

Diese Funktion prüft elementweise die Gleichheit zwischen Matrizen mit den gleichen Dimensionen.

2.7. Funktionen für elementweise skalare Operationen

Gehen wir weiter zu der Gruppe der Funktionen für elementweise skalare Operationen. Diese Gruppe ist eigentümlich darin, dass Funktionsergebnisse nicht in das ursprüngliche Array der matr Matrix platziert werden, sondern in das neue result Array. Wird jedoch das gleiche Array als die result und als matr Parameter übergeben, werden die Ergebnisse in der ursprünglichen Matrix platziert.

void MatrAddScalar(double& matr[], int numRows, int numCols, double scalar, double& result[]);

Diese Funktion fügt den Skalar Wert zu jedem Matrix-Element hinzu.

void MatrSubScalar(double& matr[], int numRows, int numCols, double scalar, double& result[]);

Diese Funktion zieht den Skalar Wert von jedem Matrix-Element ab.

void MatrMulByScalar(double& matr[], int numRows, int numCols, double scalar, double& result[]);

Diese Funktion multipliziert jedes Matrix-Element mit dem Skalar Wert.

void MatrDivByScalar(double& matr[], int numRows, int numCols, double scalar, double& result[]);

Diese Funktion dividiert jedes Matrix-Element durch den Skalar Wert.

2.8. Funktionen für Grundlegende Matrix-Oprerationen

Die Gruppe der Funktionen für grundlegende Matrix-Operationen besteht aus Funktionen zum Ausführen elementarer Handlungen - Berechnungen von Summe, Produkt und Strang, sowie Transpositionsvorgänge. Die Ergebnisse der Funktionsvorgänge (ausgenommen von MatrTrace) werden in das result Array zurückgegeben.

void MatrAddMatr(double& matr1[], double& matr2[], int numRows, int numCols, double& result[]);

Die Funktion fügt bis zu zwei Matrizen mit den gleichen Dimensionen hinzu.

void MatrSubMatr(double& matr1[], double& matr2[], int numRows, int numCols, double& result[]);

Diese Funktion subtrahiert die matr2 Matrix von der matr1 matrix. Die Matrizen müssen die gleiche Größe haben

void MatrMulMatr(
      double& matr1[], int numRows1, int numCols1,
      double& matr2[], int numRows2, int numCols2,
      double& result[], int& numRowsRes, int& numColsRes);

Diese Funktion multipliziert die matr1 Matrix mit der matr2 Matrix. Die Matrizen sollten kompatibel für Multiplikationen sein, d.h. die Anzahl der Spalten (numCols1) in der ersten Matrix sollte gleich zu der Anzahl der Zeilen (numRows2) in der zweiten Matrix sein. Die Größe der resultierenden Matrix wird zurückgegeben in referenzierten Variablen, die in die numRowsRes und numColsRes Parameter übergeben werden.

double MatrTrace(double& matr[], int numRows, int numCols);

Diese Funktion berechnet den Matrix Strang (Summe der diagonalen Elemente). Die Matrix muss quadratisch sein.

void MatrTranspose(double& matr[], int numRows, int numCols, double& result[], int& numRowsRes, int& numColsRes);

Diese Funktion transponiert die Matrix (tauscht Spalten mit Zeilen)- Die neue Matrix wird zurückgegeben in referenzierten Variablen zurückgegeben, die in die numRowsRes und numColsRes Parameter übergeben werden.

2.9. Andere Funktionen

Die Gruppe der anderen Funktionen bietet Möglichkeiten der Matrix-Inversion, Berechnung von Rängen und Determinanten, usw.

int MatrGaussianElimination(double& matr[], int numRows, int numCols, double& result[], double tolerance);

Diese Funktion steht für die Umsetzung der Gaußchen-Elimination mit Pivotisierung. Die ursprüngliche matr Matrix von numRows Zeilen und numCols Spalten wird reduziert zu einer trapezoiden (dreieckigen) Form, mit den Ergebnissen platziert in dem result Array.

Der zurückgegebene Wert ist die Anzahl der linearen unabhängigen Zeilen der Matrix (d.h. ihr Rang). Da Berechnungen zu Funktion-Rundungsfehlern führen können, ist es erforderlich einen nicht-negativen tolerance Parameterwert zu übergebender den Grad der Genauigkeit des Vergleichs bestimmt.

bool MatrGJBatchSolve(
      double& matr[], int numRows, int numCols,
      double& rhs[], int numRowsRHS, int numColsRHS,
      double& roots[], int& numRowsRoots, int& numColsRoots,
      double tolerance
      );

Diese Funktion steht für die Umsetzung der Gauß-Jordan Elimination, gedacht zum Lösen von Sätzen mehrerer Gleichungssysteme mit ein und derselben Systemmatrix.

Die gemeinsame Systemmatrix wird übergeben an matr (Datenarray), numRows und numCols (Dimensionen) Parameter. Ein Satz von rechten Vektoren wird ebenfalls als eine Matrix (der rhs Parameter) übergeben, wobei jede Spalte eine rechte Seite des berücksichtigten Systems darstellt.

Mit anderen Worten, der numRowsRHS Parameter enthält die Anzahl der Gleichungen in dem System (Anzahl der Zeilen in der Systemmatrix), während der numColsRHS Parameter die Anzahl der rechten Vektoren enthält (Anzahl der zu lösenden Systeme)

Die Ergebnisse werden zurückgegeben in Form der roots Matrix der numRowsRoots Zeilen und numColsRoots Spalten. Die Lösung für jedes System aus Gleichungen wird in der Matrixspalte platziert und entspricht der Lösung für das System der gegebenen Systemmatrix und der Spalte mit der relevanten Nummer aus der rhs Matrix. Die Funktion gibt true zurück, wenn die Lösung für den Satz an Gleichungssystemen gefunden wurde.

void MatrMinor(
      double& matr[], int numRows, int numCols,
      int rowToExclude, int colToExclude,
      double& result[], int& numRowsRes, int& numColsRes);

Diese Funktion ermittelt die kleinere Matrix, die an dem Schnittpunkt der rowToExclude Zeile und der colToExclude Spalte liegt. Die resultierenden Matrixelemente werden zurückgegeben in das result Array, während die Dimensionen in referenzierte Variablen zurückgegeben werden, die in die numRowsRes und numColsRes Parameter übergeben werden.

double MatrAlgebraicComplement(double& matr[], int numRows, int numCols, int elemRow, int elemCol, double tolerance);

Diese Funktion berechnet den algebraischen Cofaktor (kleinere mit einem Platz-Zeichen) für das am Schnittpunkt liegende Element der elemRow Zeile und elemCol Spalte. Um den Determinanten zu berechnen, verwenden wir die Gaußsche Elimination (in Form der MatrGaussianElimination Funktion) mit einem durch den tolerance Parameter festgelegten Grad an Genauigkeit.

bool MatrInvertUsingMinors(double& matr[], int numRows, int numCols, double& result[], double tolerance);

Diese Funktion berechnet die Umkehr der quadratischen matr Matrix mit einer vereinten Matrix (generiert aus algebraischen Cofaktoren der entsprechenden Matrixelemente). Asymptotische Komplexität des verwendeten Algorithmus: O(N^5). Die vereinte Matrix wird berechnet mit der MatrAlgebraicComplement Funktion (die wiederum die Gaußsche Elimination verwendet) und aus diesem Grund muss der Funktion ein nicht-negativer tolerance Parameterwert übergeben werden, der der den Grad der Genauigkeit bestimmt. Die Elemente der resultierenden Matrix werden in dem result Array platziert. Wenn die Umkehr der Matrix erfolgreich berechnet wurde (der Determinant ist ein anderer als Null), gibt die Funktion true zurück.

bool MatrInvertUsingGJ(double& matr[], int numRows, int numCols, double& result[], double tolerance);

Diese Funktion berechnet die Umkehr der gegebenen quadratischen matr Matrix durch eine angrenzende Identity Matrix, d.h. durch Lösen von N (N=numRows=numCols) Systemen linearer Gleichungen mit der MatrGJBatchSolve Funktion (die Matrix der rechten Seite ist neutral, der Grad der Genauigkeit wird festgelegt mit einem nicht-negativen tolerance Parameterwert). Asymptotische Komplexität des verwendeten Algorithmus: O(N^3). Die Elemente der resultierenden Matrix werden in dem result Array platziert. Wenn die Umkehr der Matrix erfolgreich berechnet wurde (der Determinant ist ein anderer als Null), gibt die Funktion true zurück.

double MatrDet(double& matr[], int numRows, int numCols, double tolerance);

Diese Funktion berechnet den Determinanten der quadratischen matr Matrix durch reduzieren auf einen trapezoide (dreieckige) Form. Zu diesem Zweck verwenden wir die Gaußsche Elimination mit einem tolerance Grad an Genauigkeit (Dieser Parameter muss nicht-negativ sein). Asymptotische Komplexität des Algorithmus: O(N^3).

double MatrDetTriang(double& matr[], int numRows, int numCols);

Diese Funktion berechnet den Determinant der dreieckigen matr Matrix.

double MatrRank(double& matr[], int numRows, int numCols, double tolerance);

Diese Funktion berechnet den Rang der matr Matrix durch Reduzieren zu einer trapezioden (dreieckigen) Form. Zu diesem Zweck verwenden wir die Gaußsche Elimination mit tolerance Grad an Genauigkeit (dieser Parameter muss nicht-negativ sein). Asymptotische Komplexität des verwendeten Algorithmus: O(N^3).

double MatrRankTriang(double& matr[], int numRows, int numCols, double tolerance);

Diese Funktion berechnet den Rang der matr Matrix. Diese Matrix muss Zeile für Zeile auf eine trapezoide (dreieckige) Form reduziert werden (z.B. durch Aufrufen der MatrGaussianElimination Funktion). Der nicht-negative tolerance Wert bestimmt den Grad der Genauigkeit der ersten Null-Zeile Berechnung.

void MatrComputeConnectedMatr(double& matr[], int numRows, int numCols, double& result[], double tolerance);

Diese Funktion berechnet die vereinte Matrix für die quadratische matr Matrix. Die Elemente der resultierenden Matrix werden in dem result Array platziert. Der nicht-negative tolerance Wert bestimmt den Grad der Genauigkeit bei der Berechnung algebraischer Cofaktoren.

void MatrLerpMatr(double& matr1[], double& matr2[], int numRows, int numCols, double balance, double& result[]);

Diese Funktion führt elementweise lineare Interpolation aus, zwischen den matr1 und matr2 Matrizen der gleichen Größe. Der balance Parameter steht für den lineare Interpolation Koeffizienten und muss innerhalb des Bereichs [0;1] liegen. Die Elemente der resultierenden Matrix werden zurückgegeben in das result Array.

2.10. Eingabe/Ausgabe Funktionen

Die Gruppe der Eingabe-Ausgabe Funktionen ist gedacht zum Speichern/Laden von Matrizen, sowie für das Schreiben der Debugging-Ausgabe einer Matrix in das Protokoll.

void MatrPrint(double& matr[], int numRows, int numCols);

Diese Funktion ist gedacht für das Schreiben der Debugging-Ausgabe in das Protokoll (Experten Registerkarte im Terminal). Sie gibt die Matrix Zeile für Zeile aus, unter Berücksichtigung, dass das Protokoll im Terminal in umgekehrter Reihenfolge angezeigt wird (d.h. neue Einträge erscheinen oben. Die Funktion druckt die Matrixzeilen, beginnend von dem Ende, für den Komfort der visuellen Analyse im Protokoll).

void FileWriteMatr(double& matr[], int numRows, int numCols, int handle);

Diese Funktion speichert eine Matrix (einschließlich ihrer Dimensionen) in die Datei, deren Identifikator in den handle Parameter übergeben wird. Die Datei solle offen sein in dem FILE_BIN|FILE_WRITE Modus.

void FileReadMatr(double& matr[], int& numRows, int& numCols, int handle);

Diese Funktion lädt eine Matrix von einer Datei. Zunächst werden Matrix-Dimensionen zu den referenzierenden Variablen gelesen, zu denen in den numRows und numCols Parametern übergeben wird. Das matr Array wird dann in der Größe angepasst, entsprechend der Matrixgröße, die gefolgt wird vom Laden des Inhalts des matr Array von der Datei. Der Identifikator der Datei, von der die Daten gelesen werden, wird übergeben in den handle Parameter, die Datei sollte offen sein in dem FILE_BIN|FILE_READ Modus.

Jetzt, da der Leser vertraut geworden ist mit den Funktionsbeschreibungen, können wir fortfahren um praktische Probleme mit der Bibliothek zu lösen.

3. Anwendungsbeispiel

Werfen wir einen Blick auf ein Beispiel der Ertsellung einer polynomialen Regression auf einer Reihe von Kurs-Werten mit der vorgeschlagenen Bibliothek.

Der Vorgang der Erstellung einer polynomialen Regression besteht aus der Ermittlung des polynomialen Koeffizienten f(x)=a[0]+a[1]*x+...+a[degree]*x^degree des degree Grad. Dies wird ausgeführt durch Lösen eines Systems aus linearen algebraischen Gleichungen, wobei Elemente der Systemmatrix A[degree+1][degree+1] wie folgt definiert werden: A[i][j]=(x[0]^(i+j)+x[1]^(i+j)+...+x[numPoints]^(i+j))/numPoints, während Elemente des rechten Vektor B[degree+1][1] mit der folgenden Formel bestimmt werden: B[i]=(y[0]*x[0]^i+y[1]*x[1]^i+...+y[numPoints]*x[numPoints]^i)/numPoints.

Um die Aufgabe zu lösen,, haben wir ein Skript (die LibMatrixEx.mq4 Datei in dem angehangenen Archiv), das ein Polynom erstellt und es auf dem ursprünglichen Intervall anzeigt und zu seiner Rechten (z.B. Extrapolation). Polynomwerte auf dem Extrapolation Intervall können für die Prognose der Richtung der Kursbewegung.

Das Skript wird mit drei vertikalem Linien gesteuert: zwei von ihnen sind für die Auswahl des zu analysierenden Intervalls bestimmt und das dritte bestimmt den am weitesten rechten Punkt auf dem das Plyno angezeigt wird.

Um die Operation des Skripts zu aktivieren, müssen Sie es auf das Chart ziehen und die erforderlichen Parameter einstellen: delay - Chart Aktualisierungsrate (in ms), degree - Grad des Polynom, linesMargin - anfänglicher Abstand zwischen den Steuerungslinien, linesWidth - Linienbreite des Polynom-Chart. Sie können außerdem die Farben für die vertikalen Steuerungslinien (colVLineInt und colVLineExt Parameters) und Chart-Linien (colInt und colExt Parameter) auswählen.

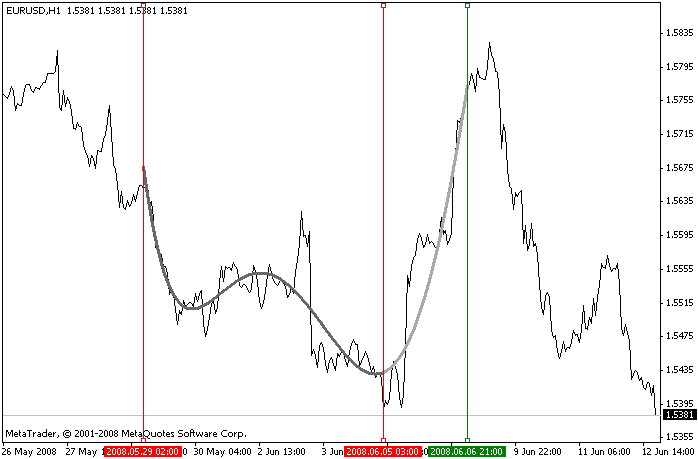
Skript Betriebsbeispiel

Lassen Sie uns die Schlüsselfunktion des Skripts begutachten, das sich mit Matrizen beschäftigt.

// creating polynomial regression
bool Regression(double& x[], double& y[], int numPoints, int polyDegree, double& poly[]) {
   // create system matrix
   double A[];
   int numRowsA = polyDegree + 1;
   int numColsA = polyDegree + 1;
   MatrSetSize(A, numRowsA, numColsA);
   // fill the matrix
   for (int row = 0; row < numRowsA; row++) {
      for (int col = 0; col < numColsA; col++) {
         int offset = MatrIndiciesToOffset(row, col, numRowsA, numColsA);
         A[offset] = SXY(x, y, numPoints, row + col, 0);
      }
   }
   // create a right hand side vector
   double B[];
   int numRowsB = polyDegree + 1;
   int numColsB = 1;
   MatrSetSize(B, numRowsB, numColsB);
   // fill the right hand side vector
   for (row = 0; row < numRowsB; row++) {
      offset = MatrIndiciesToOffset(row, 0, numRowsB, numColsB);
      B[offset] = SXY(x, y, numPoints, row, 1);
   }
   // solve a system of linear algebraic equations
   int numRowsX, numColsX;
   bool status =
      MatrGJBatchSolve(
         A, numRowsA, numColsA,
         B, numRowsB, numColsB,
         poly, numRowsX, numColsX,
         DEFAULT_TOLERANCE
      );
   if (!status) {
      Print("Error solving the system");
   }
   return (status);
}

Die Funktion übernimmt 5 Argumente. Die ersten zwei sind x und y Arrays die gedacht sind zum Speichern der Koordinaten der Punkte, durch die das Polynom gezeichnet wird. Die Anzahl der Punkte wird übergeben in den numPoints Parameter. Das vierte Argument bestimmt den Grad des betrachteten Polynoms (er muss geringer sein als die Anzahl an Punkten von mindestens 1). Das fünfte Argument ist der Verweis auf das Array das Polynom Koeffizienten empfängt.

Am Anfang der Funktion, wird die A Matrix erstellt, in der Größe angepasst und mit den obigen Formeln gefüllt. Um die Matrix-Elemente über zweidimensionale Indizes zu referenzieren, verwenden wir die MatrIndiciesToOffset Funktion, die eindimensionalen Versatz in Bezug auf den Anfang des Arrays berechnet.

Die Vektor-Spalte B wird dann auf eine ähnliche Weise gefüllt. Dem folgt der Aufruf der MatrGJBatchSolve Funkton, die das erstellte System löst, somit den Polynom Koeffizienten ermittelt.

Der Rest des Codes, der Zeilenpositionen und das Polynom ausgibt, sollte für den Leser keine Schwierigkeiten darstellen.

Fazit

Der Artikel hat in die Bibliothek für die Arbeit mit Matrizen eingeführt und die umgesetzten Funktionen und Besonderheiten besprochen.

Die Verwendung der Bibliothek wurde anhand eines Beispiels der Erzeugung polynomialer Regression einer Reihe von Kerzen Schlusskurs-Werten demonstriert.

Der Code wurde sorgfältig geprüft, aber es könnte noch Fehler geben. Sollten Sie einen Fehler entdecken, lassen Sie es mich bitte wissen.