Esperanza moral en el trading
548
4
En el presente artículo, usaremos el ducado como unidad monetaria: así preservamos la continuidad histórica. Bueno, el lector siempre podrá sustituir el ducado por cualquier otra moneda que le resulte más afín.
Esperanza matemática
En el comercio, la esperanza matemática es uno de los indicadores que ayudan a juzgar la efectividad de una estrategia comercial. Este uso de la esperanza (y mucho más) se detalla en el artículo "Matemáticas en el trading. Cómo evaluar los resultados de las transacciones comerciales".
Pero ahora estamos interesados en la definición probabilística de la esperanza matemática. Por ejemplo, le propongo un juego en el que usted tiene un 10 % de posibilidades de ganar 100 ducados y un 90 % de posibilidades de perder 10 ducados. Entonces la esperanza matemática de tal juego se verá así: E = 0,1 * 100 + 0,9 * (-10) = 1 ducado. Por lo tanto, según la esperanza matemática, podemos juzgar el rendimiento esperado. Entonces, si jugamos 100 veces a este juego, podemos suponer que nuestro depósito inicial podrá aumentar en 100 ducados.
La intuición sugiere que cuanto mayor sea la esperanza matemática, más interesante será participar en un juego así. Por ejemplo, si aumentamos las ganancias en el juego a 200 ducados, entonces la esperanza matemática también aumentará a 11, mientras que la rentabilidad esperada de 100 juegos subirá a 1100 ducados. Y si la esperanza matemática es +100500, ¡esto será ya un sueño! ¿Está de acuerdo con esta afirmación?
De ser así, hoy es uno de los días más felices de su vida. Porque ahora le propongo jugar al juego de la esperanza infinita. Solo imagine, en una hora (se puede hacer incluso más rápido) será un hiper-mega-multi-super-billonario.
Pero este juego tiene un pequeño inconveniente. Para participar en él, deberá pagar una pequeña tarifa de entrada, digamos 100 ducados. Hmm, suena un poco extraño por mi parte, mejor que la contribución sea de 50 ducados. Bueno, solo para usted y solo ahora le ofrezco un descuento: pague solo 25 ducados e iniciaremos de inmediato este maravilloso juego.
Mientras me envía la cuota de inscripción, le contaré las reglas del juego en cuestión. Entonces, primero deberá adivinar de qué lado caerá una moneda: "cara o cruz". Luego tiraré la moneda, y si acierta, le pagaré 1 ducado. La segunda apuesta le dará 2 ducados. Después del tercer intento, recibirá 4 ducados, y así sucesivamente; cada intento posterior duplicará su anterior beneficio. Imagine cuántos ducados tendré que pagarle tras cincuenta intentos. ¿Y tras cien? Semejantes números aún no se han inventado en absoluto, y toda la riqueza del mundo sería algo insignificante en comparación con sus ganancias.
Bueno, si comete un error, el juego finalizará. Puede volver a pagar la tarifa de entrada y comenzaremos desde el principio.
Algo me dice que un número apenas mayor que nadie querrá jugar a un juego así conmigo. Interesante, ¿y por qué? La respuesta es simple: por un lado, tenemos una esperanza matemática infinita:
Y por otro, nuestra voz interior nos sugiere que incluso 25 ducados será un precio demasiado alto para tal infinidad. Esta contradicción recibe el nombre de "Paradoja de San Petersburgo".
Esperanza moral
En 1738 Daniel Bernoulli publicó el trabajo "Specimen theoriae novae de mensura sortis" (Exposición de una nueva teoría sobre la medición del riesgo) . En este trabajo, el autor sugería que en cualquier juego lo importante no es maximizar la ganancia esperada, sino su utilidad para el jugador.
Esta suposición se puede ilustrar con el siguiente ejemplo. Imaginemos que hay dos jugadores diferentes. Uno dispone de un capital de 100 ducados y el otro de 1000 ducados. A ambos se les ofrece un juego con una ganancia esperada de 10 ducados. Obviamente, para el primer jugador, el juego resultará de mayor interés, ya que si gana, su capital aumentará en un 10%. Para el segundo jugador, en cambio, el capital aumentará solo en un 1%. Es decir, la misma ganancia resultará más útil para el primer jugador que para el segundo.
Usando como base esta suposición, Daniel Bernoulli creó la fórmula de la esperanza moral. Supongamos que Deposit es el capital de que dispone un jugador, Profit es la ganancia esperada, Loss la pérdida posible, y p la probabilidad de ganancia. La fórmula de la esperanza moral sería entonces:
La principal diferencia entre la esperanza moral y la esperanza matemática es que la esperanza moral depende del capital del jugador e implícitamente tiene en cuenta el riesgo del juego.
Vamos a tomar como ejemplo uno de los juegos que sugerimos anteriormente: con un 10% de posibilidades puede ganar 200 ducados y con un 90% de posibilidades puede perder 10 ducados. La esperanza matemática de este juego será la misma para todos los jugadores: 0,1*200 + 0,9*(-10) = 11 ducados. Mientras que la esperanza moral será diferente y ofrecerá un poco más de información.
Primero coloque sus ducados sobre la mesa y cuéntelos. Ahora sopese los pros y los contras y responda: ¿acepta jugar a este juego?
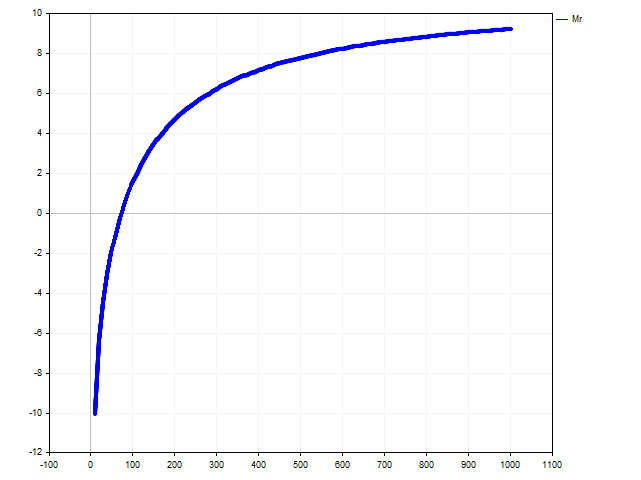
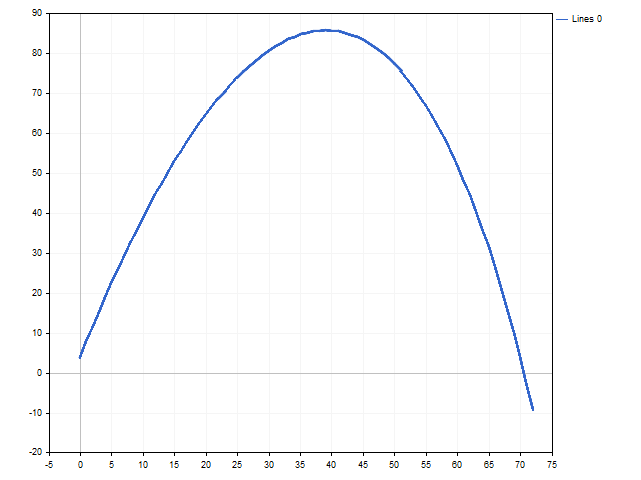
- Si ha aceptado jugar y tiene más de 73,74 ducados, entonces todo está en orden: calcule correctamente los riesgos y sus posibilidades.
- Si tiene exactamente 73,74 ducados, estará caminando por el filo de la navaja. Por el mismo filo.
- Y si tiene menos de 73,74 ducados, entonces… ¿quizás debería buscar otras formas de combatir la adicción a la adrenalina? Por ejemplo, puede intentar dar de comer en alta mar a tiburones devoradores de hombres hambrientos.
- Si ha abandonado este juego y tiene más de 73,74 ducados, es muy posible que se esté perdiendo uno de los momentos más interesantes de su vida.
Seguramente, se preguntará de dónde ha salido esta misteriosa suma de 73,74 ducados. De la esperanza moral de este juego:
Para un jugador racional, la esperanza moral debe ser estrictamente positiva:
A partir de esta desigualdad resulta sencillo encontrar la solución Deposit > 73.74. En la siguiente figura podemos ver cómo cambia la esperanza moral según el capital del jugador.
Esperanza moral en el trading
Algunas estrategias comerciales incluyen el establecimiento de stop loss y take profit. En tales estrategias comerciales, es posible usar la esperanza moral. En este caso, son posibles varias opciones para aplicar la esperanza moral.
Al abrir una posición, el tráder sabe exactamente el balance de la cuenta comercial. Además, puede valorar la probabilidad de obtener ganancias (discutiremos esto más adelante). El resto de parámetros de la posición los presentaremos como variables:
- SL – diferencia entre el precio de apertura de la posición y su stop loss en puntos (número entero positivo);
- TP – diferencia entre el precio de apertura de la posición y su take profit en puntos;
- PV – valor de un punto expresado en la divisa del depósito.
- Lot – volumen de la posición.
Entonces la esperanza moral para esta posición sería:
La primera forma de aplicar la esperanza moral solo es posible si los valores de dos de las tres variables SL, TP y Lot están preestablecidos.
Por ejemplo, al abrir una posición, establecemos el volumen de la posición y su take profit. Entonces podemos evaluar el nivel de stop loss para esta transacción. Su valor deberá ser tal que la esperanza moral se vuelva positiva. Es decir, hallaremos el valor de stop loss máximo posible.
Veamos cómo podemos hacer esto simbólicamente. Primero necesitamos encontrar el valor de la variable auxiliar:
Entonces el stop loss se verá limitado por la desigualdad:
Si hemos establecido el lote y el stop loss, entonces podremos estimar el nivel de take profit.
Entonces, el take profit para esta transacción será el siguiente:
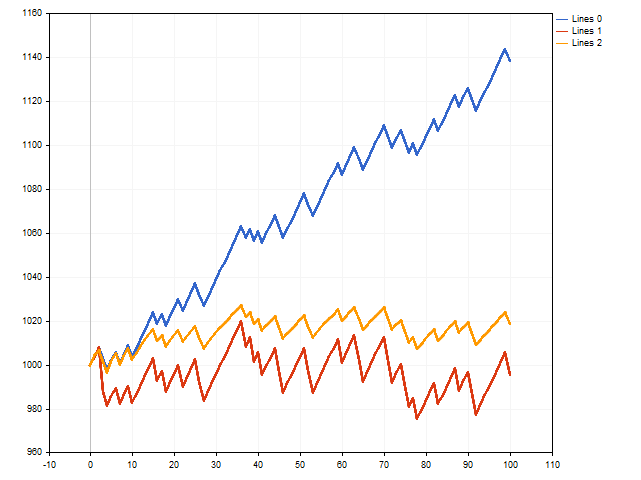
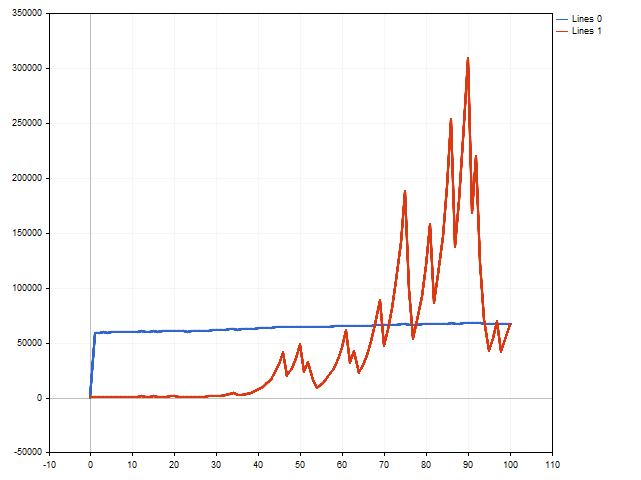
Ya nos hemos ocupado de las construcciones teóricas. Veamos ahora si podemos aplicarlas en la práctica. Para ello, escribiremos un script que simulará la ejecución de transacciones. Al mismo tiempo, comprobaremos tres opciones al mismo tiempo: con un stop loss y un take profit fijos, con un stop loss flotante y con un take profit flotante.
A primera vista, gana la opción con un stop loss y un take profit fijos (línea azul).
No obstante, recordemos que estamos utilizando el stop loss máximo y el take profit mínimo posibles. ¿Y qué sucederá si nos alejamos de estos límites y reducimos ligeramente el stop loss y aumentamos el take profit? Entonces la situación podría cambiar.
La línea roja muestra los resultados de las transacciones con un stop loss flotante, mientras que la línea naranja muestra los resultados de las transacciones con un take profit flotante. Y como podemos ver, el take profit flotante puede tener un impacto positivo en los resultados comerciales.
Esperanza moral y gestión de capital
Dividiremos la fórmula de la esperanza moral en dos partes. De manera condicional, llamaremos «rentable» a la primera parte:
La segunda, en cambio, la llamaremos «no rentable»:
Si nos fijamos bien en la parte rentable, veremos que un aumento del lote provoca su incremento. Sin embargo, el propio aumento del lote provoca una disminución en la parte no rentable. Como resultado, la parte no rentable puede adoptar un valor cero (o incluso negativo). Y entonces, la esperanza moral de tal transacción se volverá negativa. Y esto, como recordamos, no es la mejor opción: los tráders racionales no la aprueban.
Nuestra próxima idea es encontrar un valor de lote tal que las partes rentable y no rentable de la fórmula adopten simultáneamente los valores máximos posibles. Entonces la esperanza moral será máxima para los SL y TP dados. En la figura, podemos ver cómo cambia la esperanza moral a medida que aumenta el tamaño del lote.
El experimento numérico ha dado un resultado positivo. Ahora debemos deducir la fórmula para el volumen de posición óptimo. Para lograr esto, necesitaremos encontrar la derivada de la esperanza moral con respecto a la variable Lot, igualarla a cero y resolver la ecuación resultante. Como resultado, obtendremos la siguiente expresión:
Prestemos atención a la parte de la expresión encerrada entre corchetes. Aquí vemos la esperanza matemática dividida por el stop loss y el take profit. Tenga en cuenta que para calcular correctamente el lote, la esperanza matemática de la transacción deberá ser estrictamente positiva. Es decir, siempre se deberá cumplir la condición:
Por cierto, si abrimos la fracción entre corchetes, obtendremos el criterio de Kelly
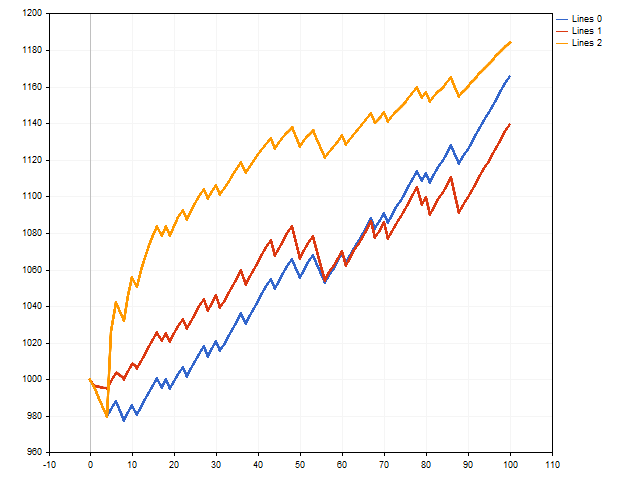
Y ahora, intentaremos simular una serie de transacciones en las que el lote se manejará con la ayuda de la esperanza moral. Aquí nos espera todo un abanico de resultados. Por ejemplo, el depósito inicial puede aumentar más de 160 veces.
No obstante, varias transacciones perdedoras seguidas pueden influir en el resultado de una forma nada positiva. En la siguiente figura, podemos observar que el depósito inicial ha aumentado unas cincuenta veces. Esto no está nada mal, si no consideramos el hecho de que en la zona del paso 90, el depósito inicial se ha incrementado unas trescientas veces.
Gestión de riesgos
Como hemos visto, la gestión de capital con ayuda de la esperanza moral puede provocar tanto ganancias impresionantes como pérdidas muy tangibles. Esto nos lleva a plantearnos la cuestión de la gestión de riesgos.
Tenemos dos formas de hacerlo. La primera y más obvia es no utilizar todo el depósito disponible en los cálculos, sino solo una parte del mismo. Por ejemplo, podemos establecer una cantidad fija. Asimismo, podemos establecer un porcentaje del balance actual. En cualquier caso, esto nos ayudará a reducir el riesgo al comerciar.
La segunda opción en cuanto a la gestión de riesgos es cambiar el cálculo de la probabilidad de una transacción rentable. Veamos con más detalle esta opción.
Supongamos que n es el número total de transacciones, mientras que m es el número de transacciones ganadoras. Entonces podemos valorar la probabilidad de ganar como:
No obstante, este enfoque no es del todo correcto, ya que de esta manera podemos estimar una frecuencia de eventos que ya han ocurrido, y lo que nosotros necesitamos obtener es la probabilidad de ganar en una transacción futura.
Digamos que ya se han realizado 15 transacciones, 10 de las cuales han sido ganadoras. Usted está a punto de abrir la siguiente posición. Entonces el número total de transacciones aumentará en 1, pero el número de transacciones ganadoras puede aumentar o permanecer igual.
Tomaremos el promedio de estas variantes y entonces la probabilidad de ganar para la posición abierta será:
Entonces hemos obtenido la estimación de Krichevsky–Trofimov, que de forma simbólica se ve así:
La adición del desplazamiento ha hecho posible una probabilidad ligeramente menor de obtener ganancias, lo cual ha redundado en un menor riesgo.
Ahora generalizaremos la estimación de la probabilidad de la forma siguiente: introduciremos un desplazamiento arbitrario s >= 1, y entonces la probabilidad de obtener ganancias será:
Estableciendo el valor de s, podemos regular el riesgo en un rango bastante amplio: cuanto mayor sea el valor de s, menor será el riesgo.
Desafortunadamente, la reducción del riesgo también afecta al volumen de ganancias obtenido. Por ello, cualquier tráder se enfrentará a una elección: un alto riesgo le permitirá obtener grandes ganancias, pero las pérdidas también podrían ser muy grandes. Un bajo riesgo, en cambio, le permitirá reducir las pérdidas, pero las ganancias serán pequeñas.
Veamos cómo el riesgo puede influir en el comercio. Para la comprobación, usaremos un asesor experto muy simple basado en la intersección de dos medias móviles. El asesor experto se ha puesto a prueba con los siguientes parámetros:
Pareja de divisas: EURUSD,
Marco temporal: H1,
Periodo de prueba: 2021.01.01 – 2022.12.31
Todos los demás parámetros serán los predeterminados.
Durante el periodo de prueba, se han realizado 419 transacciones. Y el gráfico de balance se ve así:
Para diferentes valores de riesgo, hemos obtenido los siguientes resultados.
| Risk | Total Net Profit | Balance Drawdown Absolute | Profit Factor | Expected Payoff | Recovery Factor | Margin Level |
|---|---|---|---|---|---|---|
| 0 | 42 961.51 | 2 699.05 | 1.18 | 102.53 | 1.72 | 89.20% |
| 25 | 28 932.51 | 570.27 | 1.21 | 69.05 | 1.89 | 260.70% |
| 50 | 16 836.83 | 230.64 | 1.21 | 40.18 | 1.92 | 309.53% |
Como podemos ver, la reducción del riesgo reduce las ganancias, pero puede mejorar otros parámetros de una estrategia comercial.
Conclusión
Para escribir este artículo, se han usado los siguientes programas:
| Nombre | Tipo | Descripción |
|---|---|---|
| ME SL-TP | Script | El script muestra cómo podemos cambiar la rentabilidad comercial si seleccionamos los valores de stop loss y take profit según la esperanza moral de la transacción. Parámetros del script:
|
| ME Lot | Script | El script muestra cómo el tamaño de la posición influye en la esperanza moral de una transacción. |
| ME MM | Script | El script compara la gestión de capital según la esperanza moral y el comercio con lote fijo. Al finalizar el funcionamiento, se muestra un mensaje con el resultado del comercio según ambas opciones, así como el tamaño de un lote fijo racional. |
| Two_Moving_Averages_System | Asesor | El asesor experto permite evaluar el impacto del riesgo en el rendimiento comercial. Sus parámetros son:
|
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/12134
Medimos la informatividad de los indicadores
Cómo elegir un asesor comercial: Veinte signos claros de un mal robot
Alan Andrews y sus métodos de análisis de series temporales
Ejemplo de creación de la estrategia comercial compleja Owl
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Y a qué llamamos "stop loss máximo y el take profit mínimo posibles"?, es complejo definir estos parámetros....
En este caso, estamos hablando de niveles en los que la expectativa moral sigue siendo positiva. Por ejemplo, podemos establecer un stop loss muy grande y la expectativa moral será negativa; esto es inaceptable. Es lo mismo con la toma de ganancias: no puede ser demasiado pequeña.
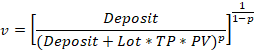
Gracias, qué valores de SL y TP fijos se han considerado para la gráfica azul? (lines 0)?. Qué ratio pérdida / beneficio tiene una expectativa moral positiva?. Por ejemplo, si considero un TP = 2*SL mi expectativa moral es positiva, pero curiosamente los AE que mejor funcionan son los que tienen un SL grande frente al TP (SL = 20*TP, por ejemplo...)
Depende de la probabilidad de una operación y un depósito rentables. El uso de un stop loss grande se debe al hecho de que es más probable un pequeño movimiento de precios. Es decir, con una relación de TP = 20 * SL, es más probable que cerremos la posición mediante una toma de ganancias. Pero esto ya se aplica a la teoría del forrajeo óptimo.