Forecasting Time Series (Part 1): Empirical Mode Decomposition (EMD) Method

Introduction

Any trader's success depends primarily on his or her ability to"take a look into the future," i.e., to guess how the price changes after a certain period of time. To solve this problem, it is important to have a wide variety of tools and features, from the latest updates on the fundamental market characteristics through the technical analysis algorithms. All of them can be enhanced to greater or lesser extent, using the mathematical methods of time series forecasting, both prices themselves and technical indicators, volatility, macroeconomic indices, trading portfolio balance, or something else being able to act as such time series.

Forecasting is a very wide-ranging topic and has already been touched upon many times on the mql5.com website. One of the first introductory and yet serious articles, Forecasting Financial Time-Series, was published back in 2008. Among many other articles and publications in the CodeBase, there are MetaTrader-ready tools offering, for instance:

• "Time Series Forecasting Using Exponential Smoothing (ES)".
• Searching for similar patterns in history, using the dynamic transformation of timeline (WmiFor+DTW);
• Back propagation (of error) neural network (BPNN);
• Kohonen neural network (SOM);

You can obtain the full list in searching across the relevant sections on the website (articles, CodeBase).

For the purpose hereof, we will extend the list of available forecasting tools with two new ones. The first one of them is based on the Empirical Mode Decomposition (EMD) method that has already been considered in the article titled Introduction to the Empirical Mode Decomposition, but not applied to forecasting. EMD is going to be considered in the first part hereof.

The second tool uses the support-vector machine (SVM) method, version Least-squares support-vector machine (LS-SVM). We are going to address it in our second part.

EMD-based forecasting algorithm

You can find a detailed introduction into the EMD technology in article Introduction to the Empirical Mode Decomposition Method. It is about decomposing a time series into strands — the so-called Intrinsic Mode Functions (IMFs). Each form is the spline interpolation of time series maximums and minimums, the extremums being first searched for the initial series. Then the IMF just found is deducted from it, whereafter the spline interpolation is performed for the extremums of the modified series, and such constructing several IMFs continues until the remainder becomes lower then the specified noise level. Visually, the results resemble Fourier series expansion; however, unlike the latter one, the typical EMD forms are not frequency-determining harmonic oscillations. Number of the IMF expansion functions obtained depends on the smoothness of the initial series and on the algorithm settings.

In the article mentioned above, ready classes are presented to compute EMD, but it proposes to obtain the decomposition result as a graph in an external HTML file. We are going to base on those classes and write necessary additions to make the algorithm predictive.

2 files were attached to the articles: CEMDecomp.mqh and CEMD_2.mqh. The second one is a slightly improved version of the first one, so we will go by the second one here. Let us copy it under the new name of EMD.mqh and include, without any changes yet, into indicator EMD.mq5.

  #include <EMD.mqh>

We will also use special classes for the simplified declaration of the array of buffer indicators, IndArray.mqh (its English description is available in the blog, the current version thereof is attached to the article). We will need many buffers, and they will be processed in a unified manner.

  #define BUF_NUM 18 // 16 IMF maximum (including input at 0-th index) + residue + reconstruction
  
  #property indicator_separate_window
  #property indicator_buffers BUF_NUM
  #property indicator_plots   BUF_NUM
  
  #include <IndArray.mqh>
  IndicatorArray buffers(BUF_NUM);
  IndicatorArrayGetter getter(buffers);

As seen, the indicator is shown in a separate window and has 18 buffers reserved to display:

• Initial series;
• 16 components of its decomposition (probably, not all of them will be used);
• Remainder ("trend"); and
• Reconstruction.

The last item is the most intriguing. The matter is that, after having obtained the IMF functions, we can sum up some (but not all) of them and obtain a smoothed version of the initial series. It is the smoothed reconstruction that will act as the source of forecasting, since it is the sum of the known splines that can be extrapolated for the bars that have not come yet (spline extrapolation). However, the forecasting depth should be limited to several bars, since the IMFs found become irrelevant as they move away from the latest known point, for which they have been obtained.

But back to file EMD.mqh. Class CEMD is defined in it, which performs all the work. The process is launched by calling the decomp method, where the time-series counting array, y, is passed. It is the size of that array that determines the length N of the proper functions — IMFResult. Method arrayprepare prepares backing arrays to compute them:

  class CEMD
  {
    private:
      int N;              // Input and output data size
      double IMFResult[]; // Result
      double X[];         // X-coordinate for the TimeSeries. X[]=0,1,2,...,N-1.
      ...
    
    public:
      int N;              // Input and output data size
      double Mean;        // Mean of input data
      ...
      
      int decomp(double &y[])
      {
        ...
        N = ArraySize(y);
        arrayprepare();
        for(i = 0; i < N; i++)
          X[i] = i;
        Mean = 0;
        for(i = 0; i < N; i++)
          Mean += (y[i] - Mean) / (i + 1.0); // Mean (average) of input data
        for(i = 0; i < N; i++)
        {
          a = y[i] - Mean;
          Imf[i] = a;
          IMFResult[i] = a;
        }
        // The loop of decomposition
          ...
          extrema(...);
          ...
        ...
      }
      
      
    private:
      int arrayprepare(void)
      {
        if(ArrayResize(IMFResult, N) != N) return (-1);
        ...
      }
  };

To increase the number of reference points, we are going to add to method decomp the new parameter, extrapolate, defining the forecasting depth. Let us increase N by the number of counts requested in extrapolate, having preliminarily saved the real length of the initial series in local variable Nf (in the code, the changes are marked with "+" and "*" for additions and changes, respectively).

      int decomp(const double &y[], const int extrapolate = 0) // *
      {
        ...
        N = ArraySize(y);
        int Nf = N;                            // + preserve actual number of input data points
        N += extrapolate;                      // + 
        arrayprepare();
        for(i = 0; i < N; i++)
          X[i] = i;
        Mean = 0;
        for(i = 0; i < Nf; i++)                // * was N
          Mean += (y[i] - Mean) / (i + 1.0);
        for(i = 0; i < N; i++)
        {
          a = y[MathMin(i, Nf - 1)] - Mean;    // * was y[i]
          Imf[i] = a;
          IMFResult[i] = a;
        }
        // The loop of decomposition
          ...
          extrema(...);
          ...
        for(i = 0; i < N; i++)
        {
          IMFResult[i + N * nIMF] = IMFResult[i];
          IMFResult[i] = y[MathMin(i, Nf - 1)] - Mean; // * was y[i]
        }
        
      }

Constructing IMFs on the bars to be forecasted starts with the last known value of the time series.

These are almost all changes necessary for forecasting. The full code of what we got is shown in the EMDloose.mqh file attached. But why EMDloose.mqh, not EMD.mqh?

The matter is that this forecasting method is not quite correct. Since we have increased the N size of all the arrays of the object, this includes the bars to be forecasted into searching for extremums, which is performed in method extrema. Technically, there are no extremums in future. All extremums formed during computations are those of the sum of spline extrapolations (without the initial series that doesn't exist in future). As a result, spline functions start adjusting to each other, trying to smooth their stacking. In a sense, it is convenient, since the prediction gets a self-balance — the oscillating process remains near the values of the time series and does not go into infinity. However, the value of such prediction is minimal — it does not characterize the initial time series anymore. However, this method may be used without doubt, and those whishing to can use it, including exactly EMDloose.mqh into the project.

To fix the problem, we will make some more modifications and get the final working version of EMD.mqh. To compare the effects provided by the two forecasting methods, we will check below how the indicator works with EMD.mqh and with EMDloose.mqh.

Well, have to get the IMF functions to be constructed in future on the splines of the last real point of the time series. In this case, the forecasting depth will have a physical (applied) constraint, since cubic splines, if they are not reconstructed, tend to infinity. This is not critical, since the forecasting depth should be limited by seceral bars at the very beginning.

The point of the changes is to save the length of the initial time series in the variable of the object, not locally in the decomp method.

  class CEMD
  {
    private:
      int N;       // Input and output data size
      int Nf;      // +
      
    public:
        int decomp(const double &y[], const int extrapolate = 0)
        {
          ...
          N = ArraySize(y);
          Nf = N;                            // + preserve actual number of input data points in the object
          N += extrapolate;                  // +
          ...
        }
  };

Then we can use variable Nf inside the extrema method, having substituted it for the increased N at relevant locations. Thus, only real extremums originating from the initial time series will be taken into consideration. It is easiest to see all changes using the context comparison of files EMD.mqh and EMDloose.mqh.

In fact, this completes the forecast algorithm. One more small step to go regarding obtaining the decomposition results. In class CEMD, method getIMF is meant for this. Initially, 2 parameters were passe into it: Destination array — x and the number of the requested IMF harmonics — nn.

  void CEMD::getIMF(double &x[], const int nn, const bool reverse = false) const
  {
    ...
    if(reverse) ArrayReverse(x); // +
  }

Here the optional parameter reverse is added, with which you can sort the array in reversed order. This is necessary to ensure working with indicator buffers, for which time-series-like indexing is convenient (0th element is the most recent).

This complete the expanding of the CEMD class for forecasting purposes, so we can go ahead with implementing an EMD-based indicator.

Indicator EMD.mq5

For demonstration purposes, the indicator will directly work with quotes; however, this approach is not exactly suitable for absolute real trading. Forecasting a price series using extrapolation suggests, at least, a news filter to eliminate strong external influences on the forecasting horizon. For shorter timeframes, night flat is probably the first choice. Besides, we can recommend longer timeframes as less sensitive to noise, or balanced synthetic baskets of several instruments.

Let us define the inputs of the indicator:

  input int Length = 300;  // Length (bars, > 5)
  input int Offset = 0;    // Offset (0..P bars)
  input int Forecast = 0;  // Forecast (0..N bars)
  input int Reconstruction = 0; // Reconstruction (0..M IMFs)

Parameters Offset and Length set the offset and the number of bars for the series to be analyzed. To facilitate the analysis of forecasts on history, parameter Offset is also presented in the interface by a dashed vertical line you can drag with the mouse within the chart and recompute the forecast interactively (note that computations may take considerable amount of time depending on the series length and shape and on the processor performance).

Parameter Forecast — number of bars to be forecasted. For rigorous algorithm EMD.mqh, it is not recommended to take a value exceeding 5-10. Larger values are allowed for the simplified algorithm EMDloose.mqh.

Parameter Reconstruction defines the number of the IMF functions that can be omitted in reconstructing the time series, so that other ones will form the forecast. If 0 is specified here, the reconstruction will completely coincide with the initial series, and forecasting is impossible (basically, it is equal to the constant — the last price value and, therefore, is meaningless). If it is set to 1, the reconstruction will get smoothed due to omitting the smallest oscillations; if 2, then two highest harmonics will be omitted, etc. If we enter a number equalling to the number of the IMF functions found, the reconstruction will coincide with the remainder ("trend"). In all those cases, the smoothed series has a forecast (its own for each combination of the number of IMFs). If a number exceeding the number of IMFs is set, then the reconstruction and forecast are undeterminate. Recommended value for this parameter is 2.

The lesser the value of Reconstruction is, the more movable and close to the initial series the reconstruction will be (it's like a short-period MA), but the forecast will be very volatile. The higher this value is, the smoother and more stable the reconstruction and forecast will be (like a longer-period MA).

In the OnInit handler, we will set the offset of buffers according to the forecasting depth.

  int OnInit()
  {
    IndicatorSetString(INDICATOR_SHORTNAME, "EMD (" + (string)Length + ")");
    for(int i = 0; i < BUF_NUM; i++)
    {
      PlotIndexSetInteger(i, PLOT_DRAW_TYPE, DRAW_LINE);
      PlotIndexSetInteger(i, PLOT_SHIFT, Forecast);
    }
    return INIT_SUCCEEDED;
  }

Indicator is computed on open prices in the bar-by-bar mode. Here are the key points of the OnCalculate handler.

We are defining the local variables and setting the indexing of the Open and Time used as the timer series.

  int OnCalculate(const int rates_total,
                  const int prev_calculated,
                  const datetime& Time[],
                  const double& Open[],
                  const double& High[],
                  const double& Low[],
                  const double& Close[],
                  const long& Tick_volume[],
                  const long& Volume[],
                  const int& Spread[])
  {

    int i, ret;
    
    ArraySetAsSeries(Time, true);
    ArraySetAsSeries(Open, true);

Ensuring the bar-by-bar mode.

    static datetime lastBar = 0;
    static int barCount = 0;
    
    if(Time[0] == lastBar && barCount == rates_total && prev_calculated != 0) return rates_total;
    lastBar = Time[0];
    barCount = rates_total;

Waiting for the sufficient amount of data.

    if(rates_total < Length || ArraySize(Time) < Length) return prev_calculated;
    if(rates_total - 1 < Offset || ArraySize(Time) - 1 < Offset) return prev_calculated;

Initializing the indicator buffers.

    for(int k = 0; k < BUF_NUM; k++)
    {
      buffers[k].empty();
    }

Distributing the local array, yy, to pass the initial series into the object and then get the results.

    double yy[];
    int n = Length;
    ArrayResize(yy, n, n + Forecast);

Filling in the array with the time series to analyze.

    for(i = 0; i < n; i++)
    {
      yy[i] = Open[n - i + Offset - 1]; // we need to reverse for extrapolation
    }

Starting the EMD algorithm using the appropriate object.

    CEMD emd;
    ret = emd.decomp(yy, Forecast);
    
    if(ret < 0) return prev_calculated;

In case of success, reading the data obtained — primarily, the number of the IMF functions and the mean value.

    const int N = emd.getN();
    const double mean = emd.getMean();

Expanding array yy, into which we will write the points of each function for future bars.

    n += Forecast;
    ArrayResize(yy, n);

Setting up visualization: Initial series, reconstruction, and forecast are displayed with bold lines, all other individual IMFs with fine lines. Since the number of IMFs changes dynamically (depending on the shape of the initial series), this setting cannot be performed once in OnInit.

    for(i = 0; i < BUF_NUM; i++)
    {
      PlotIndexSetInteger(i, PLOT_SHOW_DATA, i <= N + 1);
      PlotIndexSetInteger(i, PLOT_LINE_WIDTH, i == N + 1 ? 2 : 1);
      PlotIndexSetInteger(i, PLOT_LINE_STYLE, STYLE_SOLID);
    }

Displaying the initial time series in the last buffer (for controlling the data transferred only, since, in practice, we don't need it, for instance, from the EA code).

    emd.getIMF(yy, 0, true);
    if(Forecast > 0)
    {
      for(i = 0; i < Forecast; i++) yy[i] = EMPTY_VALUE;
    }
    buffers[N + 1].set(Offset, yy);

Distributing array sum for the reconstruction (sums of IMFs). In the loop, searching through all IMFs involved in the reconstruction and summing up the counts in this array. At the same time, putting each IMF into its own buffer.

    double sum[];
    ArrayResize(sum, n);
    ArrayInitialize(sum, 0);
  
    for(i = 1; i < N; i++)
    {
      emd.getIMF(yy, i, true);
      buffers[i].set(Offset, yy);
      if(i > Reconstruction)
      {
        for(int j = 0; j < n; j++)
        {
          sum[j] += yy[j];
        }
      }
    }

The second-to-last buffer takes the remainder and is displayed as a dotted line.

    PlotIndexSetInteger(N, PLOT_LINE_STYLE, STYLE_DOT);
    emd.getIMF(yy, N, true);
    buffers[N].set(Offset, yy);

In fact, buffers from the first to the second-to-last one contain all the decomposition harmonics in ascending order (the small ones first, then larger ones, up to the "trend").

Finally, completing the summation of the components by the counts in array sum, obtaining the final reconstruction.

    for(int j = 0; j < n; j++)
    {
      sum[j] += yy[j];
      if(j < Forecast && (Reconstruction == 0 || Reconstruction > N - 1)) // completely fitted curve can not be forecasted (gives a constant)
      {
        sum[j] = EMPTY_VALUE;
      }
    }
    buffers[0].set(Offset, sum);
    
    return rates_total;
  }

Displaying the sum together with the forecast in the zero buffer. Zero index is chosen to facilitate reading from EAs. Number of IMFs and buffers involved usually changes with a new bar coming in, so the other indexes of buffers are variable.

Some nuances are omitted in the article, regarding how to format labels and interactively work with the history offset line. Full source code is attached at the end of the article.

The only noteworthy nuance is related to that, when changing the offset of the Offset parameter using a vertical line, the indicator requests updating the chart by calling ChartSetSymbolPeriod. This function is implemented in MetaTrader 5 in such a manner that it resets the caches of all timeframes of the current symbol and rebuilds them again. Depending on the setting selected by the number of bars in the charts and on the computer performance, this process may take a remarkable time (in some cases, dozens of seconds, if there are, for instance, M1 charts with millions of bars). Unfortunately, MQL API does not provide any more efficient method of rebuilding an individual indicator. In this connection, in case this issue occurs, it is recommended to change the offset via the indicator properties dialog or decrease the number of the bars displayed on charts (terminal should be restarted). Vertical cursor line is added to ensure easy and precise positioning in the anticipated beginning of the data sample.

Let us check how the indicator works in the strict mode and in the simplified mode with the same settings (it is worth reminding that the simplified mode is obtained by recompiling with the EMDloose.mqh file, since it is not the main working mode). For EURUSD D1, we use the following settings:

• Length = 250;
• Offset = 0;
• Forecast = 10;
• Reconstruction = 2;

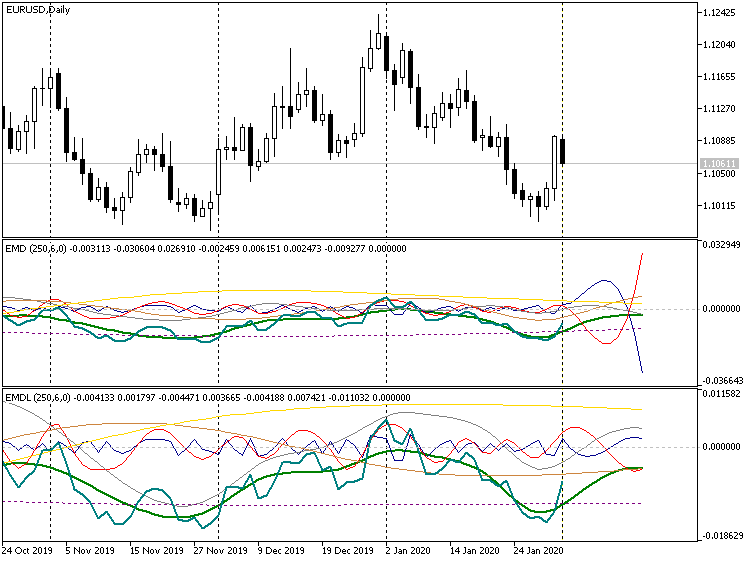
Short forecast, indicators EMD, EURUSD D1

2 indicator versions are shown in the screenshot above, the strict one on the top and the simplified one in the bottom. Note that, in the strict version, some harmonics tend to "run away" in different directions, up and down. This is why even the scale of the first indicator has become smaller than that of the second one (rescaling is a visual warning of the forecast depth inadequacy). In the simplified mode, all the decomposition components continue hovering around zero. This can be used to obtain a longer-term forecast by setting, for example, the value of 100 in the Forecast parameter. It looks nice, but usually far remote from reality. The only application of such a forecast seems to be the estimation of the future price movement range where you can try to trade on bounce inwards or on breakout.

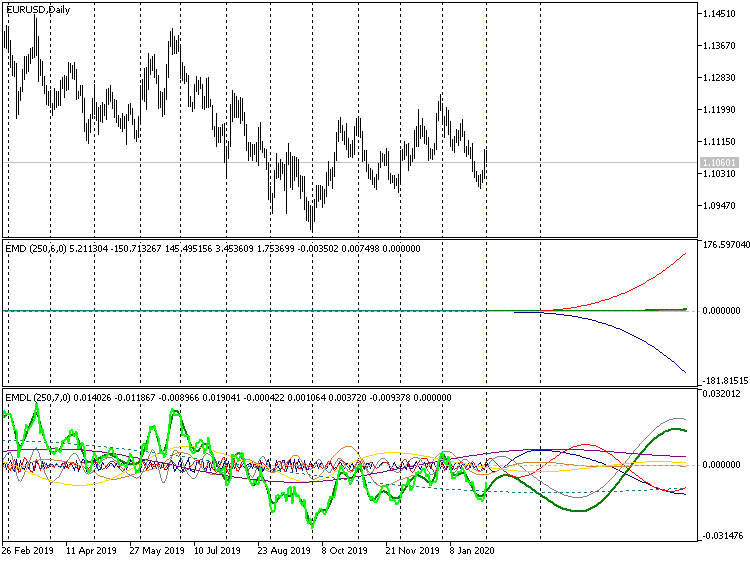
Long forecast, indicators EMD, EURUSD D1

In the strict version, this results in what we can only see the ends of the polynomials diverging into infinity, while the informative part of the chart has "collapsed" around zero.

In case of the increased forecast horizon, differences can be seen in the heading of indicators: Where initially, in both cases, 6 own functions were found (the second number in parentheses, after the amount of bars to be analyzed), then the simplified version is now using 7 ones, since, in its case, the 100 bars requested for forecasting participate in the computations of extremums. Forecasting on 10 bars does not provide such an effect (for this time series). We can suggest that Forecast = 10 is the maximum allowed but not recommended forecast length. Recommended length is 2-4 bars.

For visual reference of the reconstructed initial time series and forecast, it is easy to create a similar indicator directly displayed on the price chart, EMDPrice. Its internal structure completely follows that of the EMD indicator considered, but there is only one buffer (some IMFs are involved into computations, but not displayed to avoid overcharging the chart).

In EMDPrice, we use a short form of the OnCalculate handler, which allows us to choose the price type for computations, such as typical one, for instance. However, for any open price type, it should be taken into consideration that the indicator is computed on opening bars and, therefore, it is bar 1 that is the last formed one (i.e., having all price types). In other words, Offset can only be 0 for open prices, while in other cases, it must be at least 1.

In the screenshot below, you can see how indicator EMDPrice works with an offset to the past by 15 bars.

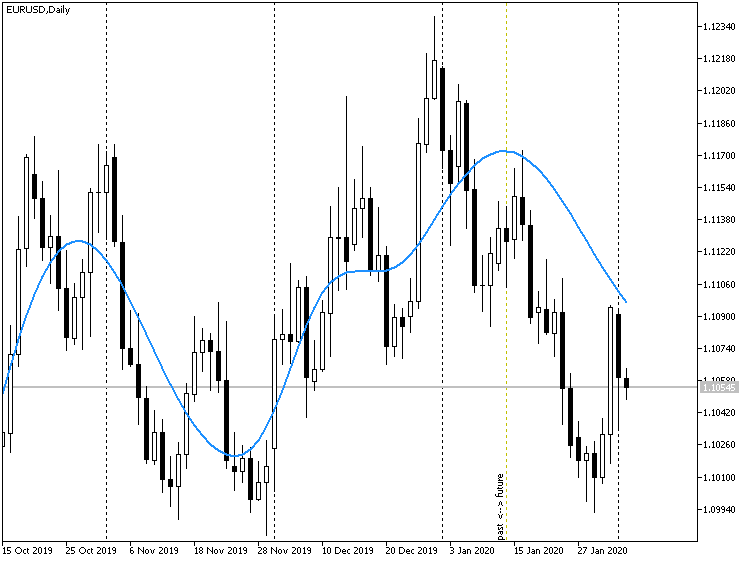
EMDPrice indicator forecast on price chart EURUSD D1, set off on history

To test the EMD indicator forecasting ability, we are going to develop a special EA.

EMD-Based Test Expert Advisor

Let us create a simple EA, TestEMD, that will create an instance of the EMD indicator and trade based on its forecasts. It will work on bar opening, since the indicator uses open prices to forecast.

Basic inputs of the EA:

• Length — time series length to be passed to the indicator;
• Forecast — number of forecast bars, to be passed to the indicator;
• Reconstruction - number of smaller harmonics to be omitted in reconstructing the forecast, to be passed to the indicator;
• SignalBar - bar number, for which the forecast value is requested from the indicator buffer.

As trading signal, we take the difference between the indicator values on the SignalBar (this parameter should be negative to look into the future to be forecasted) and on the current zero bar. Positive difference is buy signal, while the negative one is sell signal.

Since indicator EMD builds a forecast for the future, the bar numbers in SignalBar are usually negative and equal in absolute values to the values of Forecast (basically, the signal can also be taken from a less remote bar; however, in that case, it is unclear why to compute a forecast for a larger number of bars). This is a case of normal working mode when performing trade operations. In this mode, when indicator EMD is called, its Offset parameter is always zero, since we do not study any forecasts on history.

However, the EA also supports another, special non-trading mode that allows rapidly performing an optimization due to the theoretical computations of the profitability of virtual transactions on the last Forecast bars. The computation is performed sequentially on each new bar within the selected date range, and the general statistics, in form of the profit-factor of multiplying the forecast by the real price movement, is returned from OnTester. In Tester, you should select the Custom optimization criterion as the optimization price. Enter 0 to include this mode into the SignalBar parameter. At the same time, the EA itself will automatically set Offset equal to Forecast. This is exactly what allows the EA to compare the forecast and the price change on the last Forecast bars.

Of course, the EA can be optimized in the normal operation mode, together with performing trade operations and choosing any embedded optimization index. This is particularly true, because the cost-effective non-trading mode is rather rough (particularly, it does not consider spreads). However, the maximums and minimums of both fitness functions must be roughly the same.

Since a forecast can be made on several bars ahead and the relevantly directed position will be opened for the same period of time, opposedly directed positions can exist at the same time. For example, if Forecast is 3, then each position is held within the market for 3 bars, and 3 positions are open at each moment, being of different types. In this regard, a hedging account is necessary.

Full source code of the EA is attached to the article and is not described in details here. Its trading part is based on the MT4Orders library that facilitates calling trade functions. In the EA, there is no "friend-or-foe" control of orders using magic numbers, strict error processing, or setup for slippages, StopLosses and TakeProfits. The fixed lot size is set in the Lot input parameter, and it trades with market orders. If you wish to use EMD in working EAs, you can expand this test EA with the relevant functions, where necessary, or insert the part working with the EMD indicator in a similar manner to your existing EAs.

Exemplary settings for optimization are attached to the article as the TestEMD.set file. Optimization on EURUSD D1 for the year 2018 in the accelerated mode provides the following optimal "set":

• Length=110
• Forecast=4
• Reconstruction=2

Accordingly, SignalBar must be equal to minus Forecast, i.e., -4.

A single test with these settings for the period from early 2018 up to February 2020, i.e., with a forward for the year 2019 and early 2020, paints the following picture:

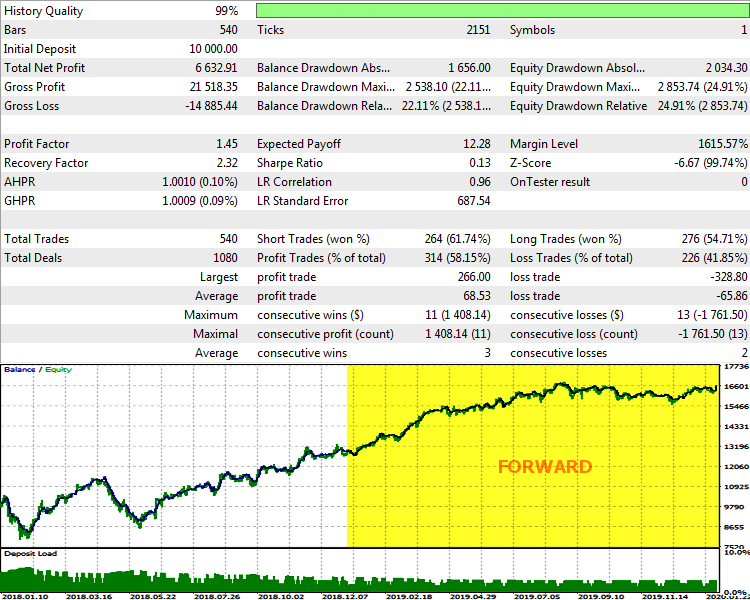
TestEMD report on EURUSD D1, 2018-2020

As we can see, the system benefits, although the indices show that there is a room for improvement. Particularly, it is logical to assume that more frequent reoptimization in a step-by-step mode and search for the step size can improve the performance of the robot.

Basically, it can be said that the EMD algorithm allows identifying on larger timeframes the fundamental, in some sense momentum fluctuations of quotes and create a profitable trading system based thereon.

EMD is not the only technology that we are going to considere herein. However, before going to the second part, we will have to "refresh" some math for studying time series.

Analysis of the Main Characteristics of Time Series in MQL — Indicator TSA

On the mql5.com website, there was already published an article titled similarly: Analysis of the Main Characteristics of Times Series. It provides a detailed consideration to computing values, such as average, median, dispersion, skewness and kurtosis factors, distribution histogram, auto correlation functions, partial autocorrelation, and much more. All this is gathered into the TSAnalysis class in the TSAnalysis.mqh file that is then used for demonstration purposes in the TSAexample.mq5 script. Unfortunately, to visualize the class performance, the approach was applied with generating an external HTML file that has to be analyzed in browser. At the same time, MetaTrader 5 provides various graphic tools to display data arrays, most significantly indicator buffers. We are going to slightly modify the class and make it more "friendly" towards indicators, whereafter we will implement an indicator that allows analyzing quotes directly in the terminal.

We will name the new file with the class TSAnalysisMod.mqh. The main operation principle remains the same: Using the Calc method, a time series is passed into the object, for which times series the entire set of indices is computed during processing. They all are divided into 2 types — scalar ones and arrays. The calling code can then read any of the characteristics.

Let us bring scalar characteristics together in a single structure of TSStatMeasures:

  struct TSStatMeasures
  {
    double MinTS;      // Minimum time series value
    double MaxTS;      // Maximum time series value
    double Median;     // Median
    double Mean;       // Mean (average)
    double Var;        // Variance
    double uVar;       // Unbiased variance
    double StDev;      // Standard deviation
    double uStDev;     // Unbiaced standard deviation
    double Skew;       // Skewness
    double Kurt;       // Kurtosis
    double ExKurt;     // Excess Kurtosis
    double JBTest;     // Jarque-Bera test
    double JBpVal;     // JB test p-value
    double AJBTest;    // Adjusted Jarque-Bera test
    double AJBpVal;    // AJB test p-values
    double maxOut;     // Sequence Plot. Border of outliers
    double minOut;     // Sequence Plot. Border of outliers
    double UPLim;      // ACF. Upper limit (5% significance level)
    double LOLim;      // ACF. Lower limit (5% significance level)
    int NLags;         // Number of lags for ACF and PACF Plot
    int IP;            // Autoregressive model order
  };

We will denote the arrays by the enumerators of TSA_TYPE:

  enum TSA_TYPE
  {
    tsa_TimeSeries,
    tsa_TimeSeriesSorted,
    tsa_TimeSeriesCentered,
    tsa_HistogramX,
    tsa_HistogramY,
    tsa_NormalProbabilityX,
    tsa_ACF,
    tsa_ACFConfidenceBandUpper,
    tsa_ACFConfidenceBandLower,
    tsa_ACFSpectrumY,
    tsa_PACF,
    tsa_ARSpectrumY,
    tsa_Size //  
  };        //  ^ non-breaking space (to hide aux element tsa_Size name)

To obtain a complete structure of TSStatMeasures with the work results, the getStatMeasures method is provided. To obtain any of the arrays using macros, methods of the same type are generated, appearing as getARRAYNAME, where ARRAYNAME corresponds with the suffix of one of the enumerators of TSA_TYPE. For example, to read a sorted times series, you should call the getTimeSeriesSorted method. All such methods have signature:

  int getARRAYNAME(double &result[]) const;

fill in the array passed, and return the number of elements.

Moreover, there is a universal method to read any array:

  int getResult(const TSA_TYPE type, double &result[]) const

Virtual method show is completely removed from the original class, as useless. Complete control of all interface-related tasks is given to the calling code.

It is convenient to process codes using the TSAnalysis class from a special indicator — TSA.mq5. Its main goal is to visualize characteristics representing arrays. If you wish, you can add to it an option of displaying scalar values, if necessary (they are printed to log now).

Since some arrays are logically interconnected in triples (for example, auto correlation function has an upper and a lower limit of 95-% confidence interval), 3 buffers are reserved in the indicator. Display styles of buffers dynamically adjust depending on the meaning of the data requested.

Indicator input parameters:

• Type — type of the requested array, enumerator TSA_TYPE;
• Length — length in bars of the analyzed times series;
• Offset — initial offset of the time series, 0 - starting point;
• Differencing — differencing mode that defines whether it should read quotes as they are or take the first-order difference;
• Smoothing — averaging period;
• Method — method of averaging;
• Price — price type (Open price by default);

Indicator is computed by bars.

This is an example of how the partial auto correlation function looks for EURUSD D1 on 500 bars, with differencing:

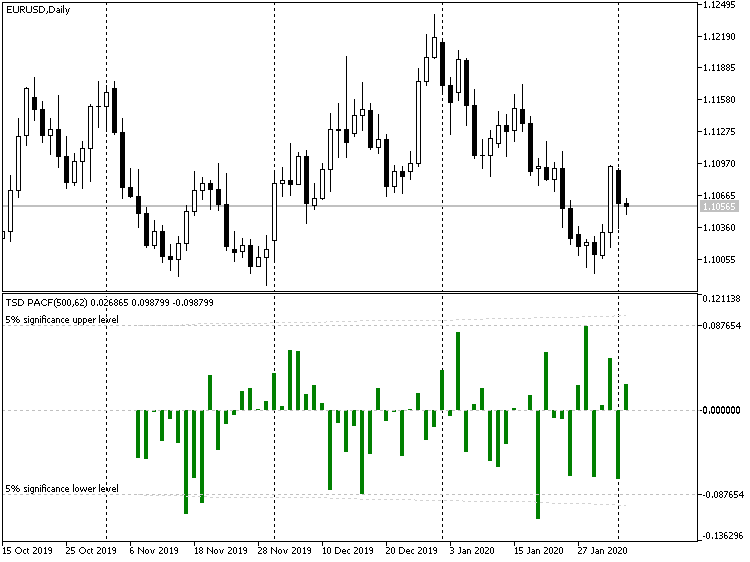
Indicator TSD, EURUSD D1

Taking the first-order differences allows increasing the stationarity (and predictability) of a series. Basically, the second-order difference will be even more stationary, the third-order one — even more, etc. However, this has its minus sides, which will be discussed later (in Part 2).

Partial autocorrelation function is not chosen by mere chance here either. We will need it at the next stage, when we go to another forecasting method. However, since we will have to study quite a large amount of materials, we have used this preparatory chapter to write this article. Moreover, statistical analysis of time series represents a universal value and can be used in other custom developments in MQL.

Conclusions

In this article, we have considered the special aspects of the empiric mode decomposition algorithm, which allow us to expand its applicability to the area of the short-term forecasting of time series. Classes, indicators and EA implemented in MQL allow using EMD-forecasting as an additional factor in making trading decisions, as well as as a part of automated trading systems. Moreover, we have updated the toolkit to perform the statistical analysis of time series, which we will need in our next article to consider forecasting by the LS-SVM method.