
预测时间序列(第 1 部分):经验分解模式(EMD)方法
概述
任何交易者的成功主要取决于他或她“透视未来”的能力,即推测一段时间周期后价格如何变化的能力。 为了解决这个问题,重要的是要拥有各种类的工具和功能,从基准市场特征的最新更新,到技术分析算法。 运用时间序列预测的数学方法、价格本身亦或技术指标两者、波动率、宏观经济指数、交易投资组合余额、或其他能够充当此类时间序列的方法,可以在某种程度上增强所有这些目标。
预测是一个涉及面很广的话题,它已在 mql5.com 网站上被多次言及。 预测财经时间序列早在 2008 年既已发表,是首先探讨且内容严谨的文章之一。 代码库当中的许多其他文章和出版物中,有众多支持 MetaTrader 的工具,例如:
- "利用指数平滑进行时间序列预测".
- 利用时间线的动态变换(WmiFor+DTW)搜索历史记录中的相似形态;
- (误差)反馈神经网络 (BPNN);
- Kohonen 神经网络 (SOM);
您可以通过搜索网站上的相关板块(文章,代码库)获得完整列表。
出于此目的,我们再将已有预测工具列表扩展两个新内容。 其中第一个是基于经验模式分解(EMD)方法,在标题为经验模式分解简介的文章中已探讨过该方法,但未将其用于预测。 本文的第一部分将研究 EMD。
第二个工具利用支持向量机(SVM)方法,版本为最小二乘支持向量机(LS-SVM)。 我们将其定位于第二部分中。
基于 EMD 的预测算法
您可以在经验模式分解方法简介中找到有关 EMD 技术的详细介绍。 它与将时间序列分解为缕有关 — 所谓的本征模式函数(IMF)。 每种形式都是时间序列最大值和最小值的样条插值,首先在初始序列里搜索极值。 然后从中推导出刚刚找到的 IMF,然后对修改后序列的极值执行样条插值,依此继续构造若干个 IMF,直至余者低于指定的噪声等级。 直观地看,结果类似于傅立叶级数展开;然而,与后者不同,典型的 EMD 形式不是由频率决定的谐波振荡。 所获 IMF 扩展函数的数量取决于初始序列的平滑度和算法设置。
在上面提到的文章中,出示了许多计算 EMD 的现成类,只是建议从外部 HTML 文件中获取分解结果作为图形。 我们会基于这些类编写必要的补充代码,从而令算法具有预测性。
文章附带了 2 个文件:CEMDecomp.mqh 和 CEMD_2.mqh。 第二个版本基于第一个略微改进,故我们在此直入第二个。 我们将其复制为新名称 EMD.mqh,并将其包含在指标 EMD.mq5 当中,无需做任何更改。
#include <EMD.mqh>
我们还将利用特殊类来简化指标缓冲区数组的声明,即 IndArray.mqh(其英文说明可在博客中找到,其当前版本已附于文末)。 我们会需要很多缓冲区,并将以统一的方式对其进行处理。
#define BUF_NUM 18 // 16 IMF maximum (including input at 0-th index) + residue + reconstruction #property indicator_separate_window #property indicator_buffers BUF_NUM #property indicator_plots BUF_NUM #include <IndArray.mqh> IndicatorArray buffers(BUF_NUM); IndicatorArrayGetter getter(buffers);
如上所示,该指标显示在一个单独的窗口中,并预留了 18 个缓冲区以供显示:
- 初始序列;
- 将其分解为 16 个分量(大概不会用到全部);
- 余数(“趋势”); 和
- 重构。
最后一项最有趣。 问题是,在获得 IMF 函数之后,我们可以对其中的一些(但不是全部)求和,并获得初始序列的平滑版本。 平滑重构不会作为预测的来源,因为它是已知样条的累加,可据其外推尚未出现的柱线(样条外推)。 然而,预测深度应限制在若干根柱线之内,因为已发现的 IMF 会随着远离最后已知点而变得无关紧要。
但回到文件 EMD.mqh。 其中定义了 CEMD 类,该类执行所有操作。 调用 decomp 方法会启动该过程,需向该方法传递时间序列计数数组 y。 正是该数组的大小确定了相应函数 IMFResult 的长度 N。 方法 arrayprepare 准备计算它们所需的后备数组:
class CEMD { private: int N; // Input and output data size double IMFResult[]; // Result double X[]; // X-coordinate for the TimeSeries. X[]=0,1,2,...,N-1. ... public: int N; // Input and output data size double Mean; // Mean of input data ... int decomp(double &y[]) { ... N = ArraySize(y); arrayprepare(); for(i = 0; i < N; i++) X[i] = i; Mean = 0; for(i = 0; i < N; i++) Mean += (y[i] - Mean) / (i + 1.0); // Mean (average) of input data for(i = 0; i < N; i++) { a = y[i] - Mean; Imf[i] = a; IMFResult[i] = a; } // The loop of decomposition ... extrema(...); ... ... } private: int arrayprepare(void) { if(ArrayResize(IMFResult, N) != N) return (-1); ... } };
为了增加参考点的数量,我们将为 decomp 方法添加新参数、外推法、定义预测深度。 我们在外推时按请求的计数值增加 N,初始序列的实际长度会预先保存在局部变量 Nf 之中(在代码里,“+” 和 “*” 标记,分别代表附加和修改)。
int decomp(const double &y[], const int extrapolate = 0) // * { ... N = ArraySize(y); int Nf = N; // + preserve actual number of input data points N += extrapolate; // + arrayprepare(); for(i = 0; i < N; i++) X[i] = i; Mean = 0; for(i = 0; i < Nf; i++) // * was N Mean += (y[i] - Mean) / (i + 1.0); for(i = 0; i < N; i++) { a = y[MathMin(i, Nf - 1)] - Mean; // * was y[i] Imf[i] = a; IMFResult[i] = a; } // The loop of decomposition ... extrema(...); ... for(i = 0; i < N; i++) { IMFResult[i + N * nIMF] = IMFResult[i]; IMFResult[i] = y[MathMin(i, Nf - 1)] - Mean; // * was y[i] } }
基于所要预测的柱线构造 IMF 时,要从时间序列的最后一个已知值开始。
这些便是预测所需的所有修改。 附件 EMDloose.mqh 文件中展示了我们得到的完整代码。 但为什么是 EMDloose.mqh,而非 EMD.mqh 呢?
问题在于这种预测方法不十分准确。 由于我们增加了对象所有数组的大小 N,而它包含搜索极值所需的预测柱线,搜索则是在 extrema 方法里执行。 从技术上讲,未来没有极值。 计算过程中形成的所有极值,都是样条外推的总和(无需未来不存在的初始序列)。 结果就是,样条函数开始彼此调整,试图令它们的堆叠平滑。 从某种意义上说,这很方便,因为预测获得了自平衡 — 振荡过程保持在时间序列值附近,且不会趋向无穷大。 不过,如此预测的价值微乎其微 — 它不再表征初始时间序列。 然而,采用该方法无需顾虑,且那些希望采用它的人,要确切地将 EMDloose.mqh 包含在项目中。
为了解决该问题,我们将进行更多修改,并得到 EMD.mqh 的最终工作版本。 为了比较两种预测方法达成的效果,我们后续将验证指标如何与 EMD.mqh 和 EMDloose.mqh 一起操作。
好吧,将来必须依据时间序列最后一个真实点的样条曲线上构建 IMF 函数。 在这种情况下,预测深度将受到物理性(应用的)约束,因为三次样条,若它们未重建,则会趋于无穷大。 这并不重要,因为在最开始时,预测深度就应受到若干柱线的限制。
修改的要点在于将初始时间序列的长度保存在对象的变量中,而非位于 decomp 方法之中。
class CEMD { private: int N; // Input and output data size int Nf; // + public: int decomp(const double &y[], const int extrapolate = 0) { ... N = ArraySize(y); Nf = N; // + preserve actual number of input data points in the object N += extrapolate; // + ... } };
然后,我们可以在 extrema 方法内使用变量 Nf,用它代替相关位置上增加的 N。 故此,只有源自初始时间序列的真实极值才会被考虑。 将文件 EMD.mqh 和 EMDloose.mqh 进行上下文比较,是观察所有修改的最简洁方式。
实际上,至此已完成了预测算法。 有关获得分解结果,还需要再走一小步。 在 CEMD 类之中,getIMF 方法是为此目的。 最初,向其中传递了 2 个参数:目标数组 — x,和 IMF 谐波请求数量 — nn。
void CEMD::getIMF(double &x[], const int nn, const bool reverse = false) const { ... if(reverse) ArrayReverse(x); // + }
此处添加了可选参数 reverse,您可以利用该参数按逆反顺序对数组进行排序。 这对于确保指标缓冲区操控是必要的,而类似于时间序列,索引更方便(第 0 个元素是最新的)。
至此完成了利用 CEMD 类进行预测的扩展,那么我们进而可以实现基于 EMD 的指标。
指标 EMD.mq5
出于演示目的,该指标将直接协同报价操作;不过,这种方法并不完全适合绝对实盘交易。 采用外推法预测价格序列,至少,建议配合一款新闻过滤器,从而消除强大外力对预测基准线的影响。 对于较短的时间帧,夜间横盘则可能是首选。 此外,我们建议您采用较长的时间帧,因为它们对噪声的敏感度较低,或者建议采用若干种金融产品平衡协合的篮子。
我们来定义指标的输入:
input int Length = 300; // Length (bars, > 5) input int Offset = 0; // Offset (0..P bars) input int Forecast = 0; // Forecast (0..N bars) input int Reconstruction = 0; // Reconstruction (0..M IMFs)
参数 “Offset” 和 “Length” 为所分析的序列设置偏移和柱线数量。 为了便于基于历史进行预测分析,界面中以垂直虚线形式示意出参数 Offset,您可在图表中用鼠标拖动,交互式地重新计算预测(请注意,计算可能需要花费大量时间,具体取决于序列 长度、形状,以及处理器性能)。
参数 Forecast — 预测的柱线数量。 对于严格的算法 EMD.mqh,建议取值不要超过 5-10。 简化算法 EMDloose.mqh 允许使用较大的值。
参数 Reconstruction 定义重构时间序列时可以省略的 IMF 函数的数量,如此其余部分即可形成预测。 如果此处指定 0,则重构将与初始序列完全一致,且不能进行预测(基本上,它等于一个常数 — 最后的价格值,因此这没意义)。 如果将其设置为 1,则由于忽略了最小的振荡,因此重构会变得更平滑;如果为 2,则将忽略两个最高谐波,依此类推。 如果输入的数字等于发现的 IMF 函数的数目,则重构将同余者吻合(“趋势”)。 在所有这些情况下,平滑后的序列都有一个预测(对于 IMF 的每种组合都有其预测)。 如果设置的数量超过 IMF 的数量,则重构和预测不确定。 此参数的建议值为 2。
Reconstruction 的值越小,则重构越容易移动,并接近初始序列(就像短线 MA),但预测会波动较大。 该值越高,重构和预测会越平滑、越稳定(就像长线 MA)。
在 OnInit 处理程序中,我们将根据预测深度设置缓冲区的偏移量。
int OnInit() { IndicatorSetString(INDICATOR_SHORTNAME, "EMD (" + (string)Length + ")"); for(int i = 0; i < BUF_NUM; i++) { PlotIndexSetInteger(i, PLOT_DRAW_TYPE, DRAW_LINE); PlotIndexSetInteger(i, PLOT_SHIFT, Forecast); } return INIT_SUCCEEDED; }
指标是在逐根柱线模式下,以开盘价计算的。 这是 OnCalculate 处理程序的关键点。
我们正在定义局部变量,并为时间序列“开盘价”和“时间”设置索引。
int OnCalculate(const int rates_total, const int prev_calculated, const datetime& Time[], const double& Open[], const double& High[], const double& Low[], const double& Close[], const long& Tick_volume[], const long& Volume[], const int& Spread[]) { int i, ret; ArraySetAsSeries(Time, true); ArraySetAsSeries(Open, true);
确保逐根柱线模式。
static datetime lastBar = 0; static int barCount = 0; if(Time[0] == lastBar && barCount == rates_total && prev_calculated != 0) return rates_total; lastBar = Time[0]; barCount = rates_total;
等待足够的数据量。
if(rates_total < Length || ArraySize(Time) < Length) return prev_calculated; if(rates_total - 1 < Offset || ArraySize(Time) - 1 < Offset) return prev_calculated;
初始化指标缓冲区。
for(int k = 0; k < BUF_NUM; k++) { buffers[k].empty(); }
分派局部数组 yy,以便将初始序列传递给对象,之后取得结果。
double yy[]; int n = Length; ArrayResize(yy, n, n + Forecast);
按照时间序列填充数组,以便进行分析。
for(i = 0; i < n; i++) { yy[i] = Open[n - i + Offset - 1]; // we need to reverse for extrapolation }
利用相应的对象启动 EMD 算法。
CEMD emd;
ret = emd.decomp(yy, Forecast);
if(ret < 0) return prev_calculated;
如果成功,则读取获得的数据 — 主要是 IMF 函数的数量和平均值。
const int N = emd.getN(); const double mean = emd.getMean();
扩展数组 yy,我们将在其内为将来的柱线写入每个函数的点数。
n += Forecast;
ArrayResize(yy, n);
设置可视化:初始系列、重建和预测均以粗线显示,所有其他 IMF 均以细线显示。 由于 IMF 的数量动态变化(取决于初始序列的形状),因此无法在 OnInit 中一次性执行此设置。
for(i = 0; i < BUF_NUM; i++) { PlotIndexSetInteger(i, PLOT_SHOW_DATA, i <= N + 1); PlotIndexSetInteger(i, PLOT_LINE_WIDTH, i == N + 1 ? 2 : 1); PlotIndexSetInteger(i, PLOT_LINE_STYLE, STYLE_SOLID); }
在最后一个缓冲区中显示初始时间序列(仅用于控制传输的数据,因为实际上,我们不需要 EA 代码中的数据)。
emd.getIMF(yy, 0, true); if(Forecast > 0) { for(i = 0; i < Forecast; i++) yy[i] = EMPTY_VALUE; } buffers[N + 1].set(Offset, yy);
为重构分派数组 sum(IMF 的总和)。 在循环中,搜索与重建有关的所有 IMF,并对该数组中的计数求和。 同时,将每个 IMF 放入其自身的缓冲区中。
double sum[]; ArrayResize(sum, n); ArrayInitialize(sum, 0); for(i = 1; i < N; i++) { emd.getIMF(yy, i, true); buffers[i].set(Offset, yy); if(i > Reconstruction) { for(int j = 0; j < n; j++) { sum[j] += yy[j]; } } }
倒数第二个缓冲区取余数,并显示为虚线。
PlotIndexSetInteger(N, PLOT_LINE_STYLE, STYLE_DOT); emd.getIMF(yy, N, true); buffers[N].set(Offset, yy);
实际上,从第一个到倒数第二个的缓冲区包含所有分解谐波,它们以升序排列(从小到大,直至“趋势”)。
最后,按数组 sum 的计数完成对分量的求和,从而获得最终的重构。
for(int j = 0; j < n; j++) { sum[j] += yy[j]; if(j < Forecast && (Reconstruction == 0 || Reconstruction > N - 1)) // completely fitted curve can not be forecasted (gives a constant) { sum[j] = EMPTY_VALUE; } } buffers[0].set(Offset, sum); return rates_total; }
在零缓冲区中显示总和,以及预测。 选择零索引是为了方便从 EA 读取。 通常,所涉及的 IMF 和缓冲区的数量会随着新柱线的变化而变化,因此缓冲区的其他索引是可变的。
在本文中忽略了一些关于如何设置标签格式,以及如何与历史偏移线交互操作的细微之处。 完整的源代码附在文章末尾。
唯一值得注意的细微差别与此相关,当使用垂直线更改 Offset 参数的偏移量时,指标会通过调用 ChartSetSymbolPeriod 请求刷新图表。 此函数按如下方式在 MetaTrader 5 中实现:重置当前品种所有时间帧的缓存,并再次重建它们。 取决于图表中柱线数量选择的设置,以及计算机性能,此过程可能会花费大量时间(在某些情况下,例如,如果 M1 图表含有数百万根柱线,则可能需要数十秒)。 不幸的是,MQL API 没有提供任何更有效的方法来重建独立指标。 在连接时,若发生此问题,建议通过指标属性对话框更改偏移量,或减少图表上显示的柱线数量(要重新启动终端)。 添加了垂直光标线,以确保在数据样本的预期起点处轻松准确地定位。
我们来查验指标在严格模式和简化模式下,按相同设置如何操作(值得提醒的是,简化模式是通过重新编译 EMDloose.mqh 文件而获得的,因为它不是主要操作模式)。 对于 EURUSD D1,我们采用如下设置:
- Length = 250;
- Offset = 0;
- Forecast = 10;
- Reconstruction = 2;
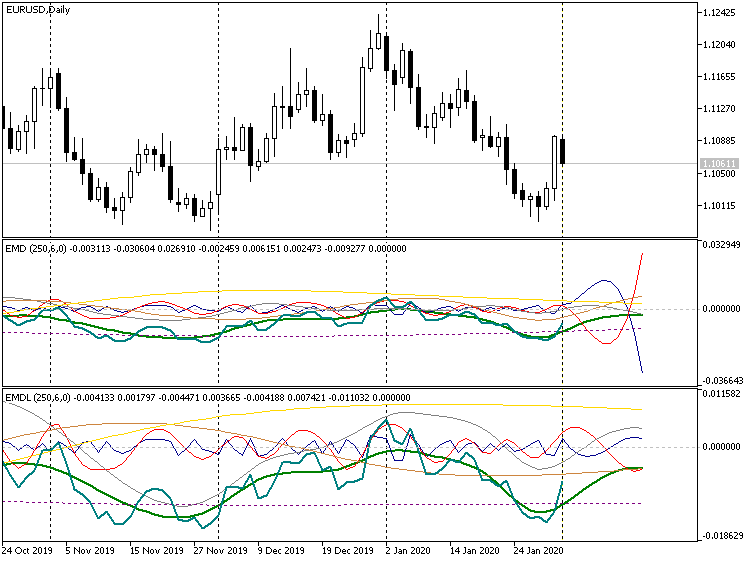
短线预测,指标 EMD,EURUSD D1
上面的屏幕截图显示了 2 个指标版本,上部是严格模式指标,下部是简化模式指标。 请注意,在严格模式版本中,某些谐波趋于在不同的方向上下波动。 这就是为什么第一个指标的刻度变得小于第二个指标的刻度(重标刻度是预测深度不足的直观警告)。 在简化模式下,所有分解分量继续在零附近徘徊。 在 “Forecast” 参数中设置例如 100 的值,可以将其用来获取长线预测。 这看起来不错,但通常离现实很远。 这种预测的唯一应用似乎是对未来价格波动范围的估测,您可以在该价格范围内尝试向内反弹、或突破时进行交易。
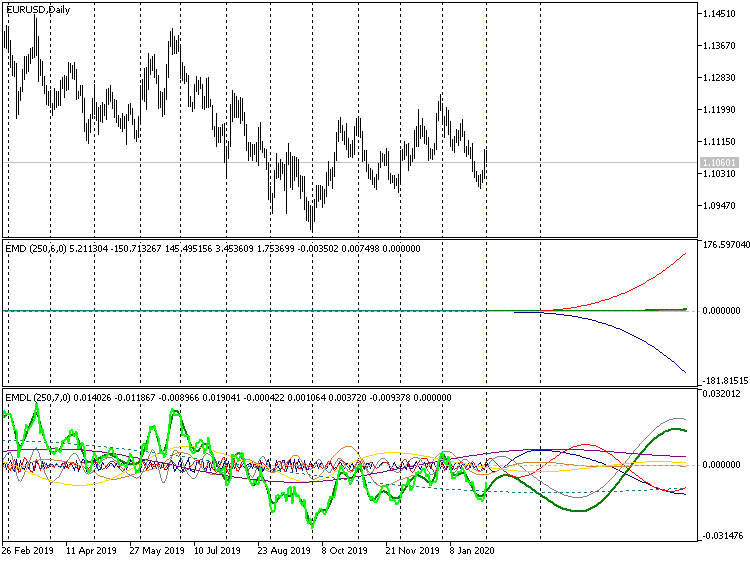
长线预测,指标 EMD,EURUSD D1
在严格模式版本中,这会导致我们只能看到多项式的末端发散到无穷大,而图表的信息部分已在零附近“崩溃”。
在增加预测范围的情况下,可以在指标的标题上看到差别:最初在两种情况下都发现了 6 个自函数(括号中的第二个数字,在所分析柱数之后),之后简化模式版本目前用到 7 个,因为在这种情况下,需要进行预测的 100 根柱线参与了极值的计算。 在 10 根柱线上进行预测不会出现这种效果(对于此时间序列)。 我们可以建议 “Forecast = 10” 是允许的最大值,但不建议预测长度。 建议长度为 2-4 根柱线。
为了直观地参考重建的初始时间序列和预测,最轻松的方式是创建一个类似于 EMDPrice 的指标,直接在价格图表上显示。 其内部结构完全遵循所研究 EMD 指标的内部结构,但只有一个缓冲区(某些 IMF 参与了计算,但为了避免图表过多故而未显示)。
在 EMDPrice 中,我们采用 OnCalculate 处理程序的简短形式,这令我们可以选择计算所用的价格类型,例如典型价格类型。 不过,对于任何开盘价格类型,都应考虑指标是基于柱线开盘价计算的,因此,最后一根完整形成的是柱线 1(即拥有所有价格类型)。 换言之,对于开盘价,“Offset” 只能为 0,而在其他情况下,必须至少为 1。
在下面的屏幕截图中,您可以看到指标 EMDPrice 如何基于偏移量为过去的 15 根柱线进行操作。
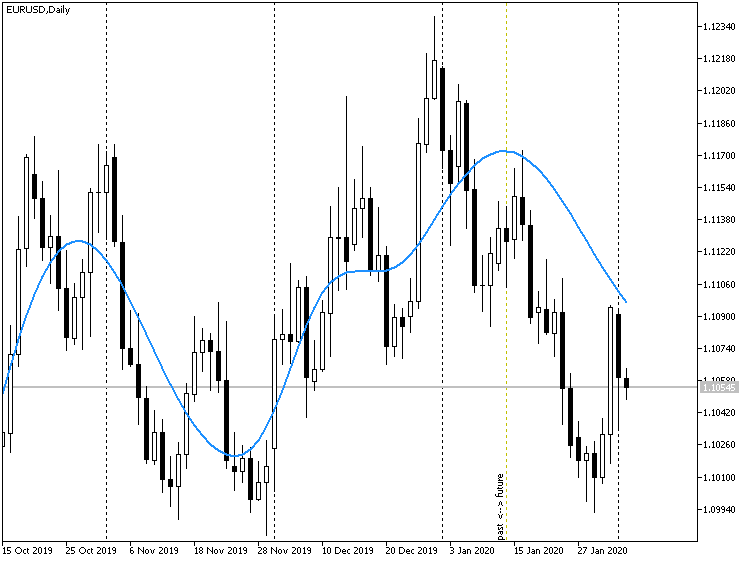
EMDPrice 指标基于价格图表 EURUSD D1 预测,设置历史记录偏移量
为了测试 EMD 指标的预测能力,我们将开发一款特殊的 EA。
基于 EMD 的测试智能交易系统
我们创建一个简单的 EA,TestEMD,它将创建 EMD 指标的实例,并据其预测进行交易。 由于它于柱线开盘时进行预测,因此指标将采用开盘价预测。
EA 的基本输入:
- Length — 传递给指标的时间序列长度;
- Forecast — 传递给指标的预测柱数量;
- Reconstruction - 传递给指标的重构预测时要忽略的较小谐波数;
- SignalBar - 柱线编号,从指标缓冲区请求其预测值。
我们取 SignalBar 上的指标值(此参数应为负值,以便查看未来的预测)与当前零号柱线之间的差值作为交易信号。 差值为正值是买入信号,为负值则是卖出信号。
由于指标 EMD 建立对未来的预测,因此 SignalBar 中的柱号通常为负,并且绝对值与 Forecast 值相等(基本上,信号也可以取自不太远的柱线;然而,在此情况下, 目前尚不清楚为什么要基于较大柱线数量计算预测)。 在执行交易操作时,这是正常操作模式的情况。 在该模式下,调用指标 EMD 时,其 Offset 参数始终为零,因为我们不探究任何基于历史记录的预测。
不过,EA 还支持另一种特殊的非交易模式,即基于最后的预测柱线进行虚拟交易,并对其获利能力进行理论计算,因此可以快速执行优化。 在选定的日期范围内,针对每根新柱线依次执行计算,将预测值乘以实际价格走势的利润因子,以该形式生成常规统计信息,并从 OnTester 返回。 在测试器中,您应该选择自定义优化条件作为优化价格。 输入 0,将该模式包含在 SignalBar 参数中。 同时,EA 会自动将 “Offset” 设置为等于 “Forecast”。 这正是令 EA 拿预测值与最后所预测柱线上价格变化进行比较的原因。
当然,EA 可以在正常操作模式下进行优化,同时可以执行交易操作,并选择任何嵌入式优化指数。 这一点尤其真实,因为具有成本效益的非交易模式相当粗糙(特别是,它不考虑点差)。 不过,两个适应度函数的最大值和最小值必须大致相同。
由于可基于之前的若干根柱线进行预测,且在相同时间段内开立同向持仓,故逆向持仓可以同时存在。 例如,如果 “Forecast” 为 3,则每笔持仓在场内持有 3 根柱线,那么每一时刻就有 3 笔持仓分属不同类型。 有关于此,需有一个对冲账户。
文章附带了 EA 的完整源代码,故于此不再赘述。 它的交易部分基于 MT4Orders 函数库,该函数库有助于调用交易功能。 在 EA 中,未利用魔幻数字进行“敌我”订单控制,也没有严格的错误处理,或设定滑点、止损和止盈。 在 “Lot” 输入参数中设置了固定的手数大小,并按市价单进行交易。 若您希望在正常运行的 EA 中使用 EMD,则您可在必要时调用相关函数,从而扩展该测试 EA,或者以类似方式在现有 EA 里插入操控 EMD 指标的部分。
用于优化的示例性设置,附于文末的 TestEMD.set 文件中。 在加速模式下针对 2018 年 EURUSD D1 的优化得到了以下最佳“设置”:
- Length=110
- Forecast=4
- Reconstruction=2
相应地,SignalBar 必须等于负的 Forecast 值,即 -4。
采用这些设置,在 2018 年初至 2020 年 2 月期间执行复盘优化,而在 2019 年和 2020 年初执行验证测试,结果如下图所示:
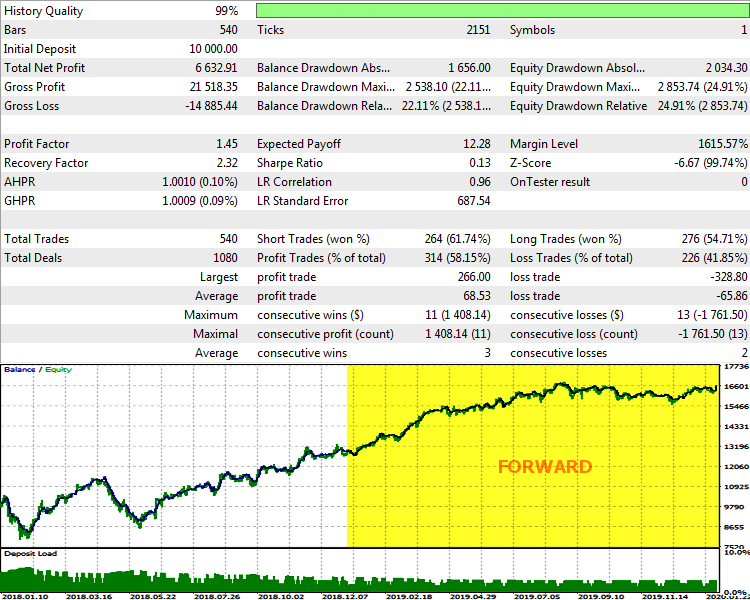
TestEMD 报告,于 EURUSD D1, 2018-2020
正如我们所见,尽管该指标表明存在改进的空间,但该系统已有收益。 特别是,逻辑上推断,以步进模式进行更频繁的重新优化,并探索步幅长度,可以提高机器人的性能。
基本上可以说,EMD 算法能够在较大时间帧基础上进行识别,从某种意义上说,报价的动量波动,并以此为基础创建可盈利的交易系统。
EMD 不是我们这里要考虑的唯一技术。 然而,在进入第二部分之前,我们为了研究时间序列,必须“更新”一些数学知识。
MQL 中时间序列的主要特征分析 — 指标 TSA
在 mql5.com 网站上已发表了一篇标题类似的文章:时间序列主要特征分析。 它为计算值(例如平均值、中位数、离散度、偏离度和峰度因子、分布直方图、自相关函数、部分自相关、等)提供了详尽研讨。 所有这些,都已收集到 TSAnalysis.mqh 文件中的 TSAnalysis 类里,然后在 TSAexample.mq5 脚本中用于演示目的。 不幸地是,出于类的性能可视化,该方法用于生成外部 HTML 文件,而该文件必须在浏览器中进行分析。 与此同时,MetaTrader 5 提供了各种图形工具来显示数据数组,最主要的是指标缓冲区。 我们将略微修改该类,并令其与指标更加“友好”,此后,我们将实现一个指标,该指标能够直接在终端中分析报价。
我们将以 TSAnalysisMod.mqh 来命名新文件。 其主要操作原理保持不变:使用 Calc 方法,将时间序列传递到对象中,在处理过程中计算整个索引集合。 它们全都划分为两种:标量类型和数组类型。 然后,调用代码可以读取任何特征。
我们将标量特征整合到一个 TSStatMeasures 结构中:
struct TSStatMeasures { double MinTS; // Minimum time series value double MaxTS; // Maximum time series value double Median; // Median double Mean; // Mean (average) double Var; // Variance double uVar; // Unbiased variance double StDev; // Standard deviation double uStDev; // Unbiaced standard deviation double Skew; // Skewness double Kurt; // Kurtosis double ExKurt; // Excess Kurtosis double JBTest; // Jarque-Bera test double JBpVal; // JB test p-value double AJBTest; // Adjusted Jarque-Bera test double AJBpVal; // AJB test p-values double maxOut; // Sequence Plot. Border of outliers double minOut; // Sequence Plot. Border of outliers double UPLim; // ACF. Upper limit (5% significance level) double LOLim; // ACF. Lower limit (5% significance level) int NLags; // Number of lags for ACF and PACF Plot int IP; // Autoregressive model order };
我们将以 TSA_TYPE 枚举来表示数组:
enum TSA_TYPE { tsa_TimeSeries, tsa_TimeSeriesSorted, tsa_TimeSeriesCentered, tsa_HistogramX, tsa_HistogramY, tsa_NormalProbabilityX, tsa_ACF, tsa_ACFConfidenceBandUpper, tsa_ACFConfidenceBandLower, tsa_ACFSpectrumY, tsa_PACF, tsa_ARSpectrumY, tsa_Size // }; // ^ non-breaking space (to hide aux element tsa_Size name)
为了得到含有操作结果的完整 TSStatMeasures 结构,提供了 getStatMeasures 方法。 若要采用宏来获取任何数组,将生成相同类型的方法,其为 getARRAYNAME,其中 ARRAYNAME 对应于多个 TSA_TYPE 枚举之一的后缀。 例如,要读取已排序时间序列,应调用 getTimeSeriesSorted 方法。 所有这些方法都具有签名:
int getARRAYNAME(double &result[]) const;
填充所传递的数组,并返回元素数字。
甚或,有一种通用方法可以读取任何数组:
int getResult(const TSA_TYPE type, double &result[]) const
虚拟方法 show 被完全从原始类中移除,因为没有用。 所有界面完整控制的相关任务交给了调用代码。
利用来自特殊指标 TSA.mq5 的 TSAnalysis 类来处理代码很方便。 其主要目标是数组的可视化特征表现。 若您希望,可以在需要时添加显示标量值的选项(目前只是将它们打印到日志)。
鉴于某些数组在逻辑上以三重互连(例如,自动相关函数的上限和下限为 95% 置信区间),因此指标中保留了 3 个缓冲区。 缓冲区的显示样式将根据请求数据的含义动态调整。
指标输入参数:
- Type — 请求的数组类型,枚举 TSA_TYPE;
- Length — 所分析时间序列的柱线长度;
- Offset — 时间序列的初始偏移量,0 - 起点;
- Differencing — 差值模式,定义是应按原样读取报价,还是采用一阶差值;
- Smoothing — 均化周期;
- Method — 均化方法;
- Price — 价格类型 (默认开盘价);
指标按柱线计算。
在 EURUSD D1,500 根柱线上自动相关函数如何查找的示例,但存在以下差异:
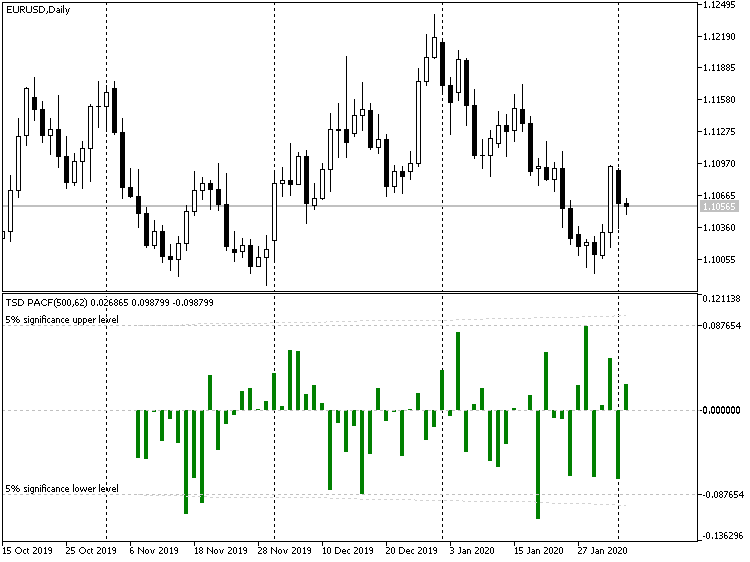
指标 TSD, EURUSD D1
采取一阶差值可以增加序列的平稳性(和可预测性)。 基本上,二阶差值将更加平稳,三阶差值 — 甚至更大,等等。 不过,这有其不利一面,这将在后面讨论(在第 2 部分中)。
这里选择部分自相关函数也非偶然。 在下一阶段,当我们转到其它预测方法时,会用到它。 但是,由于我们将要研究大量的资料,因此我们在撰写本文时用到了预备章节。 甚或,时间序列的统计分析表现出普遍的价值,可用在 MQL 的其他自定义开发当中。
结束语
在本文中,我们研究了经验模态分解算法的特殊方面,这令我们可将其扩展到时间序列的短线预测领域。 以 MQL 实现的类、指标和 EA 能够将 EMD 预测用作制定交易决策的附加因素,并可作为自动交易系统的一部分。 此外,我们已更新了工具包,以便执行时间序列的统计分析,在我们的下一篇文章中,我们将研究采用 LS-SVM 方法进行预测。
本文由MetaQuotes Ltd译自俄文
原文地址: https://www.mql5.com/ru/articles/7601
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。
 监视多币种的交易信号 (第二部分) : 应用程序可视部分的实现
监视多币种的交易信号 (第二部分) : 应用程序可视部分的实现
非常感谢你提供这篇有趣的文章,但文件无法运行,它们存在语法错误和未声明变量。
致敬
请提供您的错误日志并说明您的具体操作。
感谢 Stanislav 的精彩文章。我下载了代码,但在编译时遇到了一个错误。
错误信息如下:'Offset' -some operator expected in the line
buffers[0].set(Offset,sum);
请告诉我如何解决这个问题。
谢谢
感谢 Stanislav 的精彩文章。我下载了代码,但在编译时遇到了错误。
错误信息如下:"Offset" -some operator expected in the line
buffers[0].set(Offset,sum);
请说明如何解决这个问题。
谢谢
我刚刚重新下载了源代码,并编译了所有指标和专家,没有问题。
你做错了。请确保您在解压缩存档内容时保留了文件夹结构。
这是我将日期从 1-1-2020 更改为现在的结果